Physical Experiment and Numerical Simulation of the Artificial Recharge Effect on Groundwater Reservoir
Abstract
:1. Introduction
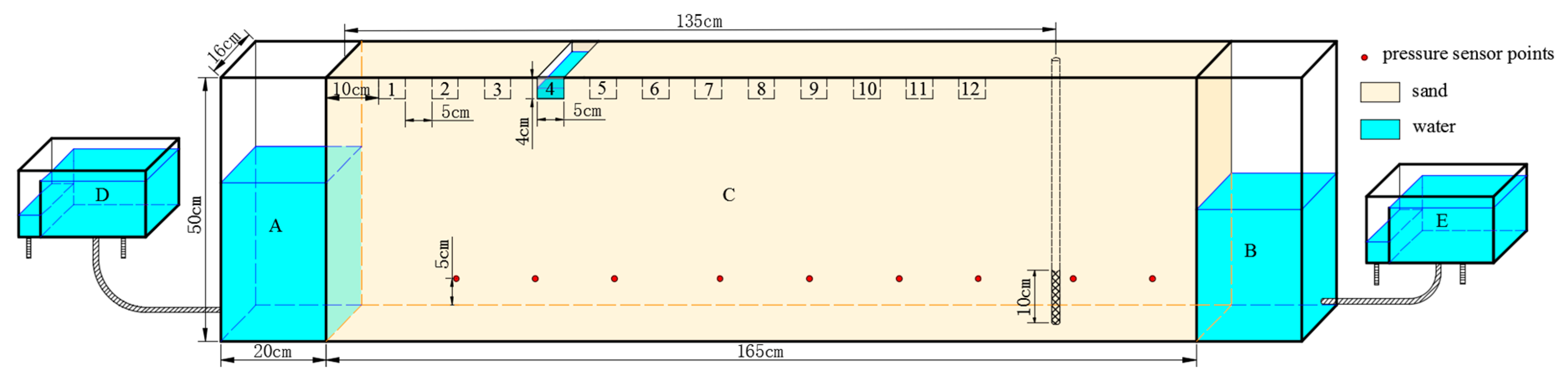
2. Physical Model
2.1. Experiment Setup
2.2. Experimental Method
2.3. Experimental Results
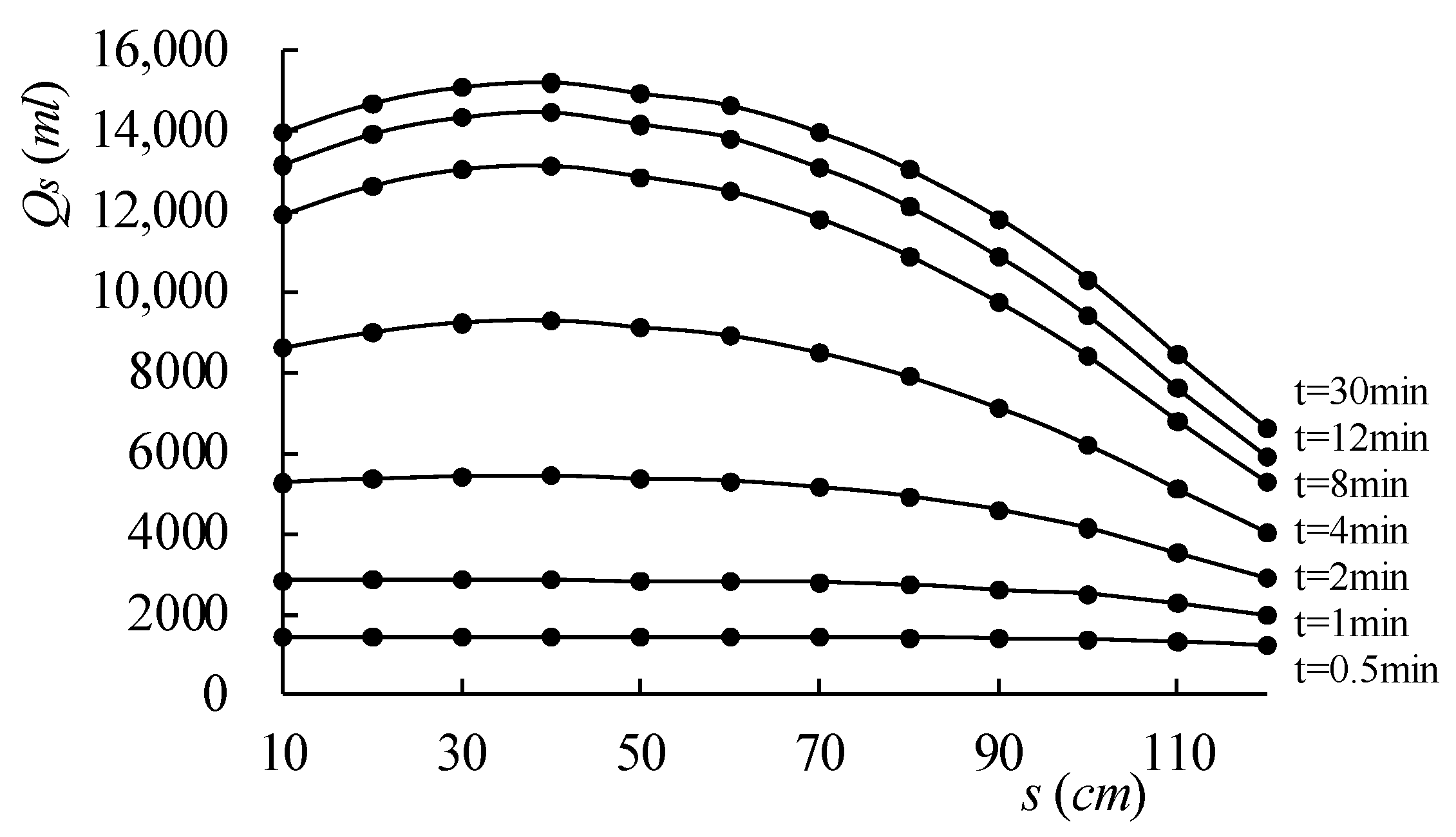
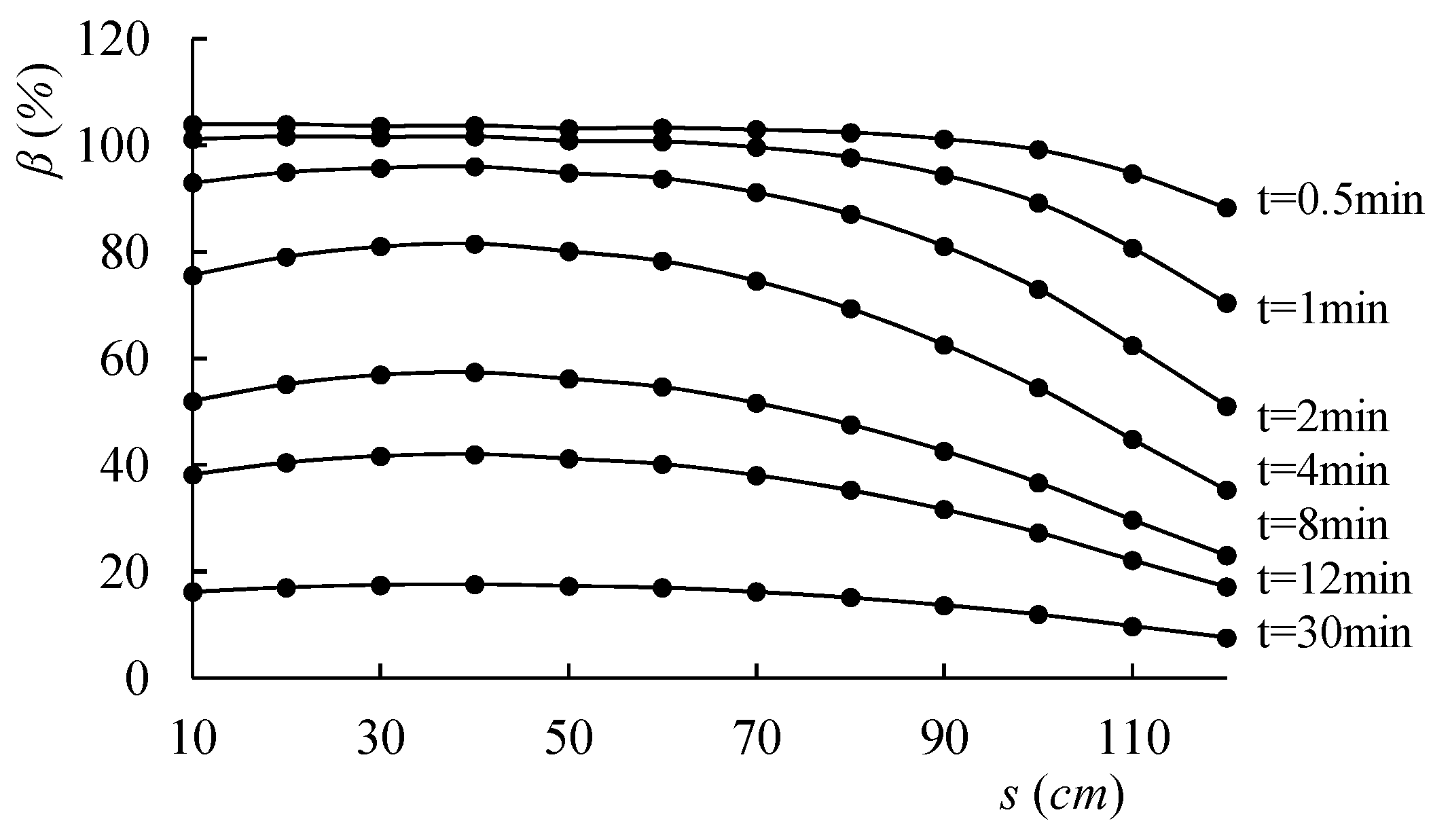
2.3.1. Effect of Relative Distance between Infiltration Basin and Pumping Well
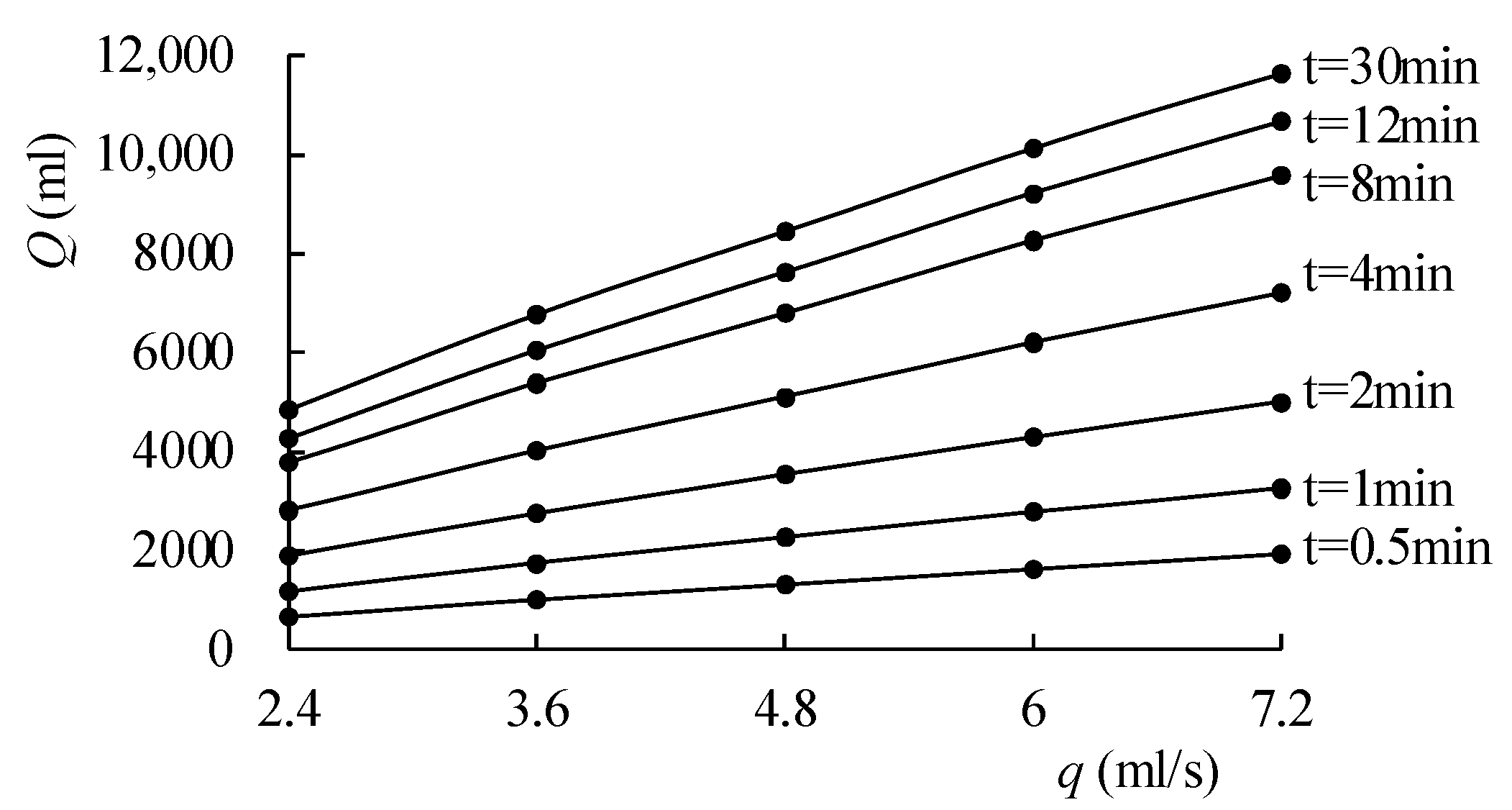
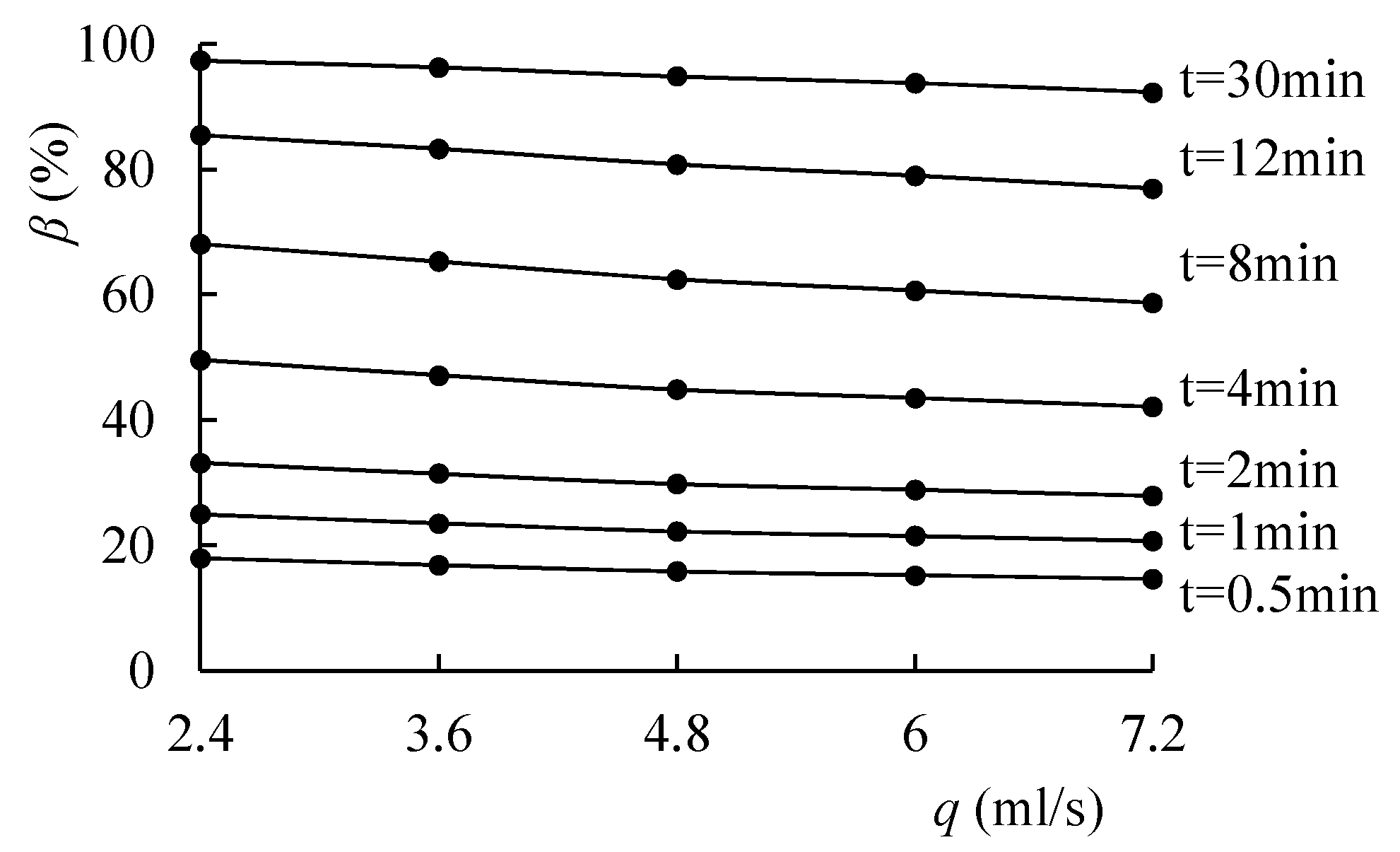
2.3.2. Effect of Recharge Intensity
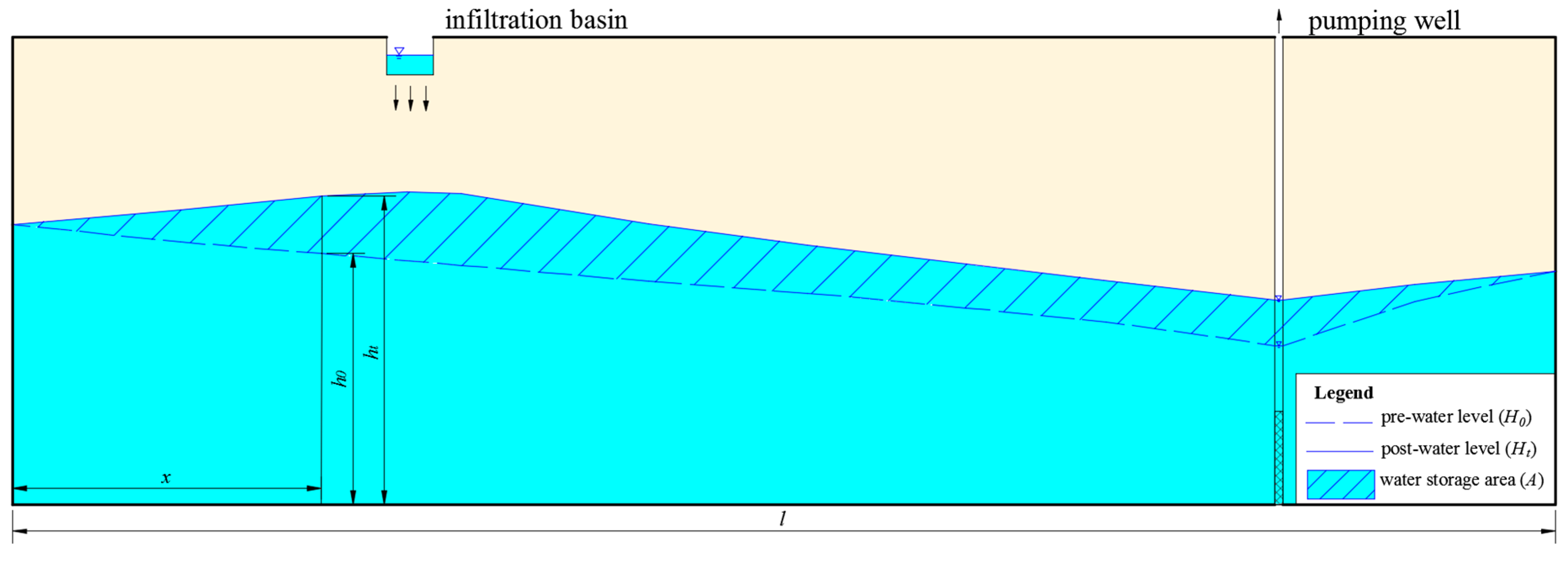
3. Numerical Simulations
3.1. Model Setup
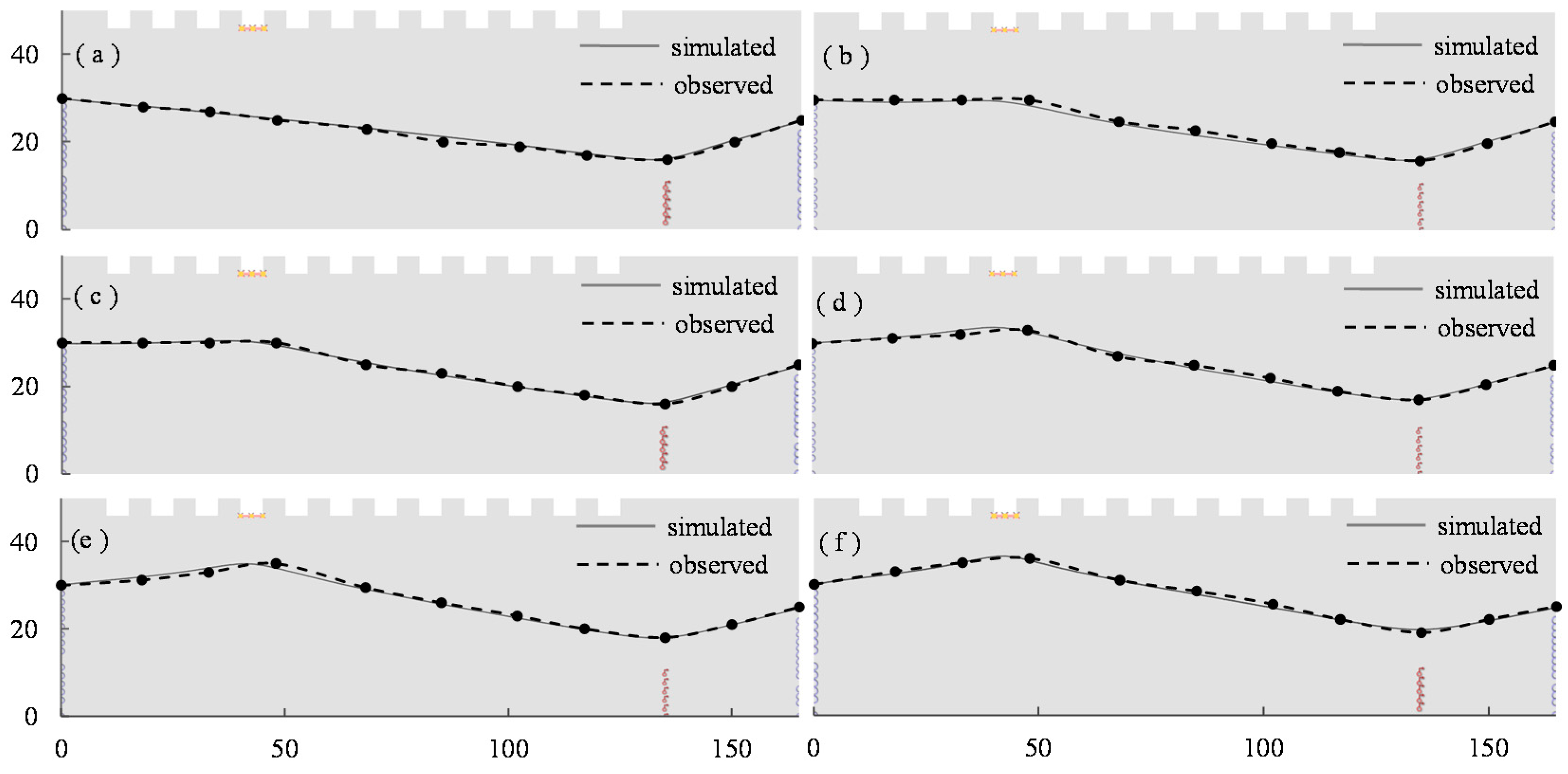
3.2. Simulation Results
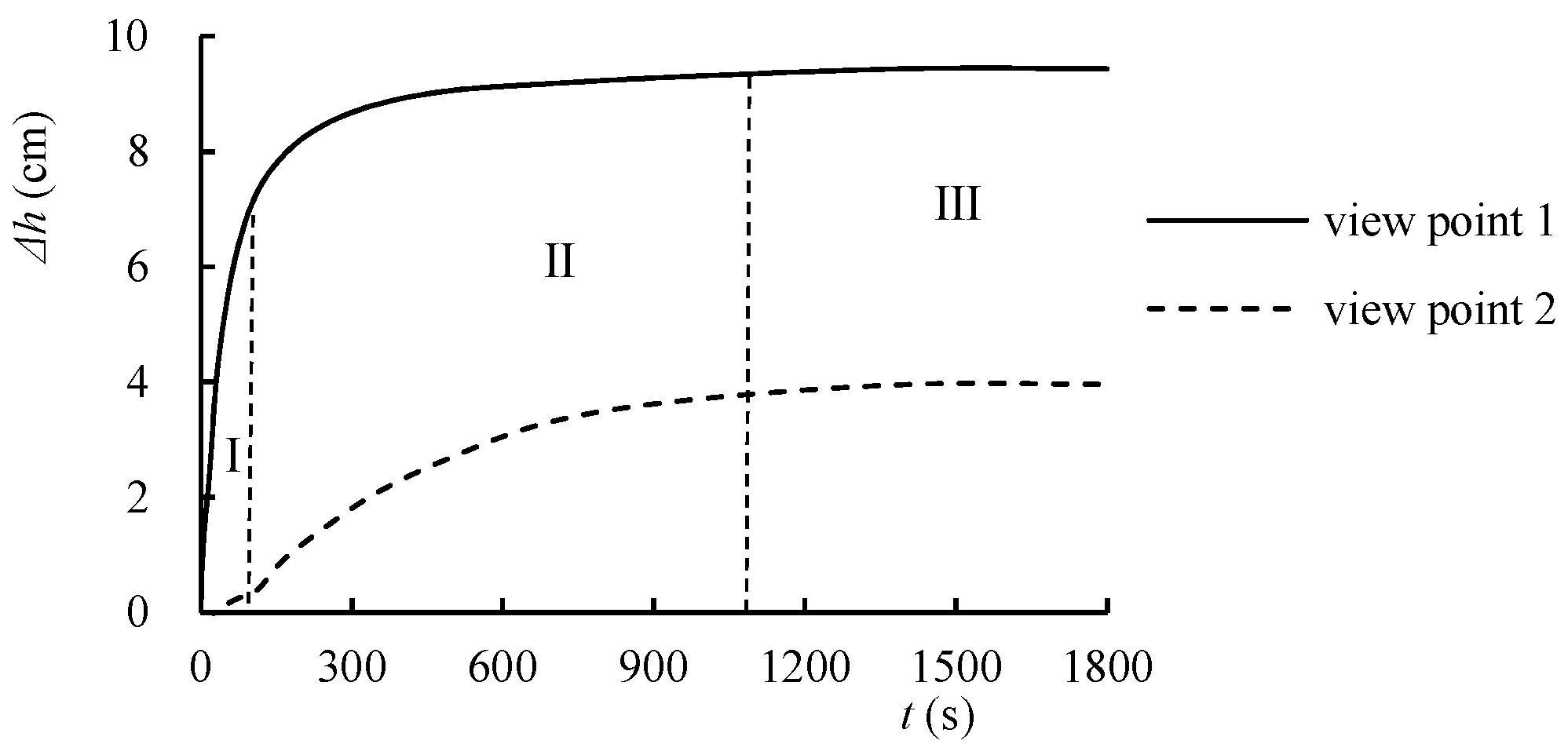
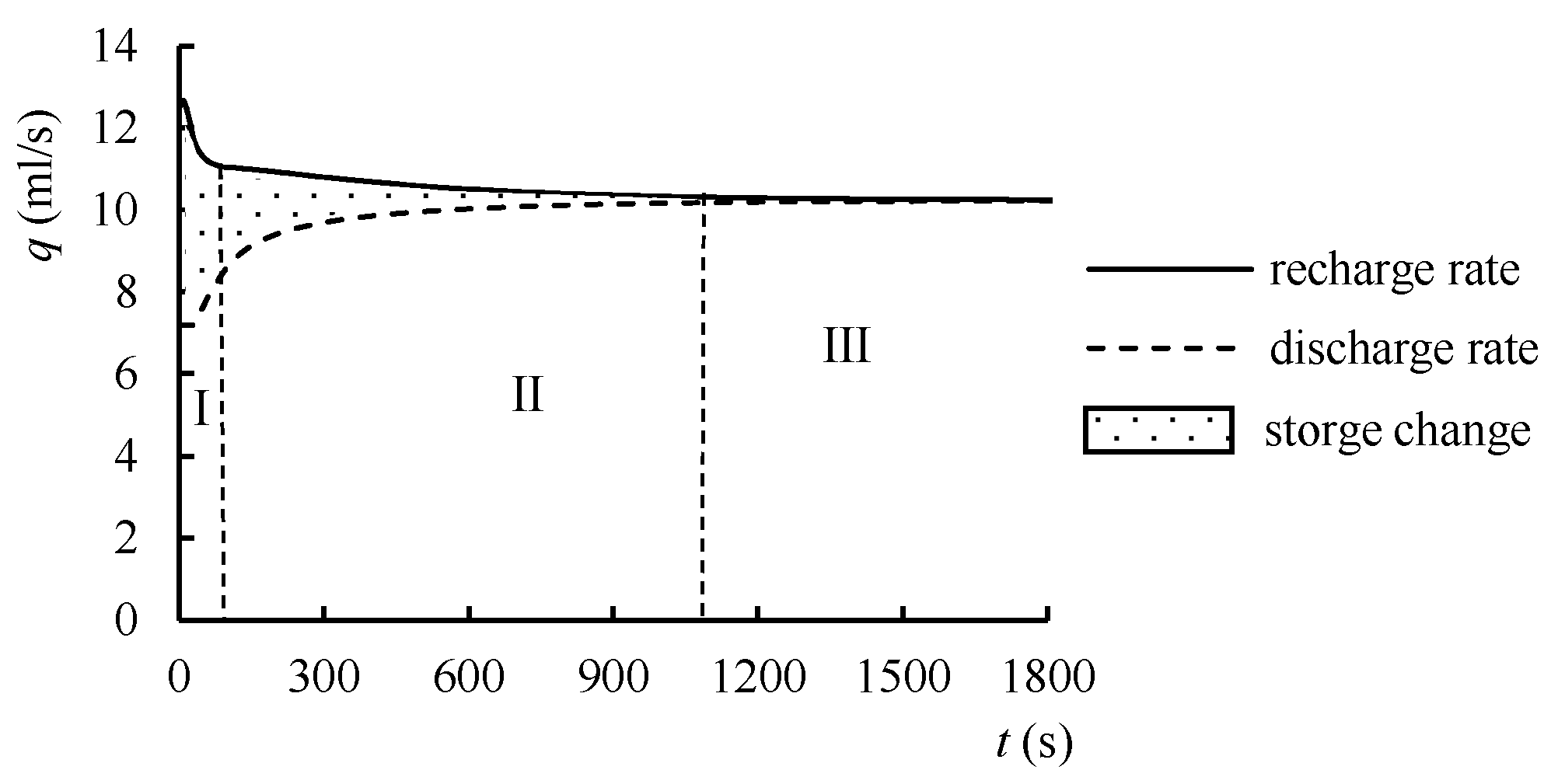
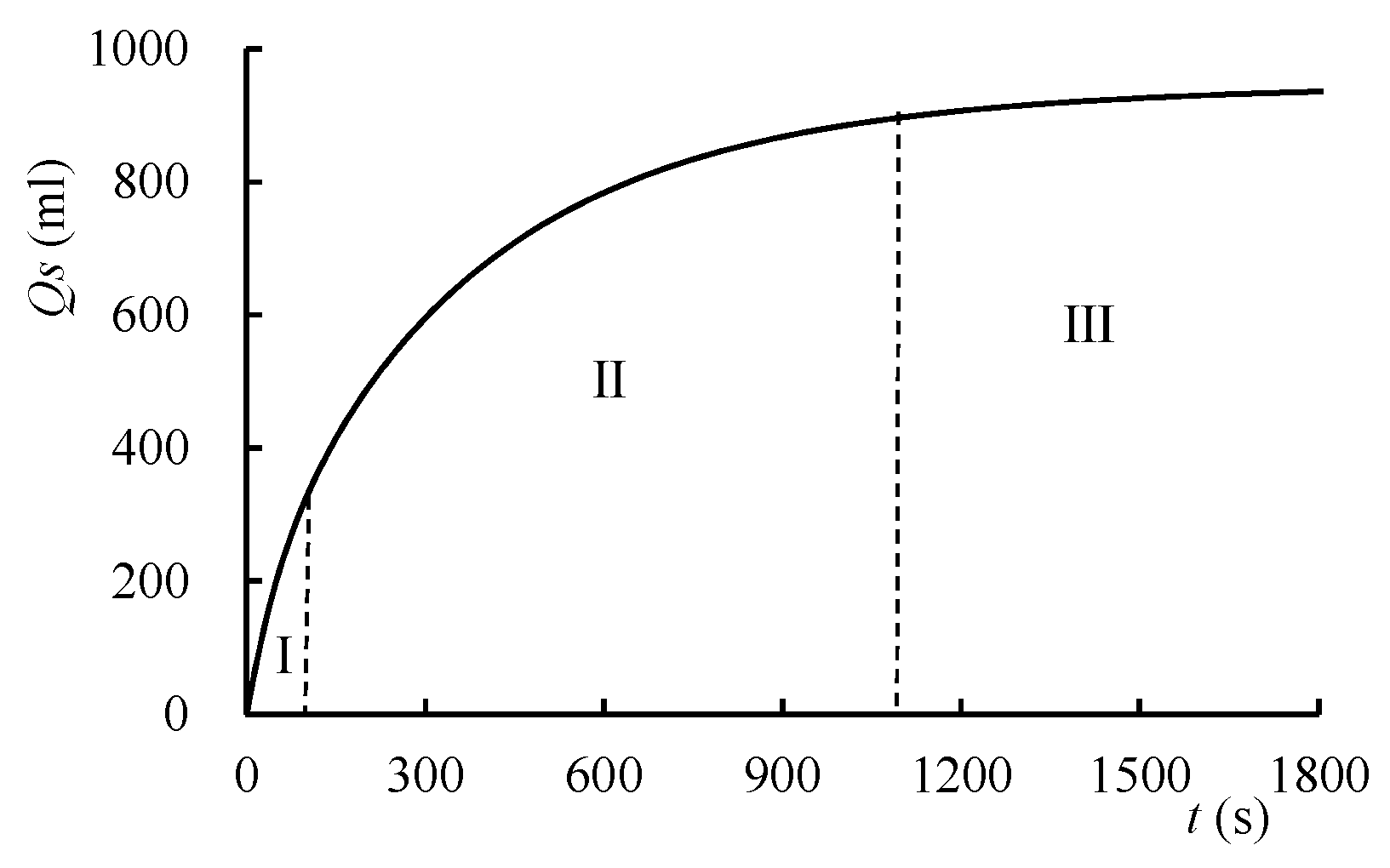
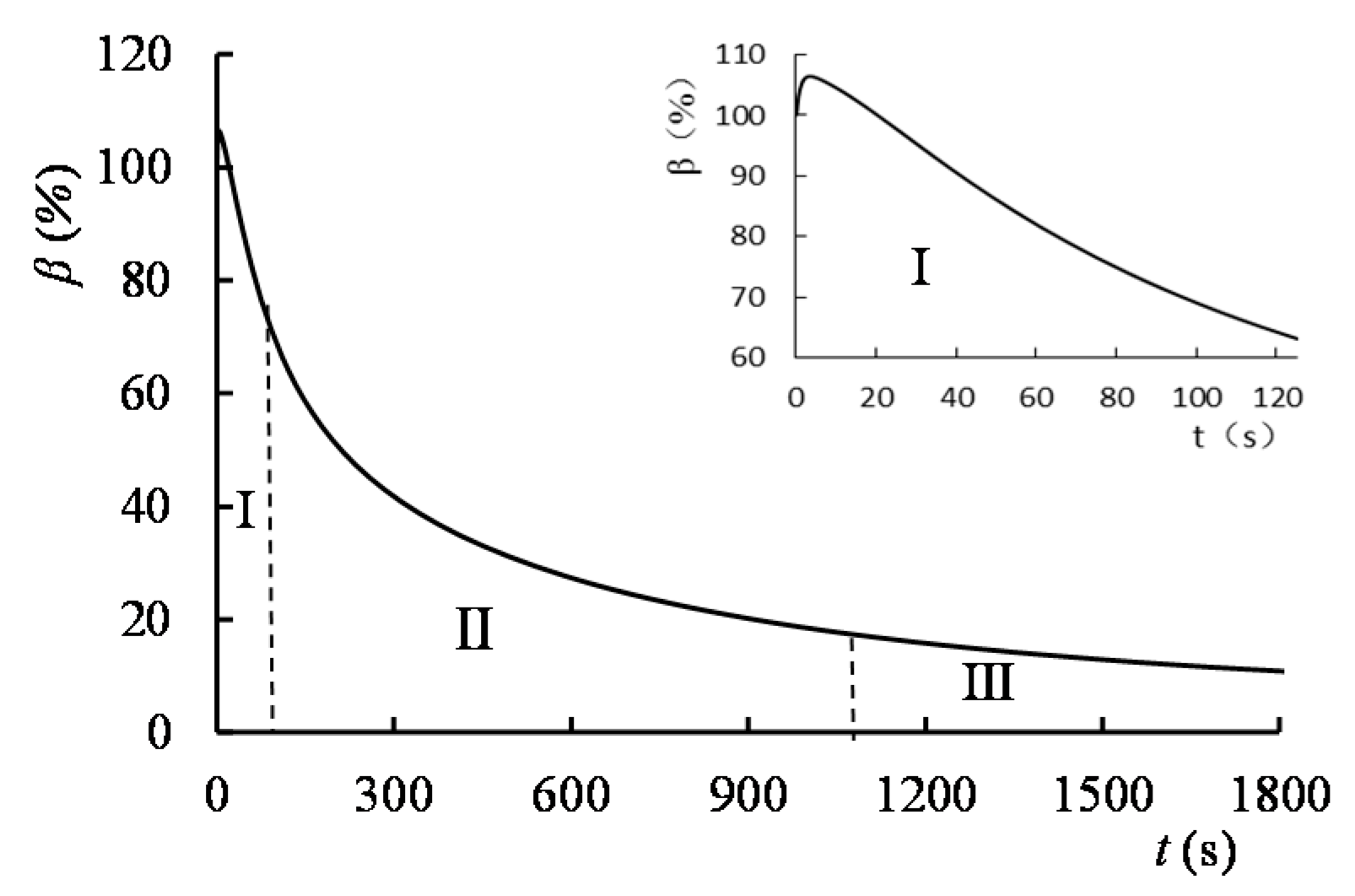
3.2.1. Analysis of Water Balance
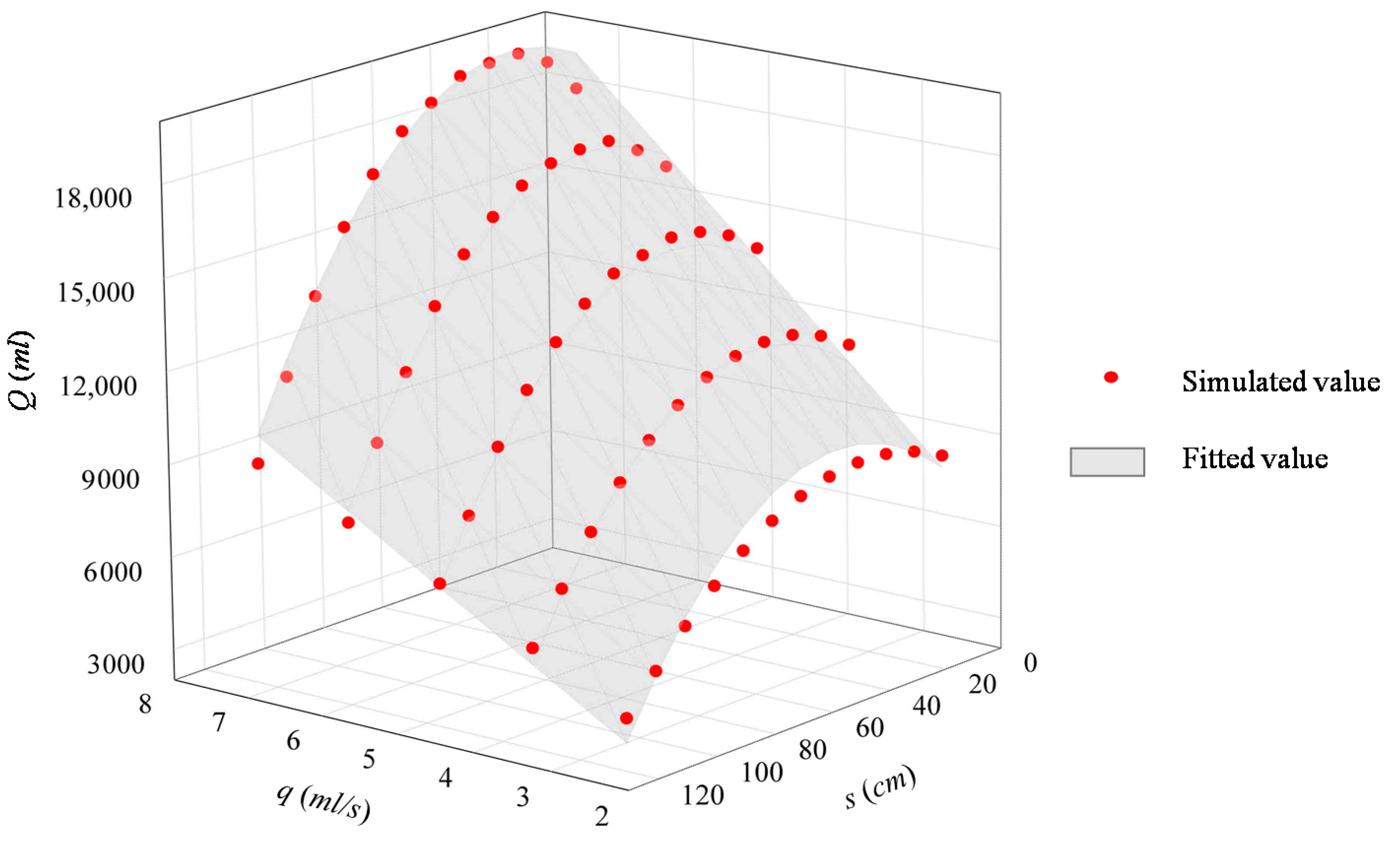
3.2.2. Analysis of Influencing Factors
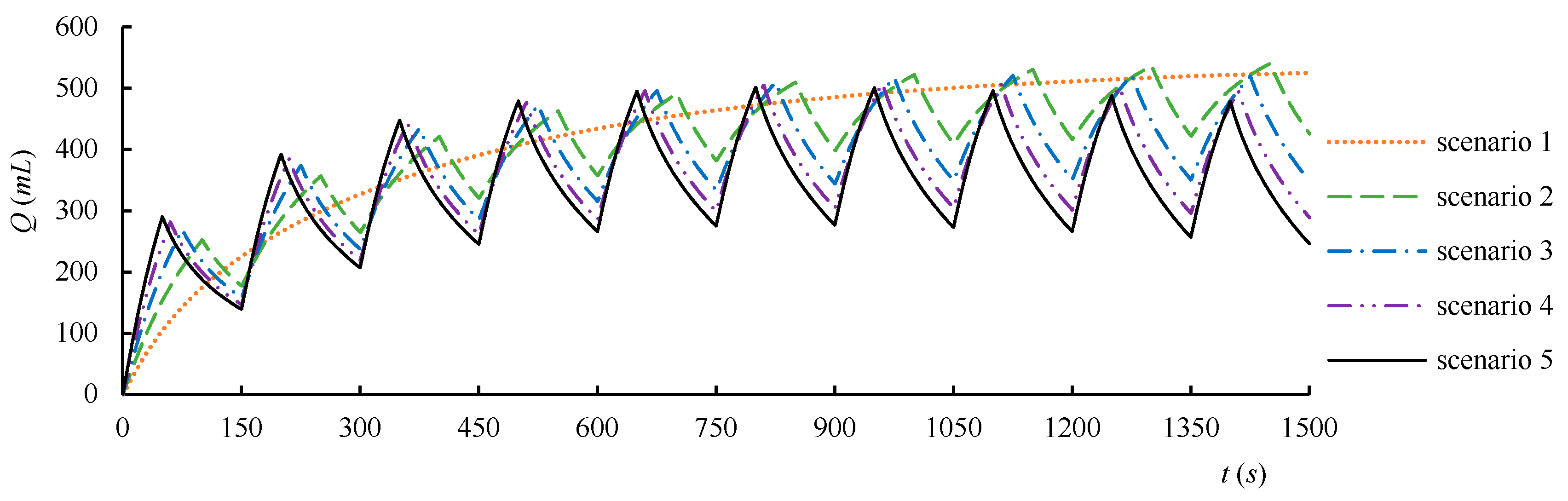
3.2.3. Analysis of the Effect of intermittent Recharge
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Scanlon, B.R.; Keese, K.E.; Flint, A.L.; Flint, L.E.; Gaye, C.B.; Edmunds, W.M.; Simmers, I. Global synthesis of groundwater recharge in semiarid and arid regions. Hydrol. Process. 2006, 20, 3335–3370. [Google Scholar] [CrossRef]
- Orellana, F.; Verma, P.; Ii, S.P.L.; Daly, E. Monitoring and modeling water-vegetation interactions in groundwater-dependent ecosystems. Rev Geophys. 2012, 50, RG3003. [Google Scholar] [CrossRef]
- Zhao, T.S. Discussion of problems for groundwater reservoir. Hydrogeol. Eng. Geol. 2002, 29, 65–67. (In Chinese) [Google Scholar]
- Li, L.W.; Shu, L.C.; Yin, Z.Z. Concept and design theory of groundwater reservoir. J. Hydraul. Eng. 2006, 13, 123–132. [Google Scholar]
- Pyne, R.D.G. Groundwater Recharge and Wells: A Guide to Aquifer Storage and Recovery; CRC Press: Boca Raton, FL, USA, 1995; p. 401. [Google Scholar]
- Ward, J.D.; Simmons, C.T.; Dillon, P.J. A theoretical analysis of mixed convection in aquifer storage and recovery: How important are density effects? J. Hydrol. 2007, 343, 169–186. [Google Scholar] [CrossRef]
- Page, D.W.; Peeters, L.; Vanderzalm, J.; Barry, K.; Gonzalez, D. Effect of aquifer storage and recovery (ASR) on recovered stormwater quality variability. Water Res. 2017, 117, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Zhang, G.; Feng, G.; Li, X.; Xie, C.; Pi, X. Flood effect on groundwater recharge on a typical silt loam soil. Water 2017, 9, 523. [Google Scholar] [CrossRef]
- Ong’Or, B.T.I.; Shu, L.C. Groundwater overdraft and the impact of artificial recharge on groundwater quality in a cone of depression, Jining, China. Water Int. 2009, 34, 468–483. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, J.C.; Xue, Y.Q.; Wang, Z.C.; Yao, Y.G.; Yan, X.X.; Wang, H.M. Land subsidence and uplift due to long-term groundwater extraction and artificial recharge in Shanghai, China. Hydrogeol. J. 2015, 23, 1851–1866. [Google Scholar] [CrossRef]
- Shi, X.Q.; Jiang, S.M.; Xu, H.X.; Jiang, F.; He, Z.F.; Wu, J.C. The effects of artificial recharge of groundwater on controlling land subsidence and its influence on groundwater quality and aquifer energy storage in Shanghai, China. Environ. Earth 2016, 75, 1–18. [Google Scholar] [CrossRef]
- Sophiya, M.S.; Syed, T.H. Assessment of vulnerability to seawater intrusion and potential remediation measures for coastal aquifers: A case study from eastern India. Environ. Earth. 2013, 70, 1197–1209. [Google Scholar] [CrossRef]
- Thompson, A.; Nimmer, M.; Misra, D. Effects of variations in hydrogeological parameters on water-table mounding in sandy loam and loamy sand soils beneath stormwater infiltration basins. Hydrogeol. J. 2010, 18, 501–508. [Google Scholar] [CrossRef]
- Nimmer, M.; Thompson, A.; Misra, D. Modeling water table mounding and contaminant transport beneath stormwater infiltration basins. J. Hydrol. Eng. 2010, 15, 963–973. [Google Scholar] [CrossRef]
- Du, S.H.; Su, X.X.; Zhang, W.J. Effective storage rates analysis of groundwater reservoir with surplus local and transferred water used in Shijiazhuang City, China. Water Resour. Manag. 2013, 27, 157–169. [Google Scholar] [CrossRef]
- Dillon, P. Future management of aquifer recharge. Hydrogeol. J. 2005, 13, 313–316. [Google Scholar] [CrossRef]
- Maréchal, J.C.; Dewandel, B.; Ahmed, S.; Galeazzi, L.; Zaidi, F.K. Combined estimation of specific yield and natural recharge in a semi-arid groundwater basin with irrigated agriculture. J. Hydrol. 2006, 329, 281–293. [Google Scholar] [CrossRef]
- Stauffer, F.; Attinger, S.; Zimmermann, S.; Kinzelbach, W. Uncertainty estimation of well catchments in heterogeneous aquifers. Water Res. 2002, 38, 20–21. [Google Scholar] [CrossRef]
- Manghi, F.; Mortazavi, B.; Crother, C.; Hamdi, M.R. Estimating regional groundwater recharge using a hydrological budget method. Water Resour. Manag. 2009, 23, 2475–2489. [Google Scholar] [CrossRef]
- Hernández-Espriú, A.; Arango-Galván, C.; Reyes-Pimentel, A.; Martínez-Santos, P.; Paz, C.P.D.L.; Macías-Medrano, S. Water supply source evaluation in unmanaged aquifer recharge zones: The mezquital valley (Mexico) case study. Water 2016, 9, 4. [Google Scholar] [CrossRef]
- Sharda, V.N.; Kurothe, R.S.; Sena, D.R.; Pande, V.C.; Tiwari, S.P. Estimation of groundwater recharge from water storage structures in a semi-arid climate of India. J. Hydrol. 2006, 329, 224–243. [Google Scholar] [CrossRef]
- Crosbie, R.S.; Binning, P.; Kalma, J.D. A time series approach to inferring groundwater recharge using the water table fluctuation method. Water Resour. Res. 2005, 41, 287–295. [Google Scholar] [CrossRef]
- Niazi, A.; Prasher, S.O.; Adamowski, J.; Gleeson, T. A system dynamics model to conserve arid region water resources through aquifer storage and recovery in conjunction with a dam. Water 2014, 6, 2300–2321. [Google Scholar] [CrossRef]
- Kasper, J.W.; Denver, J.M.; McKenna, T.E.; Ullman, W.J. Simulated impacts of artificial groundwater recharge and discharge on the source area and source volume of an Atlantic coastal plain stream, Delaware, USA. Hydrogeol. J. 2010, 18, 1855–1866. [Google Scholar] [CrossRef]
- Edwards, E.C.; Harter, T.; Fogg, G.E.; Washburn, B.; Hamad, H. Assessing the effectiveness of drywells as tools for stormwater management and aquifer recharge and their groundwater contamination potential. J. Hydrol. 2016, 539, 539–553. [Google Scholar] [CrossRef]
- Clement, T.P.; Kim, Y.C.; Gautam, T.R.; Lee, K.K. Experimental and numerical investigation of DNAPLdissolution processes in a laboratory aquifer model. Groundwater Monit. Remediat. 2004, 24, 88–96. [Google Scholar] [CrossRef]
- Hans, J.G. DHI-WASY Software FEFLOW Reference Manual; DHI WASY GmbH: Berlin, Germany, 2005. [Google Scholar]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
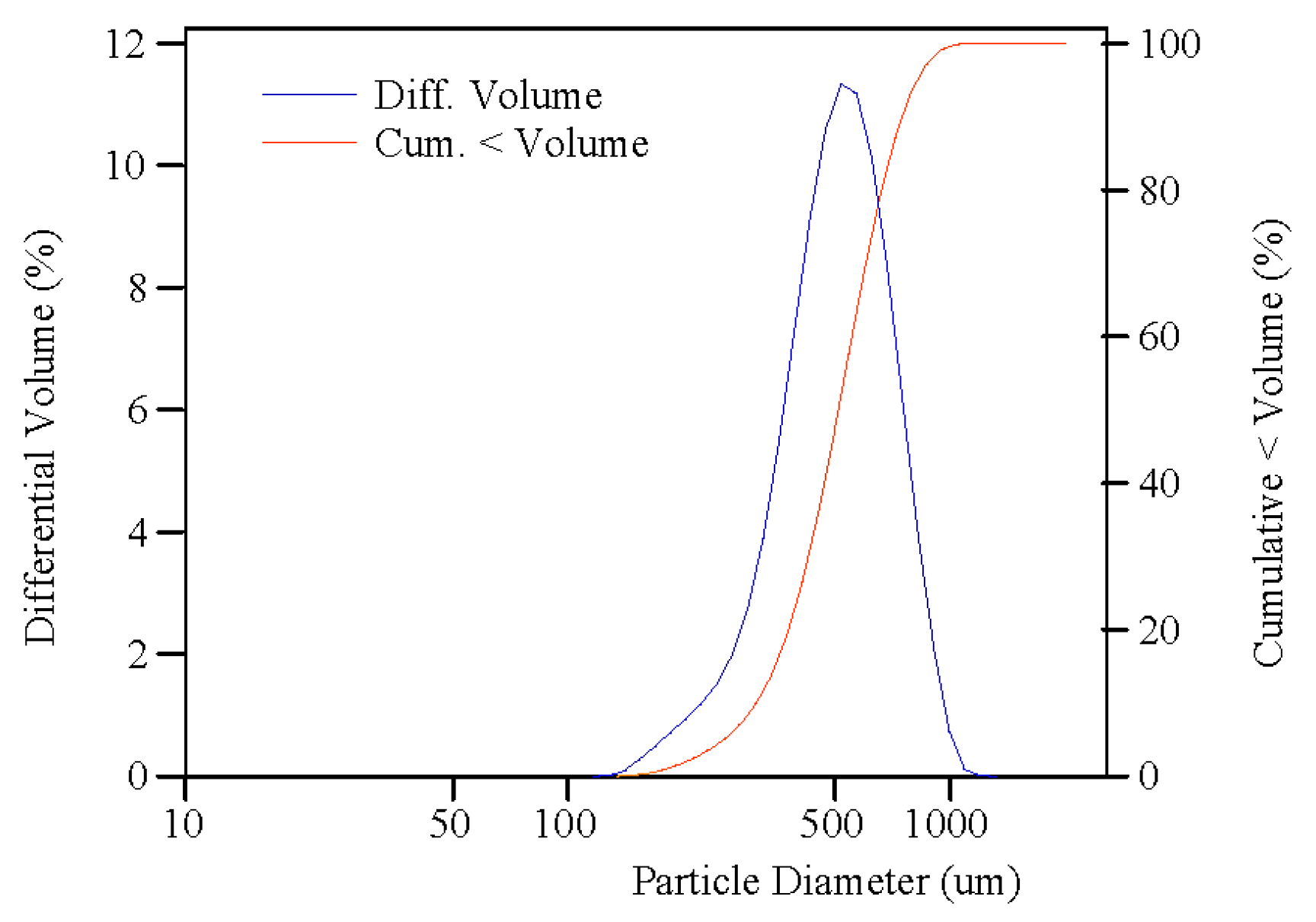



| Content (%) | <10 | <25 | <50 | <75 | <90 | Average | Mid-Value |
|---|---|---|---|---|---|---|---|
| Diameter(um) | 310.5 | 401.8 | 509.6 | 630.8 | 749.8 | 520.4 | 509.6 |
| Pressure Sensor Point | 2 | 5 | 8 |
|---|---|---|---|
| NSE | 0.973 | 0.936 | 0.797 |
| Time Period (s) | Inflow | Outflow | Storage Variation (mL) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Lateral Inflow | Artificial Recharge | Total (mL) | Lateral Outflow | Artificial Exploitation | Total (mL) | ||||||
| Quantity (mL) | Percentage (%) | Quantity (mL) | Percentage (%) | Quantity (mL) | Percentage (%) | Quantity (mL) | Percentage (%) | ||||
| 0.0 | 0.0 | - | 0.0 | - | 0.0 | 0.0 | - | 0.0 | - | 0.0 | 0.0 |
| 1.3 | 80.7 | 57.0 | 60.8 | 43.0 | 141.5 | 0.0 | 0.0 | 81.0 | 100.0 | 81.0 | 60.5 |
| 14.0 | 825.1 | 56.4 | 638.7 | 43.6 | 1463.8 | 0.0 | 0.0 | 837.5 | 100.0 | 837.5 | 626.3 |
| 32.3 | 1800.3 | 54.6 | 1495.4 | 45.4 | 3295.8 | 1.1 | 0.1 | 1936.4 | 99.9 | 1937.6 | 1358.2 |
| 79.3 | 3944.7 | 51.5 | 3717.6 | 48.5 | 7662.3 | 234.7 | 4.7 | 4758.5 | 95.3 | 4993.2 | 2669.1 |
| 145.6 | 6810.0 | 49.8 | 6874.0 | 50.2 | 13,684.0 | 1094.1 | 11.1 | 8735.2 | 88.9 | 9829.3 | 3854.7 |
| 325.5 | 14,323.1 | 48.1 | 15,475.6 | 51.9 | 29,798.7 | 4519.6 | 18.8 | 19,529.9 | 81.2 | 24,049.5 | 5749.2 |
| 581.7 | 24,470.1 | 46.9 | 27,748.2 | 53.1 | 52,218.3 | 10,231.7 | 22.7 | 34,902.2 | 77.3 | 45,133.8 | 7084.4 |
| 1244.3 | 49,380.7 | 45.3 | 59,517.9 | 54.7 | 108,898.6 | 26,141.8 | 25.9 | 74,659.8 | 74.1 | 100,801.7 | 8096.9 |
| 1800.0 | 69,855.7 | 44.8 | 86,175.5 | 55.2 | 156,031.2 | 39,776.7 | 26.9 | 108,000.0 | 73.1 | 147,776.7 | 8254.5 |
| Scenario | Scenario 1 | Scenario 2 | Scenario 3 | Scenario 4 | Scenario 5 |
|---|---|---|---|---|---|
| recharge intensity (mL/s) | 2.4 | 3.6 | 4.8 | 6 | 7.2 |
| recharge time(s) | 150 | 100 | 75 | 60 | 50 |
| interval time(s) | 0 | 50 | 75 | 90 | 100 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Y.; Shu, L.; Zhang, Y.; Wu, P.; Atlabachew Eshete, A.; Mabedi, E.C. Physical Experiment and Numerical Simulation of the Artificial Recharge Effect on Groundwater Reservoir. Water 2017, 9, 908. https://doi.org/10.3390/w9120908
Xu Y, Shu L, Zhang Y, Wu P, Atlabachew Eshete A, Mabedi EC. Physical Experiment and Numerical Simulation of the Artificial Recharge Effect on Groundwater Reservoir. Water. 2017; 9(12):908. https://doi.org/10.3390/w9120908
Chicago/Turabian StyleXu, Yang, Longcang Shu, Yongjie Zhang, Peipeng Wu, Abunu Atlabachew Eshete, and Esther Chifuniro Mabedi. 2017. "Physical Experiment and Numerical Simulation of the Artificial Recharge Effect on Groundwater Reservoir" Water 9, no. 12: 908. https://doi.org/10.3390/w9120908
APA StyleXu, Y., Shu, L., Zhang, Y., Wu, P., Atlabachew Eshete, A., & Mabedi, E. C. (2017). Physical Experiment and Numerical Simulation of the Artificial Recharge Effect on Groundwater Reservoir. Water, 9(12), 908. https://doi.org/10.3390/w9120908





