Contamination Event Detection Method Using Multi-Stations Temporal-Spatial Information Based on Bayesian Network in Water Distribution Systems
Abstract
:1. Introduction
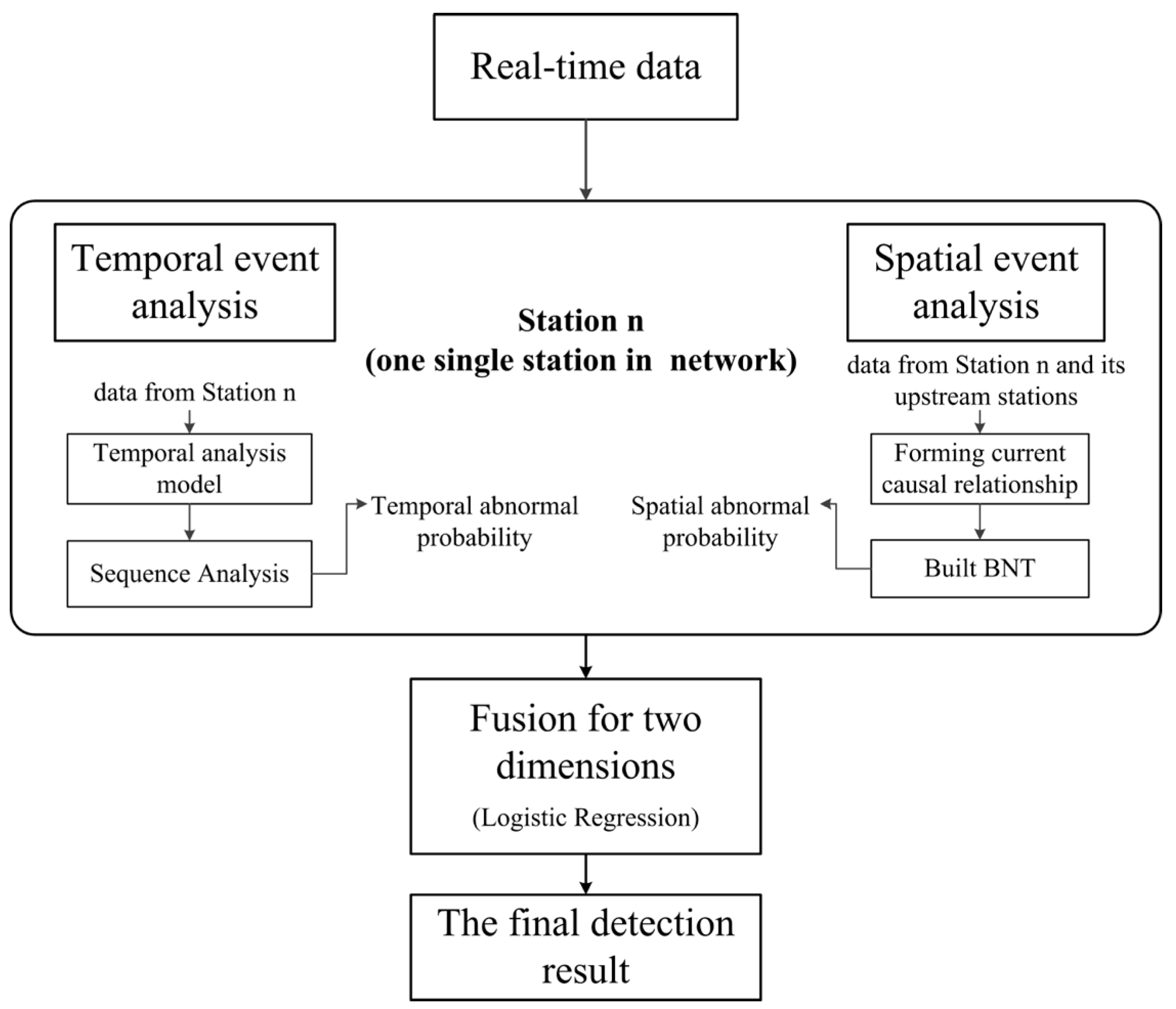
2. Methodology
2.1. Temporal Event Analysis Based on Local Information
The Threshold Model and AR Model
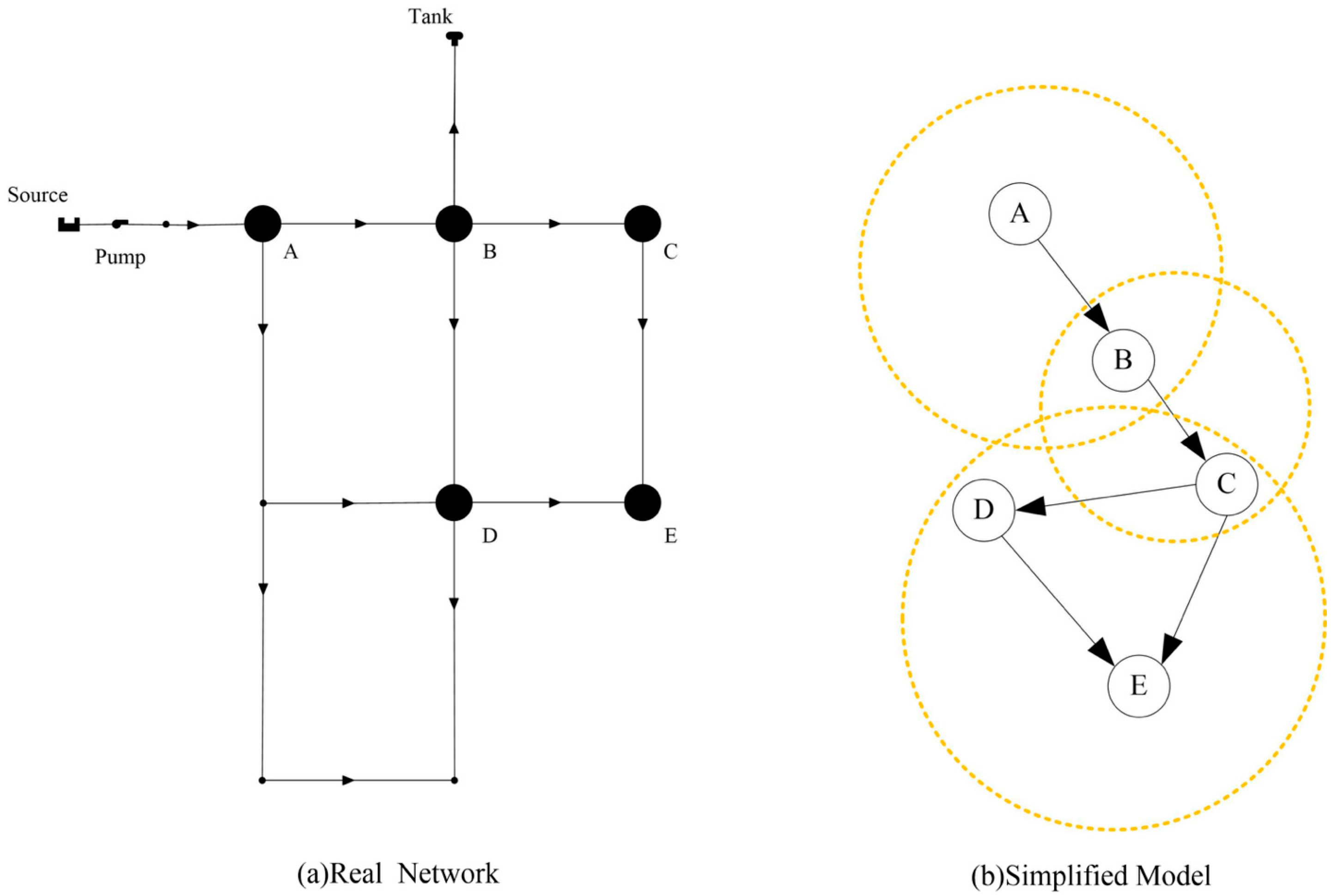
2.2. Spatial Event Analysis Using Causal Relationship Based on Multi-Stations’ Information
2.3. Fusion of Abnormal Probabilities from Temporal Dimension and Spatial Dimension
- Find a hypothesis function which is usually simplified as h function;in which
- Construct a Cost Function and it represents the deviation of the hypothesis output from the label y in training sets;where is the number of training samples.
- Use Gradient Descent to minimise the cost function .
3. Application and Experiments
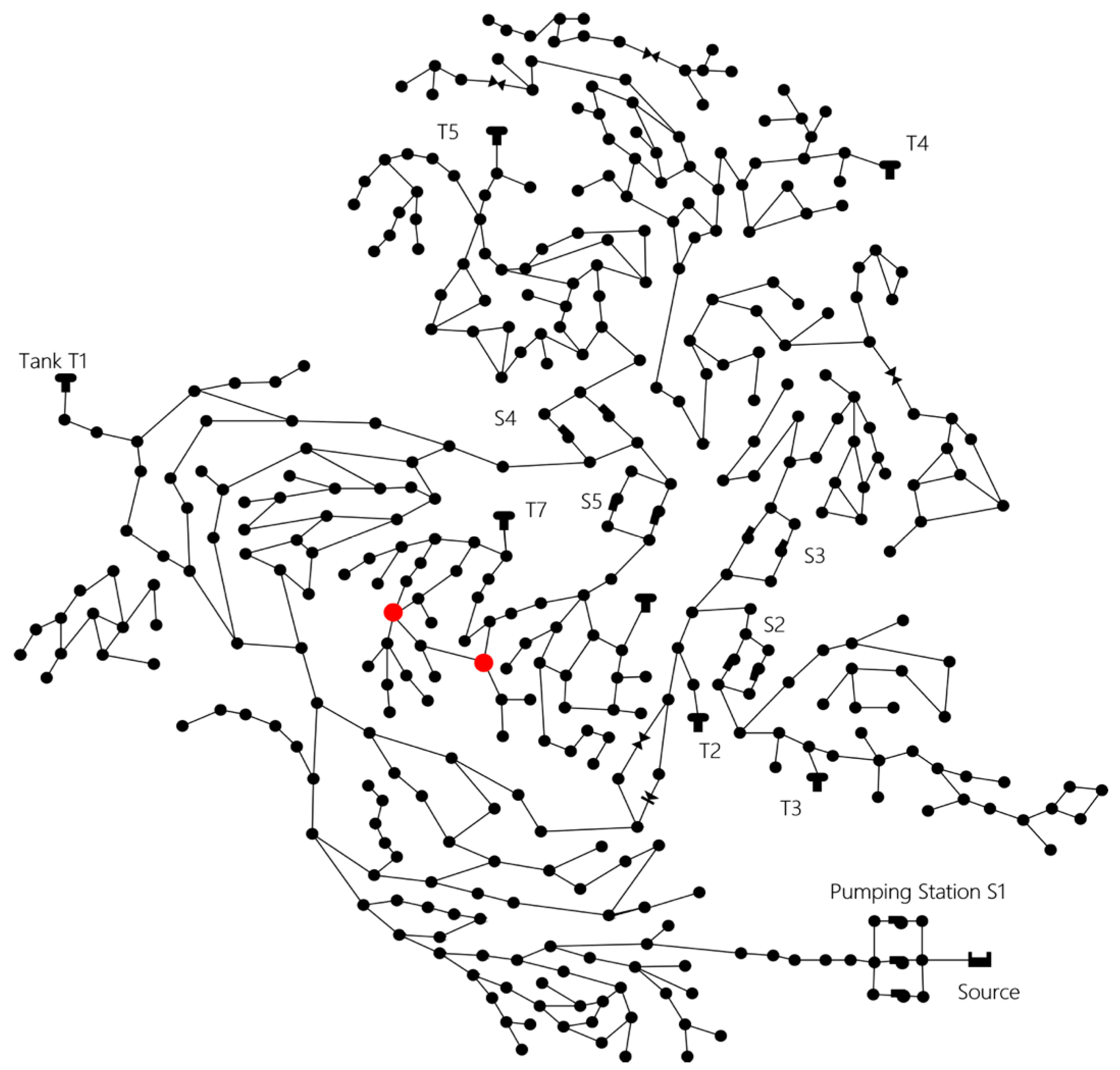
3.1. Data Formation
3.2. Experimental Procedure
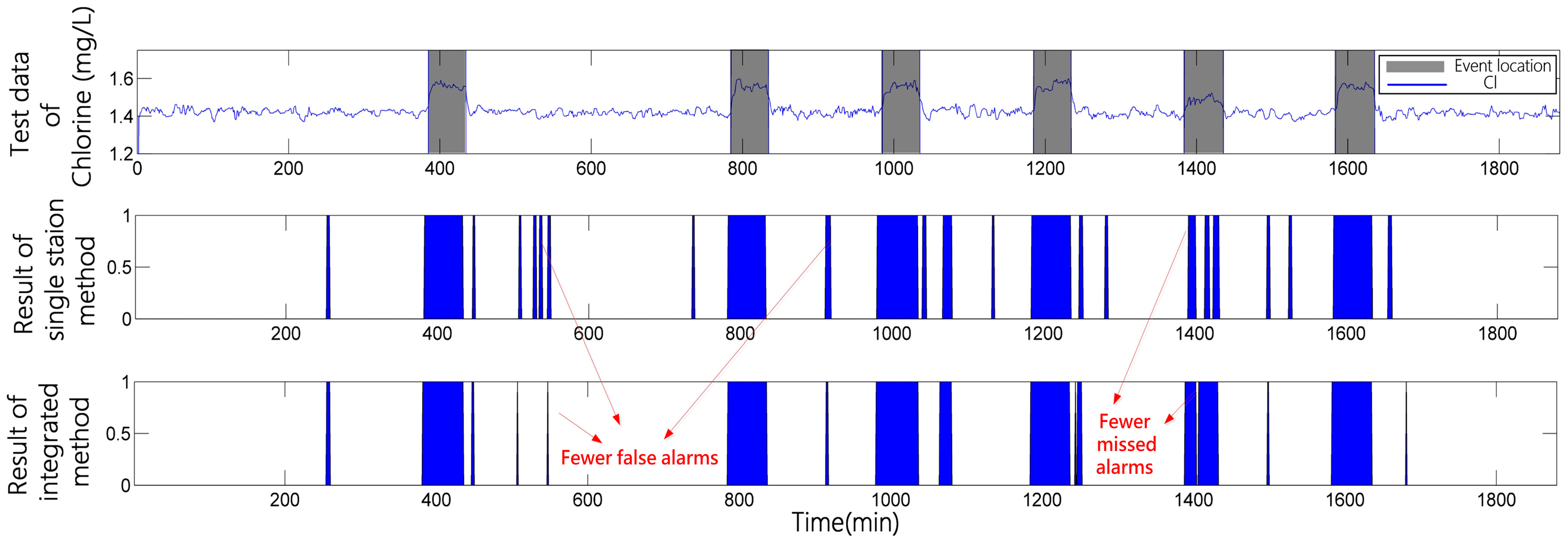
3.3. Experiment and Analysis
3.3.1. Case 1
Forming of the Bayesian Network
Temporal Analysis Based on Single Station Information
Spatial Analysis Using Causal Relationship Based on Multi-Stations Information
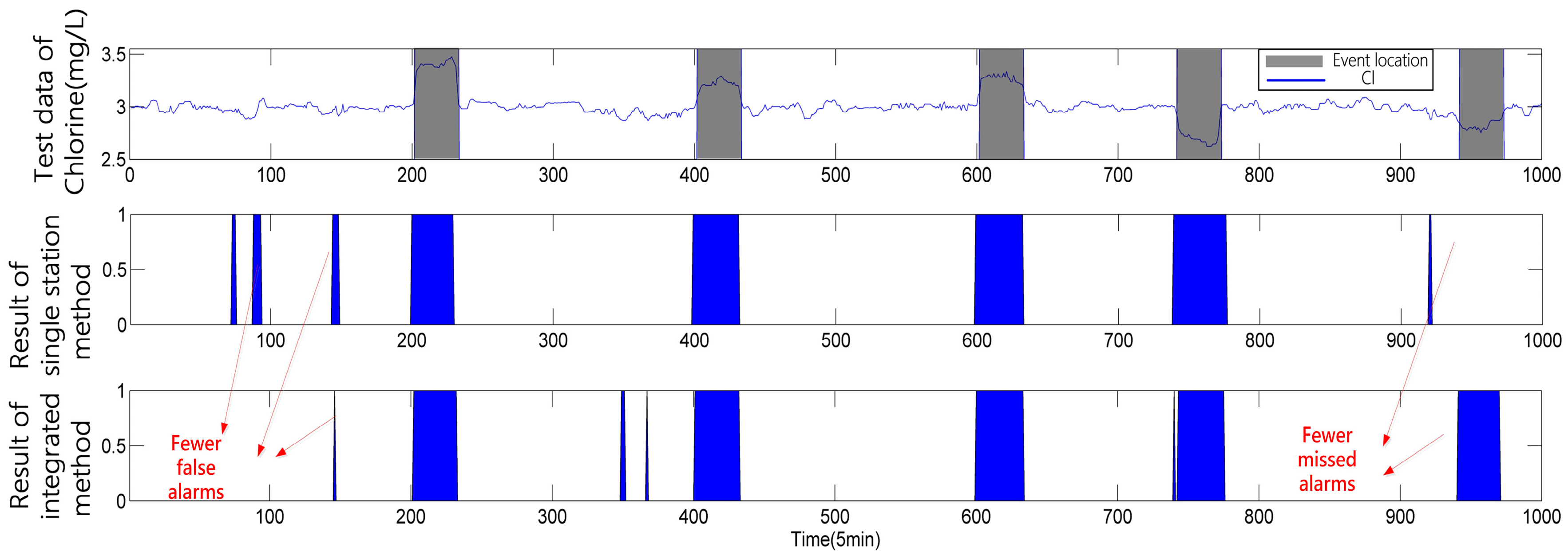
3.3.2. Case 2
Temporal Analysis Based on Single Station Information
Spatial Analysis Using Causal Relationship Based on Multi-Stations Information
4. Conclusions
- In order to build the causal relationship between stations, the discretisation of states is subjectively chosen. Thus, an expert system or a more objective method needs to be proposed for this process. Additionally, the fluctuation of the flow time between stations is uncertain, making it more difficult to obtain an accurate time in real systems. So, a more precise Bayesian Network model, such as a dynamic one, could be built with hydraulic information.
- In the section that concerned the single station temporal analysis, an improved method could be used, such as a method that uses multiple water quality indexes for higher accuracy. Although the parallel fusion method can compensate each dimension to decrease false alarms, this may be at the cost of a decrease in accuracy. Thus, better methods of fusion should be considered.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Brown, L.C.; Barnwell, T.O. The Enhanced Stream Water Quality Models QUAL2E and QUAL2E-UNCAS: Documentation and User Manual; Bibliogov: Athens, GA, USA, 1987; ISBN 9781288646760. [Google Scholar]
- Kinerson, R.S.; Kittle, J.L.; Duda, P.B. BASINS: Better Assessment Science Integrating Point and Nonpoint Sources; Springer: Boston, MA, USA, 2009; ISBN 9780387097213. [Google Scholar]
- Reed, S.; Koren, V.; Smith, M.; Zhang, Z.; Moreda, F.; Seo, D.J.; DMIP Participants. Overall distributed model intercomparison project results. J. Hydrol. 2015, 298, 27–60. [Google Scholar] [CrossRef]
- Hall, J.; Szabo, J. WaterSentinel Online Water Quality Monitoring as an Indicator of Drinking Water Contamination; Water Security Division, EPA: Washington, DC, USA, 2005. [Google Scholar]
- Jeffrey, Y.Y.; Haught, R.C.; Goodrich, J.A. Real-time contaminant detection and classification in a drinking water pipe using conventional water quality sensors: Techniques and experimental results. J. Environ. Manag. 2009, 90, 2494–2506. [Google Scholar] [CrossRef] [PubMed]
- Byer, D.E.; Carlson, K. Real-Time detection of intentional chemical contamination in the distribution system. Int. J. Electr. Comput. Eng. 2005, 1, 358–363. [Google Scholar]
- Mckenna, S.A.; Klise, K.A.; Wilson, M.P. Testing water quality change detection algorithms. In Proceedings of the 8th Annual Water Distribution System Analysis Symposium, Cincinnati, OH, USA, 27–30 August 2006. [Google Scholar]
- Arad, J.; Housh, M.; Perelman, L.; Ostfeld, A. A dynamic thresholds scheme for contaminant event detection in water distribution systems. Water Res. 2013, 47, 1899–1908. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Hou, D.; Huang, P.; Zhang, G. Multiscale water quality contamination events detection based on sensitive time scales reconstruction. In Proceedings of the 2013 International Conference on Wavelet Analysis and Pattern Recognition (ICWAPR), Tianjin, China, 14–17 July 2013. [Google Scholar]
- Klise, K.A. Water quality change detection: Multivariate algorithms. In Proceedings of the SPIE Conference on Defense and Security Symposium, Orlando, FL, USA, 9 May 2006. [Google Scholar]
- Vugrin, E.; Mckenna, S.A.; Hart, D.B. Trajectory clustering approach for reducing water quality event false alarms. In Proceedings of the World Environmental and Water Resources Congress, Kansas City, MO, USA, 17–21 May 2009. [Google Scholar]
- Modaresi, F.; Araghinejad, S. A comparative assessment of Support Vector Machines, Probabilistic Neural Networks, and K-Nearest Neighbor Algorithms for water quality classification. Water Resour. Manag. 2014, 28, 4095–4111. [Google Scholar] [CrossRef]
- O’Halloran, R.; Yang, S.; Tulloh, A.; Koltun, P.; Toifl, M. Sensor-Based water parcel tracking. In Proceedings of the 8th Annual International Symposium on Water Distribution Systems Analysis, Cincinnati, OH, USA, 27–30 August 2006. [Google Scholar]
- Koch, M.W.; Mckenna, S.A. Distributed sensor fusion in water quality event detection. J. Water Resour. Plan. Manag. 2010, 137, 10–19. [Google Scholar] [CrossRef]
- Mao, Y.; Jie, Q.; Jia, B.; Ping, P. Online event detection based on the spatio-temporal analysis in the river sensor networks. In Proceedings of the IEEE International Conference on Information and Automation, Lijiang, China, 8–10 August 2015. [Google Scholar]
- Oliker, N.; Ostfeld, A. Network hydraulics inclusion in water quality event detection using multiple sensor stations data. Water Res. 2015, 80, 47–58. [Google Scholar] [CrossRef] [PubMed]
- Stoianov, I.; Nachman, L.; Madden, S.; Tokmouline, T. PIPENET: A wireless sensor network for pipeline monitoring. In Proceedings of the 6th International Conference on Information Processing in Sensor Networks, Cambridge, MA, USA, 25–27 April 2007. [Google Scholar]
- Tsay, R.S.; Tiao, G.C. Consistent estimates of autoregressive parameters and extended sample autocorrelation function for stationary and nonstationary ARMA models. J. Am. Stat. Assoc. 1984, 79, 84–96. [Google Scholar] [CrossRef]
- Zaidi, Z.R.; Mark, B.L. Mobility tracking based on autoregressive models. IEEE Trans. Mob. Comput. 2011, 10, 32–43. [Google Scholar] [CrossRef]
- Oliker, N.; Ostfeld, A. Minimum volume ellipsoid classification model for contamination event detection in water distribution systems. Environ. Model. Softw. 2014, 57, 1–12. [Google Scholar] [CrossRef]
- Parsons, S. Probabilistic Graphical Models: Principles and Techniques by Koller Daphne and Friedman Nir; Cambridge University Press: Cambrige, MA, USA, 2011; ISBN 0262013193. [Google Scholar]
- Dawsey, W.J. Bayesian belief networks to integrate monitoring evidence of water distribution system contamination. J. Water Resour. Plan. Manag. 2006, 132, 234–241. [Google Scholar] [CrossRef]
- Rossman, L.A. EPANET Users Manual; United States Environmental Protection Agency: Cincinnati, OH, USA, 2000.
- Ostfeld, A.; Salomons, E.; Ormsbee, L.; Uber, J.G.; Bros, C.M.; Kalungi, P.; Burd, R.; Zazula-Coetzee, B.; Belrain, T.; Kang, D. Battle of the water calibration networks. J. Water Resour. Plan. Manag. 2012, 138, 523–532. [Google Scholar] [CrossRef]

| Scenario | Single Station Method | Integrated Method | ||
|---|---|---|---|---|
| TPR | FPR | TPR | FPR | |
| 1 | 0.9233 | 0.0873 | 0.9367 | 0.0310 |
| 2 | 0.8967 | 0.0342 | 0.9500 | 0.0114 |
| 3 | 0.8833 | 0.0551 | 0.9333 | 0.0234 |
| 4 | 0.9333 | 0.0582 | 0.9733 | 0.0222 |
| 5 | 0.8933 | 0.0658 | 0.9400 | 0.0506 |
| 6 | 0.9067 | 0.0532 | 0.9700 | 0.0354 |
| Average | 0.9061 | 0.0590 | 0.9501 | 0.0290 |
| Scenario | Single Station Method | Integrated Method | ||
|---|---|---|---|---|
| TPR | FPR | TPR | FPR | |
| 1 | 0.9400 | 0.0556 | 0.9800 | 0.0181 |
| 2 | 0.9063 | 0.0850 | 0.9500 | 0.0500 |
| 3 | 0.8400 | 0.0462 | 0.9467 | 0.0145 |
| 4 | 0.8750 | 0.0946 | 0.9563 | 0.0573 |
| 5 | 0.9467 | 0.0485 | 0.9533 | 0.0169 |
| 6 | 0.9125 | 0.0766 | 0.9313 | 0.0207 |
| Average | 0.9034 | 0.0678 | 0.9529 | 0.0295 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, J.; Xu, L.; Xie, X.; Hou, D.; Huang, P.; Zhang, G.; Zhang, H. Contamination Event Detection Method Using Multi-Stations Temporal-Spatial Information Based on Bayesian Network in Water Distribution Systems. Water 2017, 9, 894. https://doi.org/10.3390/w9110894
Yu J, Xu L, Xie X, Hou D, Huang P, Zhang G, Zhang H. Contamination Event Detection Method Using Multi-Stations Temporal-Spatial Information Based on Bayesian Network in Water Distribution Systems. Water. 2017; 9(11):894. https://doi.org/10.3390/w9110894
Chicago/Turabian StyleYu, Jie, Le Xu, Xiang Xie, Dibo Hou, Pingjie Huang, Guangxin Zhang, and Hongjian Zhang. 2017. "Contamination Event Detection Method Using Multi-Stations Temporal-Spatial Information Based on Bayesian Network in Water Distribution Systems" Water 9, no. 11: 894. https://doi.org/10.3390/w9110894
APA StyleYu, J., Xu, L., Xie, X., Hou, D., Huang, P., Zhang, G., & Zhang, H. (2017). Contamination Event Detection Method Using Multi-Stations Temporal-Spatial Information Based on Bayesian Network in Water Distribution Systems. Water, 9(11), 894. https://doi.org/10.3390/w9110894







