BRISENT: An Entropy-Based Model for Bridge-Pier Scour Estimation under Complex Hydraulic Scenarios
Abstract
:1. Introduction
2. The Informational Entropy Concept
3. The BRISENT Model
4. Methods
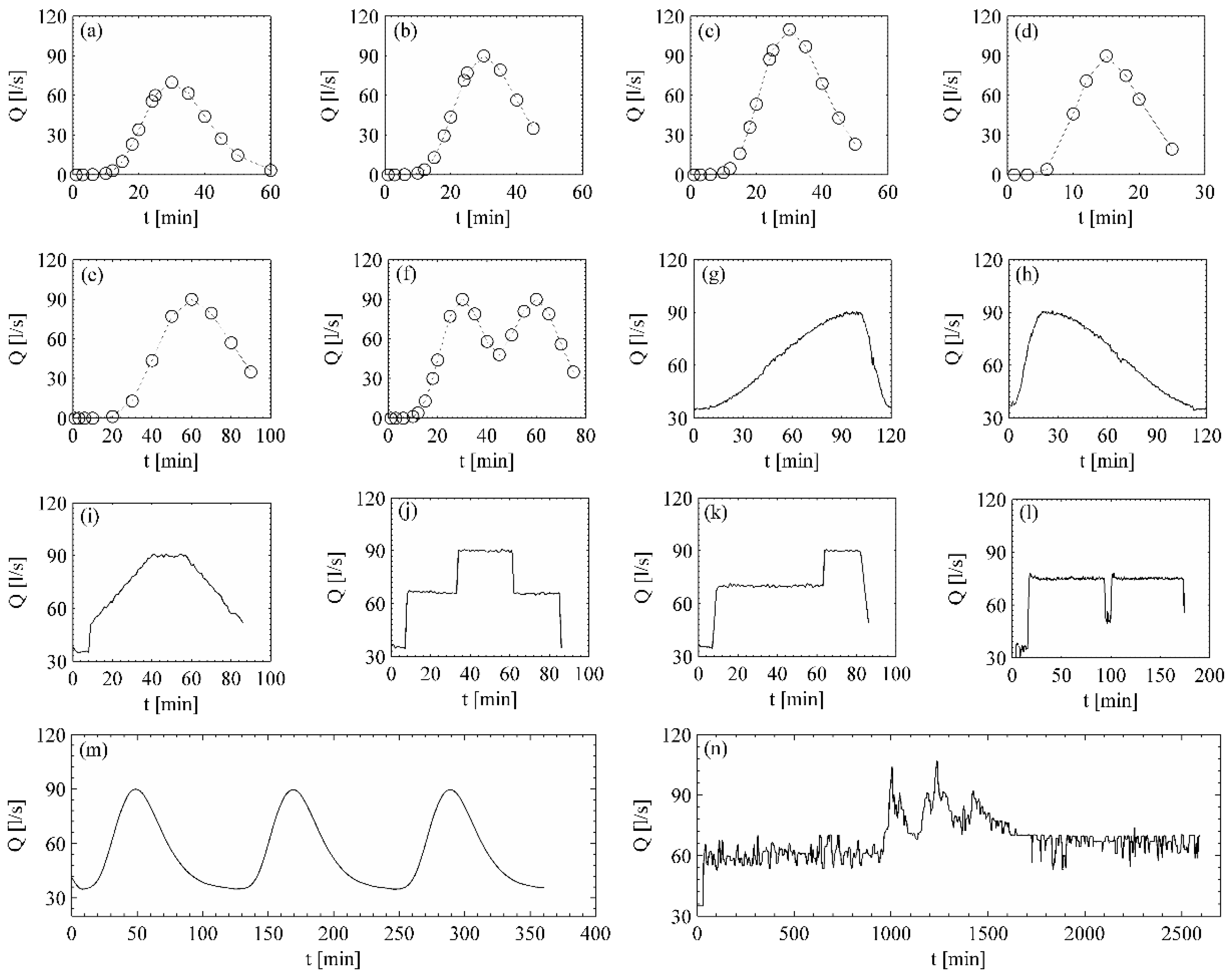
4.1. Data Characterization for λ Estimation
4.2. , , and Estimation
4.3. Calibration and Validation Procedures
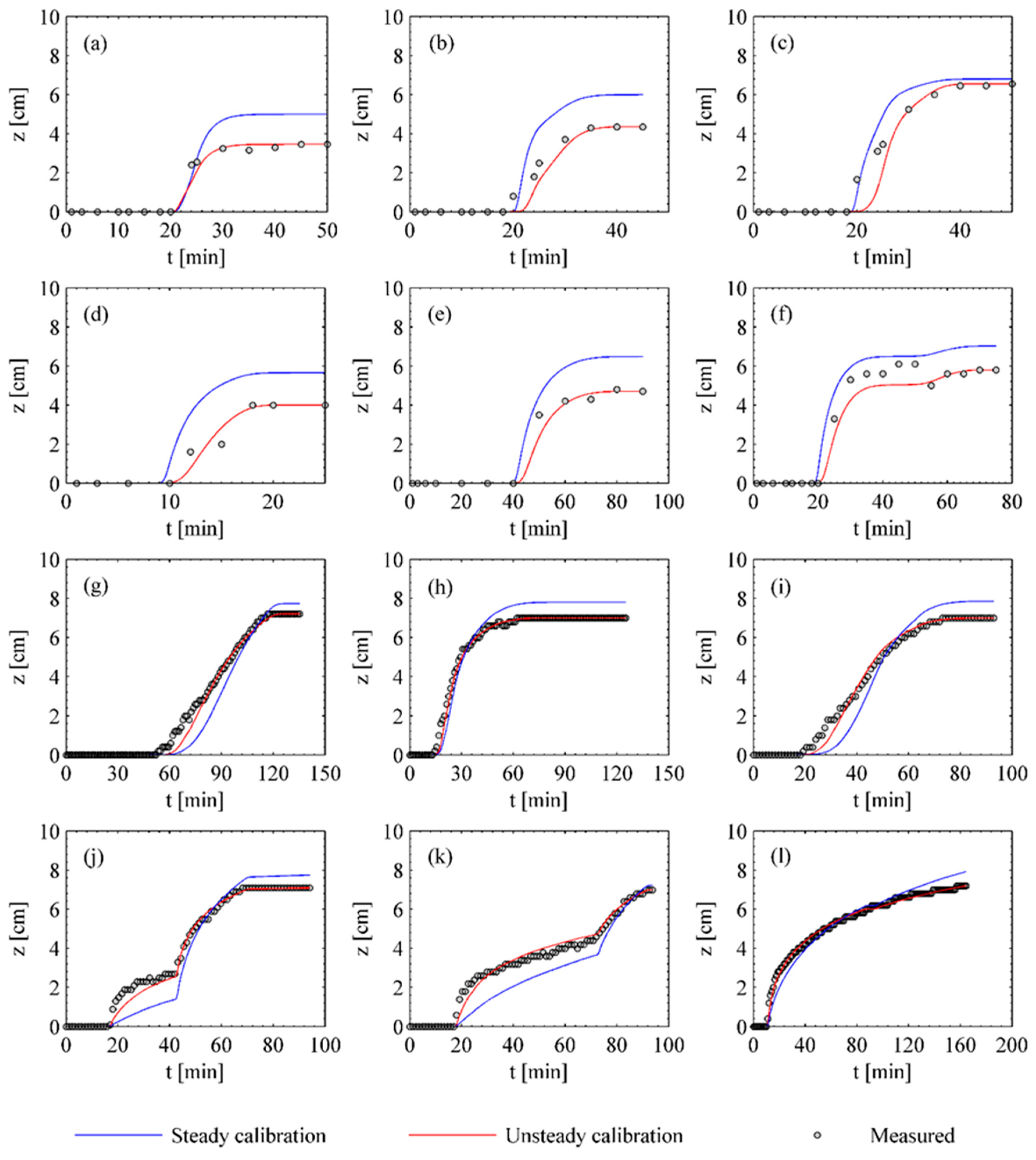
- (a)
- Calibration employing unsteady data: Each unsteady run was calibrated with the aim of finding the best performance of the model. This kind of calibration will be called “unsteady calibration” in the rest of the paper.
- (b)
- Calibration employing steady data: Two steady runs were used to calibrate the model with the aim of testing it in the most critical condition. The values of the dimensionless parameters regarding sediment properties and geometrical scale () are identical for calibration runs as well as for unsteady experiments, respectively. “2002OLIVETO32S” was used to calibrate Oliveto and Hager’s [19] unsteady runs and “2017PIZARRO01S” for the unsteady experiments of Pizarro et al. [21] and Link et al. [22]. This kind of calibration will be called “steady calibration” in the rest of the paper.
5. Results
5.1. BRISENT as a Multipurpose Model
5.1.1. BRISENT Performance under Steady Hydraulic Conditions
5.1.2. BRISENT Performance under Flood Waves
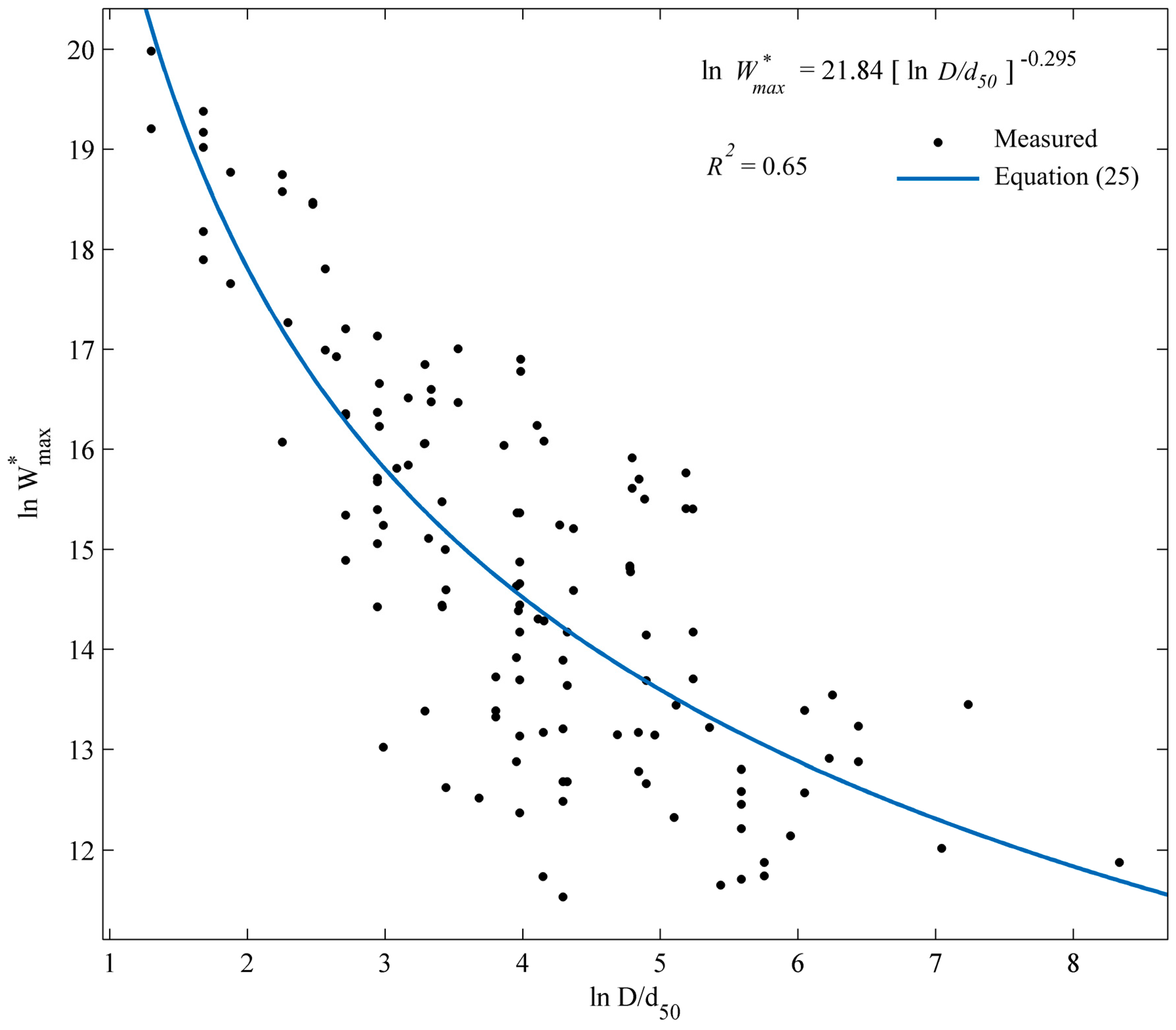
5.2. In Search of a Practical Formulation
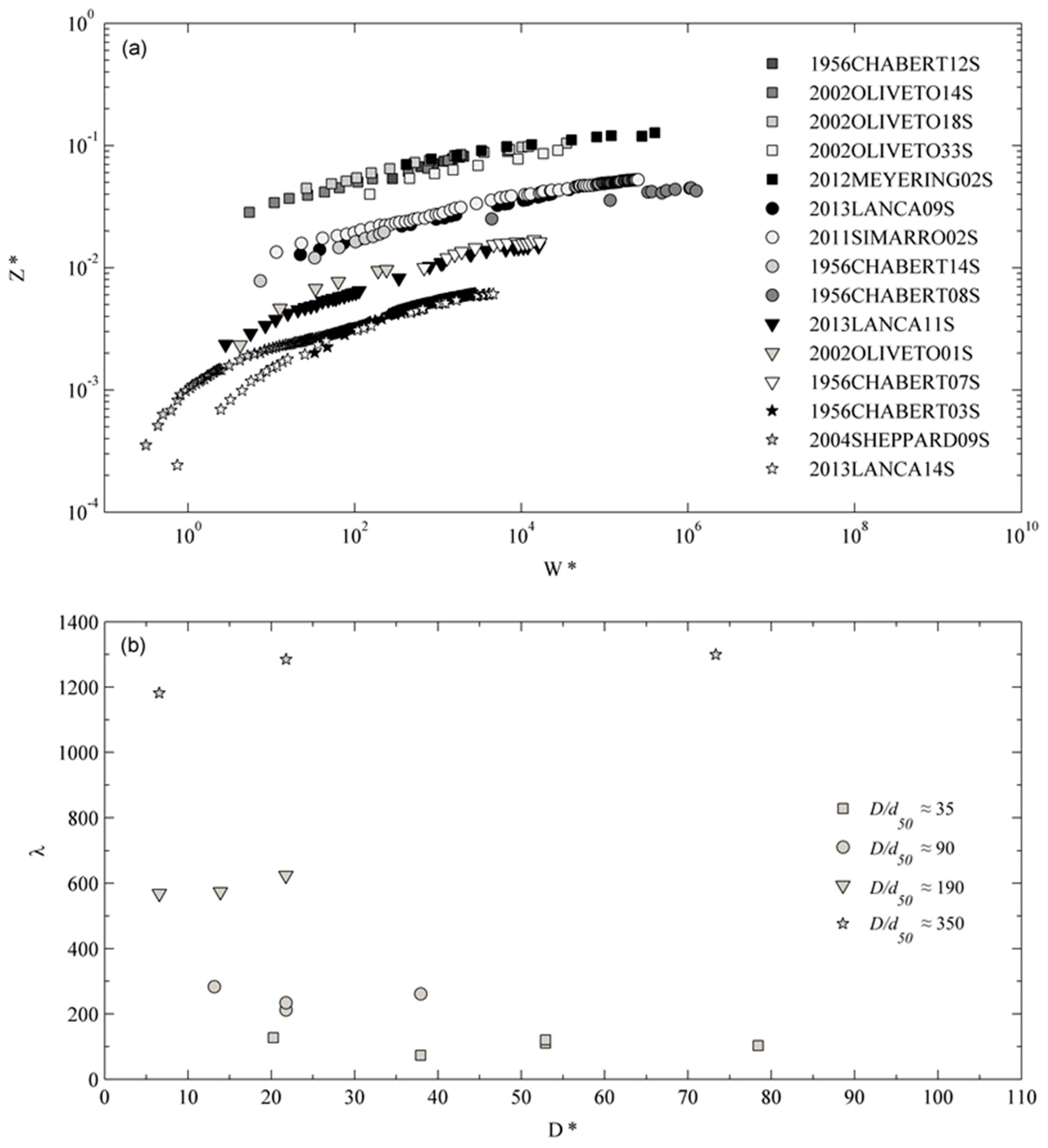
5.2.1. Effects of and on
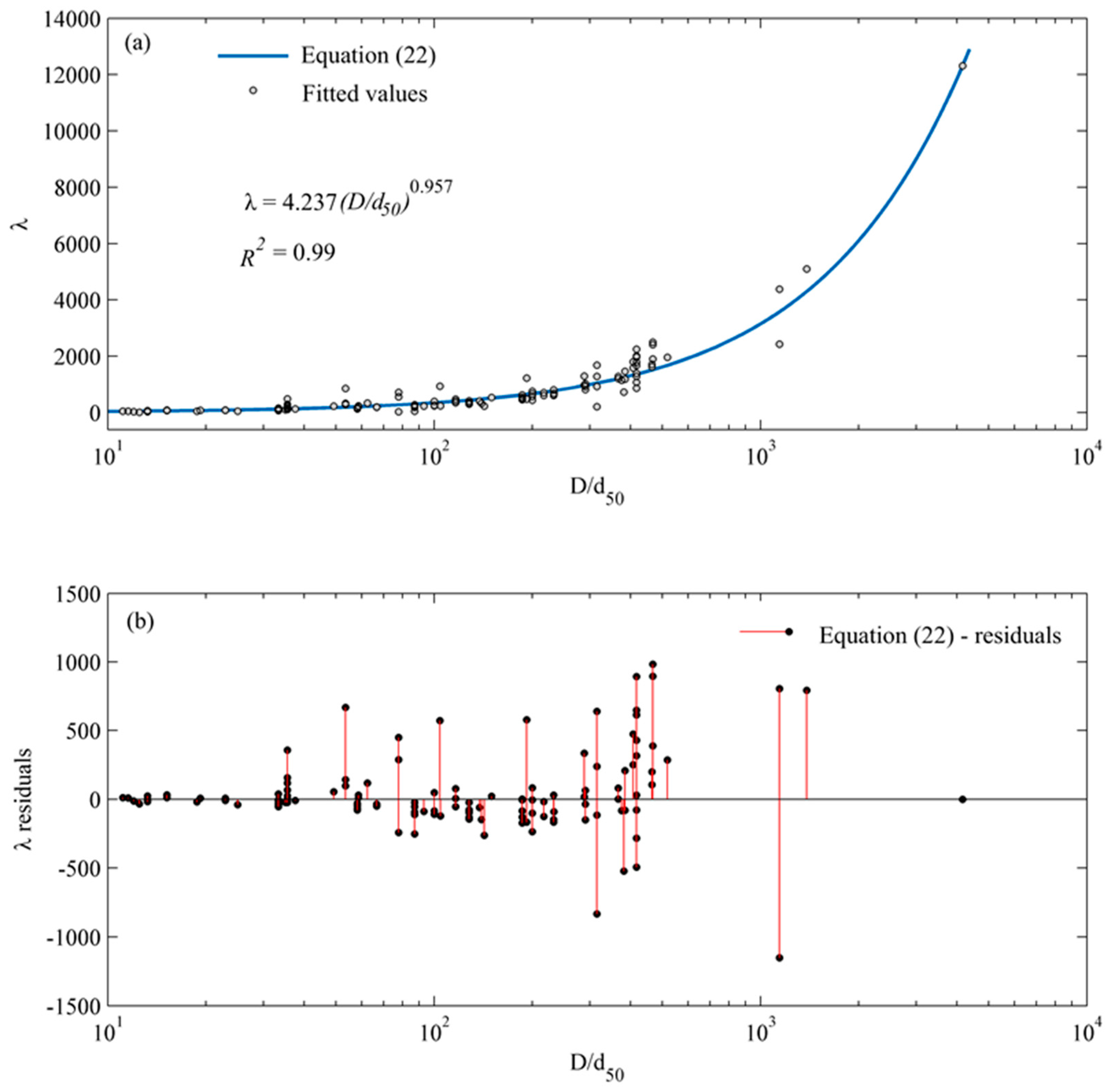
5.2.2. , , and Estimation
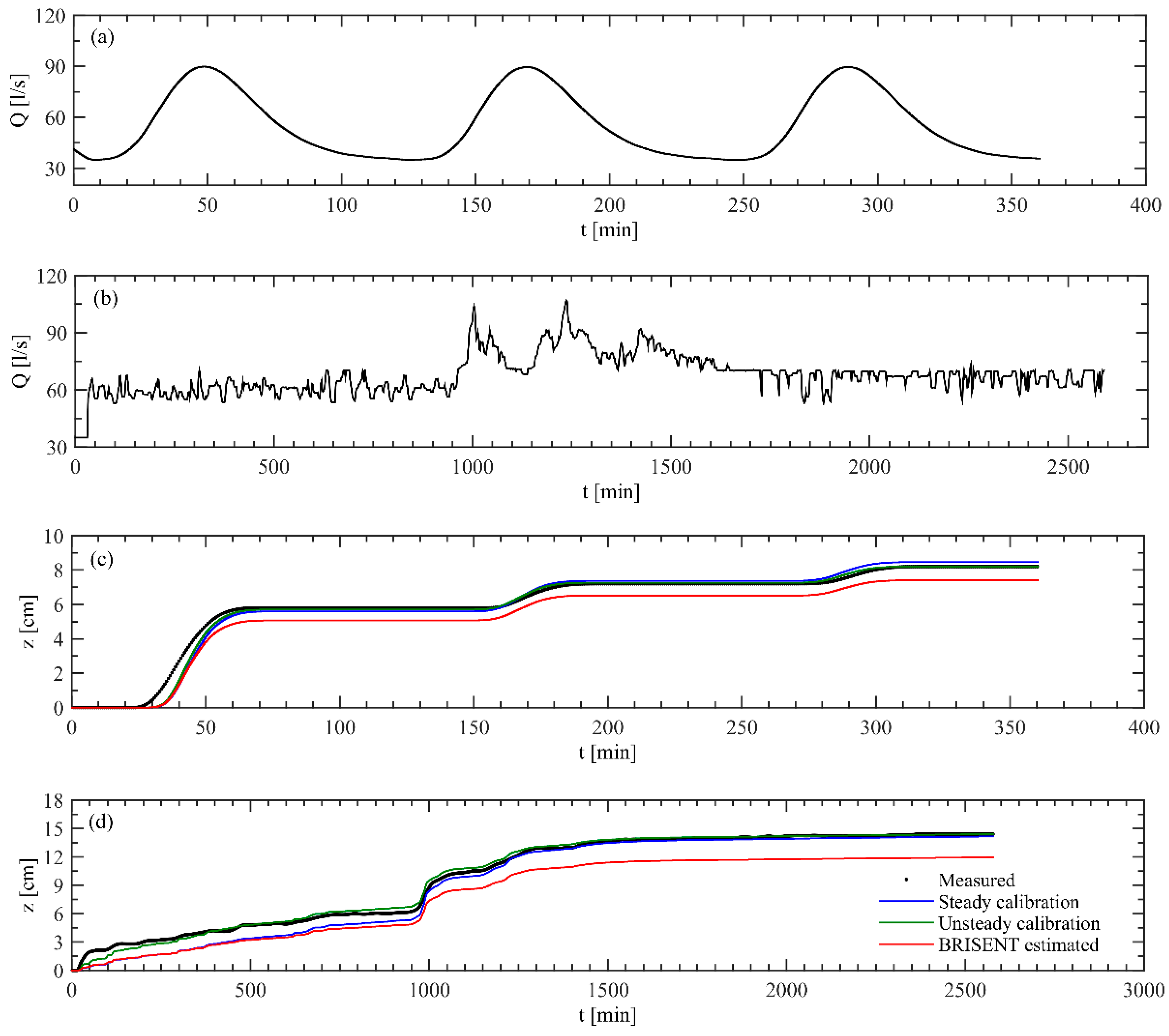
5.3. BRISENT Validation: Highly Unsteady and Multi-Peaked Hydrographs
6. Discussion
6.1. Informational Entropy and the Principle of Maximum Entropy for Pier Scour Modelling
6.2. BRISENT: A Multipurpose Model
6.3. Wide Range of the Considered Dimensionless Parameters
6.4. Applicability of the Model: Advantages and Limitations
6.5. Key Dimensionless Parameters: and
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Briaud, J.L.; Brandimarte, L.; Wang, J.; D’Odorico, P. Probability of scour depth exceedance owing to hydrologic uncertainty. Georisk Assess. Manag. Risk Eng. Syst. Geohazards 2007, 1, 77–88. [Google Scholar] [CrossRef]
- Cook, W. Bridge Failure Rates, Consequences, and Predictive Trends; Utah State University: Logan, UT, USA, 2014; ISBN 1321576021. [Google Scholar]
- Imam, B.M.; Marios, K. Causes and consequences of metallic bridge failures. Struct. Eng. Int. 2012, 22, 93–98. [Google Scholar] [CrossRef]
- Kattell, J.; Eriksson, M. Bridge Scour Evaluation: Screening, Analysis, & Countermeasures; San Dimas Technology and Development Center: San Dimas, CA, USA, 1998. [Google Scholar]
- Smith, D.W. Bridge failures. Proc. Inst. Civ. Eng. 1976, 60, 367–382. [Google Scholar] [CrossRef]
- Wardhana, K.; Hadipriono, F.C. Analysis of recent bridge failures in the United States. J. Perform. Constr. Facil. 2003, 17, 144–150. [Google Scholar] [CrossRef]
- Melville, B.W. Pier and abutment scour: Integrated approach. J. Hydraul. Eng. 1997, 123, 125–136. [Google Scholar] [CrossRef]
- Richardson, E.V.; Davis, S.R. Evaluating Scour at Bridges: Hydraulic Engineering Circular No. 18; Federal Highway Administration: Washington, DC, USA, 1995. [Google Scholar]
- Sheppard, D.M.; Melville, B.; Demir, H. Evaluation of Existing Equations for Local Scour at Bridge Piers. J. Hydraul. Eng. 2014, 140, 14–23. [Google Scholar] [CrossRef]
- Zanke, U. Kolke am Pfeiler in richtungskonstanter Strömung und unter Welleneinfluß; Universität Hannover: Hannover, Germany, 1982; Volume 54, pp. 381–416. [Google Scholar]
- Manes, C.; Brocchini, M. Local scour around structures and the phenomenology of turbulence. J. Fluid Mech. 2015, 779, 309–324. [Google Scholar] [CrossRef]
- Dey, S. Time-variation of scour in the vicinity of circular piers. Proc. Inst. Civ. Eng. Marit. Energy 1999, 136, 67–75. [Google Scholar] [CrossRef]
- Melville, B.W.; Chiew, Y.-M. Time scale for local scour at bridge piers. J. Hydraul. Eng. 1999, 125, 59–65. [Google Scholar] [CrossRef]
- Oliveto, G.; Hager, W.H. Temporal evolution of clear-water pier and abutment scour. J. Hydraul. Eng. 2002, 128, 811–820. [Google Scholar] [CrossRef]
- Sheppard, D.M.; Miller, W., Jr. Live-bed local pier scour experiments. J. Hydraul. Eng. 2006, 132, 635–642. [Google Scholar] [CrossRef]
- Lai, J.-S.; Chang, W.-Y.; Yen, C.-L. Maximum local scour depth at bridge piers under unsteady flow. J. Hydraul. Eng. 2009, 135, 609–614. [Google Scholar] [CrossRef]
- Kothyari, U.C.; Garde, R.C.J.; Ranga Raju, K.G. Temporal variation of scour around circular bridge piers. J. Hydraul. Eng. 1992, 118, 1091–1106. [Google Scholar] [CrossRef]
- López, G.; Teixeira, L.; Ortega-Sánchez, M.; Simarro, G. Estimating final scour depth under clear-water flood waves. J. Hydraul. Eng. 2014, 140, 328–332. [Google Scholar] [CrossRef]
- Oliveto, G.; Hager, W.H. Further results to time-dependent local scour at bridge elements. J. Hydraul. Eng. 2005, 131, 97–105. [Google Scholar] [CrossRef]
- Hager, W.H.; Unger, J. Bridge pier scour under flood waves. J. Hydraul. Eng. 2010, 136, 842–847. [Google Scholar] [CrossRef]
- Pizarro, A.; Ettmer, B.; Manfreda, S.; Rojas, A.; Link, O. Dimensionless effective flow work for estimation of pier scour caused by flood waves. J. Hydraul. Eng. 2017, 143. [Google Scholar] [CrossRef]
- Link, O.; Castillo, C.; Pizarro, A.; Rojas, A.; Ettmer, B.; Escauriaza, C.; Manfreda, S. A model of bridge pier scour during flood waves. J. Hydraul. Res. 2017, 55. [Google Scholar] [CrossRef]
- Sturm, T.; Sotiropoulos, F.; Landers, M.; Gotvald, T.; Lee, S.; Ge, L.; Navarro, R.; Escauriaza, C. Laboratory and 3D numerical modeling with field monitoring of regional bridge scour in Georgia. In Georgia Department of Transportation Final Project; Georgia Dept. of Transportation: Atlanta, GA, USA, 2004. [Google Scholar]
- Clubley, S.K.; Manes, C.; Richards, D.J. High resolution sonars set to revolutionise bridge scour inspections. Proc. Inst. Civ. Eng. Civ. Eng. 2015, 168, 35–42. [Google Scholar] [CrossRef]
- Prendergast, L.J.; Gavin, K. A review of bridge scour monitoring techniques. J. Rock Mech. Geotech. Eng. 2014, 6, 138–149. [Google Scholar] [CrossRef]
- Hong, J.-H.; Guo, W.-D.; Chiew, Y.-M.; Chen, C.-H. A new practical method to simulate flood-induced bridge pier scour—A case study of Mingchu bridge piers on the Cho-Shui River. Water 2016, 8, 238. [Google Scholar] [CrossRef]
- Su, C.-C.; Lu, J.-Y. Comparison of Sediment Load and Riverbed Scour during Floods for Gravel-Bed and Sand-Bed Reaches of Intermittent Rivers: Case Study. J. Hydraul. Eng. 2016, 142, 5016001. [Google Scholar] [CrossRef]
- Gaudio, R.; Grimaldi, C.; Tafarojnoruz, A.; Calomino, F. Comparison of formulae for the prediction of scour depth at piers. In Proceedings of the 1st IAHR European Division Congress, Edinburgh, UK, 4–6 May 2010. [Google Scholar]
- Gaudio, R.; Tafarojnoruz, A.; De Bartolo, S. Sensitivity analysis of bridge pier scour depth predictive formulae. J. Hydroinform. 2013, 15, 939–951. [Google Scholar] [CrossRef]
- Barbe, D.E.; Cruise, J.F.; Singh, V.P. Probabilistic approach to local bridge pier scour. Transp. Res. Rec. 1350 1992, 28–33. Available online: https://trid.trb.org/view.aspx?id=370731 (accessed on 5 November 2017).
- Johnson, P.A. Reliability-based pier scour engineering. J. Hydraul. Eng. 1992, 118, 1344–1358. [Google Scholar] [CrossRef]
- Johnson, P.A. Fault tree analysis of bridge failure due to scour and channel instability. J. Infrastruct. Syst. 1999, 5, 35–41. [Google Scholar] [CrossRef]
- Johnson, P.A.; Ayyub, B.M. Assessing time-variant bridge reliability due to pier scour. J. Hydraul. Eng. 1992, 118, 887–903. [Google Scholar] [CrossRef]
- Johnson, P.A.; Ayyub, B.M. Modeling uncertainty in prediction of pier scour. J. Hydraul. Eng. 1996, 122, 66–72. [Google Scholar] [CrossRef]
- Johnson, P.A.; Hell, T.M. Bridge Scour-A Probabilistic Approach. Infrastruct. Sussex 1996, 1, 24–30. [Google Scholar]
- Johnson, P.A.; Dock, D.A. Probabilistic bridge scour estimates. J. Hydraul. Eng. 1998, 124, 750–754. [Google Scholar] [CrossRef]
- Yanmaz, A.M.; Cicekdag, O. Composite reliability model for local scour around cylindrical bridge piers. Can. J. Civ. Eng. 2001, 28, 520–535. [Google Scholar] [CrossRef]
- Yanmaz, A.M.; Üstün, I. Generalized reliability model for local scour around bridge piers of various shapes. Turk. J. Eng. Environ. Sci. 2001, 25, 687–698. [Google Scholar]
- Johnson, P.A.; Clopper, P.E.; Zevenbergen, L.W.; Lagasse, P.F. Quantifying uncertainty and reliability in bridge scour estimations. J. Hydraul. Eng. 2015, 141, 4015013. [Google Scholar] [CrossRef]
- Flint, M.M.; Fringer, O.; Billington, S.L.; Freyberg, D.; Diffenbaugh, N.S. Historical Analysis of Hydraulic Bridge Collapses in the Continental United States. J. Infrastruct. Syst. 2017, 23, 4017005. [Google Scholar] [CrossRef]
- Robinson, D.W. Entropy and uncertainty. Entropy 2008, 10, 493–506. [Google Scholar] [CrossRef]
- Wang, Q.A. Probability distribution and entropy as a measure of uncertainty. J. Phys. A Math. Theor. 2008, 41, 65004. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Entropy: From thermodynamics to hydrology. Entropy 2014, 16, 1287–1314. [Google Scholar] [CrossRef]
- Dong, X.; Lu, H.; Xia, Y.; Xiong, Z. Decision-Making Model under Risk Assessment Based on Entropy. Entropy 2016, 18, 404. [Google Scholar] [CrossRef]
- Kvålseth, T.O. On the measurement of randomness (uncertainty): A more informative entropy. Entropy 2016, 18, 159. [Google Scholar] [CrossRef]
- Jaynes, E.T. Information theory and statistical mechanics. II. Phys. Rev. 1957, 108, 171. [Google Scholar] [CrossRef]
- Chiu, C.-L. Entropy and probability concepts in hydraulics. J. Hydraul. Eng. 1987, 113, 583–599. [Google Scholar] [CrossRef]
- Fiorentino, M.; Claps, P.; Singh, V.P. An entropy-based morphological analysis of river basin networks. Water Resour. Res. 1993, 29, 1215–1224. [Google Scholar] [CrossRef]
- Singh, V.P. Entropy theory for movement of moisture in soils. Water Resour. Res. 2010, 46, W0516. [Google Scholar] [CrossRef]
- Singh, V.P. Entropy theory for derivation of infiltration equations. Water Resour. Res. 2010, 46, W03527. [Google Scholar] [CrossRef]
- Singh, V.P. Entropy Theory in Hydraulic Engineering: An Introduction; American Society of Civil Engineers: Reston, VA, USA, 2014. [Google Scholar] [CrossRef]
- Singh, V.P. Entropy Theory in Hydrologic Science and Engineering; McGraw Hill Professional: New York, NY, USA, 2014; ISBN 0071835474. [Google Scholar]
- Moramarco, T.; Corato, G.; Melone, F.; Singh, V.P. An entropy-based method for determining the flow depth distribution in natural channels. J. Hydrol. 2013, 497, 176–188. [Google Scholar] [CrossRef]
- Hemelrijk, J. Underlining random variables. Stat. Neerl. 1966, 20, 1–7. [Google Scholar] [CrossRef]
- Breusers, H.N.C.; Nicollet, G.; Shen, H.W. Local scour around cylindrical piers. J. Hydraul. Res. 1977, 15, 211–252. [Google Scholar] [CrossRef]
- May, R.W.P.; Willoughby, I.R. Local Scour around Large Obstructions; Technical Report; Hydraulics Research: Wallingford, Oxfordshire, UK, 1990. [Google Scholar]
- Miller, W., Jr.; Sheppard, D.M. Time rate of local scour at a circular pile. In Proceedings of the First International Conference on Scour of Foundations, College Station, TX, USA, 17–20 November 2002. [Google Scholar]
- Chabert, J.; Engeldinger, P. Etude des Affouillements Autour des Piles des Ponts; Laboratoire National d’Hydraulique: Chatou, France, 1956; p. 118. (In French) [Google Scholar]
- Franzetti, S.; Larcan, E.; Mignosa, P. Erosione alla base di pile circolari di ponte: Verifica sperimentale dell’ipotesi di esistenza di una situazione finale di equilibrio. Idrotecnica 1989, 16, 135–141. [Google Scholar]
- Sheppard, D.M.; Odeh, M.; Glasser, T. Large scale clear-water local pier scour experiments. J. Hydraul. Eng. 2004, 130, 957–963. [Google Scholar] [CrossRef]
- Grimaldi, C. Non-Conventional Countermeasures Against Local Scouring at Bridge Piers. Ph.D. Thesis, The Hydraulic Engineering for Environment and Territory University, Cosenza, Italy, 2005. [Google Scholar]
- Alabi, P.D. Time Development of Local Scour at a Bridge Pier Fitted with a Collar. Master’s Thesis, University of Saskatchewan, Saskatoon, SK, Canada, 2006. [Google Scholar]
- Simarro, G.; Fael, C.M.S.; Cardoso, A.H. Estimating equilibrium scour depth at cylindrical piers in experimental studies. J. Hydraul. Eng. 2011, 137, 1089–1093. [Google Scholar] [CrossRef]
- Meyering, H. Effect of Sediment Density in Bridge Pier Scour Experiments. Ph.D. Thesis, Technical University of Braunschweig, Braunschweig, Germany, 2012. [Google Scholar]
- Lança, R.M.; Fael, C.S.; Maia, R.J.; Pêgo, J.P.; Cardoso, A.H. Clear-water scour at comparatively large cylindrical piers. J. Hydraul. Eng. 2013, 139, 1117–1125. [Google Scholar] [CrossRef]
- Giuseppe, O.; Hager, H.W. Closure to “Further Results to Time-Dependent Local Scour at Bridge Elements” by Giuseppe Oliveto and Willi H. Hager. J. Hydraul. Eng. 2006, 132, 997–998. [Google Scholar] [CrossRef]

| Authors | Run | (Days) | ||||||
|---|---|---|---|---|---|---|---|---|
| Chabert and Engeldinger [58] | 1956CHABERT01S | 0.26 | 4.29 | 6.58 | 1.65 | 192.26 | 4.00 | 0.75 |
| 1956CHABERT02S | 0.26 | 4.29 | 6.58 | 1.65 | 288.46 | 2.67 | 0.75 | |
| 1956CHABERT03S | 0.26 | 4.29 | 6.58 | 1.65 | 384.62 | 2.00 | 0.75 | |
| 1956CHABERT04S | 0.26 | 3.92 | 6.58 | 1.65 | 192.26 | 7.00 | 0.92 | |
| 1956CHABERT05S | 0.26 | 3.92 | 6.58 | 1.65 | 288.46 | 4.67 | 0.92 | |
| 1956CHABERT06S | 0.26 | 3.92 | 6.58 | 1.65 | 384.62 | 3.50 | 0.92 | |
| 1956CHABERT07S | 0.26 | 0.55 | 6.58 | 1.65 | 192.26 | 2.00 | 1.20 | |
| 1956CHABERT08S | 0.52 | 6.75 | 13.15 | 1.65 | 96.13 | 2.00 | 1.52 | |
| 1956CHABERT09S | 1.50 | 5.29 | 37.94 | 1.65 | 33.32 | 2.00 | 0.97 | |
| 1956CHABERT10S | 1.50 | 5.29 | 37.94 | 1.65 | 66.67 | 1.00 | 0.97 | |
| 1956CHABERT11S | 1.50 | 5.29 | 37.94 | 1.65 | 100.00 | 0.67 | 0.97 | |
| 1956CHABERT12S | 1.50 | 1.68 | 37.94 | 1.65 | 33.32 | 4.00 | 0.69 | |
| 1956CHABERT13S | 1.50 | 1.68 | 37.94 | 1.65 | 66.67 | 2.00 | 0.69 | |
| 1956CHABERT14S | 1.50 | 1.68 | 37.94 | 1.65 | 100.00 | 1.33 | 0.69 | |
| 1956CHABERT15S | 1.50 | 7.29 | 37.94 | 1.65 | 33.32 | 7.00 | 0.74 | |
| 1956CHABERT16S | 1.50 | 7.29 | 37.94 | 1.65 | 66.67 | 3.50 | 0.74 | |
| 1956CHABERT17S | 1.50 | 7.29 | 37.94 | 1.65 | 100.00 | 2.33 | 0.74 | |
| Zanke [10] | 1982ZANKE01S | 0.24 | 0.002 | 5.84 | 1.65 | 375.00 | 4.67 | 0.75 |
| Franzetti et al. [59] | 1989FRANZETTI01S | 2.50 | 58.13 | 30.22 | 0.18 | 19.20 | 3.00 | 0.79 |
| Oliveto and Hager [14,19] | 2002OLIVETO01S | 0.55 | 0.04 | 13.91 | 1.65 | 200.00 | 1.40 | 0.96 |
| 2002OLIVETO02S | 0.55 | 0.93 | 13.91 | 1.65 | 200.00 | 1.35 | 0.70 | |
| 2002OLIVETO03S | 0.55 | 0.44 | 13.91 | 1.65 | 200.00 | 2.75 | 0.66 | |
| 2002OLIVETO04S | 0.55 | 21.06 | 13.91 | 1.65 | 200.00 | 1.82 | 0.62 | |
| 2002OLIVETO05S | 0.55 | 0.20 | 13.91 | 1.65 | 116.36 | 2.32 | 0.62 | |
| 2002OLIVETO06S | 0.55 | 0.03 | 13.91 | 1.65 | 116.36 | 3.13 | 0.70 | |
| 2002OLIVETO07S | 0.55 | 0.89 | 13.91 | 1.65 | 116.36 | 4.69 | 0.66 | |
| 2002OLIVETO08S | 0.55 | 2.94 | 13.91 | 1.65 | 467.27 | 0.39 | 0.64 | |
| 2002OLIVETO09S | 0.55 | 0.22 | 13.91 | 1.65 | 467.27 | 0.38 | 0.79 | |
| 2002OLIVETO10S | 0.55 | 1.89 | 13.91 | 1.65 | 467.27 | 1.17 | 0.59 | |
| 2002OLIVETO11S | 3.30 | 3.95 | 52.90 | 0.42 | 15.17 | 4.99 | 0.83 | |
| 2002OLIVETO12S | 3.30 | 1.85 | 52.90 | 0.42 | 15.17 | 2.95 | 0.73 | |
| 2002OLIVETO13S | 3.30 | 0.96 | 52.90 | 0.42 | 15.17 | 1.00 | 0.84 | |
| 2002OLIVETO14S | 3.30 | 0.88 | 52.90 | 0.42 | 33.33 | 1.36 | 0.90 | |
| 2002OLIVETO15S | 3.30 | 46.88 | 52.90 | 0.42 | 33.33 | 0.96 | 0.87 | |
| 2002OLIVETO16S | 3.30 | 0.71 | 52.90 | 0.42 | 33.33 | 0.45 | 1.00 | |
| 2002OLIVETO17S | 3.30 | 2.71 | 52.90 | 0.42 | 33.33 | 0.90 | 0.77 | |
| 2002OLIVETO18S | 3.30 | 0.92 | 52.90 | 0.42 | 33.33 | 0.94 | 1.13 | |
| 2002OLIVETO19S | 3.30 | 0.88 | 52.90 | 0.42 | 77.88 | 0.58 | 0.70 | |
| 2002OLIVETO20S | 3.30 | 0.96 | 52.90 | 0.42 | 77.88 | 0.19 | 0.84 | |
| 2002OLIVETO21S | 3.30 | 2.92 | 52.90 | 0.42 | 77.88 | 0.16 | 0.66 | |
| 2002OLIVETO22S | 4.80 | 0.95 | 121.42 | 1.65 | 13.23 | 2.41 | 0.94 | |
| 2002OLIVETO23S | 4.80 | 0.92 | 121.42 | 1.65 | 13.23 | 3.19 | 0.73 | |
| 2002OLIVETO24S | 4.80 | 0.95 | 121.42 | 1.65 | 13.23 | 2.42 | 0.84 | |
| 2002OLIVETO25S | 4.80 | 0.76 | 121.42 | 1.65 | 13.23 | 1.58 | 0.68 | |
| 2002OLIVETO26S | 4.80 | 0.92 | 121.42 | 1.65 | 22.92 | 0.85 | 0.98 | |
| 2002OLIVETO27S | 4.80 | 0.59 | 121.42 | 1.65 | 22.92 | 0.87 | 0.74 | |
| 2002OLIVETO28S | 4.80 | 1.13 | 121.42 | 1.65 | 53.54 | 0.18 | 0.97 | |
| 2002OLIVETO29S | 4.80 | 0.10 | 121.42 | 1.65 | 53.54 | 0.20 | 0.75 | |
| 2002OLIVETO30S | 4.80 | 1.87 | 121.42 | 1.65 | 53.54 | 0.21 | 0.54 | |
| 2002OLIVETO31S | 4.80 | 0.46 | 121.42 | 1.65 | 104.17 | 0.12 | 0.68 | |
| 2002OLIVETO32S | 3.10 | 1.75 | 78.42 | 1.65 | 35.48 | 0.92 | 0.76 | |
| 2002OLIVETO33S | 3.10 | 0.13 | 78.42 | 1.65 | 35.48 | 0.78 | 1.14 | |
| 2005OLIVETO01U | 3.10 | 0.04 | 78.42 | 1.65 | 35.48 | 1.40 | 0.70 | |
| 2005OLIVETO02U | 3.10 | 0.03 | 78.42 | 1.65 | 35.48 | 1.57 | 0.76 | |
| 2005OLIVETO03U | 3.10 | 0.03 | 78.42 | 1.65 | 35.48 | 1.69 | 0.87 | |
| 2005OLIVETO04U | 3.10 | 0.02 | 78.42 | 1.65 | 35.48 | 1.53 | 0.81 | |
| 2005OLIVETO05U | 3.10 | 0.06 | 78.42 | 1.65 | 35.48 | 1.52 | 0.81 | |
| 2005OLIVETO06U | 3.10 | 0.05 | 78.42 | 1.65 | 35.48 | 1.45 | 0.84 | |
| Sheppard et al. [60] | 2004SHEPPARD01S | 0.22 | 3.71 | 5.57 | 1.65 | 518.18 | 10.44 | 0.91 |
| 2004SHEPPARD02S | 0.22 | 6.79 | 5.57 | 1.65 | 1386.36 | 3.90 | 0.97 | |
| 2004SHEPPARD03S | 0.80 | 15.00 | 20.24 | 1.65 | 1143.75 | 1.39 | 0.85 | |
| 2004SHEPPARD04S | 0.80 | 5.96 | 20.24 | 1.65 | 1143.75 | 0.95 | 0.87 | |
| 2004SHEPPARD05S | 0.80 | 3.67 | 20.24 | 1.65 | 381.25 | 4.16 | 0.83 | |
| 2004SHEPPARD06S | 0.80 | 1.71 | 20.24 | 1.65 | 142.50 | 11.14 | 0.87 | |
| 2004SHEPPARD07S | 2.90 | 7.83 | 73.36 | 1.65 | 315.52 | 1.33 | 0.90 | |
| 2004SHEPPARD08S | 2.90 | 13.75 | 73.36 | 1.65 | 315.52 | 0.61 | 0.84 | |
| 2004SHEPPARD09S | 2.90 | 18.67 | 73.36 | 1.65 | 315.52 | 0.32 | 0.83 | |
| 2004SHEPPARD10S | 2.90 | 25.67 | 73.36 | 1.65 | 315.52 | 0.19 | 0.76 | |
| 2004SHEPPARD11S | 0.22 | 24.17 | 5.57 | 1.65 | 4159.09 | 1.98 | 0.94 | |
| Grimaldi [61] | 2005GRIMALDI01S | 1.28 | 4.00 | 32.38 | 1.65 | 58.59 | 2.00 | 1.00 |
| 2005GRIMALDI02S | 0.86 | 6.16 | 21.75 | 1.65 | 104.65 | 2.78 | 1.00 | |
| 2005GRIMALDI03S | 0.86 | 6.09 | 21.75 | 1.65 | 139.53 | 2.08 | 1.00 | |
| Alabi [62] | 2006ALABI01S | 0.53 | 3.29 | 13.41 | 1.65 | 216.98 | 2.00 | 0.89 |
| 2006ALABI02S | 0.53 | 2.04 | 13.41 | 1.65 | 137.74 | 2.05 | 0.89 | |
| 2006ALABI03S | 0.53 | 22.13 | 13.41 | 1.65 | 216.98 | 2.00 | 0.70 | |
| Simarro et al. [63] | 2011SIMARRO01S | 0.86 | 34.90 | 21.75 | 1.65 | 87.21 | 2.13 | 0.88 |
| 2011SIMARRO02S | 0.86 | 45.60 | 21.75 | 1.65 | 93.02 | 2.00 | 0.94 | |
| 2011SIMARRO03S | 1.28 | 29.73 | 32.38 | 1.65 | 62.50 | 2.00 | 0.93 | |
| 2011SIMARRO04S | 1.28 | 24.85 | 32.38 | 1.65 | 58.59 | 2.00 | 0.93 | |
| 2011SIMARRO05S | 1.28 | 28.99 | 32.38 | 1.65 | 49.22 | 2.06 | 0.93 | |
| Meyering [64] | 2012MEYERING01S | 0.20 | 10.00 | 5.06 | 1.65 | 150.00 | 3.33 | 1.00 |
| 2012MEYERING02S | 0.80 | 10.00 | 20.24 | 1.65 | 37.50 | 3.33 | 1.00 | |
| 2012MEYERING03S | 1.60 | 10.00 | 40.47 | 1.65 | 18.75 | 3.33 | 1.00 | |
| 2012MEYERING04S | 2.50 | 10.00 | 63.24 | 1.65 | 12.00 | 3.33 | 1.00 | |
| 2012MEYERING05S | 2.60 | 10.00 | 40.66 | 0.39 | 11.54 | 3.33 | 1.00 | |
| 2012MEYERING06S | 2.70 | 10.00 | 19.77 | 0.04 | 11.11 | 3.33 | 1.00 | |
| 2012MEYERING07S | 2.00 | 0.42 | 17.64 | 0.07 | 12.50 | 13.20 | 1.00 | |
| 2012MEYERING08S | 2.00 | 0.42 | 17.64 | 0.07 | 25.00 | 6.60 | 1.00 | |
| 2012MEYERING09S | 2.00 | 0.42 | 17.64 | 0.07 | 35.00 | 4.71 | 1.00 | |
| Lança et al. [65] | 2013LANÇA01S | 0.86 | 7.08 | 21.75 | 1.65 | 127.91 | 0.50 | 0.97 |
| 2013LANÇA02S | 0.86 | 7.00 | 21.75 | 1.65 | 186.05 | 0.50 | 0.97 | |
| 2013LANÇA03S | 0.86 | 7.08 | 21.75 | 1.65 | 232.56 | 0.50 | 0.97 | |
| 2013LANÇA04S | 0.86 | 7.00 | 21.75 | 1.65 | 290.70 | 0.50 | 0.97 | |
| 2013LANÇA05S | 0.86 | 9.29 | 21.75 | 1.65 | 366.28 | 0.50 | 0.93 | |
| 2013LANÇA06S | 0.86 | 12.75 | 21.75 | 1.65 | 406.98 | 0.50 | 1.00 | |
| 2013LANÇA07S | 0.86 | 12.00 | 21.75 | 1.65 | 465.12 | 0.50 | 0.96 | |
| 2013LANÇA08S | 0.86 | 7.00 | 21.75 | 1.65 | 58.14 | 1.00 | 0.97 | |
| 2013LANÇA09S | 0.86 | 7.00 | 21.75 | 1.65 | 87.20 | 1.00 | 0.97 | |
| 2013LANÇA10S | 0.86 | 7.00 | 21.75 | 1.65 | 127.91 | 1.00 | 0.97 | |
| 2013LANÇA11S | 0.86 | 11.88 | 21.75 | 1.65 | 186.05 | 1.00 | 0.95 | |
| 2013LANÇA12S | 0.86 | 10.88 | 21.75 | 1.65 | 232.60 | 1.00 | 0.96 | |
| 2013LANÇA13S | 0.86 | 10.96 | 21.75 | 1.65 | 290.70 | 1.00 | 0.98 | |
| 2013LANÇA14S | 0.86 | 7.75 | 21.75 | 1.65 | 366.30 | 1.00 | 0.98 | |
| 2013LANÇA15S | 0.86 | 12.13 | 21.75 | 1.65 | 407.00 | 1.00 | 0.97 | |
| 2013LANÇA16S | 0.86 | 9.33 | 21.75 | 1.65 | 465.10 | 1.00 | 0.95 | |
| 2013LANÇA17S | 0.86 | 7.00 | 21.75 | 1.65 | 58.14 | 1.50 | 0.97 | |
| 2013LANÇA18S | 0.86 | 7.00 | 21.75 | 1.65 | 87.21 | 1.51 | 0.97 | |
| 2013LANÇA19S | 0.86 | 10.04 | 21.75 | 1.65 | 127.91 | 1.50 | 0.96 | |
| 2013LANÇA20S | 0.86 | 11.13 | 21.75 | 1.65 | 186.05 | 1.41 | 1.00 | |
| 2013LANÇA21S | 0.86 | 10.92 | 21.75 | 1.65 | 232.56 | 1.50 | 0.98 | |
| 2013LANÇA22S | 0.86 | 9.21 | 21.75 | 1.65 | 290.70 | 1.50 | 0.96 | |
| 2013LANÇA23S | 0.86 | 7.08 | 21.75 | 1.65 | 58.14 | 2.00 | 0.97 | |
| 2013LANÇA24S | 0.86 | 7.04 | 21.75 | 1.65 | 87.21 | 2.00 | 0.97 | |
| 2013LANÇA25S | 0.86 | 9.00 | 21.75 | 1.65 | 127.91 | 2.00 | 1.00 | |
| 2013LANÇA26S | 0.86 | 13.75 | 21.75 | 1.65 | 186.05 | 1.88 | 0.98 | |
| 2013LANÇA27S | 0.86 | 9.13 | 21.75 | 1.65 | 232.56 | 2.00 | 0.95 | |
| 2013LANÇA28S | 0.86 | 7.00 | 21.75 | 1.65 | 58.14 | 2.50 | 0.97 | |
| 2013LANÇA29S | 0.86 | 7.96 | 21.75 | 1.65 | 87.21 | 2.51 | 0.96 | |
| 2013LANÇA30S | 0.86 | 7.67 | 21.75 | 1.65 | 127.91 | 2.50 | 0.98 | |
| 2013LANÇA31S | 0.86 | 13.04 | 21.75 | 1.65 | 186.05 | 2.34 | 0.96 | |
| 2013LANÇA32S | 0.86 | 7.21 | 21.75 | 1.65 | 58.14 | 3.00 | 0.96 | |
| 2013LANÇA33S | 0.86 | 8.21 | 21.75 | 1.65 | 87.21 | 3.00 | 1.00 | |
| 2013LANÇA34S | 0.86 | 7.04 | 21.75 | 1.65 | 127.91 | 3.00 | 0.96 | |
| 2013LANÇA35S | 0.86 | 7.08 | 21.75 | 1.65 | 58.14 | 4.00 | 0.96 | |
| 2013LANÇA36S | 0.86 | 13.08 | 21.75 | 1.65 | 87.21 | 4.00 | 0.98 | |
| 2013LANÇA37S | 0.86 | 9.88 | 21.75 | 1.65 | 58.14 | 5.00 | 1.00 | |
| 2013LANÇA38S | 0.86 | 13.13 | 21.75 | 1.65 | 87.21 | 5.00 | 0.96 | |
| Link et al. [22] | 2017LINK01U | 0.36 | 0.25 | 9.11 | 1.65 | 416.67 | 1.53 | 0.87 |
| 2017LINK02U | 0.36 | 1.78 | 9.11 | 1.65 | 416.67 | 1.60 | 0.99 | |
| Pizarro et al. [21] | 2017PIZARRO01S | 0.36 | 3.59 | 9.11 | 1.65 | 416.67 | 1.47 | 0.91 |
| 2017PIZARRO02S | 0.36 | 5.97 | 9.11 | 1.65 | 416.67 | 1.53 | 0.75 | |
| 2017PIZARRO01U | 0.36 | 0.09 | 9.11 | 1.65 | 416.67 | 1.47 | 0.91 | |
| 2017PIZARRO02U | 0.36 | 0.09 | 9.11 | 1.65 | 416.67 | 1.47 | 0.91 | |
| 2017PIZARRO03U | 0.36 | 0.06 | 9.11 | 1.65 | 416.67 | 1.47 | 0.91 | |
| 2017PIZARRO04U | 0.36 | 0.07 | 9.11 | 1.65 | 416.67 | 1.47 | 0.91 | |
| 2017PIZARRO05U | 0.36 | 0.07 | 9.11 | 1.65 | 416.67 | 1.47 | 0.91 | |
| 2017PIZARRO06U | 0.36 | 0.11 | 9.11 | 1.65 | 416.67 | 1.43 | 0.78 |
| Calibration Run | Model Parameter λ | RMSE (cm) |
|---|---|---|
| 2005OLIVETO01U | 486.63 | 0.27 |
| 2005OLIVETO02U | 152.57 | 0.39 |
| 2005OLIVETO03U | 105.38 | 0.52 |
| 2005OLIVETO04U | 134.38 | 0.40 |
| 2005OLIVETO05U | 246.28 | 0.34 |
| 2005OLIVETO06U | 195.47 | 0.52 |
| 2017PIZARRO01U | 2008.72 | 0.31 |
| 2017PIZARRO02U | 1790.95 | 0.19 |
| 2017PIZARRO03U | 2254.77 | 0.29 |
| 2017PIZARRO04U | 1973.89 | 0.28 |
| 2017PIZARRO05U | 1976.10 | 0.28 |
| 2017PIZARRO06U | 1678.92 | 0.13 |
| 2002OLIVETO32S | 280.9 | 0.76 |
| 2017PIZARRO01S | 1078.86 | 0.40 |
| Experimental Run | RMSE (cm) | |
|---|---|---|
| Steady Calibration | Unsteady Calibration | |
| 2005OLIVETO01U | 0.94 | 0.27 |
| 2005OLIVETO02U | 1.17 | 0.39 |
| 2005OLIVETO03U | 0.63 | 0.52 |
| 2005OLIVETO04U | 1.57 | 0.40 |
| 2005OLIVETO05U | 1.09 | 0.34 |
| 2005OLIVETO06U | 0.83 | 0.52 |
| 2017PIZARRO01U | 0.73 | 0.31 |
| 2017PIZARRO02U | 0.71 | 0.19 |
| 2017PIZARRO03U | 0.80 | 0.29 |
| 2017PIZARRO04U | 0.82 | 0.28 |
| 2017PIZARRO05U | 0.89 | 0.28 |
| 2017PIZARRO06U | 0.42 | 0.13 |
| Minimum | 0.42 | 0.13 |
| Maximum | 1.57 | 0.52 |
| Average | 0.88 | 0.33 |
| Author | Number of Runs | Range of Selected Dimensionless Parameters | ||
|---|---|---|---|---|
| Chiew (1984) | 8 | 9.91–166.37 | 6.03–80.41 | |
| Ettema (1980) | 85 | 3.67–624.84 | 6.03–196.00 | |
| Ettema and others (2006) | 4 | 60.96–229.62 | 26.39–26.39 | |
| Graf (1995) | 3 | 47.61–71.41 | 52.77–52.77 | |
| Jones (unpublished) | 8 | 30.36–505.97 | 7.54–125.64 | |
| Melville (1997) | 4 | 19.81–31.24 | 20.10–20.10 | |
| Melville and Chiew (1999) | 9 | 39.69–73.03 | 24.12–24.12 | |
| Sheppard and others (2004) | 8 | 142.49–4159.13 | 5.53–72.87 | |
| Calibration Run | Model Parameter λ | 2017LINK01U | 2017LINK02U | |
|---|---|---|---|---|
| RMSE (cm) | RMSE (cm) | |||
| Steady calibration | 2017PIZARRO01S | 1078.86 | 0.35 | 0.81 |
| Unsteady calibration | 2017LINK01U and 2017LINK02U, respectively | 1391.84 and 1284.06, respectively | 0.21 | 0.32 |
| BRISENT estimated | --- | 1362.06 | 0.72 | 2.01 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pizarro, A.; Samela, C.; Fiorentino, M.; Link, O.; Manfreda, S. BRISENT: An Entropy-Based Model for Bridge-Pier Scour Estimation under Complex Hydraulic Scenarios. Water 2017, 9, 889. https://doi.org/10.3390/w9110889
Pizarro A, Samela C, Fiorentino M, Link O, Manfreda S. BRISENT: An Entropy-Based Model for Bridge-Pier Scour Estimation under Complex Hydraulic Scenarios. Water. 2017; 9(11):889. https://doi.org/10.3390/w9110889
Chicago/Turabian StylePizarro, Alonso, Caterina Samela, Mauro Fiorentino, Oscar Link, and Salvatore Manfreda. 2017. "BRISENT: An Entropy-Based Model for Bridge-Pier Scour Estimation under Complex Hydraulic Scenarios" Water 9, no. 11: 889. https://doi.org/10.3390/w9110889
APA StylePizarro, A., Samela, C., Fiorentino, M., Link, O., & Manfreda, S. (2017). BRISENT: An Entropy-Based Model for Bridge-Pier Scour Estimation under Complex Hydraulic Scenarios. Water, 9(11), 889. https://doi.org/10.3390/w9110889









