Greedy Algorithms for Sensor Location in Sewer Systems
Abstract
:1. Introduction
2. Methodology
2.1. Design Objectives
2.1.1. Detection Time (D)
2.1.2. Reliability (R)
2.1.3. Joint Entropy (JH)
2.1.4. Total Correlation (TC)
2.2. The Proposed Procedures
2.3. Fitness Function Evaluation
3. Results and Discussion
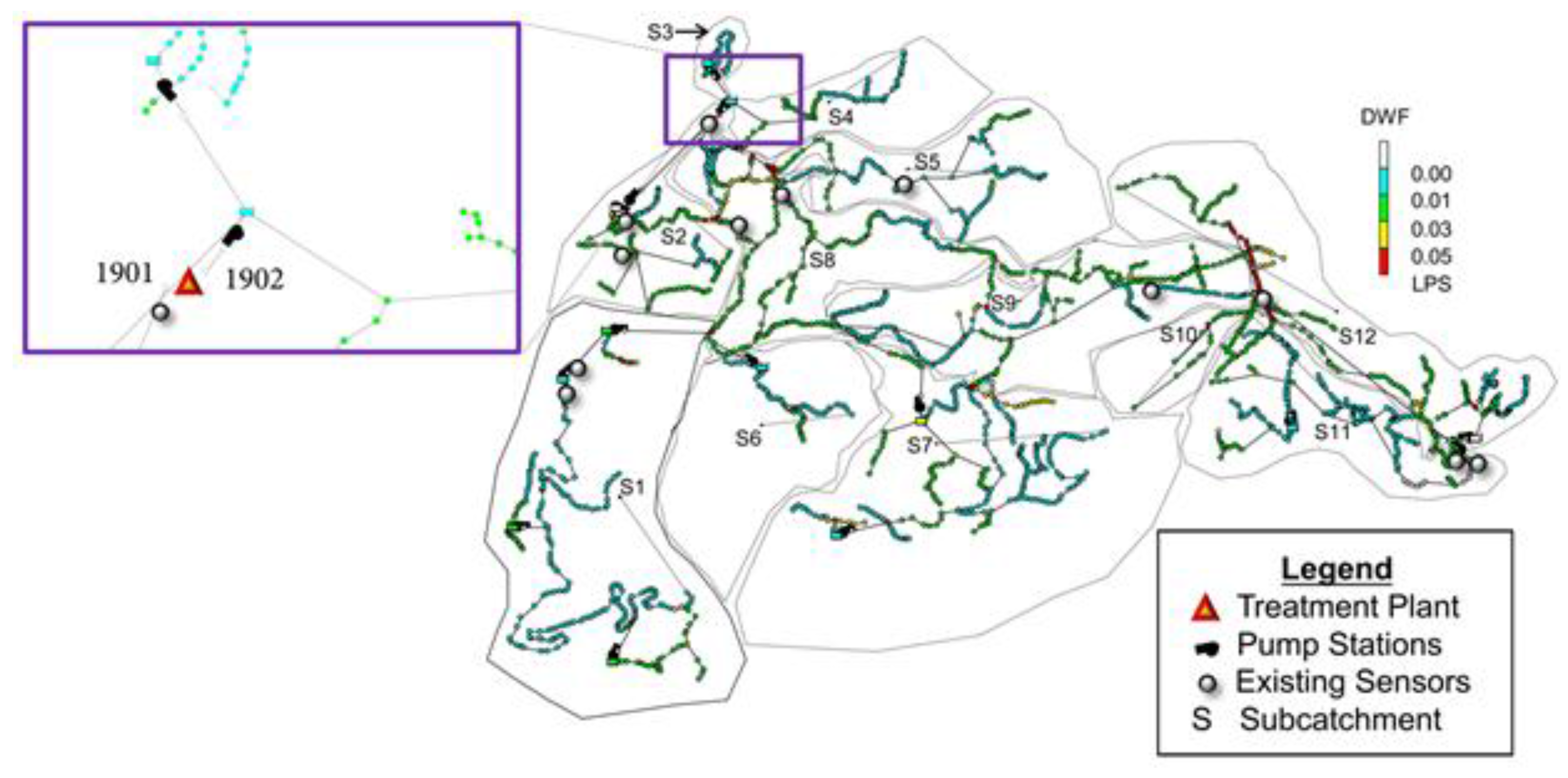
3.1. Case Study
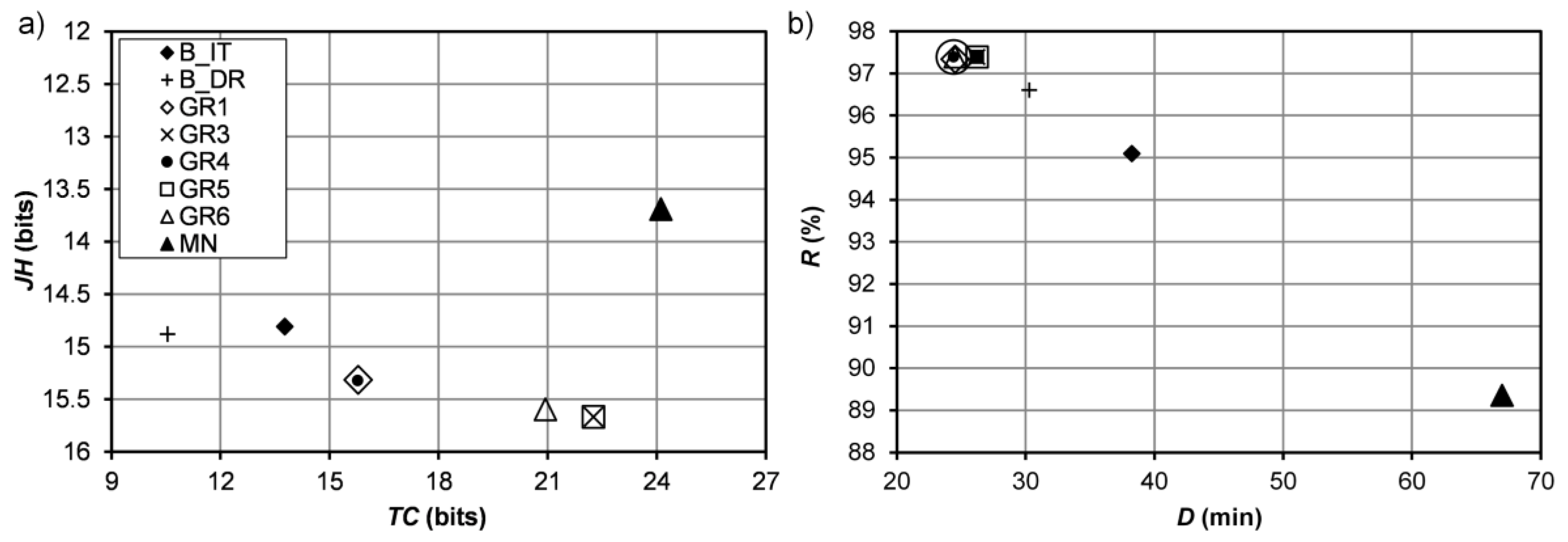
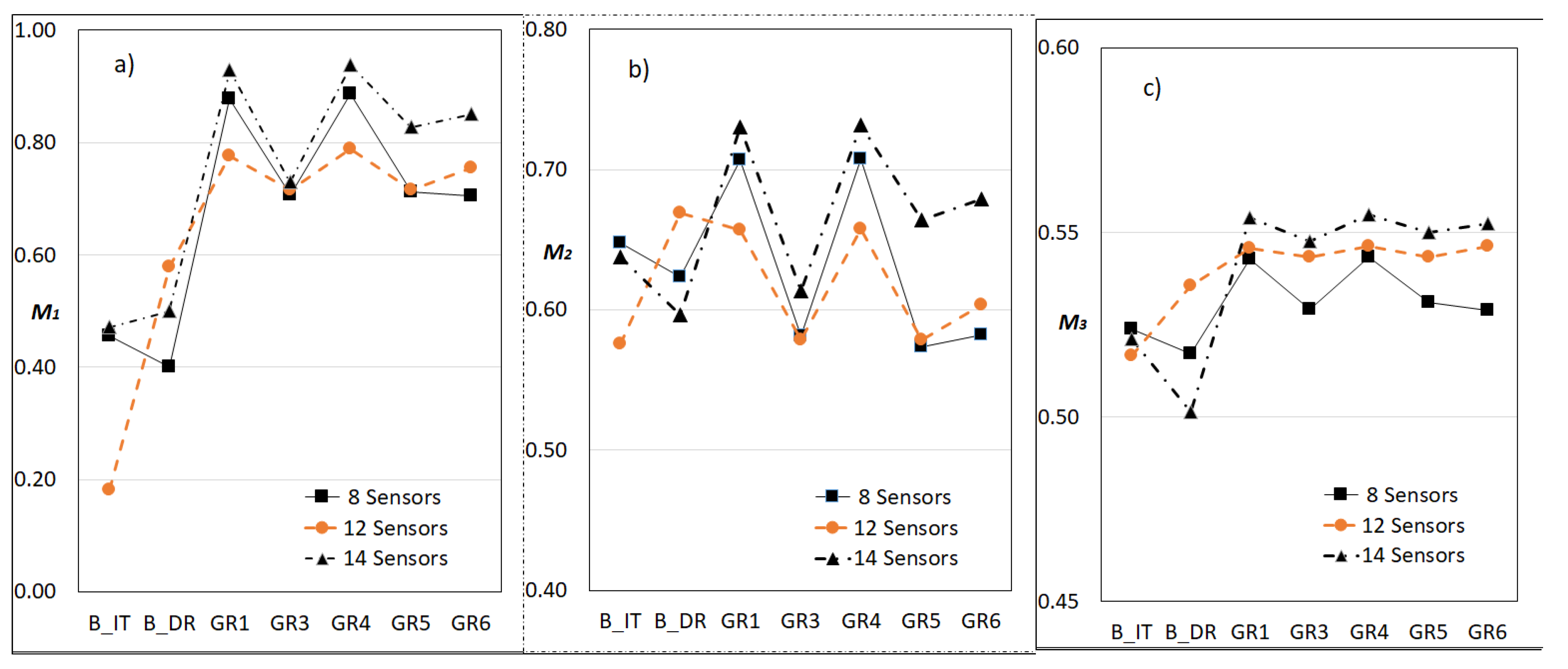
3.2. Procedures’ Comparison
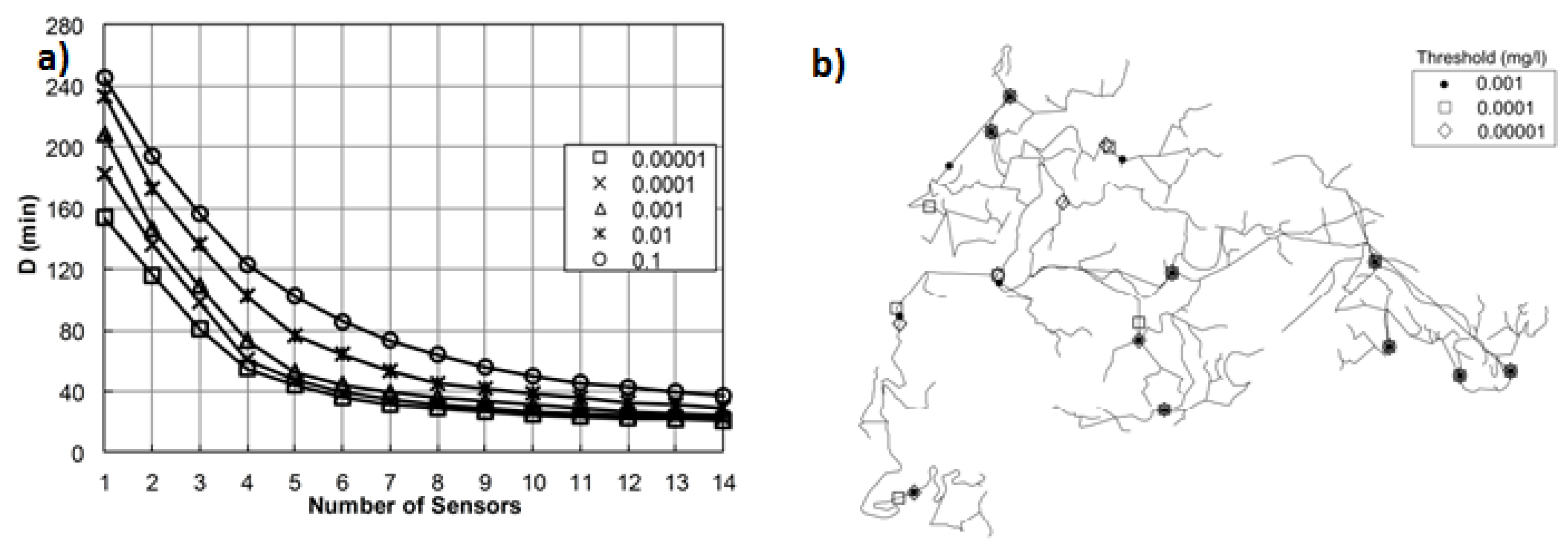
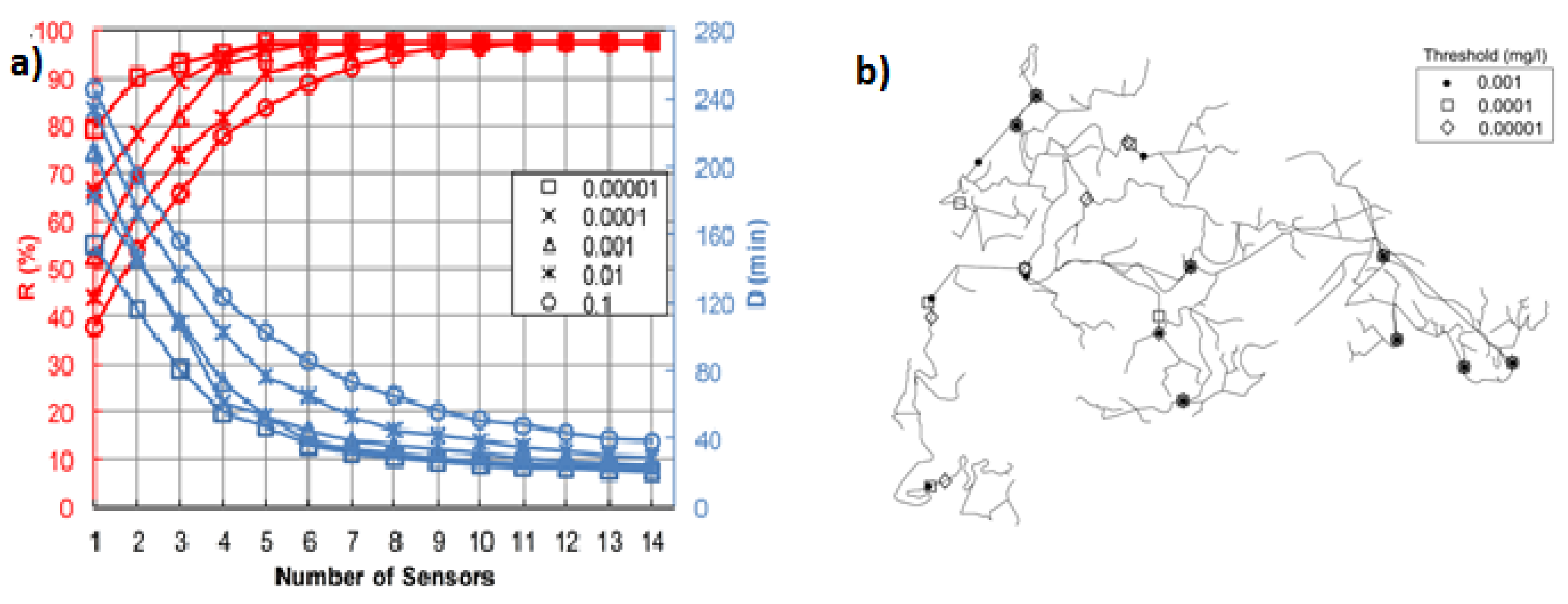
3.3. Detection Threshold Influence
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Falconer, R.A. Global water security: An introduction. Sci. Parliam. 2011, 68, 34–36. [Google Scholar]
- Pouet, M.F.; Thomas, O.; Marcoux, G. Quality survey of wastewater discharges. In Wastewater Quality Monitoring and treAtment; Quevauviller, P., Thomas, O., Van der Beken, A., Eds.; J. Wiley & Sons: Chichester, UK, 2006; pp. 275–288. [Google Scholar]
- Field, R.; Pitt, R.; Lalor, M.; Brown, M.; Vilkelis, W.; Phackston, E. Investigation of dry-weather pollutant entries into storm-drainage systems. J. Environ. Eng. 1994, 120, 1044–1066. [Google Scholar] [CrossRef]
- Irvine, K.; Rossi, M.C.; Vermette, S.; Bakert, J.; Kleinfelder, K. Illicit discharge detection and elimination: Low cost options for source identification and track down in stormwater systems. Urban Water J. 2011, 8, 379–395. [Google Scholar] [CrossRef]
- Bourgeois, W.; Burgess, J.E.; Stuetz, R.M. On-line monitoring of wastewater quality: A review. J. Chem. Technol. Biotechnol. 2001, 76, 337–348. [Google Scholar] [CrossRef]
- Llopart-Mascaró, A.; Gil, A.; Cros, J.; Alarcón, F. Guidelines for on-line monitoring of wastewater and stormwater quality. In Proceedings of the 11th International Conference on Urban Drainage, Edinburgh, Scotland, UK, 31 August–5 September 2008. [Google Scholar]
- Banik, B.K.; Di Cristo, C.; Leopardi, A. A pre-screening procedure for pollution source identification in sewer systems. Procedia Eng. 2015, 119C, 360–369. [Google Scholar] [CrossRef]
- Banik, B.K.; Di Cristo, C.; Leopardi, A.; de Marinis, G. Illicit intrusion characterization in sewer systems. Urban Water J. 2017, 14, 416–426. [Google Scholar] [CrossRef]
- Alfonso, L.; He, L.; Lobbrecht, A.; Price, R. Information theory applied to evaluate the discharge monitoring network of the Magdalena River. J. Hydoinform. 2013, 15, 211–228. [Google Scholar] [CrossRef]
- Ridolfi, E.; Alfonso, L.; Di Baldassarre, G.; Dottori, F.; Russo, F.; Napolitano, F. An entropy approach for the optimization of cross-section spacing for river modelling. Hydrol. Sci. J. 2013, 59, 126–137. [Google Scholar] [CrossRef]
- Alfonso, L.; Lobbrecht, A.; Price, R. Information theory based approach for location of monitoring water level gauges in polders. Water Resour. Res. 2010, 46, W03528. [Google Scholar] [CrossRef]
- Aral, M.M.; Guan, J.; Maslia, M.L. Optimal Design of Sensor Placement in Water Distribution Networks. J. Water Resour. Plan. Manag. 2010, 136, 5–18. [Google Scholar] [CrossRef]
- Moss, M.E.; Tasker, G.D. Intercomparison of hydrological network-design technologies. Hydrol. Sci. J. 1991, 36, 209–221. [Google Scholar] [CrossRef]
- Davar, Z.K.; Brimley, W.A. Hydrometric network evaluation: Audit approach. J. Water Resour. Plan. Manag. 1990, 116, 134–146. [Google Scholar] [CrossRef]
- Telci, I.T.; Nam, K.; Guan, J.; Aral, M.M. Optimal water quality monitoring network design for river systems. J. Environ. Manag. 2009, 90, 2987–2998. [Google Scholar] [CrossRef] [PubMed]
- Chacon-Hurtado, J.C.; Alfonso, L.; Solomatine, D.P. Rainfall and streamflow sensor network design: A review of applications, classification, and a proposed framework. Hydrol. Earth Syst. Sci. 2017, 21, 3071–3091. [Google Scholar] [CrossRef]
- Rathi, S.; Gupta, R. Sensor placement methods for contamination detection in water distribution networks: A review. Procedia Eng. 2014, 89, 181–188. [Google Scholar] [CrossRef]
- Dorini, G.; Jonkergouw, P.; Kapelan, Z.; Savic, D. SLOTS: Effective algorithm for sensor placement in water distribution systems. J. Water Resour. Plan. Manag. 2010, 136, 620–628. [Google Scholar] [CrossRef]
- Rathi, S.; Gupta, R. A simple sensor placement approach for regular monitoring and contamination detection in in water distribution networks. KSCE J. Civ. Eng. 2016, 20, 597–608. [Google Scholar] [CrossRef]
- Preis, A.; Ostfeld, A. Multiobjective contaminant sensor network design for water distribution systems. J. Water Resour. Plan. Manag. 2008, 134, 366–377. [Google Scholar] [CrossRef]
- Weickgenannt, M.; Kapelan, Z.; Blokker, M.; Savic, D.A. Risk based sensor placement for contaminant detection in water distribution systems. J. Water Resour. Plan. Manag. 2010, 136, 629–636. [Google Scholar] [CrossRef]
- Shen, H.; McBean, E. Pareto optimality for sensor placements in a water distribution system. J. Water Resour. Plan. Manag. 2011, 137, 243–248. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evolut. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Banik, B.K.; Alfonso, L.; Torres, A.S.; Mynett, A.; Di Cristo, C.; Leopardi, A. Optimal placement of water quality monitoring stations in sewer systems: An information theory approach. Procedia Eng. 2015, 119, 1308–1317. [Google Scholar] [CrossRef]
- Banik, B.K.; Alfonso, L.; Di Cristo, C.; Leopardi, A.L.; Mynett, A. Evaluation of different formulations to optimally locate pollution sensors in sewer systems. J. Water Resour. Plan. Manag. 2017, 143. Available online: http://ascelibrary.org/doi/abs/10.1061/%28ASCE%29WR.1943-5452.0000778 (accessed on 31 March 2017). [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Ostfeld, A.; Salomons, E. Optimal layout of early warning detection stations for water distribution systems security. J. Water Resour. Plan. Manag. 2004, 130, 377–385. [Google Scholar] [CrossRef]
- International Electrotechnical Commission. International Electrotechnical Commission; IEC 80000–13:2008; IEC: Geneva, Switzerland, 2013. [Google Scholar]
- Markus, M.; Vernon, K.H.; Tasker, G.D. Entropy and generalized least square methods in assessment of the regional value of stream gages. J. Hydrol. 2003, 283, 107–121. [Google Scholar] [CrossRef]
- Alfonso, L.; Lobbrecht, A.; Price, R. Optimization of water level monitoring network in polder systems using information theory. Water Resour. Res. 2010, 46, W12553. [Google Scholar] [CrossRef]
- McGill, W.J. Multivariate information transmission. Psychometrika 1954, 19, 97–116. [Google Scholar] [CrossRef]
- Watanabe, S. Information theoretical analysis of multivariate correlation. IBM J. Res. Dev. 1960, 4, 66–82. [Google Scholar] [CrossRef]
- Greco, S.; Zaniolo, C. Greedy algorithms in Datalog. Theor. Pract. Log. Prog. 2001, 1, 381–407. [Google Scholar] [CrossRef]
- Tallam, S.; Gupta, N. A concept analysis inspired greedy algorithm for test suite minimization. In CM SIGSOFT Software Engineering Notes; ACM: New York, NY, USA, 2005; Volume 31, pp. 35–42. [Google Scholar]
- Kumar, R.; Moseley, B.; Vassilvitskii, S.; Vattani, A. Fast greedy algorithms in mapreduce and streaming. In Proceedings of the Twenty-Fifth Annual ACM Symposium on Parallelism in Algorithms and Architectures, Montreal, QC, Canada, 23–25 July 2013; pp. 1–10. [Google Scholar]
- Rieckermann, J.L.; Neumann, M.; Ort, C.; Huisman, J.L.; Gujer, W. Dispersion coefficients of sewers from tracer experiments. Water Sci. Technol. 2005, 52, 123–133. [Google Scholar] [PubMed]
- Banik, B.K.; Di Cristo, C.; Leopardi, A. SWMM5 toolkit development for pollution source identification in sewer systems. Procedia Eng. 2014, 89, 750–757. [Google Scholar] [CrossRef]
- Cozzolino, L.; Della Morte, R.; Palumbo, A.; Pianese, D. Stochastic approaches for sensors placement against intentional contaminations in water distribution systems. Civ. Eng. Environ. Syst. 2011, 28, 75–98. [Google Scholar] [CrossRef]
| Procedure | GR1 | GR2 | GR3 | GR4 | GR5 | GR6 | B_IT | B_DR |
|---|---|---|---|---|---|---|---|---|
| Algorithm | GR_S | GR_S | GR_S | GR_M | GR_M | GR_M | NSGA-II | NSGA-II |
| Objectives | D | R | JH | D, R | JH, TC | D, R, JH, TC | JH, TC | D, R |
| C-Time (s) | 1.4 | 2.6 | 5200.4 | 3.8 | 2460.7 | 5205.3 | 143,415.2 | 1812.0 |
| Procedures | All |
|---|---|
| Number of sensors | From 1 to 14 |
| Detection threshold (mg/L) | 0.1, 0.01, 0.001, 0.0001, 0.00001 |
| Detection Threshold (mg/L) | 0.00001 | 0.0001 | 0.001 | 0.01 | 0.1 |
|---|---|---|---|---|---|
| JHsys (bits) | 16.74 | 16.71 | 16.64 | 16.40 | 15.70 |
| TCsys (bits) | 1895.16 | 1601.84 | 1270.35 | 948.65 | 685.80 |
| Procedure | 8 Sensors | 12 Sensors | 14 Sensors | ||||||
|---|---|---|---|---|---|---|---|---|---|
| M1 | M2 | M3 | M1 | M2 | M3 | M1 | M2 | M3 | |
| B_IT | 0.4552 | 0.6476 | 0.5237 | 0.1811 | 0.5757 | 0.5165 | 0.4715 | 0.6380 | 0.5212 |
| B_DR | 0.4000 | 0.6236 | 0.5172 | 0.5795 | 0.6690 | 0.5356 | 0.5000 | 0.5960 | 0.5013 |
| GR1 | 0.8777 | 0.7067 | 0.5429 | 0.7772 | 0.6566 | 0.5458 | 0.9293 | 0.7303 | 0.5540 |
| GR3 | 0.7073 | 0.5816 | 0.5292 | 0.7167 | 0.5785 | 0.5433 | 0.7301 | 0.6134 | 0.5476 |
| GR4 | 0.8867 | 0.7077 | 0.5433 | 0.7883 | 0.6578 | 0.5463 | 0.9378 | 0.7314 | 0.5547 |
| GR5 | 0.7132 | 0.5732 | 0.5309 | 0.7167 | 0.5785 | 0.5433 | 0.8277 | 0.6640 | 0.5501 |
| GR6 | 0.7057 | 0.5819 | 0.5289 | 0.7550 | 0.6033 | 0.5462 | 0.8509 | 0.6793 | 0.5523 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Banik, B.K.; Alfonso, L.; Di Cristo, C.; Leopardi, A. Greedy Algorithms for Sensor Location in Sewer Systems. Water 2017, 9, 856. https://doi.org/10.3390/w9110856
Banik BK, Alfonso L, Di Cristo C, Leopardi A. Greedy Algorithms for Sensor Location in Sewer Systems. Water. 2017; 9(11):856. https://doi.org/10.3390/w9110856
Chicago/Turabian StyleBanik, Bijit K., Leonardo Alfonso, Cristiana Di Cristo, and Angelo Leopardi. 2017. "Greedy Algorithms for Sensor Location in Sewer Systems" Water 9, no. 11: 856. https://doi.org/10.3390/w9110856
APA StyleBanik, B. K., Alfonso, L., Di Cristo, C., & Leopardi, A. (2017). Greedy Algorithms for Sensor Location in Sewer Systems. Water, 9(11), 856. https://doi.org/10.3390/w9110856





