Statistical and Fractal Approaches on Long Time-Series to Surface-Water/Groundwater Relationship Assessment: A Central Italy Alluvial Plain Case Study
Abstract
1. Introduction
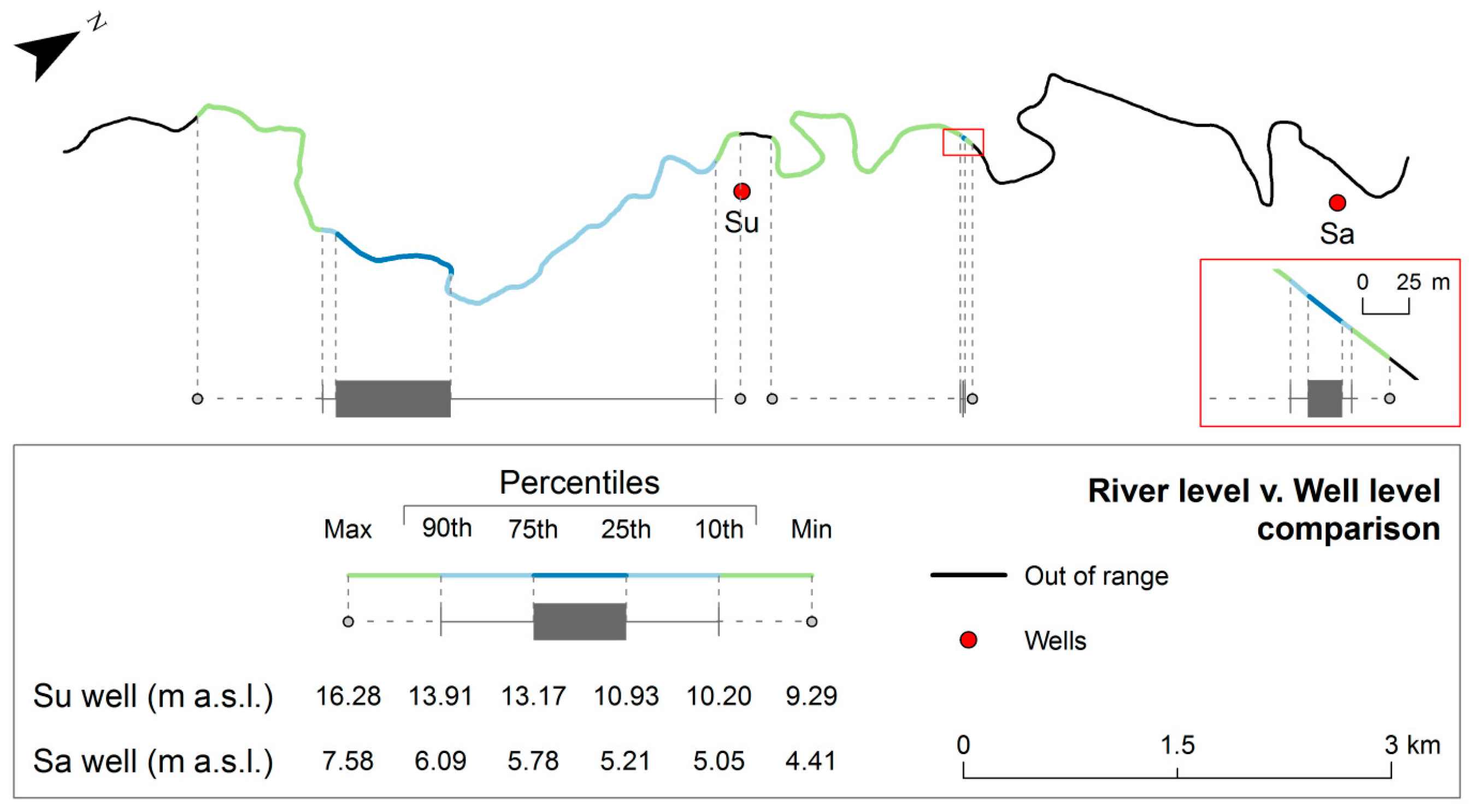
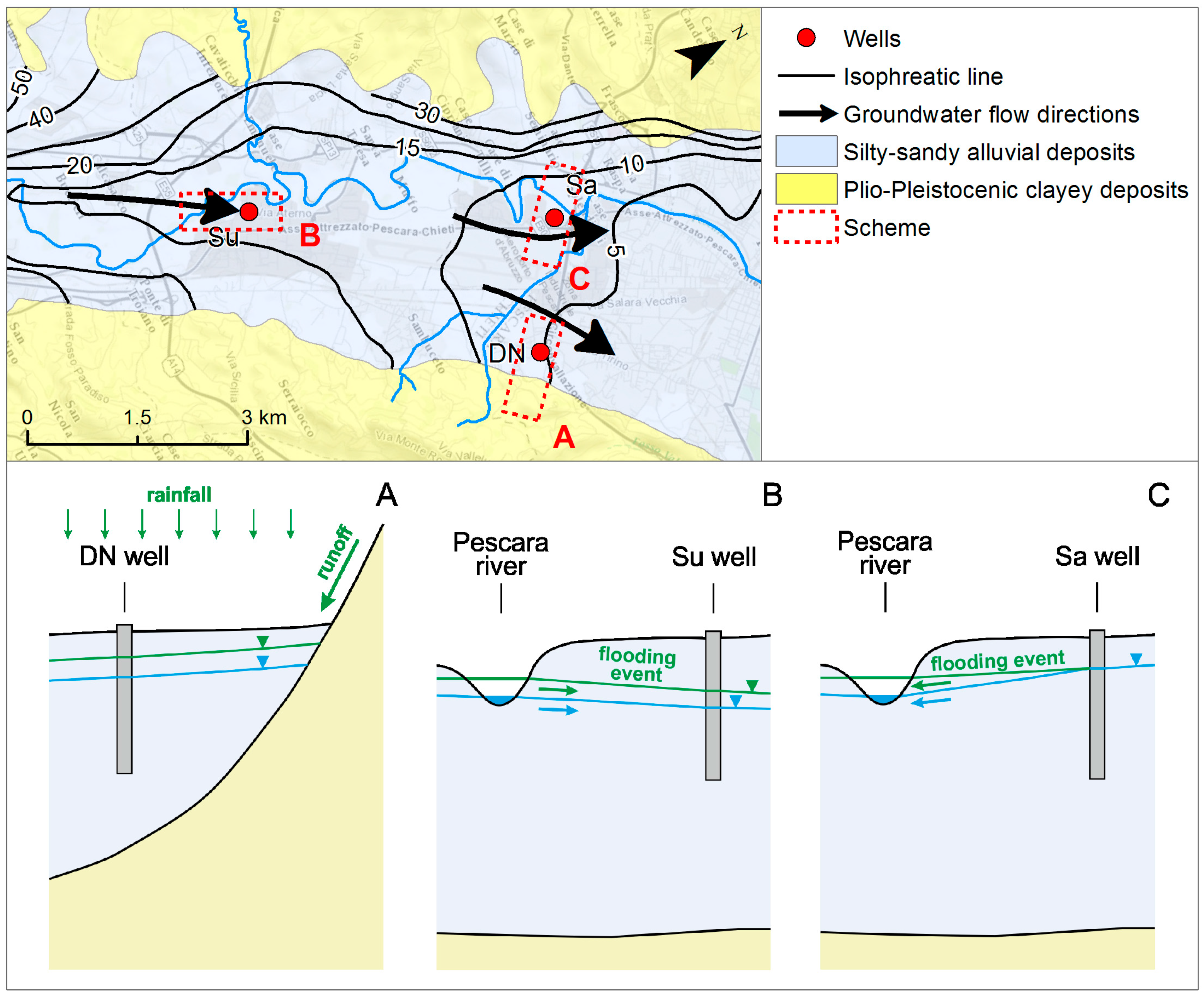
2. Study Area
3. Datasets
4. Methods
4.1. Analyses in Time Domain
4.1.1. Seasonal-Trend Decomposition Procedure Census I
4.1.2. The Autocorrelation Function
4.1.3. The Cross-Correlation Function
4.2. Analyses in Frequency Domain
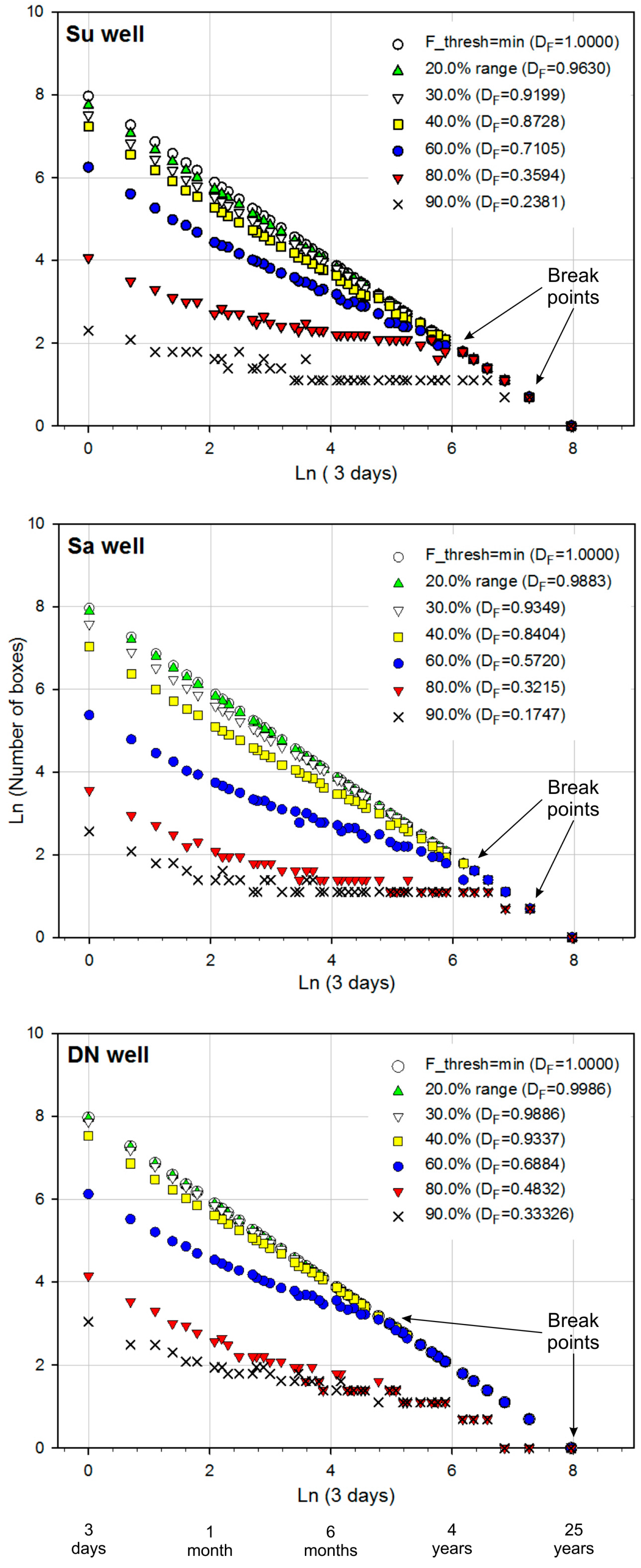
4.3. Fractal Analysis
5. Results
5.1. Descriptive Statistics
5.2. The Residual Analysis
5.3. Autocorrelation
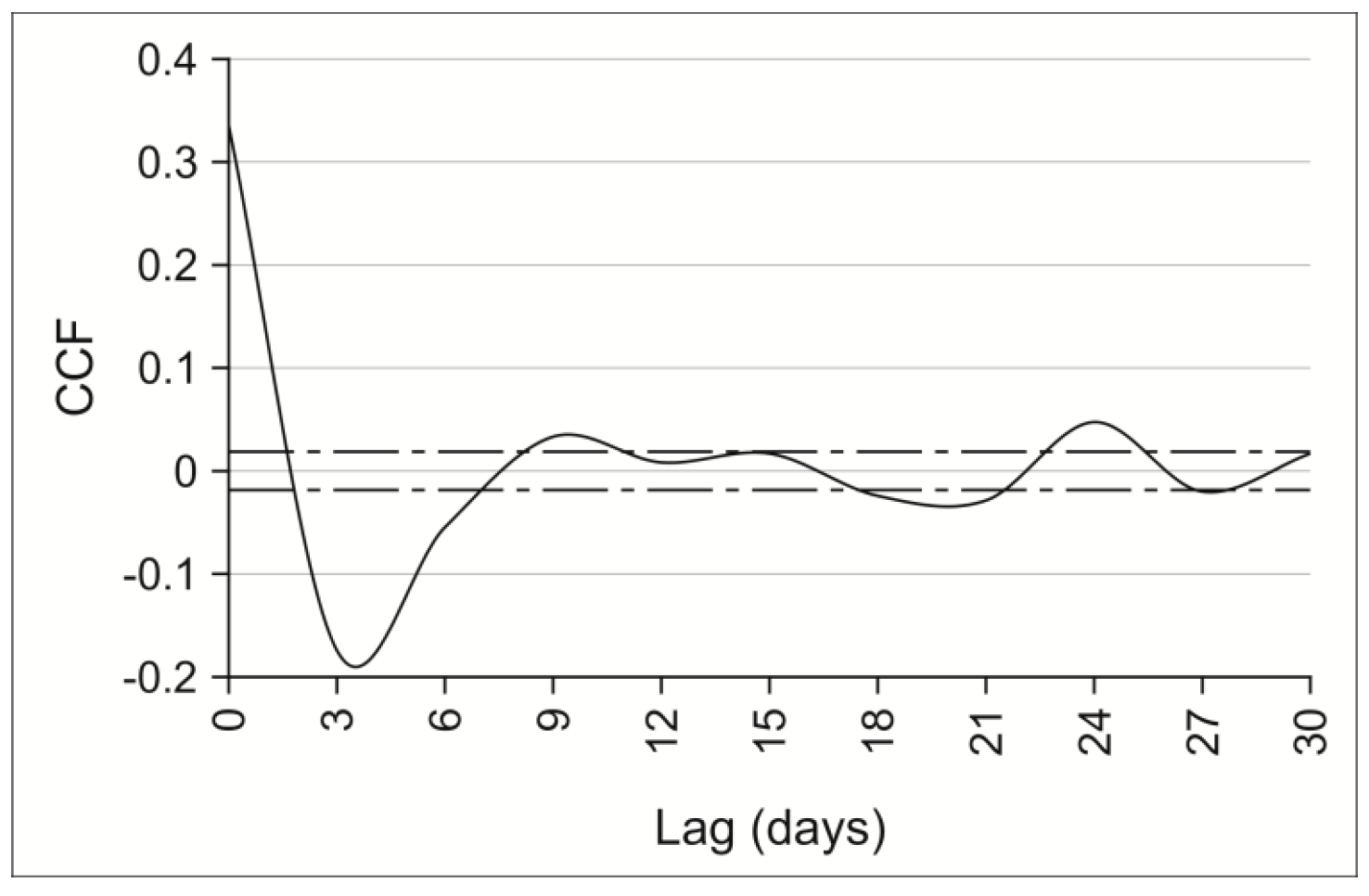
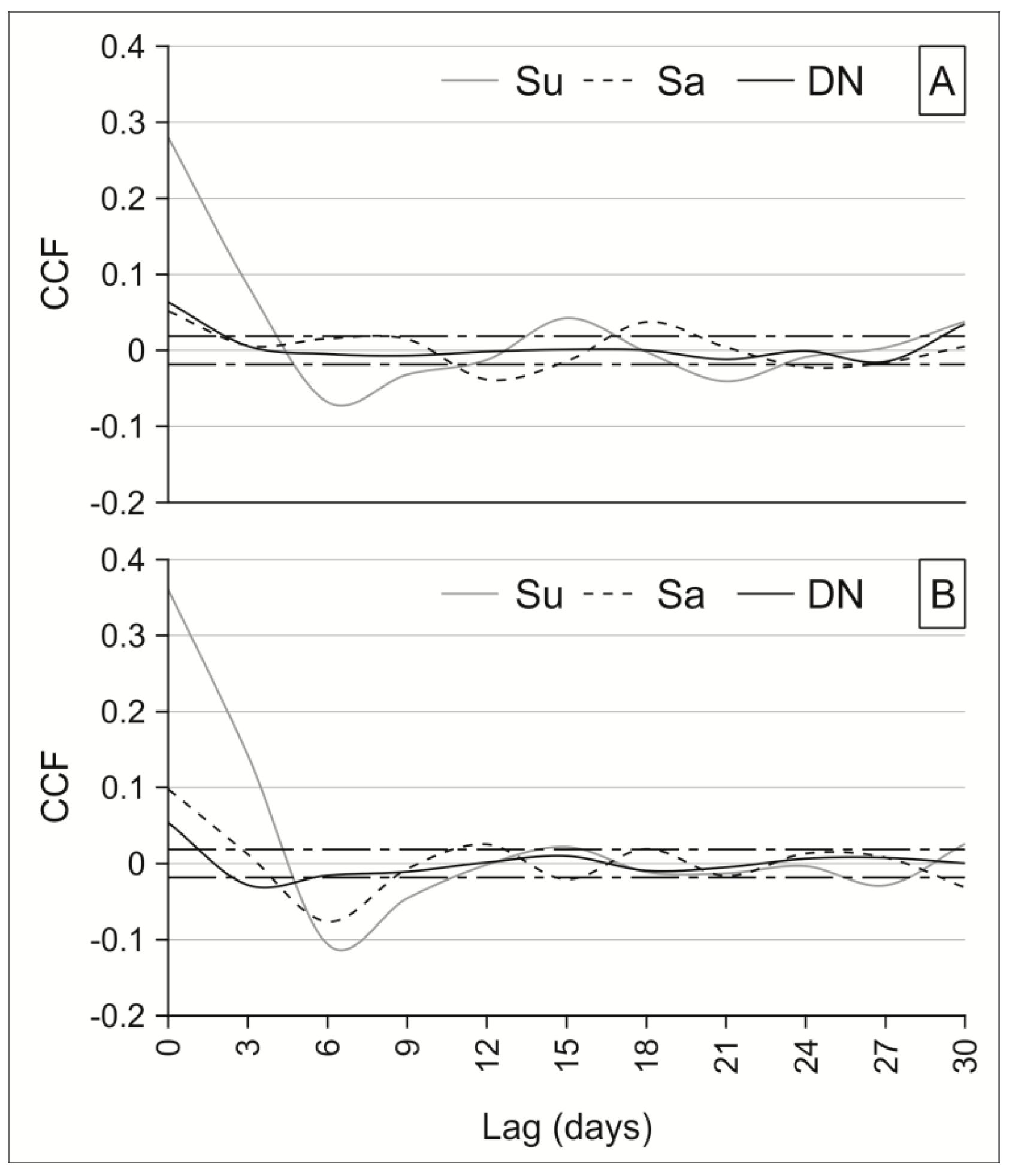
5.4. Raw Data Cross-Correlation
5.5. Residual Cross-Correlation
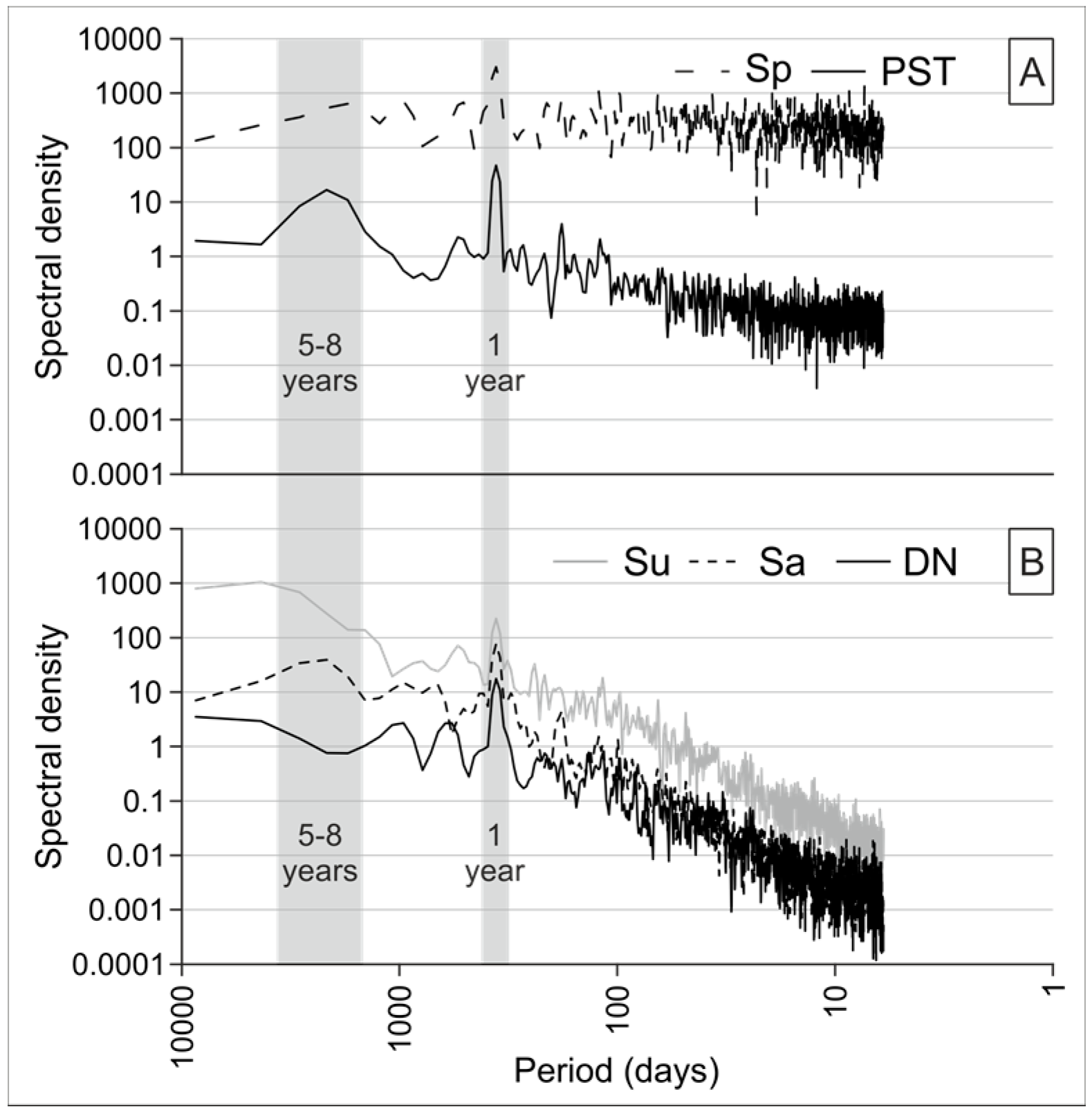
5.6. Spectral Analysis
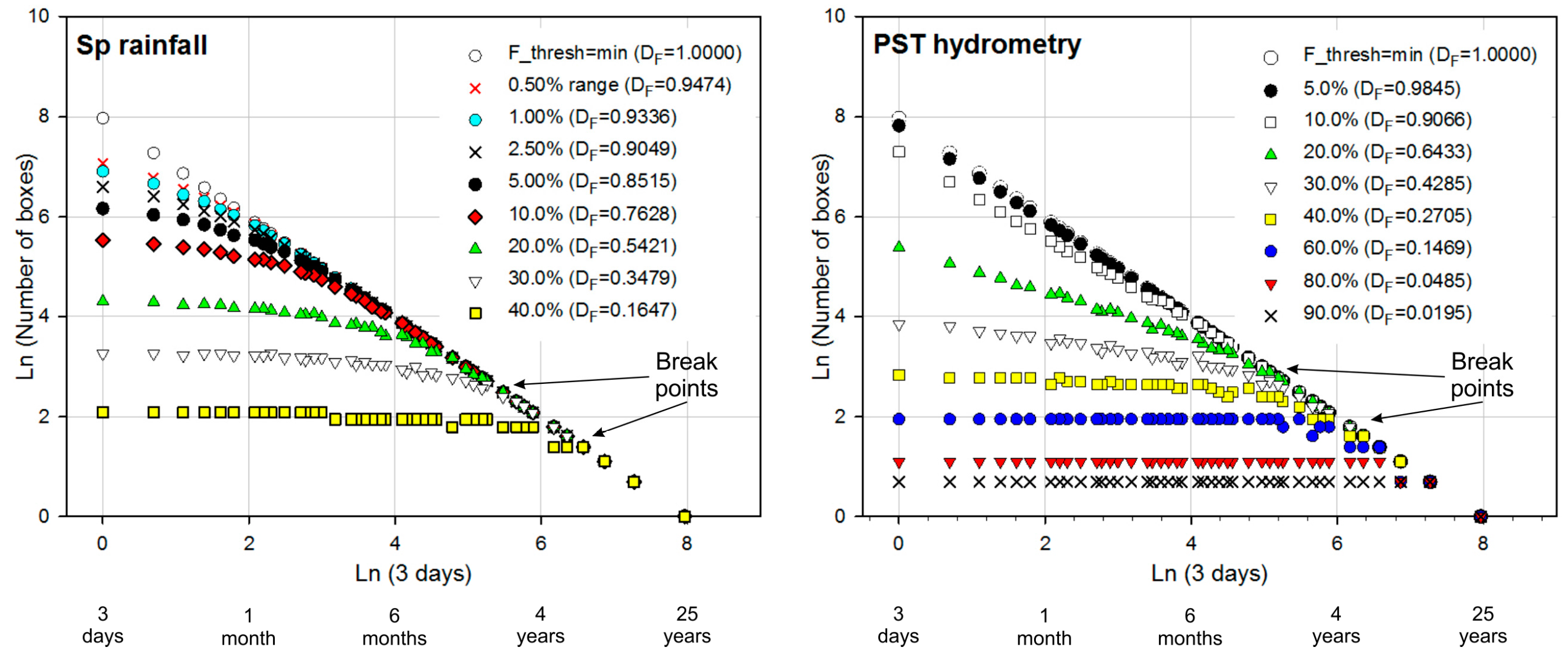
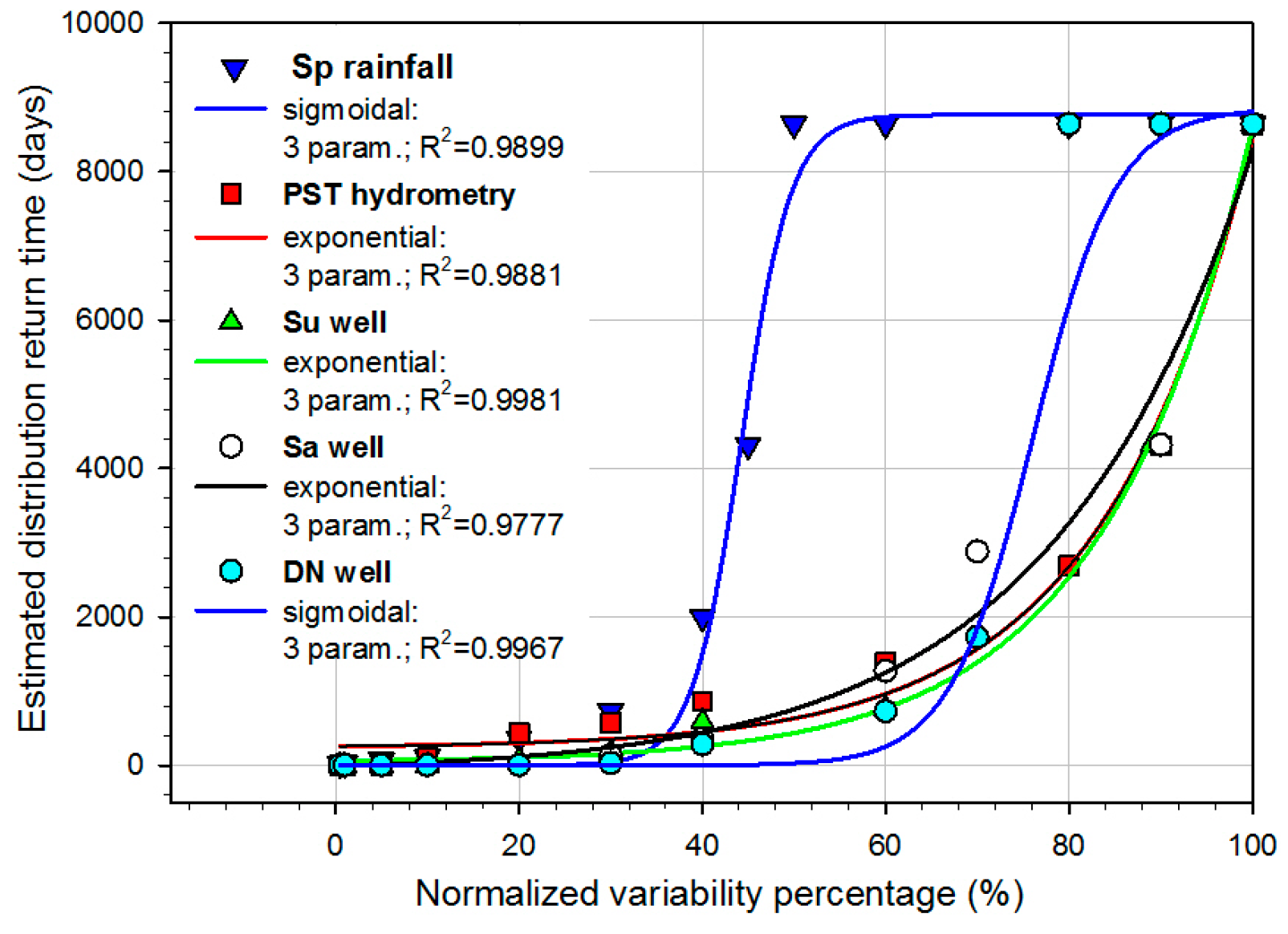
5.7. Cantor-Dust Fractal Analysis
6. Discussion
6.1. Analyses in Time Domain
6.2. Analyses in Frequency Domain
6.3. Fractal Analysis
6.4. Conceptual Model
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Mangin, A. Pour une meilleure connaissance des systemes hydrologiques à partir des analyses corrélatoire et spectrale. J. Hydrol. 1984, 67, 25–43. [Google Scholar] [CrossRef]
- Padilla, A.; Pulido-Bosch, A. Study of hydrographs of karstic aquifers by means of correlation and cross-spectral analysis. J. Hydrol. 1995, 168, 73–89. [Google Scholar] [CrossRef]
- Larocque, M.; Mangin, A.; Razack, M.; Banton, O. Contribution of correlation and spectral analyses to the regional study of a karst aquifer (Charente, France). J. Hydrol. 1998, 205, 217–231. [Google Scholar] [CrossRef]
- Thanh Tam, V.; De Smedt, F.; Batelaan, O.; Dassargues, A. Characterization of a cavern conduit system in Vietnam by time series correlation, cross-spectrum and wavelet analyses. Hydrol. Sci. J. 2004, 49, 879–900. [Google Scholar] [CrossRef]
- Panagopoulos, G.; Lambrakis, N. The contribution of time series analysis to the study of the hydrodynamic characteristics of the karst systems: Application on two typical karst aquifers of Greece (Trifilia, Almyros Crete). J. Hydrol. 2006, 329, 368–376. [Google Scholar] [CrossRef]
- Delbart, C.; Valdes, D.; Barbecot, F.; Tognelli, A.; Richon, P.; Couchoux, L. Temporal variability of karst aquifer response time established by the sliding-windows cross-correlation method. J. Hydrol. 2013, 511, 580–588. [Google Scholar] [CrossRef]
- Pasculli, A.; Audisio, C.; Lollino, G. Application of cellular automaton model for river morphological studies: CAESAR and the Pellice River (Piedmont, Italy). Rend. Online Soc. Geol. Ital. 2010, 11, 118–119. [Google Scholar]
- Pasculli, A.; Audisio, C.; Sciarra, N. Application of CAESAR for catchment and river evolution. Rend. Online Soc. Geol. Ital. 2015, 35, 224–227. [Google Scholar] [CrossRef]
- Audisio, C.; Pasculli, A.; Sciarra, N. Conceptual and numerical models applied on the river Pellice (North western Italy). In River Basins, Reservoir Sedimentation and Water Resources Engineering. Proceedings of the IAEG XII Congress; Springer International Publishing: Torino, Italy, 2015; Volume 3, pp. 327–330. [Google Scholar] [CrossRef]
- Pasculli, A.; Audisio, C. Cellular Automata modelling of fluvial evolution: Real and parametric numerical results comparison along river pellice (NW Italy). Environ. Model. Assess. 2015, 20, 425–441. [Google Scholar] [CrossRef]
- Cai, Z.; Ofterdinger, U. Analysis of groundwater-level response to rainfall and recharge estimates in fractured hard rock aquifers, NW Ireland. J. Hydrol. 2016, 535, 71–84. [Google Scholar] [CrossRef]
- Misstear, B.D.R.; Brown, L.; Johnston, P.M. Estimation of groundwater recharge in a major sand and gravel aquifer in Ireland using multiple approaches. Hydrogeol. J. 2009, 17, 693–706. [Google Scholar] [CrossRef]
- Polemio, M. Il Regime Della Falda Costiera Ionica di Metaponto. In Proceedings of the Third Conference of Geotechnical Engineering Researchers, “Il Ruolo dei Fluidi nei Problemi di Ingegneria Geotecnica”, Mondovì (Cuneo-Italy), Italy, 6–7 September 1994; pp. 135–149. Available online: www.earth-prints.org/bitstream/2122/6025/1/falda-metaponto.pdf (accessed on 15 October 2017).
- Lee, J.Y.; Lee, K.K. Use of hydrologic time series data for identification of recharge mechanism in a fractured bedrock aquifer system. J. Hydrol. 2000, 229, 190–201. [Google Scholar] [CrossRef]
- Polemio, M.; Dragone, V. Gli effetti antropici e climatici sulla disponibilità delle acque sotterranee della piana ionico-lucana. In Proceedings of the First National Congress—Italian Association of Applied and Environmental Geology, Chieti, Italy, 19–20 February 2003. [Google Scholar]
- Luque-Espinar, J.A.; Chica-Olmo, M.; Pardo-Igùzquiza, E.; Garcìa-Soldado, M.J. Influence of climatological cycles on hydraulic heads across a Spanish aquifer. J. Hydrol. 2008, 354, 35–52. [Google Scholar] [CrossRef]
- Cozzolino, M.; Piscopo, V.; Scarelli, A.; Summa, G. Analisi delle serie temporali dei dati di precipitazione e portata per la determinazione della portata sostenibile di un pozzo funzionante a carico costante. Ital. J. Eng. Geol. Environ. 2010, 2, 41–50. [Google Scholar] [CrossRef]
- Duvert, C.; Jourde, H.; Raiber, M.; Cox, M.E. Correlation and spectral analyses to assess the response of a shallow aquifer to low and high frequency rainfall fluctuations. J. Hydrol. 2010, 527, 894–907. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. The Fractal Geometry of Nature; Macmillan: New York, NY, USA, 1983. [Google Scholar]
- Turcotte, D.L. Fractal and Chaos in Geology and Geophysics; Cambridge University Press: New York, NY, USA, 1997. [Google Scholar]
- Yu, X.; Ghasemizadeh, R.; Padilla, I.Y.; Kaeli, D.; Alshawabkeh, A. Patterns of temporal scaling of groundwater level fluctuation. J. Hydrol. 2016, 536, 485–495. [Google Scholar] [CrossRef]
- Radziejewiski, M.; Kundzewicz, Z. Fractal analysis of flow of the river Warta. J. Hydrol. 1997, 200, 280–294. [Google Scholar] [CrossRef]
- Mazzarella, A. The time clustering of floodings in Venice and the Cantor dust method. Theor. Appl. Climatol. 1998, 59, 147–150. [Google Scholar] [CrossRef]
- Mazzarella, A. Multifractal dynamic rainfall processes in Italy. Theor. Appl. Climatol. 1999, 63, 73–78. [Google Scholar] [CrossRef]
- Casnedi, R. L’avanfossa abruzzese fra i fiumi Vomano e Pescara nel Pliocene inf.: Rapporti fra sedimentazione e tettonica. Studi Geologici Camerti. 1991, 357–379. [Google Scholar]
- Centamore, E.; Bigi, S.; Berti, D.; Micarelli, A.; Morelli, C. Nuovi dati sui depositi neogenici di avanfossa del Pescarese. Boll. Soc. Geol. Ital. 1992, 111, 437–447. [Google Scholar]
- D’Alessandro, L.; Miccadei, E.; Piacentini, T. Morphostructural elements of central–eastern Abruzzi: Contributions to the study of the role of tectonics on the morphogenesis of the Apennine chain. Quat. Int. 2003, 101–102, 115–124. [Google Scholar] [CrossRef]
- Parlagreco, L.; Miccadei, E.; Antonioli, F.; Gianolla, D.; Devoti, D.; Leoni, G.; Silenzi, S. New data on Holocene relative sea level along the Abruzzo coast (central Adriatic, Italy). Quat. Int. 2011, 232, 179–186. [Google Scholar] [CrossRef]
- Desiderio, G.; Nanni, T.; Rusi, S. La pianura alluvionale del fiume Pescara (Abruzzo): Idrogeologia e vulnerabilità dell’acquifero. Mem. Soc. Geol. Ital. 2001, 56, 197–211. [Google Scholar]
- Desiderio, G.; Nanni, T.; Rusi, S. La pianura del fiume Vomano (Abruzzo): Idrogeologia, antropizzazione e suoi effetti sul depauperamento della falda. Boll. Soc. Geol. Ital. 2003, 122, 421–434. [Google Scholar]
- Anibas, C.; Verbeiren, B.; Buis, K.; Chormanski, J.; De Doncker, L.; Okruszko, T.; Meire, P.; Batelaan, O. A hierarchical approach on groundwater-surface water interaction in wetlands along the upper Biebrza River, Poland. Hydrol. Earth Syst. Sci. 2012, 16, 2329–2346. [Google Scholar] [CrossRef]
- Boni, C.; Bono, P.; Capelli, G. Schema idrogeologico dell’Italia centrale. Mem. Soc. Geol. Ital. 1986, 35, 991–1012. [Google Scholar]
- Conese, M.; Nanni, T.; Peila, C.; Rusi, S.; Salvati, R. Idrogeologia della Montagna del Morrone (Appennino Abruzzese): Dati preliminari. Mem. Soc. Geol. Ital. 2001, 56, 181–196. [Google Scholar]
- Massoli-Novelli, R.; Petitta, M.; Salvati, R. La situazione idrogeologica e ambientale della Gole di Popoli (Abruzzo): Primi risultati e prospettive di ricerca. Mem. Soc. Geol. Ital. 1998, 53, 563–584. [Google Scholar]
- Nanni, T.; Rusi, S. Idrogeologia del massiccio carbonatico della montagna della Majella (Appennino centrale). Boll. Soc. Geol. Ital. 2003, 122, 173–202. [Google Scholar]
- Petitta, M.; Tallini, M. Idrodinamica sotterranea del massiccio del Gran Sasso (Abruzzo): Nuove indagini idrologiche, idrogeologiche e idrochimiche (1994–2001). Boll. Soc. Geol. Ital. 2001, 121, 343–363. [Google Scholar]
- Palmucci, W.; Rusi, S.; Di Curzio, D. Mobilisation processes responsible for iron and manganese contamination of groundwater in Central Adriatic Italy. Environ. Sci. Pollut. Res. 2016, 23, 11790–11805. [Google Scholar] [CrossRef] [PubMed]
- Palmucci, W.; Rusi, S. Boron-rich groundwater in Central Eastern Italy: A hydrogeochemical and statistical approach to define origin and distribution. Environ. Earth Sci. 2015, 72, 5139–5157. [Google Scholar] [CrossRef]
- Desiderio, G.; Folchi Vici D’Arcevia, C.; Nanni, T.; Rusi, S. Hydrogeological mapping of the highly anthropogenically influenced Peligna Valley intramontane basin (Central Italy). J. Maps. 2012, 8, 165–168. [Google Scholar] [CrossRef]
- Caschetto, M.; Barbieri, M.; Galassi, D.M.P.; Mastrorillo, L.; Rusi, S.; Stoch, F.; Di Cioccio, A.; Petitta, M. Human alteration of groundwater–surface water interactions (Sagittario River, Central Italy): Implication for flow regime, contaminant fate and invertebrate response. Environ. Earth Sci. 2014, 71, 1791–1807. [Google Scholar] [CrossRef]
- Desiderio, G.; Rusi, S.; Tatangelo, F. Caratterizzazione idrogeochimica delle acque sotterranee abruzzesi e relative anomalie. Ital. J. Geosci. 2010, 129, 207–222. [Google Scholar] [CrossRef]
- Jenkins, G.M.; Watts, D.G. Spectral Analysis and Its Applications; Holden Day: San Francisco, CA, USA, 1968. [Google Scholar]
- Chatfield, C. The Analysis of Time Series, 4th ed.; Chapman and Hall: London, UK, 1991. [Google Scholar]
- Box, G.E.P.; Jenkins, G.M.; Reinsel, G.C. Time Series Analysis: Forecasting and Control, 3rd ed.; Prentice Hall: Englewood Cliffs, NJ, USA, 1994. [Google Scholar]
- Massei, N.; Dupont, J.P.; Mahler, B.J.; Laignel, B.; Fournier, M.; Valdes, D.; Ogier, S. Investigating transport properties and turbidity dynamics of a karst aquifer using correlation, spectral, and wavelet analysis. J. Hydrol. 2006, 329, 244–257. [Google Scholar] [CrossRef]
- Fiorillo, F.; Doglioni, A. The relation between karst spring discharge and rainfall by cross-correlation analysis (Campania, southern Italy). Hydrogeol. J. 2010, 18, 1881. [Google Scholar] [CrossRef]
- Makridakis, S.G.; Wheelwright, S.C.; McGee, V.E. Forecasting: Methods and Applications, 2nd ed.; Wiley: New York, NY, USA, 1983. [Google Scholar]
- Makridakis, S.G.; Wheelwright, S.C. Forecasting Methods for Management, 5th ed.; Wiley: New York, NY, USA, 1989. [Google Scholar]
- Polemio, M.; Dragone, V. Serie storiche piezometriche delle unità idrogeologiche pugliesi: Regime piezometrico, effetti climatici ed antropici. Quad. Geol. Appl. 1999, 4, 153–162. [Google Scholar]
- Benavente, J.; Pulido-Bosch, A.; Mangin, A. Application of correlation and spectral procedures to the study of the discharge in a karstic system (Eastern Spain). In Proceedings of the Karst Water Resources Symposium, Ankara-Antalya, Turkey, 7–19 July 1985; IAHS: Wallingford, UK, 1985; Volume 161, pp. 67–75. [Google Scholar]
- Polemio, M.; Dragone, V.; Di Cagno, M. Effetti antropici e naturali sul degrado quantitativo delle acque sotterranee del Tavoliere. Quad. Geol. Appl. 1999, 4, 143–152. [Google Scholar]
- Bouchaou, L.; Mangin, A.; Chauve, P. Turbidity mechanism of water from a karstic spring: Example of the Ain Asserdoune spring (Beni Mellal Atlas, Morocco). J. Hydrol. 2002, 265, 34–42. [Google Scholar] [CrossRef]
- Imagawa, C.; Takeuchi, J.; Kawachi, T.; Chono, S.; Ishida, K. Statistical analyses and modeling approaches to hydrodynamic characteristics in alluvial aquifer. Hydrol. Process. 2013, 27, 4017–4027. [Google Scholar] [CrossRef]
- Amraoui, F.; Razack, M.; Bouchaou, L. Turbidity dynamics in karstic systems. Example of Ribaa and Bittit springs in the Middle Atlas (Morocco). Hydrol. Sci. J. 2003, 48, 971–984. [Google Scholar] [CrossRef]
- Diggle, P.D. Time Series: A Biostatistical Introduction; Oxford Statistical Science Series 5; Oxford Science Publications-Oxford University Press: Oxford, UK, 1990. [Google Scholar]
- Lee, L.J.E.; Lawrence, D.S.L.; Price, M. Analysis of water-level response to rainfall and implications for recharge pathways in the Chalk aquifer, SE England. J. Hydrol. 2006, 330, 604–620. [Google Scholar] [CrossRef]
- Delbart, C.; Valdes, D.; Barbecot, F.; Tognelli, A.; Couchoux, L. Spatial organization of the impulse response in a karst aquifer. J. Hydrol. 2016, 537, 18–26. [Google Scholar] [CrossRef]
- Acworth, R.I.; Rau, G.C.; McCallum, M.; Anderson, M.S.; Cuthbert, M.O. Understanding connected surface-water/groundwater systems using Fourier analysis of daily and sub-daily head fluctuations. Hydrogeol. J. 2015, 23, 143–159. [Google Scholar] [CrossRef]
- Andreo, B.; Jiménez, P.; Durán, J.J.; Carrasco, F.; Vadillo, I.; Mangin, A. Climatic and hydrological variations during the last 117–166 years in the south of the Iberian Peninsula, from spectral and correlation analyses and continuous wavelet analyses. J. Hydrol. 2005, 324, 24–39. [Google Scholar] [CrossRef]
- Gill, L.W.; Naughton, O.; Johnston, P.M.; Basu, B.; Ghosh, B. Characterisation of hydrogeological connections in a lowland karst network using time series analysis of water levels in ephemeral groundwater-fed lakes (turloughs). J. Hydrol. 2013, 499, 289–302. [Google Scholar] [CrossRef]
- Box, G.E.P.; Jenkins, G.M.; Reinsel, G.C. Time Series Analysis: Forecasting and Control, 4th ed.; Wiley: Hoboken, NJ, USA, 2008. [Google Scholar]
- Percival, D.B.; Walden, A.T. Spectral Analysis for Physical Applications: Multitaper and Conventional Univariate Techniques; Cambridge University Press: Cambridge, NY, USA, 1993. [Google Scholar]
- Rodriguez-Iturbe, I.; Rinaldo, A. Fractal River Basins: Chance and Self-Organization; Cambridge University Press: New York, NY, USA, 2001. [Google Scholar]
- Falconer, K.J. Fractal Geometry: Mathematical Foundations and Applications; John Wiley & Sons: New York, NY, USA, 1990. [Google Scholar]
- Zhou, X. Fractal and Multifractal Analysis of Runoff Time Series and Stream Networks in Agricultural Watersheds. Ph.D. Dissertation, Faculty of the Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, October 2004. [Google Scholar]
- Kantelhardt, J.W. Fractal and multifractal time series. In Encyclopedia of Complexity and Systems Science; Meyers, R.A., Ed.; Springer: New York, NY, USA, 2009; pp. 3754–3779. [Google Scholar]
- Svensson, C.; Olsson, J.; Berntsson, R. Multifractal properties of daily rainfall in two different climates. Water Resour. 1996, 32, 2463–2472. [Google Scholar] [CrossRef]
- Menabde, M.; Harris, D.; Seed, A.; Austin, G.; Stow, D. Multiscaling properties of rainfall and bounded random cascade. Water Resour. 1997, 33, 2823–2830. [Google Scholar] [CrossRef]
- Pandey, G.; Lovejoy, S.; Schertzer, D. Multifractal analysis of daily river flows including exstremes for basins of five to two million square kilometres, one day to 75 years. J. Hydrol. 1998, 208, 62–81. [Google Scholar] [CrossRef]
- Mazzarella, A.; Diodato, N. The alluvial events in the last two centuries at Sarno, Southern Italy: Their classification and power-law time-occurrence. Theor. Appl. Climatol. 2002, 72, 55–64. [Google Scholar] [CrossRef]
- Mazzarella, A.; Rapetti, F. Scale invariance laws in the recurrence interval of extreme floods: An application to the Upper Po River Valley (Northern Italy). J. Hydrol. 2004, 288, 264–271. [Google Scholar] [CrossRef]
- Hurst, H.E. The long term storage capacity of reservoirs. Trans. Am. Soc. Civ. Eng. 1951, 116, 770–808. [Google Scholar]
- Pasculli, A.; Sciarra, N. A fragile fracture study by fractal analysis. In Proceedings of the Annual Conference of the International Association for Mathematical Geology IAMG 2005, Toronto, ON, Canada, 21–26 August 2005. [Google Scholar]
- Liu, L.; Chen, X.; Xu, G.; Shu, L. Use of hydrologic time-series data for identification of hydrodynamic function and behavior in a karstic water system in China. Hydrogeol J. 2011, 19, 1577–1585. [Google Scholar] [CrossRef]
- Zhang, Y.; Schilling, K. Temporal scaling of hydraulic head and river base flow and its implication for groundwater recharge. Water Resour. Res. 2004, 40, W03504. [Google Scholar] [CrossRef]
- Shun, T.; Duffy, C.J. Low-frequency oscillations in precipitation, temperature, and runoff on a west facing mountain front: A hydrogeologic interpretation. Water Resour. Res. 1999, 35, 191–201. [Google Scholar] [CrossRef]
- Markovic, D.; Koch, M. Stream response to precipitation variability: A spectral view based on analysis and modelling of hydrological cycle components. Hydrol Process. 2015, 29, 1806–1816. [Google Scholar] [CrossRef]
- Zhang, Y.-K.; Li, Z. Temporal scaling of hydraulic head fluctuations: Nonstationary spectral analyses and numerical simulations. Water Resour. Res. 2005, 41, W07031. [Google Scholar] [CrossRef]
- Neves, M.C.; Costa, L.; Monteiro, J.P. Climatic and geologic controls on the piezometry of the Querença-Silves karst aquifer, Algarve (Portugal). Hydrogeol J. 2016, 24, 1015–1028. [Google Scholar] [CrossRef]
- Molénat, J.; Davy, P.; Gascuel-Odoux, C.; Durand, P. Study of three subsurface hydrologic systems based on spectral and cross-spectral analysis of time series. J. Hydrol. 1999, 222, 152–164. [Google Scholar] [CrossRef]
- Slimani, S.; Massei, N.; Mesquita, J. Combined climatic and geological forcings on the spatio-temporal variability of piezometric levels in the chalk aquifer of Upper Normandy (France) at pluridecennal scale. Hydrogeol. J. 2009, 17, 1823–1832. [Google Scholar] [CrossRef]
- Gámiz-Fortis, S.; Pozo-Vázquez, D.; Trigo, R.M.; Castro-Díez, Y. Quantifying the Predictability of Winter River Flow in Iberia. Part I: Interannual Predictability. J. Clim. 2008, 21, 2484–2502. [Google Scholar] [CrossRef]
- Labat, D. Cross wavelet analyses of annual continental freshwater discharge and selected climate. J. Hydrol. 2010, 385, 269–278. [Google Scholar] [CrossRef]
- Holman, I.P.; Rivas-Casado, M.; Bloomfield, J.P. Identifying non-stationary groundwater level response to North Atlantic ocean-atmosphere teleconnection patterns using wavelet coherence. Hydrogeol. J. 2011, 19, 1269–1279. [Google Scholar] [CrossRef]
- Tremblay, L.; Larocque, M.; Anctil, F.; Rivard, C. Teleconnections and interannual variability in Canadian groundwater levels. J. Hydrol. 2011, 410, 178–188. [Google Scholar] [CrossRef]
- El Janyani, S.; Massei, N.; Dupont, J.P.; Fournier, M.; Dörfliger, N. Hydrological responses of the chalk aquifer to the regional climatic signal. J. Hydrol. 2012, 464, 485–493. [Google Scholar] [CrossRef]
- Briciu, A.E.; Mihăilă, D. Wavelet analysis of some rivers in SE Europe and selected climate indices. Environ. Monit. Assess. 2014, 186, 6263–6286. [Google Scholar] [CrossRef] [PubMed]
- Probst, J.L.; Tardy, Y. Long range streamflow and world continental runoff fluctuations since the beginning of this century. J. Hydrol. 1987, 94, 289–311. [Google Scholar] [CrossRef]
- Labat, D. Oscillations in land surface hydrological cycle. Earth Planet. Sci. Lett. 2006, 242, 143–154. [Google Scholar] [CrossRef]
- Fendeková, M.; Pekárová, P.; Fendek, M.; Pekár, J.; Škoda, P. Global drivers effect in multi-annual variability of runoff. J. Hydrol. Hydromech. 2014, 62, 169–176. [Google Scholar] [CrossRef]
- Chiaudani, A.; Di Curzio, D.; Di Lena, B.; Palmucci, W.; Rusi, S. Preliminary analysis regarding long period rainfall-piezometric levels relationships in Abruzzo Region Peri-Adriatic area. In Proceedings of the Acts XIX Agrometeorology National Congress: New Adversities and New Services for Agroecosystems, Bologna, Italy, 14–16 June 2016. [Google Scholar]
- ISPRA-Istituto Superiore per la Protezione e la Ricerca Ambientale. Linee Guida per L’analisi e L’elaborazione Statistica di Base Delle Serie Storiche di Dati Idrologici; Manuali e Linee Guida 84/13; ISPRA: Roma, Italy, 2013.
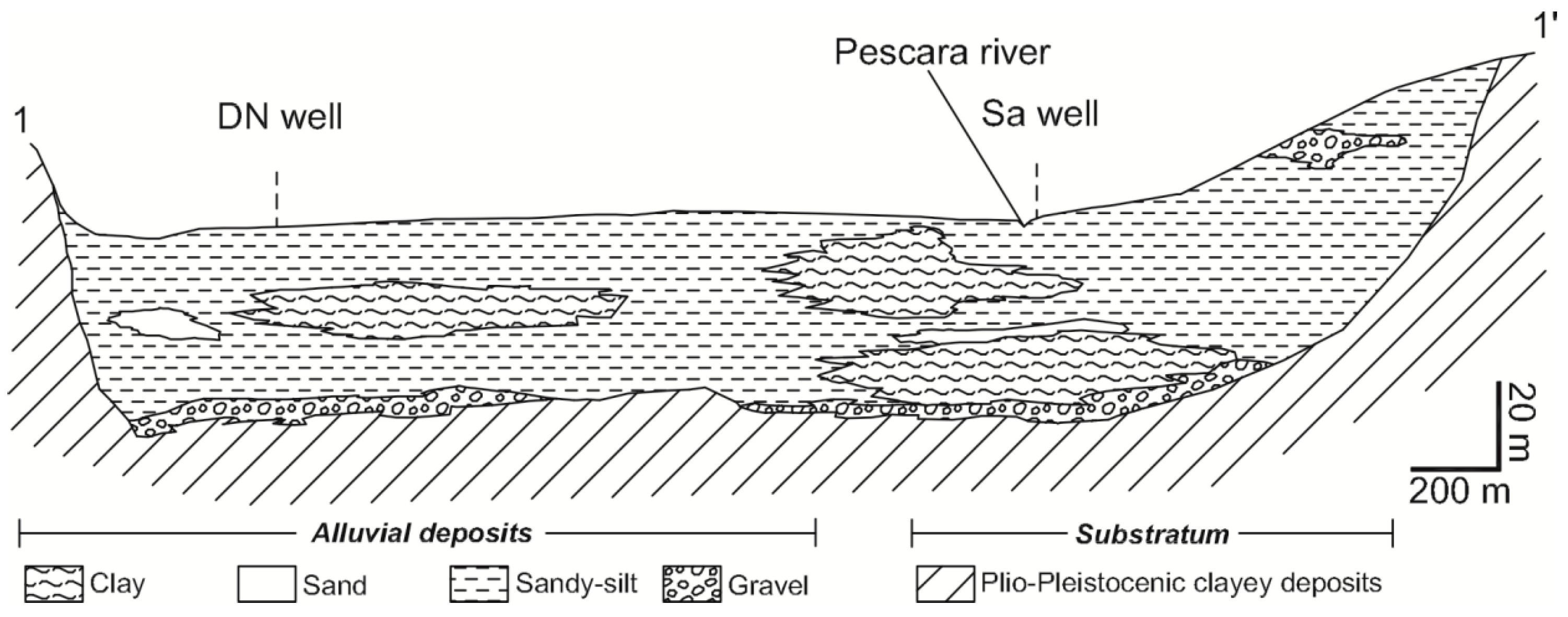
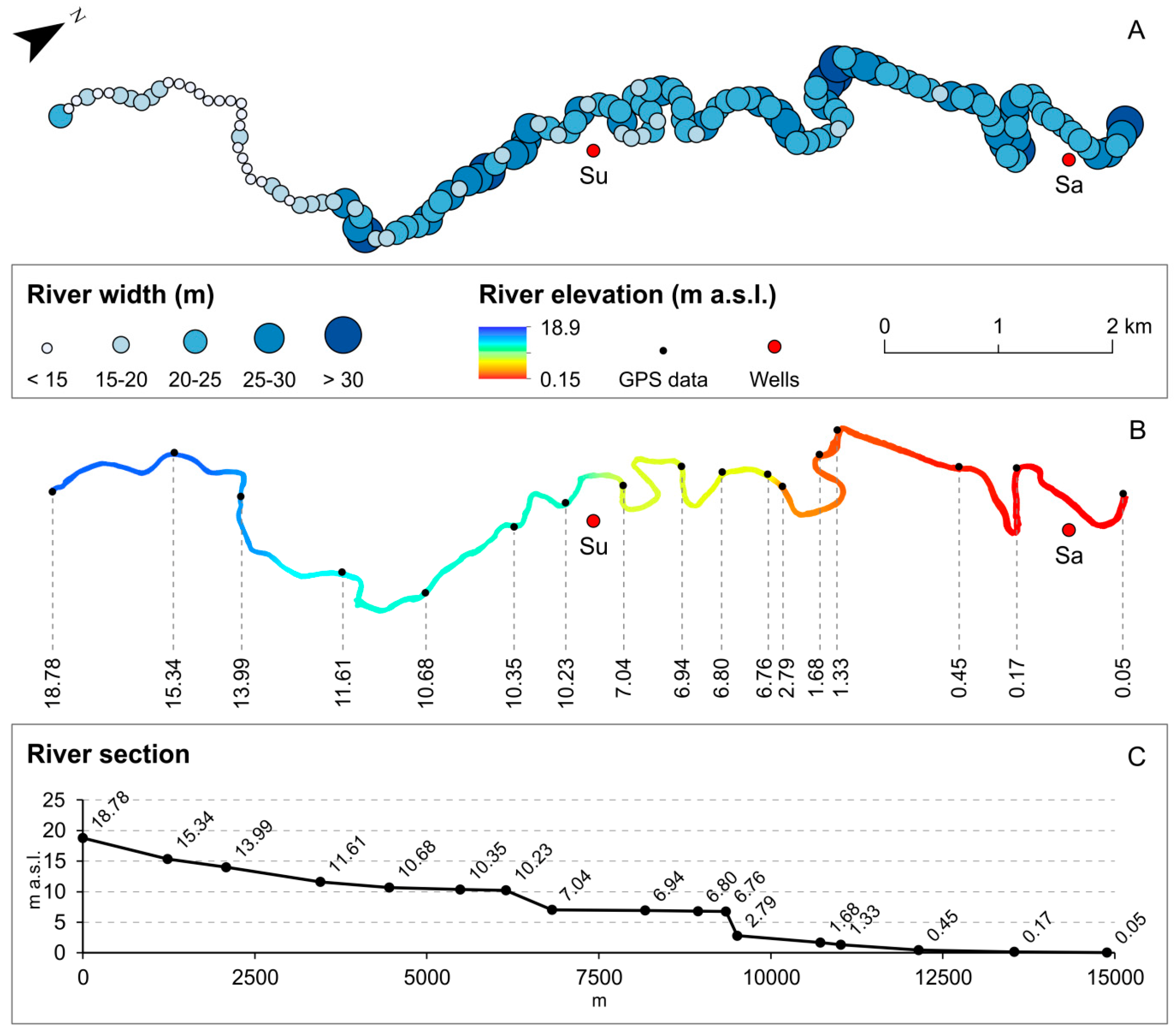
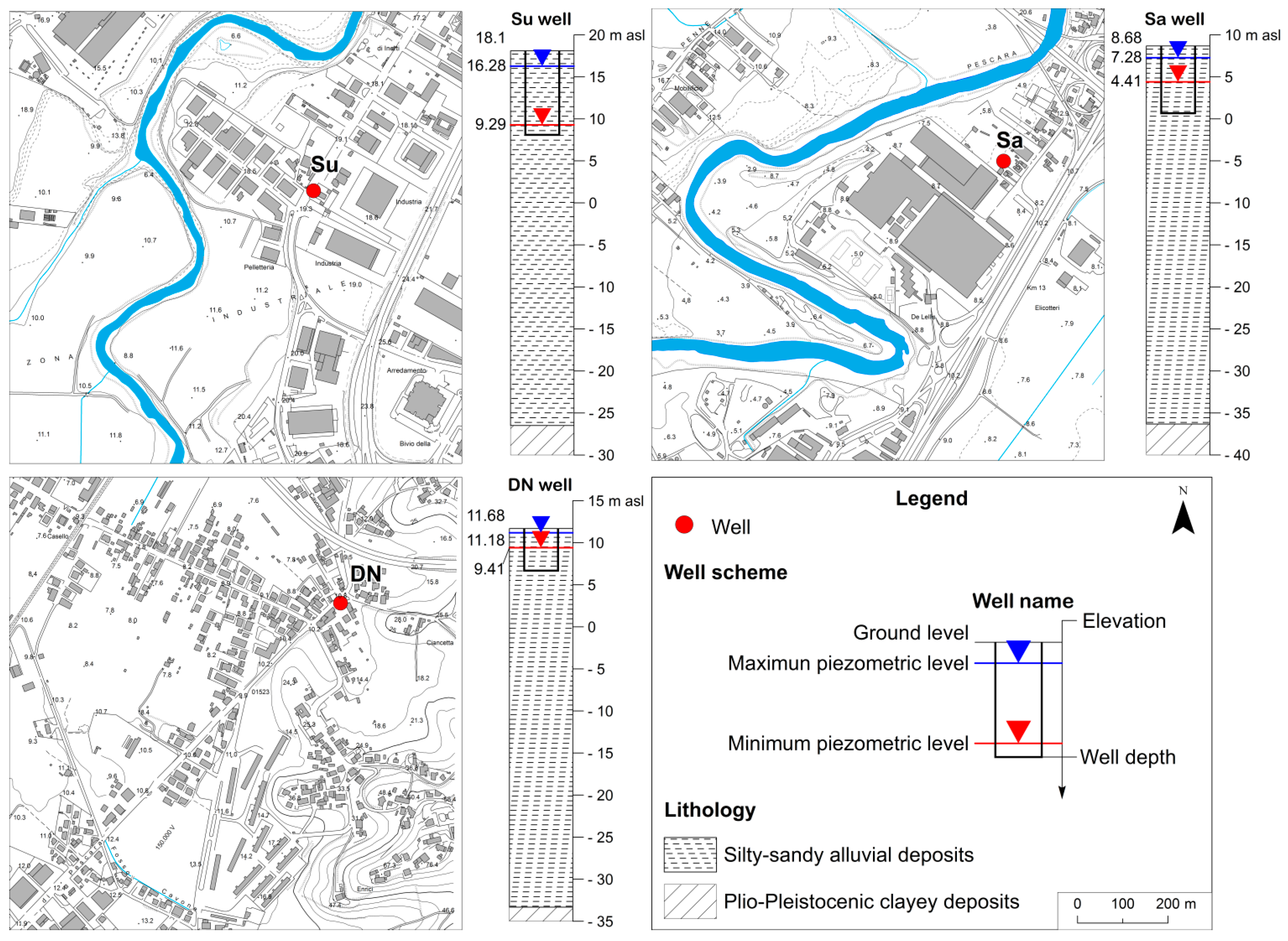
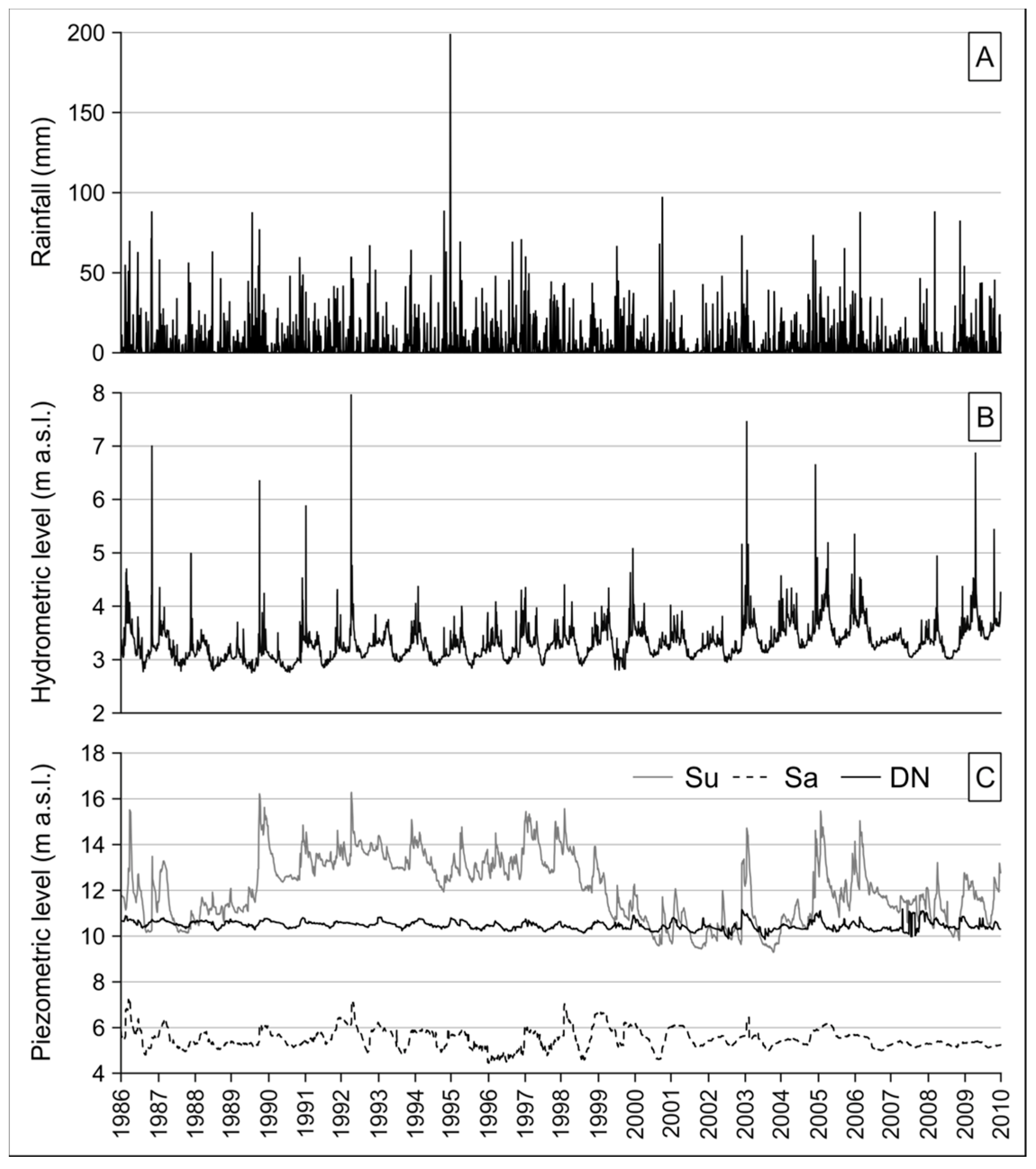

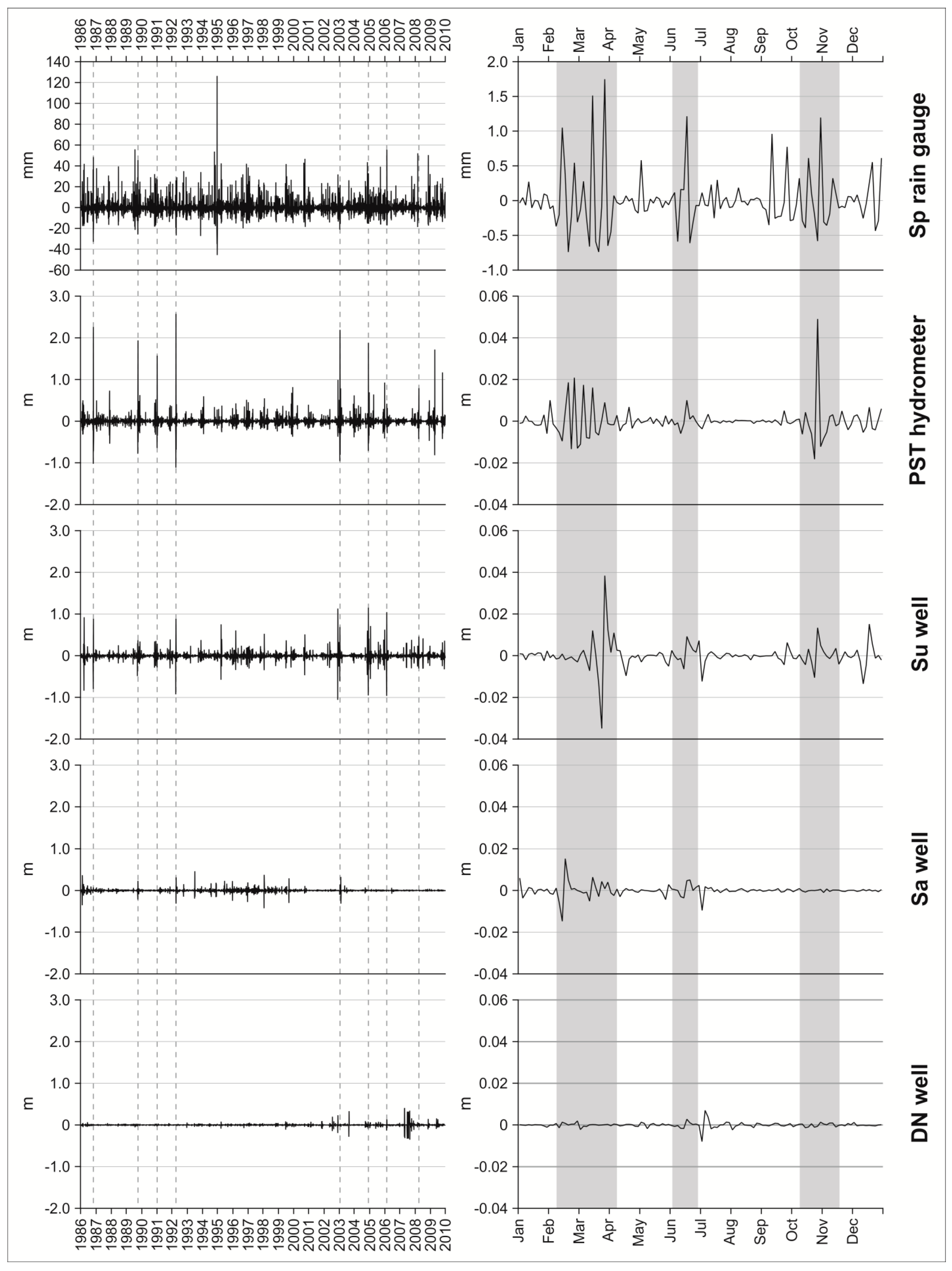
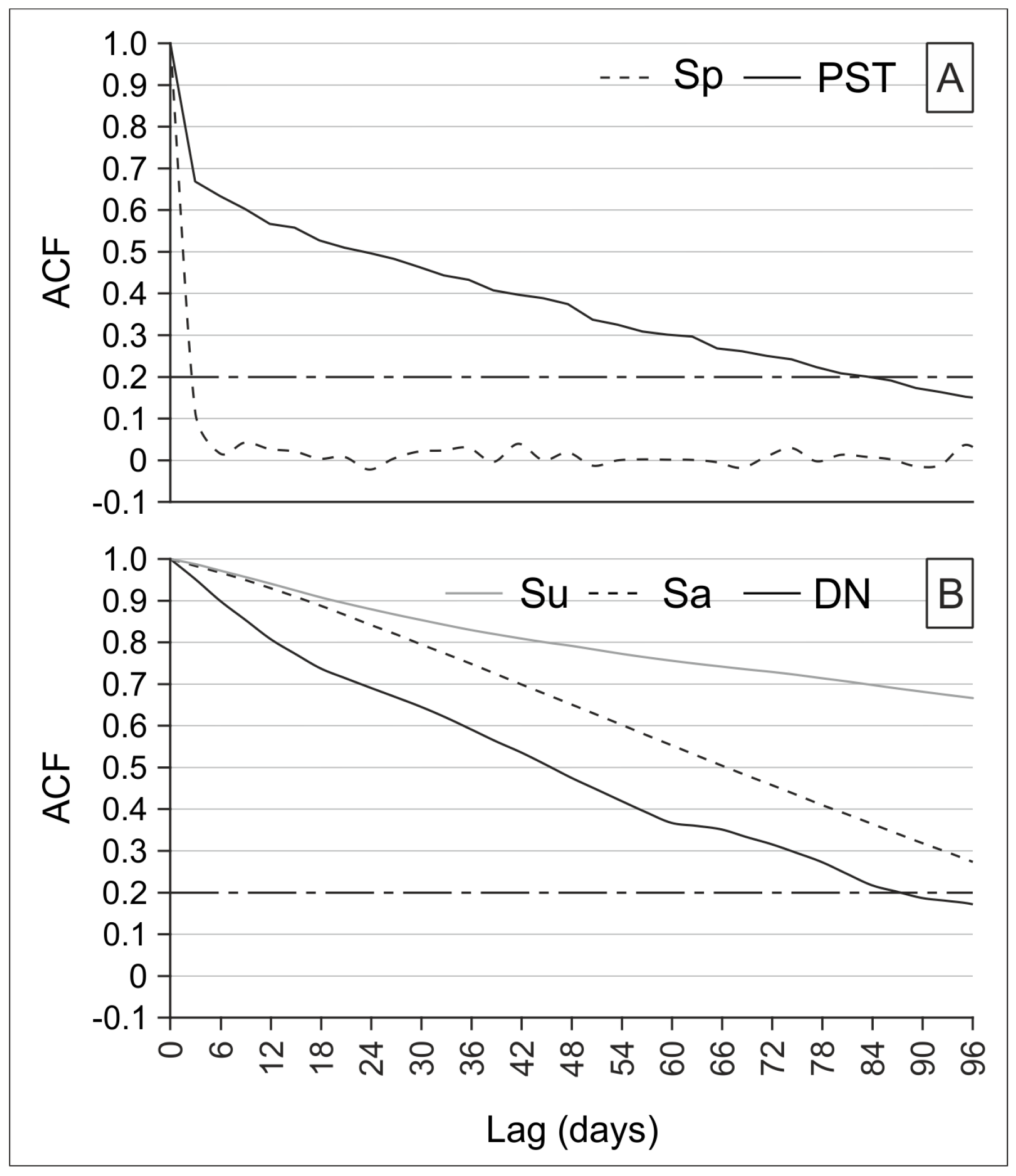
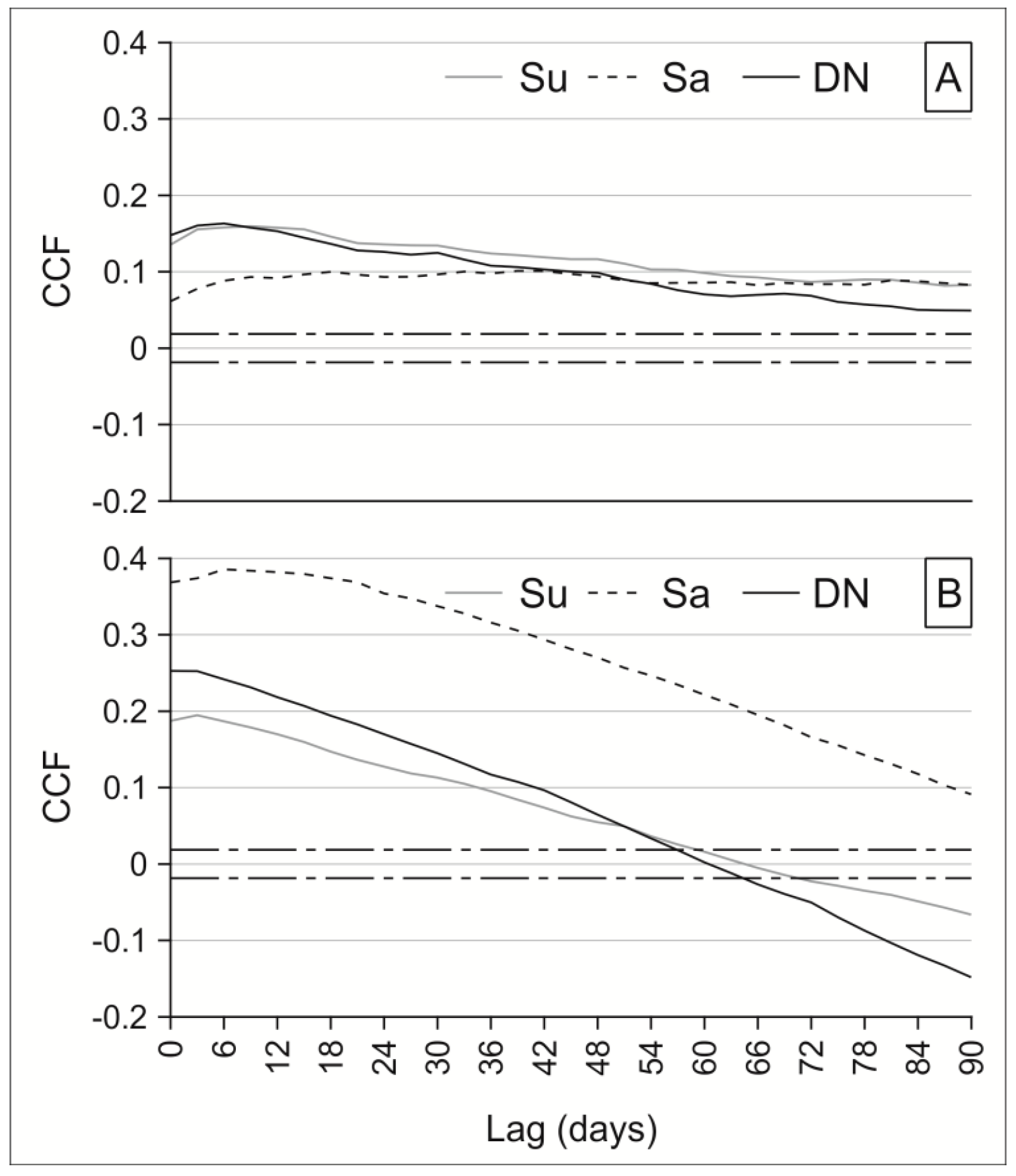
| Name | ID | Type | Elevation (m a.s.l.) | Distance from River (m) | Distance from Sea (km) |
|---|---|---|---|---|---|
| Spoltore | Sp | Rain gauge | 165.00 | 2650 | 4.4 |
| Surricchio | Su | Well | 18.10 | 250 | 8.3 |
| Sanità | Sa | Well | 8.68 | 170 | 4.1 |
| De Nicola | DN | Well | 11.68 | 1960 | 3.7 |
| Pescara S. Teresa | PST | Hydrometer | 4.51 | 0 | 7.0 |
| Type | Name | Piezometric Level (m a.s.l.) | Water Depth (m) | |||||
| Average | St. dev. | Min | Max | Average | ||||
| Well | Su | 12.06 | 1.42 | 9.29 | 16.28 | 6.70 | ||
| Sa | 5.49 | 0.43 | 4.41 | 7.28 | 3.89 | |||
| DN | 10.46 | 0.19 | 9.85 | 11.18 | 2.02 | |||
| Type | Name | Rainfall (mm) | ||||||
| Average | St. dev. | Min | Max | |||||
| Rain Gauge | Sp | 5.35 | 11.9 | 0 | 199.2 | |||
| Type | Name | Hydrometric Level (m a.s.l.) | ||||||
| Average | St. dev. | Min | Max | |||||
| Hydrometer (m) | PST | 3.33 | 0.37 | 2.74 | 7.97 | |||
| Selected F_threshold Level | Sp Rainfall | PST Hydrometry | Su Well | Sa Well | DN Well |
|---|---|---|---|---|---|
| Range = | (0–199.2) (mm) | (2.74–7.97) (m) | (9.29–16.28) (m) | (4.41–7.28) (m) | (9.85–11.18) (m) |
| L_thresh = min + 0.5 × range/100 (m) = | 0.001 | 2.77 | 9.33 | 4.42 | 9.86 |
| Fluctuation (m) = | 0.001 | 0.03 | 0.04 | 0.01 | 0.01 |
| n_events: fi,j ≥ F_threshold = 0.5% = | 1170 | 2876 | 2877 | 2879 | 2879 |
| percentage (%) = | 1170/2880 = 40.6 | 99.86 | 99.89 | 99.96 | 99.97 |
| distribution return time (DRT) (d) = | 17 (2 w) | 3 | 3 | 3 | 3 |
| L_thresh = min + 1.0 × range/100 (m) = | 0.002 | 2.79 | 9.36 | 4.44 | 9.86 |
| Fluctuation (m) = | 0.002 | 0.05 | 0.07 | 0.03 | 0.01 |
| n_events::fi,j ≥ F_threshold = 1.0% = | 998 | 2860 | 2874 | 2879 | 2879 |
| percentage (%) = | 34.7 | 99.31 | 99.79 | 99.96 | 99.97 |
| DRT (d) = | 30 (1 m) | 3 | 3 | 3 | 3 |
| L_thresh = min + 2.5 × range/100 (m) = | 0.005 | 2.87 | 9.47 | 4.48 | 9.88 |
| Fluctuation (m) = | 0.005 | 0.13 | 0.18 | 0.07 | 0.03 |
| n_events: fi,j ≥ F_threshold = 2.5% = | 730 | 2792 | 2862 | 2872 | 2878 |
| percentage (%) = | 25.3 | 96.94 | 99.38 | 99.72 | 99.93 |
| DRT (d) = | 47 (1.7 m) | 3 | 3 | 3 | 3 |
| L_thresh = min + 5.0 × range/100 (m) = | 0.01 | 3.00 | 9.64 | 4.55 | 9.92 |
| Fluctuation (m) = | 0.01 | 0.26 | 0.31 | 0.14 | 0.07 |
| n_events::fi,j ≥ F_threshold = 5% = | 474 | 2491 | 2794 | 2866 | 2876 |
| percentage (%) = | 6.5 | 86.49 | 97.01 | 99.51 | 99.86 |
| DRT (d) = | 71 (2.4 m) | 3 | 3 | 3 | 3 |
| L_thresh = min + 10 × range/100 (m) = | 0.02 | 3.26 | 9.99 | 4.70 | 9.98 |
| Fluctuation (m) = | 0.02 | 0.52 | 0.7 | 0.29 | 0.13 |
| n_events: fi,j ≥ F_threshold = 10% = | 252 | 1472 | 2684 | 2798 | 2861 |
| percentage (%) = | 8.8 | 51.11 | 93.19 | 97.15 | 99.34 |
| DRT (d) = | 107 (3.6 m) | 95 (3.2 m) | 3 | 3 | 3 |
| L_thresh = min + 20 × range/100 (m) = | 0.04 | 3.79 | 10.69 | 4.99 | 10.12 |
| Fluctuation (m) = | 0.04 | 1.05 | 1.4 | 0.58 | 0.27 |
| n_events: fi,j ≥ F_threshold = 20% = | 74 | 218 | 2313 | 2671 | 2837 |
| percentage (%) = | 2.6 | 7.569 | 80.31 | 92.74 | 98.51 |
| DRT (d) = | 361 (12 m) | 428 (14.3 m) | 69 (2.3 m) | 3 | 3 |
| L_thresh =min + 30 × range/100 (m) = | 0.06 | 4.32 | 11.40 | 5.27 | 10.25 |
| Fluctuation (m) = | 0.06 | 1.58 | 2.11 | 0.86 | 0.40 |
| n_events: fi,j ≥ F_threshold = 30% = | 26 | 47 | 1824 | 1947 | 2618 |
| percentage (%) = | 0.9 | 1.632 | 63.33 | 67.60 | 90.9 |
| DRT (d) = | 727 (24 m) | 572 (19 m) | 176 (5.9 m) | 130 (4.3 m) | 30 |
| L_thresh = min + 40 × range/100 (m) = | 0.08 | 4.84 | 12.10 | 5.56 | 10.38 |
| Fluctuation (m) = | 0.08 | 2.1 | 2.81 | 1.15 | 0.53 |
| n_events: fi,j ≥ F_threshold = 40% = | 8 | 17 | 1382 | 1139 | 1859 |
| percentage (%) = | 0.28 | 0.590 | 47.98 | 39.55 | 64.55 |
| DRT (d) = | 1995 (67 m) | 861 (29 m) | 589 (19.6 m) | 360 (12 m) | 282 |
| L_thresh = min + 60 × range/100 (m) = | 0.12 | 5.88 | 13.48 | 6.13 | 10.65 |
| Fluctuation (m) = | 0.12 | 3.14 | 4.19 | 1.72 | 0.8 |
| n_events: fi,j ≥ F_threshold = 60% = | 1 | 7 | 518 | 216 | 457 |
| percentage (%) = | 0.035 | 0.243 | 17.98 | 7.5 | 15.87 |
| DRT (d) = | 8640 (24 y) | 1392 (46 m) | 764 (25.5 m) | 1272 (42 m) | 727 (24 m) |
| L_thresh = min + 80 × range/100 (m) = | 0.160 | 6.92 | 14.88 | 6.71 | 10.91 |
| Fluctuation (m) = | 0.160 | 4.18 | 5.59 | 2.3 | 1.06 |
| n_events: fi,j ≥ F_threshold = 80% = | 1 | 3 | 58 | 35 | 63 |
| percentage (%) = | 0.035 | 0.104 | 2.014 | 1.215 | 2.19 |
| DRT (d) = | 8640 (24 y) | 2694 (7.5 y) | 2694 (7.5 y) | 2860 (7.9 y) | 8640 (24 y) |
| L_thresh = min + 90 × range/100 (m) = | 0.180 | 7.45 | 15.58 | 6.99 | 11.05 |
| Fluctuation (m) = | 0.180 | 4.71 | 6.29 | 2.58 | 1.20 |
| n_events: fi,j ≥ F_threshold = 90% = | 1 | 2 | 9 | 13 | 21 |
| percentage (%) = | 0.035 | 0.069 | 0.313 | 0.451 | 0.73 |
| DRT (d) = | 8640 (24 y) | 4310 (12 y) | 3636 (10 y) | 4186 (11.5 y) | 8640 (24 y) |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chiaudani, A.; Di Curzio, D.; Palmucci, W.; Pasculli, A.; Polemio, M.; Rusi, S. Statistical and Fractal Approaches on Long Time-Series to Surface-Water/Groundwater Relationship Assessment: A Central Italy Alluvial Plain Case Study. Water 2017, 9, 850. https://doi.org/10.3390/w9110850
Chiaudani A, Di Curzio D, Palmucci W, Pasculli A, Polemio M, Rusi S. Statistical and Fractal Approaches on Long Time-Series to Surface-Water/Groundwater Relationship Assessment: A Central Italy Alluvial Plain Case Study. Water. 2017; 9(11):850. https://doi.org/10.3390/w9110850
Chicago/Turabian StyleChiaudani, Alessandro, Diego Di Curzio, William Palmucci, Antonio Pasculli, Maurizio Polemio, and Sergio Rusi. 2017. "Statistical and Fractal Approaches on Long Time-Series to Surface-Water/Groundwater Relationship Assessment: A Central Italy Alluvial Plain Case Study" Water 9, no. 11: 850. https://doi.org/10.3390/w9110850
APA StyleChiaudani, A., Di Curzio, D., Palmucci, W., Pasculli, A., Polemio, M., & Rusi, S. (2017). Statistical and Fractal Approaches on Long Time-Series to Surface-Water/Groundwater Relationship Assessment: A Central Italy Alluvial Plain Case Study. Water, 9(11), 850. https://doi.org/10.3390/w9110850









