A Hybrid Heuristic Optimization Approach for Leak Detection in Pipe Networks Using Ordinal Optimization Approach and the Symbiotic Organism Search
Abstract
1. Introduction
2. Methodology
2.1. Flow Simulation Model
2.2. Hydraulic Transient Model
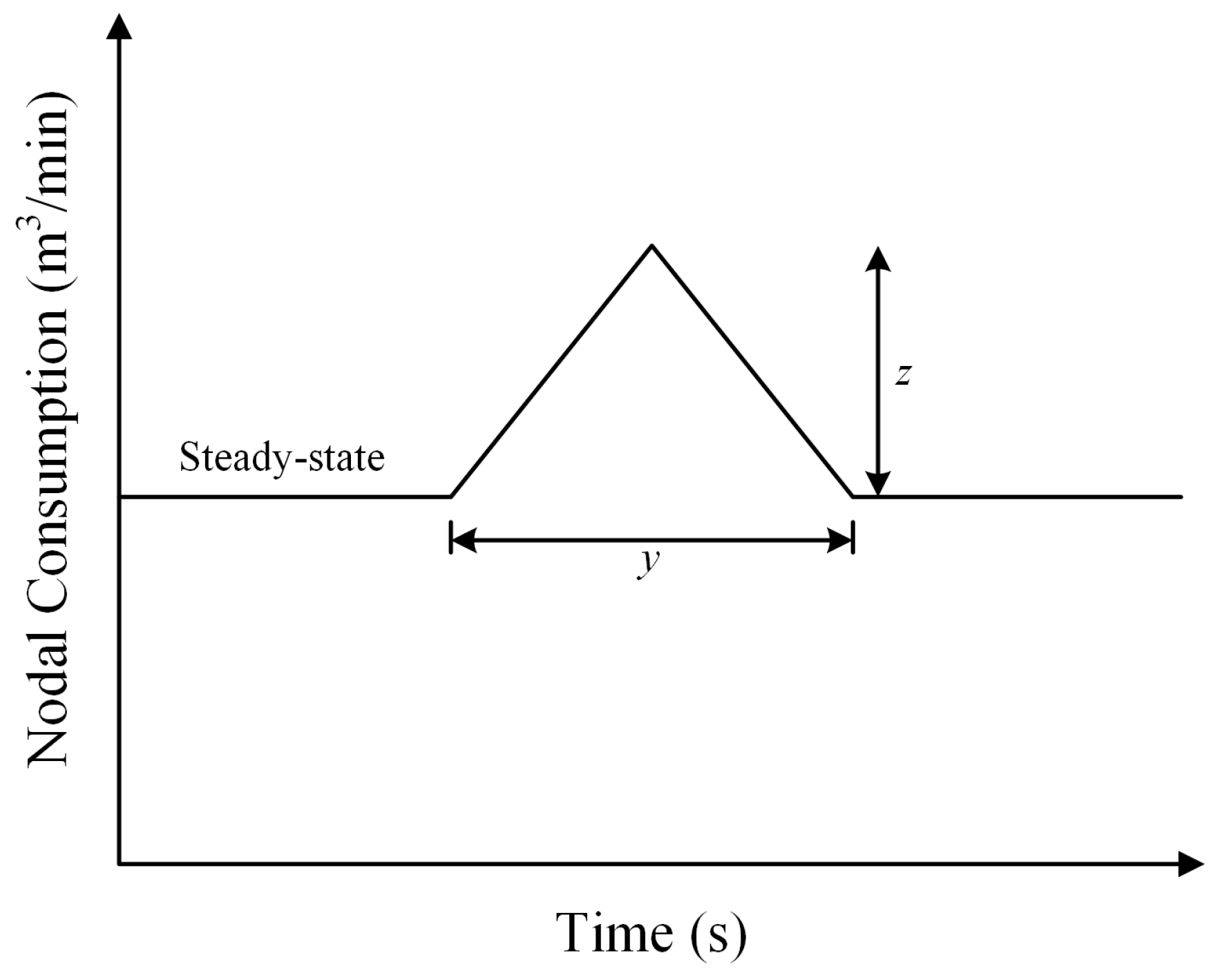
2.3. Excitation Procedure for Transient Generation
2.4. Ordinal Optimization Approach
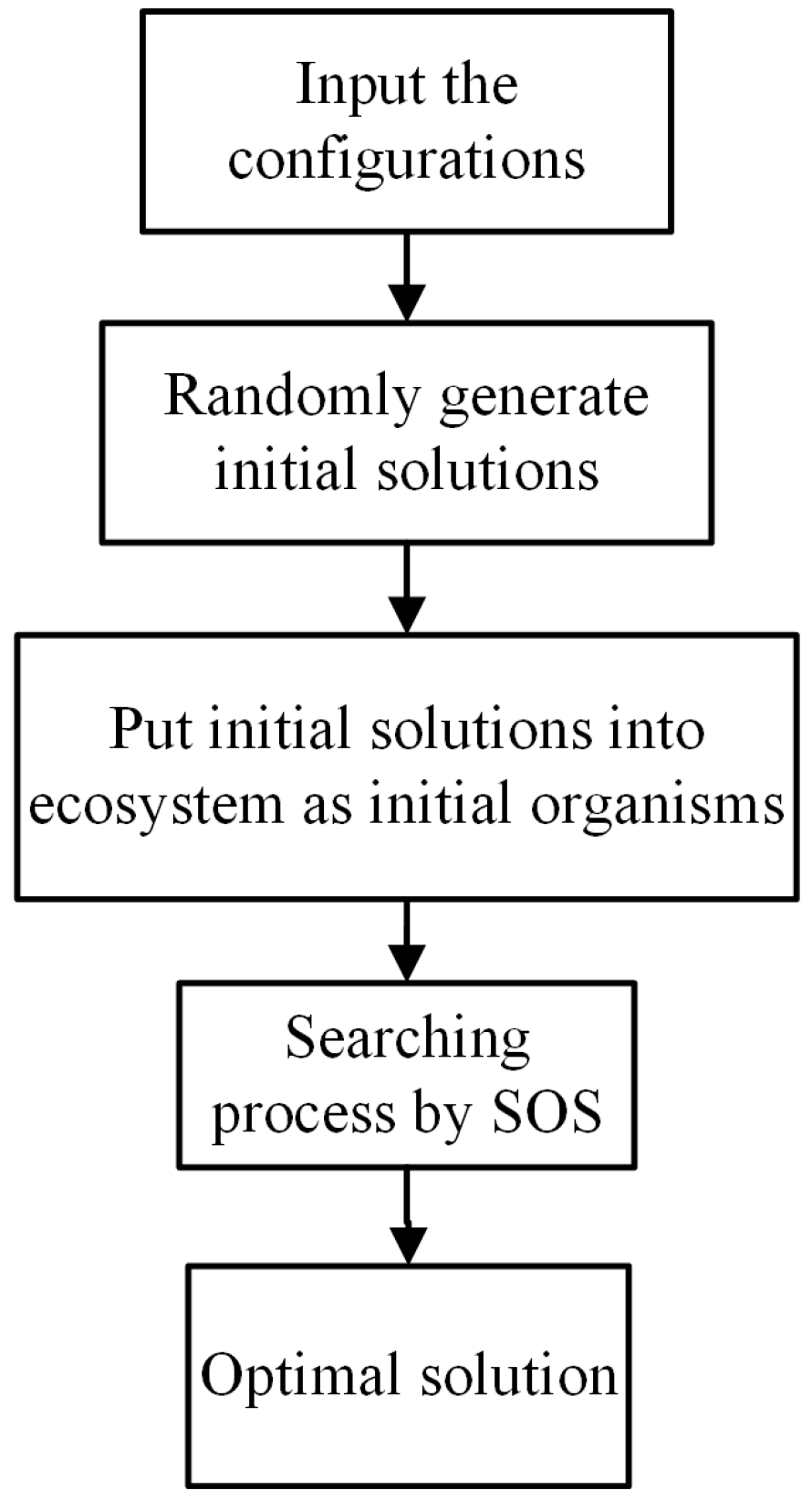
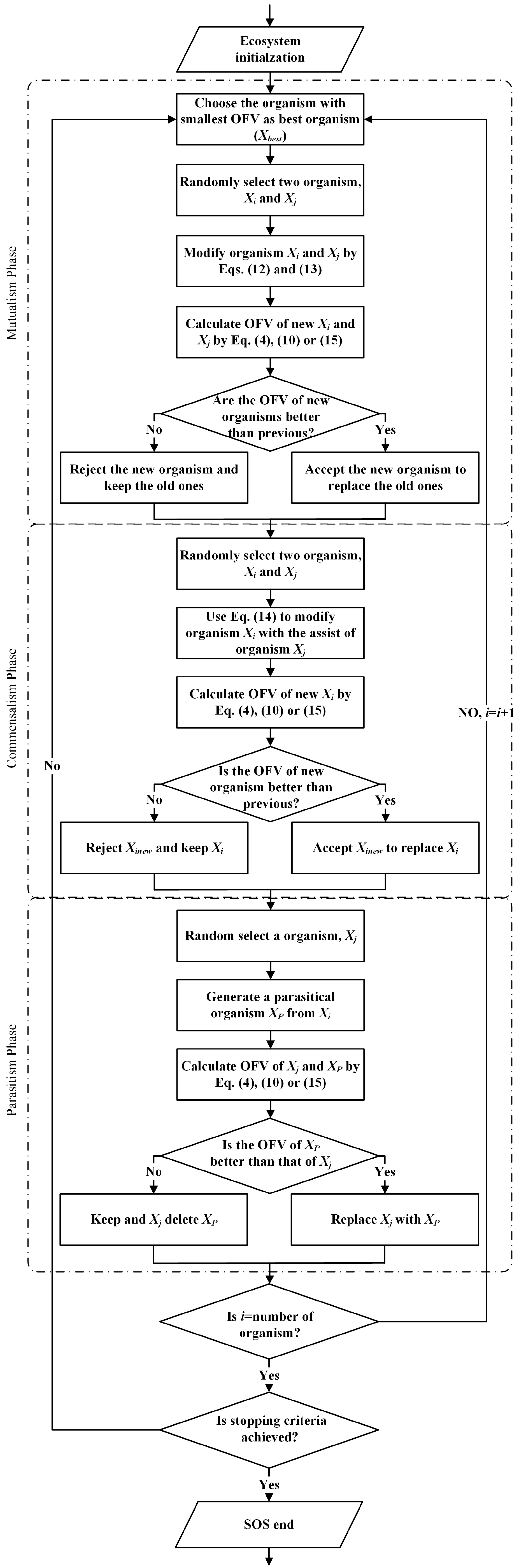
2.5. Symbiotic Organism Search (SOS)
2.5.1. Mutualism State
2.5.2. Commensalism State
2.5.3. Parasitism State
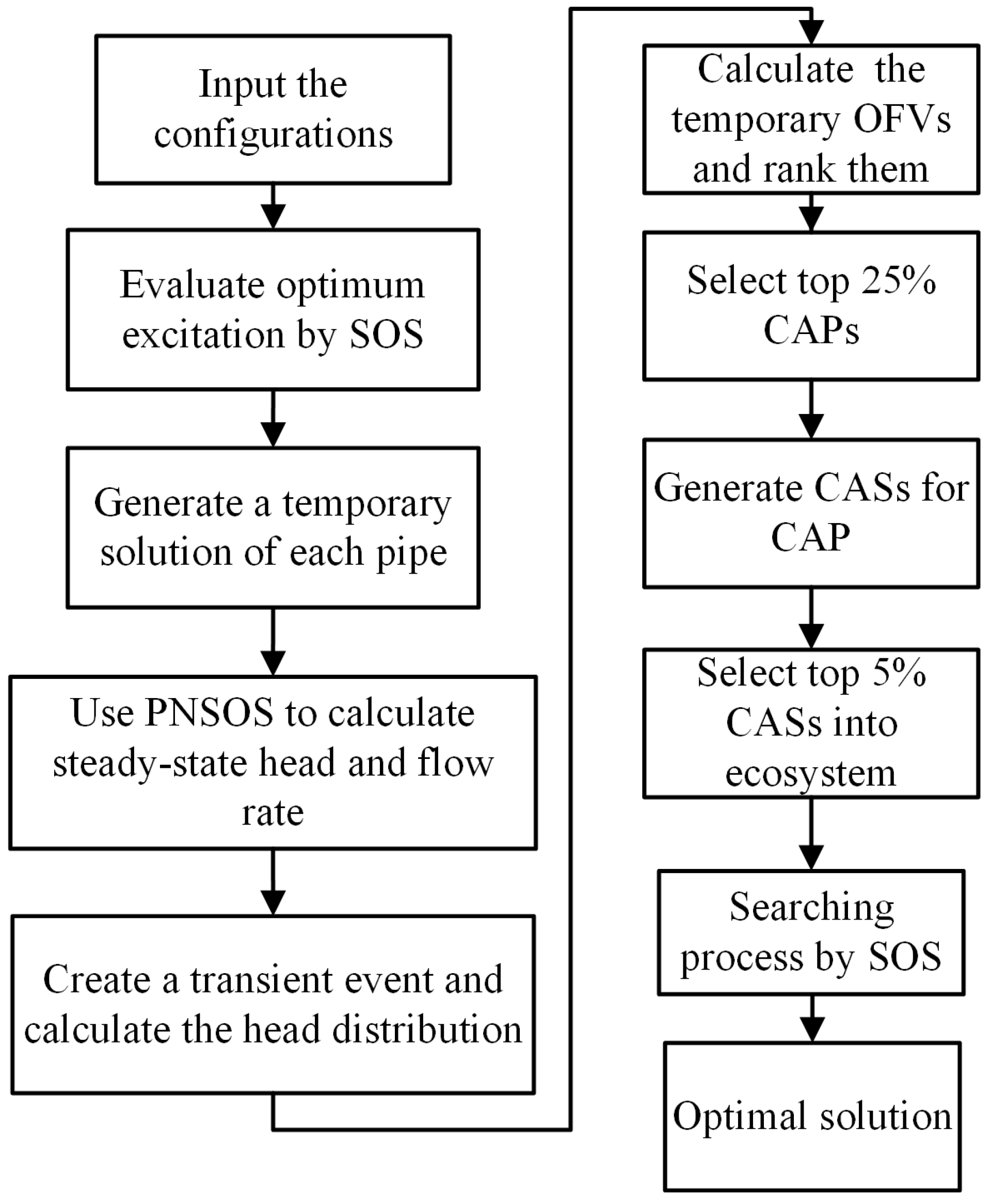
2.6. Development of LDOSOS
- Import the network configurations.
- Use SOS to determine the optimal transient generating point with its corresponding operating parameters (i.e., y: duration of outflow change, z: amount of nodal consumption variation) by maximizing Equation (10). The optimum solution is obtained when the OFV of Equation (10) does not change within four iterations.
- For the pipe sifting procedure in OOA, successively generate a temporary leak which is located at the middle of each pipe; the location and CdA of the orifices are treated as temporary solutions.
- Since the temporary leak solutions are available, PNSOS is then used to calculate the steady-state nodal heads and flow rates in the network.
- Generate a hydraulic transient event at the optimal generation point and apply Equations (7) and (8) to simulate the head distribution in the network.
- Apply Equation (15) to calculate the temporary OFV for the temporary solution of each pipe.
- Arrange all of the pipes according to the values of temporary OFVs. A quarter of pipes with smaller OFVs are chosen as candidate pipes (CAPs). Only the CAPs will be used in the further steps.
- Randomly generate 200 CASs with the information of a leaking pipe, leak location and CdAs of the orifices, and calculate their OFVs. The top 5% CASs would then be selected for the next step.
- Consider the best 5% CASs as the initial organisms for the ecosystem.
- Execute a searching process using SOS. In general, mutualism and commensalism states are used to guide the organisms toward the current best organism, and the parasitism state is applied to avoid the organism becoming stuck in a local optimal solution.
- Check whether the optimization process satisfies the stopping criterion or not. If so, the LDOSOS is then terminated; otherwise, the searching process goes on and back to the tenth step.
3. Results and Discussion
3.1. Pipe Networks Setting
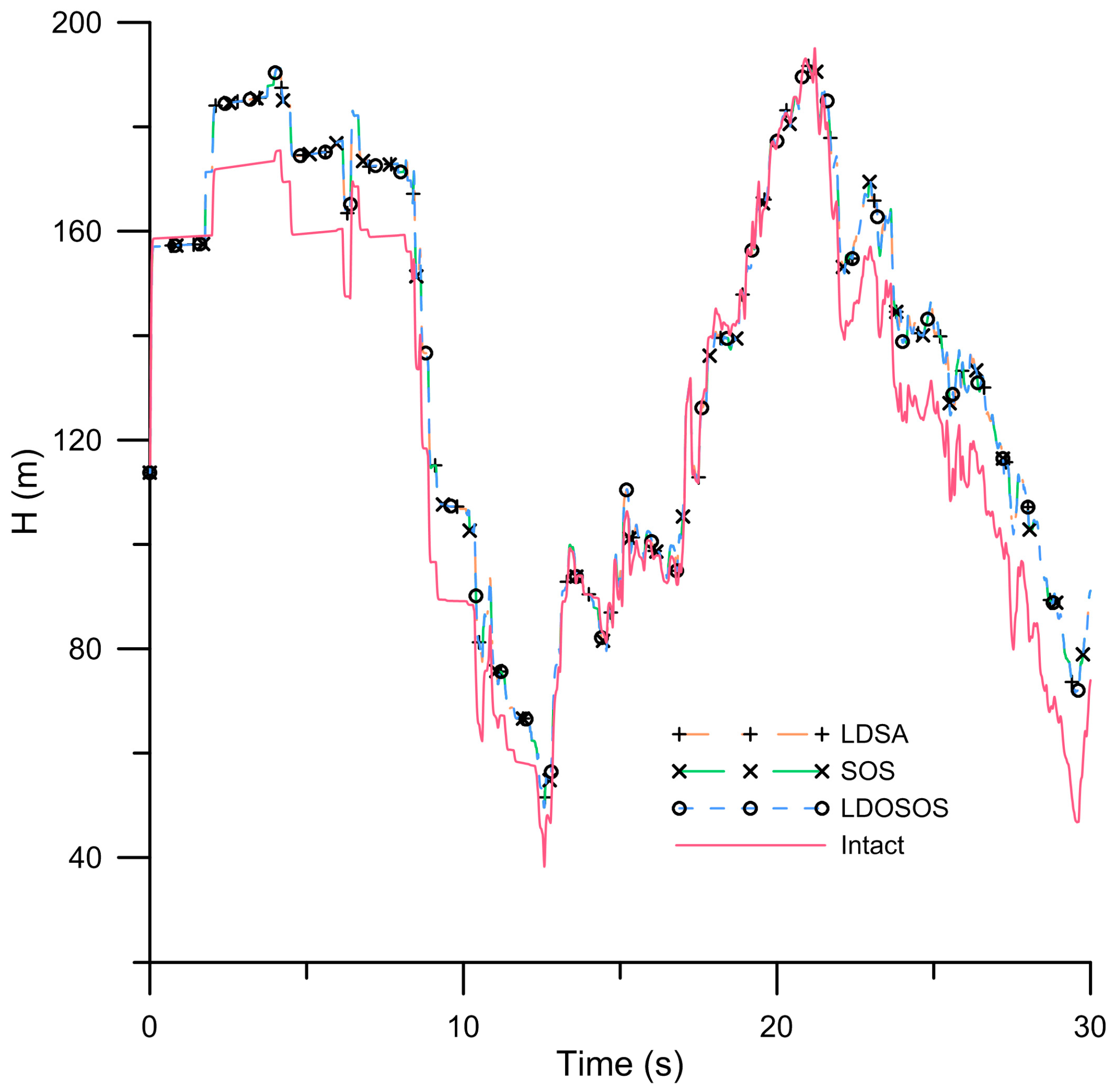
3.2. Applicability of LDOSOS to Leak Detection
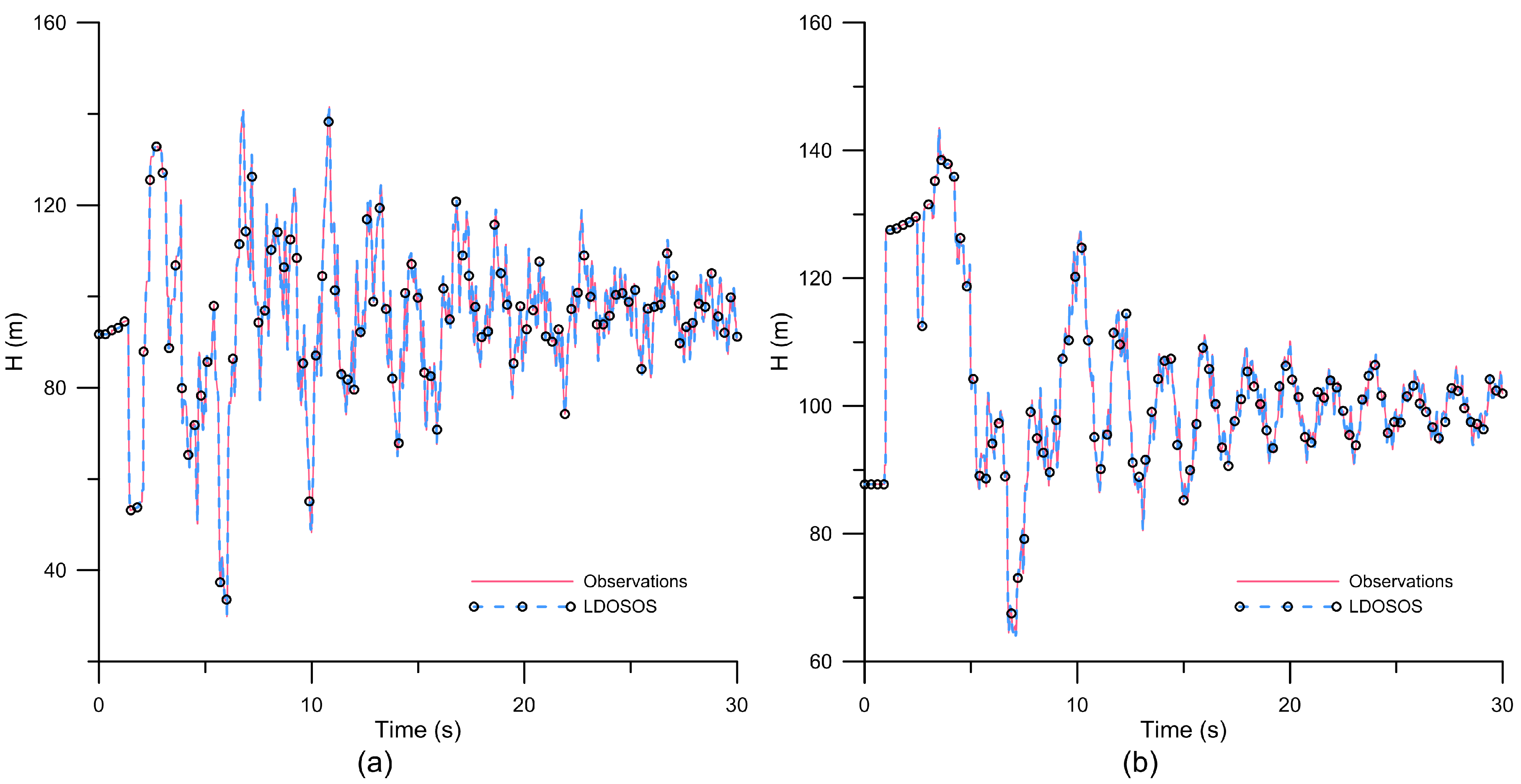
3.3. Leak Determination in WDN with Optimal Transient Operation
3.4. Measurement Error Analysis
4. Conclusions
Acknowledgments
Conflicts of Interest
References
- Thornton, J.; Sturm, R.; Kunkel, G. Water Loss Control, 2nd ed.; Mcgraw-Hill: New York, NY, USA, 2008. [Google Scholar]
- Lambert, A.O. International report: Water losses management and techniques. Water Sci. Technol. Water Supply 2002, 2, 1–20. [Google Scholar]
- Kanakoudis, V.; Tsitsifli, S. Urban water services public infrastructure projects: Turning the high level of the NRW into an attractive financing opportunity using the PBSC tool. Desalin. Water Treat. 2012, 39, 323–335. [Google Scholar] [CrossRef]
- Colombo, A.F.; Lee, P.; Karney, B.W. A selective literature review of transient-based leak detection methods. J. Hydro-Environ. Res. 2009, 2, 212–227. [Google Scholar] [CrossRef]
- Puust, R.; Kapelan, Z.; Savic, D.A.; Koppel, T. A review of methods for leakage management in pipe networks. Urban Water J. 2010, 7, 25–45. [Google Scholar] [CrossRef]
- Al-Khomairi, A. Leak detection in long pipelines using the least squares method. J. Hydraul. Res. 2008, 46, 392–401. [Google Scholar] [CrossRef]
- Shamloo, H.; Haghighi, A. Optimum leak detection and calibration of pipe networks by inverse transient analysis. J. Hydraul. Res. 2010, 48, 371–376. [Google Scholar] [CrossRef]
- Covelli, C.; Cozzolino, L.; Cimorelli, L.; Della Morte, R.; Pianese, D. A model to simulate leakage through joints in water distribution systems. Water Sci. Technol. Water Supply 2015, 15, 852–863. [Google Scholar] [CrossRef]
- Covelli, C.; Cimorelli, L.; Cozzolino, L.; Della Morte, R.; Pianese, D. Reduction in water losses in water distribution systems using pressure reduction valves. Water Sci. Technol. Water Supply 2016, 16, 1033. [Google Scholar] [CrossRef]
- Covelli, C.; Cozzolino, L.; Cimorelli, L.; Della Morte, R.; Pianese, D. Optimal location and setting of prvs in wds for leakage minimization. Water Resour. Manag. 2016, 30, 1803–1817. [Google Scholar] [CrossRef]
- Juliano, T.M.; Meegoda, J.N.; Watts, D.J. Acoustic emission leak detection on a metal pipeline buried in sandy soil. J. Pipeline Syst. Eng. Pract. 2013, 4, 149–155. [Google Scholar] [CrossRef]
- Martini, A.; Troncossi, M.; Rivola, A. Leak detection in water-filled small-diameter polyethylene pipes by means of acoustic emission measurements. Appl. Sci. 2017, 7, 2. [Google Scholar] [CrossRef]
- Martini, A.; Troncossi, M.; Rivola, A. Automatic leak detection in buried plastic pipes of water supply networks by means of vibration measurements. Shock Vib. 2015, 2015. [Google Scholar] [CrossRef]
- Martini, A.; Troncossi, M.; Rivola, A. Vibroacoustic measurements for detecting water leaks in buried small-diameter plastic pipes. J. Pipeline Syst. Eng. Pract. 2017, 8. [Google Scholar] [CrossRef]
- Yazdekhasti, S.; Piratla, K.R.; Atamturktur, S.; Khan, A. Experimental evaluation of a vibration-based leak detection technique for water pipelines. Struct. Infrastruct. Eng. 2017, 1–10. [Google Scholar] [CrossRef]
- Zahab, S.E.; Mosleh, F.; Zayed, T. An Accelerometer-Based Real-Time Monitoring and Leak Detection System for Pressurized Water Pipelines; Pipelines: Kansas City, MO, USA, 2016; pp. 257–268. [Google Scholar]
- Li, R.; Huang, H.; Xin, K.; Tao, T. A review of methods for burst/leakage detection and location in water distribution systems. Water Sci. Technol. Water Supply 2015, 15, 429–441. [Google Scholar] [CrossRef]
- Chaudhry, M.H. Applied Hydraulic Transients, 3rd ed.; Springer: New York, NY, USA, 2014. [Google Scholar]
- Vítkovský John, P.; Lambert Martin, F.; Simpson Angus, R.; Liggett James, A. Experimental observation and analysis of inverse transients for pipeline leak detection. J. Water Resour. Plan. Manag. 2007, 133, 519–530. [Google Scholar] [CrossRef]
- Vítkovský John, P.; Simpson Angus, R.; Lambert Martin, F. Leak detection and calibration using transients and genetic algorithms. J. Water Resour. Plan. Manag. 2000, 126, 262–265. [Google Scholar] [CrossRef]
- Kapelan, Z.S.; Savic, D.A.; Walters, G.A. A hybrid inverse transient model for leakage detection and roughness calibration in pipe networks. J. Hydraul. Res. 2003, 41, 481–492. [Google Scholar] [CrossRef]
- Jung, B.S.; Karney, B.W. Systematic exploration of pipeline network calibration using transients. J. Hydraul. Res. 2008, 46, 129–137. [Google Scholar] [CrossRef]
- Shamloo, H.; Haghighi, A. Leak detection in pipelines by inverse backward transient analysis. J. Hydraul. Res. 2009, 47, 311–318. [Google Scholar] [CrossRef]
- Haghighi, A.; Ramos, H.M. Detection of leakage freshwater and friction factor calibration in drinking networks using central force optimization. Water Resour. Manag. 2012, 26, 2347–2363. [Google Scholar] [CrossRef]
- Huang, Y.-C.; Lin, C.-C.; Yeh, H.-D. An optimization approach to leak detection in pipe networks using simulated annealing. Water Resour. Manag. 2015, 29, 4185–4201. [Google Scholar] [CrossRef]
- Liggett, J.A.; Chen, L.C. Inverse transient analysis in pipe networks. J. Hydraul. Eng. 1994, 120, 934–955. [Google Scholar] [CrossRef]
- Ferrante, M.; Brunone, B.; Meniconi, S. Leak detection in branched pipe systems coupling wavelet analysis and a lagrangian model. J. Water Supply Res. Technol. AQUA 2009, 58, 95. [Google Scholar] [CrossRef]
- Nazif, S.; Karamouz, M.; Tabesh, M.; Moridi, A. Pressure management model for urban water distribution networks. Water Resour. Manag. 2010, 24, 437–458. [Google Scholar] [CrossRef]
- Ferrante, M.; Brunone, B.; Meniconi, S.; Karney, B.W.; Massari, C. Leak size, detectability and test conditions in pressurized pipe systems. Water Resour. Manag. 2014, 28, 4583–4598. [Google Scholar] [CrossRef]
- Casillas, V.M.; Garza-Castañón, E.L.; Puig, V. Optimal sensor placement for leak location in water distribution networks using evolutionary algorithms. Water 2015, 7, 6496–6515. [Google Scholar] [CrossRef]
- Meniconi, S.; Brunone, B.; Ferrante, M.; Capponi, C.; Carrettini, C.A.; Chiesa, C.; Segalini, D.; Lanfranchi, E.A. Anomaly pre-localization in distribution–transmission mains by pump trip: Preliminary field tests in the milan pipe system. J. Hydroinform. 2015, 17, 377–389. [Google Scholar] [CrossRef]
- Lee, S.J.; Lee, G.; Suh, J.C.; Lee, J.M. Online burst detection and location of water distribution systems and its practical applications. J. Water Resour. Plan. Manag. 2016, 142, 04015033. [Google Scholar] [CrossRef]
- Soares, A.K.; Covas, D.I.C.; Reis, L.F.R. Leak detection by inverse transient analysis in an experimental pvc pipe system. J. Hydroinform. 2011, 13, 153–166. [Google Scholar] [CrossRef]
- Casillas Ponce, M.V.; Garza Castañón, L.E.; Cayuela, V.P. Model-based leak detection and location in water distribution networks considering an extended-horizon analysis of pressure sensitivities. J. Hydroinform. 2014, 16, 649–670. [Google Scholar] [CrossRef]
- Yeh, H.-D.; Lin, Y.-C. Pipe network system analysis using simulated annealing. J. Water Supply Res. Technol. AQUA 2008, 57, 317–327. [Google Scholar] [CrossRef]
- Mays, L.W. Water Supply Systems Security; McGraw-Hill: New York, NY, USA, 2004. [Google Scholar]
- Savić, D.A.; Banyard, J.K. Water Distribution Systems, 2nd ed.; ICE: London, UK, 2011. [Google Scholar]
- Larock, B.E.; Jeppson, R.W.; Watters, G.Z. Hydraulics of Pipeline Systems; CRC Press: Boca Raton, FL, USA, 2000. [Google Scholar]
- Vítkovský, J.; Stephens, M.; Bergant, A.; Simpson, A.; Lambert, M. Numerical error in weighting function-based unsteady friction models for pipe transients. J. Hydraul. Eng. 2006, 132, 709–721. [Google Scholar] [CrossRef]
- Duan, H.-F.; Ghidaoui, M.; Lee, P.J.; Tung, Y.-K. Unsteady friction and visco-elasticity in pipe fluid transients. J. Hydraul. Res. 2010, 48, 354–362. [Google Scholar] [CrossRef]
- Vítkovský, J.P.; Bergant, A.; Simpson, A.R.; Lambert, M.F. Systematic evaluation of one-dimensional unsteady friction models in simple pipelines. J. Hydraul. Eng. 2006, 132, 696–708. [Google Scholar] [CrossRef]
- Reddy, H.P.; Silva-Araya, W.F.; Chaudhry, M.H. Estimation of decay coefficients for unsteady friction for instantaneous, acceleration-based models. J. Hydraul. Eng. 2012, 138, 260–271. [Google Scholar] [CrossRef]
- Boulos, P.F.; Lansey, K.E.; Karney, B.W. Comprehensive Water Distribution Systems Analysis Handbook for Engineers and Planners, 2nd ed.; MWH Soft, Incorporated: Pasadena, CA, USA, 2006. [Google Scholar]
- Brunone, B. Transient test-based technique for leak detection in outfall pipes. J. Water Resour. Plan. Manag. 1999, 125, 302–306. [Google Scholar] [CrossRef]
- Meniconi, S.; Brunone, B.; Ferrante, M.; Massari, C. Small amplitude sharp pressure waves to diagnose pipe systems. Water Resour. Manag. 2011, 25, 79–96. [Google Scholar] [CrossRef]
- Brunone, B.; Ferrante, M.; Meniconi, S. Portable pressure wave-maker for leak detection and pipe system characterization. J. Am. Water Works Assoc. 2008, 100, 108–116. [Google Scholar]
- Shucksmith, J.D.; Boxall, J.B.; Staszewski, W.J.; Seth, A.; Beck, S.B.M. Onsite leak location in a pipe network by cepstrum analysis of pressure transients. J. Am. Water Works Assoc. 2012, 104, E457–E465. [Google Scholar] [CrossRef]
- Stephens, M.L.; Lambert, M.F.; Simpson, A.R. Determining the internal wall condition of a water pipeline in the field using an inverse transient. J. Hydraul. Eng. 2013, 139, 310–324. [Google Scholar] [CrossRef]
- Taghvaei, M.; Beck, S.B.M.; Boxall, J. Leak detection in pipes using induced water hammer pulses and cepstrum analysis. Int. J. COMADEM 2010, 13, 19–25. [Google Scholar]
- Haghighi, A.; Shamloo, H. Transient generation in pipe networks for leak detection. Proc. Inst. Civ. Eng. Water Manag. 2011, 164, 311–318. [Google Scholar] [CrossRef]
- Ho, Y.C.; Cassandras, C.G.; Chen, C.H.; Dai, L. Ordinal optimisation and simulation. J. Oper. Res. Soc. 2000, 51, 490–500. [Google Scholar] [CrossRef]
- Lau, T.W.E.; Ho, Y.C. Universal alignment probabilities and subset selection for ordinal optimization. J. Optim. Theory Appl. 1997, 93, 455–489. [Google Scholar] [CrossRef]
- Cheng, M.-Y.; Prayogo, D. Symbiotic organisms search: A new metaheuristic optimization algorithm. Comput. Struct. 2014, 139, 98–112. [Google Scholar] [CrossRef]
- Cheng, M.-Y.; Prayogo, D.; Tran, D.-H. Optimizing multiple-resources leveling in multiple projects using discrete symbiotic organisms search. J. Comput. Civ. Eng. 2016, 30, 04015036. [Google Scholar] [CrossRef]
- Tran, D.-H.; Cheng, M.-Y.; Prayogo, D. A novel multiple objective symbiotic organisms search (mosos) for time–cost–labor utilization tradeoff problem. Knowl-Based. Syst. 2016, 94, 132–145. [Google Scholar] [CrossRef]
- Bozorg-Haddad, O.; Azarnivand, A.; Hosseini-Moghari, S.-M.; Loáiciga, H.A. Optimal operation of reservoir systems with the symbiotic organisms search (SOS) algorithm. J. Hydroinform. 2017, 19, 507–521. [Google Scholar] [CrossRef]
- Abhulimen, K.E.; Susu, A.A. Liquid pipeline leak detection system: Model development and numerical simulation. Chem. Eng. J. 2004, 97, 47–67. [Google Scholar] [CrossRef]
- Yeh, H.-D. Theis’ solution by nonlinear least-squares and finite-difference newton’s method. Ground Water 1987, 25, 710–715. [Google Scholar] [CrossRef]
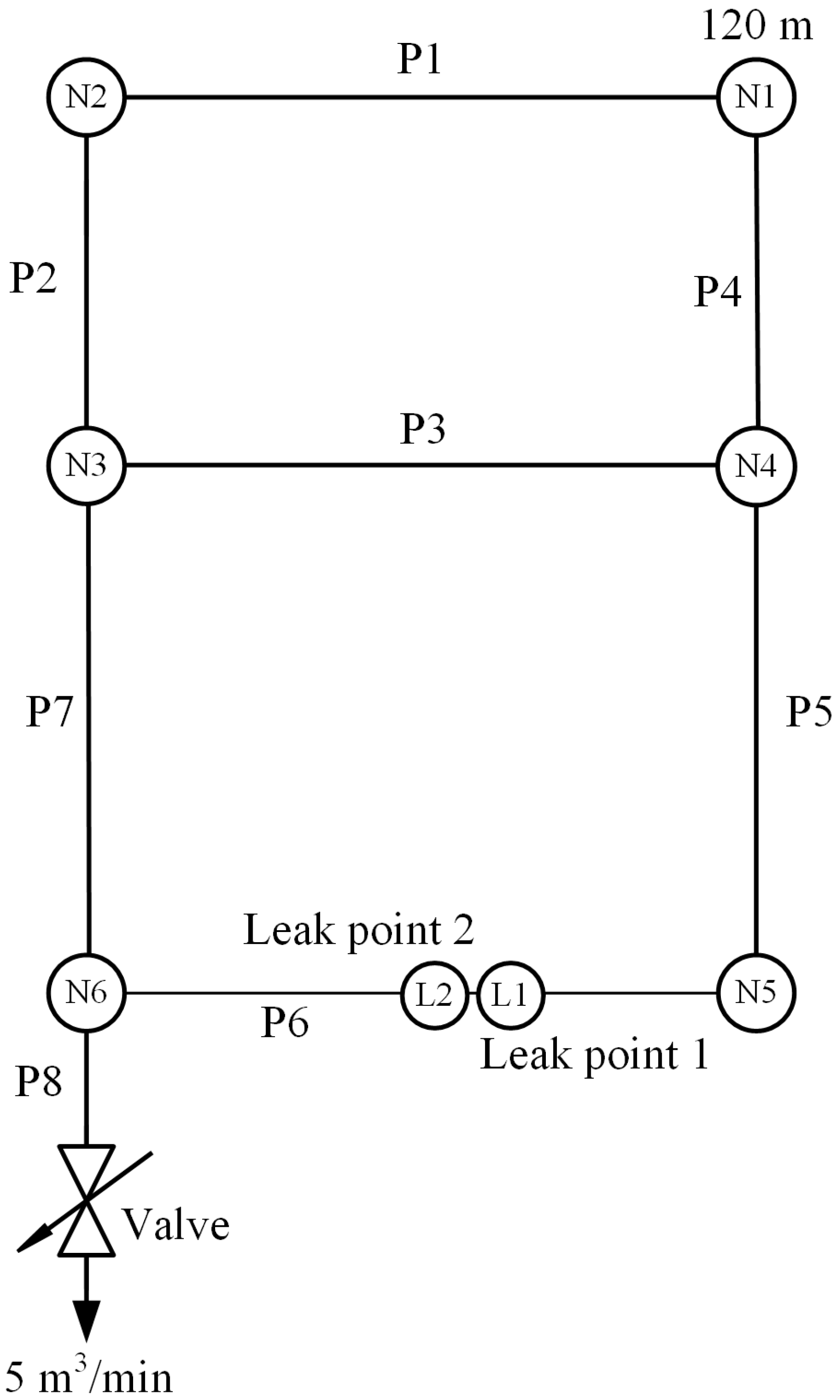
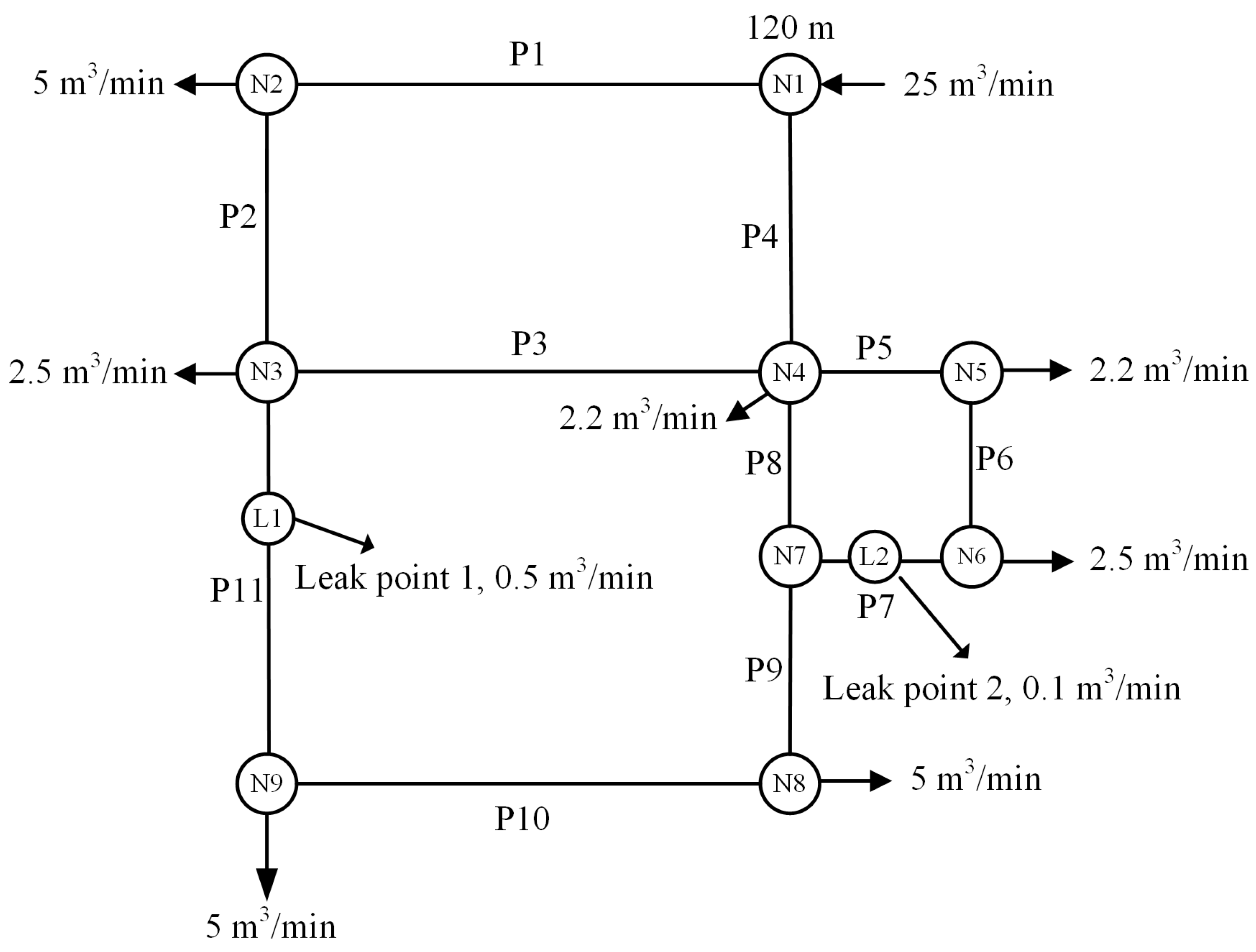
| Pipe | Node | Diameter (mm) | Length (m) | |
|---|---|---|---|---|
| Number | From | To | ||
| P1 | N1 | N2 | 305.0 | 1000.0 |
| P2 | N2 | N3 | 305.0 | 1000.0 |
| P3 | N3 | N4 | 250.0 | 1100.0 |
| P4 | N1 | N4 | 405.0 | 1250.0 |
| P5 | N4 | N5 | 355.0 | 1000.0 |
| P6 | N5 | N6 | 305.0 | 1100.0 |
| P7 | N3 | N6 | 305.0 | 1250.0 |
| P8 | N6 | Valve | 500.0 | 1000.0 |
| Pipe | Node | Diameter (mm) | Length (m) | |
|---|---|---|---|---|
| Number | From | To | ||
| P1 | N1 | N2 | 305.0 | 1000.0 |
| P2 | N2 | N3 | 305.0 | 1000.0 |
| P3 | N3 | N4 | 250.0 | 1100.0 |
| P4 | N1 | N4 | 405.0 | 1250.0 |
| P5 | N4 | N5 | 200.0 | 500.0 |
| P6 | N5 | N6 | 400.0 | 400.0 |
| P7 | N7 | N6 | 200.0 | 500.0 |
| P8 | N4 | N7 | 355.0 | 400.0 |
| P9 | N7 | N8 | 355.0 | 600.0 |
| P10 | N8 | N9 | 305.0 | 1100.0 |
| P11 | N3 | N9 | 305.0 | 1250.0 |
| Header | L1 | L2 | CPU Time (min) | Iterations | ||||
|---|---|---|---|---|---|---|---|---|
| Pipe No. | Location (m) | CdA × 10−4 (m2) | Pipe No. | Location (m) | CdA × 10−4 (m2) | |||
| Actual | 6 | 300 | 2.5 | 6 | 310 | 2.5 | - | - |
| LDSA | 6 | 300 | 2.5 | 6 | 310 | 2.5 | 372 | 9815 |
| LDSOS | 6 | 300 | 2.5 | 6 | 310 | 2.5 | 120 | 3481 |
| LDOSOS | 6 | 300 | 2.5 | 6 | 310 | 2.5 | 50 | 1469 |
| Node | y (s) | z (m3/min) | EMax |
|---|---|---|---|
| N2 | 7.2 | −5.0 | 1239 |
| N8 | 2.7 | −2.58 | 1978 |
| N9 | 3.6 | −3.22 | 1843 |
| Header | N8 | N9 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| L1 | L2 | L1 | L2 | |||||||||
| Pipe No. | Location (m) | CdA × 10−4 (m2) | Pipe No. | Location (m) | CdA × 10−4 (m2) | Pipe No. | Location (m) | CdA × 10−4 (m2) | Pipe No. | Location (m) | CdA × 10−4 (m2) | |
| Actual | 11 | 300 | 2.5 | 7 | 250 | 1 | 11 | 300 | 2.5 | 7 | 250 | 1 |
| LDOSOS | 11 | 300 | 2.499 | 7 | 250 | 1 | 11 | 300 | 2.479 | 7 | 250 | 0.964 |
| Prediction Errors | ||
|---|---|---|
| Scenario 1 | ME (m) | SEE (m) |
| Case 1 | −1.76 10−6 | 4.11 10−4 |
| Case 2 | 1.35 10−5 | 5.63 10−2 |
| Scenario 2 | ME (m) | SEE (m) |
| Case 1 | 6.13 10−6 | 8.13 10−4 |
| Case 2 | 7.41 10−5 | 6.58 10−2 |
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, C.-C. A Hybrid Heuristic Optimization Approach for Leak Detection in Pipe Networks Using Ordinal Optimization Approach and the Symbiotic Organism Search. Water 2017, 9, 812. https://doi.org/10.3390/w9100812
Lin C-C. A Hybrid Heuristic Optimization Approach for Leak Detection in Pipe Networks Using Ordinal Optimization Approach and the Symbiotic Organism Search. Water. 2017; 9(10):812. https://doi.org/10.3390/w9100812
Chicago/Turabian StyleLin, Chao-Chih. 2017. "A Hybrid Heuristic Optimization Approach for Leak Detection in Pipe Networks Using Ordinal Optimization Approach and the Symbiotic Organism Search" Water 9, no. 10: 812. https://doi.org/10.3390/w9100812
APA StyleLin, C.-C. (2017). A Hybrid Heuristic Optimization Approach for Leak Detection in Pipe Networks Using Ordinal Optimization Approach and the Symbiotic Organism Search. Water, 9(10), 812. https://doi.org/10.3390/w9100812





