The Spatial and Temporal Structure of Extreme Rainfall Trends in South Korea
Abstract
1. Introduction
2. Materials
3. Method
3.1. Block Bootstrap-Based Mann-Kendall Test
- (1)
- Estimate the test statistic S of the MK from the original time series. The test statistic S is given as follows:where and are the sequential data values, and n is the total number of observations in the time series. A positive value of test statistic S indicates an increasing trend, whereas a negative value of this quantity indicates a decreasing trend.
- (2)
- Estimate the number of significant contiguous autocorrelations k. When the autocorrelation is smaller than 5% significant level, the lag of the autocorrelation becomes k.
- (3)
- Resample the original time series a large number of times using blocks of size k + g.
- (4)
- Estimate the test statistic S for each simulated sample to produce a simulated distribution of the test statistic S.
- (5)
- Estimate the significance (p-value) of the test statistic S estimated in Step 1 using the simulated distribution from Step 3.
3.2. Modified Version of Mann-Kendall Test
3.3. Scaling Property of Extreme Rainfall Events
4. Application
5. Results
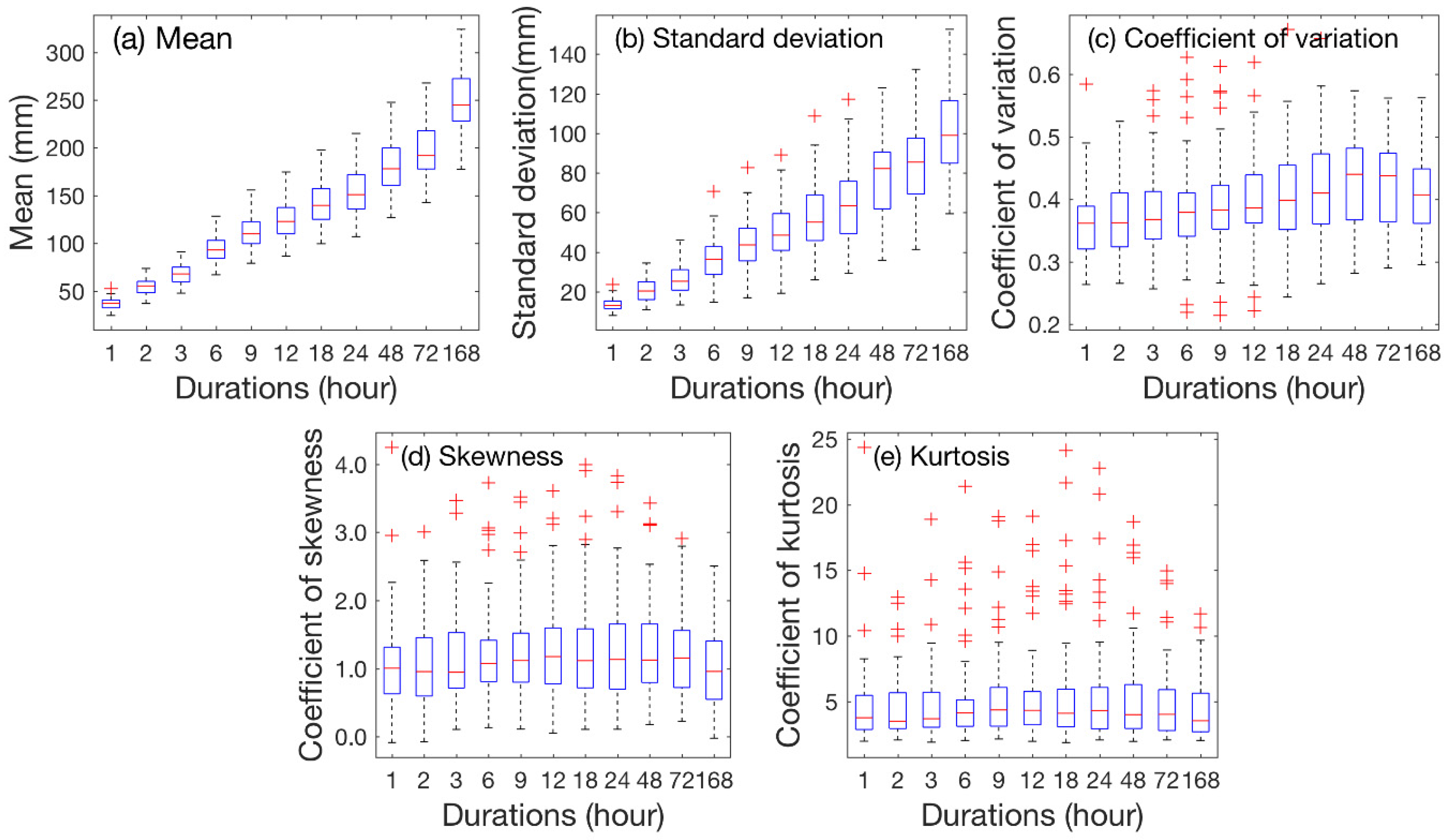
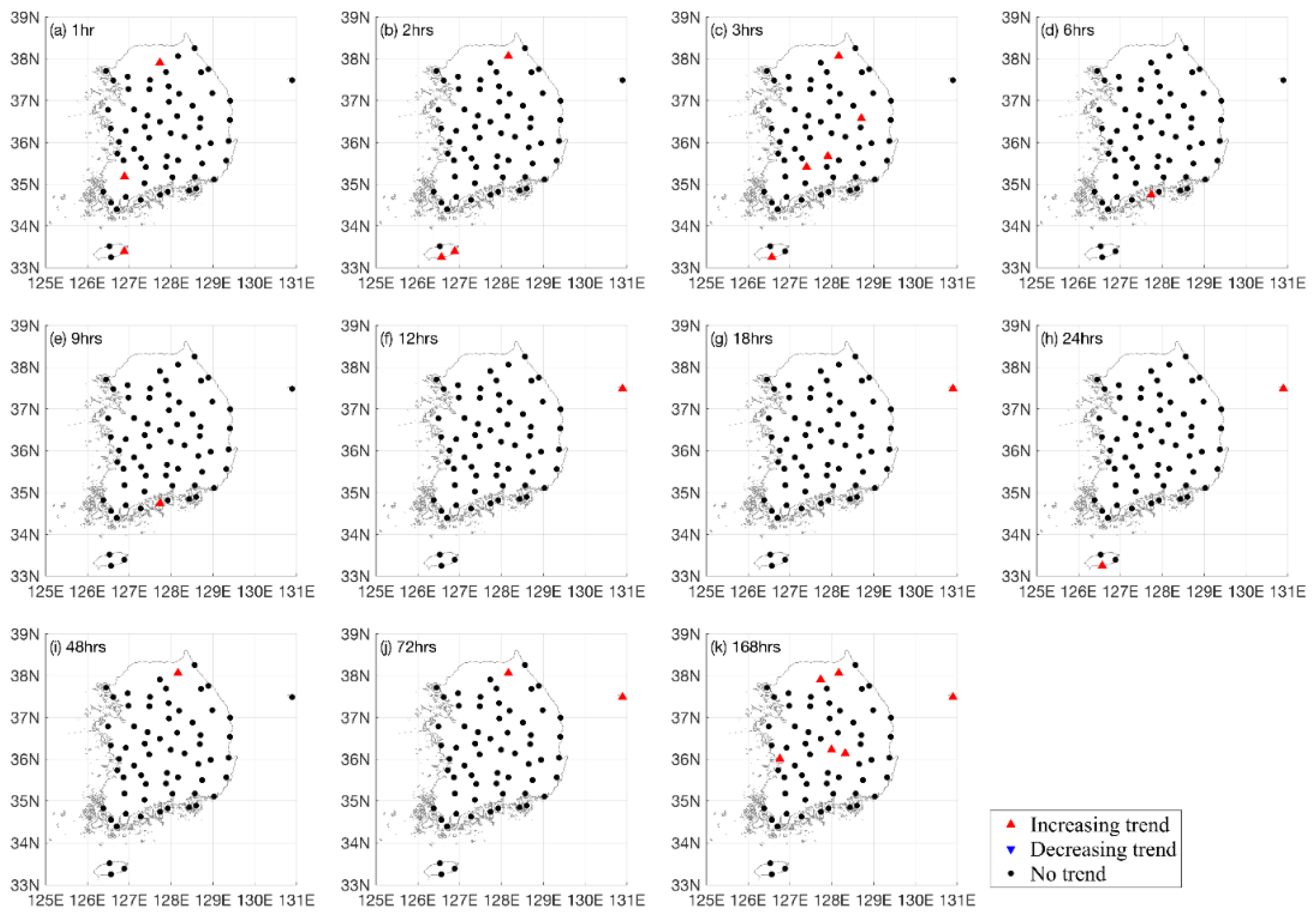
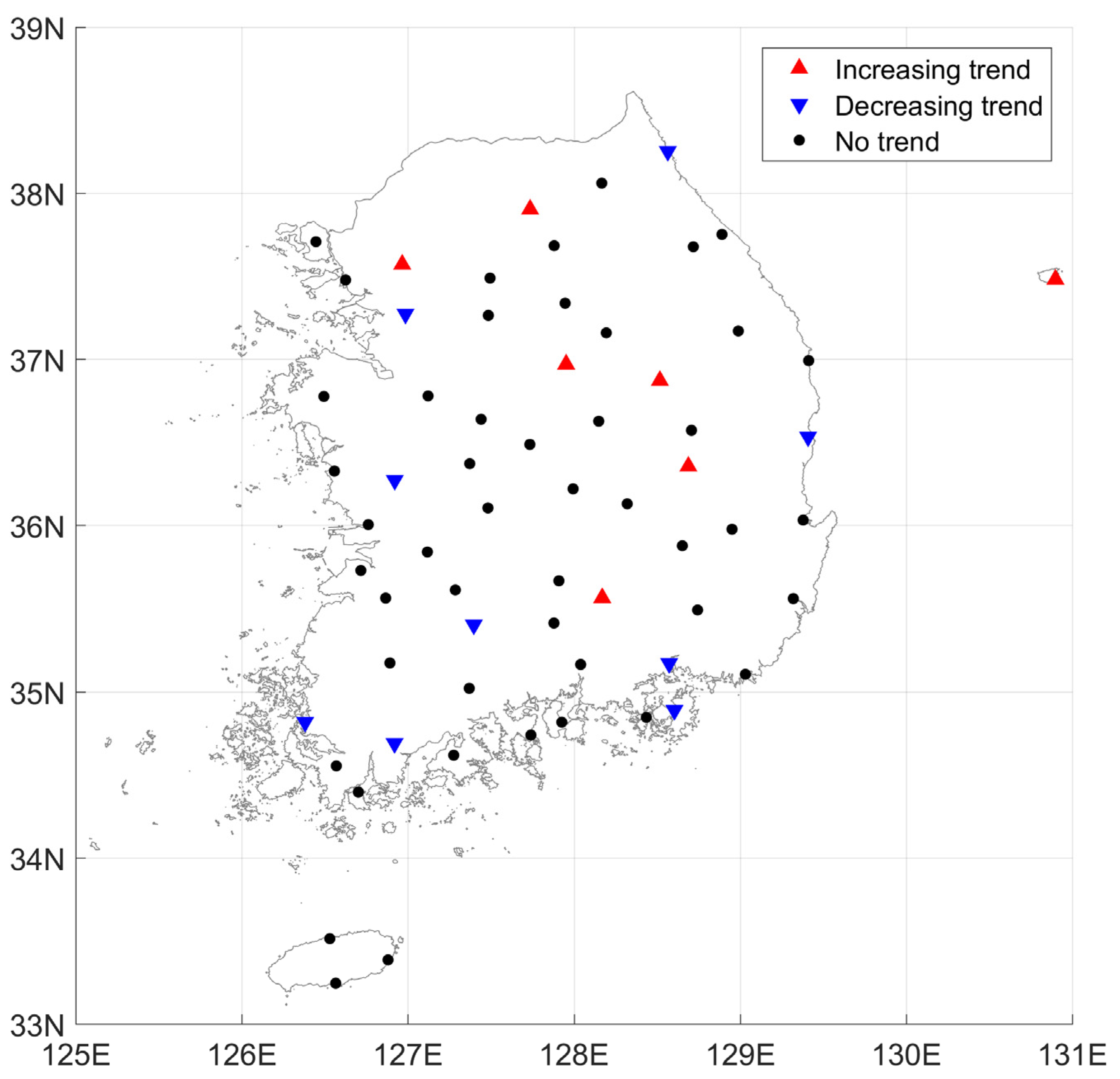
5.1. Trends in Time Series of Annual Maximum Rainfall
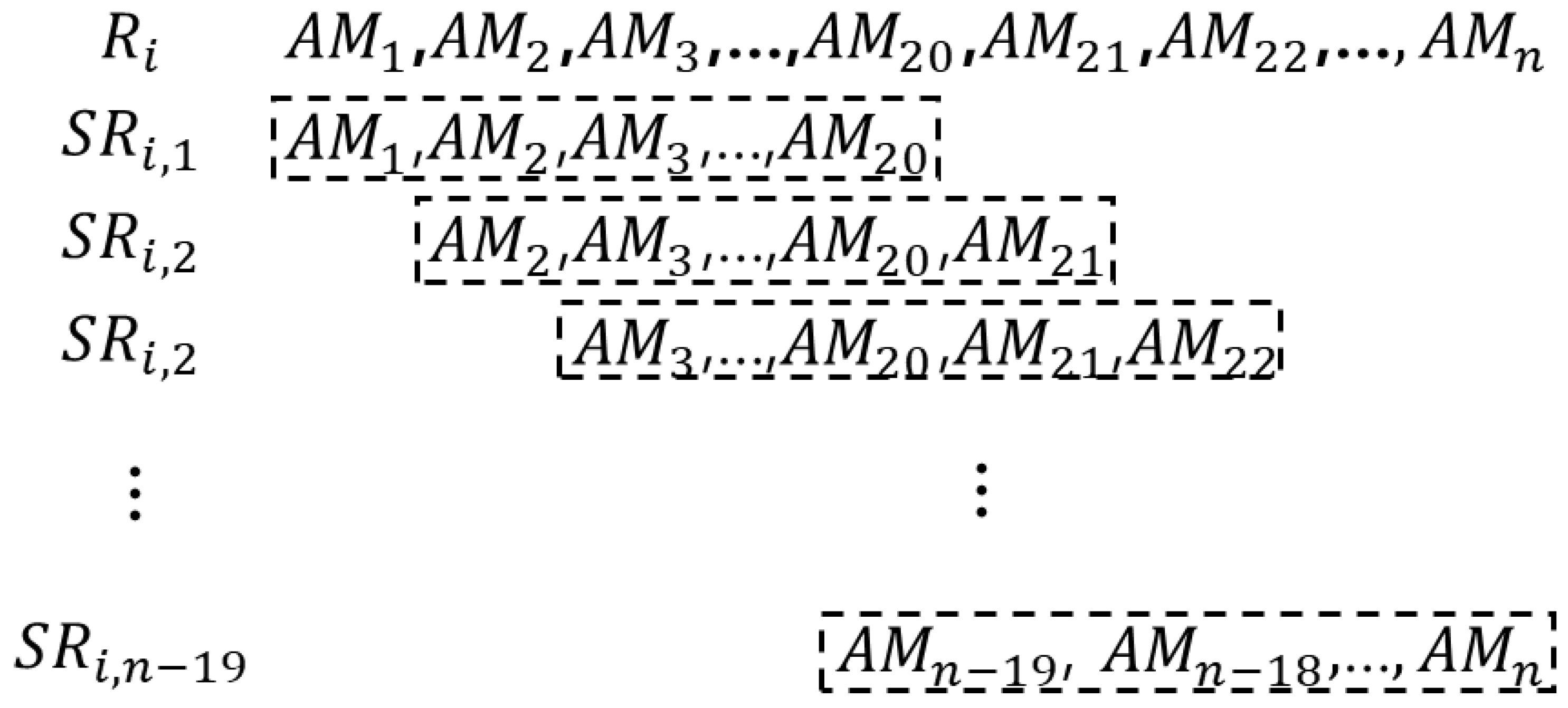
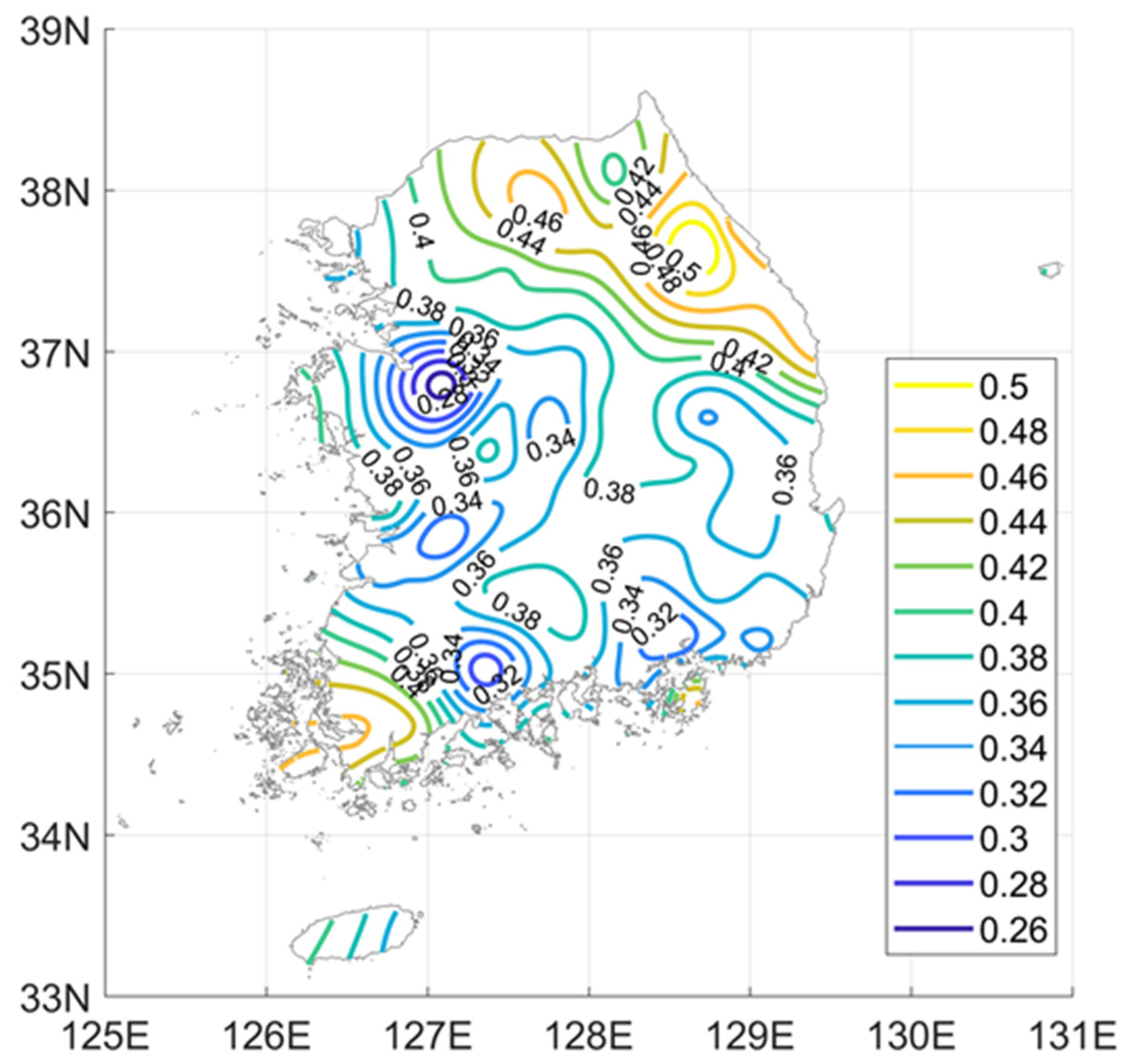
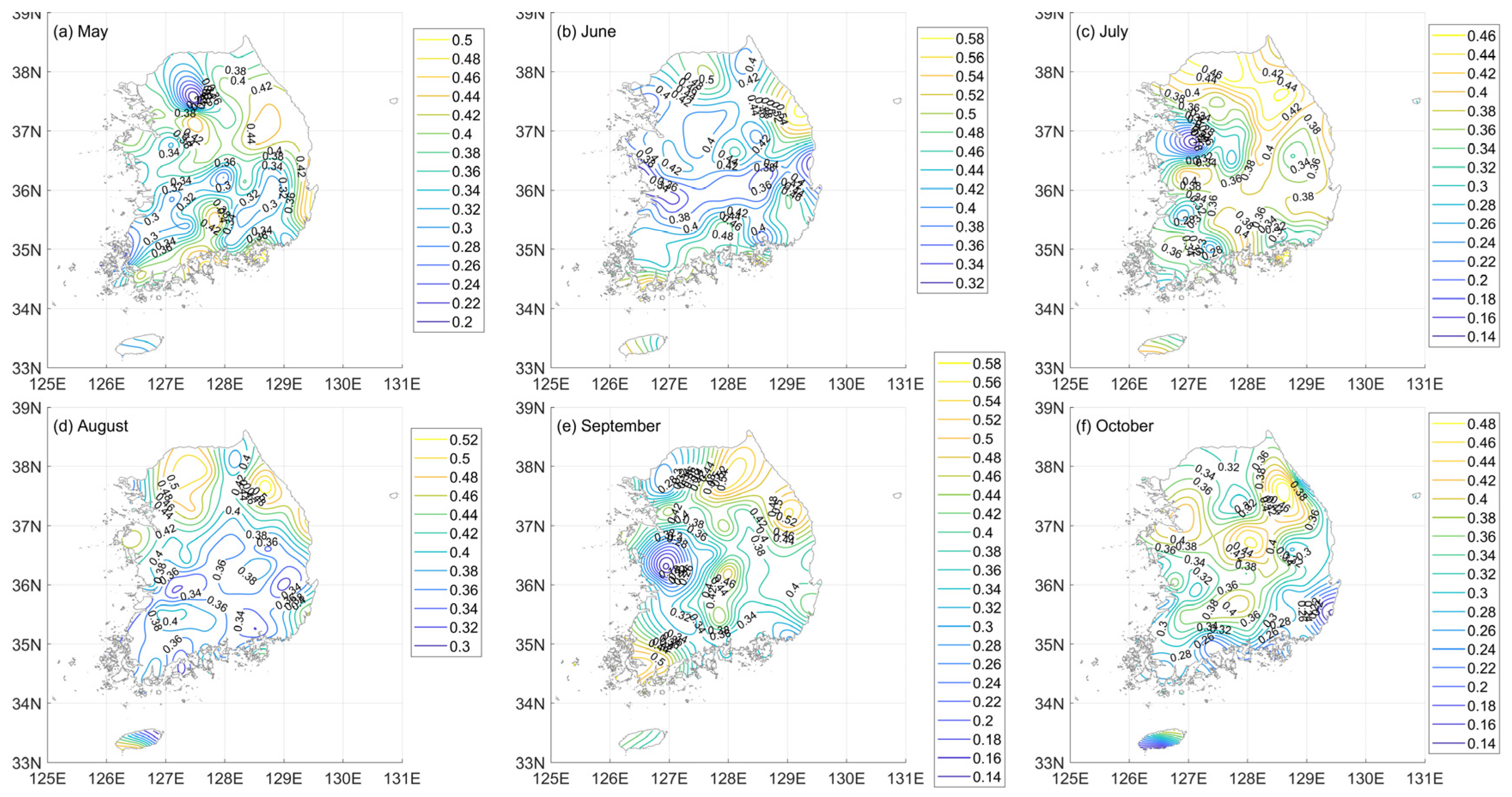
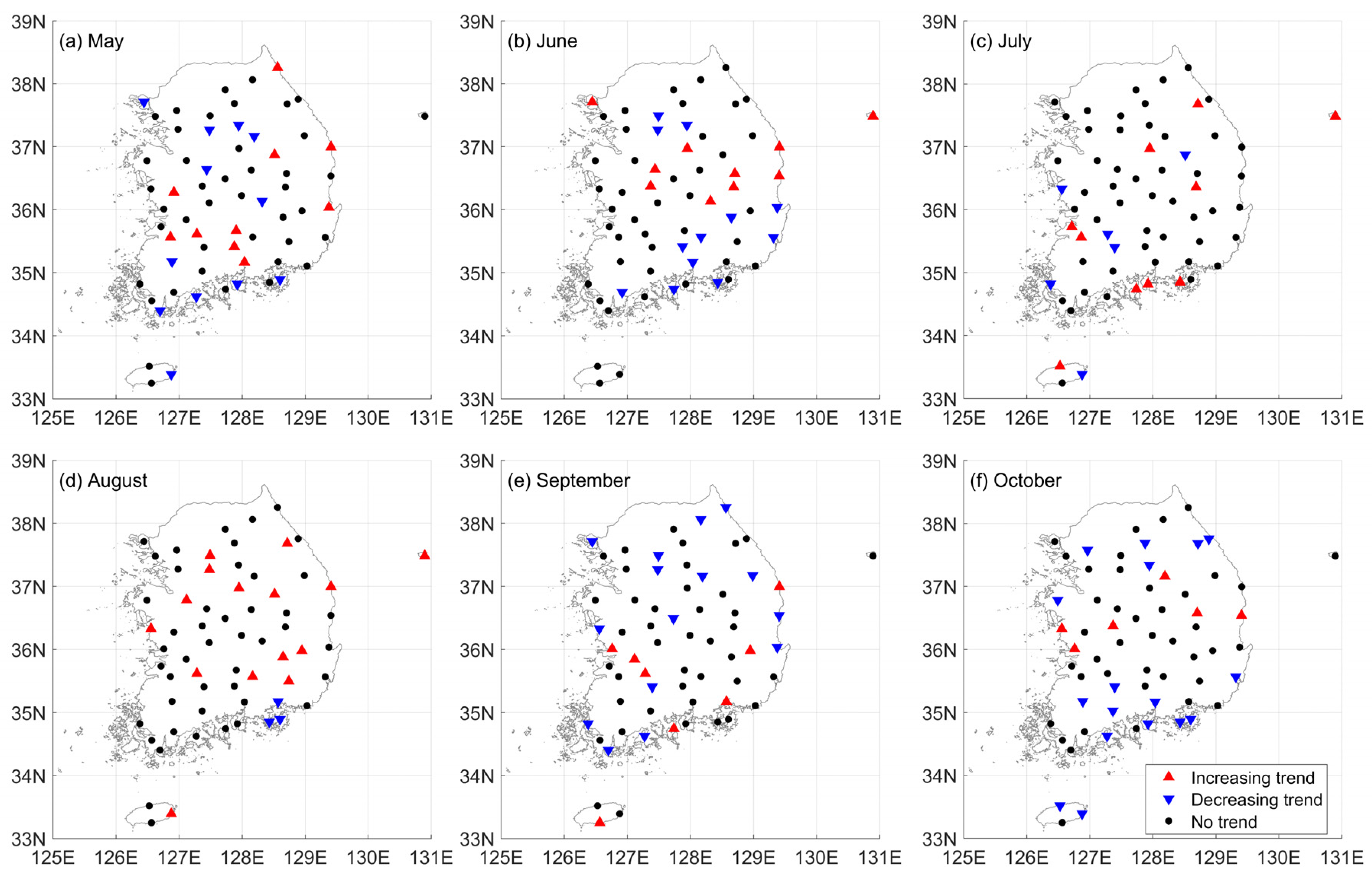
5.2. Trends in Temporal Structure of the Time Series of Annual Maximum Rainfall
6. Discussion
6.1. Characteristics of Spatial and Temporal Structure of Extreme Rainfall Trends in South Korea
6.2. Limitation of the Employed Methodology
7. Conclusions
- Significant trends are detected at a small number of stations, while no significant trends in extreme rainfall events can be found at many stations for the durations examined. Significant trends are sporadically detected at a few stations and for a few durations. There is no spatial pattern of the detected trends.
- There is large variability in the temporal structures of the extreme rainfall events. The scaling exponent estimates of the AM series in South Korea range from 0.25 to 0.5. The scaling exponent estimates in the inland part of the country are approximately 0.35. Large values of the scaling exponent are observed in the northeast, and small values of the scaling exponent are observed in the northeast. Additionally, the interannual variability in the temporal structure of the AM series is very large during the rainy season. The variations in the scaling exponent estimates during the rainy season are larger than those inferred using annual data. The spatial distribution of the scaling exponent estimates during the rainy season displays no dominant tendency. The spatial distributions of the scaling exponents for each month are dissimilar.
- Significant trends exist in the temporal structures of extreme rainfall events at many stations in South Korea. Decreasing trends are observed at many stations located in the coastal area, particularly in the southwest, whereas increasing trends are observed in the inland part of the country. The variability in the AM series with different durations in the inland part of the country is increasing over time. Additionally, the interannual variability in the trends in the temporal structure of extreme rainfall in South Korea is large. The spatial distributions of the trends for the time series of scaling exponent estimates differ by month.
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Balling, R.C., Jr.; Cerveny, R.S. Compilation and discussion of trends in severe storms in the United States: Popular perception v. Climate reality. Nat. Hazards 2003, 29, 103–112. [Google Scholar] [CrossRef]
- Garcia, J.A.; Gallego, M.C.; Serrano, A.; Vaquero, J.M. Trends in block-seasonal extreme rainfall over the Iberian Peninsula in the second half of the twentieth century. J. Clim. 2007, 20, 113–130. [Google Scholar] [CrossRef]
- Modarres, R.; da Silva, V.P.R. Rainfall trends in arid and semi-arid regions of Iran. J. Arid Environ. 2007, 70, 344–355. [Google Scholar] [CrossRef]
- Ntegeka, V.; Willems, P. Trends and multidecadal oscillations in rainfall extremes, based on a more than 100-year time series of 10 min rainfall intensities at Uccle, Belgium. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Aryal, S.K.; Bates, B.C.; Campbell, E.P.; Li, Y.; Palmer, M.J.; Viney, N.R. Characterizing and modeling temporal and spatial trends in rainfall extremes. J. Hydrometeorol. 2009, 10, 241–253. [Google Scholar] [CrossRef]
- Acero, F.J.; García, J.A.; Gallego, M.C. Peaks-over-threshold study of trends in extreme rainfall over the Iberian Peninsula. J. Clim. 2010, 24, 1089–1105. [Google Scholar] [CrossRef]
- McAfee, S.A.; Guentchev, G.; Eischeid, J.K. Reconciling precipitation trends in Alaska: 1. Station-based analyses. J. Geophys. Res.: Atmos. 2013, 118, 7523–7541. [Google Scholar] [CrossRef]
- Sarr, M.A.; Zoromé, M.; Seidou, O.; Bryant, C.R.; Gachon, P. Recent trends in selected extreme precipitation indices in senegal—A changepoint approach. J. Hydrol. 2013, 505, 326–334. [Google Scholar] [CrossRef]
- Ye, Z.; Li, Z. Spatiotemporal variability and trends of extreme precipitation in the huaihe river basin, a climatic transitional zone in east China. Adv. Meteorol. 2017, 2017, 1–15. [Google Scholar]
- Zwiers, F.W.; Kharin, V.V. Changes in the extremes of the climate simulated by CCC GCM2 under CO2 doubling. J. Clim. 1998, 11, 2200–2222. [Google Scholar] [CrossRef]
- Boo, K.O.; Kwon, W.T.; Baek, H.J. Change of extreme events of temperature and precipitation over Korea using regional projection of future climate change. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Kay, A.L.; Reynard, N.S.; Jones, R.G. RCM rainfall for UK flood frequency estimation. I. Method and validation. J. Hydrol. 2006, 318, 151–162. [Google Scholar] [CrossRef]
- Kay, A.L.; Jones, R.G.; Reynard, N.S. RCM rainfall for UK flood frequency estimation. II. Climate change results. J. Hydrol. 2006, 318, 163–172. [Google Scholar] [CrossRef]
- Wang, D.; Hagen, S.C.; Alizad, K. Climate change impact and uncertainty analysis of extreme rainfall events in the apalachicola river basin, Florida. J. Hydrol. 2013, 480, 125–135. [Google Scholar] [CrossRef]
- Shahabul Alam, M.; Elshorbagy, A. Quantification of the climate change-induced variations in intensity–duration–frequency curves in the canadian prairies. J. Hydrol. 2015, 527, 990–1005. [Google Scholar] [CrossRef]
- Lee, O.; Park, Y.; Kim, E.S.; Kim, S. Projection of korean probable maximum precipitation under future climate change scenarios. Adv. Meteorol. 2016, 2016, 1–16. [Google Scholar] [CrossRef]
- Langousis, A.; Veneziano, D.; Furcolo, P.; Lepore, C. Multifractal rainfall extremes: Theoretical analysis and practical estimation. Chaos Solitons Fractals 2009, 39, 1182–1194. [Google Scholar] [CrossRef]
- Rodríguez, R.; Navarro, X.; Casas, M.C.; Ribalaygua, J.; Russo, B.; Pouget, L.; Redaño, A. Influence of climate change on idf curves for the metropolitan area of Barcelona (Spain). Int. J. Climatol. 2014, 34, 643–654. [Google Scholar] [CrossRef]
- Bairwa, A.K.; Khosa, R.; Maheswaran, R. Developing intensity duration frequency curves based on scaling theory using linear probability weighted moments: A case study from India. J. Hydrol. 2016, 542, 850–859. [Google Scholar] [CrossRef]
- Ghanmi, H.; Bargaoui, Z.; Mallet, C. Estimation of intensity-duration-frequency relationships according to the property of scale invariance and regionalization analysis in a mediterranean coastal area. J. Hydrol. 2016, 541, 38–49. [Google Scholar] [CrossRef]
- Tan, X.; Gan, T.Y. Multifractality of Canadian precipitation and streamflow. Int. J. Climatol. 2017. [Google Scholar] [CrossRef]
- Menabde, M.; Seed, A.; Pegram, G. A simple scaling model for extreme rainfall. Water Resour. Res. 1999, 35, 335–339. [Google Scholar] [CrossRef]
- Galmarini, S.; Steyn, D.G.; Ainslie, B. The scaling law relating world point-precipitation records to duration. Int. J. Climatol. 2004, 24, 533–546. [Google Scholar] [CrossRef]
- Ceresetti, D.; Molinié, G.; Creutin, J.D. Scaling properties of heavy rainfall at short duration: A regional analysis. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Rodríguez-Solà, R.; Casas-Castillo, M.C.; Navarro, X.; Redaño, Á. A study of the scaling properties of rainfall in spain and its appropriateness to generate intensity-duration-frequency curves from daily records. Int. J. Climatol. 2017, 37, 770–780. [Google Scholar] [CrossRef]
- Jung, I.W.; Bae, D.H.; Kim, G. Recent trends of mean and extreme precipitation in Korea. Int. J. Climatol. 2011, 31, 359–370. [Google Scholar] [CrossRef]
- Park, J.-S.; Kang, H.-S.; Lee, Y.S.; Kim, M.-K. Changes in the extreme daily rainfall in South Korea. Int. J. Clim. 2011, 31, 2290–2299. [Google Scholar] [CrossRef]
- Wi, S.; Valdés, J.; Steinschneider, S.; Kim, T.-W. Non-stationary frequency analysis of extreme precipitation in South Korea using peaks-over-threshold and annual maxima. Stoch. Environ. Res. Risk Assess. 2016, 30, 583–606. [Google Scholar] [CrossRef]
- Jung, Y.; Kim, S.; Kim, T.; Heo, J.-H. Rainfall quantile estimation using scaling property in Korea. J. Korea Water Resour. Assoc. 2008, 41, 873–884. [Google Scholar] [CrossRef]
- Kim, J.-Y.; Kwon, H.-H.; Lee, B.-S. A bayesian glm model based regional frequency analysis using scaling properties of extreme rainfalls. J. Korea Soc. Civ. Eng. 2017, 37, 29–41. [Google Scholar] [CrossRef]
- Kang, H.S.; Cha, D.H.; Lee, D.K. Evaluation of the mesoscale model/land surface model (MM5/LSM) coupled model for East Asian summer monsoon simulations. J. Geophys. Res.: Atmos. 2005, 110. [Google Scholar] [CrossRef]
- Baek, H.-J.; Kim, M.-K.; Kwon, W.-T. Observed short- and long-term changes in summer precipitation over South Korea and their links to large-scale circulation anomalies. Int. J. Climatol. 2017, 37, 972–986. [Google Scholar] [CrossRef]
- Im, E.-S.; Ahn, J.-B.; Remedio, A.R.; Kwon, W.-T. Sensitivity of the regional climate of East/Southeast Asia to convective parameterizations in the RegCM3 modelling system. Part 1: Focus on the Korean Peninsula. Int. J. Climatol. 2008, 28, 1861–1877. [Google Scholar] [CrossRef]
- Lau, K.-M.; Li, M.-T. The monsoon of East Asia and its global associations—A survey. Bull. Am. Meteorol. Soc. 1984, 65, 114–125. [Google Scholar] [CrossRef]
- Kim, J.-S.; Jain, S. Precipitation trends over the Korean peninsula: Typhoon-induced changes and a typology for characterizing climate-related risk. Environ. Res. Lett. 2011, 6, 1–6. [Google Scholar] [CrossRef]
- Korea Meteorological Administration (KMA). Typhoon White Book; KMA: Seoul, Korea, 2011; p. 330. [Google Scholar]
- Von Storch, H. Misuses of statistical analysis in climate research. In Analysis of Climate Variability: Applications of Statistical Techniques Proceedings of an Autumn School Organized by the Commission of the European Community on Elba from 30 October to 6 November 1993; von Storch, H., Navarra, A., Eds.; Springer: Berlin/Heidelberg, Germany, 1999; pp. 11–26. [Google Scholar]
- Yue, S.; Pilon, P.; Phinney, B.; Cavadias, G. The influence of autocorrelation on the ability to detect trend in hydrological series. Hydrol. Process. 2002, 16, 1807–1829. [Google Scholar] [CrossRef]
- Hamed, K.H.; Rao, A. A modified mann-kendall trend test for autocorrelated data. J. Hydrol. 1998, 204, 182–196. [Google Scholar] [CrossRef]
- Yue, S.; Wang, C.Y. Applicability of prewhitening to eliminate the influence of serial correlation on the mann-kendall test. Water Resour. Res. 2002, 38, WR000861. [Google Scholar] [CrossRef]
- Yue, S.; Wang, C. The mann-kendall test modified by effective sample size to detect trend in serially correlated hydrological series. Water Resour. Manag. 2004, 18, 201–218. [Google Scholar] [CrossRef]
- Önöz, B.; Bayazit, M. Block bootstrap for mann-kendall trend test of serially dependent data. Hydrol. Process. 2012, 26, 3552–3560. [Google Scholar] [CrossRef]
- Khaliq, M.N.; Ouarda, T.B.M.J.; Gachon, P.; Sushama, L.; St-Hilaire, A. Identification of hydrological trends in the presence of serial and cross correlations: A review of selected methods and their application to annual flow regimes of Canadian rivers. J. Hydrol. 2009, 368, 117–130. [Google Scholar] [CrossRef]
- Svensson, C.; Kundzewicz, W.Z.; Maurer, T. Trend detection in river flow series: 2. Flood and low-flow index series/détection de tendance dans des séries de débit fluvial: 2. Séries d’indices de crue et d’étiage. Hydrol. Sci. J. 2005, 50, 811–824. (In French) [Google Scholar] [CrossRef]
- Yue, S.; Wang, C.Y. Regional streamflow trend detection with consideration of both temporal and spatial correlation. Int. J. Climatol. 2002, 22, 933–946. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric tests against trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods; Griffin, C., Ed.; Oxford: London, UK, 1948. [Google Scholar]
- Blain, G.C. The modified mann-kendall test: On the performance of three variance correction approaches. Bragantia 2013, 72, 416–425. [Google Scholar] [CrossRef]
- Matalas, N.C.; Langbein, W.B. Information content of the mean. J. Geophys. Res. 1962, 67, 3441–3448. [Google Scholar] [CrossRef]
- Bayley, G.V.; Hammersley, J.M. The “effective” number of independent observations in an autocorrelated time series. J. R. Stat. Soc. 1946, 8, 184–197. [Google Scholar] [CrossRef]
- Gupta, V.K.; Waymire, E. Multiscaling properties of spatial rainfall and river flow distributions. J. Geophys. Res. Atmos. 1990, 95, 1999–2009. [Google Scholar] [CrossRef]
- Burlando, P.; Rosso, R. Scaling and muitiscaling models of depth-duration-frequency curves for storm precipitation. J. Hydrol. 1996, 187, 45–64. [Google Scholar] [CrossRef]
- Nguyen, V.T.V.; Nguyen, T.D.; Wang, H. Regional estimation of short duration rainfall extremes. Water Sci. Technol. 1998, 37, 15–19. [Google Scholar]
- Ahmad, M.I.; Sinclair, C.D.; Spurr, B.D. Assessment of flood frequency models using empirical distribution function statistics. Water Resour. Res. 1988, 24, 1323–1328. [Google Scholar] [CrossRef]
- Farquharson, F.A.K.; Meigh, J.R.; Sutcliffe, J.V. Regional flood frequency analysis in arid and semi-arid areas. J. Hydrol. 1992, 138, 487–501. [Google Scholar] [CrossRef]
- Martins, E.S.; Stedinger, J.R. Generalized maximum-likelihood generalized extreme-value quantile estimators for hydrologic data. Water Resour. Res. 2000, 36, 737–744. [Google Scholar] [CrossRef]
- El-Adlouni, S.; Ouarda, T.B.M.J.; Zhang, X.; Roy, R.; Bobée, B. Generalized maximum likelihood estimators for the nonstationary generalized extreme value model. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Heo, J.H.; Kho, Y.W.; Shin, H.; Kim, S.; Kim, T. Regression equations of probability plot correlation coefficient test statistics from several probability distributions. J. Hydrol. 2008, 355, 1–15. [Google Scholar] [CrossRef]
- El-Adlouni, S.; Ouarda, T.B.M.J. Joint bayesian model selection and parameter estimation of the generalized extreme value model with covariates using birth-death markov chain monte carlo. Water Resour. Res. 2009, 45, W06403. [Google Scholar] [CrossRef]
- Heo, J.-H.; Shin, H.; Nam, W.; Om, J.; Jeong, C. Approximation of modified anderson–darling test statistics for extreme value distributions with unknown shape parameter. J. Hydrol. 2013, 499, 41–49. [Google Scholar] [CrossRef]
- Masina, M.; Lamberti, A. A nonstationary analysis for the northern adriatic extreme sea levels. J. Geophys. Res. Ocean 2013, 118, 3999–4016. [Google Scholar] [CrossRef]
- Rahman, A.; Rahman, A.; Zaman, M.; Haddad, K.; Ahsan, A.; Imteaz, M. A study on selection of probability distributions for at-site flood frequency analysis in Australia. Nat. Hazards 2013, 69, 1803–1813. [Google Scholar] [CrossRef]
- Nasri, B.; El Adlouni, S.; Ouarda, T.B. Bayesian estimation for GEV-B-Spline model. Open J. Stat. 2013, 3, 118–128. [Google Scholar] [CrossRef]
- Nguyen, C.C.; Gaume, E.; Payrastre, O. Regional flood frequency analyses involving extraordinary flood events at ungauged sites: Further developments and validations. J. Hydrol. 2014, 508, 385–396. [Google Scholar] [CrossRef]
- Overeem, A.; Buishand, A.; Holleman, I. Rainfall depth-duration-frequency curves and their uncertainties. J. Hydrol. 2008, 348, 124–134. [Google Scholar] [CrossRef]
- Villarini, G. Analyses of annual and seasonal maximum daily rainfall accumulations for Ukraine, Moldova, and Romania. Int. J. Climatol. 2012, 32, 2213–2226. [Google Scholar] [CrossRef]
- Veneziano, D.; Yoon, S. Rainfall extremes, excesses, and intensity-duration-frequency curves: A unified asymptotic framework and new nonasymptotic results based on multifractal measures. Water Resour. Res. 2013, 49, 4320–4334. [Google Scholar] [CrossRef]
- Rulfová, Z.; Buishand, A.; Roth, M.; Kyselý, J. A two-component generalized extreme value distribution for precipitation frequency analysis. J. Hydrol. 2016, 534, 659–668. [Google Scholar] [CrossRef]
- Bougadis, J.; Adamowski, K. Scaling model of a rainfall intensity-duration-frequency relationship. Hydrol. Process. 2006, 20, 3747–3757. [Google Scholar] [CrossRef]
- Borga, M.; Vezzani, C.; Fontana, G.D. Regional rainfall depth–duration–frequency equations for an alpine region. Nat. Hazards 2005, 36, 221–235. [Google Scholar] [CrossRef]
- Im, E.S.; Jung, I.W.; Bae, D.H. The temporal and spatial structures of recent and future trends in extreme indices over Korea from a regional climate projection. Int. J. Climatol. 2011, 31, 72–86. [Google Scholar] [CrossRef]
- Chang, H.; Kwon, W.-T. Spatial variations of summer precipitation trends in South Korea, 1973–2005. Environ. Res. Lett. 2007, 2, 045012. [Google Scholar] [CrossRef]
- Yu, P.-S.; Yang, T.-C.; Lin, C.-S. Regional rainfall intensity formulas based on scaling property of rainfall. J. Hydrol. 2004, 295, 108–123. [Google Scholar] [CrossRef]
- Blanchet, J.; Ceresetti, D.; Molinié, G.; Creutin, J.D. A regional GEV scale-invariant framework for intensity–duration–frequency analysis. J. Hydrol. 2016, 540, 82–95. [Google Scholar] [CrossRef]
- Soltani, S.; Helfi, R.; Almasi, P.; Modarres, R. Regionalization of rainfall intensity-duration-frequency using a simple scaling model. Water Resour. Manag. 2017, 31, 4253–4273. [Google Scholar] [CrossRef]
- Cheng, L.; AghaKouchak, A.; Gilleland, E.; Katz, R. Non-stationary extreme value analysis in a changing climate. Clim. Chang. 2014, 127, 353–369. [Google Scholar] [CrossRef]
- Vasiliades, L.; Galiatsatou, P.; Loukas, A. Nonstationary frequency analysis of annual maximum rainfall using climate covariates. Water Resour. Manag. 2015, 29, 339–358. [Google Scholar] [CrossRef]
- Cheng, L.; AghaKouchak, A. Nonstationary precipitation intensity-duration-frequency curves for infrastructure design in a changing climate. Sci. Rep. 2014, 4, 7093. [Google Scholar] [CrossRef] [PubMed]
- Sarhadi, A.; Soulis, E.D. Time-varying extreme rainfall intensity-duration-frequency curves in a changing climate. Geophys. Res. Lett. 2017, 44, 2454–2463. [Google Scholar] [CrossRef]
- Hamed, K.H. Exact distribution of the mann–kendall trend test statistic for persistent data. J. Hydrol. 2009, 365, 86–94. [Google Scholar] [CrossRef]

| No. | Name | Record Length (year) | Elevation (m) | No. | Name | Record Length (year) | Elevation (m) |
|---|---|---|---|---|---|---|---|
| 1 | Daegwallyeong | 45 | 772.43 | 33 | Yeongdeok | 44 | 41.2 |
| 2 | Jecheon | 44 | 263.1 | 34 | Pohang | 56 | 1.3 |
| 3 | Chungju | 44 | 113.7 | 35 | Namhae | 44 | 43.2 |
| 4 | Wonju | 44 | 150.7 | 36 | Geoje | 44 | 44.5 |
| 5 | Yangpyeong | 44 | 47.4 | 37 | Masan | 32 | 36.8 |
| 6 | Icheon | 44 | 90 | 38 | Tongyeong | 49 | 30.8 |
| 7 | Inje | 44 | 198.7 | 39 | Geumsan | 44 | 170.6 |
| 8 | Chuncheon | 51 | 76.8 | 40 | Chupungnyeong | 56 | 240.9 |
| 9 | Hongcheon | 44 | 146.2 | 41 | Boeun | 44 | 173 |
| 10 | Seoul | 56 | 85.5 | 42 | Daejeon | 48 | 62.6 |
| 11 | Suwon | 53 | 34.5 | 43 | Cheongju | 50 | 56.4 |
| 12 | Incheon | 56 | 69 | 44 | Buyeo | 44 | 11 |
| 13 | Ganghwa | 44 | 46.2 | 45 | Cheonan | 45 | 21.3 |
| 14 | Sokcho | 49 | 22.9 | 46 | Seosan | 49 | 25.2 |
| 15 | Gangneung | 56 | 26.1 | 47 | Gunsan | 49 | 26.9 |
| 16 | Taebaek | 32 | 714.2 | 48 | Boryeong | 44 | 17.9 |
| 17 | Andong | 39 | 140.7 | 49 | Jeonju | 56 | 61 |
| 18 | Yeongju | 44 | 210.5 | 50 | Jeongeup | 44 | 39.5 |
| 19 | Mungyeong | 44 | 170.8 | 51 | Buan | 44 | 3.6 |
| 20 | Uiseong | 44 | 82.6 | 52 | Imsil | 44 | 248 |
| 21 | Gumi | 44 | 47.4 | 53 | Namwon | 44 | 93.5 |
| 22 | Daegu | 56 | 57.3 | 54 | Wando | 45 | 27.7 |
| 23 | Yeongcheon | 44 | 93.3 | 55 | Suncheon | 43 | 74.4 |
| 24 | Geochang | 44 | 221.4 | 56 | Goheung | 44 | 53.3 |
| 25 | Hapcheon | 44 | 33 | 57 | Yoesu | 56 | 73.3 |
| 26 | Sancheong | 44 | 138.7 | 58 | Gwangju | 56 | 74.5 |
| 27 | Jinju | 48 | 27.1 | 59 | Jangheung | 44 | 44.5 |
| 28 | Miryang | 44 | 10.7 | 60 | Haenam | 44 | 4.6 |
| 29 | Ulsan | 56 | 34.6 | 61 | Mokpo | 56 | 37.4 |
| 30 | Busan | 56 | 69.2 | 62 | Jeju | 56 | 19.97 |
| 31 | Ulleungdo | 56 | 220 | 63 | Seogwipo | 56 | 50.4 |
| 32 | Uljin | 45 | 49.4 | 64 | Seongsan | 44 | 70.9 |
| No. | Scaling Exponent | Standard Deviation | No. | Scaling Exponent | Standard Deviation |
|---|---|---|---|---|---|
| 1 | 0.5166 (0.4392, 0.5472) | 0.0321 | 33 | 0.3776 (0.3287, 0.4408) | 0.0290 |
| 2 | 0.4010 (0.3653, 0.4410) | 0.0195 | 34 | 0.3756 (0.3054, 0.4255) | 0.0277 |
| 3 | 0.3598 (0.3160, 0.4201) | 0.0290 | 35 | 0.3638 (0.3443, 0.3927) | 0.0124 |
| 4 | 0.3963 (0.3533, 0.4288) | 0.0191 | 36 | 0.4412 (0.3606, 0.4822) | 0.0317 |
| 5 | 0.3988 (0.3419, 0.4589) | 0.0327 | 37 | 0.3075 (0.2722, 0.3664) | 0.0237 |
| 6 | 0.3968 (0.3225, 0.4662) | 0.0381 | 38 | 0.3674 (0.3330, 0.4074) | 0.0180 |
| 7 | 0.3974 (0.3429, 0.4792) | 0.0369 | 39 | 0.3435 (0.3194, 0.3719) | 0.0133 |
| 8 | 0.4729 (0.4404, 0.4960) | 0.0145 | 40 | 0.3814 (0.3561, 0.4089) | 0.0135 |
| 9 | 0.4494 (0.3963, 0.4802) | 0.0209 | 41 | 0.3234 (0.2499, 0.4053) | 0.0414 |
| 10 | 0.3966 (0.3268, 0.4547) | 0.0324 | 42 | 0.3846 (0.3488, 0.4022) | 0.0138 |
| 11 | 0.3848 (0.3240, 0.4333) | 0.0279 | 43 | 0.3628 (0.3048, 0.4048) | 0.0271 |
| 12 | 0.3648 (0.3196, 0.4087) | 0.0227 | 44 | 0.3638 (0.2252, 0.4147) | 0.0569 |
| 13 | 0.3529 (0.3287, 0.3924) | 0.0141 | 45 | 0.2500 (0.1527, 0.3987) | 0.0803 |
| 14 | 0.4524 (0.3737, 0.4998) | 0.0375 | 46 | 0.3813 (0.2830, 0.4498) | 0.0420 |
| 15 | 0.4576 (0.3634, 0.4677) | 0.0393 | 47 | 0.3858 (0.2818, 0.4657) | 0.0486 |
| 16 | 0.4472 (0.3721, 0.5121) | 0.0351 | 48 | 0.3859 (0.2413, 0.4578) | 0.0598 |
| 17 | 0.3392 (0.3004, 0.3966) | 0.0247 | 49 | 0.3052 (0.2858, 0.3269) | 0.0105 |
| 18 | 0.3897 (0.3406, 0.4484) | 0.0281 | 50 | 0.3418 (0.2643, 0.3896) | 0.0360 |
| 19 | 0.3903 (0.3593, 0.4173) | 0.0150 | 51 | 0.3235 (0.2882, 0.3569) | 0.0172 |
| 20 | 0.3760 (0.3417, 0.3990) | 0.0147 | 52 | 0.3695 (0.3219, 0.4038) | 0.0209 |
| 21 | 0.3777 (0.3549, 0.3975) | 0.0108 | 53 | 0.3733 (0.3368, 0.3990) | 0.0158 |
| 22 | 0.3620 (0.3331, 0.3915) | 0.0149 | 54 | 0.4136 (0.3217, 0.4851) | 0.0415 |
| 23 | 0.3501 (0.3124, 0.3906) | 0.0205 | 55 | 0.2873 (0.245, 0.3846) | 0.0464 |
| 24 | 0.3723 (0.3327, 0.4148) | 0.0217 | 56 | 0.3749 (0.2969, 0.4518) | 0.0424 |
| 25 | 0.3469 (0.3171, 0.3787) | 0.0159 | 57 | 0.3915 (0.3475, 0.4234) | 0.0194 |
| 26 | 0.3907 (0.3753, 0.4087) | 0.0085 | 58 | 0.3708 (0.3257, 0.3978) | 0.0192 |
| 27 | 0.3680 (0.3391, 0.3992) | 0.0158 | 59 | 0.4395 (0.3393, 0.4892) | 0.0443 |
| 28 | 0.3645 (0.3303, 0.4036) | 0.0182 | 60 | 0.4587 (0.3434, 0.4980) | 0.0493 |
| 29 | 0.3629 (0.2490, 0.4624) | 0.0549 | 61 | 0.4518 (0.3377, 0.4954) | 0.0523 |
| 30 | 0.3443 (0.2929, 0.3903) | 0.0257 | 62 | 0.3907 (0.3332, 0.4231) | 0.0228 |
| 31 | 0.3972 (0.3092, 0.4518) | 0.0364 | 63 | 0.3755 (0.2724, 0.4636) | 0.0498 |
| 32 | 0.4694 (0.4274, 0.4934) | 0.0175 | 64 | 0.3479 (0.2877, 0.3900) | 0.0268 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jung, Y.; Shin, J.-Y.; Ahn, H.; Heo, J.-H. The Spatial and Temporal Structure of Extreme Rainfall Trends in South Korea. Water 2017, 9, 809. https://doi.org/10.3390/w9100809
Jung Y, Shin J-Y, Ahn H, Heo J-H. The Spatial and Temporal Structure of Extreme Rainfall Trends in South Korea. Water. 2017; 9(10):809. https://doi.org/10.3390/w9100809
Chicago/Turabian StyleJung, Younghun, Ju-Young Shin, Hyunjun Ahn, and Jun-Haeng Heo. 2017. "The Spatial and Temporal Structure of Extreme Rainfall Trends in South Korea" Water 9, no. 10: 809. https://doi.org/10.3390/w9100809
APA StyleJung, Y., Shin, J.-Y., Ahn, H., & Heo, J.-H. (2017). The Spatial and Temporal Structure of Extreme Rainfall Trends in South Korea. Water, 9(10), 809. https://doi.org/10.3390/w9100809





