1. Introduction
Climate change is advancing globally [
1], and its impacts are growing on our planet. Some are already underway and others will occur in the near future. In Europe, land and sea temperatures are increasing; precipitation patterns are changing, generally making wet regions wetter, particularly in the winter, and dry regions drier, particularly in the summer; sea ice coverage, glacier volume and snow cover are decreasing and sea levels are rising; and climate-related extremes such as heat waves, heavy precipitation and droughts are increasing in frequency and intensity in many regions [
2].
Increasing pressure on water distribution, in terms of growing demand and decreasing availability due to climate change, require the adoption of appropriate optimization strategies in order to develop correct and efficient management of available resources. Over the last decades, optimization methods have been widely applied in water resources problems and many optimization models have been developed. These state-of-the-art models have been reviewed by several authors [
3,
4,
5,
6,
7]. Optimization of water systems follows different approaches, changing with the scale on which the system is analyzed, and various types of optimization techniques have been proposed.
In the context of climate change, due to the variability of rainfall and the scarcity of water, the conflicts between different uses, as well as the current structural and management problems must be overcome.
With regards to proper management strategy, the use of new sources of water supply seems to be a challenge, while the use of unconventional water resources, such as the reuse of waste water, is receiving more attention [
8,
9,
10,
11,
12,
13].
Optimization models and mixed simulation—optimization models have also been widely used for drinking water distribution systems. Specifically, drinking water distribution systems analysis and planning has been studied using linear programming (LP), nonlinear programming (NLP) and integer linear programming (ILP), together with the most recent probabilistic heuristic algorithms. Many of these models have been developed for solving least-cost design problems, with additional consideration of other aspects such as reliability and operational efficiency [
14,
15,
16,
17,
18,
19]. The pursuit of the optimal management of these systems also requires the improvement of water systems by reducing structural and management deficiencies, the risk analysis associated with the vulnerability of drinking water systems [
20] and the proper allocation of available water resources [
21].
Proper allocation of water resources is an important optimization problem and many studies have been conducted on this issue. In the last decades, problems related to the correct allocation of water resources have been assuming a growing interest in relation to hydrological regime changes and growing demand in different sectors. In this context, optimal distribution of available resources includes the ability to respond to the needs of different users and to promote equilibrium between economic, social and environmental aspects. Previously, several studies have been developed in this field with different approaches and conceptual models. Yamout and El-Fadel [
22] proposed and applied a multi-sectoral model for water resource allocations and management. Zhanping and Juncan [
23] proposed an optimization model for the optimal planning of complex water systems with multiple supply sources and multiple users, taking into account environmental considerations. Sun and Zeng [
24] adopted the optimization theory of the dynamic programming principle to build the Weinan city water resources optimization allocation model. Bai, Liu and Wang [
25] developed an optimal model for water allocation and water distribution network management where objectives include cost and water conservation. Ni, Liu, Ren and Yang [
26] investigated the optimal allocation of water resources for an urban water management system through a model based on multi-agent modeling technology.
In this context, the sustainable management of drinking water resource systems requires the establishment of local districts of a proper size where the service can be provided with adequate levels of efficiency. The best delimitation of such districts must take into account three different types of objectives: (1) political and administrative—making use of regional, provincial or municipal boundaries; (2) technical—identifying management areas comprising a homogeneous storage and distribution system; and (3) socio-economic—identifying the area where the lowest rate of application is sustainable. It should be noted that these goals are not always compatible and it is often necessary to prioritize some of them over others. The easiest and most frequent choice prioritizes the optimization of homogeneous infrastructure systems within defined administrative boundaries. In this context, the concept of sustainable water management requires the optimization of resource allocation in order to meet the demand even in a scenario of reduced water availability due to climate change. The goal of achieving the lowest water usage rate is of interest not only in relation to operating costs and economic management optimization, but also in relation to financial optimization of investment plans. In fact, the optimization of new pipelines has a positive impact on water tariffs. An immediate prediction of infrastructure developments is informed by parametric evaluations of the amount of work to be carried out, such as kilometers of networks. With the aim of proper management of investment plans, there is a need for fast and accurate methodological forecasting tools for drinking water systems optimization which are capable of accounting for possible future scenarios of reduction in water availability due to the effects of, for example, climate change or evolution of demand.
According to this approach, this paper identifies and compares water resource optimization solutions achieved in the province of Crotone (Calabria region, Southern Italy) through the redefinition of the distribution system, taking into account both current water availability and possible future reduction in water availability due to the scenarios projected by climate change analyses.
2. Materials and Methods
Climate change impact has been assessed by means of a simulation provided by the COSMO-Climate Limited-area Modeling (CCLM) [
27] Regional Climate Model (RCM) using the Representative Concentration Pathway (RCP) 4.5 [
28] in the context of the EURO-CORDEX initiative (
www. euro-cordex.net; a detailed description of the initiative can be found in [
29]). The CCLM model performed dynamic downscaling of the MPI-ESM-LR (Max Planck Institute Earth System Model at base resolution) General Circulation Model (GCM) and was applied at a resolution of 0.11° (approximately 12.5 km) both during the control period (1971–2005) and the future scenario (2016–2050). Further downscaling at an adequate resolution for the hydrological analysis needed in this study was performed with a distributed water balance model [
30]. The model simulated soil moisture and groundwater content dynamics, snow accumulation and melting, evapotranspiration, baseflow and subsurface/surface runoff on a 5-km resolution regular grid with a monthly time step, using temperature and precipitation provided by the RCM as climatic drivers. In addition, vegetation and soil properties were also needed as static input for the model, but they were considered constant over time both in the control period and future scenarios. The reliability of the water balance model has been widely tested on the entire regional territory of Calabria [
30,
31,
32]. The model, which assumed five years of acceleration in both the control period and in the future scenario, was able to assess changes in water resources availability for the climate change scenario and to proceed to the water scheme optimization.
The optimization model used in this paper is a least—cost optimization model aimed at identifying the proper allocation of drinking water resources, as proposed in [
21] and revised in [
33].
The optimization model analyzes the water resources available in a territory in relation to the demand of the users in order to determine the possible transfer of water resources in the territory by different schemes. The rationalization of water resources can be obtained through a review of the existing drinking water systems and the identification of optimal solutions to resource allocation. The model returns as output an ideal water supply system which is able to achieve optimal allocation in terms of the minimum overall cost for the completion of the supply system. This approach requires the solution of an optimization problem based on a nonlinear objective function, which is proportional to the cost of transferring water resources.
The optimization model was developed in MATLAB using the “fmincon” function, which allows an accurate and expeditious computational evaluation of the optimal solutions.
The model is defined as follows:
given m source nodes (springs, wells, intakes), each one characterized by a water availability (annual average flow) (L/s), labeled as ai, where i = 1, 2, …, m;
and fixed n destination nodes (users), each one characterized by a user demand (annual average demand) (L/s), labeled as bj, where j = 1, 2, …, n;
with the flow Qij (L/s) transferred from source node i to destination node j;
and the cost Cij of the transferring of Qij.
Then, the optimal allocation configuration is the one that minimizes the total cost of the whole water distribution system:
Regarding the cost, the method mainly refers to the cost of building the infrastructure, which can be considered as a function of the diameter
D and can be expressed in monomial form as in [
34]:
where the constants
K and
α depend on pipeline material.
The specific modeling of the cost function is that proposed in [
21] and revised in [
33]:
where the parameters depend on the type of material, its class, and the state of the pipeline material; in particular,
Lij is the distance between nodes
i and
j, and
Yij = hi −
hj is the corresponding piezometric head difference.
The solution of the optimal water allocation problem requires that the decision variables Qij are determined such that the cost function (3) is minimized and appropriate constraints, described later, are satisfied. The required solution is the set of links between source and destination nodes that represents the optimal water allocation in the analyzed area.
Constraints of physical and planning limitations have been imposed on the model to represent the actual operational characteristics of a given water resources system. With respect to the investigated problem, the following considerations are relevant.
Total water supplied from each source node
i cannot exceed the maximum water supply capacity of the source:
In order to achieve proper water allocation, the water demand of each user node
j has to be fulfilled. The water resources balance between the water supply and water demand constraint is written as follows:
Water quantity has to satisfy the condition:
Finally, the following constraint is considered to exclude the construction of pump stations:
Note that, if demand exceeds supply, it is necessary to introduce a dummy source with the assigned supply:
Since the source does not really exist, no transportation from it will occur, so the cost can be set to zero.
In the case where supply exceeds demand, it is necessary to introduce a dummy destination to which will be assigned a demand equal to:
Since no transport takes place, the cost can be set to zero.
The model determines the optimal distribution of available water resources in a given area. If water distribution systems already exist in the analyzed area, then they can be evaluated as further constraints. Specifically, cost
Cij is set to zero if source node
i is connected to destination node
j by an existing pipeline:
However, the possible flow rate
Qij between already connected nodes
i and
j cannot exceed the maximum value of
allowed by the existing pipeline:
If the available information only includes the total flow that can be supplied to a user node
j by the
Nj subsets of its existing connections, then the constraints on actual flow rates for
j can be expressed as follows:
where
identifies the
sth subset composed by n
s source nodes already connected to
j, and
is the maximum total flow allowed from this subset.
The results obtained by solving this model are the variables Qij, which permit the calculation of the amount of resources that the generic source i can provide to the generic destination j. Regarding the dummy destination, the flow transferred from the generic source node to that destination is to be considered as a surplus of water that remains at the source node itself.
The model may require several iterations. For example, some links between sources and destinations, as predicted by the model, may not be feasible due to orographic, structural, or other problems. These problems may, in turn, render the necessary infrastructural works for the transfer of resources unaffordable and/or impossible. However, the base solution can be improved by imposing supplementary constraints on the links requiring improvement and running the model through additional iterations.
In the model, the choice to make gravity pipes the only option is in accordance with the aim of reducing energy costs for new connections. Furthermore, in this first version of the model, the installation of new pipes in parallel is not a requirement because the maximum flow is already applied.
3. Case Study
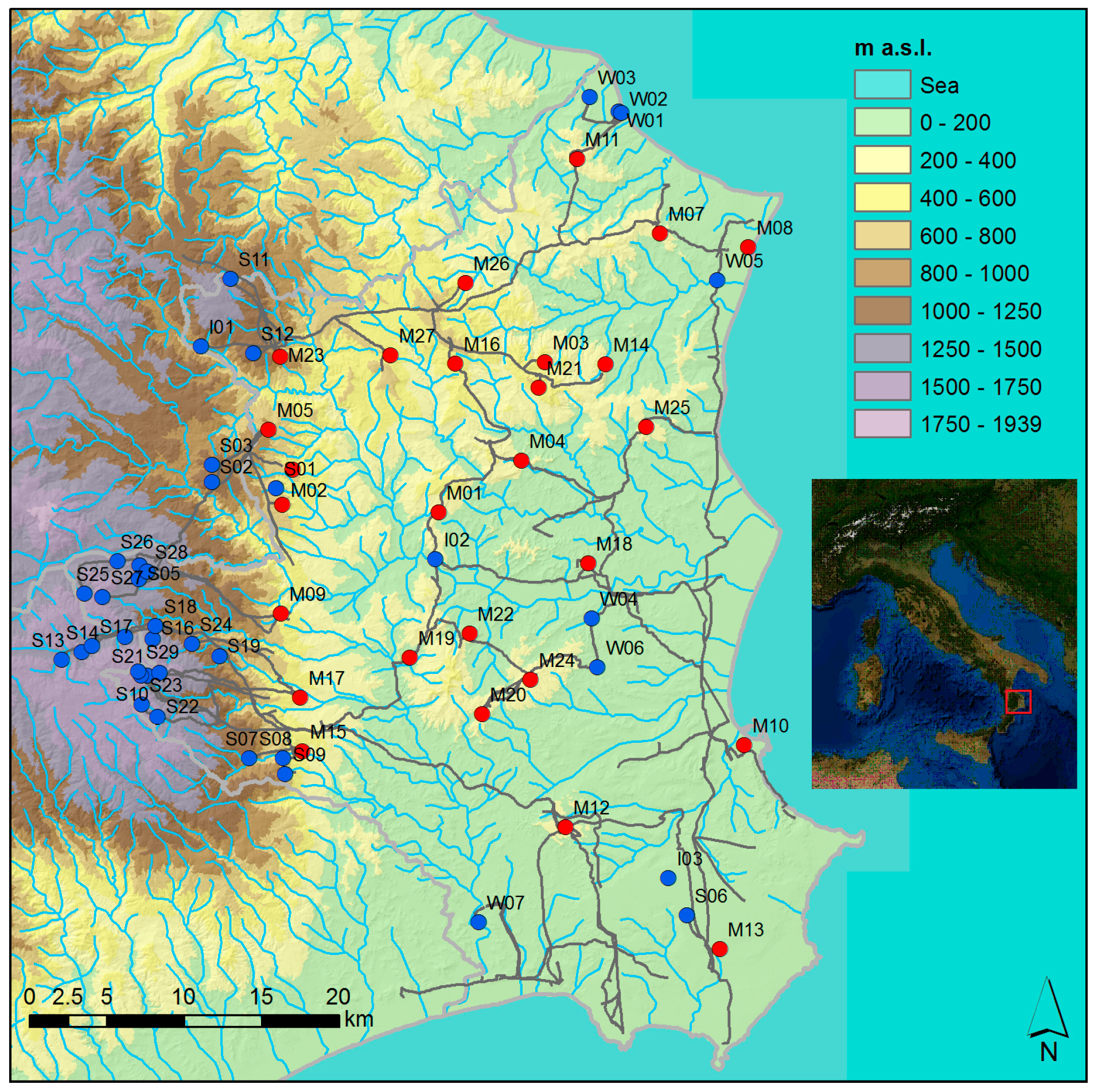
The case study was conducted in the area corresponding to the province of Crotone (1717 km
2) in southern Italy. In this area, 29 springs, 3 intakes and 7 wells are available, for a total drinking water availability of 1534.8 L/s (
Table 1). As shown in
Table 2, total water demand by municipalities is 922.8 L/s [
35].
Drinking water distribution is carried out within the province of Crotone through six regional water supply systems together with some small municipal systems (
Figure 1). The comparison between the water resources distributed by these supply systems and the water needs shows that, although availability exceeds demand, water distribution is not balanced and that, especially in summer, several municipalities are affected by water shortage.
In this case, the availability exceeds the demand, therefore it is necessary to formulate the problem by introducing a dummy destination. The optimization problem is characterized by source nodes, destination nodes and decision variables Qij have to be determined in order to minimize the cost (Equation (3)).
With regards to the K and α parameters of Equation (3), on the basis of the characteristics of the existing pipelines in the case study area, the value α is posed as equal to 1, while the parameter K can be left in parametric form because it does not influence the minimum cost configuration.
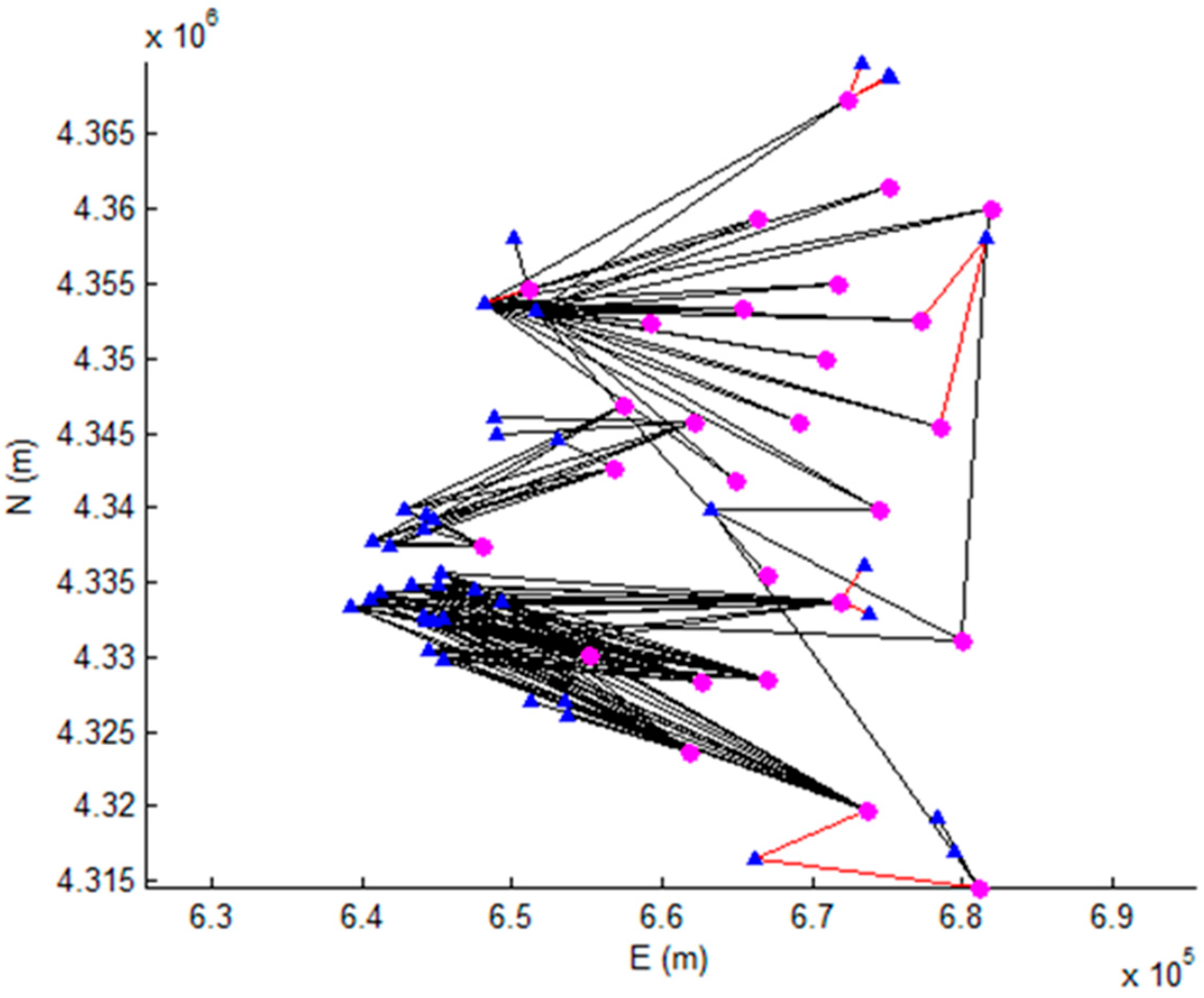
Figure 2 is a graphic representation of the links between the source nodes and the destination nodes of the current schema of the drinking water systems.
4. Results
Given the current unbalanced distribution of the available water resources, an effective optimization solution is needed. Considering the sensitivity of the analyzed area to climate change [
36], it is also worthwhile evaluating the optimization of the system with respect to the expected availability of water resources in climate change scenarios.
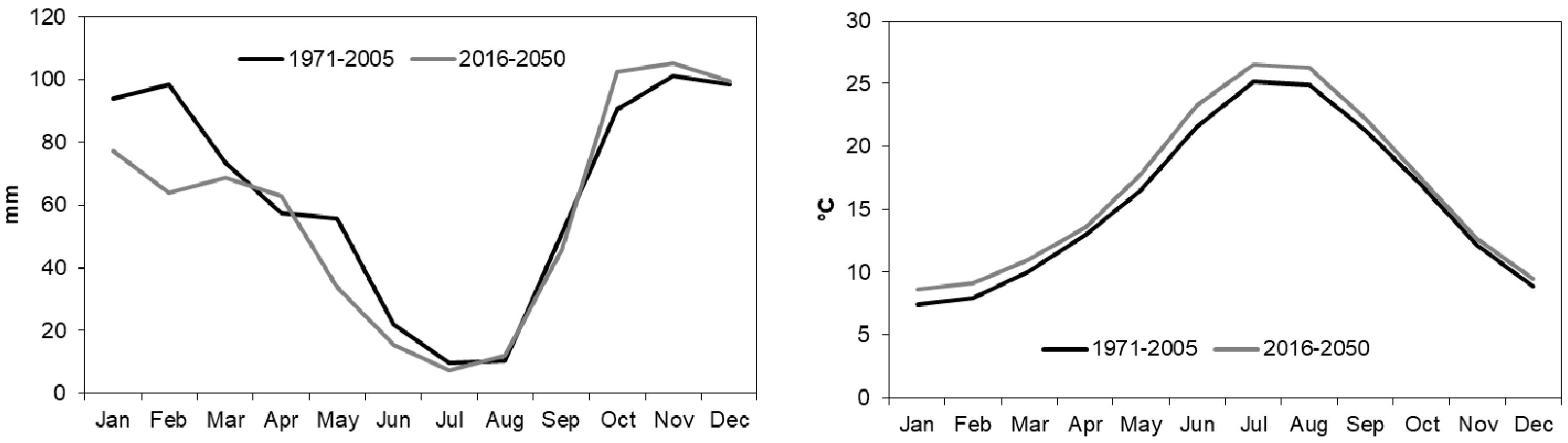
The future scenario has been projected by means of the CCLM simulation. The model was previously tested in the control period 1971–2005 against observations and produced acceptable results. Specifically, the average yearly precipitation simulated in the province of Crotone was 762.6 mm, against 791.9 mm observed. The seasonal behavior was also well reproduced in general, with the main underestimates being in winter (especially for December and January, about −20 mm/month on average) and some overestimates in spring (especially for May, +25 mm/month on average). Temperature, however, was reproduced almost perfectly, with an average yearly simulated value of 15.5 °C (15.8 °C observed) and monthly discrepancies always less than 1 °C.
The study did not use a bias correction procedure for several reasons. First, performance of the CCLM model as compared with observations in the control period was deemed acceptable enough to not require the inclusion of such procedures. Additionally, the implementation of these methods is not straightforward, and many recent studies have been addressing basic questions concerning their effectiveness and even the need for them, e.g., [
37,
38].
Results of the future scenario analysis (2016–2050 with RCP4.5) show an average reduction in precipitation of 8.9% and an average increase in temperature of 1.0 °C for the whole province of Crotone.
Figure 3 shows the projected monthly change for both precipitation (left) and temperature (right). Precipitation reduction is particularly relevant for winter (up to −35% in February) and, secondarily, for late spring, while some small increase is projected for autumn. Temperature increase concerns the whole year, with peaks around +1.5 °C for summer, while a lower increase of around +0.5 °C is forecasted for the last months of the year.
Precipitation changes in terms of quantity and seasonal distribution significantly affect the surface water balance and the availability of water resources. The distributed water balance model of [
30] to determine the impact of climate change on the different components of the hydrological cycle was used for a detailed study of each of the source nodes. For all the available source nodes, dedicated simulations were performed, assuming that:
if the source node is a spring, then the percent change of future water availability is evaluated considering changes in the baseflow variable and assuming that the hydrogeological basin corresponds to the drainage basin;
if the source node is a well, then the related variable is the control of groundwater content, assuming both that the hydrogeological basin corresponds to the drainage basin and that the well is currently fully exploited, therefore any reduction due to climate change would immediately affect water availability from the well;
if the source node is an intake from a stream, then the related variable is the total runoff. In this case, some assumptions were also made, for example that any reduction in total runoff would linearly affect the quantity of water taken from the stream, without taking into account any possible flow regulation or issues related to environmental flow requirements.
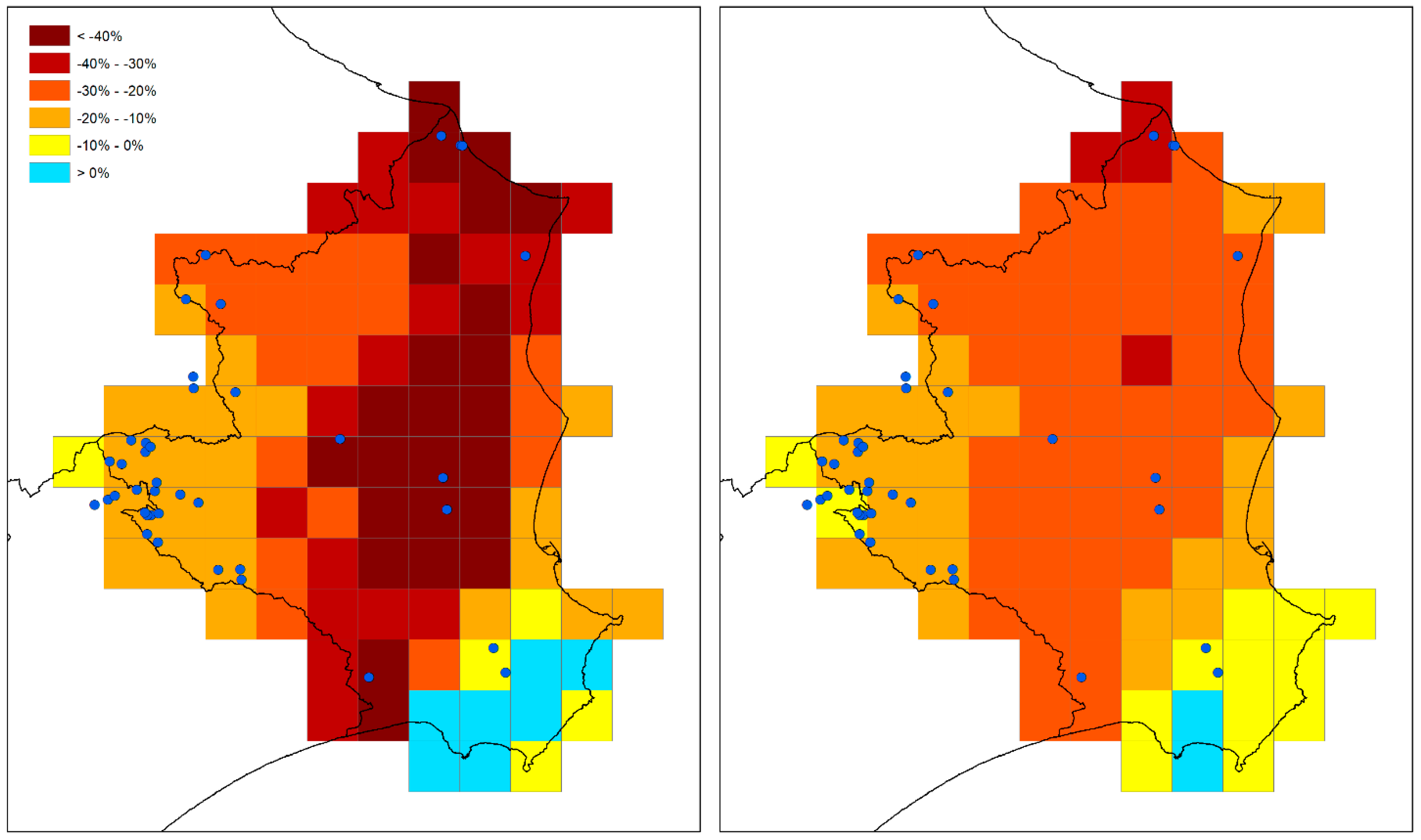
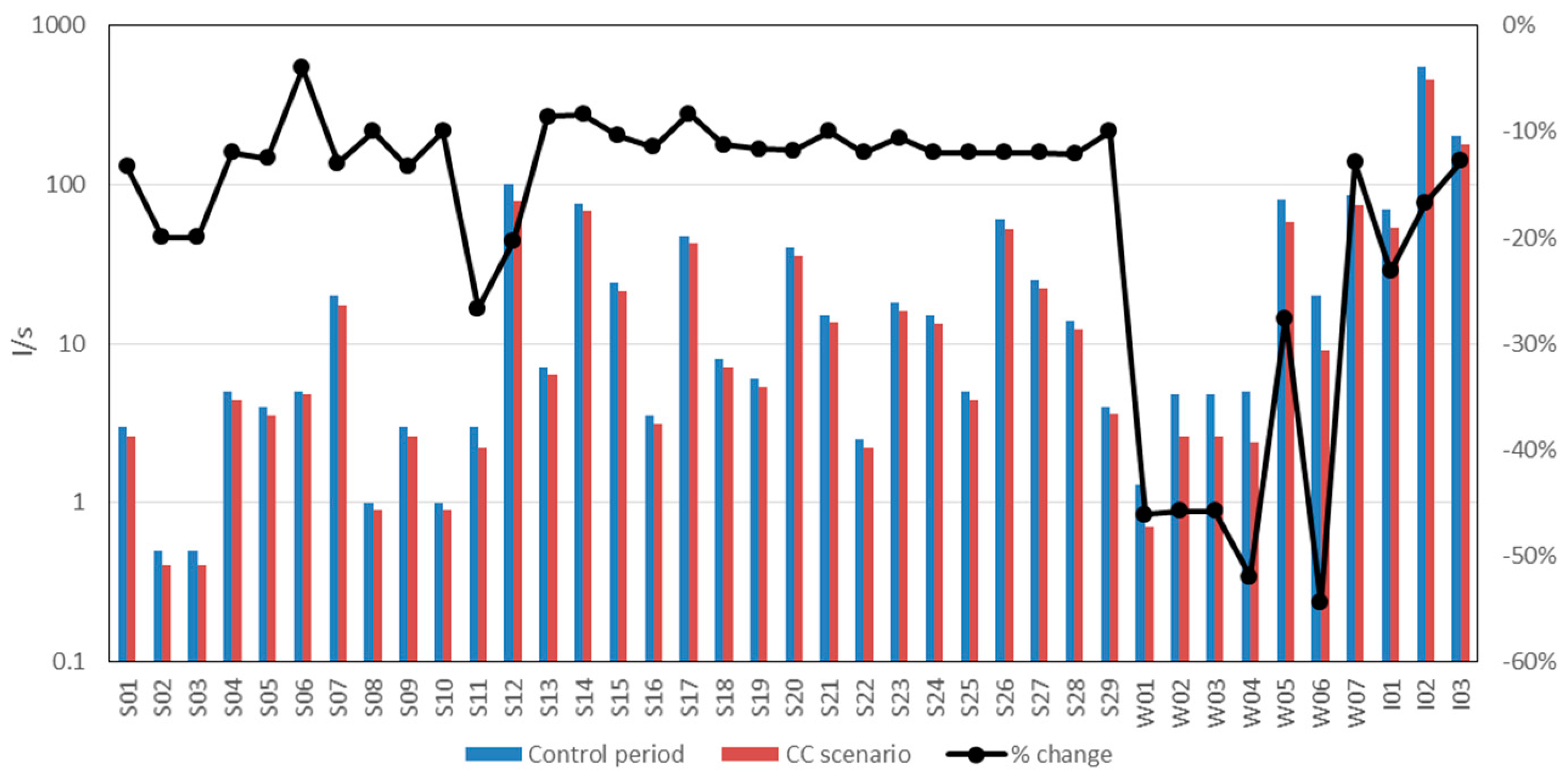
Figure 4 provides an overall picture of the projected changes in baseflow and total runoff in the province of Crotone. The average total runoff reduction for each of the 5-km resolution cells was considered to be about 19%, while the average contribution to the baseflow decreases on a cell-by-cell basis of about 25%. The main reductions are projected to occur in the central areas of the province where not many source nodes are present. Percentage increase concerns areas with low absolute precipitation values (i.e., the southeast of the province), which cannot contribute significantly to enhance overall water availability.
Table 3 and
Figure 5 show the projected changes in the available flow from each of the 39 source nodes. The reduction in available volumes ranged between 3% and 54%.
The optimization model was first applied to the current hydrological scenario; then, the hydrological model, based on CCLM results, was applied to the future hydrological scenario. This modeling was based on both the current and future available volumes and the various percentage reductions for the different source nodes identified. In contrast with the present condition, the model presents a balanced distribution of resources with regards to availability and needs.
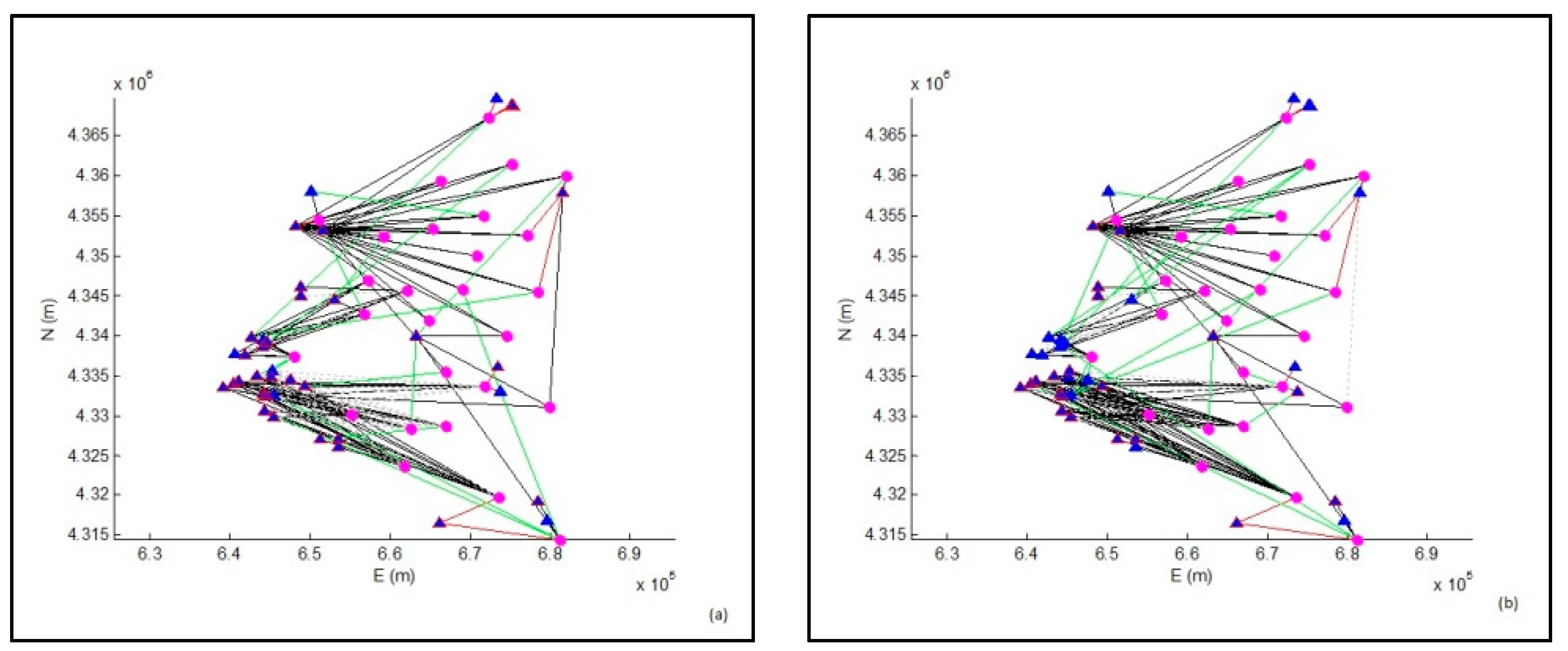
This solution was compared with that obtained by considering the current availability of water resources. A graphic representation of the results obtained is depicted in
Figure 6.
For the current and future scenarios, the model outputs identify suitable solutions for the distribution of water resources in order to satisfy the demand.
For both solutions, it is necessary to modify the overall water system in terms of:
redefining large water schemes with regards to the elimination of some existing links between individual source nodes and destination nodes, and the identification of new links to be built;
redefining, albeit less significantly, the resource distribution of the supply works related to the smallest schemes.
Table 4 and
Table 5 point out several differences between the two scenarios regarding the transferable volumes, the links between source nodes and destination nodes, and the new infrastructures to be developed. In the case of the optimization solution identified with regards to current water availability, a final network of 2230.5 km would be achieved (the existing network has a length of 2632.3 km). The optimization solution identified network sections maintained in operation, others to be deleted, and 16 new connections to be constructed, for a total of 352.7 km to be implemented. Overall, this solution, compared to a topological abstraction of the network, results in a reduction of the overall length of the entire system of about 15%.
In the context of the future hydrological scenario, the solution provided by the optimization model identified 17 new connections to be built, for a total of 383.7 km of new connections. In this case, considering the network sections to be maintained or eliminated, and the new connections to be made, this solution, compared to a topological abstraction of the network, results in a reduction in the overall length of the entire system of about 4%.
This difference is obviously due to significant variations in water resources available in each of the 39 source nodes.
The comparison between the optimization solutions for the climate change and current scenarios shows an absolute difference of 31 km of new connections, excluding the new connections required in both solutions. This difference shows the impact of climate change on optimization results and confirms the usefulness of planning interventions based on climate change scenario optimization. In fact, the latter solution ensures an optimal resource distribution with respect to the expected reductions in water availability due to climate change and at the same time satisfies current demands. Conversely, if an investment plan considers only the current optimization results (and not the climate change scenario), the investment would have to be increased in future (assuming a reasonable reliability of climate change projections) as 250 km of connections realized in relation to current scenario would no longer be needed in the climate change scenario. Therefore, the results obtained from this study highlight the importance of applying optimization procedures which take into account the effects of climate change in order to perform a more accurate analysis and plan of interventions to solve local supply problems.
5. Conclusions
Research on the correct allocation of water resources is becoming increasingly important due to the reduction of water availability and the increasing competition between different users. This paper presented two optimization solutions with regards to the problem of available resources allocation. In particular, for the case study of the province of Crotone, the optimization solution for current water availability was compared to the optimization solution for the expected reduced availability of water resources due to climate change. The province of Crotone is a territory with an agricultural and tourist vocation and is characterized by a sufficient availability of drinking water, but by an unbalanced distribution. The sensitivity of the territory to climate change will likely worsen this situation. It was shown that, even considering an intermediate climate change scenario (RCP4.5), reduction in precipitation is significant, and it is amplified in the hydrological outflow.
The comparison between the optimization solutions achieved with the climate change scenario and the control period showed:
in both cases, the need to redefine the large distribution schemes;
a significantly different redefinition of the water systems in terms of resource distribution and connections between supply sources and users;
the viable feasibility of climate change adaptation measures, provided that overall water resources availability is still sufficient (as in the proposed case study) and proper planning actions are adopted.
The proposed methodology responds to the need for predicting optimized network developments by providing its total length and the length of new connections required, allowing the evaluation of the financial impact within an investment plan. This flexible approach, which in future research developments will also be applied to more complex cases where water availability is not assured in future scenarios, is of interest to water service providers and, in general, to stakeholders committed to achieving the most sustainable water tariff.
The results achieved highlight the importance of and the need for assessing the effects of climate change in water resource planning in order to provide a more adequate planning strategy able to guarantee a better distribution of resources and fulfillment of demand.