Next Article in Journal
Sunshine Duration Variability in Haihe River Basin, China, during 1966–2015
Next Article in Special Issue
Participatory Irrigation Management and Irrigation Water Use Efficiency in Maize Production: Evidence from Zhangye City, Northwestern China
Previous Article in Journal / Special Issue
Adapting to Variable Water Supply in the Truckee-Carson River System, Western USA
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Water
Volume 9
Issue 10
10.3390/w9100769
water-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Application of Hydrological Model PRMS to Simulate Daily Rainfall Runoff in Zamask-Yingluoxia Subbasin of the Heihe River Basin

by
Fei Teng
1,
Wenrui Huang
1,2,*,
Yi Cai
1,
Chunmiao Zheng
3 and
Songbin Zou
4
1
Department of Hydraulic Engineering, College of Civil Engineering, Tongji University, 1239 Siping Road, Shanghai 200092, China
2
Department of Civil & Environmental Engineering, FAMU-FSU College of Engineering, Florida State University, 2525 Pottsdamer Street, Tallahassee, FL 32310, USA
3
Center for Water Research, College of Engineering, Peking University, Beijing 100080, China
4
Cold and Arid Regions Research Institute, Chinese Academy of Sciences, Lanzhou 730000, China
*
Author to whom correspondence should be addressed.
Water 2017, 9(10), 769; https://doi.org/10.3390/w9100769
Submission received: 2 July 2017 / Revised: 19 September 2017 / Accepted: 21 September 2017 / Published: 9 October 2017
(This article belongs to the Special Issue Sustainable Water Management within Inland River Watershed)
Browse Figures
Versions Notes

Abstract

:
The Precipitation-Runoff Modeling System (PRMS) has been applied to simulate rainfall runoff in Zamask-Yingluoxia subbasin of the Heihe River Basin in this study. By using observed data in the subbasin, the model has been calibrated by comparing model simulations of daily stream flow to observed data at Yinglouxia station for the period of summer in 2004. Then model verification was conducted by keeping the same model parameters for the simulation of the period from 1 January 2003 to 31 December 2006. Results from model verification indicate that the model is able to provide good accuracy of simulations of daily rainfall runoff and river flow at Yinglouxia station, with a Nash-Sutcliffe Efficiency coefficient of 0.90 and the root-mean-square error of 15.7 m3/s. The error of maximum peak flow is 6.9 m3/s (1.8%) and the error of mean flow is 1.4 m3/s (2.5%). Comparing to previous studies, results indicate the improvement of model accuracy in simulations of daily rainfall runoff. The calibrated and verified hydrological model can be used to support flood hazard mitigations and water resource management in the Zamask-Yingluoxia subbasin.

1. Introduction

Heihe River, which is the second longest inland river in Northwest China, originates from north of Qilian Mountain with a length of 800 km. Most precipitation in the Heihe River Basin is concentrated in the upstream mountain region. In addition, Qilian Mountain has a glacier in its high-elevation area, which generates runoff via the ice melt or glacier-melt process. Upstream became the runoff formation area of the Heihe River Basin (Kang et al. [1]) which supports the water resource usage in the midstream agriculture development and downstream ecological conservation of the Heihe River Basin (Figure 1). Annual precipitation is between 300 and 700 mm, which is mainly concentrated in the summer (Zou et al. [2]). Although the Heihe River Basin is located in the arid/semi-arid region, it has still suffered flood disasters (Yi et al. [3]) with serious casualties and property losses several times (e.g., flood events in July 1954, August 1996 and August 2011). Flooding may also cause effects on hydraulic structures (Ratha and Sarkar [4]). In addition, drought is also a serious problem in the Heihe River Basin. Cai et al. [5] indicated that, due to the long-term loss of glacial storage in the upper Heihe River Basin as an effect of climate change, the water shortage in the arid Heihe River Basin will be intensified. Wang et al. [6] detected the impact of increasing land use on hydrologic processes in the Heihe River Basin. It shows that with the continuous expansion of the cultivated land area in the basin, the runoff has decreased observably since 1967. The shortage of water resource has become a restricting factor in the local economy and society’s developments (Jiao et al. [7,8]). The runoff from the mountain region accounts for a high proportion of the water resources in Heihe River’s midstream and downstream region. Because of the Heihe River Basin suffering the risk of both flood and drought, water resource management becomes an issue of concern. There is a certain amount of research about flow prediction or water resource management in the Heihe River Basin due to rapid economic development, population growth, urbanization and climate change (Nian et al. [9]). Water resource management and irrigation management in the Heihe River Basin has been explored in recent studies (Cai et al. [10]; Tian et al. [11]; Huang et al. [12]; Zou et al. [2]). Mountain runoff changes have to be understood in order to satisfy the water resource needs for the development of the Heihe River Basin (Kang et al. [1]), while there is a great uncertainty of the water volumes from mountain sources (Qin et al. [13]).
Most previous hydrological models in the upstream region of the Heihe River Basin are used to simulate monthly stream flow at Yingluoxia State (e.g., Luo et al. [14]; Zou et al. [2]) because of the limit of insufficient data for a large basin for accurate daily flow simulations. For example, lacking rainfall stations to resolve the spatial variations of rainfall in the hydrological model simulations can make it difficult to produce accurate model simulations of daily runoff. The outlet of Heihe River’s upstream mountain region is located at the Yingluoxia hydrologic station, which is also the boundary between the upstream and midstream regions of Heihe River. It had been chosen as the control point to calibrate the simulated stream flow from the upstream region. Due mainly to the insufficient meteorological, geological and hydrologic data in this region, previous studies could only provide accurate simulations of monthly average flow (Kang et al. [1]; Huang et al. [15]). The research also indicated that Qilian Mountain’s snowmelt process and groundwater transport are important factors in streamflow simulation in the Heihe River Basin (Huang et al. [15]; Zhou et al. [16]). Some recent time series methods, such as the neural network model (Shoaib et al. [17]) and binary-coded particle swarm optimization (Taormina and Chau [18]), have shown improvement of rainfall runoff simulations. Kisi et al. [19] conducted rainfall-runoff process modeling using soft computing techniques. Granata et al. [20] presented vector regression for rainfall-runoff modeling in urban drainage. Alizadeh et al. [21] presented a new approach with a combination of wavelet transform and artificial neural network to simulate rainfall runoff. Results of this study demonstrate that a reliable prediction of the rainfall and runoff process both for one and two months ahead can be achieved. Although time series model methods have advantages in fast simulations, they are unable to resolve spatial distributions of rainfall runoff, the effects of land cover changes, and the components of flows.
Some researchers in recent years have tried to improve the accuracy of daily streamflow simulations for the upstream or midstream region of the Heihe River Basin. For some studies’ hydrologic modeling of the large upstream basin, the small number of data stations in the Heihe River’s mountain region may be the major limitation for model calibrations. Xia et al. [22] simulated the rainfall runoff in Heihe River’s upstream mountainous basin with a distributed time-variant gain model, which coupled with snowmelt process. Chen et al. [23,24] simulated the outflow at Yingluoxia from the upstream basin via a distributed water-heat coupled model (DWHC) with the test of different spatial interpolation methods to calculate the daily meteorological data. Although it shows some improvement over the simulations using distributed hydrologic models, results still need to improve to agree with the observed series. Jiao et al. [8] used a Spatial Modeling Environment (SME) model to simulate the streamflow at Yingluoxia station from the upstream Heihe River Basin model, with the model’s simulated flow higher than the observed data. Li et al. [25] and Wu et al. [26] applied SWAT to simulate daily rainfall runoff in the upper and midstream of the Heihe River Basin, which showed improvement of model accuracy with the correlation coefficient of 0.89. Li et al. [27] conducted hydrological modeling that covers both upstream and midstream regions, and compared a distributed hydrological model’s (GISMOD) performance. Its simulation of Yingluoxia station indicated the improvement of accuracy over previous studies that the monthly flow is acceptable with the Nash-Sutcliffe efficiency (NSE) of 0.9. However, model predictions of daily flow by Li et al. [27] were underestimated. Previous studies of rainfall runoff modeling in the upstream Heihe River Basin show the needs for further improvements of model accuracy for flood simulations, especially more accurate simulations of peak flow for flood hazard mitigation. In addition, coupling surface and ground water modeling is also important for water resource management. The PRMS hydrological model has been used as a module in a coupled ground-water and surface-water flow model (GSFLOW), and it has been applied in daily rainfall-runoff modeling. Therefore, the PRMS hydrological model was selected for our study to provide: (1) more accurate predictions of storm-induced daily rainfall runoff for flood predictions and hazard mitigations; and (2) a calibrated surface runoff module for the coupled surface and groundwater modeling by the GSFLOW model.
In this study, hydrological modeling study of rainfall runoff is conducted in the Zamask-Yingluoxia subbasin (Figure 1), a relatively small watershed near the border of upstream and midstream regions of the Heihe River Basin. Within the study area, there are observed data from several hydrological measurement stations that can be used to specify model boundaries and used for model calibration and verifications (Figure 2). Observed data include daily stream inflows in the Qilian and Zamask rivers, daily outflow at Yinglouxia station, and daily rainfall at three hydrological stations. With better data than those previous studies in larger regions with insufficient data, especially rainfall stations, more accurate model calibration and verification can be made to provide a more reliable storm runoff model to support flood hazard predictions and a surface water module for coupling surface and groundwater modeling.

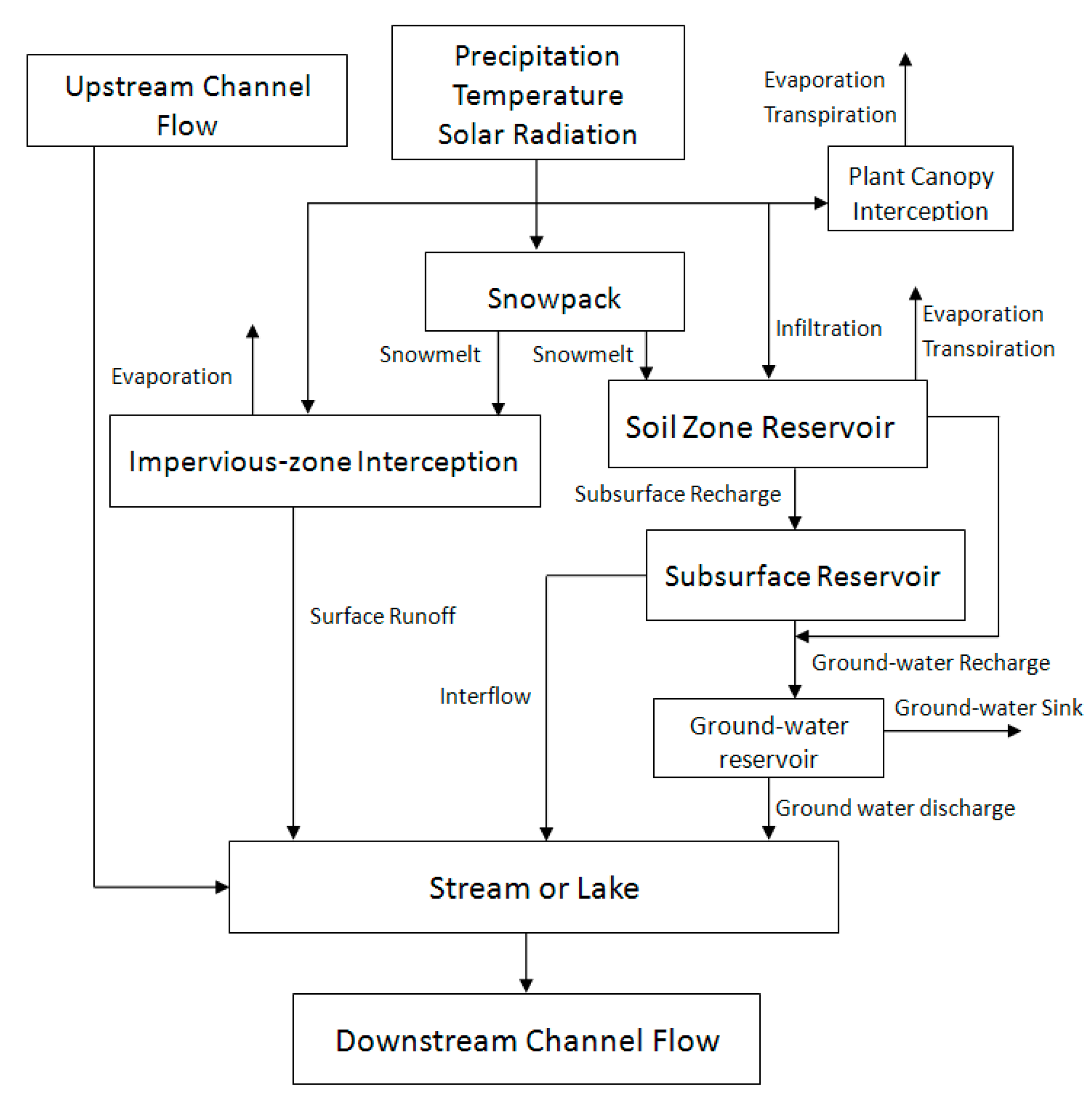
2. Hydrologic Model Descriptions

The Precipitation-Runoff Modeling System (PRMS, Denver, Colorado, USA), is a deterministic, distributed-parameter, physical process-based modeling system developed by the United States Geological Survey (USGS) to evaluate the response of various combinations of climate and land use on streamflow and general watershed hydrology (Markstrom et al. [28]). PRMS’s modular design allows users to selectively couple the modules in the module library or even to establish a self-design model. It has been widely applied in the research of rainfall-runoff modeling. It was proved to be a reliable hydrologic model. PRMS discretizes the area of a watershed into a network of hydrologic response units (HRU). Each HRU integrates the interaction of climate, plant canopy, impervious-zone interception, surface runoff, subsurface flow, groundwater, streamflow routing, evaporation, and snowpack (Figure 3). The model simulates the hydrologic processes of a watershed using a series of reservoirs that represent a volume of finite or infinite capacity. Water is collected and stored in each reservoir for simulation of flow, evapotranspiration, and sublimation. Surface runoff, subsurface flow, and groundwater provide the water to the drainage network segments. Surface runoff from rainfall is computed using a contributing area concept. A reservoir routing method is used to compute subsurface flow which is a rapid movement of water from unsaturated zone to stream channel. The groundwater is conceptualized as a linear reservoir and is assumed to be the source of all baseflow. Streamflow could be computed according to the sum of surface runoff, subsurface flow, and groundwater discharge that reaches the stream network. However, PRMS also provides a Muskingum flow-routing method to compute streamflow to and from individual stream segments in the streamflow module. The module enables the phase of flood wave to be adjusted by parameter Kinematic wave coefficient (K_coef) that represents the travel time of the flood wave in each segment. Surface runoff is an important element of streamflow. The most influential elements of surface runoff and infiltration module in PRMS are HRU’s area, surface storage depression, impervious area, and type of variable source area. These parameters determine the water’s transformation and storage from precipitation to surface runoff.
The PRMS model has been applied to some rainfall runoff and snowmelt modeling. Niswonger et al. [29] applied the PRMS model to an integrated decision support system. Markstrom and Hay [30] (2009) used the model to investigate watershed responses to climate change. Hay et al. [31] applied PRMS to a snowmelt-dominant watershed. Hay et al. [32] and Christiansen et al. [33] evaluated climate change impacts on rainfall runoff by PRMS model simulations. Dressler et al. [34] conducted an evaluation of snow water equivalent for mountain basins in the PRMS model. Markstrom et al. [35] integrated the PRMS model into a ground and surface water flow model GSFLOW, in which the PRMS model was applied to perform a long-term hydrologic process.

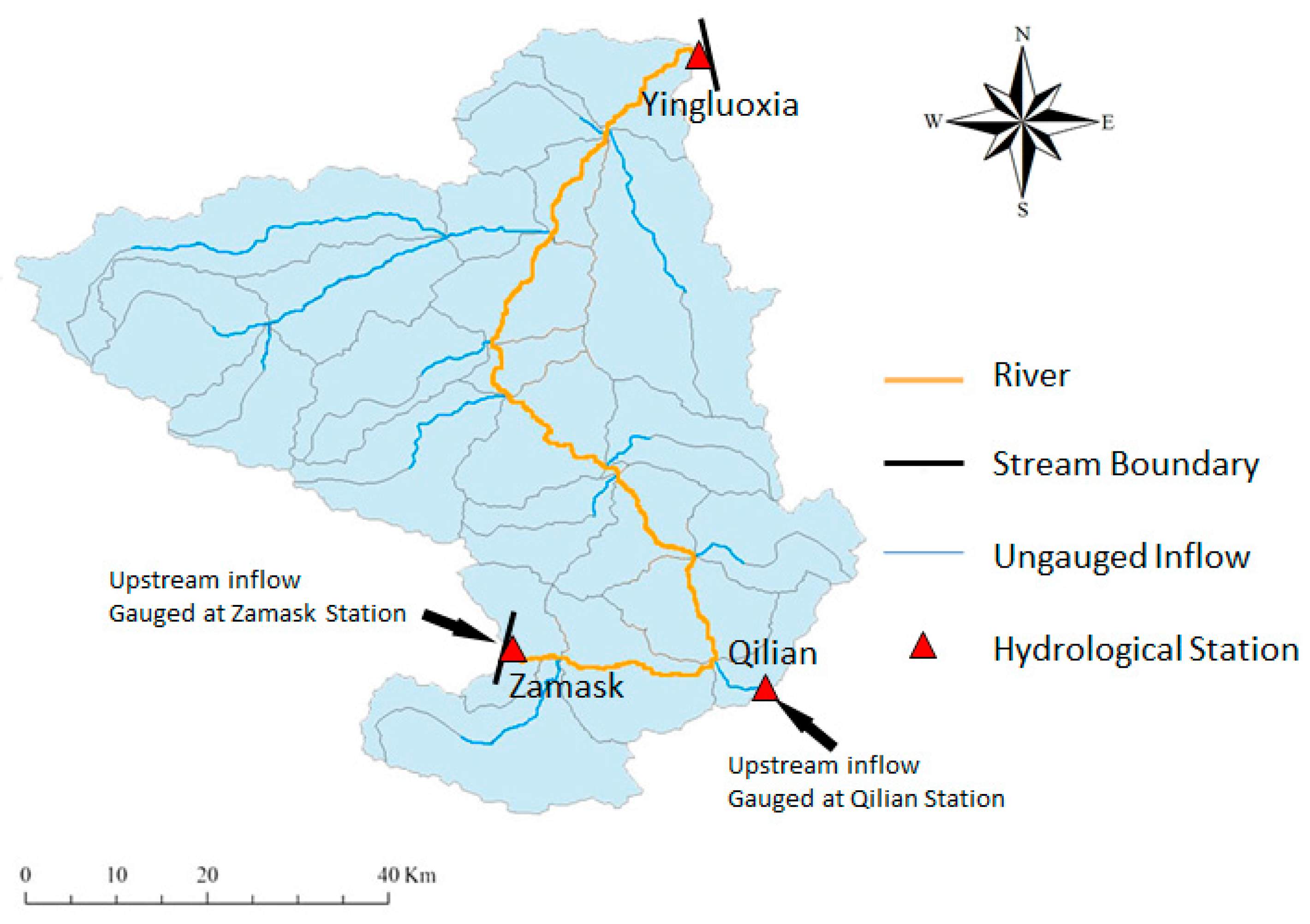
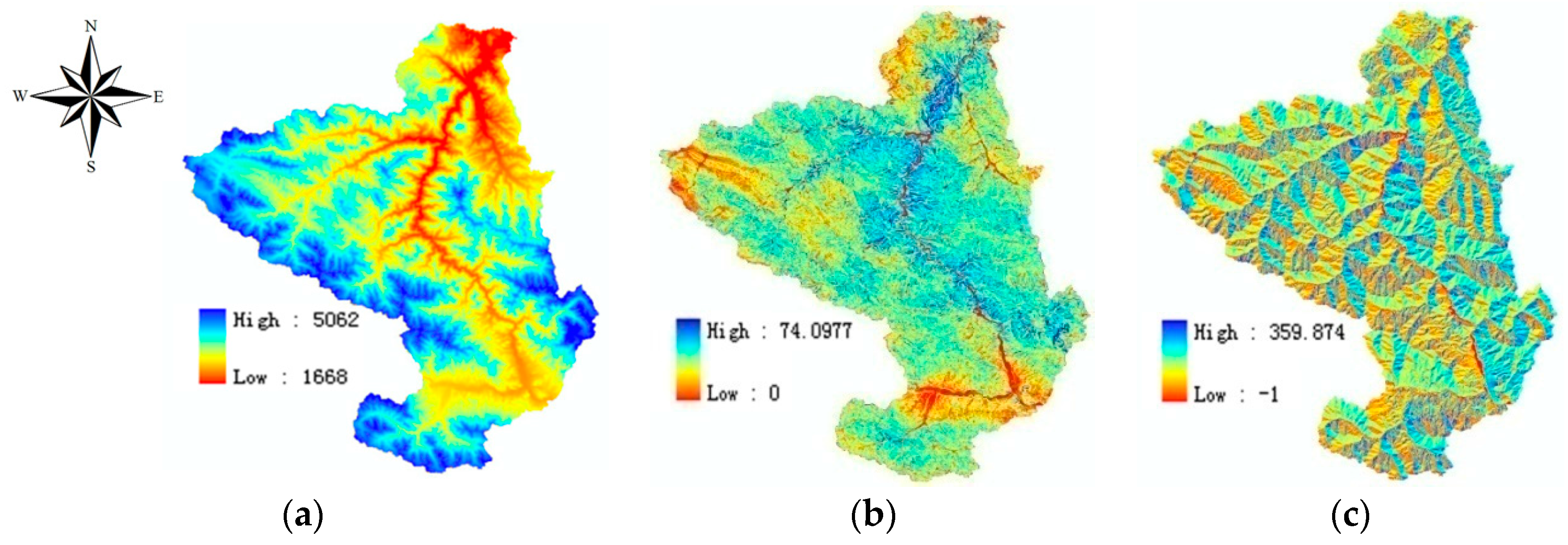
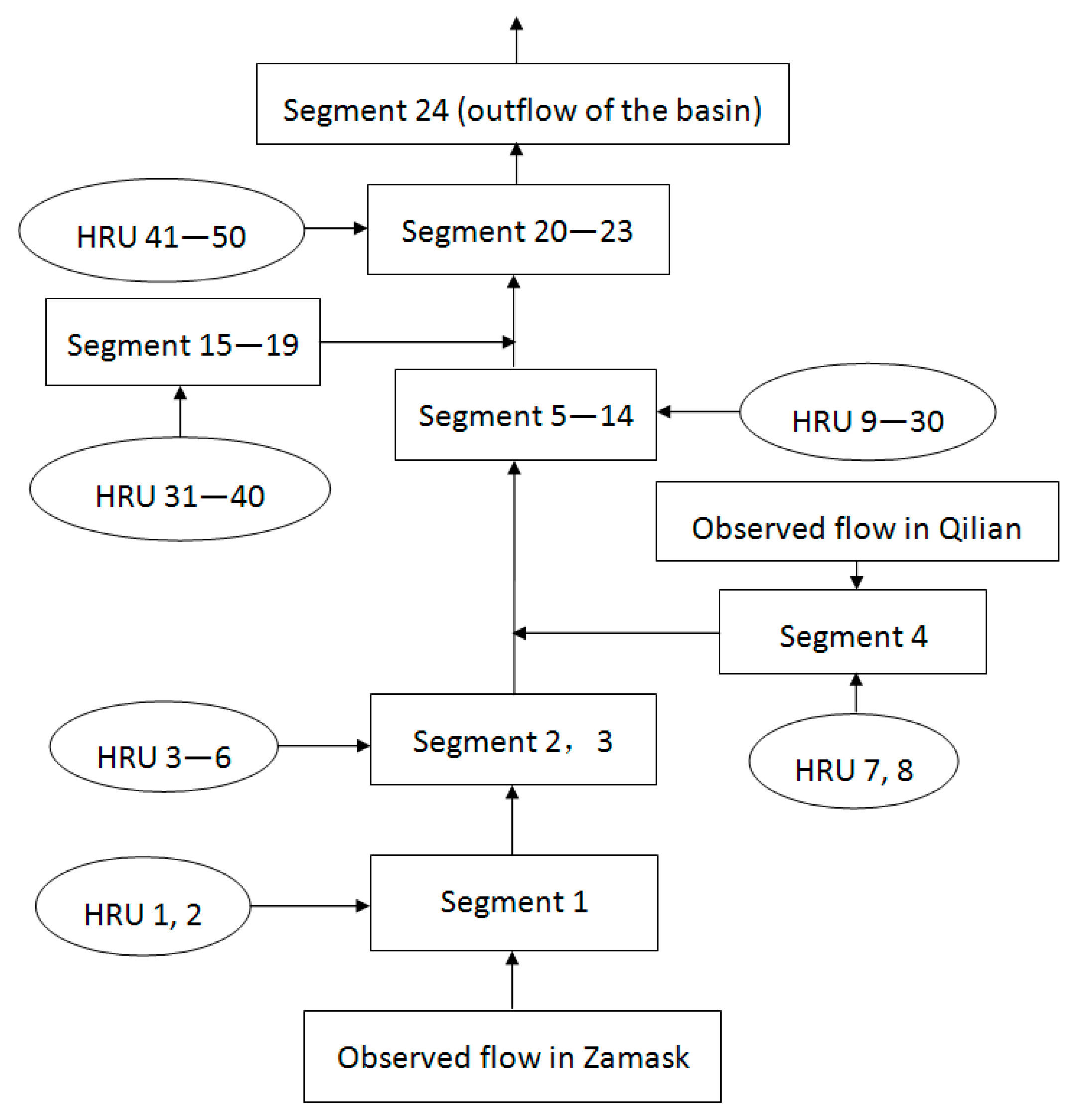
3. Hydrologic Model Setup

The watershed area from Zamask hydrologic station and Qilian station to the Yingluoxia hydrologic station was selected to establish the PRMS model. The study watershed has an area of 2934 km2 and 104-km-long channel of Heihe River. The observed hydrologic, meteorological and geographic data were obtained from the Data Management Center of the Heihe Project (Data Management Center of Heihe Project [36]). There are three hydrologic stations located in this region. Zamask station is the upper boundary of Heihe River in the study region. Qilian station is located at the end of Babaohe River in the region, which is Heihe River’s tributary. Yingluoxia station is the outlet of the watershed, so it was set as the lower boundary. These three stations provide hydrologic and meteorological data such as discharge, precipitation, temperature, transpiration, and solar radiation (Figure 2).
The hydrologic model network for the Zamask-Yingluoxia Basin, consisting of HRUs and segments, was set up based on hydrologic and physical characteristics such as drainage boundaries, land-surface altitude, slope, and aspect (Figure 4); plant type and cover; land use; distribution of precipitation, temperature, and solar radiation, and so on, based on the GSFLOW user manual (Markstrom et al. [35]). Fifty HRUs and 24 segments were obtained from the digital elevation model’s (DEM) data processing in ArcGIS. Parameters of the basin’s geographic information (e.g., HRU’s area, slope, aspect, latitude and elevation), soil type, land uses, segments’ length and topological structure were classified and transformed into the format that PRMS could adapt in each HRU (Figure 5). The spatial distribution of the stations was used to analyze the weighted rainfall in HRUs in the Zamask-Yingluoxia Basin. Time series of rainfall were matched to the HRUs according to the stations’ locations. Other parameters as shown in Table 1 were initialized with default values and calibrated to match the observed data.

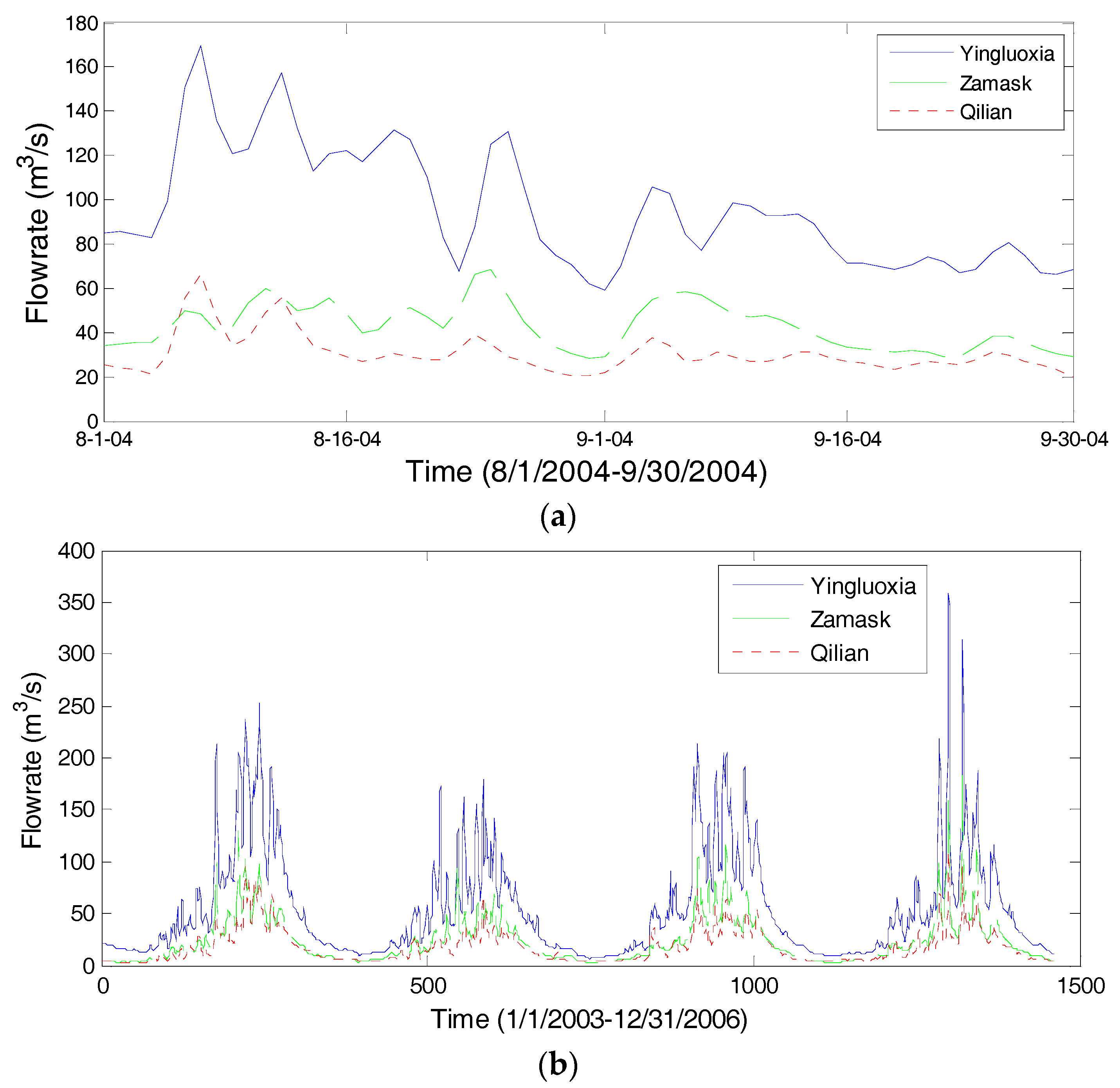
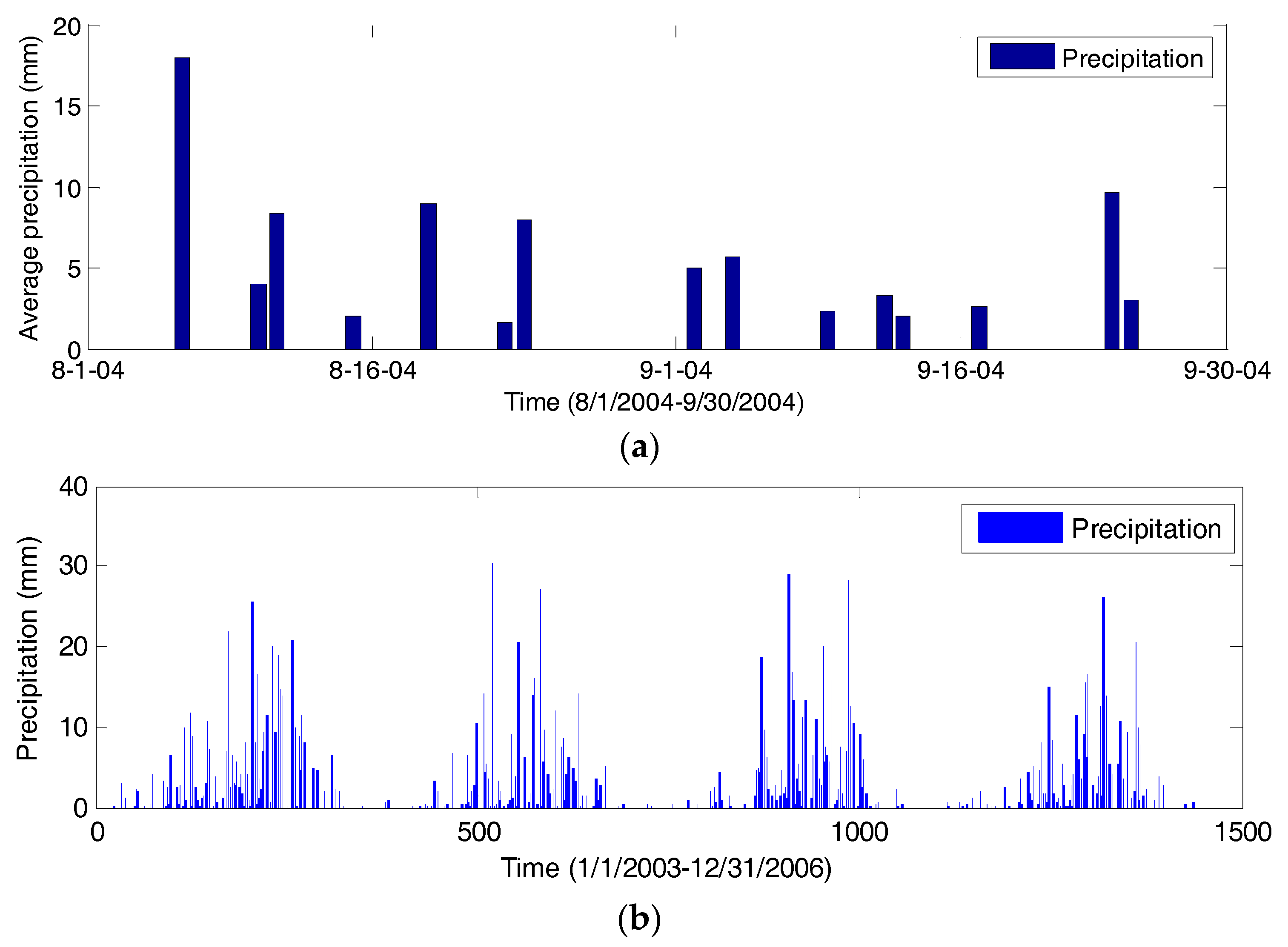
4. Boundary Conditions

The observed daily discharge at the Zamask station and Qilian hydrological stations were used as the upstream inflows of the Zamask-Yingluoxia Basin. Yingluoxia station’s observed daily discharge was used to calibrate and verify the PRMS’s simulation of the daily flow at the basin’s outlet. In this study, the daily flow from 1 August to 30 September 2004 was chosen for calibration, while long-term data series from 1 January 2003 to 31 December 2006 were used for verification (Figure 6). Qilian station provided data of temperature and solar radiation. Because of the HRUs having different elevations, data series of Qilian’s temperature were modified in each HRU according to the difference of elevation with Qilian station. The vertical rate of temperature’s change is −8 degrees centigrade per kilometer (Wang et al. [37]). Combined evapotranspiration is often responsible for returning 50% or even 60% of precipitation back to the atmosphere (HEC-HMS User’s Manual [38]). Precipitation data were available in three hydrological observation stations in Qilian Station, Zamask Station, and Yingluoxia Station. The Thiessen polygon method was used to interpolate the precipitation from observation stations to the HRU. The simulation time’s average daily precipitation for model calibration during 1 August–30 September 2004 and model verification during 1 January 2003–31 December 2006 were shown in Figure 7.

5. Daily Flow Modeling

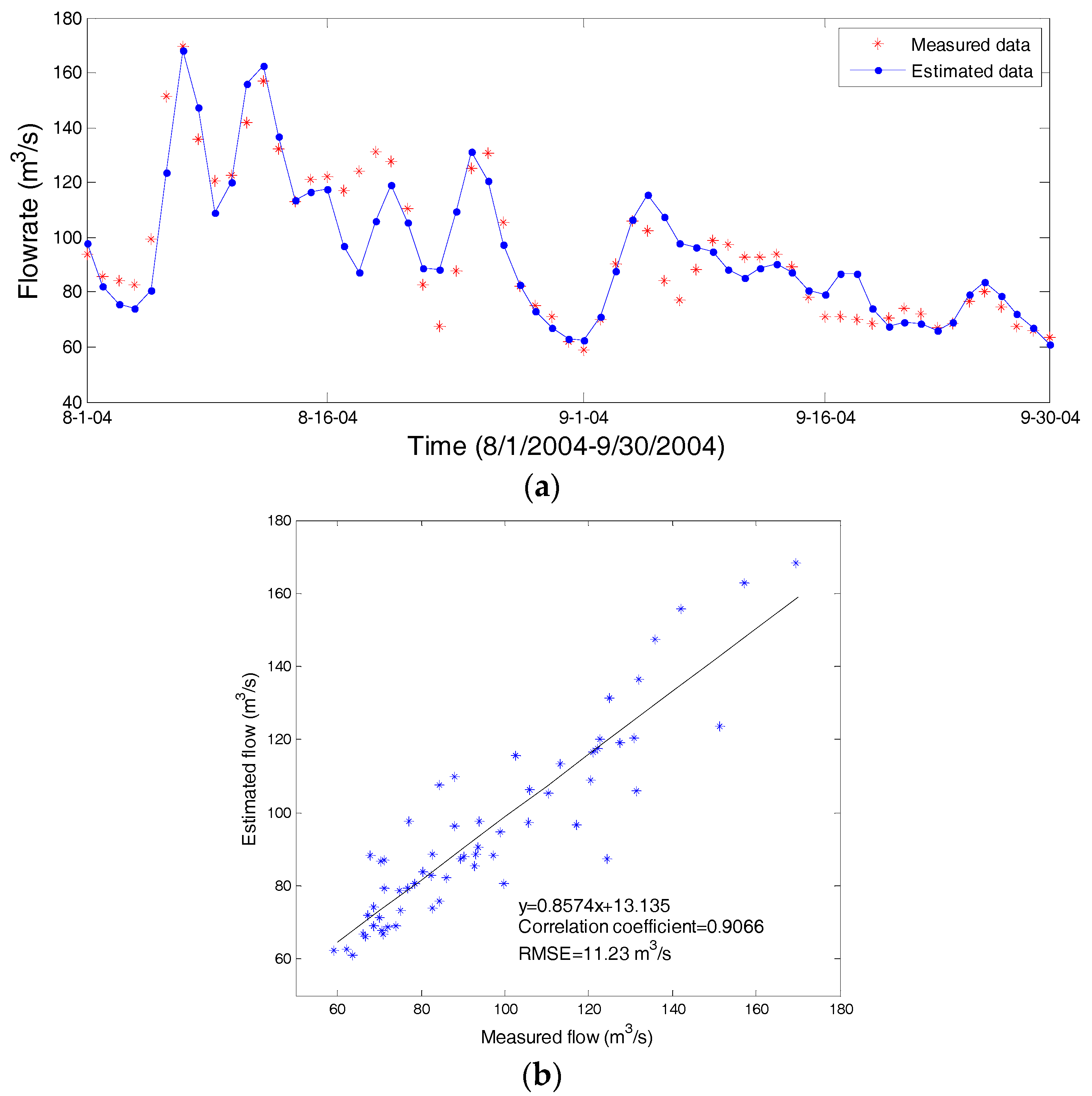
5.1. Model Calibration

Daily stream flow from 1 August to 30 September 2004 was used for the model’s calibration. During calibration, initial estimates of the range of the hydrological model parameters were based on the characteristics of the hydrological and soil types in the study area. Parameters were adjusted to achieve a satisfactory comparison between simulated and observed flow at Yingluoxia station. Some previous studies of PRMS modeling provide a series of parameters’ value to initialize the model (Chang et al. [39]; Mazi et al. [40]). The rest of the parameters were initialized as the recommended default value by the user manual (Markstrom et al. [35]).
Major calibrated parameters of PRMS belong to surface runoff, subsurface flow, groundwater, and streamflow routing modules (Table 1). The first three module’s outputs determine the value of the hydrograph while the streamflow routing module takes charge of the phase of flow. For example, sro_to_dprst, standing for the fraction of pervious and impervious surface runoff that flows into surface depressions, was set to 0.5. The hydrograph of peak flow would become sharp if the value decreased, which means more precipitation in HRU’s impervious area transformed into surface runoff and drained into the stream channel immediately. The remaining precipitation would be stored in the basin’s depression area at first. Then they would infiltrate into the ground and finally transform into subsurface flow, groundwater discharge, or a groundwater reservoir. Therefore, the hydrograph would become flat if this parameter increased. The key parameter in the stream routing module is kinematic wave coefficient (K_coef), which presents a flow’s travel time from upstream to downstream in a segment. It was obtained through dividing each stream length by wave velocity. The velocity in the mountain region is usually more than 5 km/h. The increase of this value would delay the phase of the flow.
During the simulation time, remarkable precipitation occurred on 6, 11, and 24 August. This time period was used for rainfall runoff’s calibration. Moreover, little rainfall in September provided the conditions to calibrate the parameters about baseflow. After model calibration, the hydrographs of observed and simulated flow at Yingluoxia station match well (Figure 8a). Observed flood peak occurred at 7 August with a flow of 169.5 m3/s. The simulated peak value at the same time is 168.1 m3/s so that the error is 1.4 m3/s (or 0.8%). The hydrographs of measured and estimated flow have a correlation coefficient of 0.91, while their root mean square error (RMSE) is 11.23 m3/s (Figure 8b). With a Nash-Sutcliffe efficiency of 0.82, the result indicates that model calibration is satisfactory.

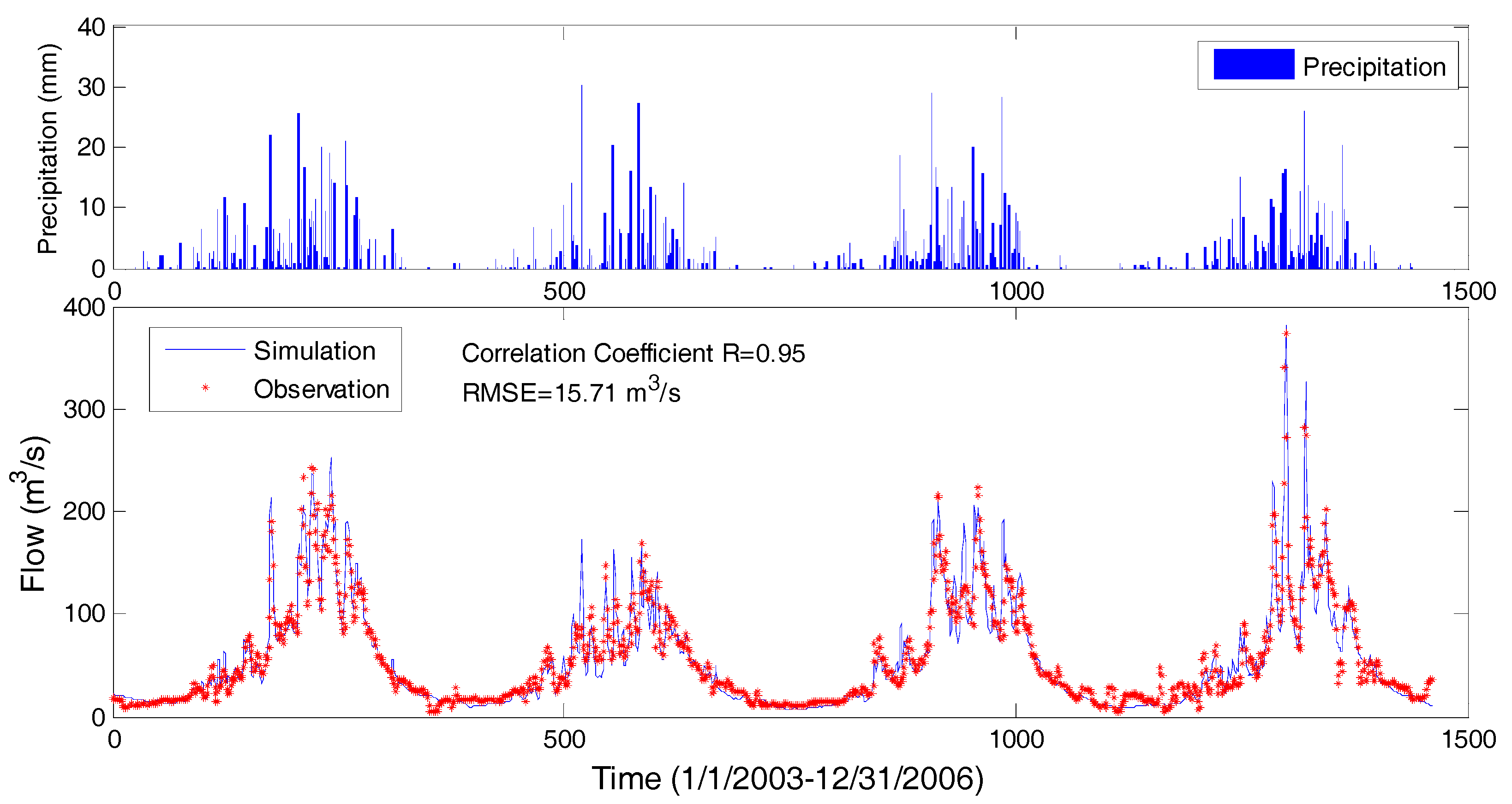
5.2. Model Verification

The calibrated PRMS model was further verified for the four-year period from 1 January 2003 to 31 December 2006. Model simulations match well with observations with the correlation coefficient of 0.95 and RMSE of 15.7 m3/s (Figure 9). The Nash-Sutcliffe efficiency is 0.90 in the model verification. The maximum flow of 373.8 m3/s was measured at Yingluoxia station on 22 July 2006. The simulated maximum flow was 380.7 m3/s on the same date. The error of the maximum flow was 6.9 m3/s (or 1.8%), and the error of mean flow was 1.4 m3/s (2.5%). All those statistics as shown from Table 2 from present study are better than those from previous studies, showing the improvement of model accuracy.
The results of calibration and verification indicated that the model is capable of simulating the rainfall-runoff process correctly in daily scale with high correlation coefficients and low RMSE. In particular, model simulations of rainfall runoff in the four high flow seasons (or rainy seasons during summer and fall) in the four years of verification period match well with observations of flows. Therefore, PRMS’s modeling at Zamask-Yingluoxia Basin is satisfactory for flood predictions.

6. Discussion

Model calibrations and verifications indicate that the PRMS model can provide good accuracy to predict daily rainfall runoff in the Zamask-Yingluoxia subbasin. Statistic comparisons between the present study and previous studies are given in Table 2, which show good improvement of model accuracy over previous studies for predicting daily flow at Yinglouxia station. Therefore, the data set in the subbasin of Zamask-Yingluoxia used in this study may be able to provide a good test case for other larger-scale models (such as an upstream basin model or midstream basin model) in the upstream region of the Heihe River Basin to identify the potential problems for model improvement (such as increasing the number of rainfall stations). In fact, hydrological modeling in a larger basin scale are even more important for water resources management, while the modeling in a smaller subbasin can be used to validate and test models for model improvement.
The calibrated and verified hydrological model can be used as a useful tool to support flood hazard predictions and water resources management in the Zamask-Yingluoxia subbasin of the Heihe River Basin. According to the simulation of the rainfall-runoff processes in the Zamask-Yingluoxia subbasin, the flow rate rises quickly at the beginning of a flood event, while the rate at which it falls is slower than the rate at which it rises. The time for alarm is short in case of a flood event. As a result, the prediction of heavy precipitation and flood must be treated seriously. A high-time resolution hydrologic model should be established to describe detailed rainfall-runoff processes. It is important to reduce the extreme flood peak so that the hydrograph would be flat. Reservoirs with different operation scenarios may be used in flood controls and preventions. The model’s simulation also indicates that the range between high flow and low flow at Yingluoxia station is large at the outlet of the Zamask-Yingluoxia subbasin, which means the downstream basins may have the risk of suffering both flood and drought in a short time period. To avoid the flow rate being either too low or too high, storing and allocating water resources scientifically is necessary. Flood events in the Zamask-Yingluoxia subbasin should be converted into a kind of resource for usage in drought seasons that benefit the development of the basin. During wet seasons in the Heihe River Basin, it is helpful to prepare moderate artificial reservoirs to store the extra discharge in Zamask-Yingluoxia subbasin. After the flood event, the stored water resource could be released gradually to the lower stream basin.
In the simulation from the year 2003 to 2006, the weights of major components of stream flow were analyzed. Surface runoff, subsurface runoff (interflow), and groundwater recharge took different percentages of water quantity of stream flow discharge with the value of 48.4%, 21.0%, and 30.6% (Table 3). The result indicates that rainfall runoff is the main source for the Zamask-Yingluoxia subbasin. Its direct drainage (surface runoff) and indirect drainage (subsurface flow) provide nearly 70% of the subbasin’s stream discharge. Although the velocity of groundwater recharge is low, it lasts for long and has a steady status. As a result, the water quantity from groundwater recharge is also important, especially during the drought period. Groundwater could be regarded as an important supplement for the Zamask-Yingluoxia subbasin’s water resource usage.
Because of the upstream basin is the runoff formation area of the Heihe River Basin, the water resource it generates is valuable for the arid or semi-arid areas in midstream or downstream basins. Good management of water resources in the Zamask-Yingluoxia subbasin is important for achieving water usage requirements in the midstream and downstream Heihe River Basin. In the Heihe River’s upstream basin, it is necessary to focus on the control of flood disasters. The vegetation ecosystem in Heihe River’s upstream basin is the fundamental guarantee for the water resource system. Deterioration of the vegetation canopy would destroy the water circulation process of the basin. To enhance the capacity of water conservation, the protection of canopy in the upstream basin should be paid more attention. Another method to utilize the extra water resources is transporting them to the downstream desert directly during wet seasons. The limitation of water usage during its transport can provide a fair amount of water resources for the downstream basin.

7. Conclusions

In order to investigate the hydrological process in the Zamask-Yingluoxia subbasin in the upper Heihe River Basin, a PRMS hydrological model has been applied to the subbasin where an observed data are available from three hydrological stations. Daily flow data series of the Yingluoxia hydrologic station, located at the outlet of the mountain region of the Heihe River Basin, was used for PRMS’s calibration and verification. Results indicate that the PRMS model has been successfully applied in the Zamask-Yingluoxia subbasin. The correlation coefficients between measured and estimated daily flow at the Yingluoxia station are equal to or above 0.9 in both model calibration and verification. Root mean square errors are 11.2 and 15.7 m3/s, and errors of maximum peak flows are 1.4 and 6.9 m3/s, for calibration and verification, respectively. Results show good improvement of the modeling accuracy over previous studies (as shown in Table 2) for simulations of daily rainfall runoff and flow at Yinglouxia station. Therefore, the results of this study can provide more reliable model predictions of flood events for flood mitigation in the region. In addition, the calibrated PRMS model can be used as a surface water module in the coupled surface and ground water flow model GSFLOW for studying surface-ground water interaction.

Acknowledgments

This study is partially supported by the National Natural Science Foundation of China (Nos. 91225301 and 41571031), and National Special Scientific and Technology Grant (No. 2014ZX07405002D). Special thanks go to the Center for Water Research of Beijing University, and Cold and Arid Regions Science Data Center at Lanzhou for providing the data.

Author Contributions

Fei Teng conducted the model applications, Wenrui Huang directed and supervised the modeling study and manuscript preparation, Yi Cai performed GIS data analysis, Songbing Zou and Chunmiao Zheng provided data for model calibration and applications.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Kang, E.; Cheng, G.; Lan, Y. A model for simulation the response of runoff from the mountains watersheds of inland river basins in the arid area of northwest China to climate changes. Sci. China Ser. D Earth Sci. 1999, 29, 48–54. [Google Scholar]
  2. Zou, S.B.; Ruan, H.W.; Lu, Z.X.; Yang, D.W.; Xiong, Z.; Yin, Z.L. Runoff Simulation in the Upper Reaches of Heihe River Basin Based on the RIEMS–SWAT Model. Water 2016, 8, 455. [Google Scholar] [CrossRef]
  3. Yi, Q.; Chen, X.; Xie, Y. Comparison and analysis between flood event 52.7 and 96.8 in Heihe River Basin. Inn. Mong. Water Resour. 2004, 97, 60–61. [Google Scholar]
  4. Ratha, D.; Sarkar, A. Analysis of flow over backward facing step with transition. Front. Struct. Civ. Eng. 2015, 9, 71–81. [Google Scholar] [CrossRef]
  5. Cai, Y.; Huang, W.; Teng, F.; Gu, S. Effects of changing climate on glacier shrinkage and river flow in the Upper Heihe River Basin, China. J. Coast. Res. 2014, 121–128. [Google Scholar] [CrossRef]
  6. Wang, G.; Liu, J.; Kubota, J.; Chen, L. Effects of land-use changes on hydrological processes in the middle basin of the Heihe River, northwest China. Hydrol. Process. 2007, 32, 1370–1382. [Google Scholar] [CrossRef]
  7. Jiao, W.; Xu, Z. A distributed runoff model for the mountainous region of the Heihe River Basin (China) based on the spatial modeling environment (SME) I: Model structure and equations. Environ. Earth Sci. 2013, 68, 881–888. [Google Scholar] [CrossRef]
  8. Jiao, W.; Xu, Z. A distributed runoff model for the mountainous region of the Heihe River Basin (China) based on the spatial modeling environment (SME) II: Model calibration and validation. Environ. Earth Sci. 2013, 69, 2189–2197. [Google Scholar] [CrossRef]
  9. Nian, Y.; Li, X.; Zhou, J.; Hu, X. Impact of land use change on water resourceallocation in the middle reaches of the Heihe River Basin in northwestern China. J. Arid Land 2014, 6, 273–286. [Google Scholar] [CrossRef]
  10. Cai, Y.; Huang, W.; Teng, F.; Wang, B.; Ni, K.; Zheng, C. Spatial variation of river-groundwater interactions from upstream mountain to midstream oasis and downstream desert in Heihe River Basin, China. Hydrol. Res. 2015, 47, 501–520. [Google Scholar] [CrossRef]
  11. Tian, Y.; Zheng, Y.; Wu, B.; Wu, X.; Liu, J.; Zheng, C.M. Modeling surface water-groundwater interaction in arid and semi-arid regions with intensive agriculture. Environ. Model. Softw. 2015, 63, 170–184. [Google Scholar] [CrossRef]
  12. Huang, W.; Cai, Y.; Chao, Y.N.; Teng, F.; Xu, S.D.; Wang, B.B. Neural Network Modelling of Flow in Yinluoxia Station Based on Flow in Zhamashike Station in Heihe River, China. Adv. Intell. Syst. Res. 2015, 123, 206–209. [Google Scholar]
  13. Qin, J.; Ding, Y.; Yang, G. The hydrological linkage of mountains and plains in the arid region of northwest China. Chin. Sci. Bull. 2013, 58, 3140–3147. [Google Scholar] [CrossRef]
  14. Luo, K.; Tao, F.; Deng, X.; Moiwo, J.P. Changes in potential evapotranspiration and surface runoff in 1981–2010 and the driving factors in Upper Heihe River Basin in Northwest China. Hydrol. Process. 2017, 31, 90–103. [Google Scholar] [CrossRef]
  15. Huang, Q.; Zhang, W. Improvement and application of GIS-based distributed SWAT hydrological modeling on high altitude, cold, semi-arid catchment of Heihe River Basin, China. J. Nanjing For. Univ. Nat. Sci. Ed. 2004, 28, 22–26. [Google Scholar]
  16. Zhou, J.; Li, X.; Wang, G.; Hu, H.; Sha, Z.; Leavesley, G.; Markstorm, S.; Viger, R. An Improved Precipitation-Runoff Model Based on MMS and its Application in the Upstream Basin of Heihe River. J. Nat. Resour. 2008, 23, 724–736. [Google Scholar]
  17. Shoaib, M.; Shamseldin, A.Y.; Melville, B.W. Comparative study of different wavelet based neural network models for rainfall–runoff modeling. J. Hydrol. 2014, 515, 47–58. [Google Scholar] [CrossRef]
  18. Taormina, R.; Chau, K.W. Data-driven input variable selection for rainfall–runoff modeling using binary-coded particle swarm optimization and Extreme Learning Machines. J. Hydrol. 2015, 529, 1617–1632. [Google Scholar] [CrossRef]
  19. Kisi, O.; Shiri, J.; Tombul, M. Modeling rainfall-runoff process using soft computing techniques. Comput. Geosci. 2013, 51, 108–117. [Google Scholar] [CrossRef]
  20. Granata, F.; Gargano, R.; de Marinis, G. Support vector regression for rainfall-runoff modeling in urban drainage: A comparison with the EPA’s storm water management model. Water 2016, 8, 69. [Google Scholar] [CrossRef]
  21. Alizadeh, M.J.; Kavianpour, M.R.; Kisi, O.; Nourani, V. A new approach for simulating and forecasting the rainfall-runoff process within the next two months. J. Hydrol. 2017, 548, 588–597. [Google Scholar] [CrossRef]
  22. Xia, J.; Wang, G.; Tan, G.; Ye, A.; Huang, G.H. Development of distributed time-variant gain model for nonlinear hydrological systems. Sci. China Ser. D Earth Sci. 2005, 48, 713–723. [Google Scholar] [CrossRef]
  23. Chen, R.; Lu, S.; Kang, E.; Ji, X.; Zhang, Z.; Yang, Y.; Qing, W. A distributed water-heat coupled model for mountainous watershed of an inland river basin of Northwest China (I) model structure and equations. Environ. Geol. 2008, 53, 1299–1309. [Google Scholar] [CrossRef]
  24. Chen, R.; Lu, S.; Kang, E.; Ji, X.; Zhang, Z.; Yang, Y.; Qing, W. A distributed water-heat coupled model for mountainous watershed of an inland river basin in Northwest China (II) using meteorological and hydrological data. Environ. Geol. 2008, 55, 17–28. [Google Scholar] [CrossRef]
  25. Li, Z.; Deng, X.; Wu, F.; Hasan, S. Scenario Analysis for Water Resources in Response to Land Use Change in the Middle and Upper Reaches of the Heihe River Basin. Sustainability 2015, 7, 3086–3108. [Google Scholar] [CrossRef]
  26. Wu, F.; Zhan, J.; Güneralp, İ. Present and future of urban water balance in the rapidly urbanizing Heihe River Basin, Northwest China. Ecol. Model. 2015, 318, 254–264. [Google Scholar] [CrossRef]
  27. Li, L.; Xu, Z.; Zhao, J.; Su, L. A distributed hydrological model in the Heihe River Basin and its potential for estimating the required irrigation water. Hydrol. Res. 2017, 48, 191–213. [Google Scholar] [CrossRef]
  28. Markstrom, S.L.; Regan, R.S.; Hay, L.E.; Viger, R.J.; Webb, R.M.T.; Payn, R.A.; LaFontaine, J.H. PRMS-IV, the Precipitation-Runoff Modeling System; version 4. U.S. Geological Survey (Reston, VA, USA) Techniques and Methods, 2015, Book 6, Chap. B7; p. 158. Available online: https://pubs.usgs.gov/tm/6b7/ (accessed on 13 February 2016).
  29. Niswonger, R.G.; Allander, K.K.; Jenton, A.E. Collaborative modelling and integrated decision support system analysis of a developed terminal lake basin. J. Hydrol. 2014, 517, 521–537. [Google Scholar] [CrossRef]
  30. Markstrom, S.L.; Hay, L.E. Integrated watershed scale response to climate change for selected basins across the United States. Water Resour. Impact 2009, 11, 8–10. [Google Scholar]
  31. Hay, L.E.; Leavesley, G.H.; Clark, M.P.; Markstrom, S.L.; Viger, R.J.; Umemoto, M. Step-wise, multiple objective calibration of a hydrologic model for a snowmelt-dominated watershed. J. Am. Water Resour. Assoc. 2006, 42, 877–890. [Google Scholar] [CrossRef]
  32. Hay, L.E.; Wilby, R.L.; Leavesley, G.H. A comparison of delta change and downscaled GCM scenarios for three mountainous basins in the United States. J. Am. Water Resour. Assoc. 2000, 36, 387–397. [Google Scholar] [CrossRef]
  33. Christiansen, D.E.; Markstrom, S.L.; Hay, L.E. Impacts of climate change on growing season in the United States. Earth Interact. 2011, 15, 1–17. [Google Scholar] [CrossRef]
  34. Dressler, K.A.; Leavesley, G.H.; Bales, R.C.; Fassnacht, S.R. Evaluation of gridded snow water equivalent and satellite snow cover products for mountain basins in a hydrologic model. Hydrol. Process. 2006, 20, 673–688. [Google Scholar] [CrossRef]
  35. Markstrom, S.L.; Niswonger, R.G.; Regan, R.S.; Prudic, D.E.; Barlow, P.M. GSFLOW—Coupled Ground-Water and Surface-Water Flow Model Based on the Integration of the Precipitation-Runoff Modeling System (PRMS) and the Modular Ground-Water Flow Model (MODFLOW-2005); U.S. Geological Survey: Reston, VA, USA, 2008. [Google Scholar]
  36. Data Management Center of Heihe Project. Available online: http://www.heihedata.org/data (accessed on 5 November 2014).
  37. Wang, H.; Zhang, B.; Jin, X. Analysis of temporal and spatial variation of temperature and precipitation in Qilian mountain area based on GIS. J. Desert Res. 2009, 29, 1196–1202. [Google Scholar]
  38. U.S. Army Corps of Engineers. Hydrologic Modeling System (HEC-HMS) User Manual; version 4.2.0; Hydrologic Engineering Center: Davis, CA, USA, 2016.
  39. Chang, H.; Jung, I.-W. Spatial and temporal changes in runoff caused by climate change in a complex large river basin in Oregon. J. Hydrol. 2010, 388, 186–207. [Google Scholar] [CrossRef]
  40. Mazi, K.; Koussis, A.D.; Restrepo, P.J.; Koutsoyiannis, D. A groundwater-based, objective-heuristic parameter optimisation method for a precipitation-runoff model and its application to a semi-arid basin. J. Hydrol. 2004, 290, 243–258. [Google Scholar] [CrossRef]
Water 09 00769 g001 550
Figure 1. Zamask-Yingluoxia subbasin (a) of the Heihe River Basin (b), Northwest China.
Figure 1. Zamask-Yingluoxia subbasin (a) of the Heihe River Basin (b), Northwest China.
Water 09 00769 g001
Water 09 00769 g002 550
Figure 2. Segments, hydrological response units, and data station locations in the Zamask-Yingluoxia subbasin. Data of precipitation and flow are available in three hydrological stations.
Figure 2. Segments, hydrological response units, and data station locations in the Zamask-Yingluoxia subbasin. Data of precipitation and flow are available in three hydrological stations.
Water 09 00769 g002
Water 09 00769 g003 550
Figure 3. Schematic diagram of a watershed and its climate inputs simulated by the Precipitation-Runoff Modeling System (PRMS).
Figure 3. Schematic diagram of a watershed and its climate inputs simulated by the Precipitation-Runoff Modeling System (PRMS).
Water 09 00769 g003
Water 09 00769 g004 550
Figure 4. Geographic data of the subbasins: (a) Elevation; (b) Slope; (c) Aspect.
Figure 4. Geographic data of the subbasins: (a) Elevation; (b) Slope; (c) Aspect.
Water 09 00769 g004
Water 09 00769 g005 550
Figure 5. Hydrological model structure for the Zamask-Yingluoxia Basin.
Figure 5. Hydrological model structure for the Zamask-Yingluoxia Basin.
Water 09 00769 g005
Water 09 00769 g006 550
Figure 6. Measured flows from hydrologic stations with upstream inflows from Zamask and Qilian stations: (a) flow from August to September 2004; (b) flow from January 2003 to December 2006.
Figure 6. Measured flows from hydrologic stations with upstream inflows from Zamask and Qilian stations: (a) flow from August to September 2004; (b) flow from January 2003 to December 2006.
Water 09 00769 g006
Water 09 00769 g007 550
Figure 7. Averaged observed precipitation in the Zamask-Yingluoxia subbasin: (a) Precipitation from August to September 2004; (b) Precipitation from January 2004 to December 2006.
Figure 7. Averaged observed precipitation in the Zamask-Yingluoxia subbasin: (a) Precipitation from August to September 2004; (b) Precipitation from January 2004 to December 2006.
Water 09 00769 g007
Water 09 00769 g008 550
Figure 8. Comparison of measured and estimated flows at Yingluoxia station during the model calibration period from 1 August to 30 September 2004: (a) stream flow; (b) correlation.
Figure 8. Comparison of measured and estimated flows at Yingluoxia station during the model calibration period from 1 August to 30 September 2004: (a) stream flow; (b) correlation.
Water 09 00769 g008
Water 09 00769 g009 550
Figure 9. Comparison of measured and estimated flows at Yingluoxia station during the model verification period from 1 January 2003 to 31 December 2006.
Figure 9. Comparison of measured and estimated flows at Yingluoxia station during the model verification period from 1 January 2003 to 31 December 2006.
Water 09 00769 g009
Table
Table 1. Major calibrated parameters’ value of PRMS.
Table 1. Major calibrated parameters’ value of PRMS.
ModuleParametersMean Value
Surfacedprst_flow_coef:
Coefficient in linear flow routing equation for open surface depressions		0.2
sro_to_dprst:
Fraction of pervious and impervious surface runoff that flows into surface depressions; the remainder flows to a stream network		0.5
smidx_coef:
Coefficient in non-linear contributing area algorithm		0.22
Soilpref_flow_den:
Decimal fraction of the soil zone available for preferential flow		0.11
ssr2gw_rate:
Linear coefficient in the equation used to compute gravity drainage to PRMS groundwater reservoir		0.3
Baseflowgwflow_coef:
Linear coefficient to route water in groundwater reservoir to streams		0.02
ReachK_coef:
Travel time of flood wave from one segment to the next downstream segment, called the Muskingum storage coefficient		1.3
Table
Table 2. Statistics comparison of model simulations and observations of daily flow at Yingluoxia station by different rainfall-runoff modeling studies.
Table 2. Statistics comparison of model simulations and observations of daily flow at Yingluoxia station by different rainfall-runoff modeling studies.
Model Name (Authors)Water-Heat Coupled Model (Chen, et al. [24])Model Based on SME 3 (Jiao and Xu [8])GISMOD 4 (Li et al. [27])SWAT (Li et al. [25]; Wu et al. [26])PRMS (Present Study)
RegionHeihe upstream basinHeihe upstream basinHeihe upstream basinHeihe upstream and midstream basinZamask-Yingluoxia subbasin
Period Calibration Verification2000
1999		2000
1995–1999		1990–19932009
2010		8–9/2004
2003–2006
Correlation coefficient0.77Not availableNot available0.87 (calib. 1), 0.89 (verif.)0.90 (calib.),
0.95 (verif.)
Nash-Sutcliffe efficiency coefficient0.6270.46–0.620.7–0.710.88 (calib.), 0.87 (verif.)0.82 (calib.),
0.90 (verif.)
Root mean square error (m3/s)34.9Not availableNot availableNot available11.2 (calib.),
15.7 (verif.)
Error of maximum flow (m3/s)130 2 (calib.), 350 (verif.)60 (calib.),
30 (verif.)		Not available30 (calib.),
35 (verif.)		1.4 (calib.),
6.9 (verif.)
Notes: 1 Calib. = calibration; verif. = verification; 2 Except present study, errors of maximum flows in previous studies are approximately obtained from the figures in the references. 3 Spatial Modeling Environment (SME); 4 Distributed hydrological model (GISMOD).
Table
Table 3. Major components in stream flow as the results of rainfall runoff from model simulations between 1 January 2003 and 31 December 2006.
Table 3. Major components in stream flow as the results of rainfall runoff from model simulations between 1 January 2003 and 31 December 2006.
Components of Stream FlowSurface RunoffInterflowGroundwater Recharge
Percentage of the stream flow48.4%21.0%30.6%

Share and Cite

MDPI and ACS Style

Teng, F.; Huang, W.; Cai, Y.; Zheng, C.; Zou, S. Application of Hydrological Model PRMS to Simulate Daily Rainfall Runoff in Zamask-Yingluoxia Subbasin of the Heihe River Basin. Water 2017, 9, 769. https://doi.org/10.3390/w9100769

AMA Style

Teng F, Huang W, Cai Y, Zheng C, Zou S. Application of Hydrological Model PRMS to Simulate Daily Rainfall Runoff in Zamask-Yingluoxia Subbasin of the Heihe River Basin. Water. 2017; 9(10):769. https://doi.org/10.3390/w9100769

Chicago/Turabian Style

Teng, Fei, Wenrui Huang, Yi Cai, Chunmiao Zheng, and Songbin Zou. 2017. "Application of Hydrological Model PRMS to Simulate Daily Rainfall Runoff in Zamask-Yingluoxia Subbasin of the Heihe River Basin" Water 9, no. 10: 769. https://doi.org/10.3390/w9100769

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop