Integrating Artificial Neural Networks into the VIC Model for Rainfall-Runoff Modeling
Abstract
:1. Introduction
2. Integrating ANNs with the VIC Model
2.1. Variable Infiltration Capacity Model
2.2. Artificial Neural Networks
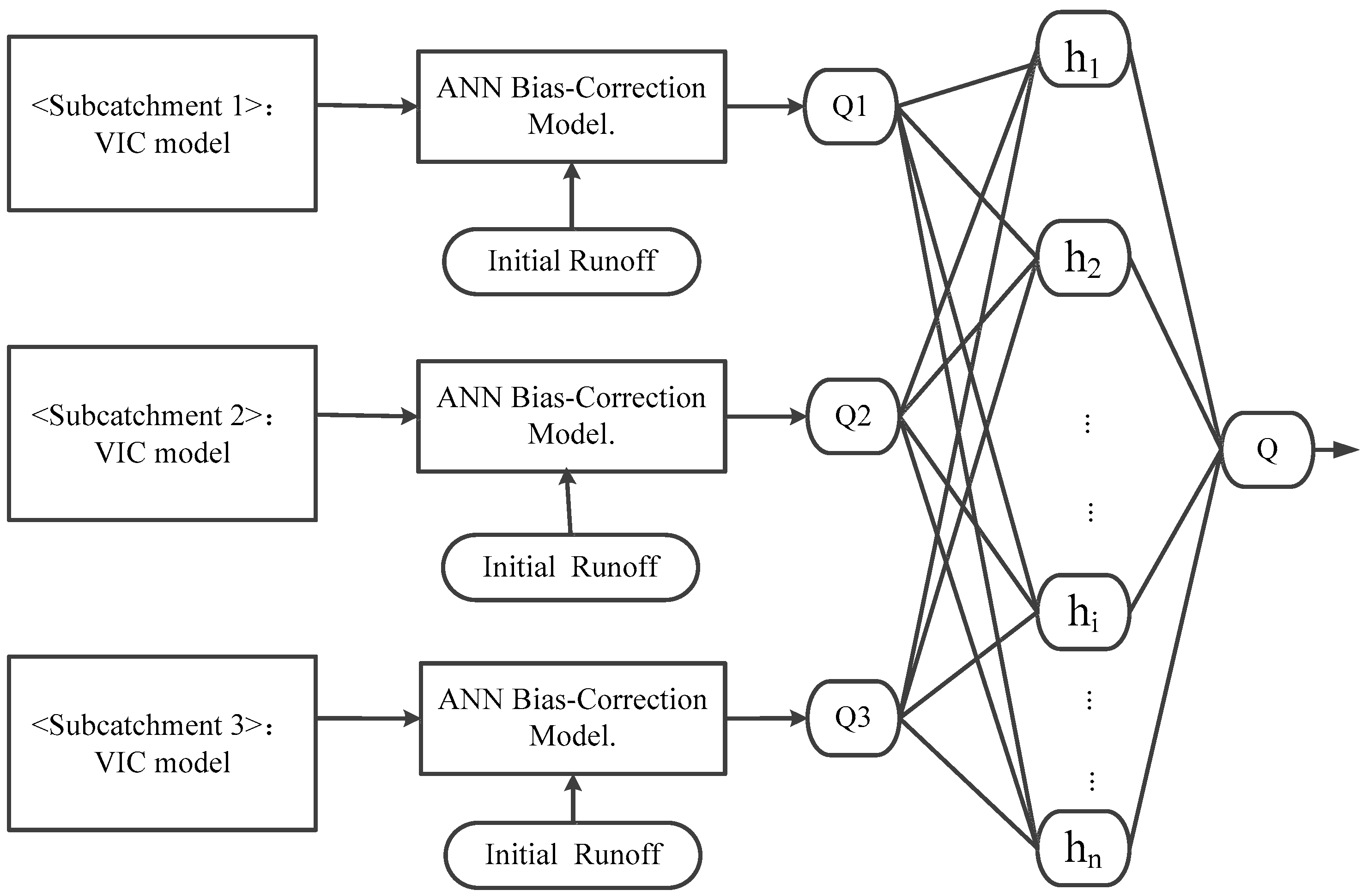
2.3. Hybrid VIC and ANN Model
3. Model Application and Case Study
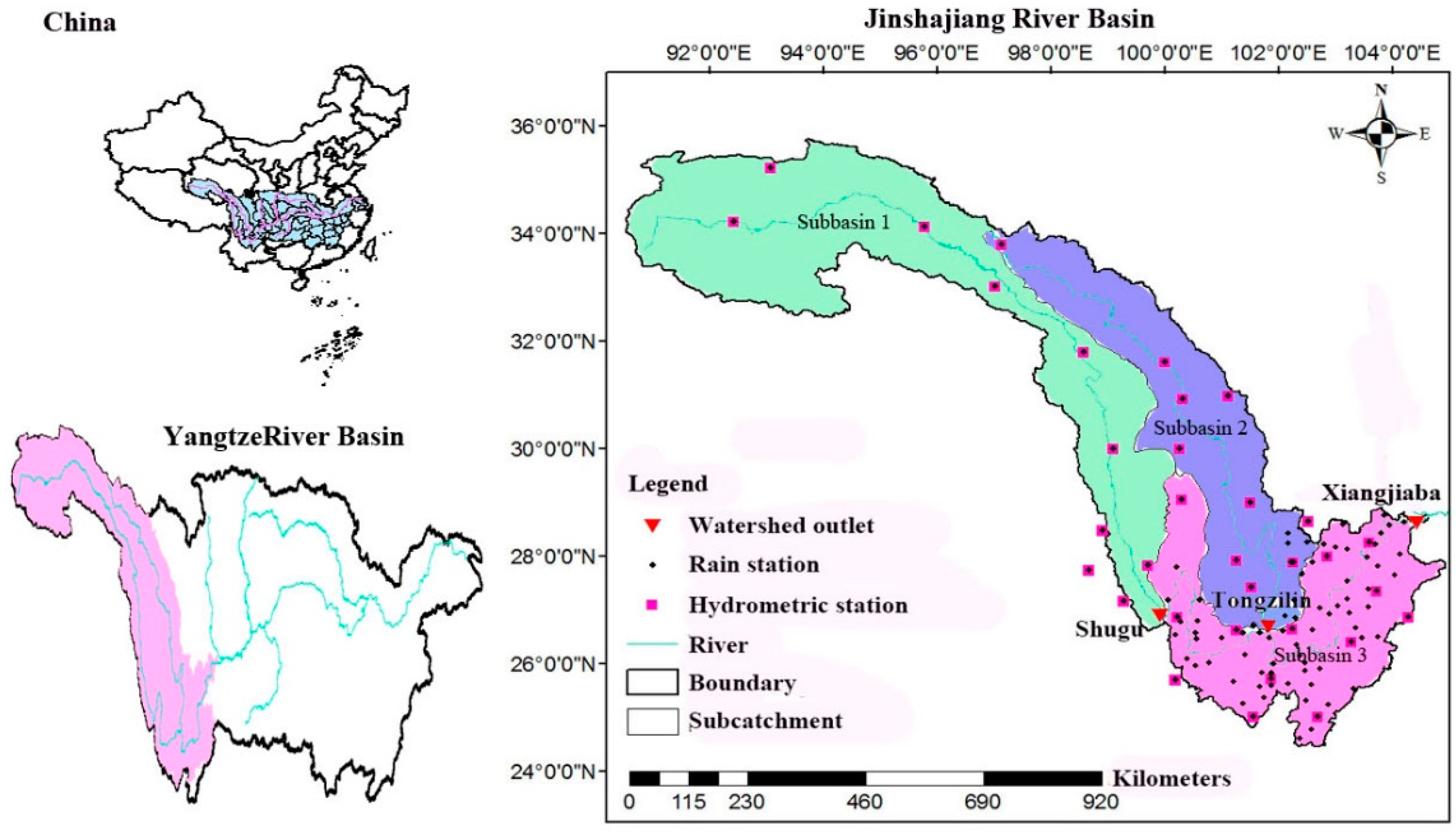
3.1. Study Area
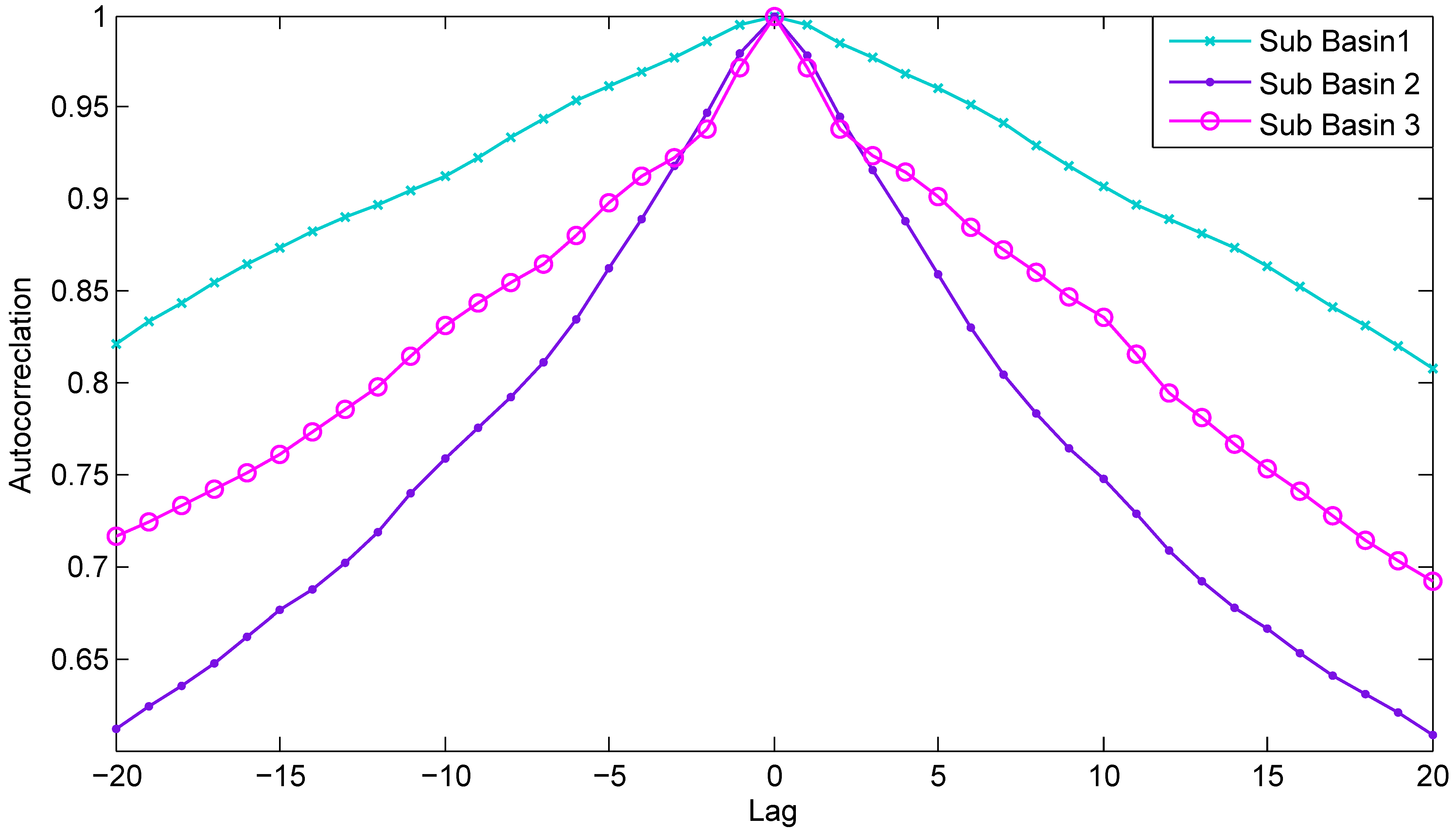
3.2. Data Preparation
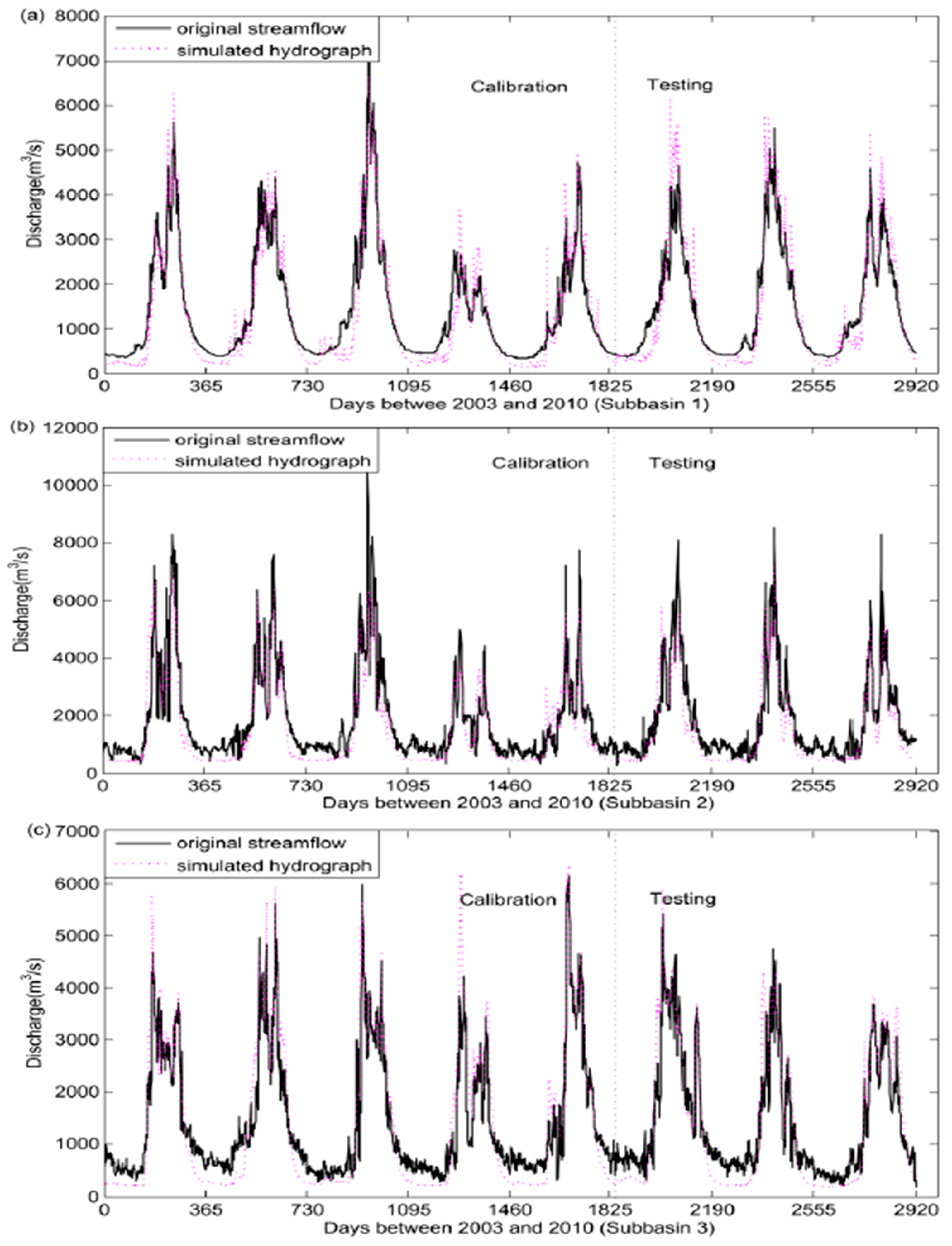
3.3. Calibrating the VIC Model
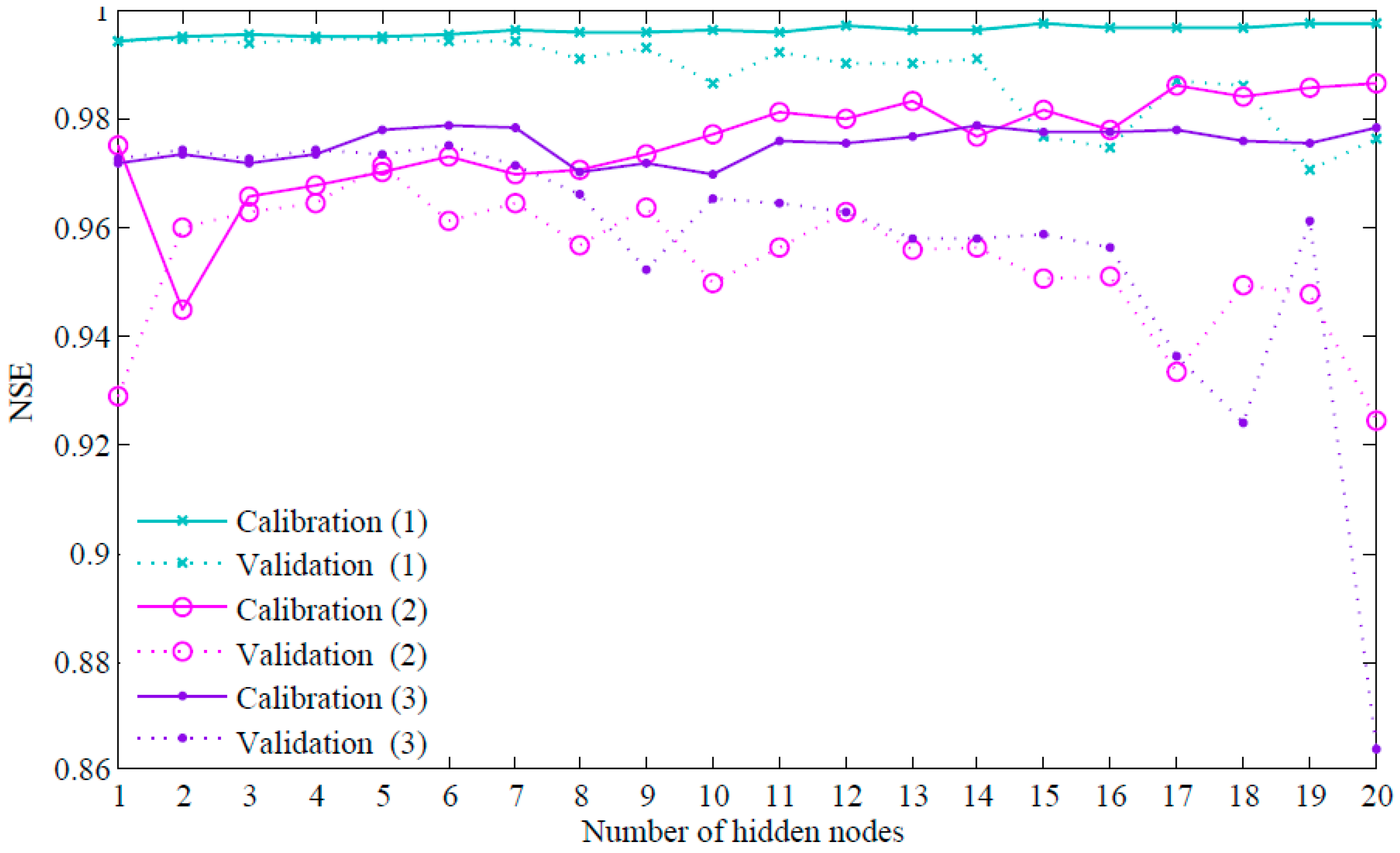
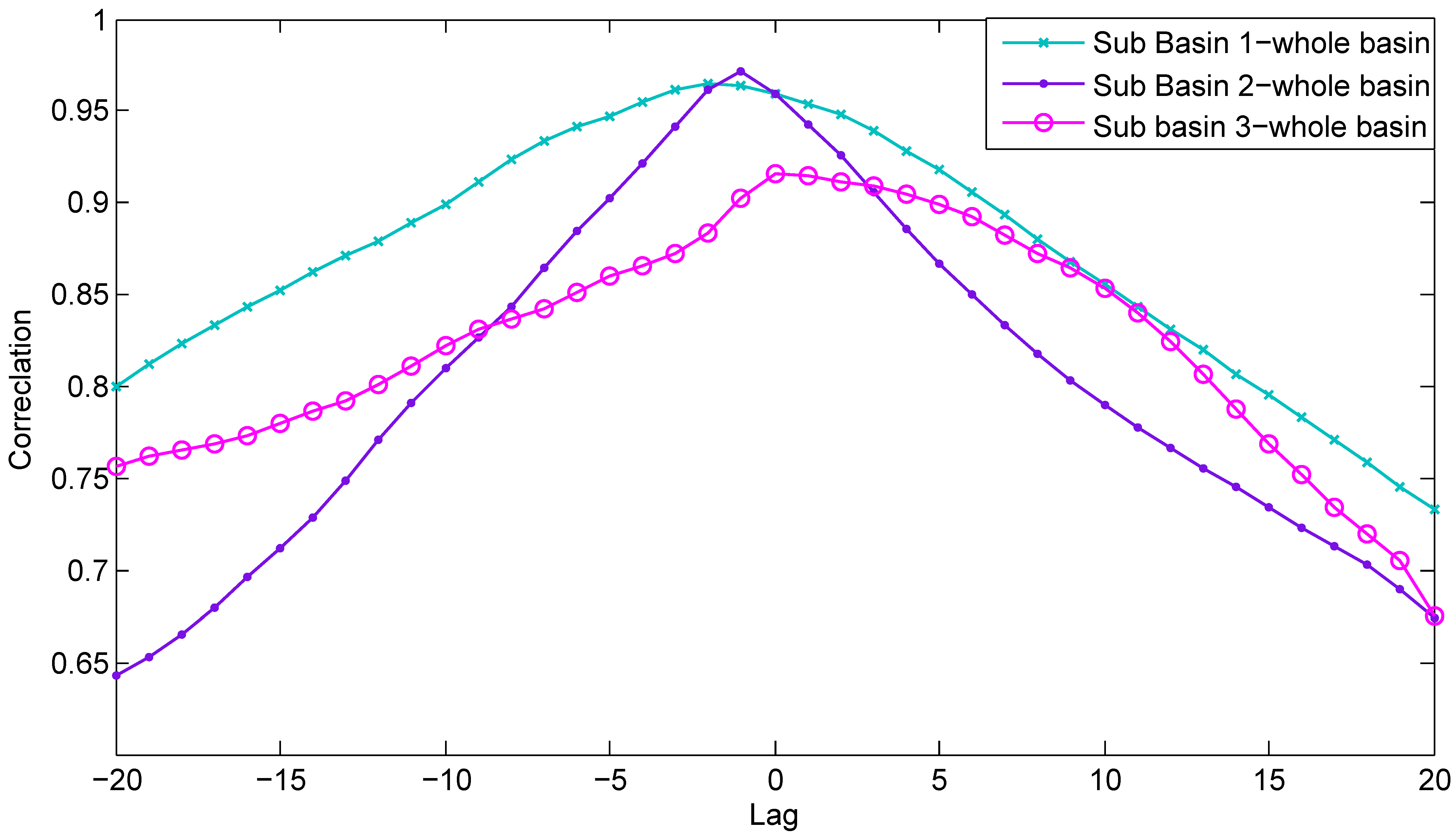
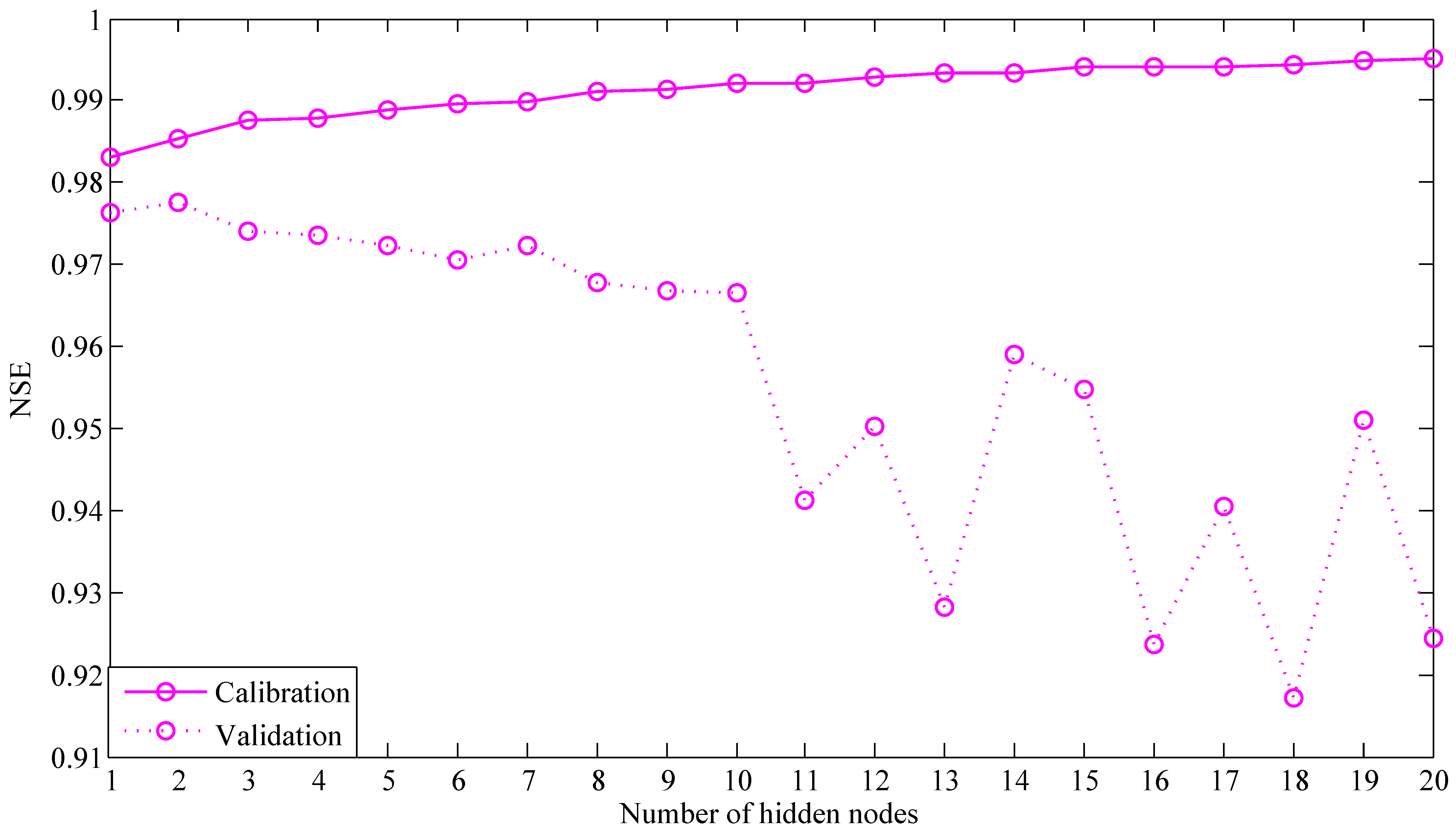
3.4. Configuring the ABCM
- Calculate , …, and for Subbasin 1; , …, and for Subbasin 2; , , and for Subbasin 3.
- Let Ei(t) plus be the corrected flow of each subbasin.
- Determine the optimal number of hidden neurons of each subbasin’s ABCM by trial-and-error.
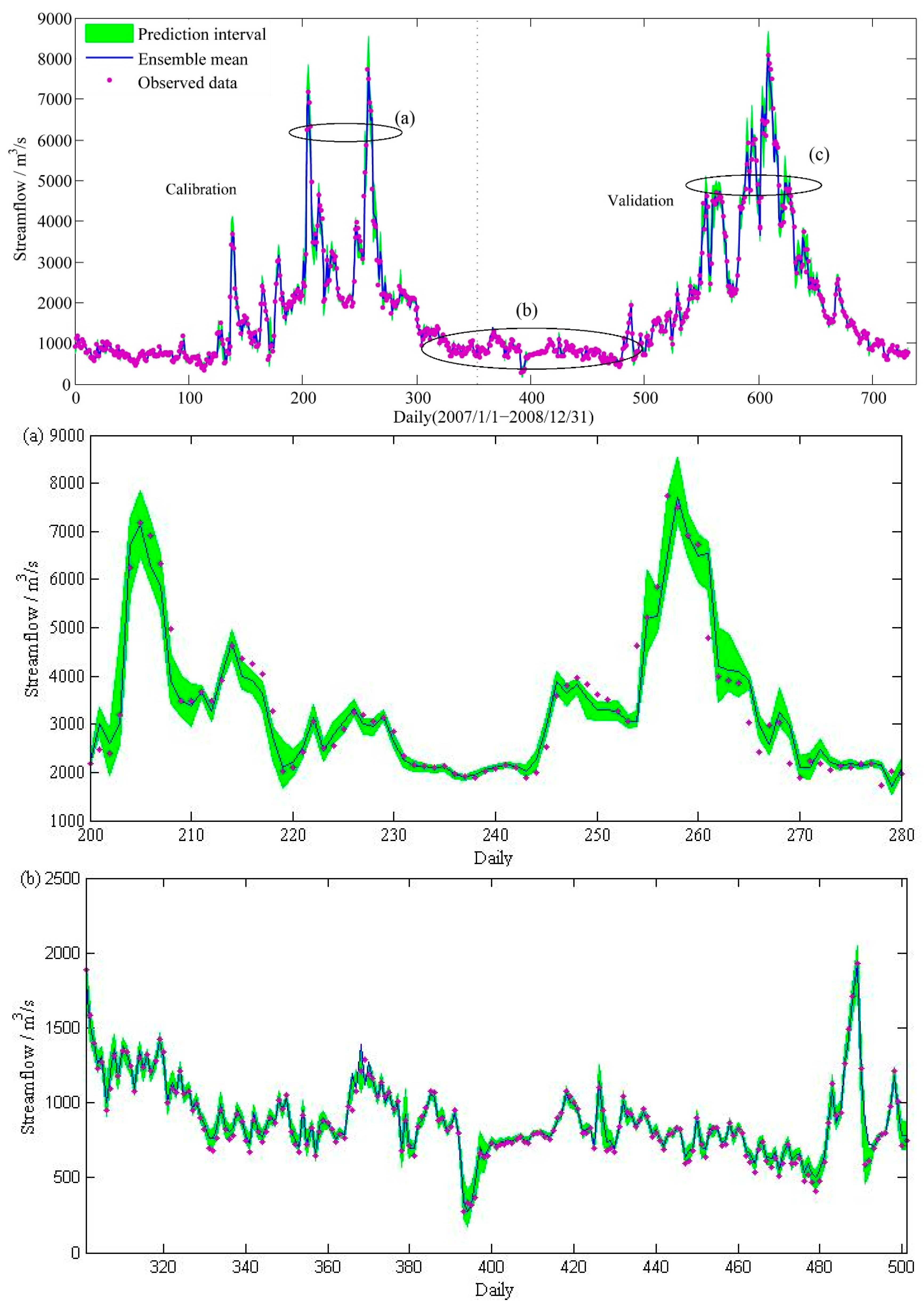
3.5. Configuring the ARM
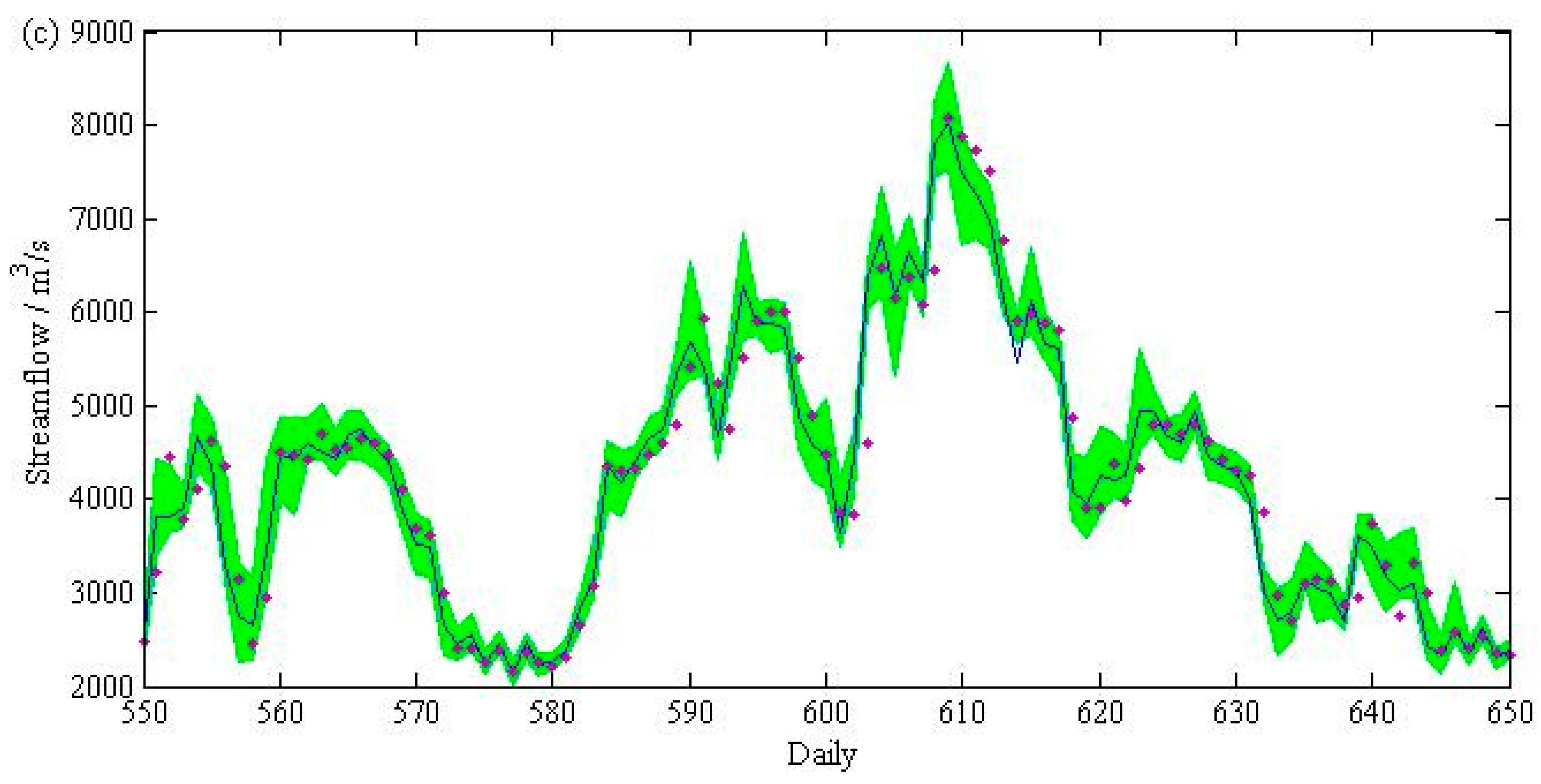
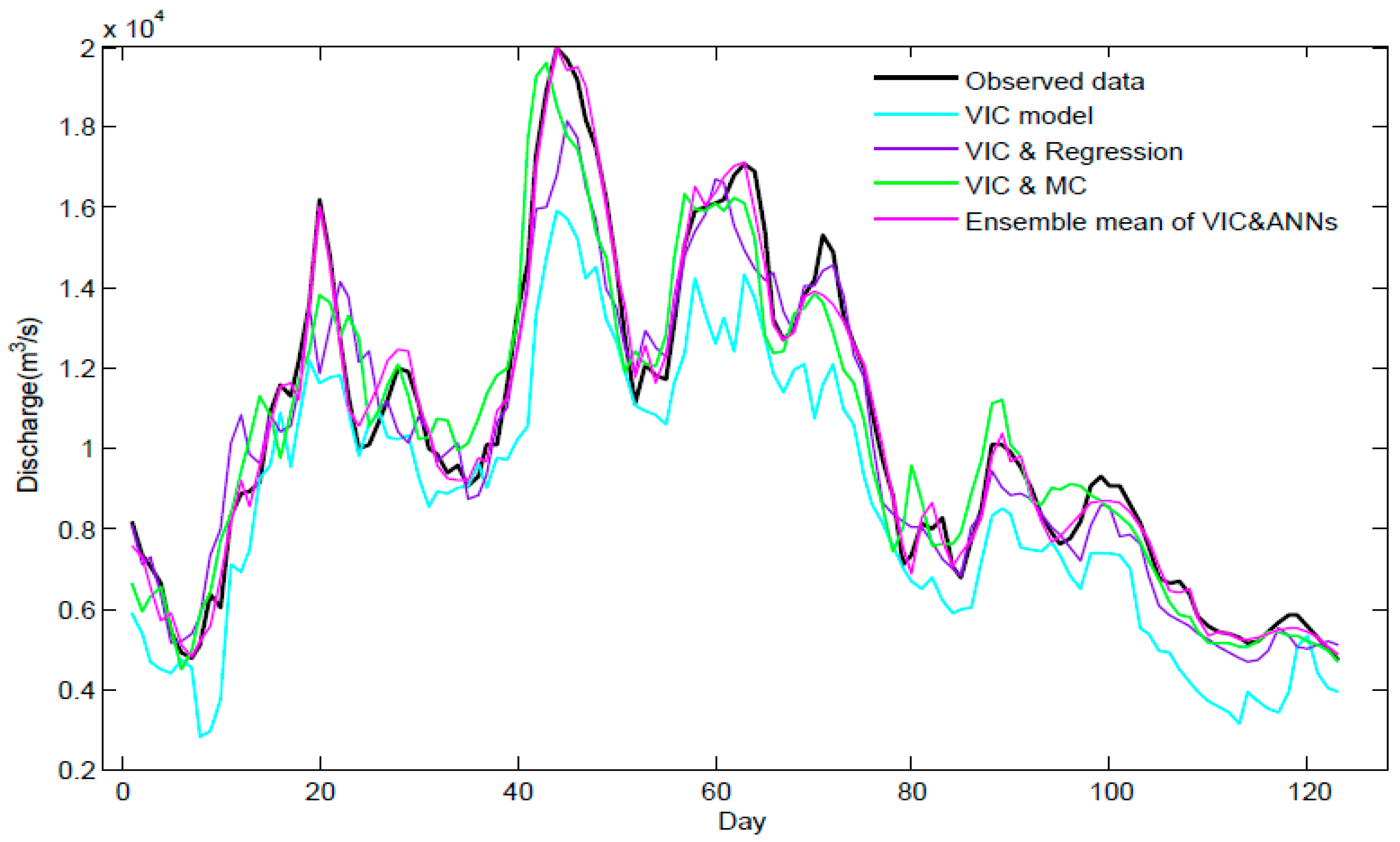
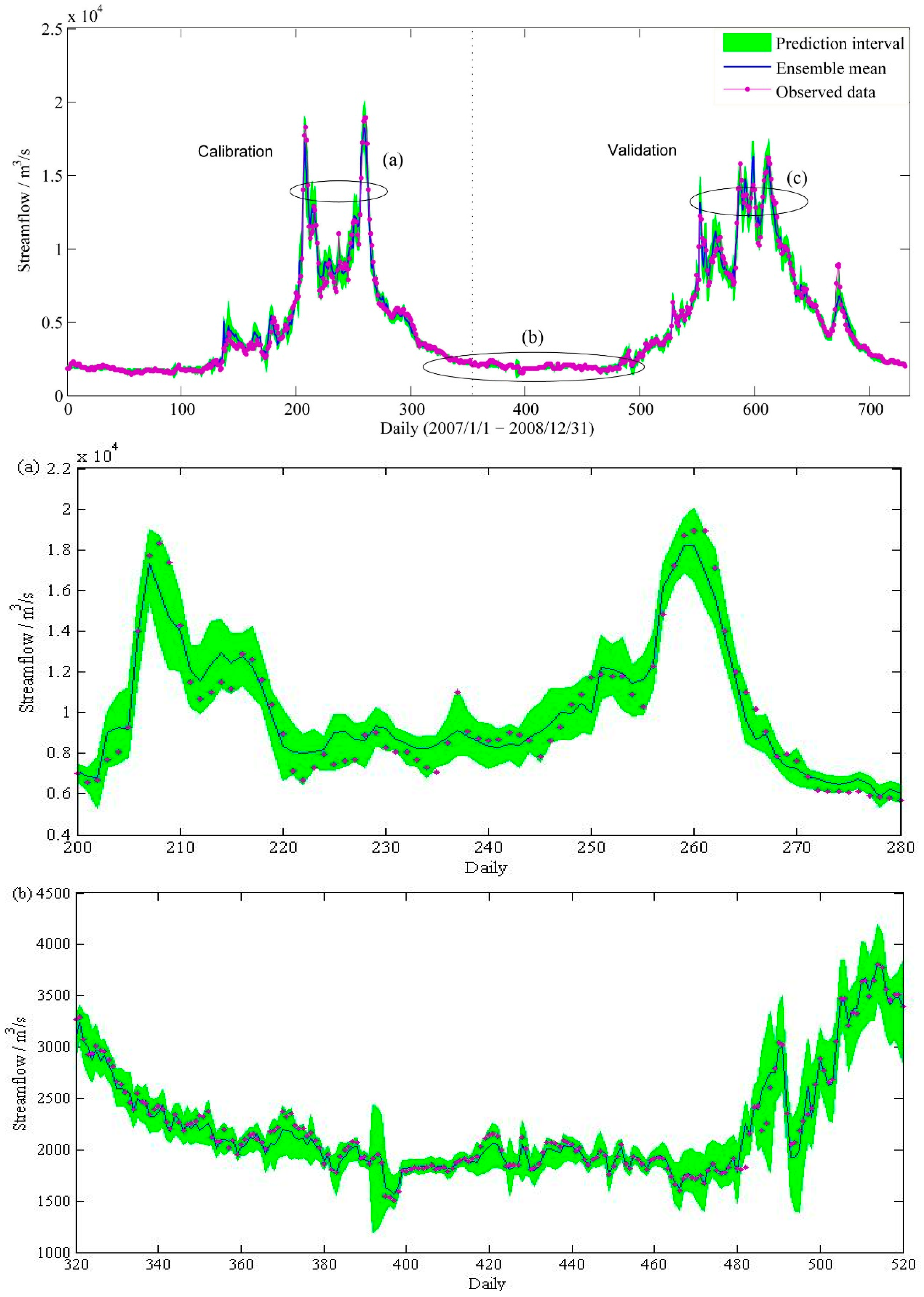
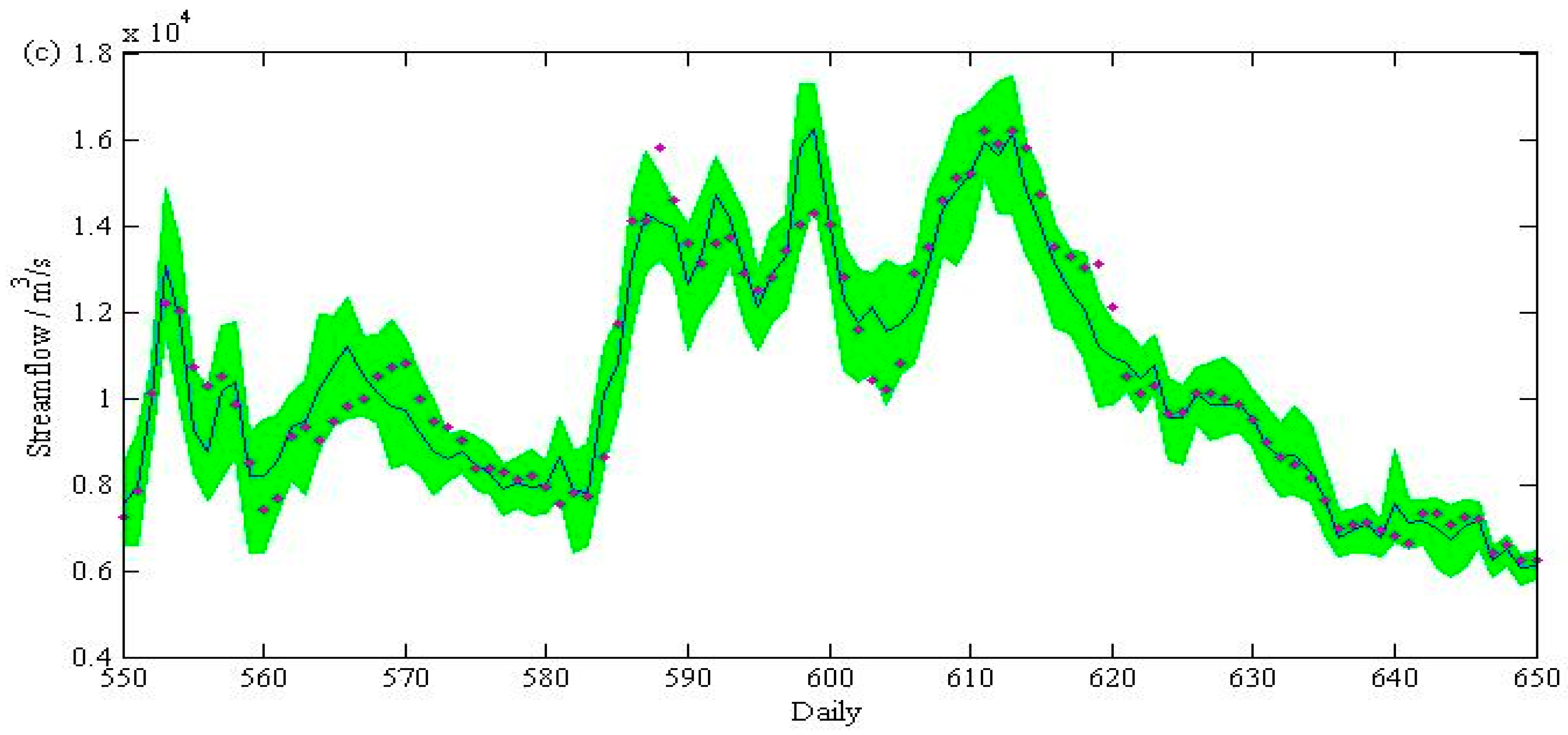
4. Results and Discussion
5. Summary and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Liang, X. A simple hydrologically based model of land-surface water and energy fluxes for general-circulation models. J. Geophys. Res. 1994, 99, 14415–14428. [Google Scholar] [CrossRef]
- Liang, X. Surface soil moisture parameterization of the VIC-2L model: Evaluation and modification. Glob. Planet. Chang. 1996, 13, 195–206. [Google Scholar] [CrossRef]
- Liang, X.; Xie, Z.H.; Huang, M.Y. A new parameterization for surface and groundwater interactions and its impact on water budgets with the variable infiltration capacity (VIC) land surface model. J. Geophys. Res. 2003, 108. [Google Scholar] [CrossRef]
- Nijssen, B.; Schnur, R.; Lettenmaier, D.P. Global retrospective estimation of soil moisture using the variable infiltration capacity land surface model, 1980–1993. J. Clim. 2001, 14, 1790–1808. [Google Scholar] [CrossRef]
- Nijssen, B. Predicting the discharge of global rivers. J. Clim. 2001, 14, 3307–3323. [Google Scholar] [CrossRef]
- You, Q.; Min, J.; Zhang, W.; Pepin, N.; Kang, S. Comparison of multiple datasets with gridded precipitation observations over the Tibetan Plateau. Clim. Dyn. 2015, 45, 791–806. [Google Scholar] [CrossRef]
- You, Q.L.; Min, J.Z.; Kang, S.C.; Pepin, N. Poleward expansion of the tropical belt derived from upper tropospheric water vapour. Int. J. Climatol. 2015, 35, 2237–2242. [Google Scholar] [CrossRef]
- Mo, K.C.; Lettenmaier, D.P. Hydrologic prediction over the conterminous United States using the national multi-model ensemble. J. Hydrometeorol. 2014, 15, 1457–1472. [Google Scholar] [CrossRef]
- Park, D.; Markus, M. Analysis of a changing hydrologic flood regime using the Variable Infiltration Capacity model. J. Hydrol. 2014, 515, 267–280. [Google Scholar] [CrossRef]
- Eum, H.I.; Dibike, Y.; Prowse, T.; Bonsal, B. Inter-comparison of high-resolution gridded climate data sets and their implication on hydrological model simulation over the Athabasca Watershed, Canada. Hydrol. Process. 2014, 28, 4250–4271. [Google Scholar]
- Warrach-Sagi, K.; Wulfmeyer, V.; Grasselt, R.; Ament, F.; Simmer, C. Streamflow simulations reveal the impact of the soil parameterization. Meteorol. Z. 2008, 17, 751–762. [Google Scholar] [CrossRef]
- Tan, A.; Adam, J.C.; Lettenmaier, D.P. Change in spring snowmelt timing in Eurasian Arctic rivers. J. Geophys. Res. 2011, 116. [Google Scholar] [CrossRef]
- Wu, H.; Adler, R.F.; Tian, Y.; Huffman, G.J.; Li, H.; Wang, J. Real-time global flood estimation using satellite-based precipitation and a coupled land surface and routing model. Water Resour. Res. 2014, 50, 2693–2717. [Google Scholar] [CrossRef]
- Eum, H.I.; Yonas, D.; Prowse, T. Uncertainty in modelling the hydrologic responses of a large watershed: A case study of the Athabasca river basin, Canada. Hydrol. Process. 2014, 28, 4272–4293. [Google Scholar] [CrossRef]
- Lohmann, D.; Raschke, E.; Nijssen, B.; Lettenmaier, D.P. Regional scale hydrology: I. Formulation of the VIC-2L model coupled to a routing model. Hydrol. Sci. J. 1998, 43, 131–141. [Google Scholar]
- Lohmann, D.; Raschke, E.; Nijssen, B.; Lettenmaier, D.P. Regional scale hydrology: II. Application of the VIC-2L model to the Weser River, Germany. Hydrol. Sci. J. 1998, 43, 143–158. [Google Scholar]
- Gao, C.; Gemmer, M.; Zeng, X.; Liu, B.; Su, B.; Wen, Y. Projected streamflow in the Huaihe river basin (2010–2100) using artificial neural network. Stoch. Environ. Res. Risk Assess. 2010, 24, 685–697. [Google Scholar] [CrossRef]
- Huo, Z.; Feng, S.; Kang, S.; Huang, G.; Wang, F.; Guo, P. Integrated neural networks for monthly river flow estimation in arid inland basin of Northwest China. J. Hydrol. 2012, 420, 159–170. [Google Scholar] [CrossRef]
- Dumedah, G.; Walker, J.P.; Chik, L. Assessing artificial neural networks and statistical methods for infilling missing soil moisture records. J. Hydrol. 2014, 515, 330–344. [Google Scholar] [CrossRef]
- Chang, F.J.; Lin, C.H.; Chang, K.C.; Kao, Y.H.; Chang, L.C. Investigating the interactive mechanisms between surface water and groundwater over the Jhuoshuei river basin in central Taiwan. Paddy Water Environ. 2014, 12, 365–377. [Google Scholar] [CrossRef]
- Burchard-Levine, A.; Liu, S.; Vince, F.; Li, M.; Ostfeld, A. A hybrid evolutionary data driven model for river water quality early warning. J. Environ. Manag. 2014, 143, 8–16. [Google Scholar] [CrossRef] [PubMed]
- Yilmaz, A.G.; Imteaz, M.A.; Jenkins, G. Catchment flow estimation using artificial neural networks in the mountainous Euphrates basin. J. Hydrol. 2011, 410, 134–140. [Google Scholar] [CrossRef]
- Aziz, K.; Rahman, A.; Fang, G.; Shrestha, S. Application of artificial neural networks in regional flood frequency analysis: A case study for Australia. Stoch. Environ. Res. Risk Assess. 2014, 28, 541–554. [Google Scholar] [CrossRef]
- Chang, F.J.; Chiang, Y.M.; Tsai, M.J.; Shieh, M.C.; Hsu, K.; Sorooshian, S. Watershed rainfall forecasting using neuro-fuzzy networks with the assimilation of multi-sensor information. J. Hydrol. 2014, 508, 374–384. [Google Scholar] [CrossRef]
- Okkan, U.; Fistikoglu, O. Evaluating climate change effects on runoff by statistical downscaling and hydrological model GR2M. Theor. Appl. Climatol. 2014, 117, 343–361. [Google Scholar] [CrossRef]
- Abramowitz, G.; Pitman, A.; Gupta, H.; Kowalczyk, E.; Wang, Y.P. Systematic bias in land surface models. J. Hydrometeorol. 2007, 8, 989–1001. [Google Scholar] [CrossRef]
- ASCE Task Committee on Artificial Neural Networks in Hydrology. Artificial neural networks in hydrology: I Preliminary concepts. J. Hydrol. Eng. 2000, 5, 115–123. [Google Scholar]
- ASCE Task Committee on Artificial Neural Networks in Hydrology. Artificial neural networks in hydrology: II Hydrologic applications. J. Hydrol. Eng. 2000, 5, 124–137. [Google Scholar]
- Lee, D.S.; Jeon, C.O.; Park, J.M.; Chang, K.S. Hybrid neural network modeling of a full-scale industrial wastewater treatment process. Biotechnol. Bioeng. 2002, 78, 670–682. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.Y.; Adams, B.J. Integration of artificial neural networks with conceptual models in rainfall-runoff modeling. J. Hydrol. 2006, 318, 232–249. [Google Scholar] [CrossRef]
- Jain, A.; Srinivasulu, S. Integrated approach to model decomposed flow hydrograph using artificial neural network and conceptual techniques. J. Hydrol. 2006, 317, 291–306. [Google Scholar] [CrossRef]
- Song, X.M.; Kong, F.Z.; Zhan, C.S.; Han, J.W. Hybrid optimization rainfall-runoff simulation based on Xinanjiang model and artificial neural network. J. Hydrol. Eng. 2012, 17, 1033–1041. [Google Scholar] [CrossRef]
- Elshorbagy, A.; Corzo, G.; Srinivasulu, S.; Solomatine, D.P. Experimental investigation of the predictive capabilities of data driven modeling techniques in hydrology—Part 1: Concepts and methodology. Hydrol. Earth Syst. Sci. 2010, 14, 1931–1941. [Google Scholar] [CrossRef]
- Kasiviswanathan, K.S.; Cibin, R.; Sudheer, K.P.; Chaubey, I. Constructing prediction interval for artificial neural network rainfall runoff models based on ensemble simulations. J. Hydrol. 2013, 499, 275–288. [Google Scholar] [CrossRef]
- Liang, X.; Xie, Z.H. Important factors in land-atmosphere interactions: Surface runoff generations and interactions between surface and groundwater. Glob. Planet. Chang. 2003, 38, 101–114. [Google Scholar] [CrossRef]
- Todini, E. The ARNO rainfall–runoff model. J. Hydrol. 1996, 175, 339–382. [Google Scholar] [CrossRef]
- Zeng, X.; Zbigniew, W.; Zhou, J.Z.; Su, B.D. Discharge projection in the Yangtze River basin under different emission scenarios based on the artificial neural networks. Quat. Int. 2012, 282, 113–121. [Google Scholar] [CrossRef]
- Chen, J.Y.; Adams, B.J. Semidistributed form of the Tank model coupled with Artificial Neural Networks. J. Hydrol. Eng. 2006, 11, 408–417. [Google Scholar] [CrossRef]
- Tiwari, M.K.; Song, K.Y.; Chatterjee, C.; Gupta, M.M. River-flow forecasting using higher-order neural networks. J. Hydrol. Eng. 2012, 17, 655–666. [Google Scholar] [CrossRef]
- Bowden, G.J.; Dandy, G.C.; Maier, H.R. Input determination for neural network models in water resources applications. Part 1-background and methodology. J. Hydrol. 2005, 301, 75–92. [Google Scholar]
- Bowden, G.J.; Dandy, G.C.; Maier, H.R. Input determination for neural network models in water resources applications. Part 2. Case study: Forecasting salinity in a river. J. Hydrol. 2005, 301, 93–107. [Google Scholar]
- Jinshajiang River Basin in China. Data Center for Resources And Environmental Sciences, Chinese Academy of Sciences (RESDC). Available online: http://www.resdc.cn/data.aspx?DATAID=141 (accessed on 12 May 2016).
- Raje, D.; Priya, P.; Krishnan, R. Macroscale hydrological modelling approach for study of large scale hydrologic impacts under climate change in Indian river basins. Hydrol. Process. 2014, 28, 1874–1889. [Google Scholar] [CrossRef]
- Ponce, V.M.; Yevjevich, V. Muskingum-Cunge method with variable parameters. J. Hydraul. Div. 1978, 104, 124–137. [Google Scholar] [CrossRef]
- Getirana, A.C.V.; Boone, A.; Peugeot, C. Evaluating LSM-Based Water Budgets over a West African Basin Assisted with a River Routing Scheme. J. Hydrometeorol. 2014, 15, 2331–2346. [Google Scholar] [CrossRef]
- Nayak, P.C.; Sudheer, K.P.; Rangan, D.M.; Ramasastri, K.S. Short-term flood forecasting with a neurofuzzy model. Water Resour. Res. 2005, 41. [Google Scholar] [CrossRef]
- Ye, L.; Zhou, J.Z.; Zeng, X.F.; Guo, J.; Zhang, X.X. Multi-objective optimization for construction of prediction interval of hydrological models based on ensemble simulations. J. Hydrol. 2014, 519, 925–933. [Google Scholar] [CrossRef]
- Zhang, Y.; You, Q.; Chen, C.; Ge, J. Impacts of climate change on streamflows under RCP scenarios: A case study in Xin River Basin, China. Atmos. Res. 2016, 178–179, 521–534. [Google Scholar]
| Model | Catchment | Calibration | Validation | ||
|---|---|---|---|---|---|
| NSE | RE | NSE | RE | ||
| (%) | (%) | (%) | (%) | ||
| VIC Model | Subbasin 1 | 86.63 | 8.73 | 85.39 | 1.34 |
| Subbasin 2 | 78.46 | −18.61 | 78.23 | −20.3 | |
| Subbasin 3 | 78.82 | −16.07 | 77.44 | −16.57 | |
| Catchment | Calibration | Validation | ||
|---|---|---|---|---|
| NSE | RE | NSE | RE | |
| (%) | (%) | (%) | (%) | |
| Subbasin 1 | 99.76 (99.68–99.75) | 0.09 (−0.04–0.11) | 99.72 (99.65–99.73) | 0.47 (0.08–0.62) |
| Subbasin 2 | 97.92 (96.81–98.24) | 1.73 (1.35–2.23) | 97.63 (96.19–98.87) | 1.94 (1.25–3.12) |
| Subbasin 3 | 97.81 (96.29–98.23) | 1.85 (1.07–2.14) | 97.19 (95.82–96.64) | 2.13 (2.34–3.97) |
| Model | Calibration | Validation | ||
|---|---|---|---|---|
| NSE | RE | NSE | RE | |
| (%) | (%) | (%) | (%) | |
| VIC | 78.03 | −21.51 | 78.47 | −20.02 |
| VIC and MC | 95.77 | −1.53 | 95.34 | −0.85 |
| VIC and Regression | 95.62 | −1.74 | 95.11 | −1.2 |
| VIC and ANN | 98.89 (98.24–98.92) | 0.43 (0.24–0.46) | 97.76 (96.73–97.85) | −0.86 (−1.11–0.14) |
| Model Phase | Category | POC (%) | Prediction Band with Respect to Ensemble Mean (%) | No. of Patterns | % of Total Data |
|---|---|---|---|---|---|
| Calibration | Complete flow | 64.45 | 8.74 | 1826 | 100 |
| Low flow | 58.98 | 6.83 | 1213 | 66.40 | |
| Medium flow | 72.36 | 11.43 | 515 | 28.20 | |
| High flow | 90.63 | 12.03 | 98 | 5.39 | |
| Validation | Complete flow | 66.92 | 10.89 | 1096 | 100 |
| Low flow | 59.15 | 8.44 | 675 | 61.62 | |
| Medium flow | 76.95 | 12.08 | 338 | 30.86 | |
| High flow | 89.49 | 13.07 | 83 | 7.52 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, C.; Zhou, J.; Tayyab, M.; Zhu, S.; Zhang, H. Integrating Artificial Neural Networks into the VIC Model for Rainfall-Runoff Modeling. Water 2016, 8, 407. https://doi.org/10.3390/w8090407
Meng C, Zhou J, Tayyab M, Zhu S, Zhang H. Integrating Artificial Neural Networks into the VIC Model for Rainfall-Runoff Modeling. Water. 2016; 8(9):407. https://doi.org/10.3390/w8090407
Chicago/Turabian StyleMeng, Changqing, Jianzhong Zhou, Muhammad Tayyab, Shuang Zhu, and Hairong Zhang. 2016. "Integrating Artificial Neural Networks into the VIC Model for Rainfall-Runoff Modeling" Water 8, no. 9: 407. https://doi.org/10.3390/w8090407
APA StyleMeng, C., Zhou, J., Tayyab, M., Zhu, S., & Zhang, H. (2016). Integrating Artificial Neural Networks into the VIC Model for Rainfall-Runoff Modeling. Water, 8(9), 407. https://doi.org/10.3390/w8090407






