Drinking and Cleaning Water Use in a Dairy Cow Barn

1. Introduction

Water is used in dairy farming for producing feed crops, processing feed, watering the animals, cleaning and disinfecting the barn and equipment, and cooling the milk and the barn. Cultivation of feed crops accounts for the highest share of water use in dairy farming [1,2,3,4,5]. In rainfed farming, this water is provided by the natural water cycle. Access to precipitation is assured by the access to the land and does not lead to additional costs [6]. The water used in the barn is mainly provided by technical means and represents part of the technical water [6]. This technical water accounts for less than 5% of total water use in German dairy farming [2], but it is diverted from its natural cycle and so must be paid for. Hence particular attention is paid to the use of technical water. The amount of technical water used in barns depends on the equipment and management of the dairy farm.

Several studies have investigated water use for drinking, cleaning, and disinfection. The drinking water demand of lactating cows has been investigated by several authors, including Cardot et al. [7], Holter and Urban [8], Meyer et al. [9], and Murphy et al. [10]. All authors estimated the daily drinking water intake of cows depended on influencing factors such as the milk yield of the cows, live weight, dry matter content of the feed, dry matter intake, day of the year, rainfall, temperature, and sodium intake. Not all authors used the same variables to estimate drinking water intake. Some of the variables were dependent on each other; for example, the dry matter intake depended on the live weight of the animals, and the milk yield on the dry matter intake. Including the day of the year in the estimation [8] should indicate the temperature change during the year, while Meyer et al. [9] and Murphy et al. [10] included the mean or the minimum temperature. The investigations were conducted for cows in early to mid-lactation and covered a period of at most 16 weeks.

Scientific investigations of the cleaning water demand in the barn are scarce [11]. The cleaning water demand has mainly been investigated by public authorities and consulting agencies [12,13,14,15,16,17], and the available studies do not describe in detail how the cleaning water demand was measured and estimated. Water for cleaning in the dairy barn is used for different situations, including for the process of milking, which requires cleaning and disinfection of the milking equipment, the milking parlour, and the milk cooling tank. Cleaning the equipment and cooling tank is computer-controlled, so the water needs are constant within the same system. However, different systems are available, such as hot water cleaning and circulation cleaning. The cleaning water demand of the milking parlour depends on the area, the worker, the system, and the farm management. For example, a high-pressure cleaner needs less water than a hose. Sometimes less water could be used to achieve the same cleaning result, but workers are urged to use more water because the additional water is needed to keep slurry pumpable. Hence, without information on the methods used to measure and estimate the cleaning water demand, application to a specific barn remains uncertain.

The aim of this study was to investigate the technical water use in a dairy cow barn on a commercial dairy farm in North-East Germany by taking detailed measurements of the drinking and cleaning water demand over a period of two years. Regression functions of the drinking water demand over the whole lactation cycle were developed and compared with existing regression functions and methods to test the equations for their accuracy. Two milking systems were compared with respect to technical water demand per cow, kg milk, and milking. Daily and annual variations in the water demand are displayed for groups of cows with different milk yields. Understanding of how much cleaning water is used is improved. Detailed portioning of the cleaning water demand to the main contributors is outlined and recommendations to reduce the water use are given.

2. Materials and Methods

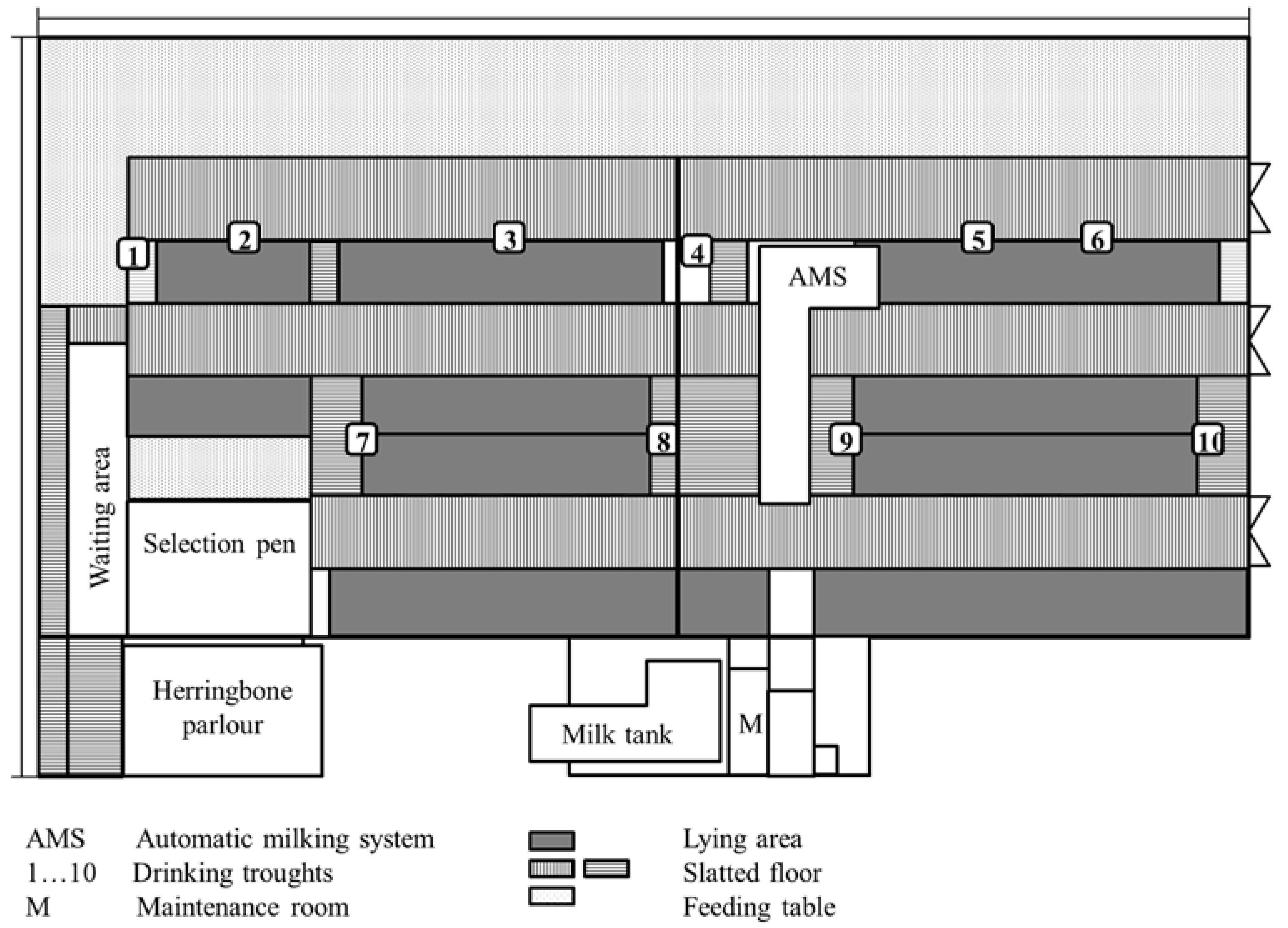
2.1. Milking Systems

The dairy farm investigated is located in North-East Germany and manages 675 ha arable land. The farm keeps on average 210 milking cows and 180 calves and heifers. The dairy cow barn is 70 m long and 30 m wide. Two milking systems are established on the farm—an automatic milking system (AMS) with two single boxes and a 2 × 7 herringbone milking parlour (HBP). A group of cows is associated with each milking system, but the cows are moved between the systems during lactation depending on their milk yield and the milking intensity: for the first two weeks after calving, the cows are milked in the HBP; between the 15th and 170th day in milk, they are milked in the AMS; and after the 170th day in milk until the end of lactation, they are milked in the HBP again. The milk yield is recorded at each milking for every cow in the AMS. The two single boxes of the AMS have an area of 35 m² and are cleaned with a hose. For the milk yield of the cows in the HBP, the data of the monthly milk performance testing was taken into account. The HBP has an area of 70 m² and is cleaned with a hose and a high-pressure cleaner. The milk is collected by a milk truck every two days. The milk tanks are cleaned automatically after emptying.

The cows in the AMS group were fed a total mixed ration of 5.3% alfalfa silage, 22.3% grass silage, 50.0% maize silage, 1.2% straw, 8.4% rape seed meal, 3.9% soy bean meal, 7.7% concentrate (DEUKA MK 204), and 1.2% minerals and vitamins, providing a dry matter intake of 23 kg per cow per day with a dry matter content of 39.8%. The cows in the HBP group were fed a total mixed ratio of 45.2% grass silage, 47.5% maize silage, 6.1% rape seed meal, and 1.2% minerals and vitamins, providing a dry matter intake of 17.4 kg per cow per day with a dry matter content of 35%. The composition, dry matter intake, and dry matter content of each diet was ruminant appropriate, being similar to those reported by Krauß et al. [2].

2.2. Water Metering

To investigate the technical water use of lactating cows in the barn of the commercial dairy farm, 38 water meters (Itron Inc.; Liberty Lake, Washington, WA, USA) were installed at various points of water withdrawal on 23 February 2012. The water withdrawal was measured in as much detail as the installation of the water pipes allowed over a period of more than two years, up to 08 May 2014. The water meters were chosen based on the expected flow rates and pipe diameters, to minimize any flow-rate-dependent measuring inaccuracies. This was important, as there were differences between the readings of the water meters in the pipe and the water meters at the points of withdrawal from the pipe—these differences may have resulted from measurement inaccuracies of the water meters or leakage from the pipe, but the latter was assumed here since it was not possible to distinguish between these effects. Complete datasets are available for 802 of the 806 days. Four datasets were excluded from the analyses because of missing values of the water meters.

A ground plan of the barn and the drinking troughs is shown in Figure 1. The cows in the AMS-group were in the right part of the barn and the cows in the HBP-group were in the left part of the barn. The water was supplied by a single bore and its quality was checked by the farm management; the drinking water was proven to be of a quality suitable for human consumption. The main pipe had a water meter and was split into six smaller pipes. Four of the pipes supplied the drinking troughs, one the AMS, and one the milk tank room. Each group of cows had access to five drinking troughs, and water meters were installed in front of the troughs. Troughs 1, 2, 3 and 4 were supplied by pipe 1. Troughs 5 and 6 were supplied by pipe 2. Troughs 7 and 8 were supplied by pipe 3. Troughs 9 and 10 were supplied by pipe 4. Every pipe had a water tap for drawing cleaning water as well as a water meter for calculating use of cleaning water and detecting leaks. The cleaning water demand of the milking system, the milk tank of the HBP, and the milk tank of the AMS was measured using three hot water meters and three cold water meters. The high pressure cleaner and the hose in the HBP each had a water meter to measure the water use for cleaning the surface of the HBP. The udder brush had a hot water meter and a cold water meter, and the disinfection of the milking units had its own water meter. A hot water meter and a cold water meter were installed in each AMS box. Pipe 5 supplied these four water meters and had its own water meter to detect leaks. In the milk tank room, four water meters were installed to measure the use of cleaning water for the floor of the milk tank room, the milk churn, the workers’ hands, and their workwear.

The water meters transmitted their count wirelessly to a collector every hour. The collector transmitted the counts daily to an access point and this transmitted the data to a file transfer protocol (FTP) server. The drinking water intake of the cows and the cleaning water demand of the milk tank, the milking system, and the surface of the milking parlour were measured separately for each group. There was also nonspecific withdrawal which cannot be allocated to one of the milking systems, such as water used for cleaning the floor of the milk tank room, the milk cans, and the workers’ clothes.

2.3. Technical Water

The term “technical water” is used in the calculation of water use indicators at farm scale [6]. Technical water W_tech (m³) means the water that is provided by technical means in contrast to water which reaches the farm via precipitation, surface, or subsurface flows. W_tech (m³) is subdivided at farm scale into irrigation water W_irri (m³) and tap water W_tap (m³) [6]. In this study the technical water use focuses on water use in the dairy barn W_tech-barn (m³). W_tech-barn (m³) can be split into the drinking water demand of the cows W_drink-cow (m³) and the cleaning water demand W_clean (m³) [3].

2.4. Regression Functions of the Drinking Water Demand

The measurements of drinking water intake on the commercial farm in North-East Germany were compared with the following regression functions from literature [7,8,9,10]:

$$W_{\text{drink}-\text{cow}\_\text{daily}}=-26.65+1.54\times \text{DMI}+1.33\times Y_{\text{milk}}+0.89\times \text{DMC}+0.58\times T_{\text{min}}-0.30\times \text{RF }\left(R^2=0.45\right)$$

(1)

$$W_{\text{drink}-\text{cow}\_\text{daily}}=-32.39+2.47\times \text{DMI}+0.6007\times Y_{\text{milk}}+0.6205\times \text{DMC}+0.0911\times \text{DOY}-0.000257\times {\text{DOY}}^2\left(R^2=0.69\right)$$

(2)

$$W_{\text{drink}-\text{cow}\_\text{daily}}=-26.12+1.516\times T_{\text{mean}}+1.299\times Y_{\text{milk}}+0.0058\times {\text{m}}_{\text{b}}+0.406\times {\text{In}}_{\text{Na}}\left(R^2=0.60\right)$$

(3)

$$W_{\text{drink}-\text{cow}\_\text{daily}}=15.99+1.58\times \text{DMI}+0.90\times Y_{\text{milk}}+0.05\times {\text{In}}_{\text{Na}}+1.20\times T_{\text{min}}\left(R^2=0.59\right)$$

(4)

where the daily drinking water intake of cows is W_{drink-cow_daily} (L·day⁻¹), the milk yield of the cows Y_milk (kg·day⁻¹), the live weight of the animals m_b (kg), the dry matter content of the feed DMC (%), the dry matter intake DMI (kg), day of the year DOY (−), rainfall RF (mm·day⁻¹), mean ambient temperature T_mean (°C), minimum ambient temperature T_min (°C), and sodium intake In_Na (g·day⁻¹).

The mean, minimum and maximum temperature and the rainfall were measured by the nearest station (19 km) of the German Meteorological Service and provided by the ATB-Modeling Database [18].

2.5. Statistical Analyses

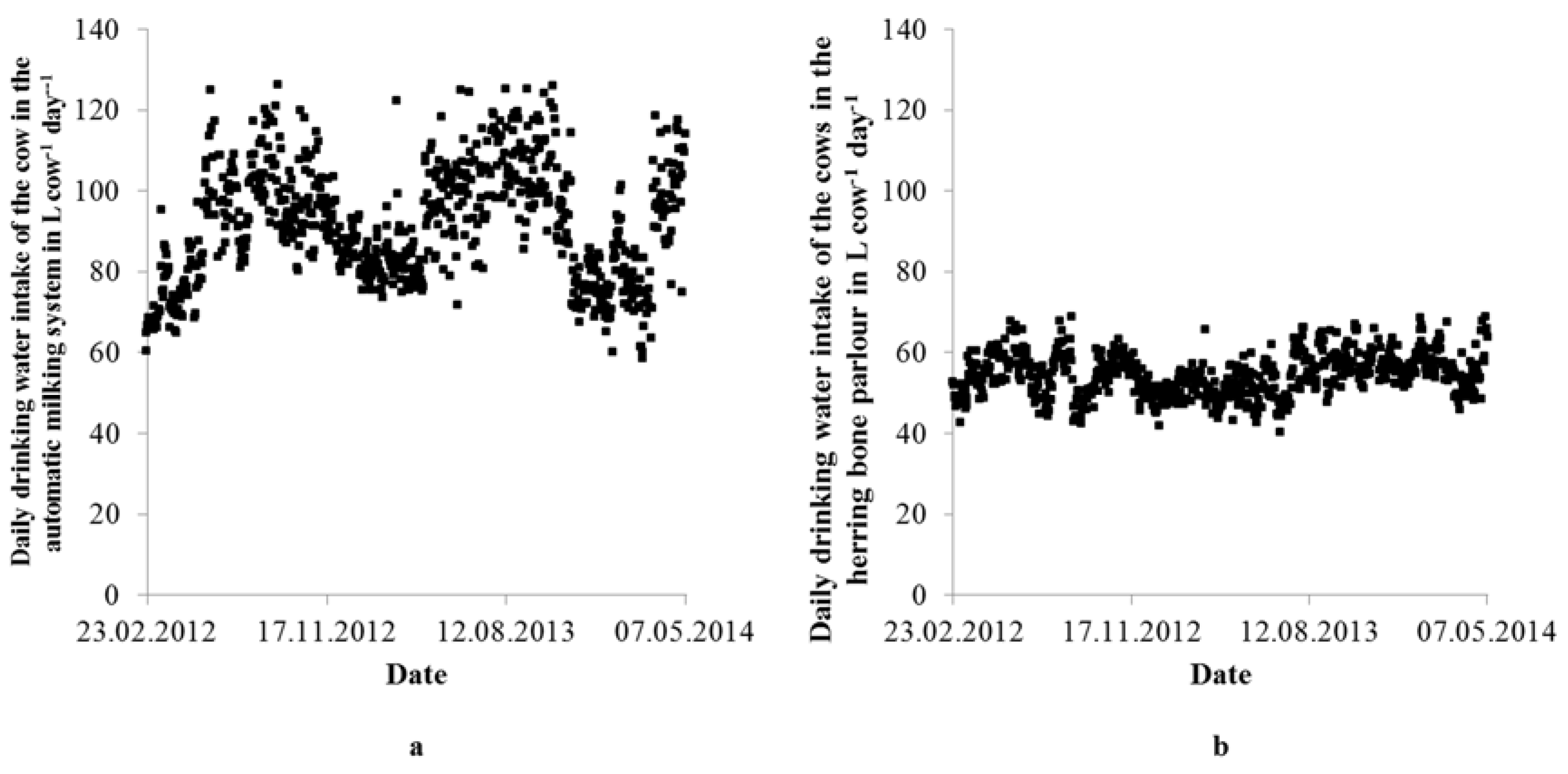
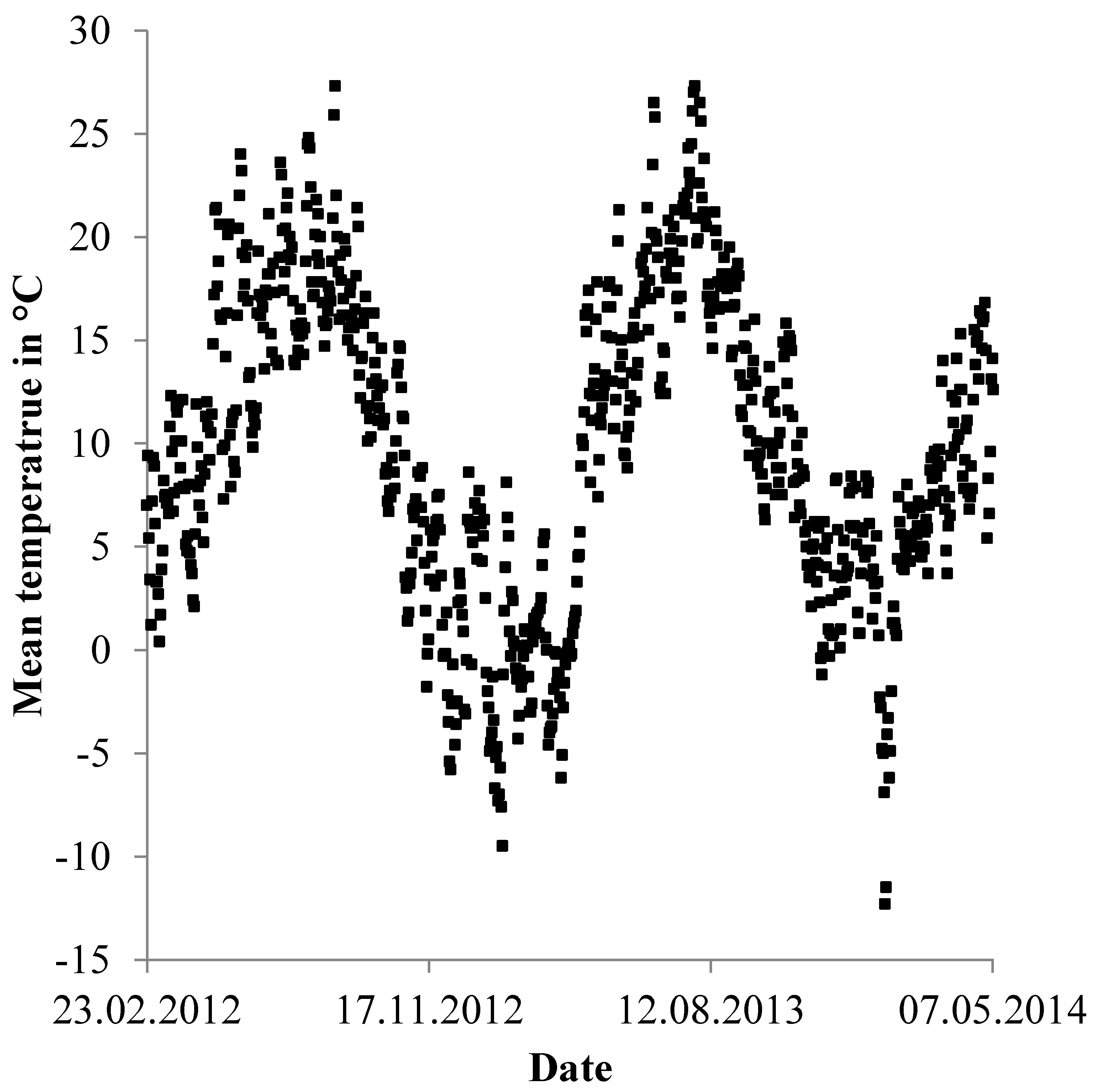
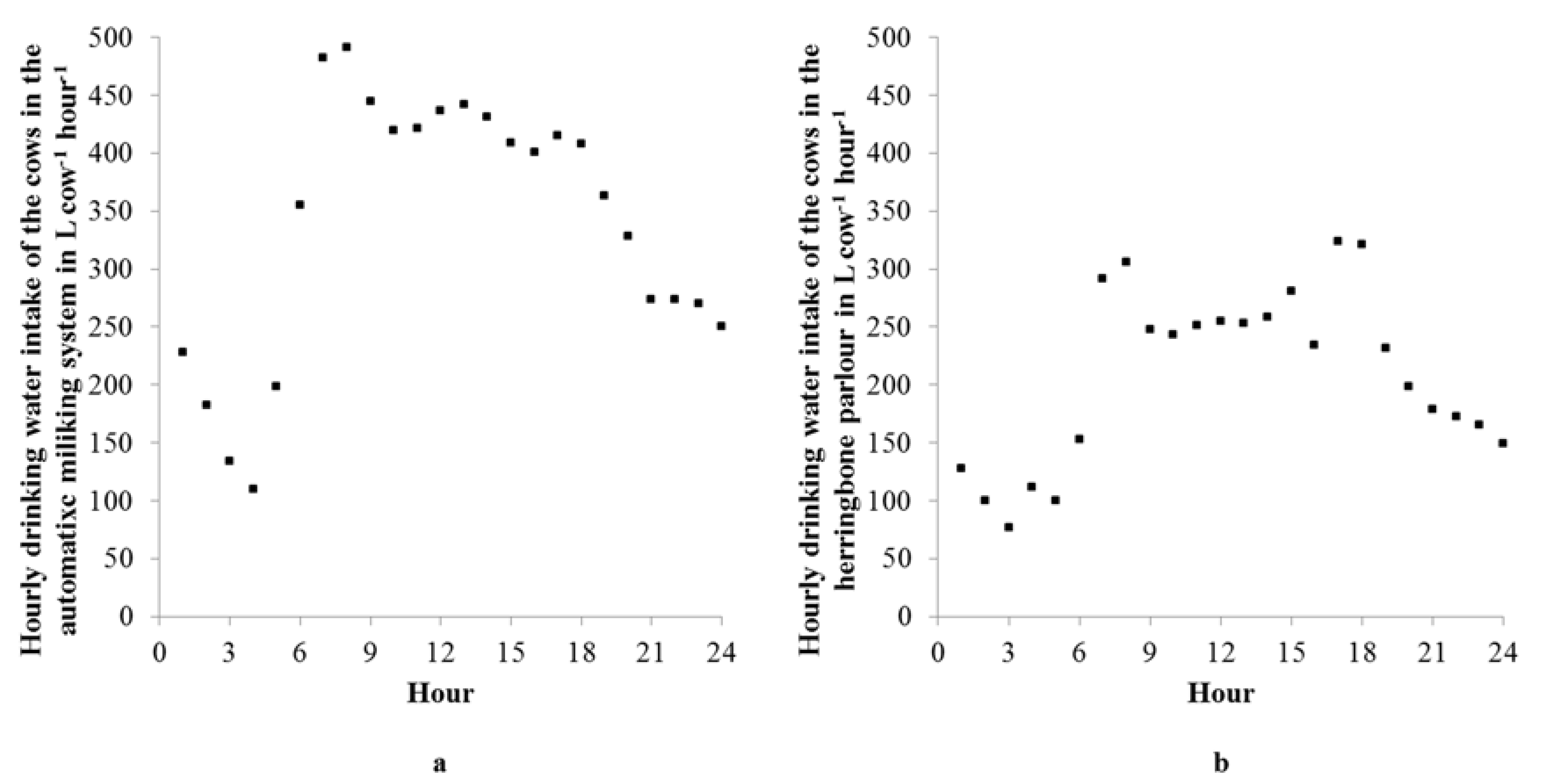
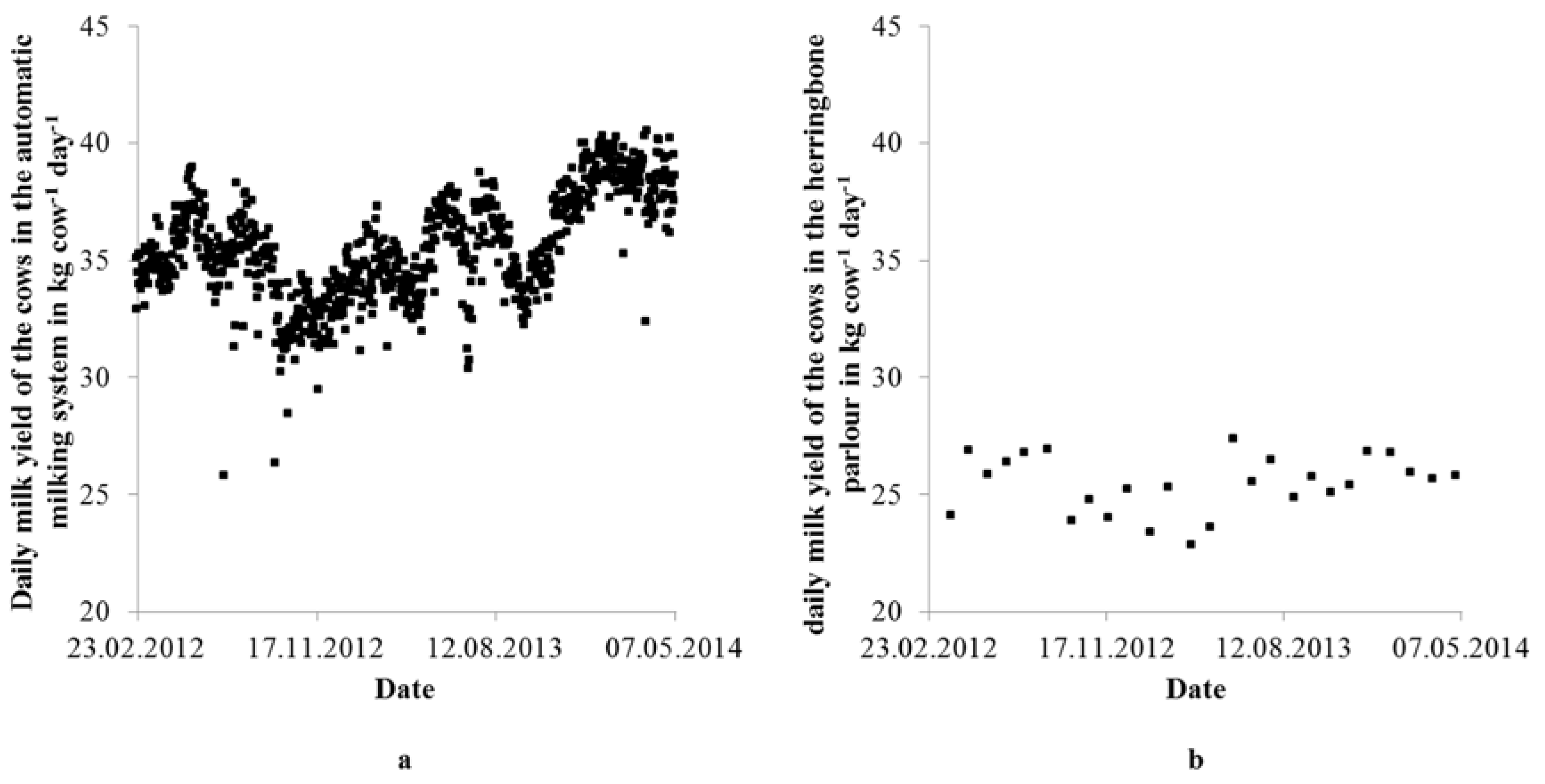
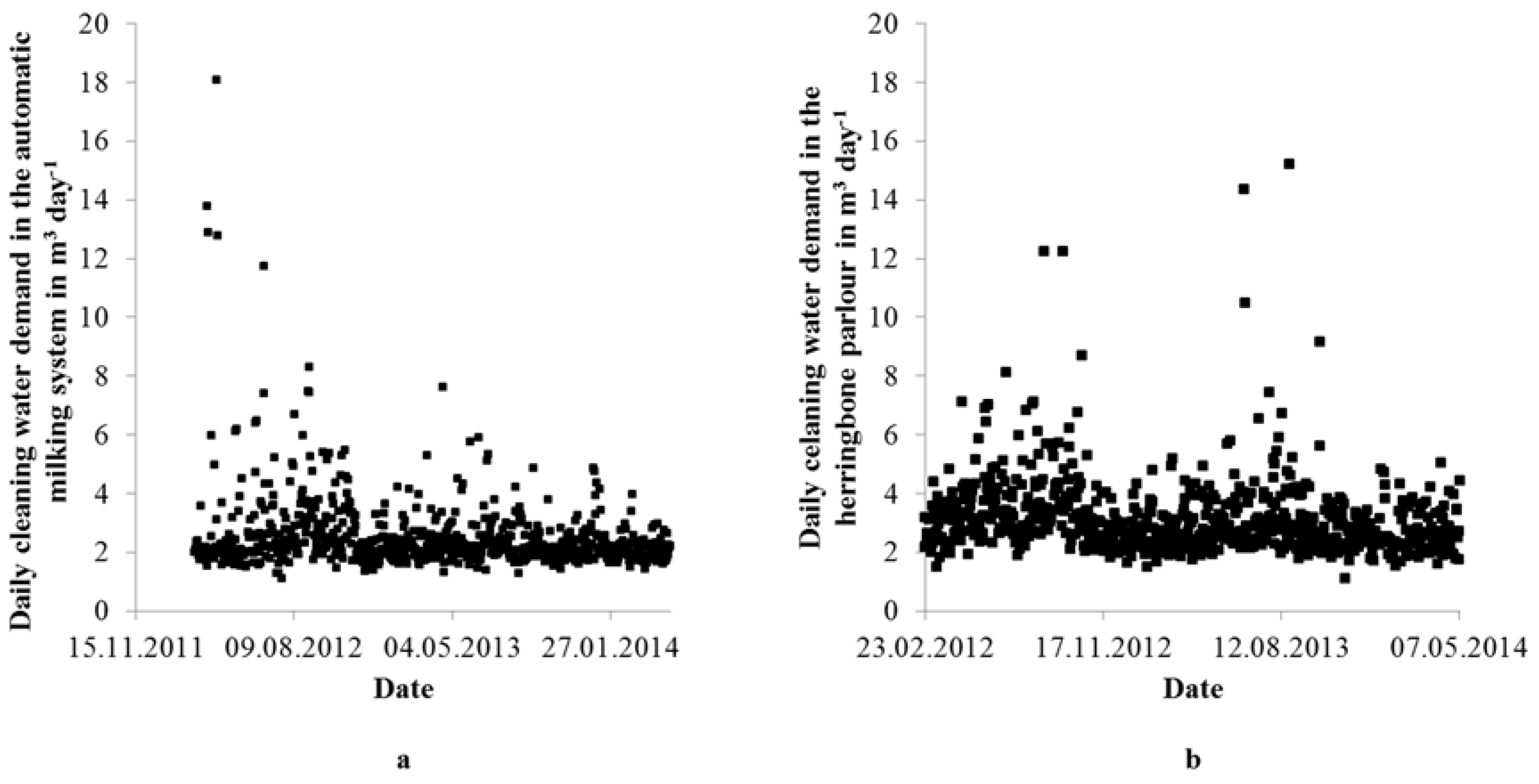
The hourly data of the water meters and the milk yield data of the cows were checked for completeness. Outliers in the drinking water dataset were eliminated if the values were higher than the threshold of 1.96 × SD [19]. By contrast, outliers in the cleaning water dataset were not eliminated because various factors within a farmstead could legitimately result in these higher values.

The data were analyzed with the software SAS 9.4 (SAS Institute Inc., Cary, NC, USA) and the procedure Proc MEANS to obtain the mean values and standard deviations (SDs). The regression function of the daily drinking water intake was estimated using Proc REG, with the average daily mean temperature and the daily milk yield included as independent variables. The means of the regression functions obtained by Cardot et al. [7], Holter and Urban [8], Meyer et al. [9] and Murphy et al. [10] were compared with the measured values from this study using Proc TTEST.

The performances of the previously published regression functions and the function developed in this study were evaluated by comparing the measured and modeled daily drinking water demands. An ordinary parametric least squares linear regression test with the coefficient of determination (R²) was used to assess the goodness of fit [19]. In addition, the Nash-Sutcliffe efficiency (NSE), logarithmic Nash-Sutcliffe efficiency (NSElog), Root mean square error (RMSE), ratio of the root mean square error to the standard deviation of measured data (RSR) and percent BIAS (PBIAS), were used for model evaluation following Moriasi [20], Ellis et al. [21], and Tedeschi [22].

3. Results and Discussion

3.1. Drinking Water Demand

The daily drinking water intake per cow throughout the observation period is shown in Figure 2. The drinking water demand of the cows in the AMS showed a seasonal response, being highest in the summer and lowest in the winter. This corresponds with the changes of the daily mean air temperature during the year (Figure 3). Cardot et al. [7], Holter and Urban [8], Meyer et al. [9] and Murphy et al. [10] also identified the drinking water intake as dependent on the temperature or season. The drinking water intake of the cows in the HBP did not show such a seasonal response. Since the group of cows in the HBP was more heterogeneous than in the AMS, the effects of temperature on drinking water intake may have been leveled out.

The drinking water intake changed not only over the year, but also during the day (Figure 4). Between 05:00 and 21:00 h the cows drink 80% of their daily water intake. During this time the workers were in the barn and it was lit. The peak of drinking water intake was observed between 07:00 and 08:00 h for the cows in the AMS, and between 07:00 and 08:00 h and between 17:00 and 18:00 h for the cows in the HBP. This was expected, since the cows in the HBP were milked at these times, and cows drink large amounts of water after milking [7].

The milk yields were needed to calculate the drinking water demand per kg milk and to assess the accuracy of the available regression functions for estimating the drinking water demand of dairy cows. Milk yields are shown in Figure 5 and

Table 1. Milk yield, measured and estimated drinking water intake of the cows.

Measured or Estimated Value	Mean	SD 1	Min 2	Max 3
Automatic milking system
Number of cows	87.9	4.0	78.0	101.0
Milk yield (kg·cow−1·day−1)	35.5	9.6	0.0	83.9
Daily drinking water intake (L·cow−1·day−1)
own measurements	91.1	14.3	58.5	126.2
calculated according to Cardot et al. [7]	95.7 4	4.9	82.2	108.4
calculated according to Holter and Urban [8]	76.3 4	2.8	68.5	81.1
calculated according to Meyer et al. [9]	84.2 4	12.9	51.9	114.2
calculated according to Murphy et al. [10]	92.8	8.1	69.2	113.2
Herringbone milking parlour (HBP)
Number of cows	91.8	6.2	73.0	101.0
Milk yield (kg·cow−1·day−1)	25.4	7.5	2.9	65.3
Daily drinking water intake (L·cow−1·day−1)
own measurements	54.4	5.3	40.2	121.7
calculated according to Cardot et al. [7]	69.2 4	4.6	55.6	81.0
calculated according to Holter and Urban [8]	53.0 4	2.7	46.5	56.9
calculated according to Meyer et al. [9]	68.9 4	12.1	36.7	97.9
calculated according to Murphy et al. [10]	74.4 4	8.4	49.2	95.2

Notes: ¹ standard deviation; ² minimum; ³ maximum; ⁴ significant difference to own measurements (p ≤ 0.001).

. The average milk yield of the 88 cows milked in the AMS was 35.5 kg milk per cow per day, with an average of 2.8 milkings per day and 12.7 kg milk per milking. On average, 92 cows were milked twice per day in the HBP, with an average milk yield of 25.4 kg milk per cow per day or 12.7 kg per milking. Figure 5 is more detailed for the AMS, as milk yield data was available for each milking in contrast to the data for milk yield in the HBP.

The 88 cows in the AMS group drink on average 8.0 m³ of water per day. This is equivalent to 91.1 L water per cow per day, or 2.6 L per kg milk. Holter and Urban [8] suggested a rule of thumb of 2 L drinking water per kg milk, which is 77% lower than the measured value. The diet provided 34.8 L water, which represented 27% of the total water intake. The calculation of the drinking water demand according to Meyer et al. [9] leads to an underestimation of the drinking water demand by 6.9 L per day, and according to Holter and Urban [8] to an underestimation by 14.8 L per day, while using the regression function of Cardot et al. [7] the drinking water demand was overestimated by 4.6 L per day. The difference between the measured minimum and maximum water intake is 67.7 L per day, while the range of estimated values includes 26 L [7], 13 L [8], 62 L [9] and 44 L [10].

The 92 cows in the HBP group drank on average 5.0 m³ of water per day, representing a mean drinking water demand of 54.4 L water per cow per day or 2.1 L per kg milk. This was 10% more than Holter and Urban’s [8] rule of thumb. The diet provided 32 L water, which was 36% of the total water intake.

The measured drinking water demand of the cows in the AMS and the HBP, the milk yield of the cows (kg·cow⁻¹·day⁻¹) and the mean temperature (°C) were used to develop a new regression function for the modeling of the daily drinking water demand of cows in the barn (W_{drink-cow_daily}):

$$W_{drink-cow\_daily}= -27.93 + 0.49 \times mean temperature + 3.15 \times milk yield \left(R^2=0.67\right)$$

(5)

A comparison of the measured and modeled daily drinking water demand is provided in

Table 2. Summary statistics for previously published regression functions and the function developed in this study for the two milking systems.

Model Evaluation Statistics	Estimated Value	Cardot et al. [7]	Holter and Urban [8]	Meyer et al. [9]	Murphy et al. [10]	This Study
Standard regression	Slope	1.30	1.54	0.94	1.33	0.97
	y-intercept	−34.36	−26.66	0.96	−38.10	1.09
	Pearson’s correlation coefficient (R)	0.86	0.87	0.63	0.77	0.82
	Coefficient of determination (R2)	0.74	0.75	0.39	0.59	0.67
Dimensionless	Nash-Sutcliffe efficiency (NSE)	−0.15	−0.53	−0.44	−1.11	0.51
	Logarithmic transformed NSE (NSElog)	−0.60	0.12	−0.56	−1.98	0.59
Error index	Root mean square error (RMSE)	15.12	14.79	17.06	17.89	12.18
	RMSE-observations standard deviation ratio (RSR)	0.80	0.70	0.84	0.71	0.57
	BIAS	9.74	−8.05	3.89	10.92	−0.01
	Percent bias (PBIAS)	13.4	−11.1	5.4	15	−0.01

. It was found that the function developed in this study was closest to the perfect slope of 1, while the function of Meyer et al. [9] had the smallest y-intercept. A slope of 1 and a y-intercept of 0, using standard regression, indicate that the model perfectly fits the measured data [23]. The coefficient of determination (R²) shows the proportion of the variance in the measured data that is explained by the model, with values closer to 1 indicating less error variance. The regression functions had R² values ranging from 0.45 [7] to 0.69 [8], indicating that the regression functions did not include all of the parameters that affect the water intake of the cows. However, since values >0.5 are generally considered acceptable [24,25], all of these models were more or less acceptable. All of the previously published regression functions were based on investigations that were conducted from early to mid-lactation [7,8,9,10], and so did not cover the period of lactation when the milk yield—and hence the drinking water demand—is lower. By contrast, in the present study, the cows milked in the HBP were at the end of lactation. Therefore, this may explain why the calculated drinking water demand from all regression functions, except that of Holter and Urban [8], was significantly higher than our measured values from the HBP.

Only the function developed in this study showed acceptable NSE and NSElog values of >0.5, although the function of Holter and Urban [8] also resulted in an acceptable value of >0 for NESlog; the peaks resulting from a larger drinking water demand affected this model’s performance. In general, model simulation with dimensionless model evaluation statistics can be considered satisfactory if NSE > 0.50 and RSR < 0.70, and if PBIAS < 25% for streamflow [20]. By contrast, an NSE value < 0.0 shows that the mean observed value is a better predictor than the simulated value, indicating unacceptable performance. The logarithmic transformed NSE (NSElog) lowers the tendency of the NSE to overvalue large peaks.

The function developed in this study also showed the lowest RMSE, RSR, and BIAS error indices. RSR values of 0 indicate a perfect fit using the absolute error index statistic, and so the RSR values for the other functions (>0.70) must be considered unsatisfactory. Residual variance is the difference between the measured and simulated values, and is often estimated by the residual mean square or root mean square error (RMSE). The lower the RSR, the lower the RMSE, which indicates a better model simulation performance. The BIAS was larger for the previously published functions, which measures the average tendency of the simulated constituent values to be larger or smaller than the measured data.

In the literature studies of Cardot et al. [7], Holter and Urban [8], Meyer et al. [9], and Murphy et al. [10], more parameters influencing water intake were investigated than were finally included in the new regression function. It cannot be ruled out that these parameters could have a greater influence on the water intake of the cows in this study. Using the regression function of the earliest study predicted the water intake best, although the genetics, physiology, and milk yield of the cows has changed over the years. Further reasons for the difference between estimated and measured drinking water intake may be factors that were not investigated, such as rank fights, sexual cycle, and disturbance caused by external factors.

Our regression function includes only two parameters, since others such as live weight, dry matter intake, or sodium intake were not measured in this commercial dairy herd. The coefficients of the parameters in this function are not comparable with other studies, since every study includes its own parameters in the regression functions. The coefficient and hence the influence of the milk yield on drinking water intake in this study is comparable to the other regression functions. This can be explained by the interdependence of the different parameters, for example a higher dry matter intake will lead to a higher milk yield. If the dry matter intake is not included in the regression function, a part of its influence will be compensated by the milk yield parameter [26]. The R² of our regression function is 0.67, which lies between the R² of Cardot et al. [7] at 0.74 and that of Murphy [10] at 0.59.

3.2. Cleaning Water Demand

The daily cleaning water demand of the HBP and the AMS is shown in Figure 6. Neither milking system showed a seasonal pattern for cleaning water demand. The cleaning water demand was higher in the HBP than in the AMS. The daily cleaning water demand ranged from 1.1 m³ to 18.1 m³ in the AMS and from 1.1 m³ to 15.2 m³ in the HBP.

For cleaning the AMS, on average 2.5 m³ water was used per day (

Table 3. Comparison of the water demand of the milking systems.

Water Demand	Unit	Mean	Standard Deviation	Min	Max
Automatic milking system (AMS)
Cleaning water demand
per day	m3·day−1	2.5	1.3	1.1	18.1
per cow and day	L·cow−1·day−1	28.6	14.8	11.8	207.9
per kg milk	L·kg·milk−1	0.8	0.4	0.4	6.1
Herringbone milking parlour (HBP)
Cleaning water demand
Total	m3·day−1	3.1	1.3	1.1	15.2
of the milk tank	m3·day−1	0.1	0.1	0	0.5
of the milking equipment	m3·day−1	0.7	0.3	0.3	6.9
for udder cleaning	m3·day−1	0.3	0.1	0.1	2.2
for surface cleaning	m3·day−1	2.0	1.1	0.9	9.3
per cow and day	L·cow−1·day−1	33.8	14.1	12.5	170.8
per kg milk	L·kg·milk−1	1.3	0.5	0.5	6.5

). Per cow per day, 28.6 L water was needed. Related to the milk yield of the cows, 0.8 L water was used per kg milk to clean the AMS. The cleaning of the milk tank required 0.2 m³ water per day or 7% of the total water use in the AMS.

For cleaning the HBP, 3.1 m³ water was used per day (Figure 6, Table 3). Per cow per day 33.8 L water was used, which is 5.2 L per day or 18% more than in the AMS. For cleaning the surface of the milking parlour 2.0 m³ water was used. Fourteen litres of cleaning water per square metre was used in the HBP. Cleaning of the milking system required 0.7 m³ water per day and cleaning of the udder prior to milking 0.3 m³ per day. 0.1 m³ water per day was used for cleaning the milk tank, which is 4% of the total technical water use. Related to the milk yield, 1.3 L per kg milk was used for cleaning.

Leaks amount to 1% of the measured technical water use in the barn and were mainly caused by disrupted hoses. Hose disruption seldom occurred (5 times during the observation period), but can result in high water loss if this happens at night and is only detected hours later in the morning when the first workers enter the barn.

The high cleaning water use in the HBP was caused by the cleaning system and the fact that there was no incentive to save water. The cleaning was performed with a high-pressure cleaner and a hose with a large diameter. The water was supplied via the farm’s own bore, so that no costs were incurred for the water, only energy costs for pumping. Furthermore, the water was deliberately added to the slurry to keep it pumpable. This leads to high water demand for cleaning the surface of the parlour.

In the studies by Jensen [12] and Rasmussen and Pedersen [14], the cleaning water use was 0.2–0.4 L water per kg milk, which is less than half of what we measured. In their studies the AMS were optimized for low water use and were operated with the maximum number of cows. The higher water demand by the commercial farm in our study was also explained by withdrawal of water which was not directly used to clean the AMS, but to clean the barn of the cows in the AMS. Chapagain and Hoekstra [27] estimated the cleaning water demand in their calculation of the virtual water at 22 L per cow per day, which is 6.6 L less than measured in the AMS and 11.8 L less than in the HBP. A cleaning water demand of 0.3 L water per kg milk was estimated in a life cycle assessment study by Eide [28] for Norwegian conditions, which is 60% less than in this study. KTBL [13] estimated 2 L per square meter for cleaning an HBP, which is one seventh of what we measured.

In the AMS the share of drinking water demand was 76% and the share of cleaning water 24% of the total technical water demand. This is comparable with the results of Drastig et al. [1]. In the HBP, 62% of the water was needed for drinking and 38% for cleaning. The difference is explained by the higher cleaning water demand per cow and the lower drinking water demand per cow in the HBP. It is difficult to make general statements about reductions of the water demand in a dairy barn, since regression functions of the water demand only cover up to two thirds of the influencing parameters. The variation in cleaning water demand between the milking systems was less than the water demand for cleaning the surface of the parlours. Cleaning of the milking system was computer-controlled, while the surface of the parlour was cleaned by hand. The soiling depends on the cows. The water demand can be reduced by educating the workers to reduce water use, by using high-pressure cleaners or mechanical cleaning methods such as a brush. The cleaning water demand per liter of milk could be reduced with more milk milked per cleaning cycle, if the total cleaning water demand cannot be reduced. This could be achieved with more cows, if the barn allows, or higher milk yields of the cows. The findings of this study with respect to the cleaning water demand are only applicable to this particular barn with its milking and cleaning systems. Therefore, further detailed measurements in other barns are required to make general statements about methods for reducing the cleaning water demand.

3.3. Relation of Technical Water Demand to Total Water Demand for Milk Production

The relation of the technical water demand to the total water demand for milk production is shown in

Table 4. Relation of technical water demand obtained in this study to total water demand for milk production from various references.

Reference	Approach	Fractions of Water Use	Total Water Demand in L·kg−1·milk	Share of Drinking Water	Share of Cleaning Water	Share of Technical Water
of Total Water Demand in %
de Boer et al. [30]	Life cycle assessment	evaporation of transport of feed or electricity production, evapotranspiration of feed cultivation, unused irrigation water, water embodied in crop or animal products, tap water for industrial or agricultural processes	66	-	-	8.0
Sultana et al. [31]	Consumptive water use	water consumption from feed and other inputs, e.g., drinking, servicing, manufacturing inputs and capital goods	1833	1.0	4.0	5.5
Chapagain and Hoestra [27]	Water footprint	evapotranspiration for plant growth, ground/surface water consumed, drinking and service water	735	0.6	0.2	0.8
Mekonnen and Hoekstra [32]	Water footprint	evapotranspiration for plant growth, ground/surface water consumed, drinking and service water, freshwater required to dilute the load of pollutants to ambient water quality standards	1020	1.1	0.8	2.0
Zonderland- Thomassen and Ledgard [33]	Water footprint	evapotranspiration for plant growth, ground/surface water consumed, freshwater required to dilute the load of pollutants to ambient water quality standards	1015	1.0	1.0	2.0
Peden et al. [4]	Livestock water productivity	transpiration, evaporation, downstream discharge, degradation and contamination of water	1269	<2.0	-	-
Singh and Kishore [34]	Water productivity	irrigation water use for crop production, drinking water	2040	1.2	-	-
Brown et al. [35]	Virtual water	rain water, irrigation water, the water requirements of feed, drinking and service water for animals, water required for processing	-	0.4	0.006	-
Atzori et al. [36]	Net water footprint index	evapotranspiration including rain water, soil water, and irrigation water, drinking water, service water	26–408	-	-	2–40

. The technical water demand in the HBP was 89 L per cow per day and in the AMS 121 L per cow per day. Given a water demand between 600 and 700 L per kg milk for the production of feed, according to the farm water productivity approach [2] the measured water demand for drinking was 0.4% of total water demand. The relation of cleaning water to total water demand was 0.1% for the AMS and 0.2% for the HBP. The share of the technical water demand was about 10 times higher than the share of the indirect water demand for farm buildings in total water demand of 0.05% [29]. If the water demand for feed production is estimated with a life cycle approach [30] the relation of drinking and cleaning water demand is 8.0%. Calculating the water demand for feed production according to the water footprint concept, the drinking water demand would be between 0.6% [27] and 1.1% [29] and the cleaning water demand between 0.2% [27] and 0.8% [29]. The technical water demand per cow was in the range estimated in the studies mentioned, while its percentage of the total water demand was lower due to the high milk yield of the cows. Hence the technical water demand per kg milk is low.

4. Conclusions

The technical water demand of the commercial dairy farm investigated is influenced by the milking system, the management, environmental factors, and the milk yield. The drinking water intake corresponds with the ambient temperature and the milk yield. The cleaning water demand in the automatic milking system is lower per cow per day than in the herringbone parlour. The technical water demand in the barn could be lowered by reducing the cleaning water demand. The total technical water use in the barn makes a minor contribution to water use in dairy farming compared with the water use for feed production.