Estimating Loess Plateau Average Annual Precipitation with Multiple Linear Regression Kriging and Geographically Weighted Regression Kriging
Abstract
:1. Introduction
2. Study Area and Data
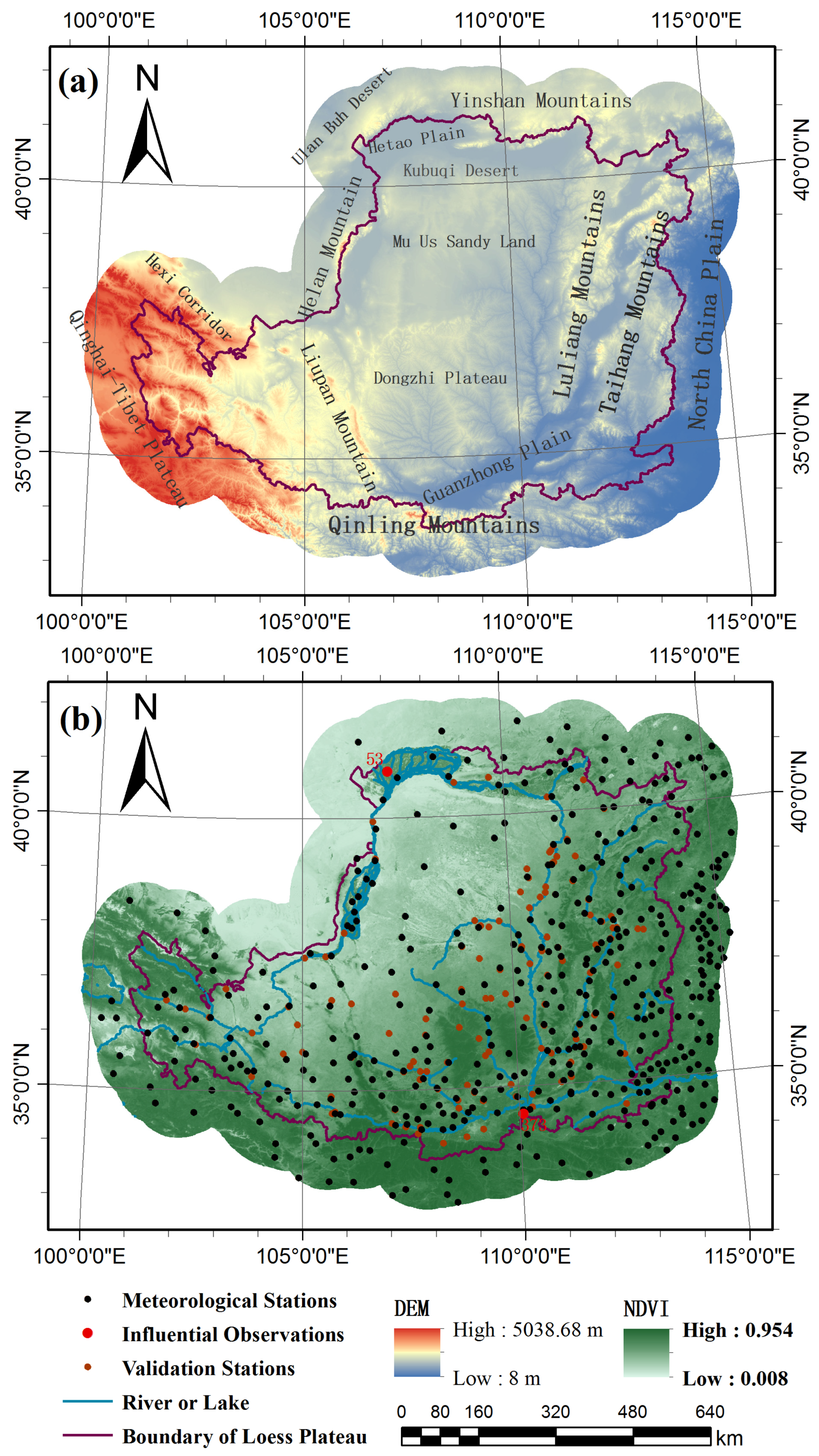
2.1. Study Area
2.2. Data Sets and Data Processing
3. Methods
3.1. Logit Transformation and Exploratory Data Analysis Methods
3.2. Interpolation Techniques: Multiple Linear Regression Kriging (MLRK) and Geographically Weighted Regression Kriging (GWRK)
3.2.1. Regression Kriging
3.2.2. Multiple Linear Regression Kriging
3.2.3. Geographically Weighted Regression Kriging
3.3. Validation Techniques
4. Results
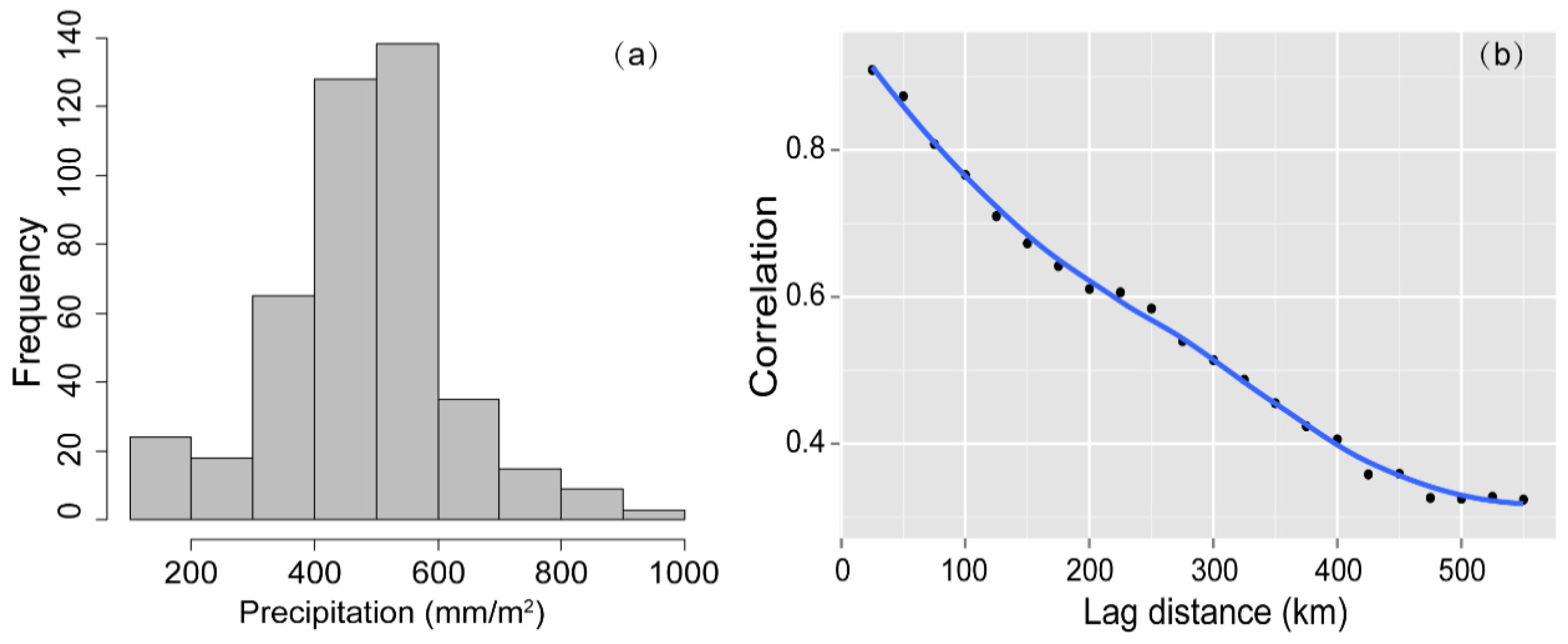
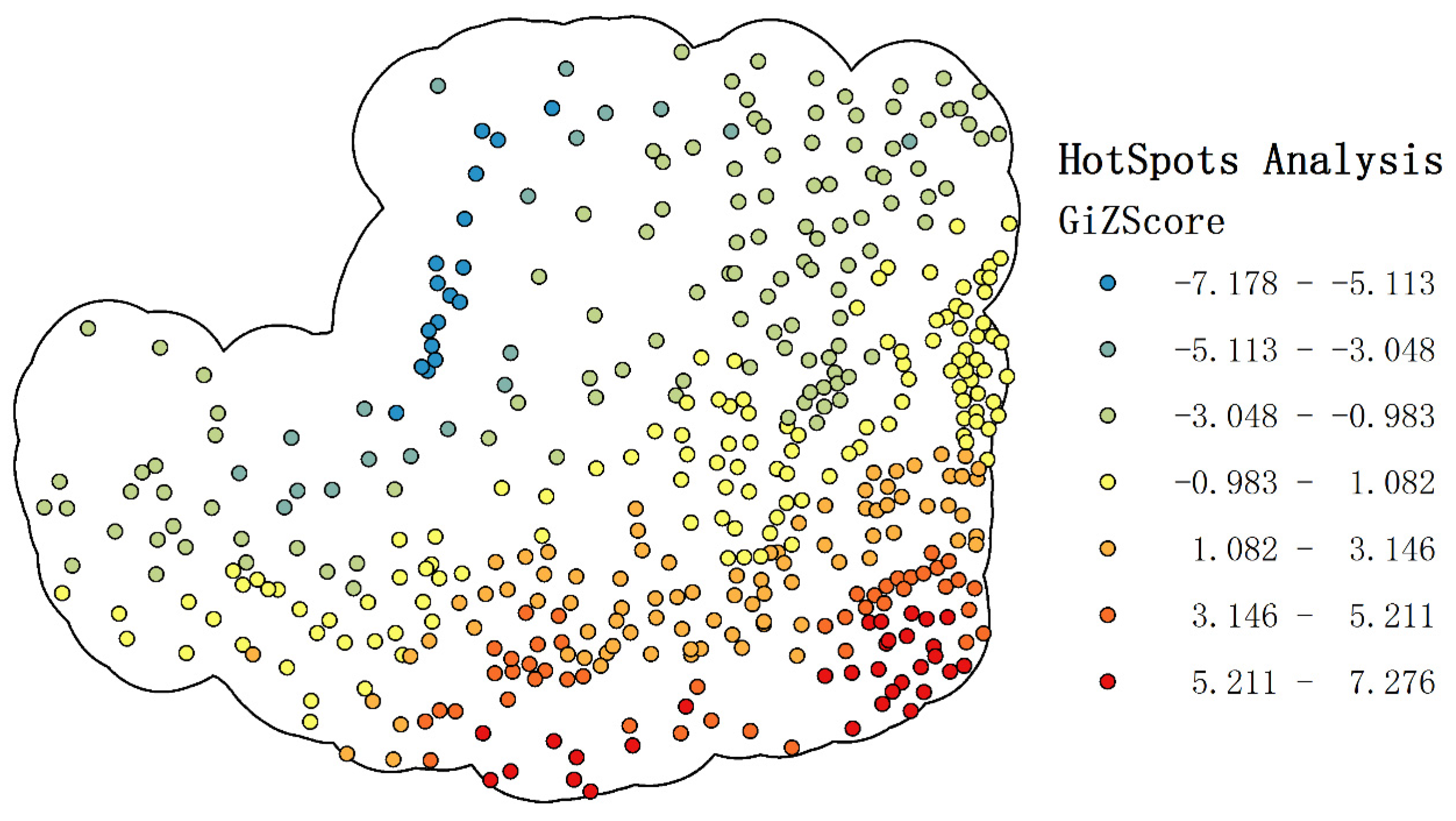
4.1. Spatial Autocorrelation
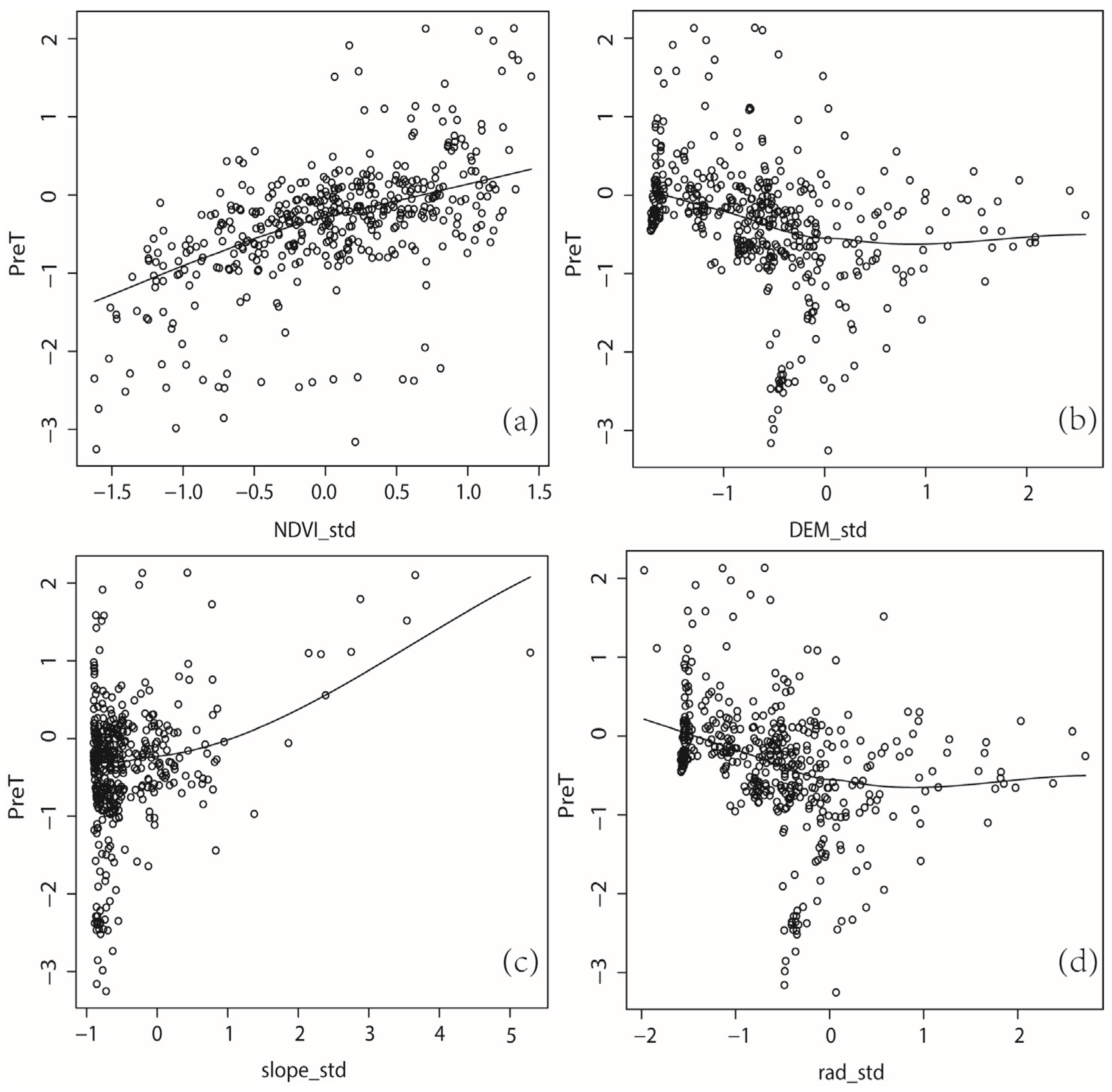
4.2. Exploratory Data Analysis
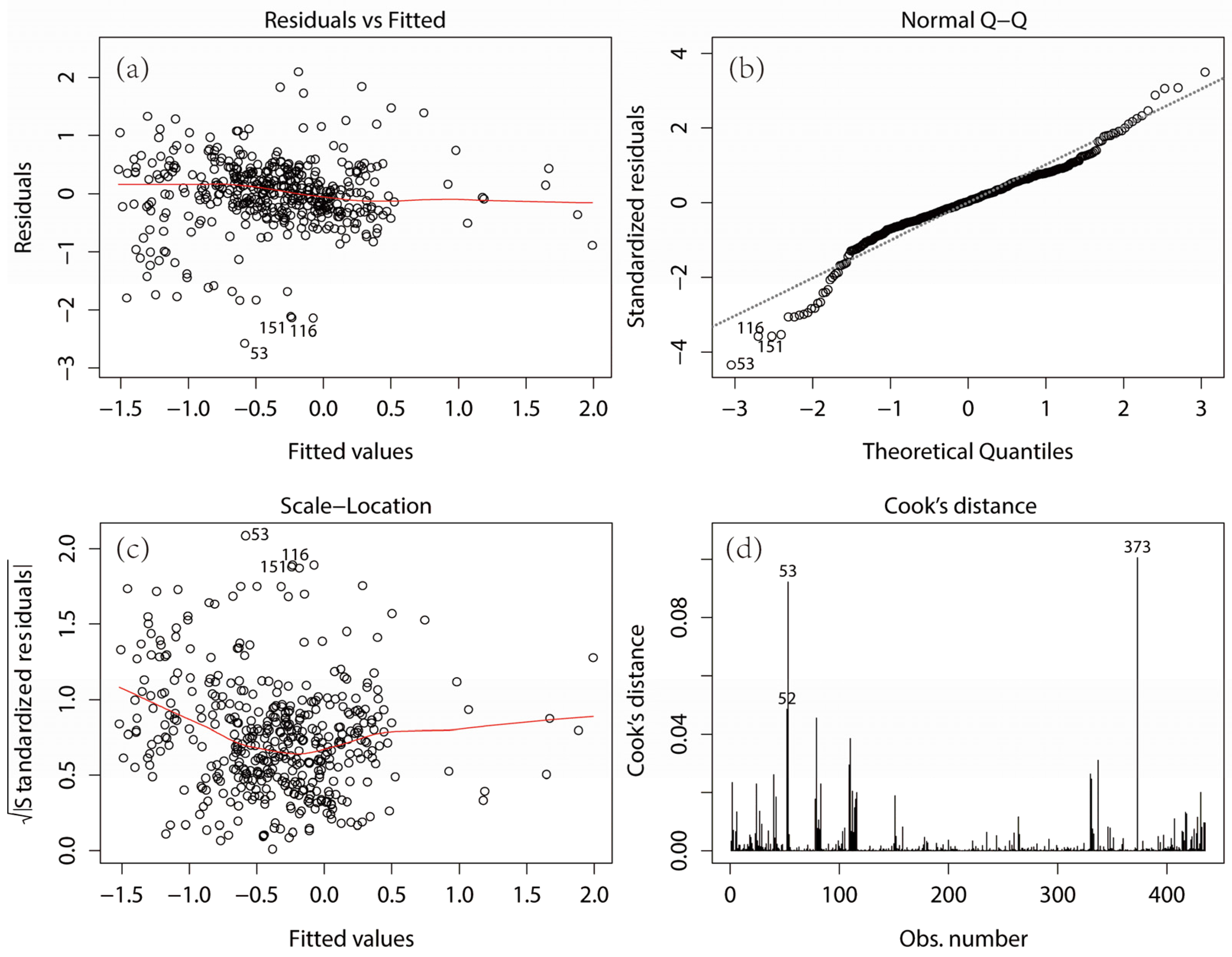
4.3. Diagnosis and Evaluation of Regression
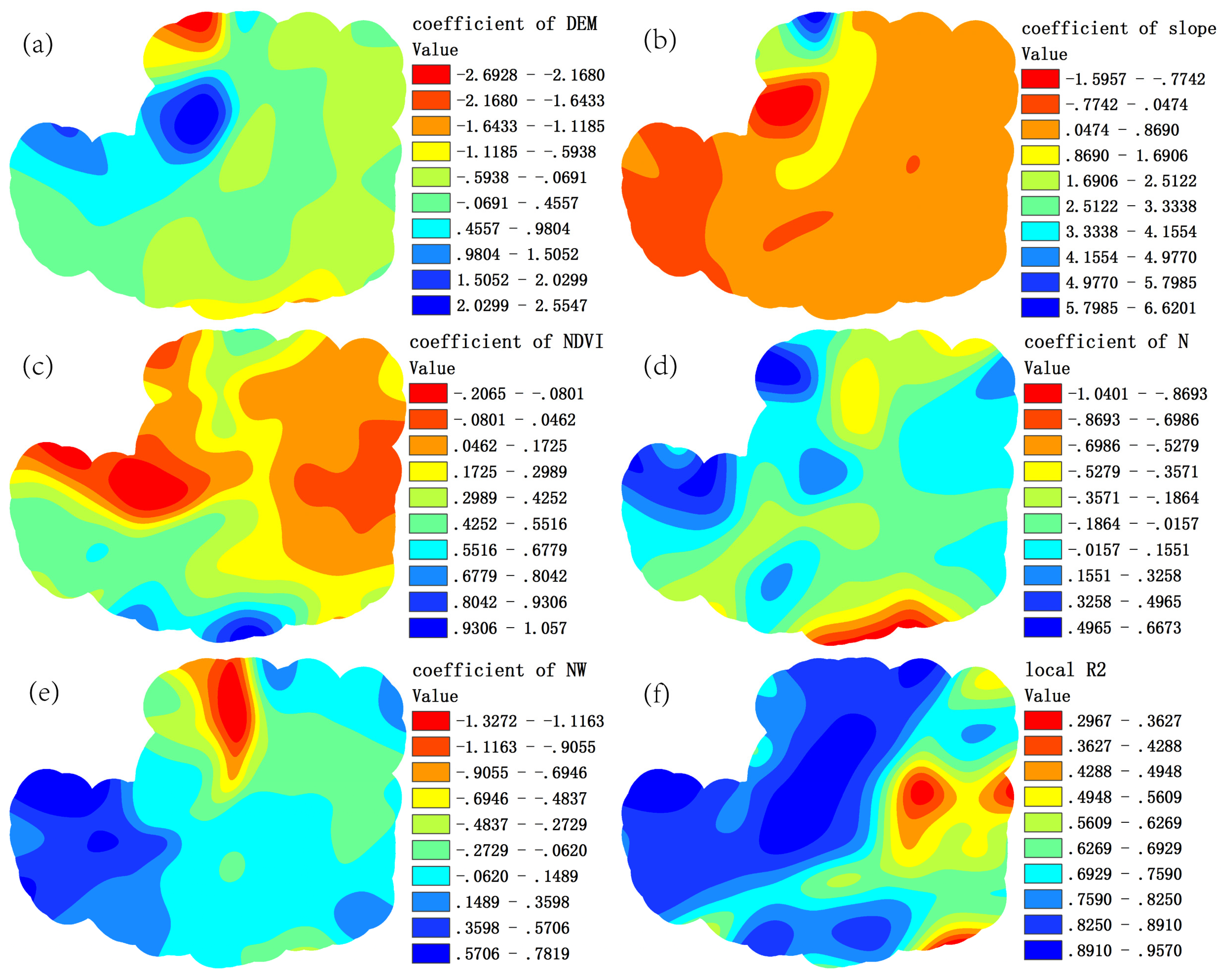
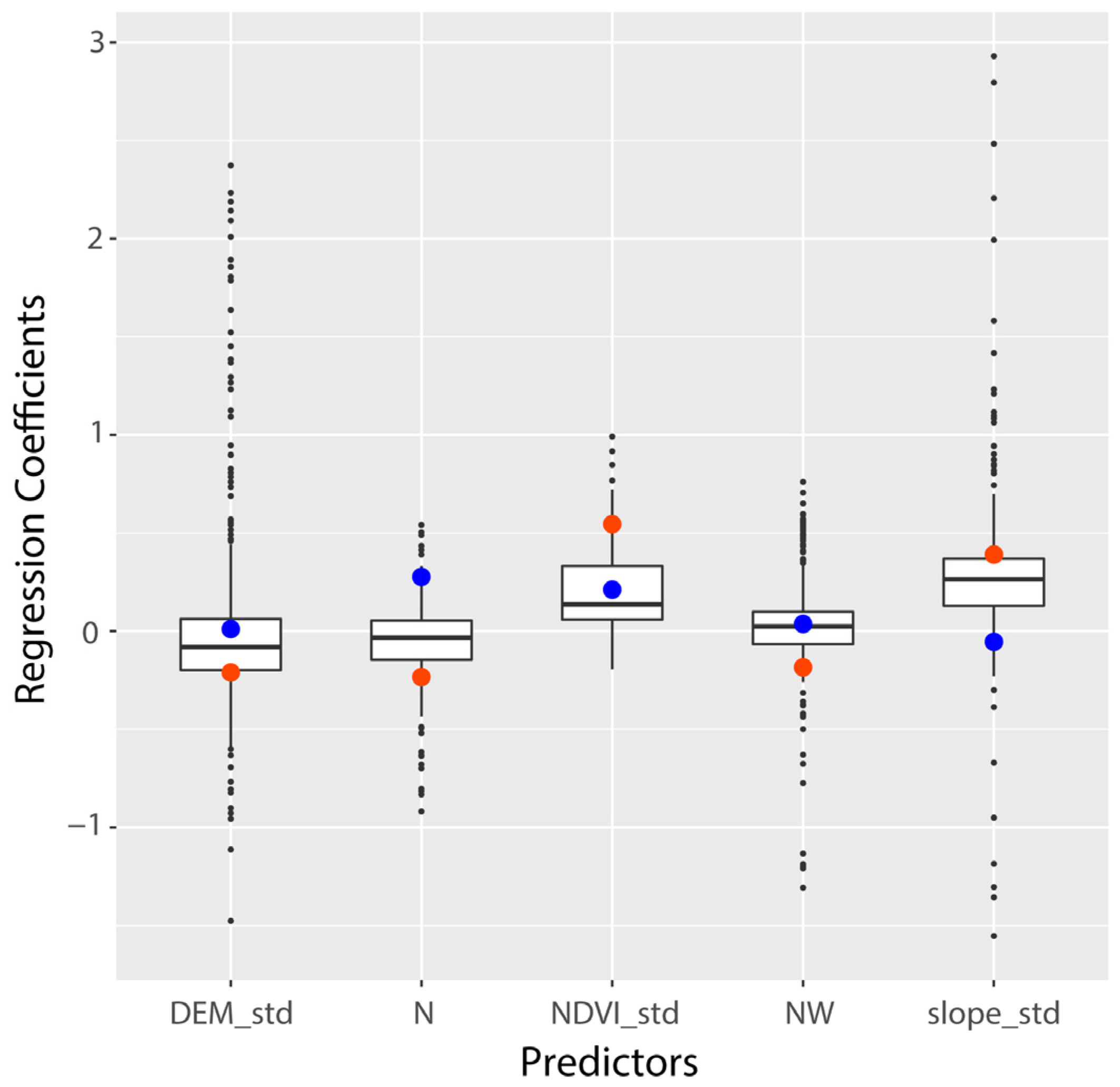
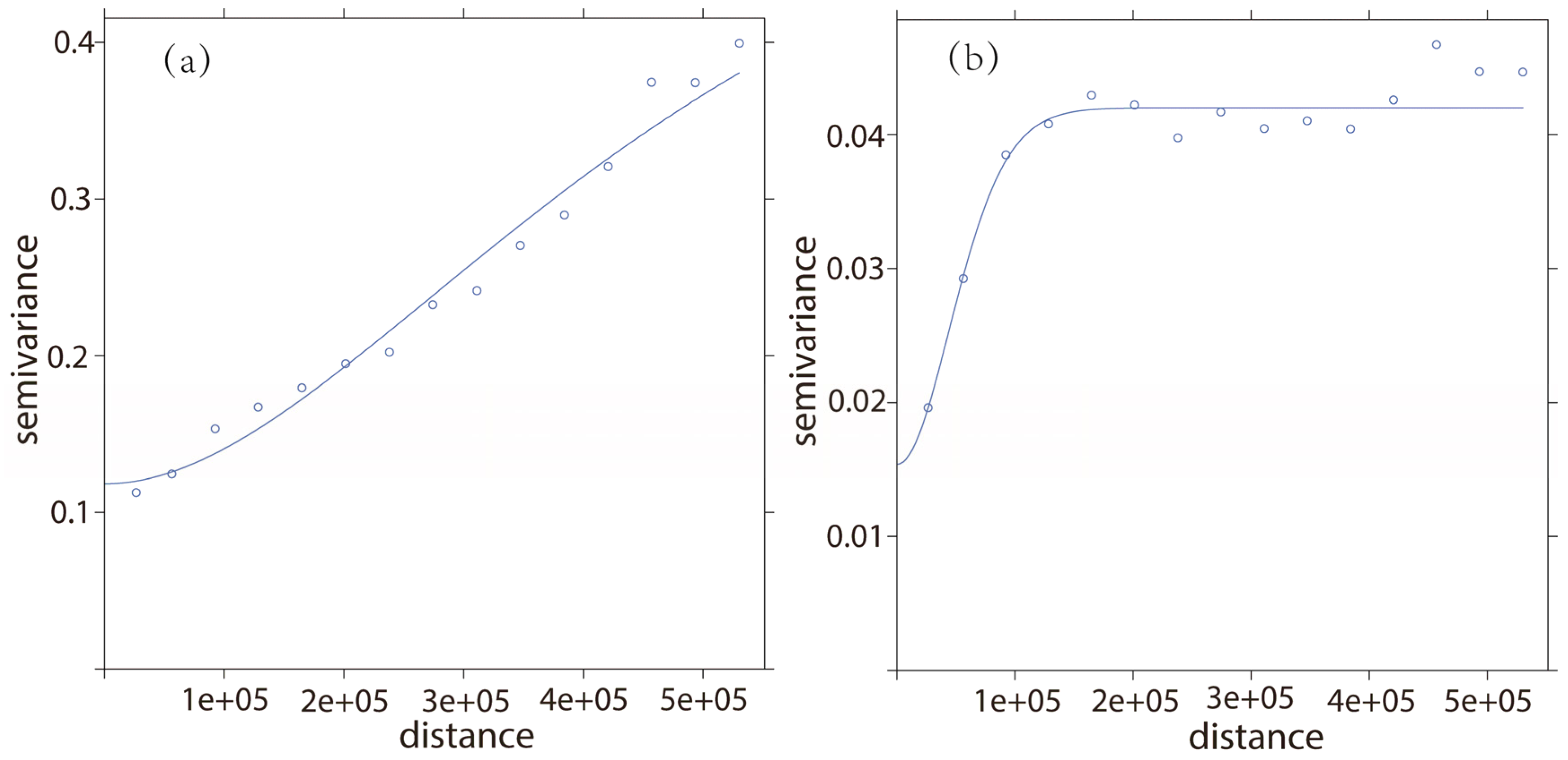
4.4. Regression Residuals Interpolation
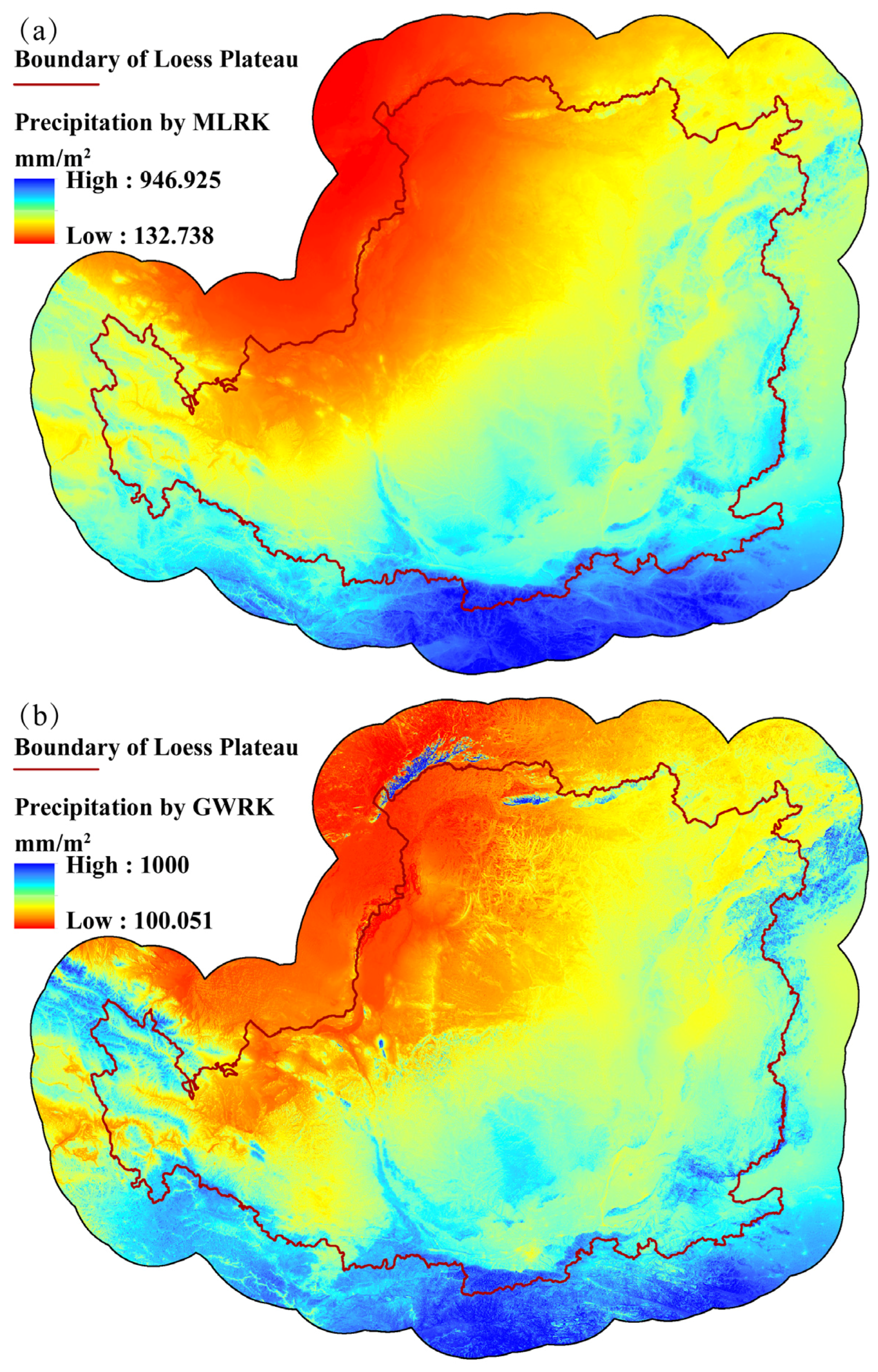
4.5. Validation of MLRK and GWRK
5. Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| CV | Cross-Validation |
| DEM | Digital Elevation Model |
| DEM_std | Standardized Normal Variable of Digital Elevation Model |
| E | Dummy Variable of East Aspect |
| GWR | Geographically Weighted Regression |
| GWRK | Geographically Weighted Regression Kriging |
| MAE | Mean Absolute Error |
| MAEr | Mean Absolute Relative Error |
| ME | Mean Error |
| MEr | Mean Relative Error |
| MLR | Multiple Linear Regression |
| MLRK | Multiple Linear Regression Kriging |
| N | Dummy Variable of North Aspect |
| NE | Dummy Variable of Northeast Aspect |
| NW | Dummy Variable of Northwest Aspect |
| NDVI | Normalized Difference Vegetation Index |
| NDVI_std | Standardized Normal Variable of Normalized Difference Vegetation Index |
| OK | Ordinary Kriging |
| OLS | Ordinary Least Squares |
| PRE | Annual Average Precipitation from meteorological stations |
| PreT | Logit-Transformed Precipitation |
| rad_std | Standardized Normal Variable of Solar Radiation |
| RK | Regression Kriging |
| RMSE | Root Mean Square Error |
| slope_std | Standardized Normal Variable of Slope |
| S | Dummy Variable of South Aspect |
| SE | Dummy Variable of Southeast Aspect |
| Ste. | Matern with Stein’s Parameterization |
| SW | Dummy Variable of Southwest Aspect |
| W | Dummy Variable of West Aspect |
References
- Taesombat, W.; Sriwongsitanon, N. Areal rainfall estimation using spatial interpolation techniques. Sci. Asia 2009, 35, 268–275. [Google Scholar] [CrossRef]
- Li, X.; Gao, S. Precipitation Modeling and Quantitative Analysis; Springer Science & Business Media: Dordrecht, The Netherlands, 2012. [Google Scholar]
- Shi, T.; Yang, X.; Christakos, G.; Wang, J.; Liu, L. Spatiotemporal interpolation of rainfall by combining BME theory and satellite rainfall estimates. Atmosphere 2015, 6, 1307–1326. [Google Scholar] [CrossRef]
- Mair, A.; Fares, A. Comparison of rainfall interpolation methods in a mountainous region of a tropical island. J. Hydrol. Eng. 2010, 16, 371–383. [Google Scholar] [CrossRef]
- Sun, W.; Zhu, Y.; Huang, S.; Guo, C. Mapping the mean annual precipitation of China using local interpolation techniques. Theor. Appl. Climatol. 2015, 119, 171–180. [Google Scholar] [CrossRef]
- Xu, W.; Zou, Y.; Zhang, G.; Linderman, M. A comparison among spatial interpolation techniques for daily rainfall data in Sichuan Province, China. Int. J. Climatol. 2015, 35, 2898–2907. [Google Scholar] [CrossRef]
- Jin, Q.; Shi, M.; Zhang, J.; Wang, S.; Hu, Y. Calibration of rainfall erosivity calculation based on TRMM data: A case study of the upriver basin of Jiyun River, North China. Sci. Soil Water Conserv. 2015, 13, 94–102. (In Chinese) [Google Scholar]
- Seo, Y.; Kim, S.; Singh, V.P. Estimating spatial precipitation using regression kriging and artificial neural network residual kriging (RKNNRK) hybrid approach. Water Resour. Manag. 2015, 29, 2189–2204. [Google Scholar] [CrossRef]
- Wong, D.W.; Yuan, L.; Perlin, S.A. Comparison of spatial interpolation methods for the estimation of air quality data. J. Expo. Sci. Environ. Epid. 2004, 14, 404–415. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Hong, Y.; Xie, P.; Gao, J.; Niu, Z.; Kirstetter, P.; Yong, B. Variational merged of hourly gauge-satellite precipitation in Chia: Preliminary results. J. Geophys. Res. Atmos. 2015, 120, 9897–9915. [Google Scholar] [CrossRef]
- Sideris, I.V.; Gabella, M.; Erdin, R.; German, U. Real-time radar-rain-gauge merging using spatio-temporal co-kriging with external drift in the alpine terrain of Switzerland. Q. J. R. Meteor. Soc. 2014, 140, 1097–1111. [Google Scholar] [CrossRef]
- Newman, A.J.; Clark, M.P.; Craig, J.; Nijssen, B.; Wood, A.; Gutmann, E.; Mizukami, N.; Brekke, L.; Arnold, J.R.; Arnold, J.R. Gridded ensemble precipitation and temperature estimates for the contiguous United States. J. Hydrometeorol. 2015, 16, 2481–2500. [Google Scholar] [CrossRef]
- Xie, P.; Xiong, A.Y. A conceptual model for constructing high-resolution gauge-satellite merged precipitation analyses. J. Geophys. Res. Atmos. 2011, 116, D21106. [Google Scholar] [CrossRef]
- Michaelides, S.C. (Ed.) Precipitation: Advances in Measurement, Estimation and Prediction; Springer Science & Business Media: Berlin, Germany, 2007; pp. 131–169.
- Bajat, B.; Pejović, M.; Luković, J.; Manojlović, P.; Ducić, V.; Mustafić, S. Mapping average annual precipitation in Serbia (1961–1990) by using regression kriging. Theor. Appl. Climatol. 2013, 112, 1–13. [Google Scholar] [CrossRef]
- Masson, D.; Frei, C. Spatial analysis of precipitation in a high-mountain region: Exploring methods with multi-scale topographic predictors and circulation types. Hydrol. Earth Syst. Sci. 2014, 18, 4543–4563. [Google Scholar] [CrossRef]
- Hutchinson, M.F. Interpolating mean rainfall using thin plate smoothing splines. Int. J. Geog. Inf. Syst. 1995, 9, 385–403. [Google Scholar] [CrossRef]
- Ninyerola, M.; Pons, X.; Roure, J.M. A methodological approach of climatological modelling of air temperature and precipitation through GIS techniques. Int. J. Clim. 2000, 20, 1823–1841. [Google Scholar] [CrossRef]
- Bostan, P.A.; Heuvelink, G.B.M.; Akyurek, S.Z. Comparison of regression and kriging techniques for mapping the average annual precipitation of Turkey. Int. J. Appl. Earth Obs. 2012, 19, 115–126. [Google Scholar] [CrossRef]
- Li, J.; Heap, A.D. Spatial interpolation methods applied in the environmental sciences: A review. Environ. Model. Softw. 2014, 53, 173–189. [Google Scholar] [CrossRef]
- Odeha, I.O.A.; McBratney, A.B.; Chittleborough, D.J. Spatial prediction of soil properties from landform attributes derived from a digital elevation model. Geoderma 1994, 63, 197–214. [Google Scholar] [CrossRef]
- Hengl, T.; Heuvelink, G.B.; Stein, A. A generic framework for spatial prediction of soil variables based on regression-kriging. Geoderma 2004, 120, 75–93. [Google Scholar] [CrossRef]
- Song, X.; Brus, D.; Liu, F.; Li, D.; Zhao, Y.; Yang, J.; Zhang, G. Mapping soil organic carbon content by geographically weighted regression: A case study in the Heihe River Basin, China. Geoderma 2016, 261, 11–22. [Google Scholar] [CrossRef]
- Kumar, S.; Lal, R.; Liu, D. A geographically weighted regression kriging approach for mapping soil organic carbon stock. Geoderma 2012, 189, 627–634. [Google Scholar] [CrossRef]
- Wang, Q.X.; Fan, X.H.; Qin, Z.D.; Wang, M.B. Change trends of temperature and precipitation in the Loess Plateau Region of China, 1961–2010. Global Planet. Chang. 2012, 92, 138–147. [Google Scholar] [CrossRef]
- Harris, P.; Fotheringham, A.S.; Crespo, R.; Charlton, M. The use of geographically weighted regression for spatial prediction: An evaluation of models using simulated data sets. Math Geosci. 2010, 42, 657–680. [Google Scholar] [CrossRef]
- Li, Z.; Zheng, F.L.; Liu, W.Z.; Flanagan, D.C. Spatial distribution and temporal trends of extreme temperature and precipitation events on the Loess Plateau of China during 1961–2007. Quat. Int. 2010, 226, 92–100. [Google Scholar] [CrossRef]
- Wei, J.; Zhou, J.; Tian, J.; He, X.; Tang, K. Decoupling soil erosion and human activities on the Chinese Loess Plateau in the 20th century. Catena 2006, 68, 10–15. [Google Scholar] [CrossRef]
- Wang, K.; Zhang, C.; Li, W. Comparison of geographically weighted regression and regression kriging for estimating the spatial distribution of soil organic matter. GISci. Remote Sens. 2012, 49, 915–932. [Google Scholar] [CrossRef]
- Xin, Z.; Yu, X.; Li, Q.; Lu, X.X. Spatiotemporal variation in rainfall erosivity on the Chinese Loess Plateau during the period 1956–2008. Reg. Environ. Chang. 2011, 11, 149–159. [Google Scholar] [CrossRef]
- Pebesma, E.J. Multivariable geostatistics in S: The gstat package. Comput. Geosci. 2004, 30, 683–691. [Google Scholar] [CrossRef]
- Hengl, T. A Practical Guide to Geostatistical Mapping, 2nd ed.; University of Amsterdam: Amsterdam, The Netherlands, 2009. [Google Scholar]
- Fotheringham, A.S.; Brunsdon, C.; Charlton, M. Geographically Weighted Regression: The Analysis of Spatially Varying Relationships; John Wiley & Sons Ltd.: Chichester, UK, 2002. [Google Scholar]
- Cleveland, W.S. Robust locally weighted regression and smoothing scatterplots. J. Am. Stat. Assoc. 1979, 74, 829–836. [Google Scholar] [CrossRef]
- Lado, L.R.; Polya, D.; Winkel, L.; Berg, M.; Hegan, A. Modelling arsenic hazard in Cambodia: A geostatistical approach using ancillary data. Appl. Geochem. 2008, 23, 3010–3018. [Google Scholar] [CrossRef]
| Variables | PRE | DEM_std | NDVI_std | rad_std | slope_std | N | NE | E | SE | S | W | NW | SW |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PRE | 1 | – | – | – | – | – | – | – | – | – | – | – | – |
| DEM_std | −0.331 ** | 1 | – | – | – | – | – | – | – | – | – | – | – |
| NDVI_std | 0.600 ** | −0.386 ** | 1 | – | – | – | – | – | – | – | – | – | – |
| rad_std | −0.349 ** | 0.968 ** | −0.385 ** | 1 | – | – | – | – | – | – | – | – | – |
| slope_std | 0.315 ** | 0.286 ** | 0.097 * | 0.172 ** | 1 | – | – | – | – | – | – | – | – |
| N | −0.134 ** | 0.022 | −0.042 | −0.009 | −0.090 | 1 | – | – | – | – | – | – | – |
| NE | −0.019 | 0.069 | −0.080 | −0.011 | 0.067 | −0.138 ** | 1 | – | – | – | – | – | – |
| E | 0.051 | 0.011 | 0.074 | 0.010 | −0.029 | −0.133 ** | −0.172 ** | 1 | – | – | – | – | – |
| SE | 0.028 | −0.086 | 0.061 | −0.039 | −0.096 * | −0.148 ** | −0.191 ** | −0.185 ** | 1 | – | – | – | – |
| S | 0.080 | −0.127 ** | 0.061 | −0.068 | −0.035 | −0.127 ** | −0.164 ** | −0.158 ** | −0.176 ** | 1 | – | – | – |
| W | 0.014 | 0.052 | −0.068 | 0.114 * | 0.095 * | −0.123 * | −0.159 ** | −0.153 ** | −0.170 ** | −0.146 ** | 1 | – | – |
| NW | −0.033 | 0.052 | −0.027 | −0.014 | 0.091 | −0.103 * | −0.133 ** | −0.128 ** | −0.142 ** | −0.122 * | −0.118 * | 1 | – |
| SW | 0.014 | 0.052 | −0.068 | 0.114 * | 0.095 * | −0.123 * | −0.159 ** | −0.153 ** | −0.170 ** | −0.146 ** | 1.000 ** | −0.118 * | 1 |
| PreT | 0.985 ** | −0.306 ** | 0.578 ** | −0.324 ** | 0.309 ** | −0.133 ** | −0.011 | 0.052 | 0.023 | 0.080 | 0.021 | −0.051 | 0.021 |
| Models | R2 | Adjusted R2 | Residuals SE | F-statistic | p-Value |
|---|---|---|---|---|---|
| a * | 0.4481 | 0.4338 | 0.6046 | 31.23 | <2.2 × 10−16 |
| b ** | 0.4465 | 0.4400 | 0.6012 | 69.21 | <2.2 × 10−16 |
| Coefficients | Estimate | Std. Error | t Value | P(>|t|) |
|---|---|---|---|---|
| a | −0.2110 | 0.0404 | −5.224 | 2.73 × 10−7 *** |
| b | 0.3903 | 0.0466 | 8.376 | 7.89 × 10−16 *** |
| c | 0.5449 | 0.0477 | 11.414 | <2 × 10−16 *** |
| d | −0.2341 | 0.0986 | −2.375 | 0.0180 * |
| e | −0.1856 | 0.1019 | −1.821 | 0.0692 |
| f | −0.2903 | 0.0414 | −7.022 | 8.64 × 10−12 *** |
| Residuals | Model | Nugget (C0) (km2/m4) | Partial Sill (C) (km2/m4) | Range (m) | Kappa | C0/(C0 + C) (%) |
|---|---|---|---|---|---|---|
| MLR | Ste. | 0.1,182 | 0.4151 | 590,950.4 | 1.9 | 22.16 |
| GWR | Ste. | 0.01,537 | 0.02,665 | 66,963.64 | 10 | 36.58 |
| Method | Adjusted R2 | ME (mm/m2) | MEr (%) | MAE (mm/m2) | MAEr (%) | RMSE (mm/m2) |
|---|---|---|---|---|---|---|
| MLRK | 0.87 | −20.88 | −3.82 | 30.85 | 6.58 | 40.05 |
| GWRK | 0.85 | −9.80 | −1.29 | 35.75 | 7.78 | 43.24 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, Q.; Zhang, J.; Shi, M.; Huang, J. Estimating Loess Plateau Average Annual Precipitation with Multiple Linear Regression Kriging and Geographically Weighted Regression Kriging. Water 2016, 8, 266. https://doi.org/10.3390/w8060266
Jin Q, Zhang J, Shi M, Huang J. Estimating Loess Plateau Average Annual Precipitation with Multiple Linear Regression Kriging and Geographically Weighted Regression Kriging. Water. 2016; 8(6):266. https://doi.org/10.3390/w8060266
Chicago/Turabian StyleJin, Qiutong, Jutao Zhang, Mingchang Shi, and Jixia Huang. 2016. "Estimating Loess Plateau Average Annual Precipitation with Multiple Linear Regression Kriging and Geographically Weighted Regression Kriging" Water 8, no. 6: 266. https://doi.org/10.3390/w8060266
APA StyleJin, Q., Zhang, J., Shi, M., & Huang, J. (2016). Estimating Loess Plateau Average Annual Precipitation with Multiple Linear Regression Kriging and Geographically Weighted Regression Kriging. Water, 8(6), 266. https://doi.org/10.3390/w8060266







