1. Introduction
As the current demand for freshwater in many regions outweighs the available supply, the need to effectively manage freshwater as a resource has become greater than ever with hydrologic forecast modeling playing a key role in its management. Fortunately, this increased obligation has been met with rapid technological advancements allowing for the development of hydrologic prediction models of high accuracy. One key aspect of hydrologic modeling is rainfall–runoff modeling, where streamflow, indicating the availability of water in a catchment, is forecasted for a multitude of purposes, such as drought management, flood control, the design of hydraulic structures, hydropower generation, maintenance of minimum ecological requirements, and municipal and irrigational supply. The time-varying, spatially-distributed, and non-linear nature of runoff generation is influenced by an array of interconnected and diverse factors that can be hard to define [
1]. These factors include storm characteristics, climatic characteristics influencing meteorological shifts, the catchment’s initial state, as well as the geomorphological characteristics of a catchment. As a result, numerous modeling techniques have been implemented to model these systems. Early methods, such as Mulvaney’s Rational Method [
2], focused on deriving empirical relationships between influencing factors to predict runoff or peak discharge [
3], while modern methods rely heavily on computational power and can be categorized as either physically-based, conceptual, or data-driven models. The simplest and easiest to implement of the modern computational methods are referred to as data-driven models and require at a minimum only past streamflow and rainfall data [
4]. Physically based and conceptual models also often require expertise for the implementation of sophisticated mathematical tools [
5]. Instead, data-driven models are able to capture the relationships driving the transformation of precipitation into streamflow by relying on information rooted within the hydrologic time-series.
Numerous data-driven techniques have been implemented to portray the nonlinear and non-stationary relationship between rainfall and runoff for specific catchments. Of these, genetic programming (GP) has proven advantageous over other methods as it self-optimizes both parameter coefficients and the functional relationships between input variables while excluding the user’s need to optimize model architecture, proving key advantages over more popularized data-driven techniques, such as artificial neural network models [
6]. A number of studies highlight the effectiveness of GP for forecasting hydrologic events. Parasuraman
et al. [
7] used the GP to model the evapotranspiration process, relying on a number of variables and comparing results with those of an ANN and the traditional Penman-Monteith (PM) method, with results indicating that GP and ANNs performed similarly, with both outperforming the PM method. Havlíček
et al. [
1] combined GP with a set of conceptual functions resulting in improved streamflow forecasting when compared to stand-alone GP and ANN models. Aytek
et al. [
8] used gene expression programming, a subset of GP, to model streamflow, determining that GP performed with similar results compared to feed forward back propagation ANNs. Mehr
et al. [
9] compared linear genetic programming (LGP) to a hybrid wavelet analysis-artificial neural network for modeling a series of gauge stations, concluding that LGP outperformed the neural network. Srinivasulu
et al. [
10] implemented a series of ANN models for streamflow predictions at Lock and Dam 10 on the Kentucky River, with the best performing model being trained through a real-coded genetic algorithm.
Numerous examples highlighting the effectiveness of incorporating data-driven techniques into hybrid designs can be found in literature (e.g., [
11,
12]). Nourani
et al. [
13] developed a hybrid wavelet transform and adaptive neural-fuzzy interface system model to decompose daily runoff and precipitation time-series, applying each decomposed signal as input data to predict runoff one time-step ahead. Kisi
et al. [
14] used a similar technique, but instead with genetic programming as the symbolic regression method. Wang
et al. [
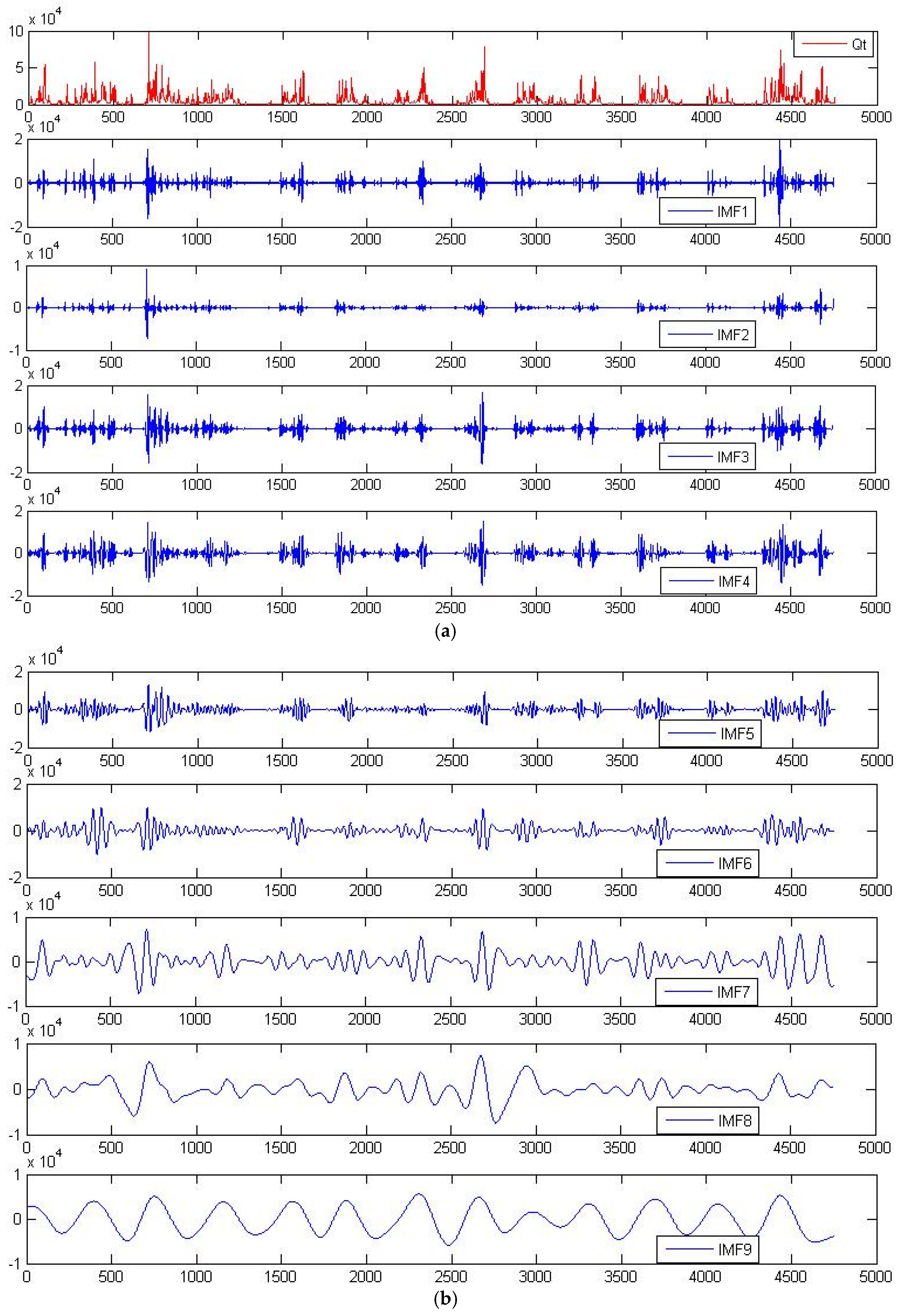
15] applied an ensemble empirical mode decomposition-particle swarm optimization–support vector machine hybrid model to first decompose a precipitation time-series into its respective sub-series, then selected the parameters with the highest impact, and lastly predicted monthly runoff one time-step ahead. The ensemble empirical mode decomposition (EEMD) has shown great promise in the decomposition of nonlinear and non-stationary time-series while avoiding the
a priori user-derived data assumptions required in more popularized methods such as wavelet transform [
16]. To separate data into like clusters, the unsupervised classification technique of a self-organizing map (SOM) is implemented as it has shown a high propensity for classifying multidimensional data onto a two-dimensional space [
17]. Srinivasulu
et al. [
10] noted the applicability of this method when coupled with an ANN and its superiority in handling noisy data when compared to other methods such as k-means clustering. Another example of its application in hydrology is found in Ismail
et al. [
18], who grouped historic river flow data through an SOM for the prediction of monthly streamflow using a least squares support vector machine model. Numerous other studies have attempted to model streamflow predictions by dividing input data through hydrograph characteristics, or have attempted to use data-driven modeling to make predictions multiple time-steps ahead (e.g., [
19,
20,
21,
22,
23]).
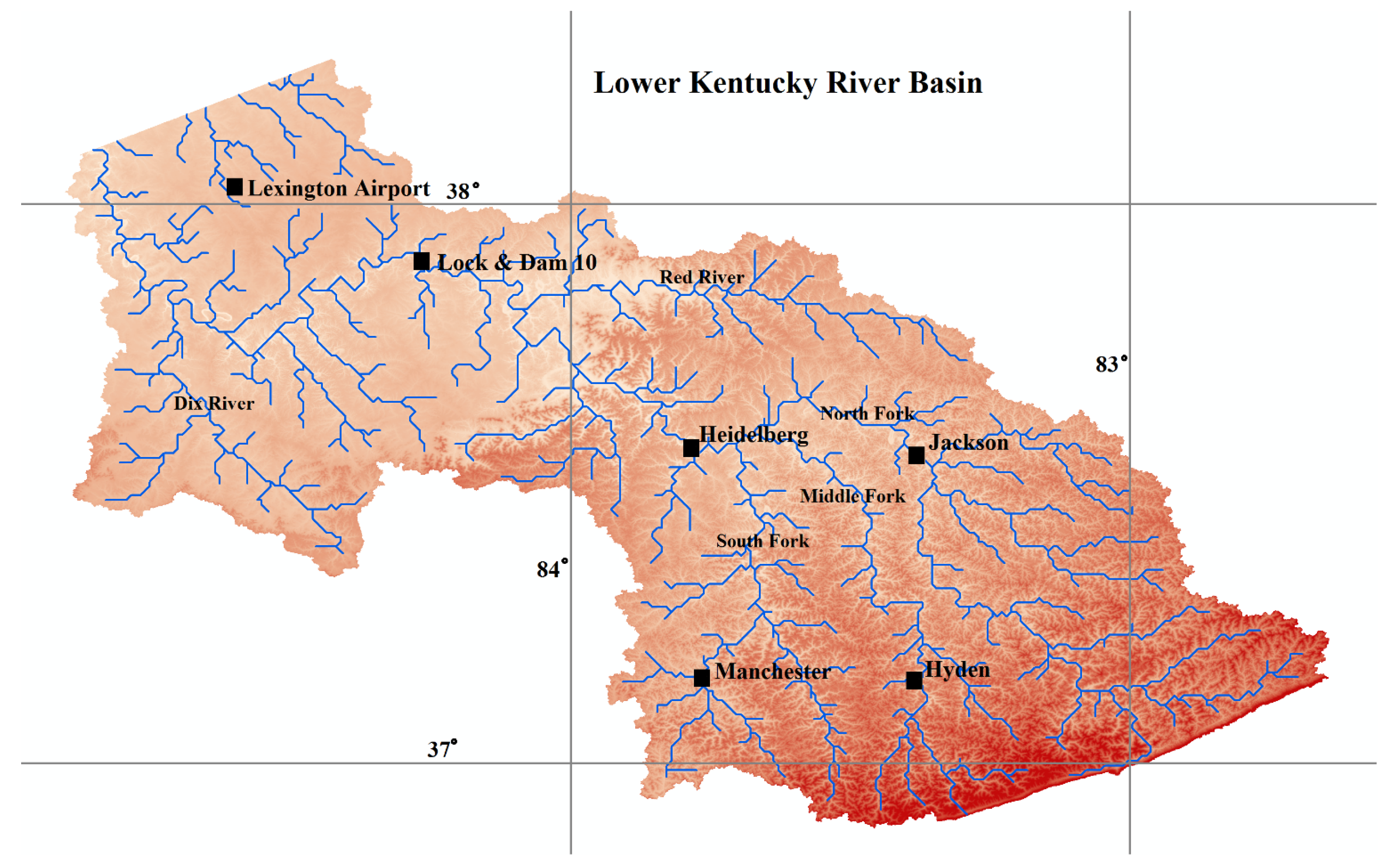
The objectives of this study are to (a) investigate the applicability of LGP for modeling the rainfall–runoff process; (b) to explore the impact of preprocessing the runoff data through EEMD and clustering the input space through an SOM on the predictive capability of LGP; (c) to assess the seasonal effects of runoff for the study area by grouping the input information into high and low flow seasons; (d) to report the ability of LGP to fit to datasets representing the rising and falling trends of the hydrograph; and (e) to determine the ability of the hybrid design for making predictions multiple time-steps ahead. Rainfall and discharge data was derived from the Kentucky River Basin, with forecasts being made for daily average streamflow values. Each produced model was evaluated based on a set of statistical measures.
4. Results and Discussion
Results for the ability of each model to capture discharge at Lock and Dam 10 along the Kentucky River are listed below for the different objectives of this study. Each model was evaluated based on the seven statistical parameters discussed in the previous section.
Table 5 and
Table 6 present the performance parameters for the first objective of models, which focused on assessing LGP’s ability to capture streamflow within the basin. LGP-1 shows the strong autocorrelation of runoff information when capturing streamflow within the models. Conversely, it was found that oversupplying LGP models with too many days of precipitation information lead to significant reductions in the performance of the models. For example, including P(
t), P(
t−1), and P(
t−2) with three days of past runoff resulted in an AARE of 50.23 and NMBE of 2.90. This model is labeled LGP 1.7 and can be found in the
supplementary material in Tables S2 and S3. It is noted in [
37] that including precipitation beyond the catchments lag time can lead to a loss in the predictive capability of data-driven models. The lag time to Lock and Dam 10 has been reported as two days [
38]. LGP-2 & LGP-3 display the strength of LGP for creating data-driven models capturing streamflow. Although LGP-2 displayed a stronger AARE and with fewer variables, LGP-3 outperformed LGP-2 in most of the other statistical parameters, aside from capturing the peak flow in the dataset. When compared to the best performing ANN model published in [
10], LGP-2 & LGP-3 posted stronger validation AARE values, with similar statistical values for the other validation set parameters. The strongest ANN model published in [
10] can be found in
Table 5. It was trained through a genetic algorithm and run over the same datasets as the models produced in this study.
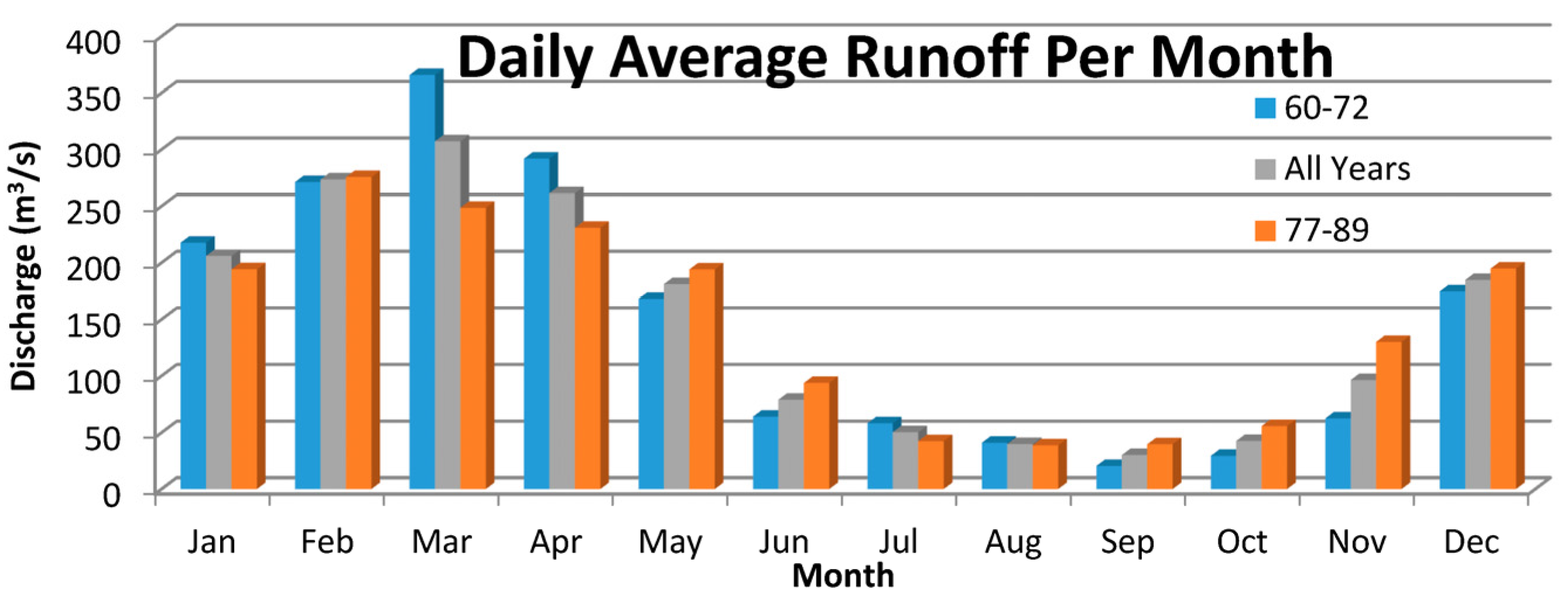
Modeling the low and high flow seasons for the basin separately shows a strong under-prediction during the low flow seasons, as indicated by the NMBE in LGP-4. Of the dates associated with the highest relative error in LGP-2 & LGP-3, a majority occurred during months of low flow, suggesting an altered dynamic to the environment during these periods, with potential causes being increased infiltration from the underlying karst geology as the ground becomes less saturated from loss of snowmelt and warmth, increased evaporation of water from pooling along the lock system, and increased municipal and irrigational usage during summer months. LGP-5 shows a greater ease for LGP to model the falling portions of the hydrograph in comparison with the rising trends. Examining the rising portions of the hydrograph’s output shows large degrees of relative error associated with the over-prediction of streamflow on days of small changes in actual streamflow after heavy precipitation, with these events occurring during the low flow season. Additionally, modeling the effect of precipitation error on model performance shows a greater degree of error associated with the undervalued precipitation estimations as compared to overestimations (
Tables S6 and S7).
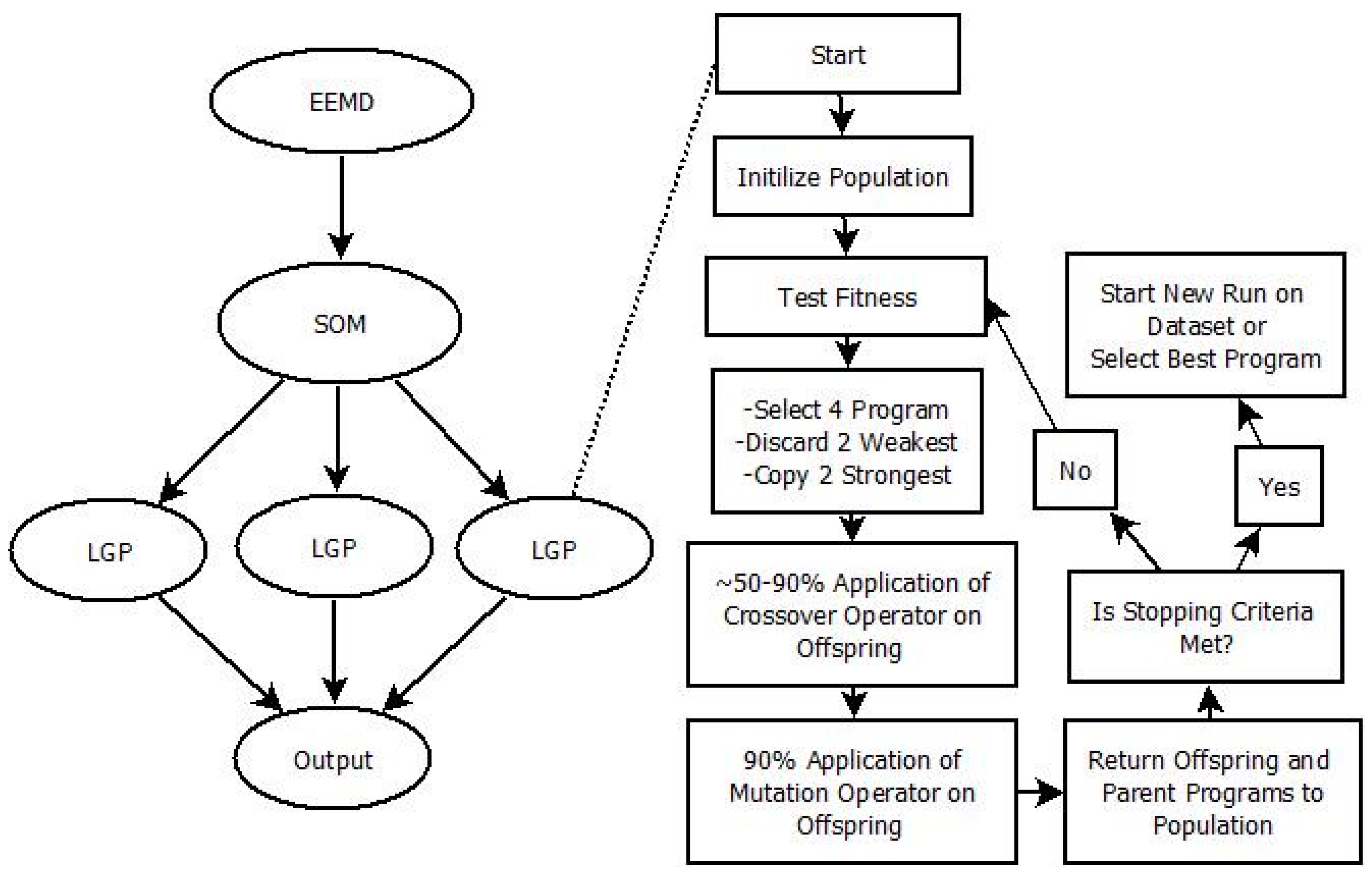
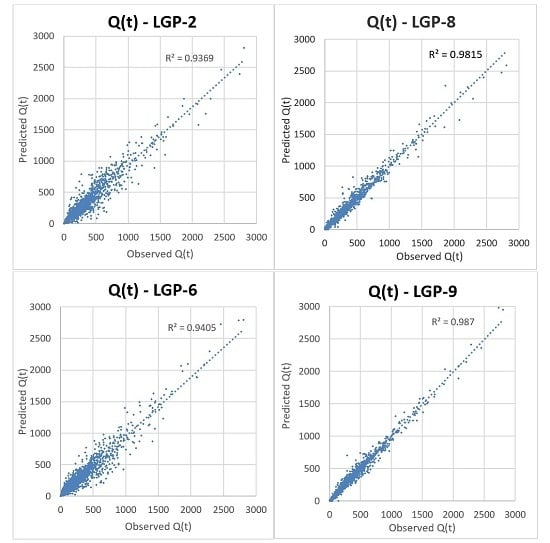
LGP-6 through LGP-9 were assessed incorporating LGP into hybrid designs, with the results presented in
Table 7. LGP-6 & LGP-7 were created for direct comparison with LGP-2 & LGP-3 and included an SOM to classify the input space before LGP application on each class. When comparing LGP-6 with LGP-2 it is seen that classifying the input space did not provide a significant reward for the added computation requirement, as some parameters slightly improved (NRMSE,
Eper,
E) and others regressed (AARE, NMBE). Comparing LGP-7 to LGP-3 resulted in more parameters that improved, but again, the improvements were not enough to justify the added computation requirement and time. LGP-8, which utilized IMF data derived from EEMD in addition to standard rainfall and precipitation information, showed major improvement in reducing AARE and improving
E &
Eper, while better-predicting values further from the mean, as indicated by its NRMSE. From the set of EEMD included models that resulted in LGP-8, consistently stronger AARE,
E,
I, NRMSE, and
Eper values were found, although it appeared to create a negative bias for %MF. These models, including others, are included in the
supplementary material. Further improvement was seen when an SOM was utilized to classify EEMD and standard information before LGP application, as indicated by LGP-9. Of the different designs presented, LGP-9 resulted in the largest reduction in error, with an AARE of 10.122, the strongest Nash-Sutcliffe of 0.987, strongest
Eper of 0.931, the strongest ability to predict values away from the mean, with an NRMSE of 0.182, and very low magnitude of over-predicting, with and NMBE of 0.161. Utilizing an SOM in conjunction with EEMD-derived runoff information was shown to significantly improve the performance of models created through LGP.
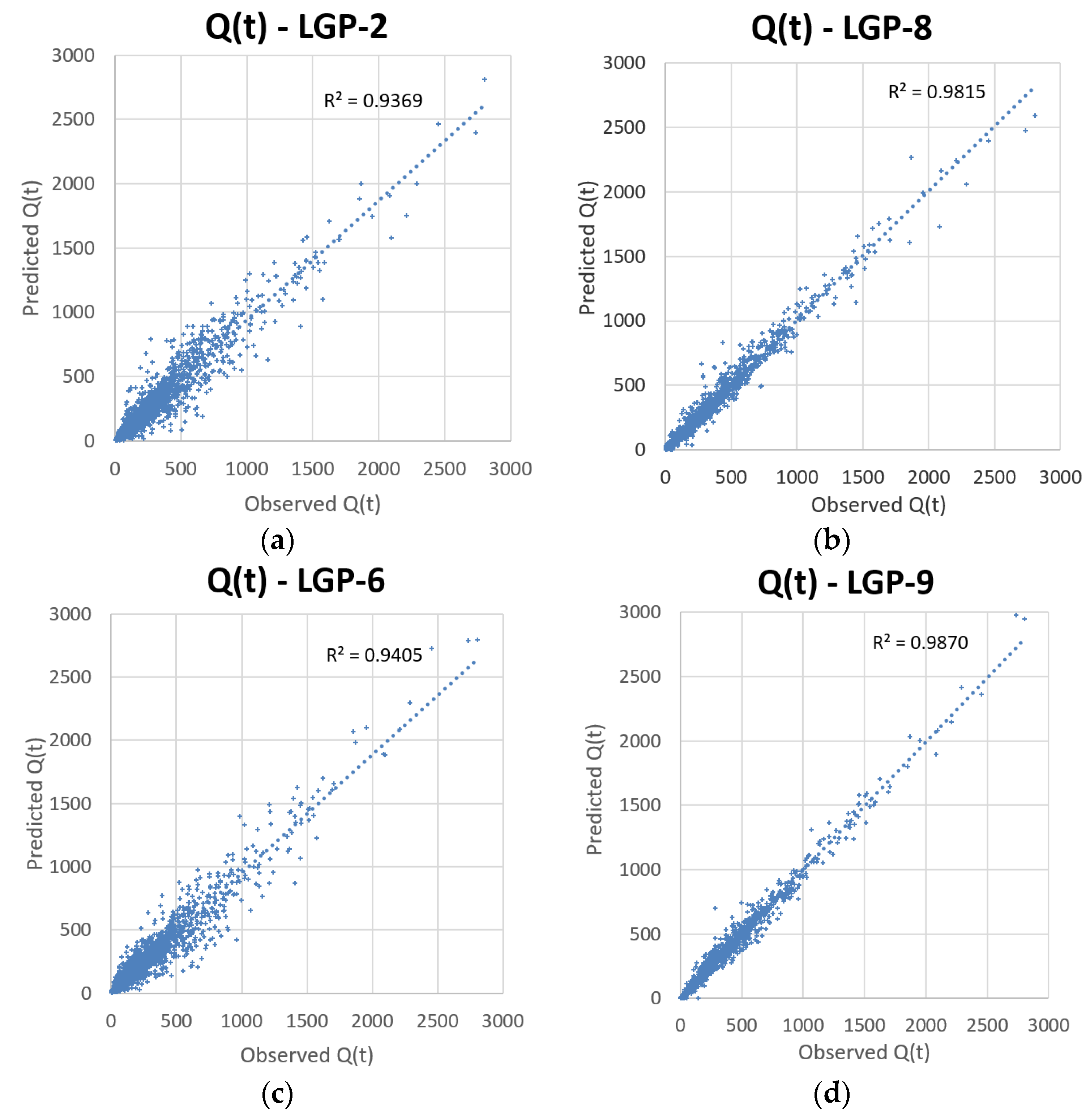
Figure 7 shows a scatter-plot comparison between LGP-2, LGP-6, LGP-8, and LGP-9 for capturing streamflow.
Table 8 displays a comparison of the low, medium, and high magnitude flows for select models. Intervals were derived from generated intervals of streamflow information through an SOM, but were also guided through observable values. The flow intervals composed of low flows between 0 and 28.2 m
3/s, medium flows between 28.2 and 282.3 m
3/s, and high flows above 282.3 m
3/s. LGP-2, which utilized LGP as a standalone application, resulted in an extremely strong AARE, which was not reproduced for any other LGP standalone models created during trial and error, which likely signifies that it is an extreme outlier linear genetic program for this individual basin. LGP-3, LGP-8, & LGP-9 each show more difficulty in predicting low magnitude flows compared to medium and high magnitude flows, with LGP-9 reporting the best results for each interval.
The third and primary objective of this study was to determine the practicality of the method by assessing its ability to predict multiple time-steps ahead.
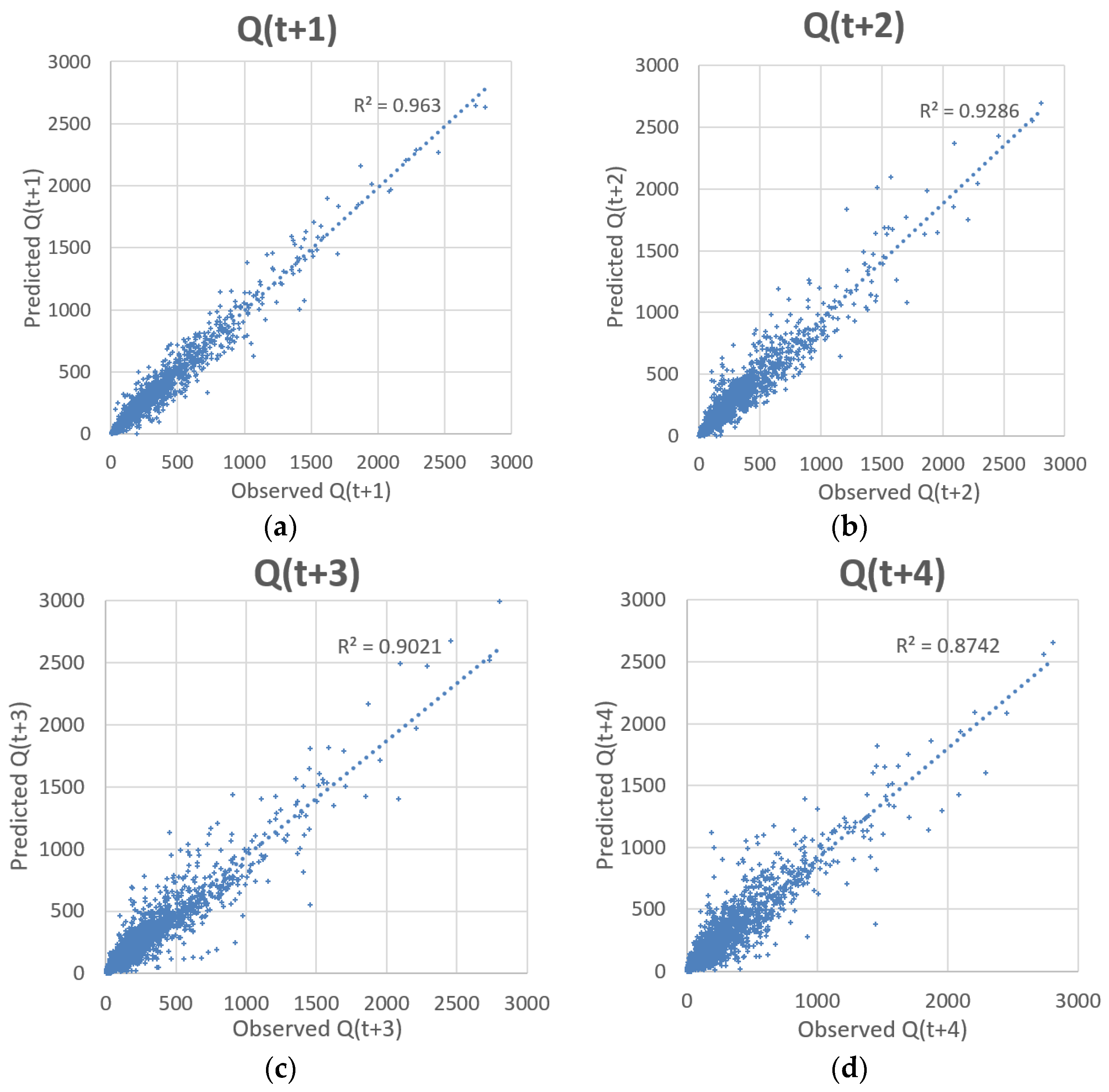
Table 9 displays the statistical performance of the EEMD-SOM-LGP architecture for predicting streamflow at Lock and Dam 10 along the Kentucky River Basin up to 4 days ahead. The hybrid design depicts strong values for predicting streamflow up to two days ahead with acceptable values that can give a good indication on streamflow for days three and four.
Figure 8 compares the ability of the EEMD-SOM-LGP design to predict streamflow at different time-steps.
Other model designs were assessed but are not reported (
Tables S11–S18). For example, using LGP as a standalone was deemed non-effective, as considerable lag developed between observed and predicted values. To account for the need to include the basin’s response to precipitation when using LGP as a standalone application, models could incorporate forecasted precipitation information, although at the expense of new issues. Utilizing an EEMD-LGP design eliminated this lag and returned strong results, although not as effective as when incorporating an SOM into the model design. For example, at Q(
t+3), the EEMD-LGP model returned an AARE of 47.832, an
E of 0.889, and an
Eper of 0.522, while the EEMD-SOM-LGP design returned an AARE of 43.365, an
E of 0.902, and an
Eper of 0.591 at Q(
t+3). Utilizing the EEMD-SOM-LGP design also minimized the negative effect on %MF, as values without the application of the SOM were all negative and in double digits. For comparative purposes, these models can be found in the
supplementary material.
Figure 9 compares LGP-10 with LGP as a standalone application for predicting streamflow at three days ahead.
5. Conclusions
This study focused on assessing the effectiveness of LGP as a standalone application and in hybrid designs with EEDM and an SOM to capture streamflow, while also focusing on the ability of the hybrid design to forecast streamflow multiple time-steps ahead. Daily average rainfall and streamflow data from the Kentucky River Basin were utilized to develop each of the models, with a number of different statistical parameters being used to evaluate their performance.
The findings from this study suggest that LGP works very well when utilized with EEMD-derived runoff data, and even better when an SOM is utilized to create separate data classes composed of EEMD-derived runoff information and observed values with each class being run as a separate model. Selecting the appropriate IMFs is largely up to the user’s knowledge of the data, with the five highest frequency IMFs being determined to provide the greatest degree of predictive performance in regards to this catchment.
Utilizing LGP as a standalone application to capture streamflow resulted in very similar findings when compared to the best performing ANN model from [
10], which was developed over the same dataset and input variables and trained through a genetic algorithm. Classifying the input space through an SOM before modeling each class through LGP did not prove to be worthwhile without the inclusion of EEMD-derived runoff subcomponents. When EEMD-derived runoff subcomponents were utilized with LGP, all the statistical parameters significantly improved, aside from %MF. Including all three techniques together in an EEMD-SOM-LGP structure resulted in the strongest performance of all the reported models. The design also proved highly effective for making predictions multiple time-steps ahead.
The fast processing environments of LGP, SOM, and EEMD make them very good data-driven techniques for forecast modeling, especially when utilized together. Streamlining all the techniques into a single application would benefit forecast modelers. As the findings from this study are preliminary in nature, they should be reinforced on additional basins and for forecasting other natural signals. Also, developing a more comprehensive method for the selection of the appropriate IMF components could be investigated and implemented, likely further improving results.