Bivariate Drought Analysis Using Streamflow Reconstruction with Tree Ring Indices in the Sacramento Basin, California, USA
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area and Data
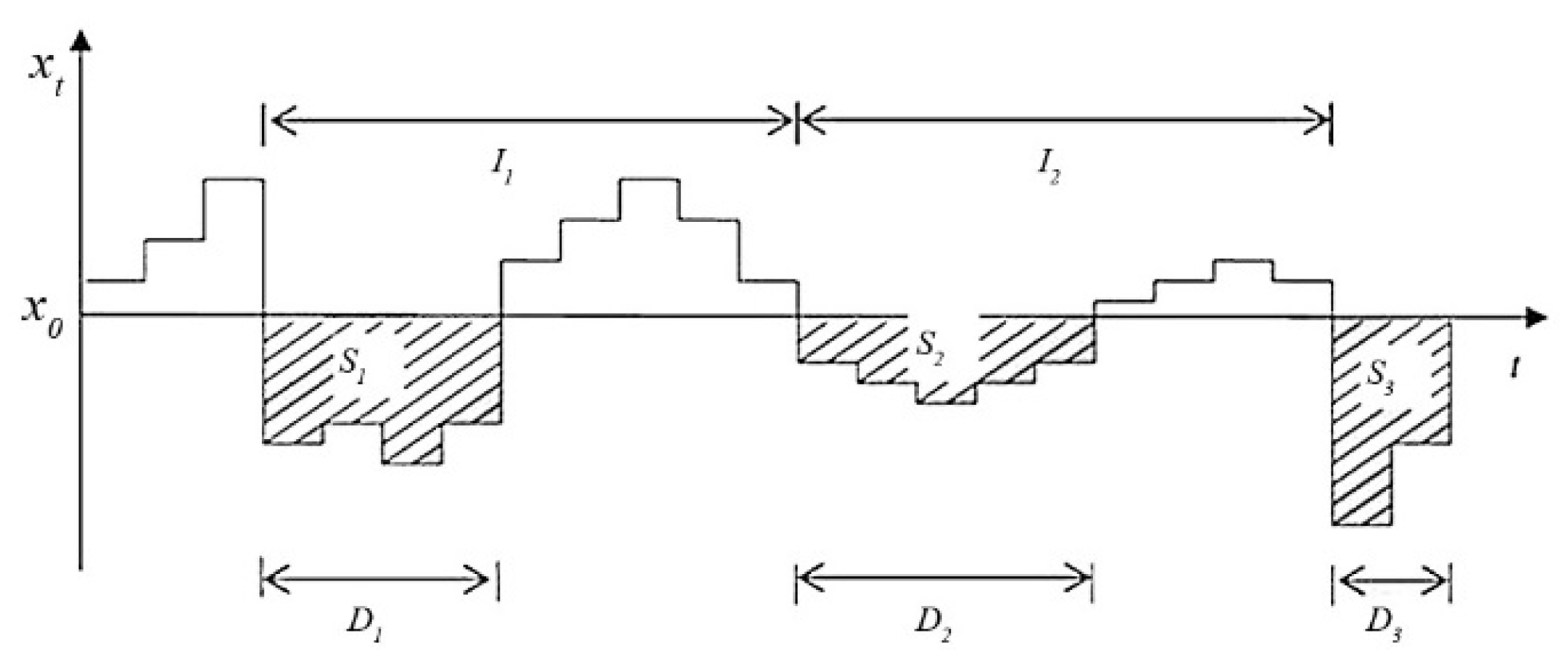
2.2. Drought Definition Using the Run Theory
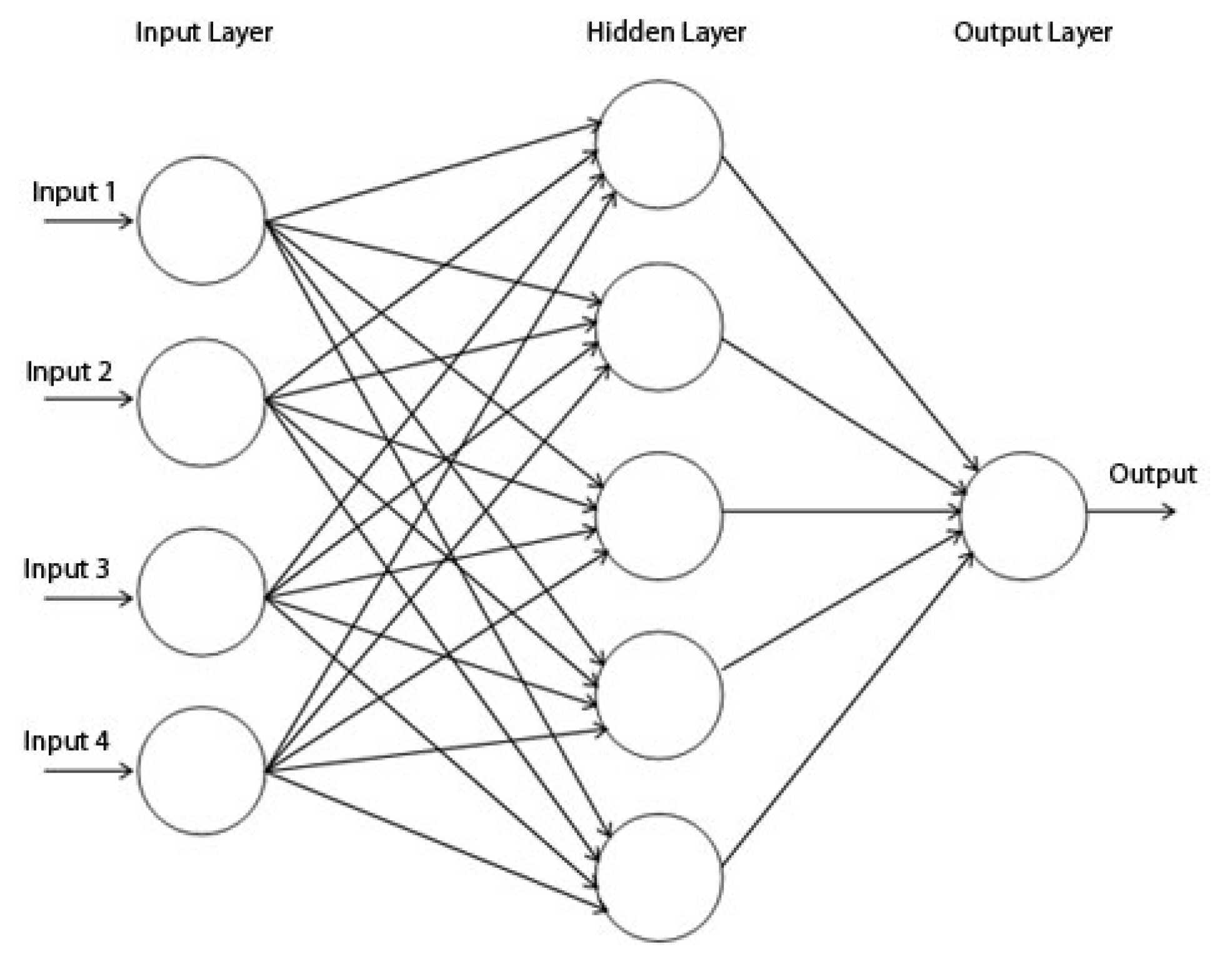
2.3. Artificial Neural Network
2.4. Drought Frequency Analysis Based on Copula
3. Results and Discussion
3.1. Tree-Ring Data Screening
3.2. Reconstructed ANN Model Calibration and Validation
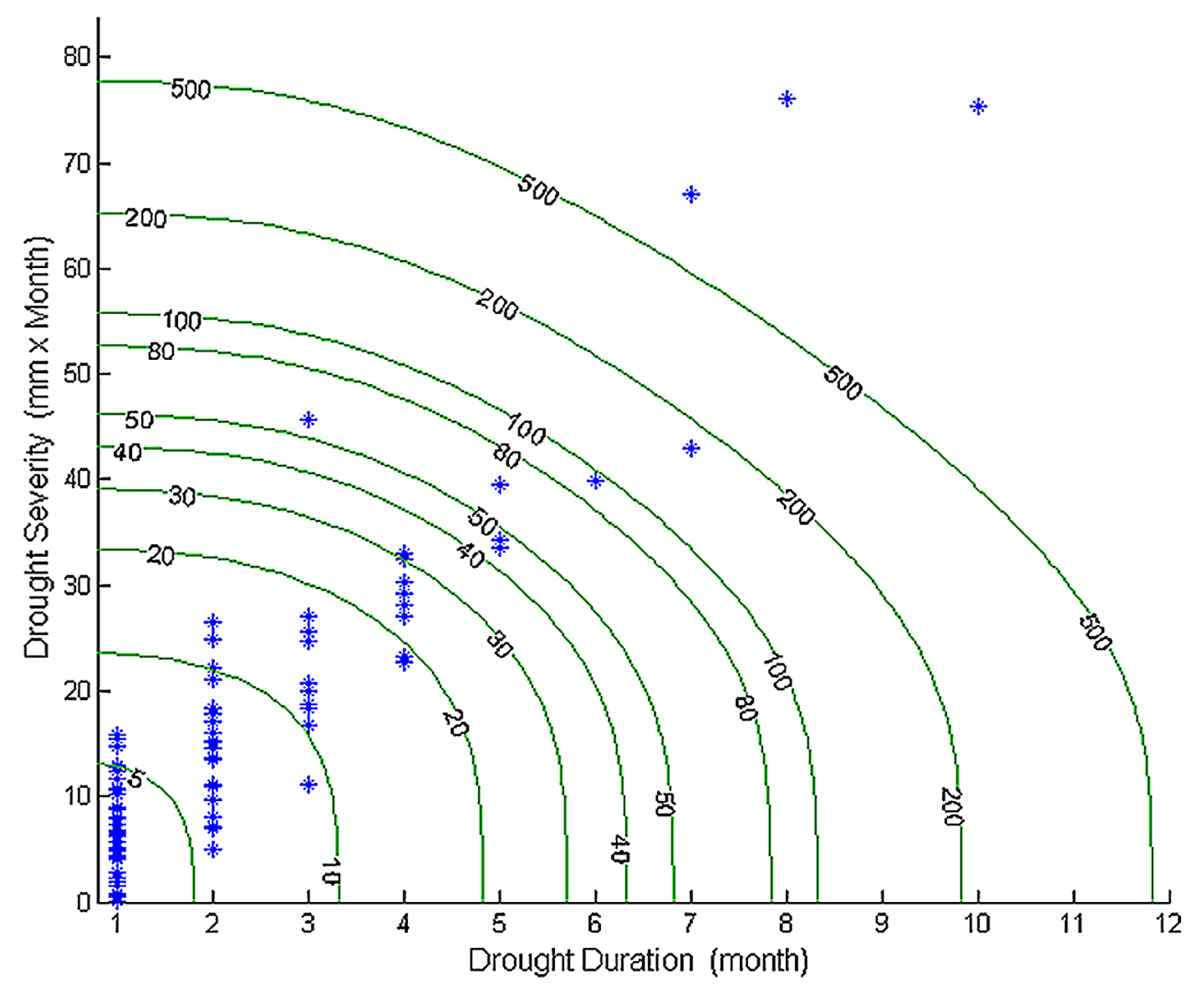
3.3. Bivariate Drought Analysis and Discussion
4. Conclusions
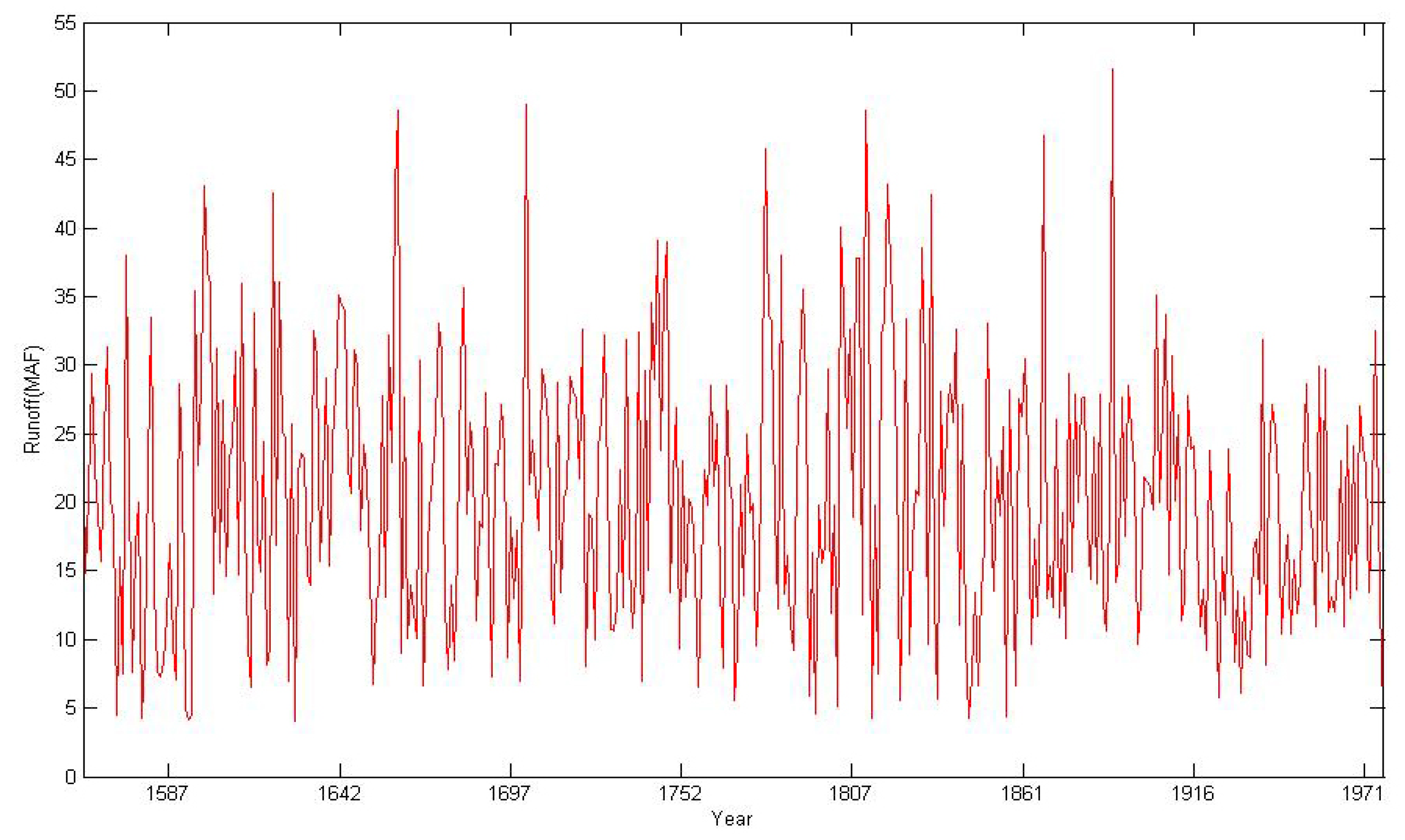
- The past streamflow for the period from 1560 to 1871 is reconstructed with the ANN model and tree-ring data, which was found to be the appropriate predictor. As shown by calibration and validation results from 1872 to 1977, the R2 and Nash values are 0.7 or higher. It is therefore concluded that the ANN model reconstructs streamflow of the Sacramento River satisfactorily.
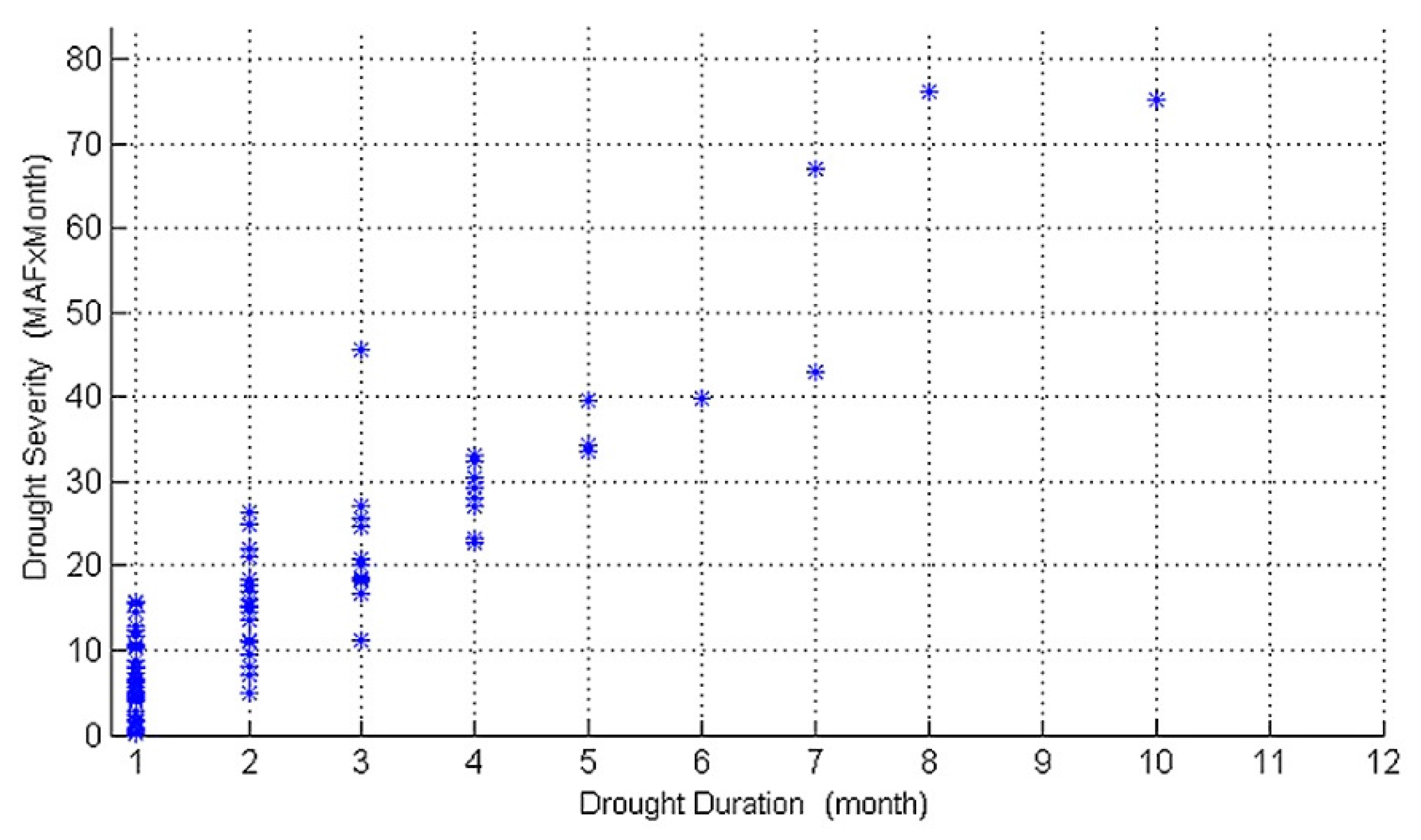
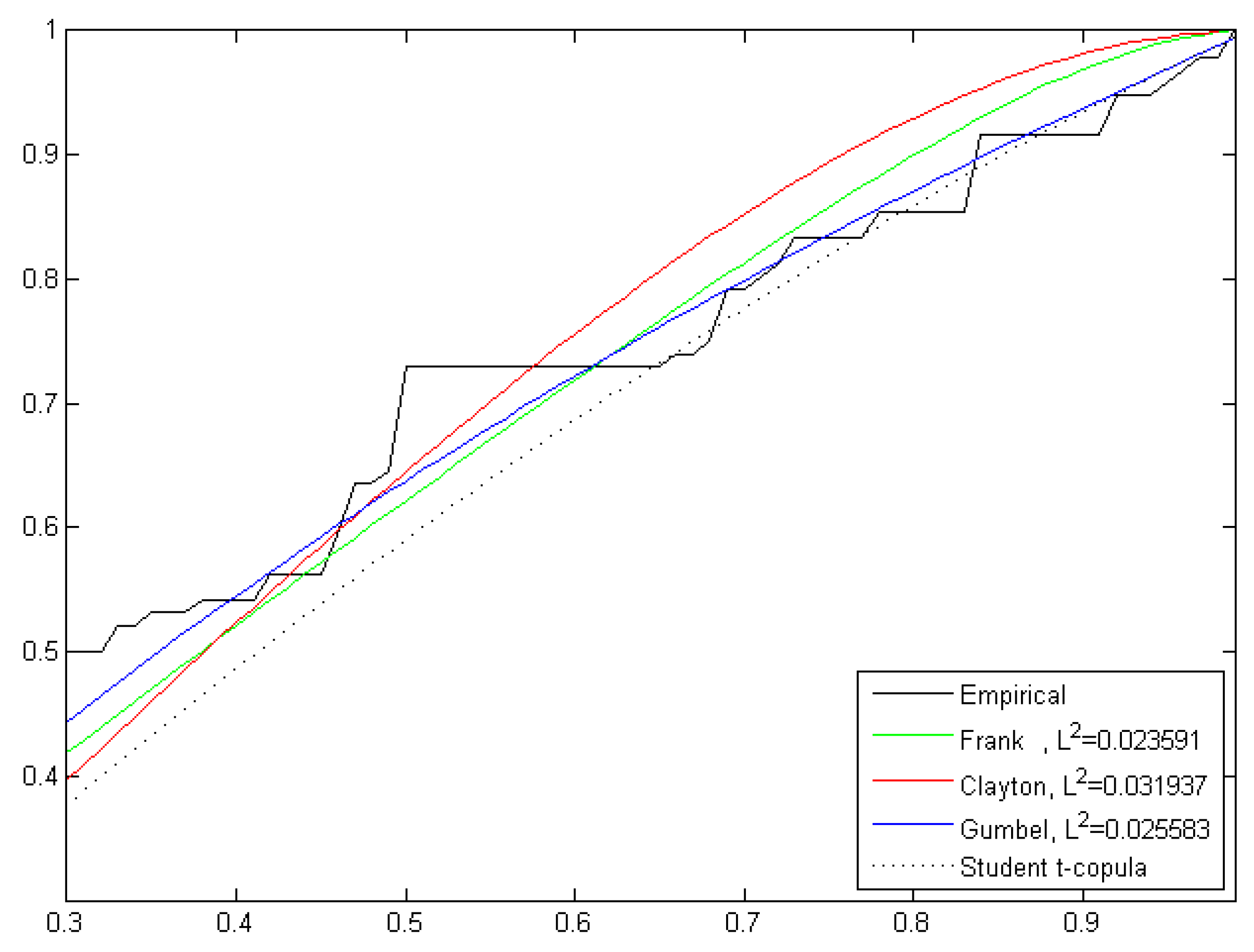
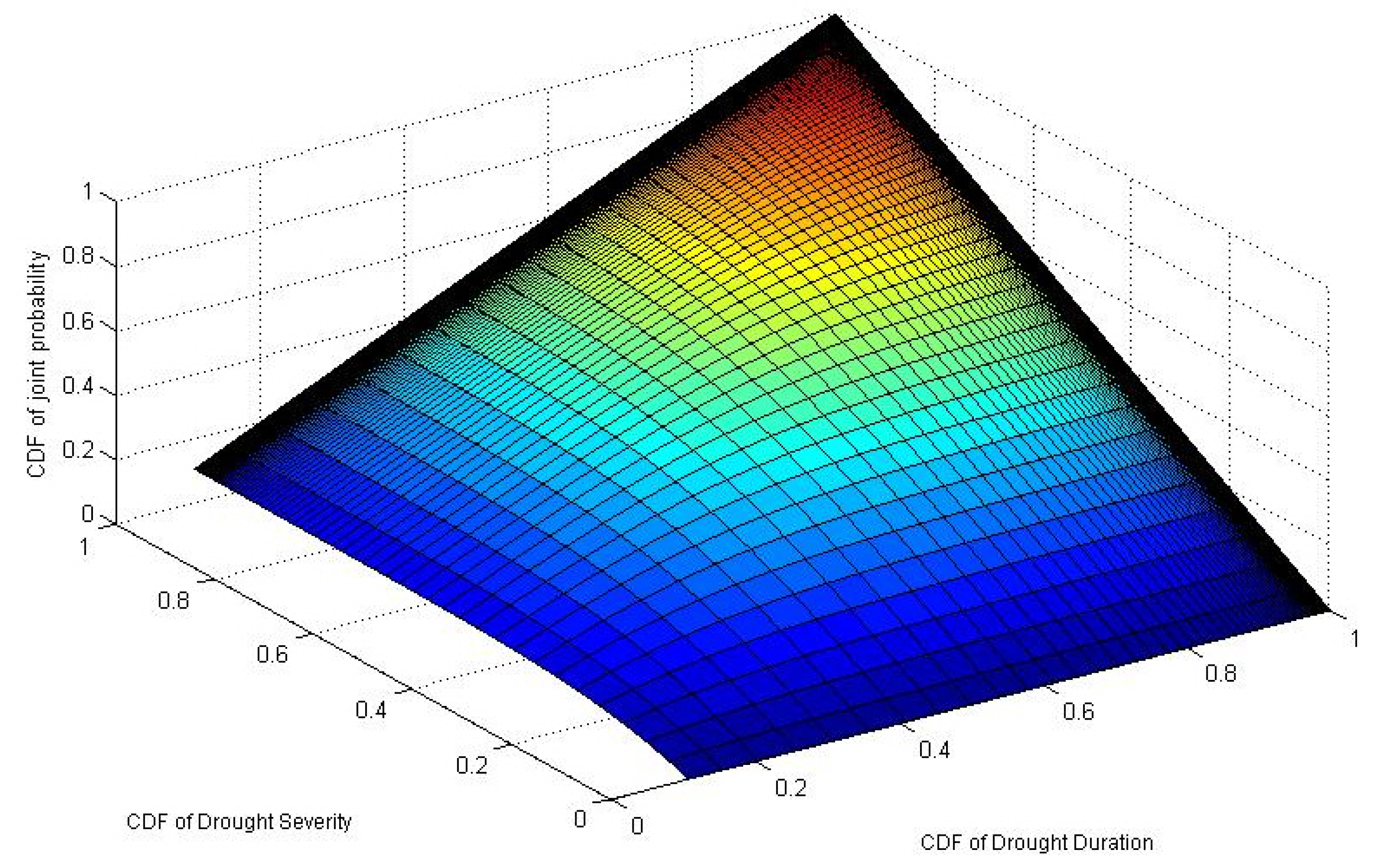
- Drought characteristics in the Sacramento River basin have strong correlation with each other. The Archimedean copula is found to be appropriate for bivariate drought frequency analysis.
- It is shown that a drought with a 20-year return period or longer will cause actual water shortages in the perspective of water supply to the southern California area. Hence, it could be considered an appropriate critical level of droughts for actual water shortages.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Wang, B.; Jhun, J.G.; Moon, B.K. Variability and singularity of Seoul, South Korea, rainy season (1778–2004). J. Clim. 2007, 20, 2572–2580. [Google Scholar] [CrossRef]
- Mun, J.W.; Lee, D.Y. Tree-ring data application for drought mitigation. J. Korean Soc. Hazard Mitig. 2011, 11, 70–78. (In Korean) [Google Scholar]
- Kim, H.S.; Hwang, S.H.; Kim, J.H. Reconstruction of River Flows Using Tree-Ring Series and Neural Network. J. Korean Soc. Civ. Eng. 1998, 18, 583–589. [Google Scholar]
- Ferguson, C.W. Bristlecone Pine: Science and Esthetics A 7100-year tree-ring chronology aids scientists; old trees draw visitors to California mountains. Science 1968, 159, 839–846. [Google Scholar] [CrossRef] [PubMed]
- Fritts, H.C. Tree-ring analysis: A tool for water resources research. Eos Trans. Am. Geophys. Union 1969, 50, 22–29. [Google Scholar] [CrossRef]
- Fritts, H.C. Tree Rings and Climate; Academic Press Inc.: New York, NY, USA, 1976. [Google Scholar]
- Hughes, M.K.; Xiangding, W.; Xuemei, S.; Garfin, G.M. A preliminary reconstruction of rainfall in north-central China since AD 1600 from tree-ring density and width. Quat. Res. 1994, 42, 88–99. [Google Scholar] [CrossRef]
- Díaz, S.C.; Touchan, R.; Swetnam, T.W. A tree-ring reconstruction of past precipitation for Baja California Sur, Mexico. Int. J. Climatol. 2001, 21, 1007–1019. [Google Scholar] [CrossRef]
- Cleaveland, M.K.; Stahle, D.W.; Therrell, M.D.; Villanueva-Diaz, J.; Burns, B.T. Tree-ring reconstructed winter precipitation and tropical teleconnections in Durango, Mexico. Clim. Chang. 2003, 59, 369–388. [Google Scholar] [CrossRef]
- Gray, S.T.; Fastie, C.L.; Jackson, S.T.; Betancourt, J.L. Tree-ring-based reconstruction of precipitation in the Bighorn Basin, Wyoming, since 1260 AD. J. Clim. 2004, 17, 3855–3865. [Google Scholar] [CrossRef]
- Liu, Y.; Cai, Q.; Shi, J.; Hughes, M.K.; Kutzbach, J.E.; Liu, Z.; An, Z. Seasonal precipitation in the south-central Helan Mountain region, China, reconstructed from tree-ring width for the past 224 years. Can. J. For. Res. 2005, 35, 2403–2412. [Google Scholar] [CrossRef]
- Liu, Y.; Ma, L.; Leavitt, S.W.; Cai, Q.; Liu, W. A preliminary seasonal precipitation reconstruction from tree-ring stable carbon isotopes at Mt. Helan, China, since AD 1804. Glob. Planet. Chang. 2004, 41, 229–239. [Google Scholar] [CrossRef]
- Schneuwly, D.M.; Stoffel, M. Tree-ring based reconstruction of the seasonal timing, major events and origin of rockfall on a case-study slope in the Swiss Alps. Nat. Hazards Earth Syst. Sci. 2008, 8, 203–211. [Google Scholar] [CrossRef]
- Frank, D.; Esper, J. Characterization and climate response patterns of a high-elevation, multi-species tree-ring network in the European Alps. Dendrochronologia 2005, 22, 107–121. [Google Scholar] [CrossRef]
- Cook, E.R.; Jacoby, G.C. Tree-ring-drought relationships in the Hudson Valley, New York. Science 1977, 198, 399–401. [Google Scholar] [CrossRef] [PubMed]
- Stockton, C.W.; Meko, D.M. Drought Recurrence in the Great Plains as Reconstructed from Long-Term Tree-Ring Records. J. Clim. Appl. Meteorol. 1983, 22, 17–29. [Google Scholar] [CrossRef]
- Graumlich, L.J. Precipitation variation in the Pacific Northwest (1675–1975) as reconstructed from tree rings. Ann. Assoc. Am. Geogr. 1987, 77, 19–29. [Google Scholar] [CrossRef]
- Till, C.; Guiot, J. Reconstruction of precipitation in Morocco since 1100 AD Based on Cedrus atlantica tree-ring widths. Quat. Res. 1990, 33, 337–351. [Google Scholar] [CrossRef]
- Meko, D.; Stockton, C.W.; Boggess, W.R. The Tree-ring Record of Severe Sustained Drought. J. Am. Water Resour. Assoc. 1995, 31, 789–801. [Google Scholar] [CrossRef]
- Stahle, D.W.; Cook, E.R.; Cleaveland, M.K.; Therrell, M.D.; Meko, D.M.; Grissino-Mayer, H.D.; Luckman, B.H. Tree-ring data document 16th century mega drought over North America. EOS Trans. Am. Geophys. Union 2000, 81, 121–125. [Google Scholar] [CrossRef]
- Raffalli-Delerce, G.; Masson-Delmotte, V.; Dupouey, J.L.; Stievenard, M.; Breda, N.; Moisselin, J.M. Reconstruction of summer droughts using tree-ring cellulose isotopes: A calibration study with living oaks from Brittany (western France). Tellus B 2004, 56, 160–174. [Google Scholar] [CrossRef]
- Li, J.; Gou, X.; Cook, E.R.; Chen, F. Tree-ring based drought reconstruction for the central Tien Shan area in northwest China. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Li, J.; Chen, F.; Cook, E.R.; Gou, X.; Zhang, Y. Drought reconstruction for north central China from tree rings: The value of the Palmer drought severity index. Int. J. Climatol. 2007, 27, 903–909. [Google Scholar] [CrossRef]
- Tian, Q.; Gou, X.; Zhang, Y.; Peng, J.; Wang, J.; Chen, T. Tree-ring based drought reconstruction (AD 1855–2001) for the Qilian Mountains, northwestern China. Tree Ring Res. 2007, 63, 27–36. [Google Scholar] [CrossRef]
- Mishra, A.K.; Singh, V.P. Drought modeling—A review. J. Hydrol. 2011, 403, 157–175. [Google Scholar] [CrossRef]
- Agüero, J.D.L.C.; Rodríguez, F.J.G. Morphometric stock structure of the Pacific sardine Sardinops sagax (Jenyns, 1842) off Baja California, Mexico. In Morphometrics; Springer: Berlin, Germany; Heidelberg, Germany, 2004. [Google Scholar]
- Stockton, C.W.; Meko, D.M. A long-term history of drought occurrence in western United States as inferred from tree rings. Weatherwise 1975, 28, 244–249. [Google Scholar] [CrossRef]
- Gray, S.T.; Betancourt, J.L.; Fastie, C.L.; Jackson, S.T. Patterns and sources of multidecadal oscillations in drought-sensitive tree-ring records from the central and southern Rocky Mountains. Geophys. Res. Lett. 2003, 30. [Google Scholar] [CrossRef]
- Helama, S.; Meriläinen, J.; Tuomenvirta, H. Multicentennial megadrought in northern Europe coincided with a global El Niño–Southern Oscillation drought pattern during the Medieval Climate Anomaly. Geology 2009, 37, 175–178. [Google Scholar] [CrossRef]
- Ropelewski, C.F.; Halpert, M.S. North American precipitation and temperature patterns associated with the El Niño/Southern Oscillation (ENSO). Monthly Weather Rev. 1986, 114, 2352–2362. [Google Scholar] [CrossRef]
- Davi, N.K.; Jacoby, G.C.; D’Arrigo, R.D.; Baatarbileg, N.; Jinbao, L.; Curtis, A.E. A tree-ring-based drought index reconstruction for far-western Mongolia: 1565–2004. Int. J. Climatol. 2009, 29, 1508–1514. [Google Scholar] [CrossRef]
- Touchan, R.; Funkhouser, G.; Hughes, M.K.; Erkan, N. Standardized precipitation index reconstructed from Turkish tree-ring widths. Clim. Chang. 2005, 72, 339–353. [Google Scholar] [CrossRef]
- Liang, E.; Shao, X.; Liu, H.; Eckstein, D. Tree-ring based PDSI reconstruction since AD 1842 in the Ortindag Sand Land, east Inner Mongolia. Chin. Sci. Bull. 2007, 52, 2715–2721. [Google Scholar] [CrossRef]
- Shiau, J.T. Fitting drought duration and severity with two-dimensional copulas. Water Resour. Manag. 2006, 20, 795–815. [Google Scholar] [CrossRef]
- Chbouki, N. Spatio-Temporal Characteristics of Drought as Inferred from Tree-Ring Data in Morocco. Ph.D. Thesis, University of Arizona, Tucson, AZ, USA, 1992. [Google Scholar]
- Shiau, J.T.; Modarres, R. Copula-based drought severity-duration-frequency analysis in Iran. Meteorol. Appl. 2009, 16, 481–489. [Google Scholar] [CrossRef]
- Rajsekhar, D.; Singh, V.P.; Mishra, A.K. Multivariate drought index: An information theory based approach for integrated drought assessment. J. Hydrol. 2015, 526, 164–182. [Google Scholar] [CrossRef]
- Hao, Z.; AghaKouchak, A. Multivariate standardized drought index: A parametric multi-index model. Adv. Water Resour. 2013, 57, 12–18. [Google Scholar] [CrossRef]
- Brown, J.F.; Wardlow, B.D.; Tadesse, T.; Hayes, M.J.; Reed, B.C. The Vegetation Drought Response Index (VegDRI): A new integrated approach for monitoring drought stress in vegetation. GISci. Remote Sens. 2008, 45, 16–46. [Google Scholar] [CrossRef]
- Tadesse, T.; Wardlow, B.D.; Brown, J.F.; Svoboda, M.D.; Hayes, M.J.; Fuchs, B.; Gutzmer, D. Assessing the vegetation condition impacts of the 2011 drought across the US Southern Great Plains using the Vegetation Drought Response Index (VegDRI). J. Appl. Meteorol. Climatol. 2015, 54, 153–169. [Google Scholar] [CrossRef]
- Alley, W.M. The Palmer Drought Severity Index: Limitations and assumptions. J. Clim. Appl. Meteorol. 1984, 23, 1100–1109. [Google Scholar] [CrossRef]
- Shafer, B.A.; Dezman, L.E. Development of a Surface Water Supply Index (SWSI) to assess the severity of drought conditions in snowpack runoff areas. In Proceedings of the Western Snow Conference, Reno, Nevada, April 1982; pp. 164–175.
- Valipour, M. Use of surface water supply index to assessing of water resources management in Colorado and Oregon. Adv. Agric. 2013, 3, 631–640. [Google Scholar]
- González, J.; Valdés, J.B. Bivariate drought recurrence analysis using tree ring reconstructions. J. Hydrol. Eng. 2003, 8, 247–258. [Google Scholar] [CrossRef]
- Vangelis, H.; Spiliotis, M.; Tsakiris, G. Drought severity assessment based on bivariate probability analysis. Water Resour. Manag. 2011, 25, 357–371. [Google Scholar] [CrossRef]
- Murtin, C.M.; Murtin, F. Education Inequalities among World Citizens: 1870–2000. 2006. Working Paper. Available online: http://www.eea-esem.com/files/papers/EEA-ESEM/2006/2780/EducationInequality.pdf (accessed on 21 March 2016).
- Sklar, A. Fonctions de Repartition `a n Dimensions et Leura Marges; Publication de l’Institut de Statistique de l’Université de Paris: Paris, France, 1959; pp. 229–231. (In French) [Google Scholar]
- Shiau, J.T.; Feng, S.; Nadarajah, S. Assessment of hydrological droughts for the Yellow River, China, using copulas. Hydrol. Process. 2007, 21, 2157–2163. [Google Scholar] [CrossRef]
- Serinaldi, F.; Bonaccorso, B.; Cancelliere, A.; Grimaldi, S. Probabilistic characterization of drought properties through Copulas. Phys. Chem. Earth 2009, 34, 596–605. [Google Scholar] [CrossRef]
- Song, S.; Singh, V.P. Meta-elliptical copulas for drought frequency analysis of periodic hydrologic data. Stoch Environ. Res. Risk Assess. 2010, 24, 425–444. [Google Scholar] [CrossRef]
- Mirabbasi, R.; Anagnostou, E.N.; Fakheri-Fard, A.; Dinpashoh, Y.; Eslamian, S. Analysis of meteorological drought in northwest Iran using the Joint Deficit Index. J. Hydrol. 2013, 492, 35–48. [Google Scholar] [CrossRef]
- Chen, L.; Singh, V.P.; Guo, S.; Mishra, A.K.; Guo, J. Drought Analysis Using Copulas. J. Hydrol. Eng. 2012, 18, 797–808. [Google Scholar] [CrossRef]
- Vergni, L.; Todisco, F.L.; Mannocchi, F. Analysis of agricultural drought characteristics through a two-dimensional copula. Water Resour. Manag. 2015, 29, 2819–2835. [Google Scholar] [CrossRef]
- Huang, S.; Huang, Q.; Chang, J.; Chen, Y.; Xing, L.; Xie, Y. Copulas-Based Drought Evolution Characteristics and Risk Evaluation in a Typical Arid and Semi-Arid Region. Water Resour. Manag. 2014, 29, 1489–1503. [Google Scholar] [CrossRef]
- Reddy, M.J.; Singh, V.P. Multivariate modeling of droughts using copulas and meta-heuristic methods. Stoch. Environ. Rese. Risk Assess. 2014, 28, 475–489. [Google Scholar] [CrossRef]
- Mishra, A.; Singh, V.P.; Desai, V. Drought characterization: A probabilistic approach. Stoch. Environ. Res. Risk Assess. 2009, 23, 41–55. [Google Scholar] [CrossRef]
- Jacoby, G.C.; Cook, E.R. Past temperature variations inferred from a 400-year tree-ring chronology from Yukon Territory, Canada. Arct. Alp. Res. 1981, 13, 409–418. [Google Scholar] [CrossRef]
- Grissino-Mayer, H.D.; Fritts, H.C. The International Tree-Ring Data Bank: An enhanced global database serving the global scientific community. Holocene 1997, 7, 235–238. [Google Scholar] [CrossRef]
- Cook, E.R. A time series analysis approach to tree-ring standardization (Dendrochronology, Forestry, Dendroclimatology, Autoregressive process). Ph.D. Thesis, University of Arizona, Tucson, AZ, USA, 1985. [Google Scholar]
- California Data Exchange Center. Available online: http://cdec.water.ca.gov/index.html (accessed on 12 May 2015).
- Yevjevich, V. An objective approach to definitions and investigations of continental hydrologic droughts. In Hydrologic Paper; Colorado State University: Fort Collins, CO, USA, 1967. [Google Scholar]
- Kwak, J.; Kim, D.; Kim, S.; Singh, V.P.; Kim, H. Hydrological drought analysis in Namhan river basin, Korea. J. Hydrol. Eng. 2014, 19. [Google Scholar] [CrossRef]
- Serinaldi, F.; Grimaldi, S. Fully nested 3-Copula: Procedure and application on hydrological data. J. Hydrol. Eng. 2007, 12, 420–430. [Google Scholar] [CrossRef]
- Yu, K.X.; Xiong, L.; Gottschalk, L. Derivation of low flow distribution functions using copulas. J. Hydrol. 2014, 508, 273–288. [Google Scholar] [CrossRef]
- Wong, G.; Lambert, M.F.; Metcalfe, A.V. Trivariate copulas for characterization of droughts. ANZIAM J. 2008, 49, 306–315. [Google Scholar]
- Sadri, S.; Burn, D.H. Copula-based pooled frequency analysis of droughts in the Canadian Prairies. J. Hydrol. Eng. 2012, 19, 277–289. [Google Scholar] [CrossRef]
- Chen, Y.D.; Zhang, Q.; Xiao, M.; Singh, V.P. Evaluation of risk of hydrological droughts by the trivariate Plackett copula in the East River basin (China). Nat. Hazards 2013, 68, 529–547. [Google Scholar] [CrossRef]
- Saghafian, B.; Mehdikhani, H. Drought characterization using a new copula-based trivariate approach. Nat. Hazards 2014, 72, 1391–1407. [Google Scholar] [CrossRef]
- Black, P.E. Watershed Hydrology; John Wiley & Sons: Hoboken, NJ, USA, 1991. [Google Scholar]
- Hopfield, J.J. Neural networks and physical systems with emergent collective computational abilities. Proc. Natl. Acad. Sci. USA 1982, 79, 2554–2558. [Google Scholar] [CrossRef] [PubMed]
- Rosenblatt, F. The perceptron: A probabilistic model for information storage and organization in the brain. Psychol. Rev. 1958, 65, 386–408. [Google Scholar] [CrossRef] [PubMed]
- Battiti, R. Accelerated backpropagation learning: Two optimization methods. Complex. Syst. 1989, 3, 331–342. [Google Scholar]
- Gill, P.E.; Murray, W.; Wright, M.H. Practical Optimization; Academic Press: New York, NY, USA, 1981. [Google Scholar]
- Bourquin, J.; Schmidli, H.; van Hoogevest, P.; Leuenberger, H. Advantages of Artificial Neural Networks (ANNs) as alternative modelling technique for data sets showing non-linear relationships using data from a galenical study on a solid dosage form. Eur. J. Pharm. Sci. 1998, 7, 5–16. [Google Scholar] [CrossRef]
- Meko, D.M.; Therrell, M.D.; Baisan, C.H.; Hughes, M.K. Sacramento river flow reconstructed to AD 869 from tree rings. J. Am. Water Resour. Assoc. 2001, 37, 1029–1039. [Google Scholar] [CrossRef]
- Basheer, I.A.; Hajmeer, M. Artificial neural networks: Fundamentals, computing, design, and application. J. Microbiol. Methods 2000, 43, 3–31. [Google Scholar] [CrossRef]
- AghaKouchak, A. Entropy–Copula in Hydrology and Climatology. J. Hydrometeorol. 2014, 15, 2176–2189. [Google Scholar] [CrossRef]
- Saad, C.; El Adlouni, S.; St-Hilaire, A.; Gachon, P. A nested multivariate copula approach to hydrometeorological simulations of spring floods: The case of the Richelieu River (Québec, Canada) record flood. Stoch. Environ. Res. Risk Assess. 2015, 29, 275–294. [Google Scholar] [CrossRef]
- Rodriguez, J.C. Measuring financial contagion: A copula approach. J. Empir. Financ. 2007, 14, 401–423. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks: A Comprehensive Foundation, 2nd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 1999. [Google Scholar]
- Maier, H.R.; Dandy, G.C. Neural networks for the prediction and forecasting of water resources variables: A review of modelling issues and applications. Environ. Model. Softw. 2000, 15, 101–124. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Khandakar, Y. Automatic Time Series for Forecasting: The Forecast Package for R; Department of Econometrics and Business Statistics, Monash University: Melbourne, Australia, 2007. [Google Scholar]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Vogel, R.M.; Hosking, J.R.; Elphick, C.S.; Roberts, D.L.; Reed, J.M. Goodness of fit of probability distributions for sightings as species approach extinction. Bull. Math. Biol. 2009, 71, 701–719. [Google Scholar] [CrossRef] [PubMed]
- El Adlouni, S.; Ouarda, T.B. Joint Bayesian model selection and parameter estimation of the generalized extreme value model with covariates using birth-death Markov chain Monte Carlo. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Carle, D. Introduction to Water in California; University of California Press: Berkeley, CA, USA, 2004. [Google Scholar]
- Paulson, R.W.; Chase, E.B.; Roberts, R.S.; Moody, D.W. National Water Summary 1988–89: Hydrologic Events and Floods and Droughts (No. 2375); US Government Printing Office: Washington, DC, USA, 1991. [Google Scholar]
- Poulin, A.; Huard, D.; Favre, A.C.; Pugin, S. Importance of tail dependence in bivariate frequency analysis. J. Hydrol. Eng. 2007, 12, 394–403. [Google Scholar] [CrossRef]

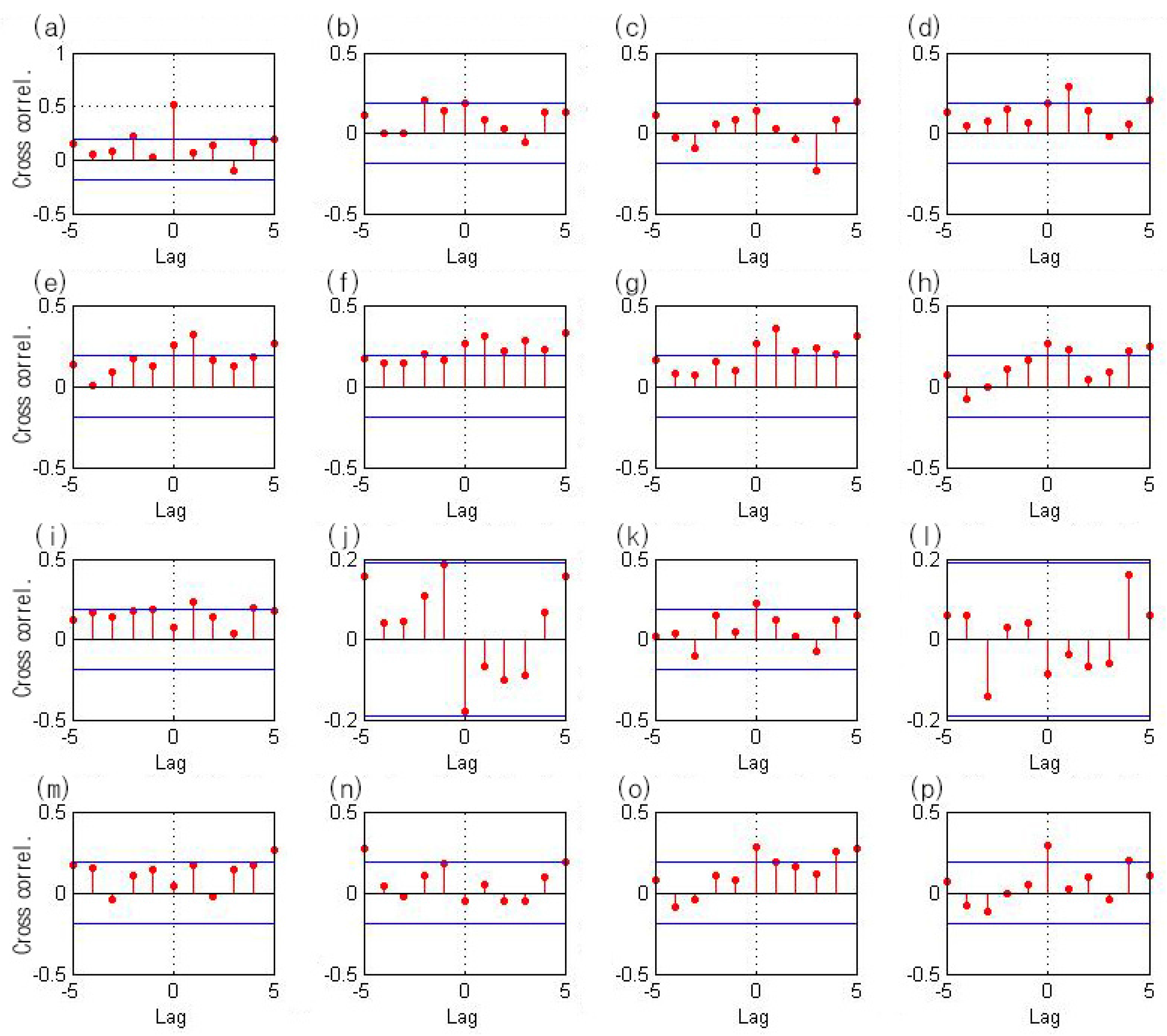

| Category | Index in Figure 1 | ID | Name | Site Location | Tree Ring Species | ||
|---|---|---|---|---|---|---|---|
| Lat (degree) | Lon (degree) | Height (EL.m) | |||||
| Tree ring sites | 7 | ANTEP | Antelope Lake | 40.15 | −120.6 | 1480 | Pinus jeffreyi Balf |
| 7 | ANTEP | Antelope Lake | 40.15 | −120.6 | 1480 | Pinus ponderosa Douglas ex C. Lawson | |
| 3 | CALAM | Calamity Creek | 43.98 | −118.8 | 1464 | Juniperus occidentalis Hook | |
| 6 | DALTON | Dalton Reservoir | 41.62 | −120.7 | 1531 | Pinus ponderosa Douglas ex C. Lawson | |
| 14 | DEVILS | Devil’s Dance Floor | 37.75 | −119.75 | 2084 | Pinus jeffreyi Balf | |
| 9 | DONNER | Donner Summit | 39.32 | −120.35 | 2265 | Pinus jeffreyi Balf | |
| 11 | FELKN | Felkner Ridge | 39.5 | −122.67 | 1494 | Pinus lambertiana Douglas | |
| 2 | FREDER | Frederick Butte | 43.58 | −120.45 | 1494 | Juniperus occidentalis Hook | |
| 5 | HAGER | Hager Basin Reservoir | 41.77 | −120.75 | 1524 | Juniperus occidentalis Hook | |
| 10 | HELLS | Hell’s Half Acre | 39.6 | −122.95 | 1922 | Pinus jeffreyi Balf | |
| 8 | LEMON | Lemon Canyon | 39.57 | −120.25 | 1859 | Pinus jeffreyi Balf | |
| 15 | PIUTE | Piute Mountain | 35.53 | −118.43 | 1975 | Pinus jeffreyi Balf | |
| 13 | SNOWHT | Snow White Ridge | 38.13 | −120.05 | 1731 | Pinus ponderosa Douglas ex C. Lawson | |
| 16 | SORREL | Sorrel Peak | 35.43 | −118.28 | 2011 | Pinus jeffreyi Balf | |
| 1 | SPRING | Spring Canyon | 44.9 | −118.93 | 1366 | Juniperus occidentalis Hook | |
| 4 | STEENS | Steens Mountain | 42.67 | −118.92 | 1656 | Juniperus occidentalis Hook | |
| 13 | STJOHN | St. White Mountain | 39.43 | −122.68 | 1555 | Pinus ponderosa Douglas ex C. Lawson | |
| Flow site | S | SBB | Sac. River, Abv bend bridge | 40.29 | –122.19 | 56.6 | - |
| F | FTO | Feather River, Oroville | 39.52 | –121.55 | 45.4 | - | |
| Y | YRS | Yuba River, Smartville | 39.24 | –121.27 | 85.3 | - | |
| A | AMF | American River, Folsom | 38.68 | –121.18 | 0 | - | |
| Copula Family | Copula func., | Generator func., | Parameter (α) |
|---|---|---|---|
| Clayton | |||
| Frank | |||
| Gumbel |
| Period | Mean (MAF) | Median (MAF) | Standard Deviation (MAF) | Skewness |
|---|---|---|---|---|
| Observed (1872–1977) | 18.9 | 17.6 | 7.8 | 0.8 |
| Reconstructed (1560–1871) | 20.4 | 19.8 | 9.6 | 0.6 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kwak, J.; Kim, S.; Kim, G.; Singh, V.P.; Park, J.; Kim, H.S. Bivariate Drought Analysis Using Streamflow Reconstruction with Tree Ring Indices in the Sacramento Basin, California, USA. Water 2016, 8, 122. https://doi.org/10.3390/w8040122
Kwak J, Kim S, Kim G, Singh VP, Park J, Kim HS. Bivariate Drought Analysis Using Streamflow Reconstruction with Tree Ring Indices in the Sacramento Basin, California, USA. Water. 2016; 8(4):122. https://doi.org/10.3390/w8040122
Chicago/Turabian StyleKwak, Jaewon, Soojun Kim, Gilho Kim, Vijay P. Singh, Jungsool Park, and Hung Soo Kim. 2016. "Bivariate Drought Analysis Using Streamflow Reconstruction with Tree Ring Indices in the Sacramento Basin, California, USA" Water 8, no. 4: 122. https://doi.org/10.3390/w8040122
APA StyleKwak, J., Kim, S., Kim, G., Singh, V. P., Park, J., & Kim, H. S. (2016). Bivariate Drought Analysis Using Streamflow Reconstruction with Tree Ring Indices in the Sacramento Basin, California, USA. Water, 8(4), 122. https://doi.org/10.3390/w8040122








