Abstract
Paute-Cardenillo (owned by Celec Ep-Hidropaute) is a dam with maximum height 135 m located in the Paute River in Ecuador. Its hydroelectric production will be integrated at the National Electric System of Ecuador with an installed capacity of 600 MW which will produce 3300 GWh per year. To evaluate the stability and safety of the structure, it is necessary to ascertain the shape and dimensions of the scour generated downstream from the dam. We studied the scour, due to the operation of the free surface spillway (700 m3/s) and half-height outlets (1760 m3/s), with three complementary procedures: empirical formulae obtained in models and prototypes, semi-empirical methodology based on pressure fluctuations-erodibility index and computational fluid dynamics simulations. The free surface weir could generate a scour around 21 m, while the intermediate outlet could reach the intact rock, located 34 m below the initial river bed. A pre-excavated basin is proposed and the velocities and pressures are analyzed. The results demonstrated the suitability of combining different methodologies to achieve an adequate resolution of this complex phenomenon.
1. Dam Characteristic
The Paute-Cardenillo Dam, located in Ecuador, is a double curvature arch dam with a maximum height of 135 m to the foundations (Figure 1a). Considering as the reference the Universal Transverse Mercator (UTM) system with the projection PSAD 56 (Provisional South American Datum 1956) corresponding to area 17 of the Southern Hemisphere, the top level is 926 meters above mean sea level (MASL), while the normal maximum water level is 924 MASL. The river bed consists of a layer of 24 m of alluvial, below which there is a layer of 10 m of weathered rock (Figure 1b). Table 1 shows the particles characteristics size of the alluvial (24 m) and the weathered rock (10 m) in the Paute River.
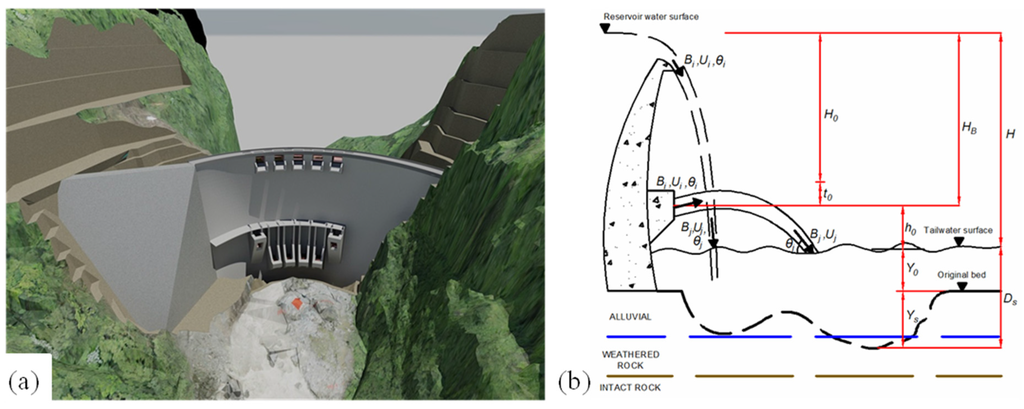
Figure 1.
Paute-Cardenillo Dam (a) Three-dimensional view; (b) Scheme of scour.

Table 1.
Particles characteristic size of the bed material.
The dam has a free surface weir controlled by five folded gates (7.20 m × 5.60 m) designed to spill a flow of Q4 = 700 m3/s (return period TR = 4 years) and a half-height outlet with two almost symmetrical ducts (5.00 m × 5.80 m). Considering the maximum normal operating level (924 m), the intermediate outlet design flow is Q40 = 1760 m3/s (return period TR = 40 years). Hence, the total design flow of the weir and half-height outlet is Q100 = 2340 m3/s (return period TR = 100 years). The bottom outlet consists of four radial gates (5.00 m × 6.80 m). According to Consorcio PCA [1], the total discharge capacity of the dam is Q10000 = 5520 m3/s (return period TR = 1000 years).
2. Empirical Formulae
We estimated the scour hole for flows of various return periods. In the study, we examined 31 formulae. Some of the classical formulae are Schoklitsch [2], Veronese-B [3], Eggenberger [4]. A number of more recent formulae were also considered, such as: Taraimovich [5], INCYTH [6], Mason [7], Liu [8], Bombardelli and Gioia [9], Suppasri [10], and Pagliara et al. [11]. Most of the equations were obtained by dimensional and statistical analysis of data obtained in Froude scale reduced models, with few formulae based on prototypes and many obtained for the ski-jump.
As discharge is produced by a free surface weir and in pressure conditions by an intermediate outlet, we modified the general expression which provides the following simplified general expression:
where Ds is the scour depth below tailwater level, Y0 the tailwater depth, Ys the scour depth below the original bed, Γ an experimental coefficient, q the specific flow, Hn the net energy head, g the gravitational acceleration, and d the characteristic size of bed material.
In Equation 1 and in Figure 1b, x, y, z, v and w are empirical exponents defined by regression or optimization, t0 the energy loss in the duct, Hn = H0 = HB − t0 the net energy head at the exit of the outlet, H the falling height from reservoir level to tailwater level (ski-jump and free surface weir), h0 the vertical distance between the outlet exit and the tailwater level, Bi, Ui, θi the thickness, velocity and angle of the jet in initial condition, Bj, Uj, θj the total thickness, velocity and angle of the jet in the impingement conditions.
After considering the results obtained with the 31 formulae, the equations whose values were out of the range of the mean value ± 1 standard deviation were not considered when recalculating the mean value and the standard deviation. This filtering process was repeated twice. Table 2 and Table 3 show the coefficients corresponding to five simplified and general formulae whose scour values fall in the range of the mean value ± 1 standard deviation at each specific flow rate.

Table 2.
Coefficients of five simplified scour formulae.

Table 3.
Five general scour formulae.
Figure 2 shows the results obtained for the free surface weir. We indicated the range of the mean value ± 1 standard deviation. The maximum scour that is possible to simulate is until the weathered rock depth (total scour 34 m) because the intact rock represents a rigid boundary condition in the empirical formulae of scour. Considering the mean value for the design flow (700 m3/s), the scour could reach a depth of 17 m. However, taking into account the mean value + 0.50 standard deviation, then the design flow fully penetrates the alluvial (scour 24 m). Considering the mean value + 1 standard deviation, the design flow could reach the intact rock layer (scour 34 m).
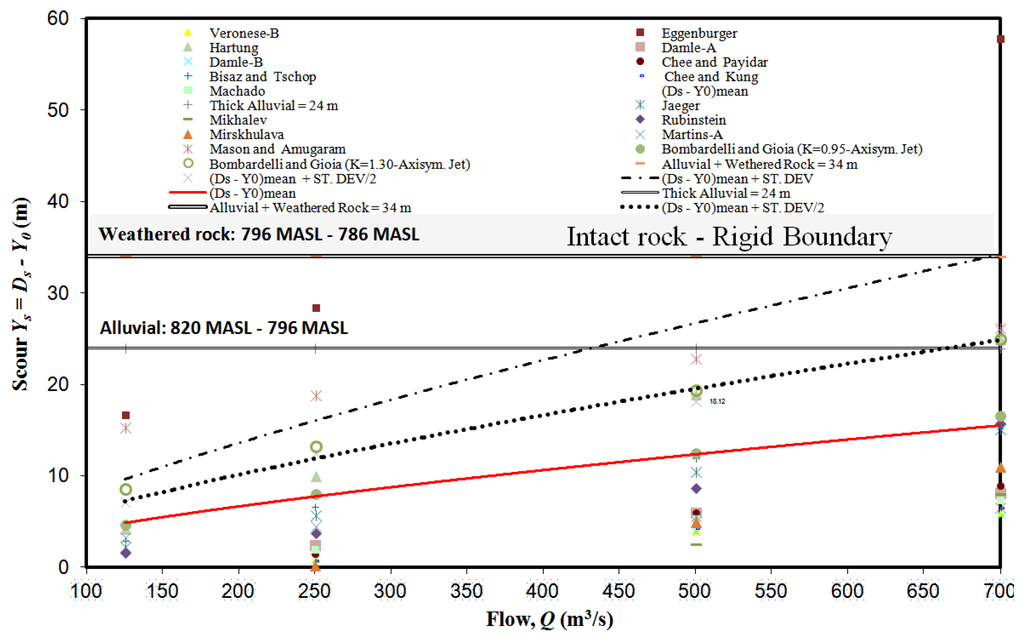
Figure 2.
Scour of alluvial and weathered rock for the free surface weir.
Figure 3 shows the results obtained for the half-height outlet. The range of the mean value ± 1 standard deviation and 0.50 standard deviation are indicated. For mean values the jet would scour the alluvial layer (24 m) with a return period flow Q22 = 1320 m3/s. The design flow (Q40 = 1760 m3/s) would penetrate over 32 m and not reach the intact rock. However, with the mean value + 0.50 standard deviation, the flow of 1550 m3/s would already completely erode the weathered rock layer (scour 34 m).
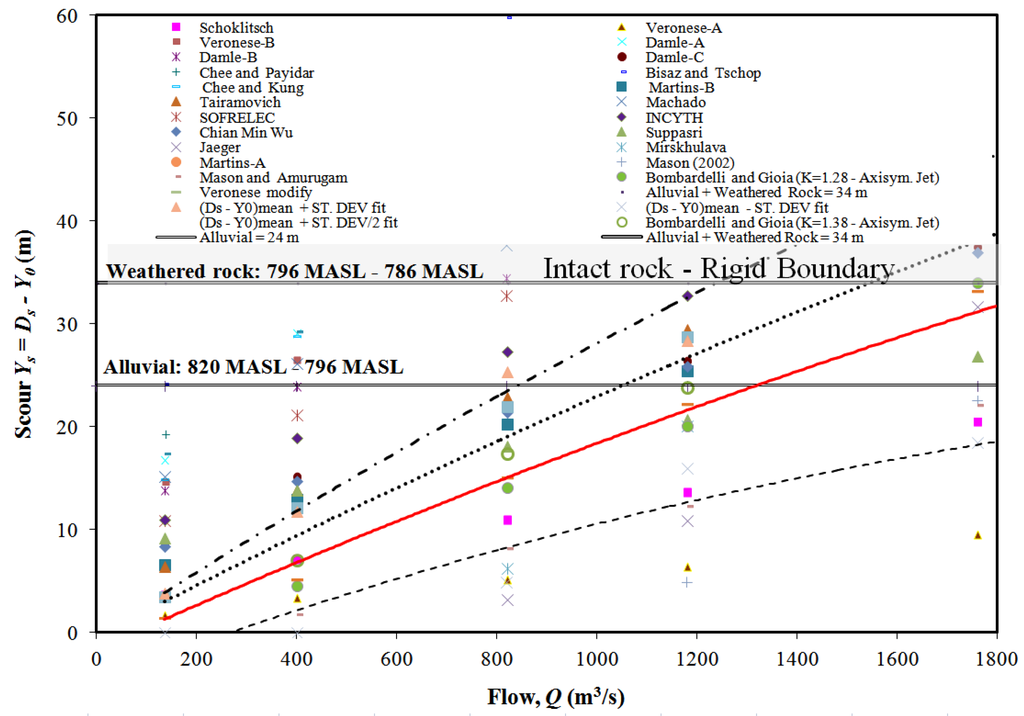
Figure 3.
Scour of alluvial and weathered rock for the half-height outlet.
3. Semi-Empirical Methodology
The erodibility index is based on an erosive threshold that relates the magnitude of relative erosion capacity of water and the relative capacity of a material (natural or artificial) to resist scour. There is a correlation between the stream power or magnitude of the erosive capacity of water (P) and a mathematical function [f(K)] that represents the relative capacity of the material to resist erosion.
Scour in turbulent flow is not a shear process. It is caused by turbulent and fluctuating pressures. Quantification of pressure fluctuations of incident jets in stilling basins has been studied mainly by Ervine and Falvey [20], Ervine et al. [21], Castillo [22], Castillo et al. [23], Bollaert and Schleiss [24], Castillo and Carrillo [25,26], and Castillo et al. [27,28]. Some of the main results of these papers have been included in FEMA [29].
The dynamic pressures of jets are a function of the turbulence intensity at the discharge conditions, length of the jet flight, diameter (circular jet) or thickness (rectangular jet) in impingement jet conditions, and water cushion depth. Annandale [30,31] summarized and established a relationship between the stream power and the erodibility index for a wide variety of materials and flow conditions. Stream power per unit of area available of an impingement jet is:
where γ is the specific weight of water, Q the flow discharge, H the fall height or the upstream energy head (see Figure 1b), and A the jet area on the impact surface. The jet area was estimated using the equations of the impingement jet thickness for the free falling jet case [27,28], in which the falling distance and the specific flow are considered.
The impingement jet thickness formula is obtained as:
where Bg is the thickness due to gravity effect, ξ the jet lateral spread distance due to the turbulence effect, q the specific flow, H the fall height, and h is the energy head at the crest weir. φ = KφTu, with Tu being the turbulence intensity and Kφ an experimental parameter (1.14 for circular jets and 1.24 for the three-dimensional nappe flow case).
The erodibility index is defined as:
where Ms is the number of resistance of the mass, Kb the number of the block size, Kd the number of resistance to shear strength on the discontinuity contour, and Js the number of structure relative of the grain.
The threshold of rock strength to the stream power, expressed in kW/m2, is calculated and based on the erodibility index K.
Table 4 and Table 5 show the formulae of the parameters and the values of the different variables considered and their respective calculus. The values of the different variables were obtained from the geotechnical study of the Paute-Cardenillo Dam [32].

Table 4.
Erodibility indexes parameters (adapted from Annandale [31]).

Table 5.
Semi-empirical methodology. Input and calculated values.
The dynamic pressure in the bottom of the stilling basin is based on two components: the mean dynamic pressure (Cp) and the fluctuating dynamic pressure (Cp'). We can use these dynamic pressure coefficients as estimators of the stream power reduction coefficients, by the effect of the jet disintegration in the air and their diffusion in the stilling basin (Annandale [31]). Hence, the dynamic pressures are also a function of the fall height to disintegration height ratio (H/Lb) and water cushion to impingement jet thickness (Y/Bj). Thus, the total dynamic pressure can be expressed as:
where Cp(Y/Bj) is the mean dynamic pressure coefficient, Cp'(Y/Bj) the fluctuating dynamic pressure coefficient, Pjet the stream power per unit of area, and F the reduction factor of the fluctuating dynamic pressure coefficient. In the rectangular jet case (nappe flow), Castillo et al. [27] adjusted the formulae to calculate the disintegration height (Lb), and the mean and fluctuating dynamic pressure coefficients (Cp and Cp', respectively) by using new laboratory data (see Figure 4, Figure 5 and Figure 6). These formulae were used to estimate the Ptotal value.
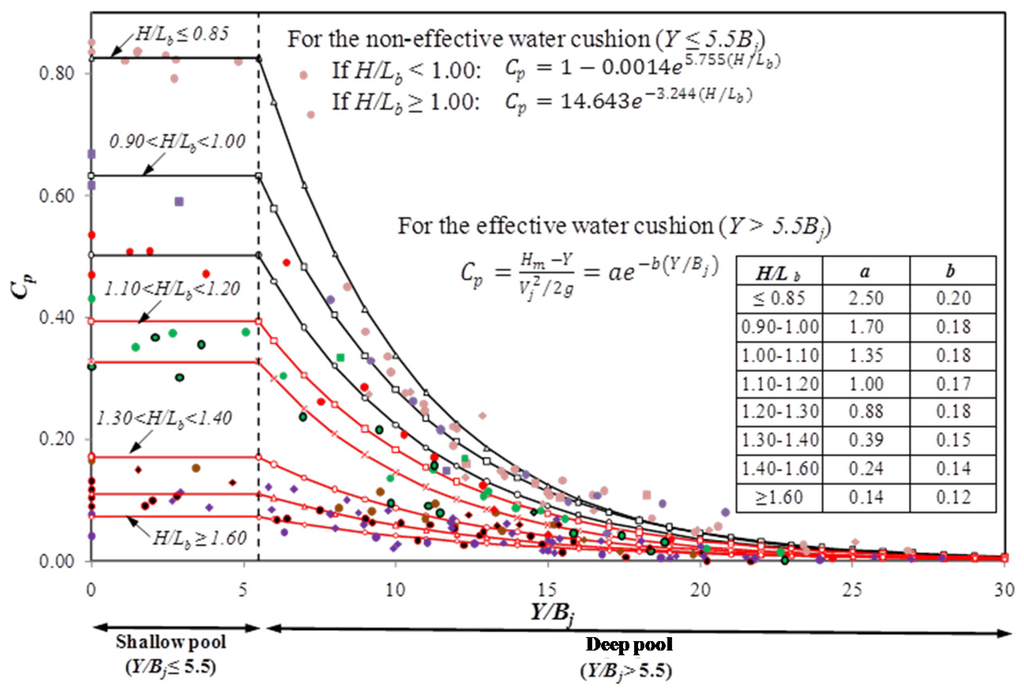
Figure 4.
Mean dynamic pressure coefficient (Cp) for the nappe flow case in function of ratios Y/Bj and H/Lb (Castillo et al. [27]).
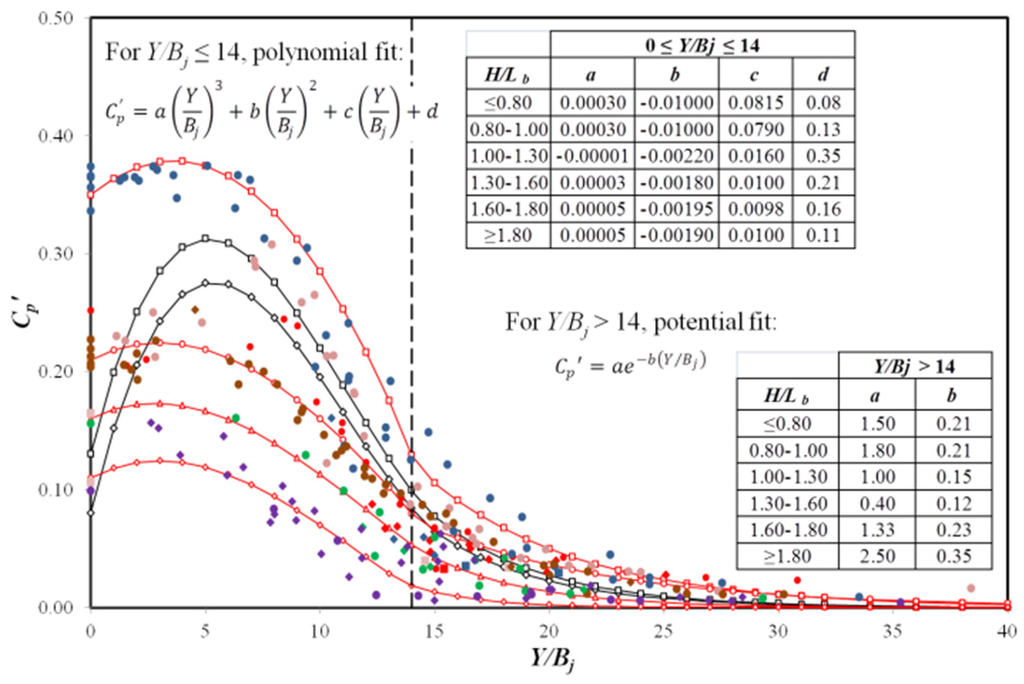
Figure 5.
Fluctuating dynamic pressure coefficient (Cp') for the nappe flow case in function of ratios Y/Bj and H/Lb (Castillo et al. [27]).
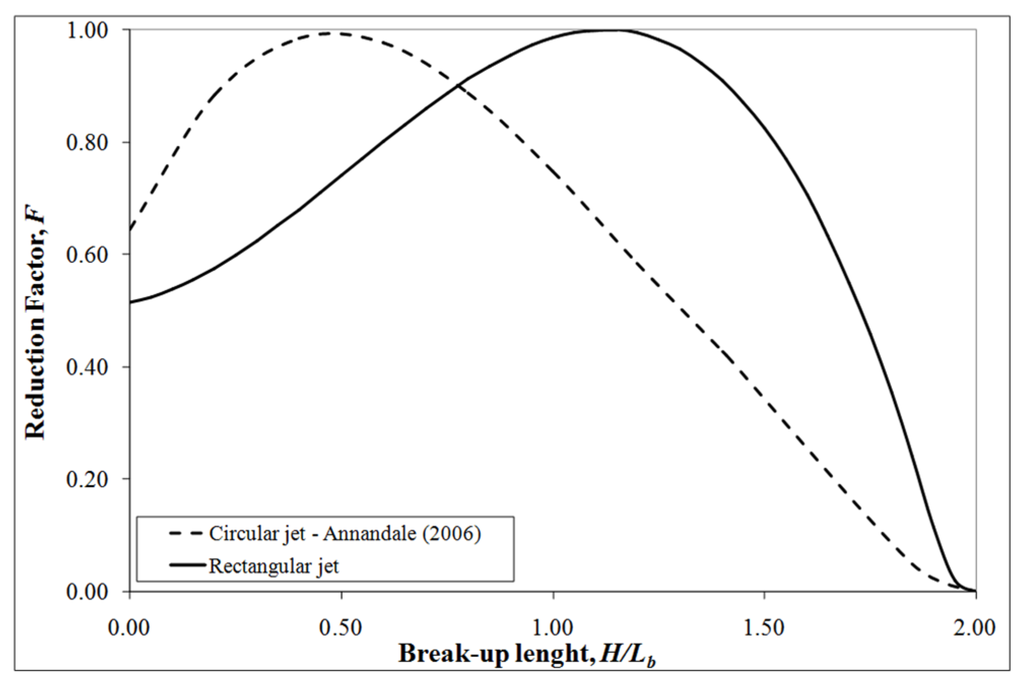
Figure 6.
Reduction factor F of fluctuating dynamic pressure coefficient in function of ratio H/Lb and the jet type (Castillo et al. [27]).
Table 6 shows the results obtained in the three types of material existent in the place of the dam and considering a concrete slab of 20 MPa characteristic strength.

Table 6.
Values of the parameters to estimate the Erodibility Index (K) and then the Power Threshold (Prock) for bed layers (water cushion depth Ds = 24 m).
In Figure 7 the stream power of the free surface weir jet is indicated, together with the power threshold of alluvial, weathered and intact rock. Considering a water cushion depth Ds = 24 m (tailwater depth Y0 = 6 m), the flow rate of 500 m3/s would have the power to erode the weathered rock, although the design flow of 700 m3/s, would not have enough power to reach the intact rock. This confirms that the maximum scour of the free surface weir could be near to Ds = 26 m (alluvial 20 m, tailwater depth Y0 = 6 m).
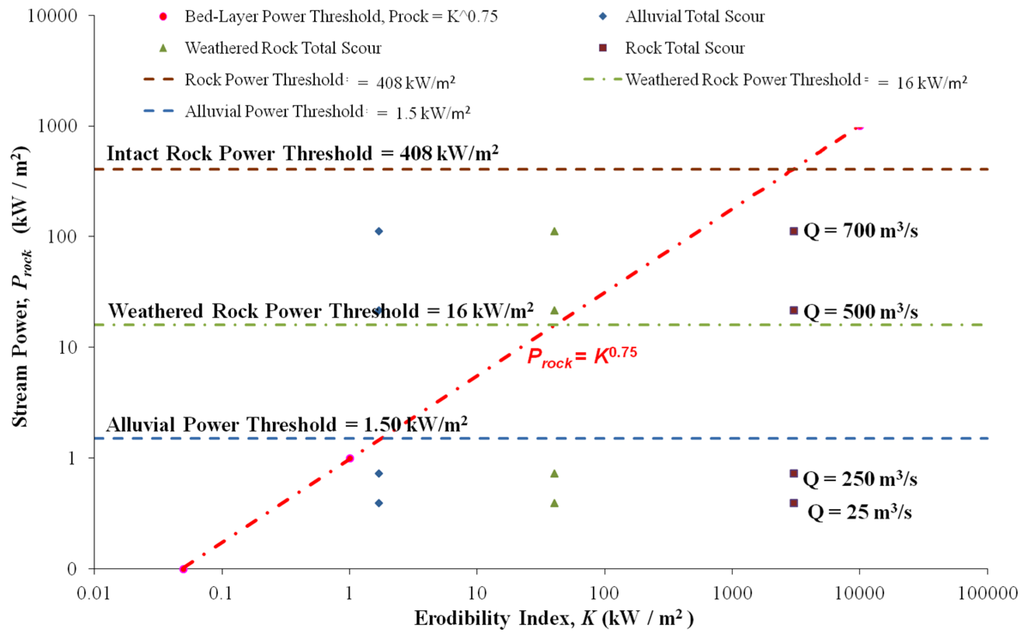
Figure 7.
Stream power of the jet for different flows as a function of the erodibility. Alluvial, weathered rock and intact rock indexes (Ys = 18 m, Y0 = 6 m) for the free surface weir.
We can observe that the half-height outlet case does not correspond strictly with the circular nor rectangular (nappe flow) jet case. For circular jets, the Cp and Cp' are valid for H/Lb ≤ 0.50 (Ervine et al. [21]). However, for the design flow (Q40 = 1760 m3/s) the H/Lb = 1.67. For this reason the calculations in Figure 8 were carried out using the rectangular jet analogy.
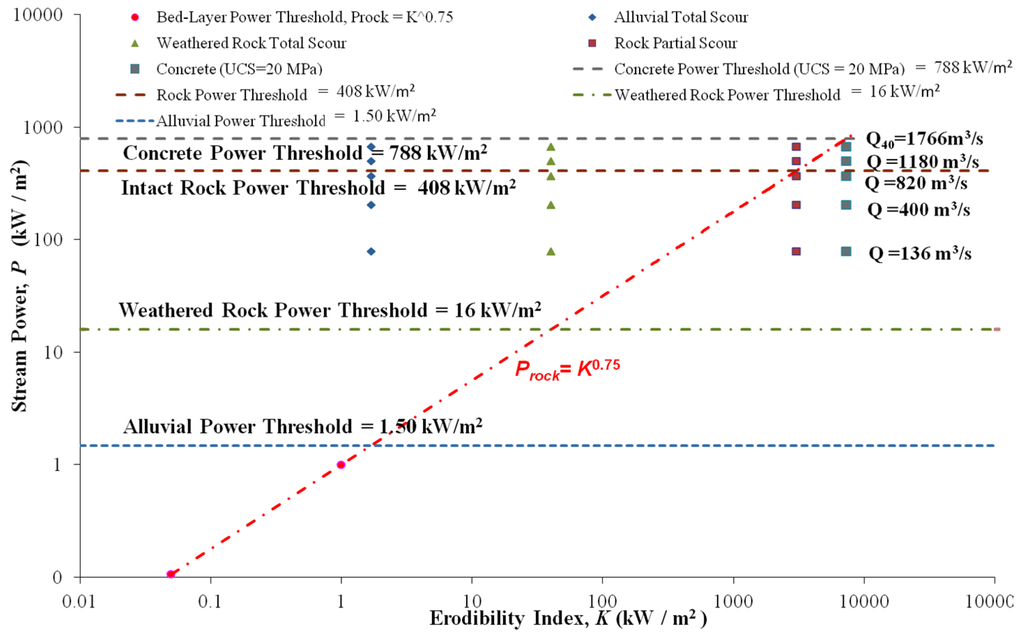
Figure 8.
Stream power of the jet for different flows as a function of the erodibility. Alluvial, weathered rock and intact rock indexes (Ys = 18 m, Y0 = 6 m) for the half-height outlet.
The stream power threshold of weathered rock (Pweathered_rock = 16 kW/m2) does not resist the flow of the annual return period (Qma = 136 m3/s). The intact rock stream power (Prock = 408 kW/m2) could resist up to a flow return period of 5 years (Q5 = 820 m3/s). The Q10 = 1180 m3/s would exceed the intact rock strength, while the design flow reaches a significant scour in the intact rock. As a solution to the scour, a concrete slab of 20 MPa characteristic strength and thickness of 2 m (Pconc = 788 kW/m2) is placed directly on the alluvial level (796 MASL). The geometry of the pre-excavated basin should be similar to the geometry of the basin that would be formed with the flow Q40 = 1766 m3/s. Figure 8 indicates that the concrete slab would resist the power stream of the design flow (Pjet = 666 kW/m2).
4. Numerical Simulation
As a complement of the empirical and semi-empirical methodologies, we carried out three-dimensional mathematical model simulations. These programs allow a more detailed characterization and, thus, a detailed study of local effects of the sediments transport. We used the Computational Fluid Dynamics (CFD) program FLOW-3D. It solves the Navier-Stokes equations discretized by finite differences and incorporates various turbulence models, a sediment transport model (Meyer-Peter and Müller, [33]) and an empirical model of bed erosion (Mastbergen and Von den Berg [34]; Brethour and Burnham [35]), together with a method for calculating the free surface of the fluid without solving the air component TrueVOF™ (Hirt and Nichols [36]).
In order to simulate the proper functioning of the free surface weir, we carried out several simulations by means of sensitivity analysis: air entrainment models, turbulence models, mesh size and type of solver, among others (Castillo and Carrillo [25,26]). We compared pressures obtained in the stagnation point and their associated mean dynamic pressure coefficients with the parametric methodology. Principal data for the analysis were q = 19.44 m2/s and H = 120.00 m. With these data, the calculated impingement jet thickness was Bj = 1.46 m.
During the mesh size sensitivity analysis [25,26], we obtained the most accurate results by using a mesh size of 0.20 m. In the solver options, we selected the stability and convergence method and the free surface solved with the split Lagrangian method. Table 7 compares the mean pressure and the mean dynamic pressure coefficient obtained by the non-effective water cushion case, while Figure 9 shows the pressure signal calculated on the stagnation point with FLOW-3D and the mean value of the register.

Table 7.
Comparison of pressures and Cp for the free surface weir, considering a water cushion Y0 = 2 m (Castillo and Carrillo [25,26]).
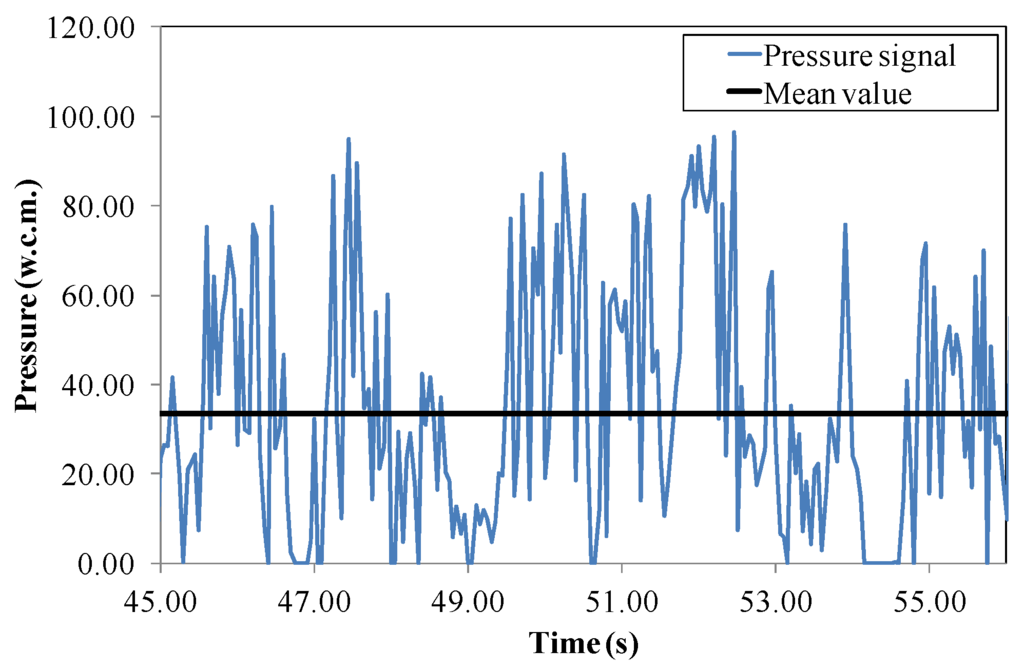
Figure 9.
Pressure signal on the stagnation point for the free surface weir calculated with FLOW-3D, considering a water cushion Y0 = 2 m.
The simulations of the half-height outlet were easier to perform, due to the size of the ducts and the falling jets. The sensitivity analysis was performed in a similar way as with the free surface weir [25,26]. The study showed that with a mesh size of 1.00 m (Figure 10), pressures on the bottom of the plunge pool were almost similar to the parametric methodology.
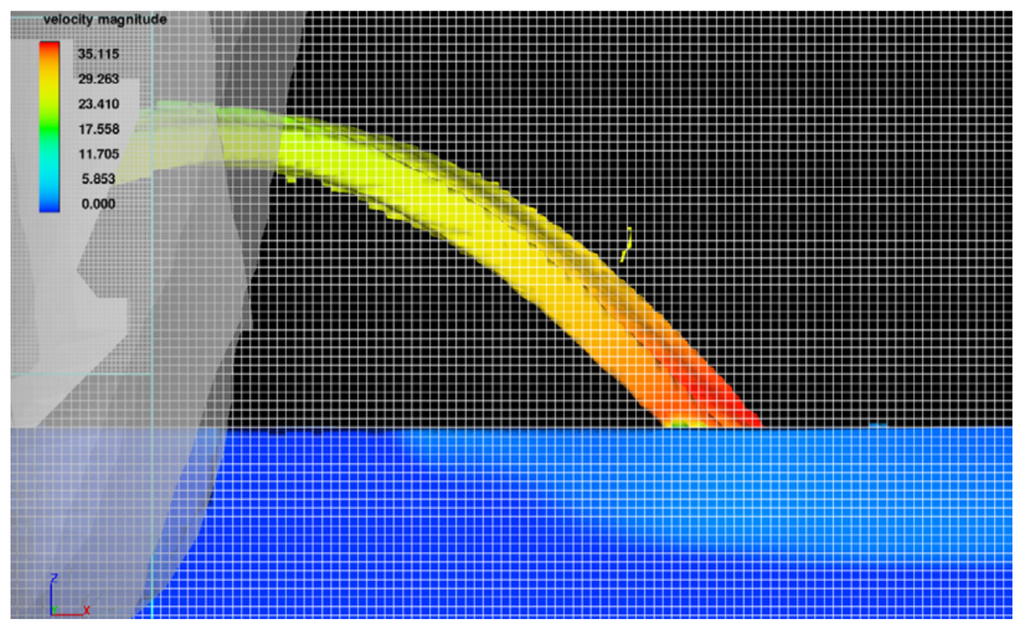
Figure 10.
Mesh size of the half-height outlet simulations.
The sediment scour model of FLOW-3D estimates the motion of sediment flow by predicting the erosion, advection and deposition of sediment. This is done by considering two states in which sediment can exist: suspended and packed sediment. Suspended sediment is typically of low concentration and advects with fluid flow. Packed sediment exists in the computational domain at the critical packing fraction (we used value 0.70 considering the existing field data). Only a thin surface layer of grains of the packed sediment can move in the form of bed-load transport.
Suspended sediment is transported by advection along with the fluid. FLOW-3D assumes there are totally N sediment species. The transport equation for each sediment species i is:
where cs,i is the concentration of the suspended sediment, in units of mass per unit volume and is the mean velocity of the fluid-sediment mixture. The momentum balances for each sediment species and the fluid-sediment mixture are:
where us,i is the velocity of sediment species i; ρs,i the density of the sediment species i; fs,i the volume fraction of sediment species i; Pr the pressure; Ki the coefficient of quadratic drag for species i; F includes body and viscous forces; ur,i is the relative velocity between the velocity (us,i) of sediment species i and the fluid velocity (uf), and is density of fluid-sediment mixture.
Subtracting Equation (8b) from Equation (8a) gives
where udrift,i = us,i − is the velocity needed to compute the transport of sediment due to drift. Assuming that the motion of the sediment is nearly steady at the scale of the computational time and that the advection term is small (i.e., for small drift velocity udrift), the result of Equation (9) is
where Ki is the drag function and combines shape drag and Stokes drag (Flow Science [37]). The correction to account for particle/particle interactions is an experimentally determined relation referred to as the Richardson-Zaki [38] correlation. Table 8 shows the principal relations to calculate the sediment scour model in FLOW-3D.

Table 8.
Principal relations to calculate the sediment scour model in FLOW-3D.
Sediment is entrained by the picking up and re-suspension of packed sediment due to shearing and small eddies at the packed sediment interface. The empirical model used in FLOW-3D is based on Mastbergen and Von den Berg [34]. The first step to computing the critical Shields number is calculating the dimensionless parameter and from this, the dimensionless critical Shields parameter is computed using the Soulsby-Whitehouse equation (Soulsby [39]). The critical Shields parameter can be modified for sloping surfaces to include the angle of repose. The local Shields number is computed based on the local shear stress, τ. It is assumed that the Nikuradse roughness of the bed surface is proportional to the local mean grain diameter in packed sediment: ks = crough d50,packed. We used the default value of the proportional constant crough = 1.0. The entrainment lift velocity of sediment is then computed with Mastbergen and Von den Berg expression and as a function of the dimensionless particle diameter, (see Table 8). The entrainment velocity ulift,i is then used to compute the amount of packed sediment that is converted into suspended sediment, effectively acting as a mass source of suspended sediment at the packed bed interface. Once converted to suspended sediment, the sediment subsequently advects and drifts.
Bed-load transport is the sediment transport due to rolling or bouncing over the surface of the packed bed of sediment. The model currently used in FLOW-3D is from Meyer-Peter and Muller [33]. This model predicts the volumetric flow of sediment per unit width over the surface of the packed bed:
where the typical value of (Van Rijn [40]) and which has been used in our different simulations (5 and 13 for low and high sediment transport, respectively). Φi is related to the volumetric bed-load transport rate per unit width, qbi. The bed-load thickness of the saltating sediment is estimated with the Van Rijn [40] relation (see Table 8). To compute the motion of the sediment in each computational cell, the value of qb,i is converted into a velocity by . The direction of the motion is determined from the motion of the liquid adjacent to the packed bed interface. Therefore, the volumetric flux is , where is the direction of the fluid-sediment mixture adjacent to the packed interface, and the resulting bed-load velocity, ubedload,i, is used to transport the packed sediment.
Settling and entrainment of grains are opposite processes and often occur at the same time. In the 3D scour model, the settling velocity is related to the drift velocity near bed as ; where ns is the outward pointing normal to the packed bed interface.
The model in FLOW-3D v.11.1 is fully coupled with fluid flow. The fundamental difference from the previous version is that the packed bed is described by the FAVORTM technique. At each time step, area and volume fractions describing the packed sediments are calculated throughout the domain. However, the maximum size of the particle that this version can manage is over 35 mm (Flow Science [37]). For this reason, simulations were carried out in a Froude similitude scale 1:50 and the results transformed to prototype scale. The model had 4,159,233 cells and the scour reached the steady state after 60 s of simulation. With this setting, the time required to solve the problem was approximately 26.00 days in an Intel(R) Core(TM) i7-2600 CPU @3.40 GHz processor and 24.0 GB RAM.
In Figure 11 we can observe the scour obtained with the CFD simulation. Scour depth was 21 m, which is greater than the calculated with the mean value of the empirical formulae (17 m) and similar to the semi-empirical methodology (~ 20 m).
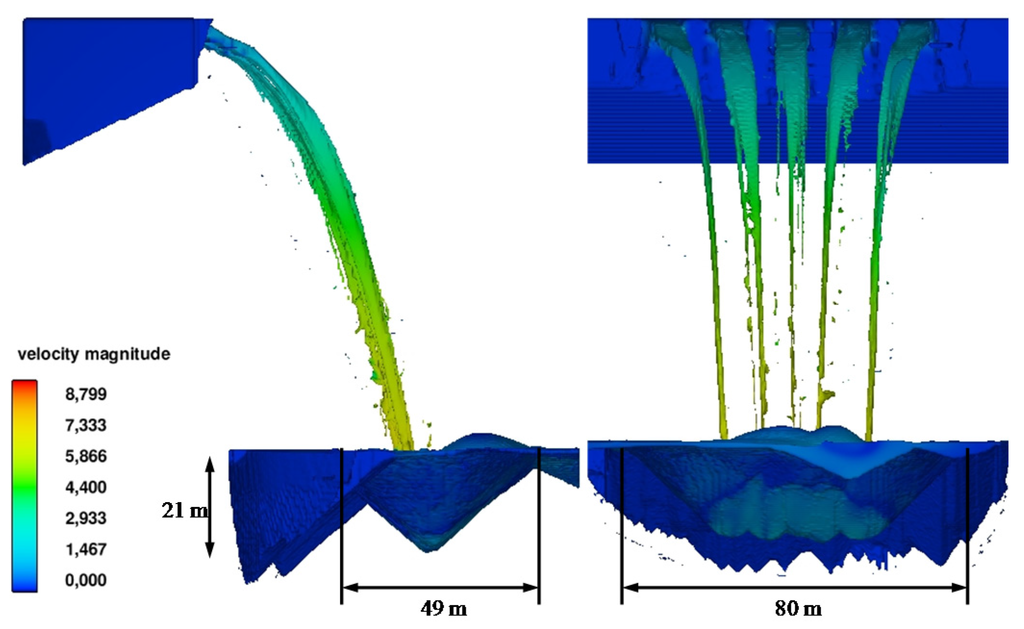
Figure 11.
Scour bowl due to the free surface weir jet. Bilayer simulation: alluvial 24 m and weathered rock 10 m (Units in m/s. Froude scale 1:50. Prototype impingement velocity = 6.1 × 501/2 = 43.13 m/s).
However this value is a maximum threshold of scour because 1:50 scale modeling contains scale effects that are difficult to quantify.
To simulate the half-height outlet (two rectangular ducts of 5.00 m × 5.80 m), the selection of the mesh size is a function of their dimensions and of the thickness of the falling jets. Figure 12 shows the scour shape and size simulated considering bilayer material (alluvial 24 m and weathered rock 10 m).
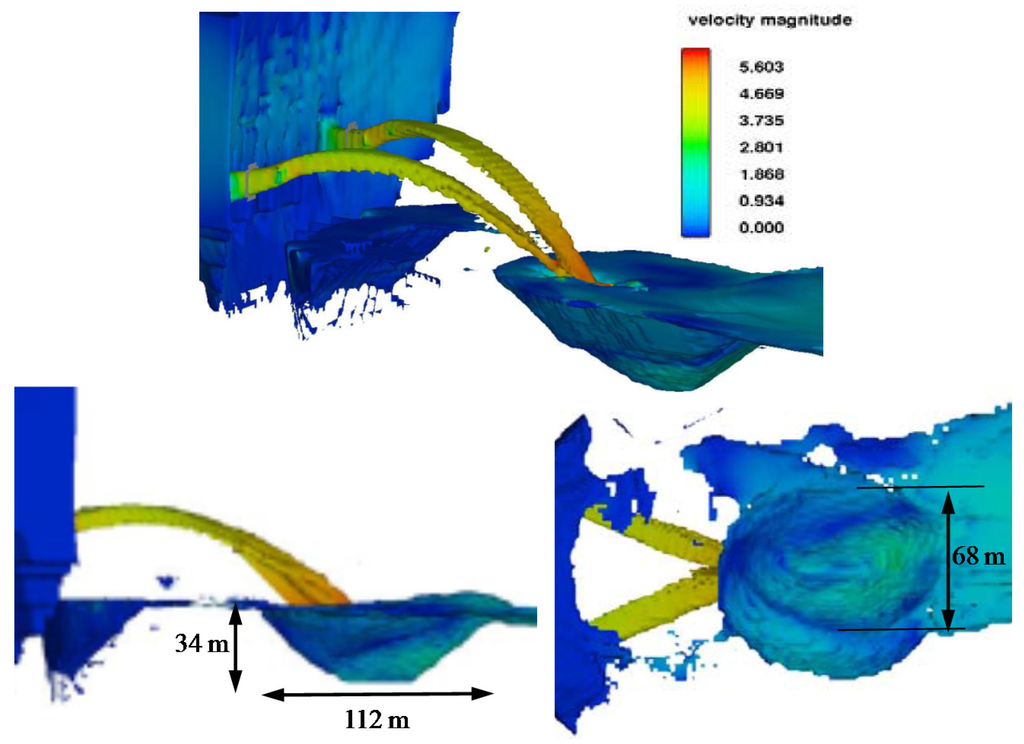
Figure 12.
Scour bowl due to the half-height outlet. Bilayer simulation: alluvial 24 m and weathered rock 10 m. (Units in m/s. Froude scale 1:50. Prototype impingement velocity = 5.4 × 501/2 = 38.18 m/s).
The mesh consisted of hexahedral elements of 0.02 m (equivalent to 1.00 m in prototype scale using the Froude similitude). The inlet boundary condition considered the flow and the water height in the design condition, and outflow condition in the downstream condition. The domain consisted in 2,177,770 active cells. The time-step size was controlled by stability and convergence criteria. Pressures obtained in the stagnation point and their associated mean dynamic pressure coefficients were compared with the parametric methodology. After 50 s of simulation (4.75 × 106 s of CPU, 7.2 days of elapsed time), the maximum scour depth reached the intact rock (34 m). This value is a bit bigger than that obtained with the mean value adjustment of the empirical formulae (32 m), is equal to the mean value + 0.50 standard deviation (34 m), and a bit smaller than the semi-empirical methodology whose value was greater than 34 m (alluvial 24 m, weathered rock 10 m and intact rock > 2 m).
Table 9 summarizes the maximum scour obtained by the free surface weir and by the half height outlets when the design flow is considered.

Table 9.
Comparison of scour obtained by different methods for free surface weir and half-height outlet.
For the empirical formulae, three values have been considered: the mean value of the 31 formulae considered (Ys), the mean value + 0.50 standard deviation (Ys + 0.50 SD), and the mean value + 1 standard deviation (Ys + SD). The scour obtained with the different methodologies are in agreement.
As far as the numerical simulation is concerned, the scour shape was analyzed considering the intact rock as non-erodible. The upstream face of the scour occurred approximately 85 m downstream from the dam. The plant scour was nearly 112 m long and 68 m wide.
Considering the place of the dam, the scour would reach the left natural slope and could cause landslides. A pre-excavated stilling basin shape has been proposed in order to adjusted to the geometry and the space available (Figure 13). In Figure 14 we can observe that the free surface weir jets are disintegrated in impingement conditions (H/Lb = 1.31 according to lab measurements). The velocities reach 43 m/s and are reduced to 6 m/s by diffusion in the water cushion. The instantaneous pressures on the bottom reach 28 m and correspond to hydrostatic pressure of the water cushion.
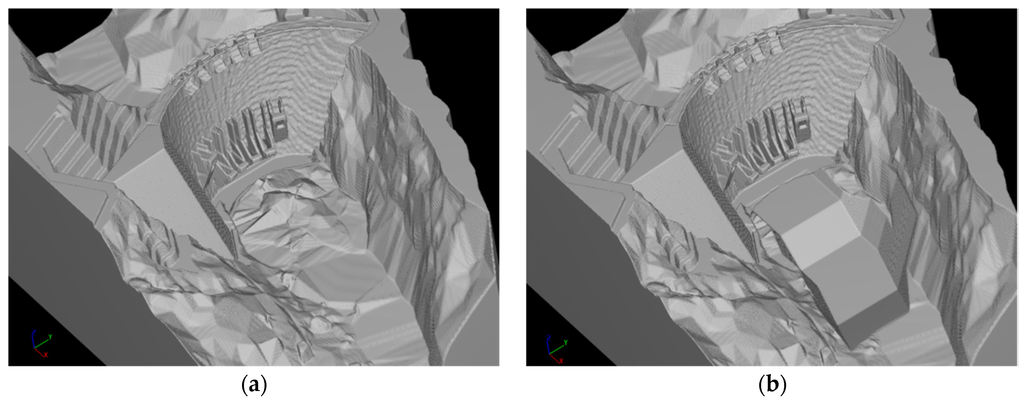
Figure 13.
Pre-excavated basin. (a) Initial condition; (b) geometry proposed.
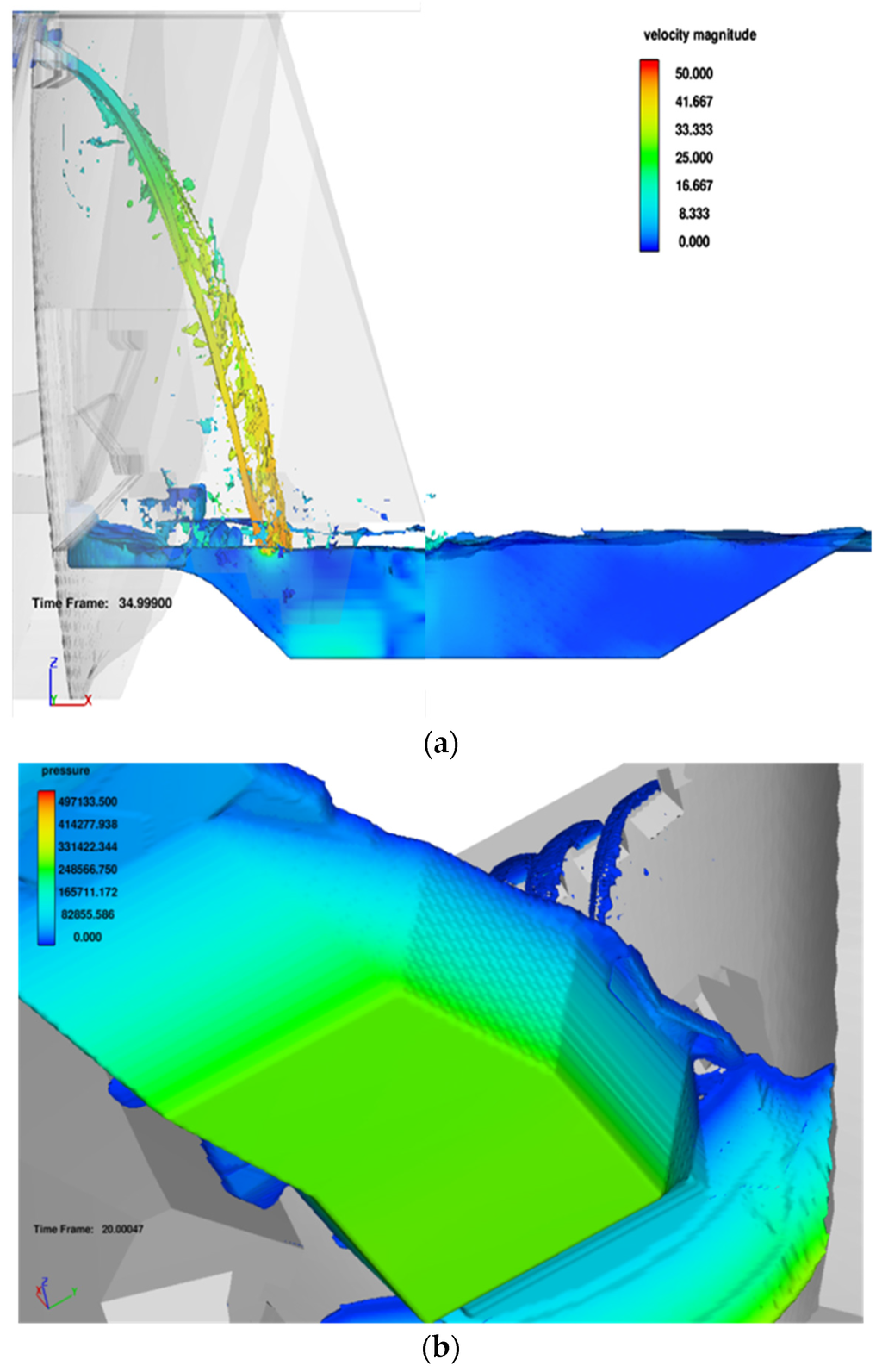
Figure 14.
Lateral and spatial views of the free surface weir jets in the air and in the pre-excavated stilling basin (Prototype scale. Units in m/s and in Pascal): (a) Velocities; (b) Pressures (Q = 700 m3/s).
For the half-height outlets, the velocities in spatial and lateral views are shown (Figure 15). The high velocity of the impingement jet is reduced by diffusion effect in the water cushion to 20 m/s. We can observe that there is very strong flow recirculation of vertical and horizontal axis. At the end of the pre-excavated stilling basin velocity is reduced to around 6 m/s.
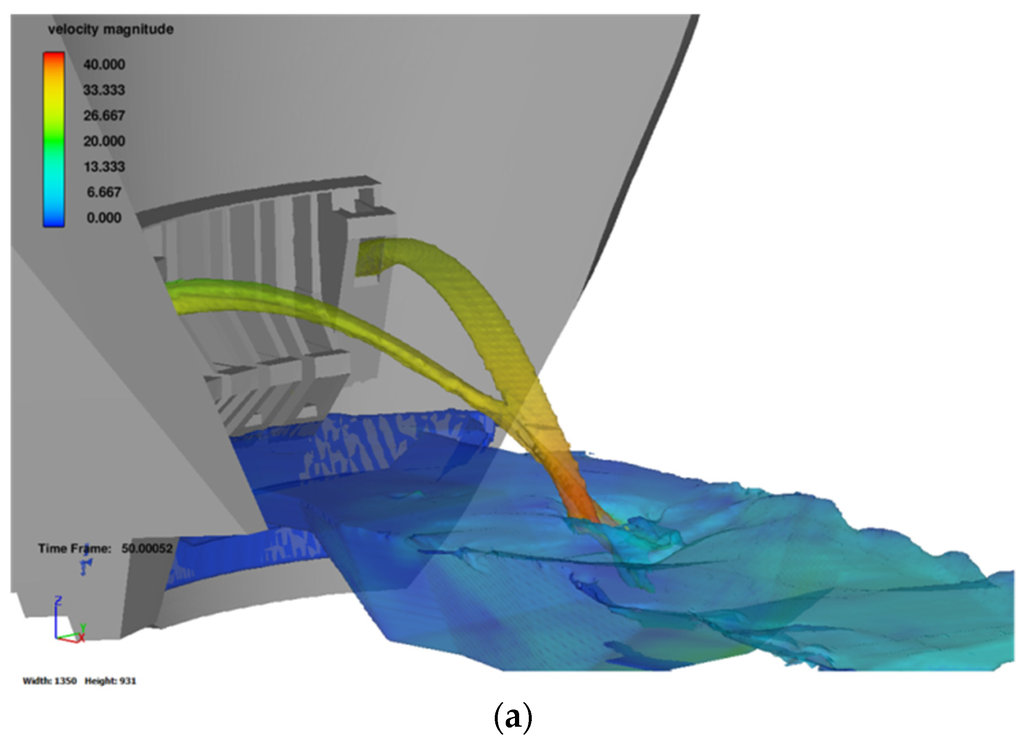
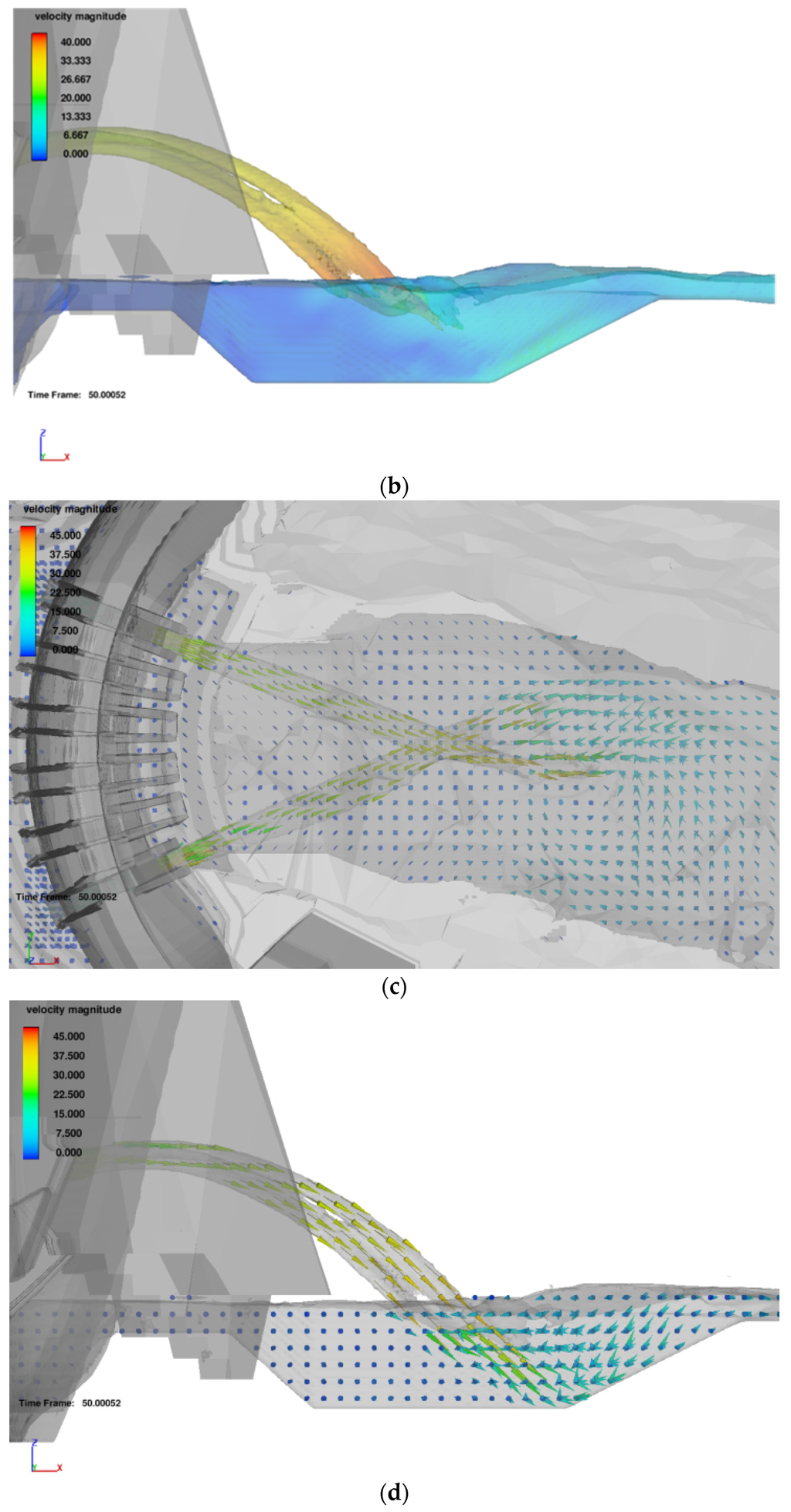
Figure 15.
Flow velocity in the air and in the pre-excavated stilling basin (Prototype scale. Units in m/s): (a) Spatial view of the half-height outlet; (b) Lateral view of the half-height outlet; (c) Top view of the velocity vectors with the half-height outlet; (d) Lateral view of the velocity vectors with the half-height outlet.
Figure 16 shows the total pressures in the pre-excavated stilling basin when the two ducts of the half-height outlet are working (Q = 1760 m3/s) and when only one duct only is working (Q = 880 m3/s), respectively.
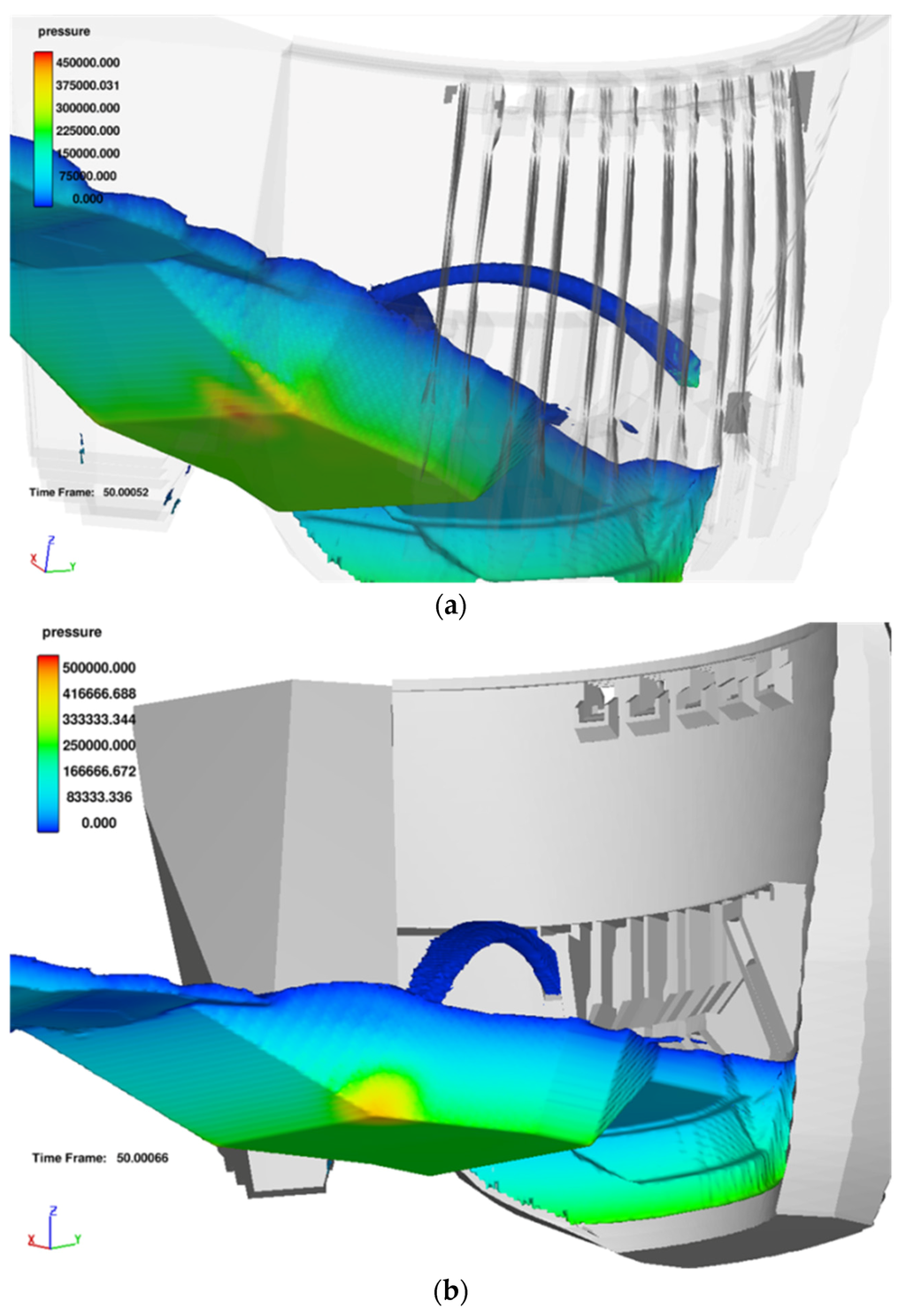
Figure 16.
Spatial views of pressures in the pre-excavated stilling basin (Prototype scale. Units in Pascal): (a) Working two ducts of half-height outlet (Q = 1760 m3/s); (b) Working one duct of half-height outlet (Q = 880 m3/s).
We can observe that when two ducts work, the total pressure reaches 45 m on the basin bottom. However, if only one duct is working, then the pressure reaches 50 m. The reduction of 5 m of total pressure is due to the impact of the jets in the air (see Figure 15).
5. Conclusions
In this paper, similar results have been obtained by solving the problem from three different perspectives: empirical formulations, pressure fluctuations-erodibility index and CFD simulations. From them, the only method to determine whether intact rock can resist the erosive action of the discharge devices of the dam is the semi-empirical methodology based on pressure fluctuations-erodibility index.
The results demonstrate the suitability of combining methodologies to solve complex phenomena. Thus, numerical simulations were used to complement the classical formulations, allowing a better understanding of the physical phenomena in order to obtain an adequate solution. The methodology leads us to propose a pre-excavated stilling basin.
The basin would allow the generation of an effective water cushion. Besides this, it would reduce the sedimentation due to the excavation and the material transported by the river, especially during the flushing operations of the reservoir (Castillo et al. [41]). The pre-excavated basin would also help to produce a symmetric and regular flow, reducing the risk of potential landslides.
Sensitivity analysis must be performed to prove the models are robust to various inputs, and not only to one single scenario. Some parameters need to be considered to reduce this uncertainty in numerical modeling including the turbulence parameters. A laboratory scale model should be made to compare the results with the other methodologies.
Acknowledgments
This work was supported by the Ministerio de Economía y Competitividad (Spain) and the FEDER (grant no. BIA2011-28
756-C03-02). We are grateful to CELEC EP-Hidropaute and the Consorcio POYRY-Caminosca Asociados for the data provided. The first author acknowledges the support of the Ministerio de Educación, Cultura y Deporte of España through the program PRX 14/00367, which allowed him to develop a stay as a Visiting Scholar Researcher at the Department of Civil and Environmental Engineering of the University of California, Davis, from April to October, 2015. We thank very much Fabián Bombardelli from the University of California, Davis, for his comments on an earlier version of the manuscript.
Author Contributions
Luis G. Castillo carried out the analysis and application of the empirical and semi-empirical methodology, provided the application case study, and analyzed the results and written works. José M. Carrillo carried out the numerical simulations and participated in written works. Both authors reviewed and contributed to the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| A | jet area on the impact surface; |
| Bg | thickness of the jet due to gravity effect; |
| Bi | thickness of the jet in initial condition; |
| Bj | thickness of the jet in the impingement conditions; |
| CD,i | drag coefficient for sediment species i; |
| Cp | mean dynamic pressure coefficient; |
| Cp′ | fluctuating dynamic pressure coefficient; |
| Cr | coefficient of relative density; |
| crough | proportional constant of local mean grain diameter in packed sediment (default value 1.0); |
| cs,i | concentration of the suspended sediment, |
| Ds | scour depth below tailwater level; |
| d | characteristic particle diameter; |
| di | characteristic size of bed material in which i % is smaller in weight; |
| d50,packed | local mean grain diameter in packed sediment: |
| ds,i | diameter of sediment species i; |
| dm | average particle size of the bed material; |
| d∗ | dimensionless particle diameter; |
| f | residual friction angle of the granular earth material; |
| fb,i | volume fraction of sediment i in the bed-load layer; |
| fs | total volume fraction of sediment; |
| fs,i | volume fraction of sediment species i; |
| F | reduction factor of the fluctuating dynamic pressure coefficient; |
| F | body and viscous forces; |
| g | gravitational acceleration; |
magnitude of the gravitational vector; | |
| H | fall height; |
| Hn | net energy head; |
| h | energy head at the crest weir; |
| h0 | vertical distance between the outlet exit and the tailwater level; |
| Ja | join wall alteration number; |
| Jn | join set number; |
| Jr | joint wall roughness number; |
| Js | number of structure relative of the grain; |
| Jx, Jy, Jz | discontinuity spacing; |
| K | erodibility index; |
| Kb | number of the block size; |
| Kd | number of resistance to shear strength on the discontinuity contour; |
| Ki | coefficient of quadratic drag for species i; |
| Kφ | experimental parameter; |
| ks | Nikuradse roughness of the bed surface; |
| Lb | disintegration height; |
| Ms | number of resistance of the mass; |
| ns | outward pointing normal to the packed bed interface; |
| P | relative capacity of the material to resisting erosion; |
| Pjet | stream power per unit of area; |
| Pr | pressure; |
| Q | flow; |
| Qi | flow with return period i; |
| q | specific flow; |
| qbi | volumetric bed-load transport rate per unit width; |
| Re | Reynolds number; |
dimensionless parameter to computing the critical Shields number; | |
| RQD | rock quality designation; |
| SD | Standard deviation; |
| SPT | standard penetration test; |
| TR | return period; |
| t0 | energy loss in the duct; |
| Ui | velocity of the jet in the initial condition; |
| Uj | velocity of the jet in the impingement conditions; |
mean velocity of the fluid-sediment mixture; | |
direction of the fluid-sediment mixture adjacent to the packed interface; | |
| ubedload,i | velocity magnitude of bed-load; |
| ubedload,i | vector velocity of bed-load; |
| udrift,i | velocity of the sediment due to drift; |
| uf | fluid velocity; |
| ulift,i | entrainment lift velocity of sediment; |
| ur,i | relative velocity between the velocity of sediment species i and the fluid velocity; |
| usettling,i | velocity magnitude of settling; |
| us,i | velocity of sediment species i; |
drift velocity to account for particle/particle interactions; | |
| UCS | unconfined compressive strength; |
| x, y, z, v, w | empirical exponents defined by regression or optimization; |
| Y | water cushion depth; |
| Y0 | tailwater depth; |
| Ys | scour depth below the original bed; |
| αi | entrainment parameter (recommended value 0.018); |
| β | air-water relationship; |
| βi | proportionality constant of Meyer-Peter and Müller equation; |
| Γ | experimental coefficient; |
| γ | specific weight of water; |
| γr | reference unit weight of rock (27·103 N/m3); |
| δi | bed-load thickness; |
| ζ0 | Richardson-Zaki coefficient; |
| ζuser | coefficient of Richardson-Zaki coefficient (default value 1.0); |
| ζ | exponent of Richardson-Zaki relation; |
| θi | local Shields number based on the local shear stress, angle of the jet in the initial conditions; |
| θj | angle of the jet in the impingement conditions; |
dimensionless critical Shields parameter; | |
dimensionless critical Shields parameter for sloping surfaces to include the angle of repose; | |
| μf | dynamic viscosity of fluid; |
| ξ | jet lateral spread distance due to the turbulence effect; |
| ρ | water density; |
density of fluid-sediment mixture; | |
| ρr | mass density of the rock; |
| ρs | density of sediment; |
| ρs,i | density of the sediment species i; |
| τ | shear stress; |
| Φi | dimensionless bed-load transport rate; |
| φ | parameter (φ = KφTu); |
| φ | residual friction angle of the granular earth material. |
References
- Consorcio PCA. FASE B: Informe de Factibilidad, Anexo 6, Hidráulica; Consorcio PCA: Quito, Ecuador, 2012. (In Spanish) [Google Scholar]
- Schoklitsch, A. Kolkbildung unter Über-fallstrahlen. Wasserwirtschaft 1932, 25, 341–343. (In German) [Google Scholar]
- Veronese, A. Erosioni di fondo a valle di uno scarico. Ann. Lavori Pubblici 1937, 75, 717–726. (In Italian) [Google Scholar]
- Eggenberger, W. Die Kolkbildung Bei Einem Uberstromen und Bei Der Kombination Uberstromen-Unterstromen. Ph.D. Thesis, ETH Zürich, Zurich, Switzerland, 1943. [Google Scholar]
- Taraimovich, I.I. Deformation of channels below high-head spillways on rock foundations. J. Power Technol. Eng. 1978, 12, 917–923. [Google Scholar] [CrossRef]
- INCYTH-LHA. Estudio Sobre Modelo del Aliviadero de la Presa Casa de Piedra, Informe Final; DOH-044-03-82; Laboratorio de Hidráulica-Instituto Nacional del Agua: Ezeiza, Argentina, 1982. (In Spanish) [Google Scholar]
- Mason, P.J. Effects of air entrainment on plunge pool scour. J. Hydraul. Eng. 1989, 115, 385–399. [Google Scholar] [CrossRef]
- Liu, P. A new method for calculating depth of scour pit caused by overflow water jets. J. Hydraul. Res. 2005, 43, 695–701. [Google Scholar] [CrossRef]
- Bombardelli, F.A.; Gioia, G. Scouring of granular beds by jet-driven axisymmetric turbulent cauldrons. Phys. Fluids 2006, 18, 88–101. [Google Scholar] [CrossRef]
- Suppasri, A. Hydraulic Performance of Nam Ngum 2 Spillway; Asian Institute of Technology: Pathumthani, Thailand, 2007. [Google Scholar]
- Pagliara, S.; Amidei, M.; Hager, W.H. Hydraulics of 3D Plunge Pool Scour. J. Hydraul. Eng. 2008, 134, 1275–1284. [Google Scholar] [CrossRef]
- Hartung, W. Die Kolkbildung hinter Uberstromen wehren im Hinblick auf eine beweglich Sturzbettgestaltung. Die Wasser Wirtsch. 1959, 49, 309–313. (In German) [Google Scholar]
- Chee, S.P.; Padiyar, P.V. Erosion at the base of flip buckets. Eng. J. Can. 1969, 52, 22–24. [Google Scholar]
- Bisaz, E.; Tschopp, J. Profundidad de erosión al pie de un vertedero para la aplicación de corrección de arroyos en quebradas empinadas. In Proceedings of the Fifth Congreso Latinoamericano de Hidráulica (IAHR), Lima, Peru, 23–28 October 1972; pp. 447–456. (In Spanish)
- Martins, R. Scouring of rocky riverbeds by free-jet spillways. Int. Water Power Dam Constr. 1975, 27, 152–153. [Google Scholar]
- Machado, L.I. O Sistema de Dissipacao de Energia Proposto para a Barragem de Xingo. In Transactions of the International Symposium on the Layout of Dams in Narrow Gorges; ICOLD: Rio de Janeiro, Brazil, 1982. [Google Scholar]
- Jaeger, C. Uber die Aehnlichkeit bei flussaulichen Modellversuchen. Wasserkr. Wasserwirtsch. 1939, 34, 269. (In German) [Google Scholar]
- Rubinstein, G.L. Laboratory Investigation of Local Erosion on Channel Beds Below High Overflow Dams. Trans Coordinating Conferences on Hydraulic Engineering Iss VII Conference on Hydraulics of High Head Water Discharge Structures; Gosenergoizdat: Moscow, Russia, 1963. [Google Scholar]
- Mirtskhulava, T.E. Alguns Problemas da Erosao nos Leitos dos Rios. Moscow. Trans. No 443do; Laboratório Nacional de Engenharia Civil: Lisbon, Portugal, 1967. (In Portuguese) [Google Scholar]
- Ervine, D.A.; Falvey, H.R. Behavior of turbulent jets in the atmosphere and plunge pools. ICE Proc. 1987, 83, 295–314. [Google Scholar]
- Ervine, D.A.; Falvey, H.R.; Whiters, W. Pressure Fluctuations on Plunge Pool Floors. J. Hydraul. Res. 1997, 35, 257–259. [Google Scholar] [CrossRef]
- Castillo, L.G. Aerated jets and pressure fluctuation in plunge pools. In Proceedings of the 7th International Conference on Hydroscience and Engineering, Philadelphia, PA, USA, 10–13 September 2006.
- Castillo, L.G.; Puertas, J.; Dolz, J. Discussion about Scour of rock due to the impact of plunging high velocity jets Part I: A state-of-the-art review. J. Hydraul. Res. 2007, 45, 853–858. [Google Scholar] [CrossRef]
- Bollaert, E.F.R.; Schleiss, A. Scour of rock due to the impact of plunging high velocity jets. Part 1: A state-of-the-art review. J. Hydraul. Res. 2003, 41, 451–464. [Google Scholar] [CrossRef]
- Castillo, L.G.; Carrillo, J.M. Scour estimation of the Paute-Cardenillo Dam. In Proceedings of the International Perspectives on Water Resources & the Environment, Quito, Ecuador, 8–10 January 2014.
- Castillo, L.G.; Carrillo, J.M. Characterization of the dynamic actions and scour estimation downstream of a dam. In Dam Protections against Overtopping and Accidental Leakage; CRC Press: Madrid, Spain, 2015; pp. 231–243. [Google Scholar]
- Castillo, L.G.; Carrillo, J.M.; Blázquez, A. Plunge pool mean dynamic pressures: A temporal analysis in nappe flow case. J. Hydraul. Res. 2015, 53, 101–118. [Google Scholar] [CrossRef]
- Castillo, L.G.; Carrillo, J.M.; Sordo-Ward, A. Simulation of overflow nappe impingement jets. J. Hydroinform. 2014, 16, 922–940. [Google Scholar] [CrossRef]
- Federal Emergency Management Agency. FEMA P-1015, Technical Manual: Overtopping Protection for Dams. Best Practices for Design, Construction, Problem Identification and Evaluation, Inspection, Maintenance, Renovation, and Repair. Available online: https://www.fema.gov/es/media-library/assets/documents/97888 (accessed on 5 December 2014).
- Annandale, G.W. Erodibility. J. Hydraul. Res. 1995, 33, 471–494. [Google Scholar] [CrossRef]
- Annandale, G.W. Scour Technology: Mechanics and Engineering Practice; McGraw-Hill: New York, NY, USA, 2006. [Google Scholar]
- Consorcio PCA. FASE B: Informe de Factibilidad, Anexo 8, Geotécnica; Consorcio PCA: Quito, Ecuador, 2012. (In Spanish) [Google Scholar]
- Meyer-Peter, E.; Müller, R. Formulas for Bed-Load Transport. In Proceedings of the Second Meeting, International Association for Hydraulic Structures Research, Stockholm, Sweden, 7 June 1948; pp. 39–64.
- Mastbergen, D.R.; Van den Berg, J.H. Breaching in fine sands and the generation of sustained turbidity currents in submarine canyons. Sedimentology 2003, 50, 625–637. [Google Scholar] [CrossRef]
- Brethour, J.; Burnham, J. Modeling Sediment Erosion and Deposition with the FLOW-3D Sedimentation & Scour Model; Flow Science Technical Note, FSI-10-TN85; Flow Science, Inc.: Santa Fe, Mexico, 2010; pp. 1–22. [Google Scholar]
- Hirt, C.W.; Nichols, B.D. Volume of Fluid (VOF) Method for the Dynamics of Free Boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Flow Science, Inc. FLOW-3D Users Manual Version 11.0; Flow Science, Inc.: Santa Fe, Mexico, 2014. [Google Scholar]
- Richardson, J.F.; Zaki, W.N. Sedimentation and fluidization (Part I). Trans. Inst. Chem. Eng. 1954, 32, 35–53. [Google Scholar]
- Soulsby, R. Chapter 9: Bedload transport. In Dynamics of Marine Sand; Thomas Telford Publications: London, UK, 1997. [Google Scholar]
- Van Rijn, L. Sediment transport, Part I: Bed load transport. J. Hydraul. Eng. 1984, 110, 1431–1456. [Google Scholar] [CrossRef]
- Castillo, L.G.; Carrillo, J.M.; Álvarez, M.A. Complementary Methods for Determining the Sedimentation and Flushing in a Reservoir. J. Hydraul. Eng. 2015, 141, 05015004. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).