Semi- vs. Fully-Distributed Urban Stormwater Models: Model Set Up and Comparison with Two Real Case Studies
Abstract
:1. Introduction
2. Semi- and Fully-Distributed Modeling Approaches
2.1. Conceptual Basis of Semi-Distributed and Fully Distributed Models
- Initial losses: The main difference is related to the representation of the depression storage. Depression storage is the stormwater that is retained in small depressions on the overland surface (puddle forming) and in pores of surface materials, both in impervious and pervious areas (surface wetting) [30]. In SD models, these two phenomena are usually considered with a constant value or a single value that is subtracted directly from the rainfall and is dependent on subcatchments’ slope and surface type [31]. In FD models, due to the finer resolution, the overland flow module can account for more detailed depressions that origin puddle forming [28].
- Continuing losses: The main difference is related to the infiltration modeling. Infiltration is the percentage of rainfall draining into the soil. In SD models, infiltration is estimated for each subcatchment based on soil saturation, and subtracted from the rainfall before being applied to the model. In FD models, rainfall is applied directly to the overland mesh and infiltration is estimated for each 2D element, based on soil saturation and water depth. Therefore, infiltration predicted by FD models takes into account the runoff quantity on the overland surface, and can capture infiltration into permeable surfaces of runoff routed from upstream impermeable areas.
- Runoff routing: In SD models, the generated runoff is transformed by the rainfall–runoff module into an inflow hydrograph that is usually applied to the sewer flow module. In FD models, the generated runoff is directly applied to the overland flow module and routed in the overland surface. SD runoff routing functions are based on both physically based as well as empirical or conceptual methods, with resolutions defined by subcatchments sizes [32,33]. FD runoff routing is simulated by applying physically based approaches with resolutions defined by the surface overland mesh. While FD models enable the representation of the real connection between impervious and pervious areas on the surface, SD models usually merge the runoff discharges to sewers from impervious and pervious area of subcatchments, unless the subcatchments are either pervious or impervious. In addition, runoff volumes captured by surface ponds are captured by FD models, since they consider the runoff on the overland mesh, whereas in SD models can neglect these volumes depending on subcatchment delineation and their discharge definition.
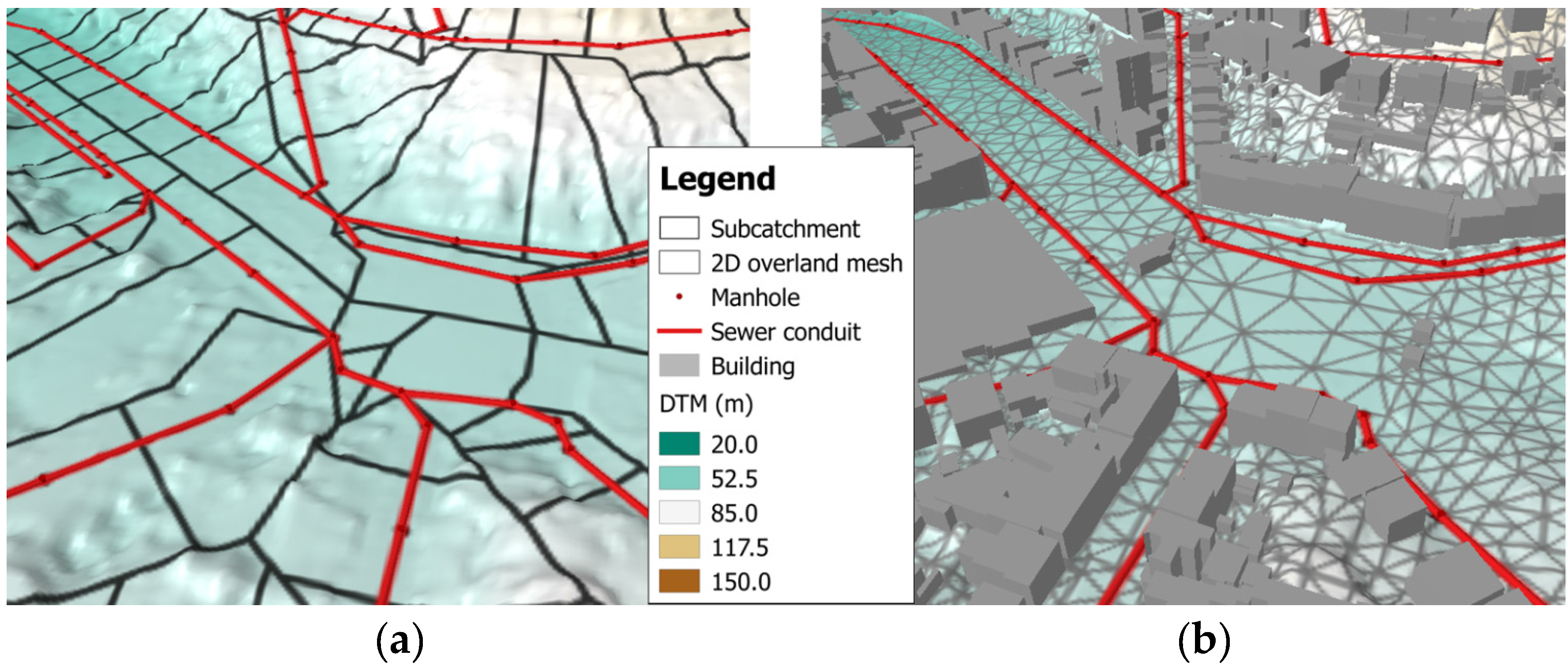
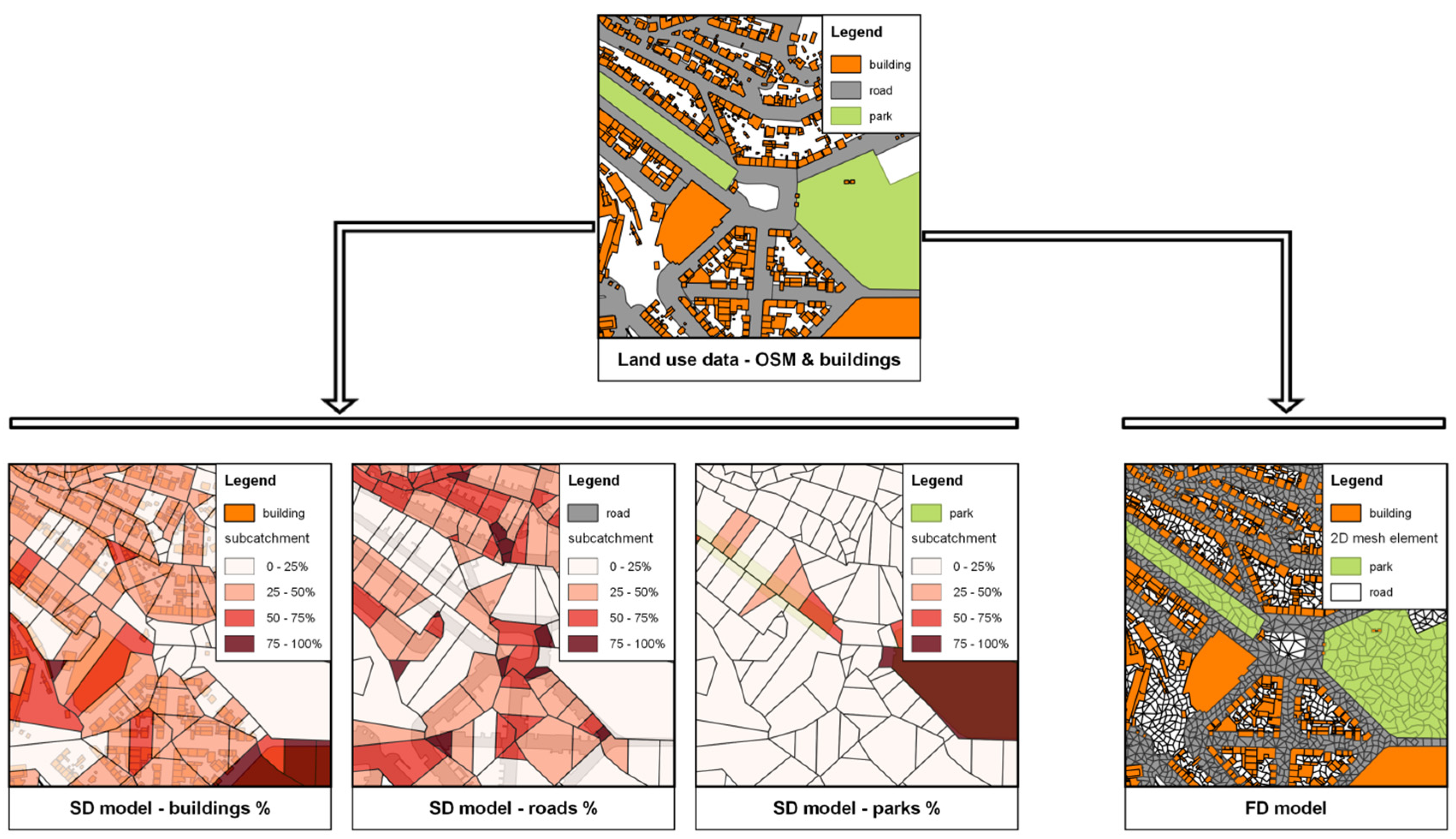
2.2. Model Building Process
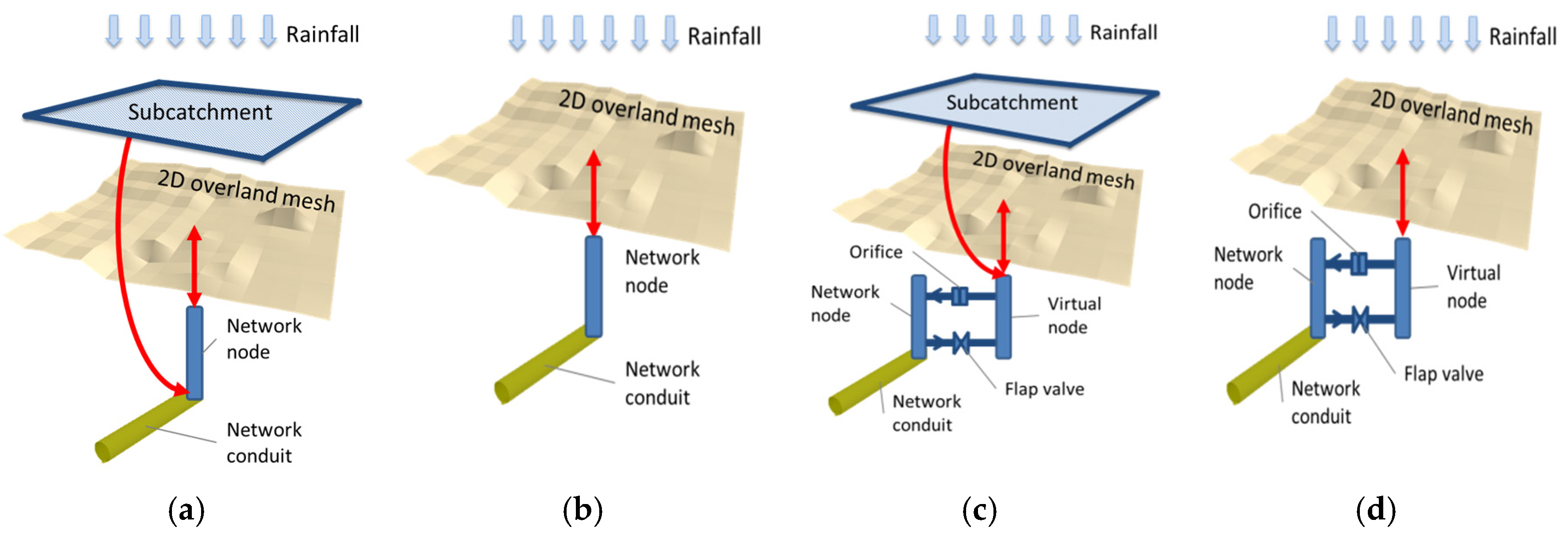
2.3. Connections between Modules and Inlet Capacity
3. Case Studies
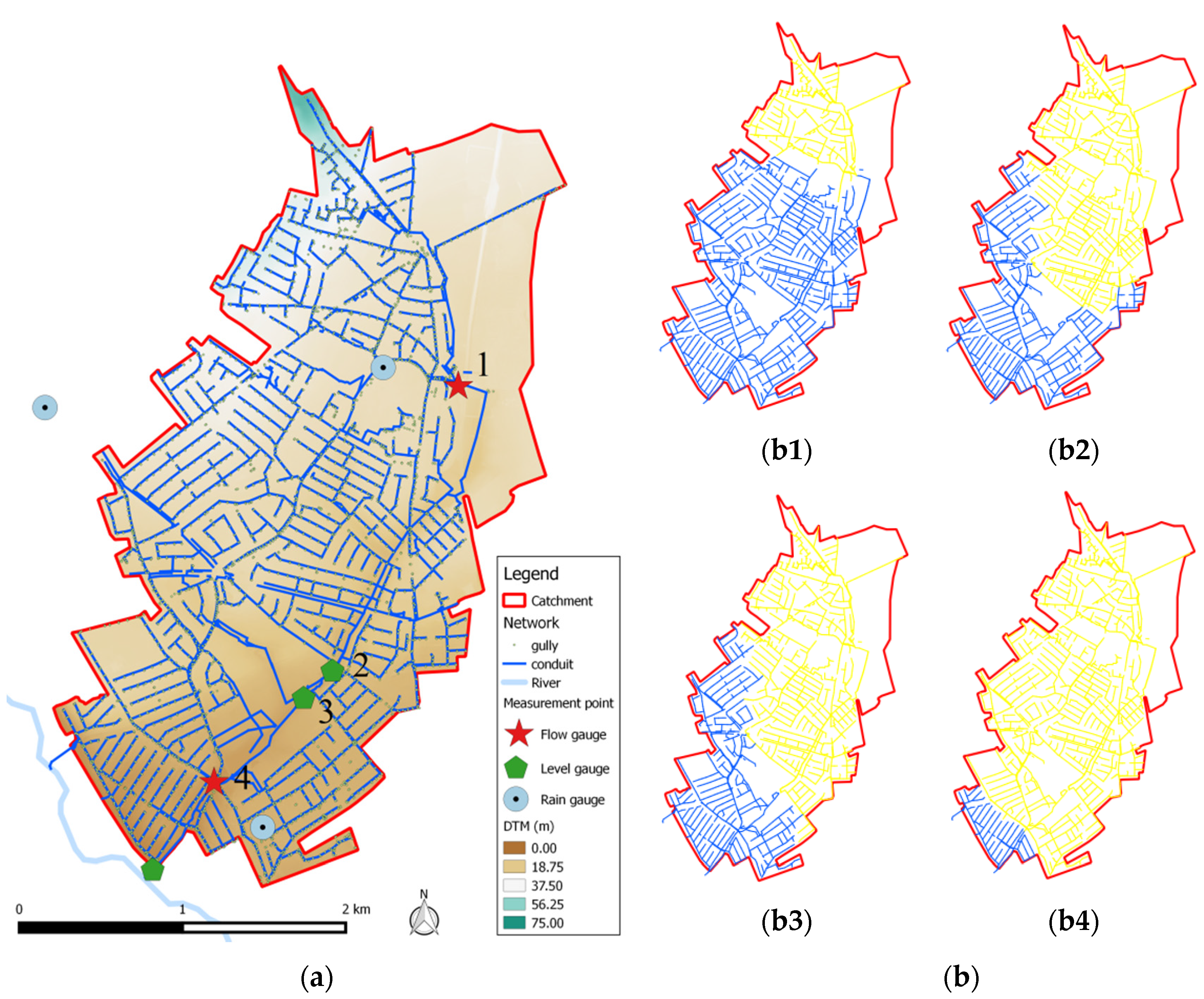
3.1. Cranbrook Case Study
3.2. Zona Central Case Study
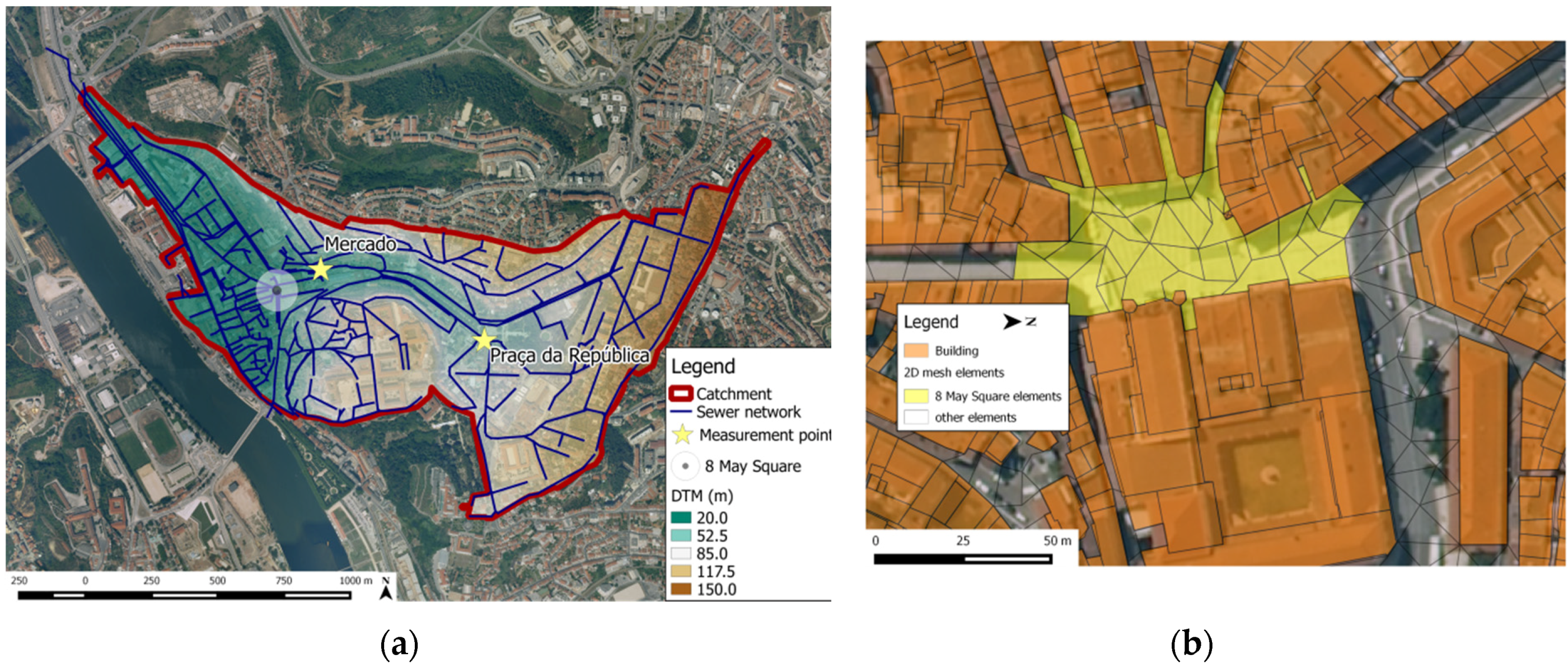
4. Results and Discussion
4.1. Cranbrook Case Study
| Event ID * | Start | End | Duration (h) | Maximum Rainfall (mm/h) | Total Rainfall Depth (mm) | Average Rainfall Intensity (mm/h) |
|---|---|---|---|---|---|---|
| 141212 | 12 December 2014 1:30 A.M. | 12 December 2014 8:00 A.M. | 6.5 | 12 | 10.9 | 2 |
| 150103 | 3 January 2015 3:50 A.M. | 3 January 2015 5:00 P.M. | 13.2 | 12 | 16.6 | 1 |
| 150108 | 8 January 2015 7:30 A.M. | 8 January 2015 2:30 P.M. | 7.0 | 12 | 11.6 | 2 |
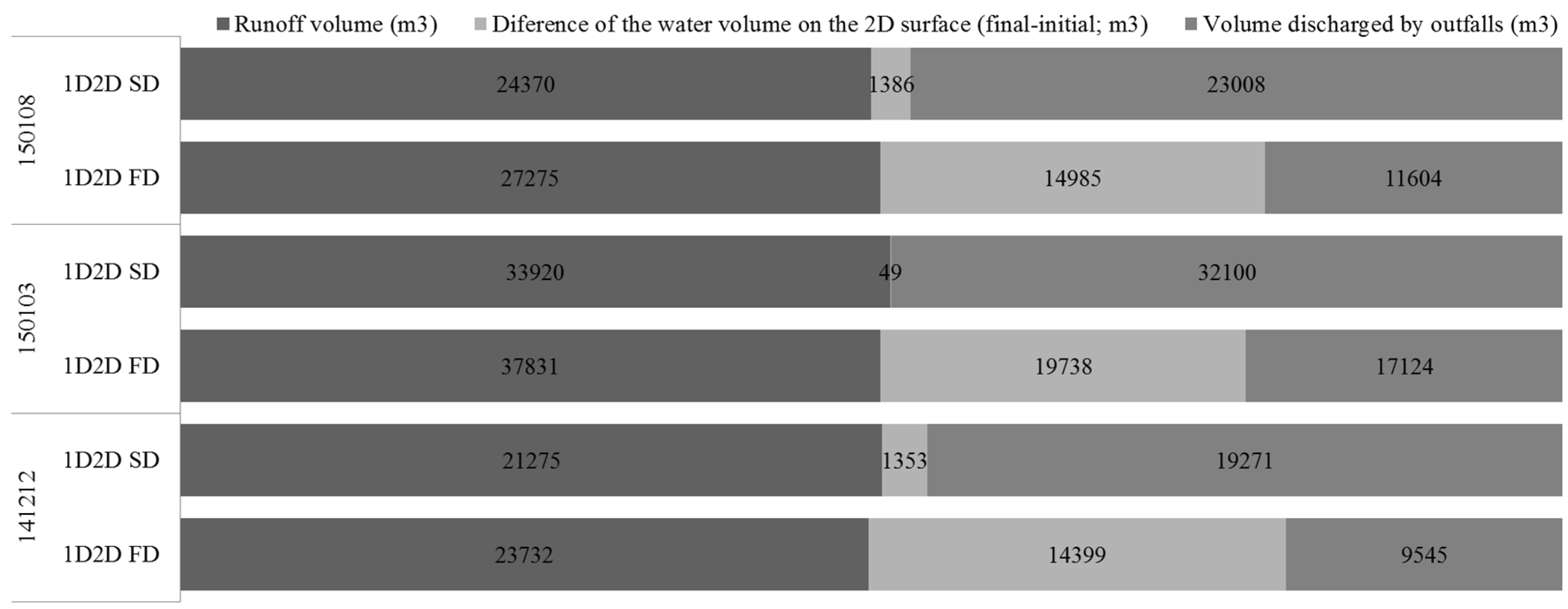
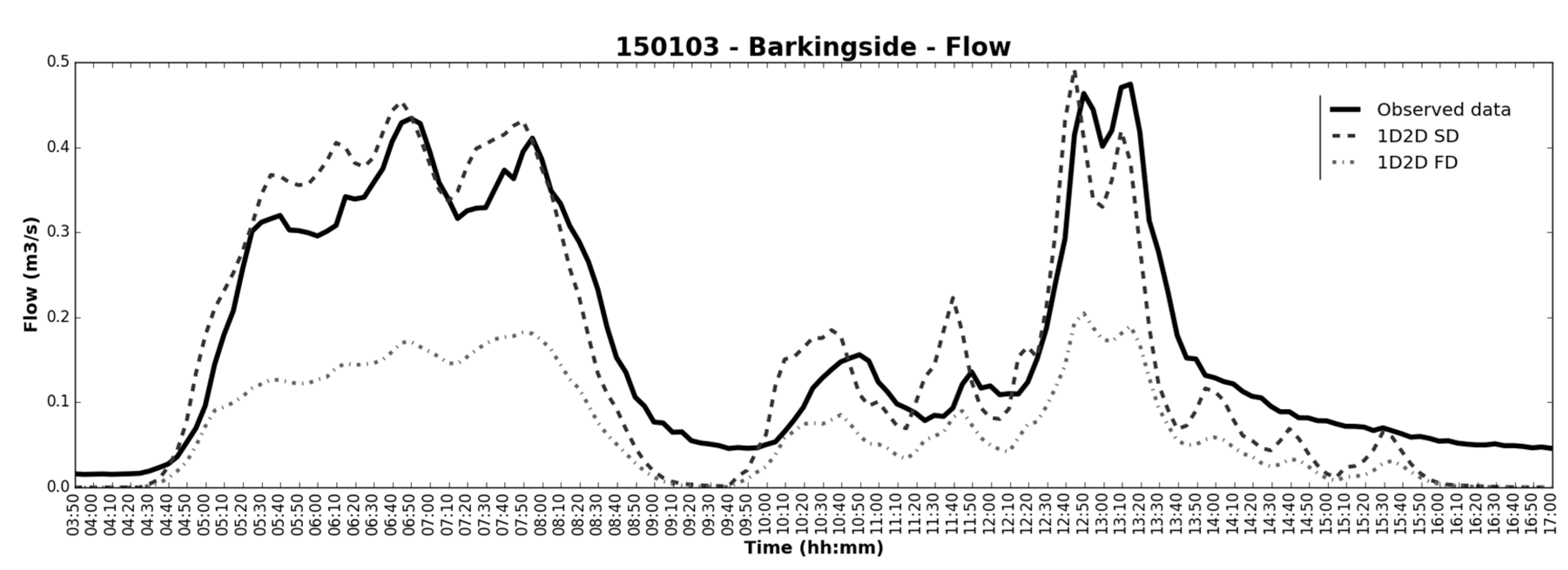
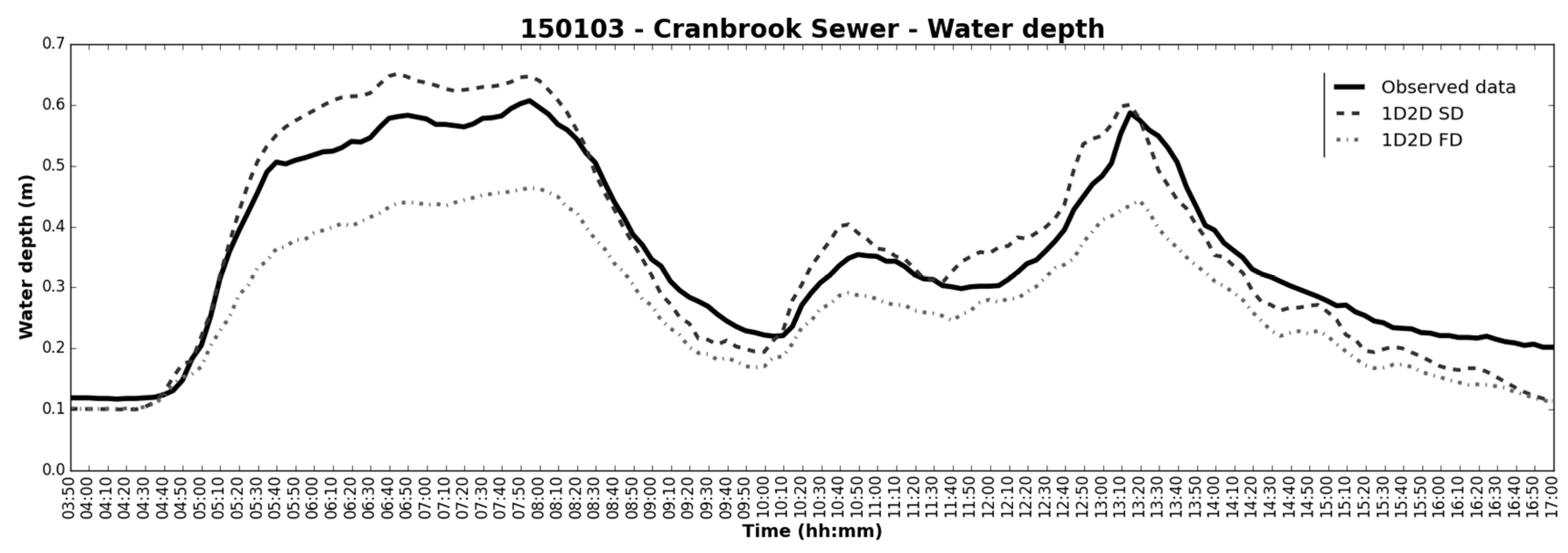
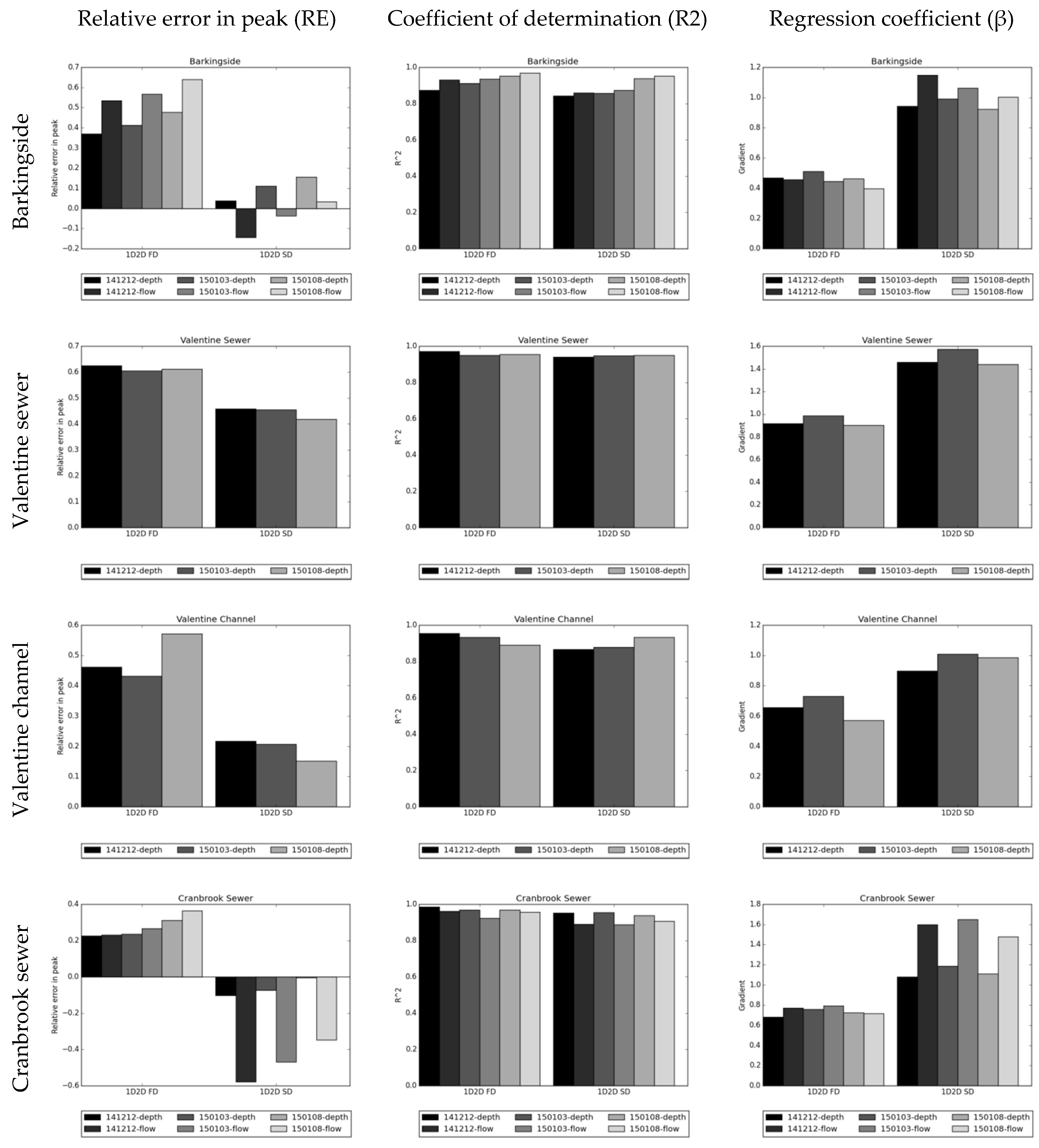
- Relative error (RE) in peak (Figure 10, left column):where is the relative error in the peak results () compared to the peak in observed data (). RE was applied to flow and water depth peaks. Positive values indicate underestimation by the peak results and negative values imply overestimation. The RE has the advantage of being a “tangible” statistic that evaluates the performance of a critical parameter such as the peak flow or water depth. It is important to note that very large RE can be obtained when low values are evaluated, even if the absolute difference in peak is small.In general, for all simulated events the RE is higher in FD than in SD models, which means that FD underestimates results against observed data. In the Cranbrook sewer sensor, the SD model predicted accurate water depths but overestimated flows. This can be due to the location of the sensor in a zone where turbulence can occur and affect monitoring data accuracy. In the FD model this variation does not occur, because both water depth and flows results are smoothened and underestimated. In conclusion, while the SD model captured water depth and flow peaks, the FD model underestimated these results.
- Coefficient of determination (R2) (Figure 10, middle column) and Regression coefficient (β) (Figure 10, right column): Resulting from a simple linear regression analysis applied between each simulated results time series and the observed data. These two statistics provide an indication of how well the results replicate observed data, both in terms of pattern (R2) and accuracy (β). The R2 measure ranges from 0 to 1 and describes how much of the observed data variability is according with the simulated results. In practical terms, R2 provides a measurement of the similarity between the patterns of the observed data time series and the simulated results time series, i.e., indicates how the hydrodynamics are captured by the model. The regression coefficient, β, is employed to provide supplementary information to the R2. β 1 represents good agreement in the magnitude of observed data and results time series; β 1 means the results are overestimated against observed data (by a factor of β); and β 1 means the results are underestimated against observed data (by a factor of β).For most simulated events, the R2 is close to 1 for both SD and FD models, which implies that the variations of modeling results match the observed data, i.e., the models can capture the hydrodynamics of observed data. The differences between SD and FD models are not so evident, but FD models tend to have higher R2, which suggest that they have the potential to better represent the dynamic behavior of stormwater flows in urban catchments.The β is in general closer to 1 for SD model results, which indicates that SD results are matching the observed data more accurately than FD ones. The exceptions in the results analysis can be noticed in the data for the Valentines and the Cranbrook Sewer sensors. For the Valentines Sewer sensor, network elements tend to overestimate water depths in the SD model. For the Cranbrook Sewer sensor, the errors in observed flow data due to turbulence also affect this indicator as verified for the RE. These two aspects are not verified in the FD model as it underestimates overall results.Combining the R2 and the β results, it can be concluded that SD and FD models capture the hydrodynamics registered and the SD model tend to capture the magnitude of observed data while FD model underestimates it.
4.2. Zona Central Case Study
| Event Name * | Start | End | Duration (h) | Maximum Rainfall (mm/h) | Total Rainfall Depth (mm) | Average Rainfall Intensity (mm/h) | Return Period (yr.) |
|---|---|---|---|---|---|---|---|
| 060609 | 9 June 2006 2:50 P.M. | 9 June 2006 4:30 P.M. | 1.7 | 144.0 | 36.6 | 22.0 | 50 |
| 061025 | 25 October 2006 12:30 A.M. | 25 October 2006 5:30 A.M. | 5.0 | 102.0 | 56.6 | 11.3 | 50 |
| 080921 | 21 September 2008 3:10 P.M. | 21 September 2008 5:20 P.M. | 2.2 | 60.6 | 21.4 | 9.9 | 5 |
| 131224 | 24 December 2013 6:40 A.M. | 24 December 2013 6:00 P.M. | 11.3 | 31.5 | 48.9 | 4.3 | 5 |


| Event | Max Water Depth (m) | Flooding Volume (m3) | Flooding Area (m2) | |||
|---|---|---|---|---|---|---|
| SD | FD | SD | FD | SD | FD | |
| 060609 | 0.44 | 0.11 | 275 | 68 | 1092 | 324 |
| 061025 | 0.51 | 0.25 | 360 | 138 | 1693 | 630 |
| 080921 | 0.10 | 0.08 | 63 | 42 | 324 | 248 |
| 131224 | 0.14 | 0.06 | 79 | 34 | 569 | 248 |
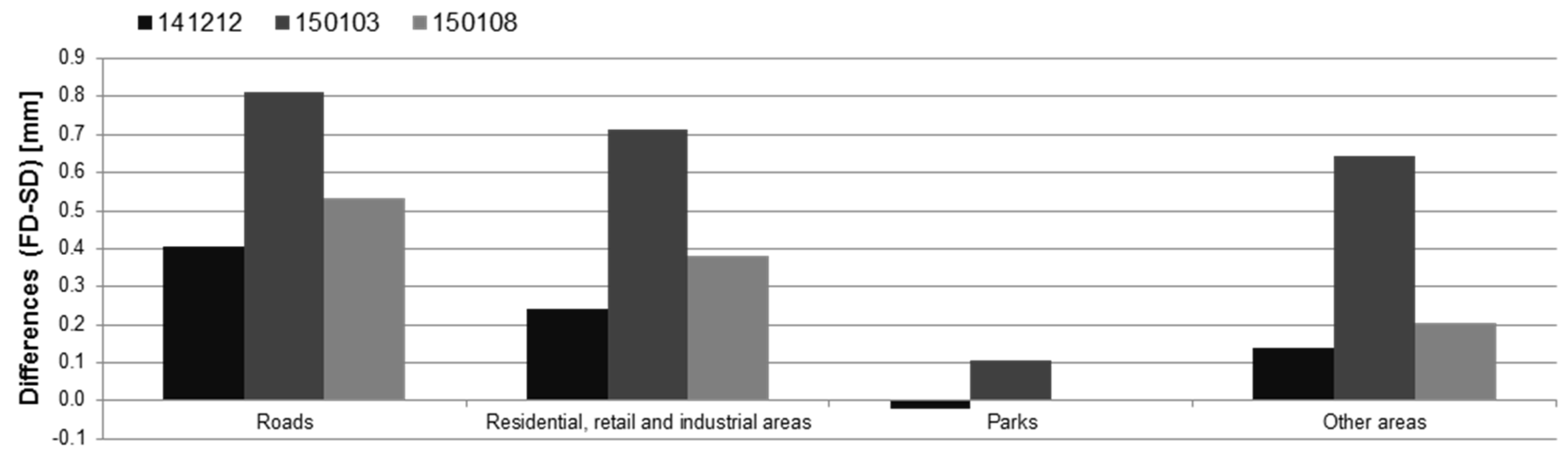
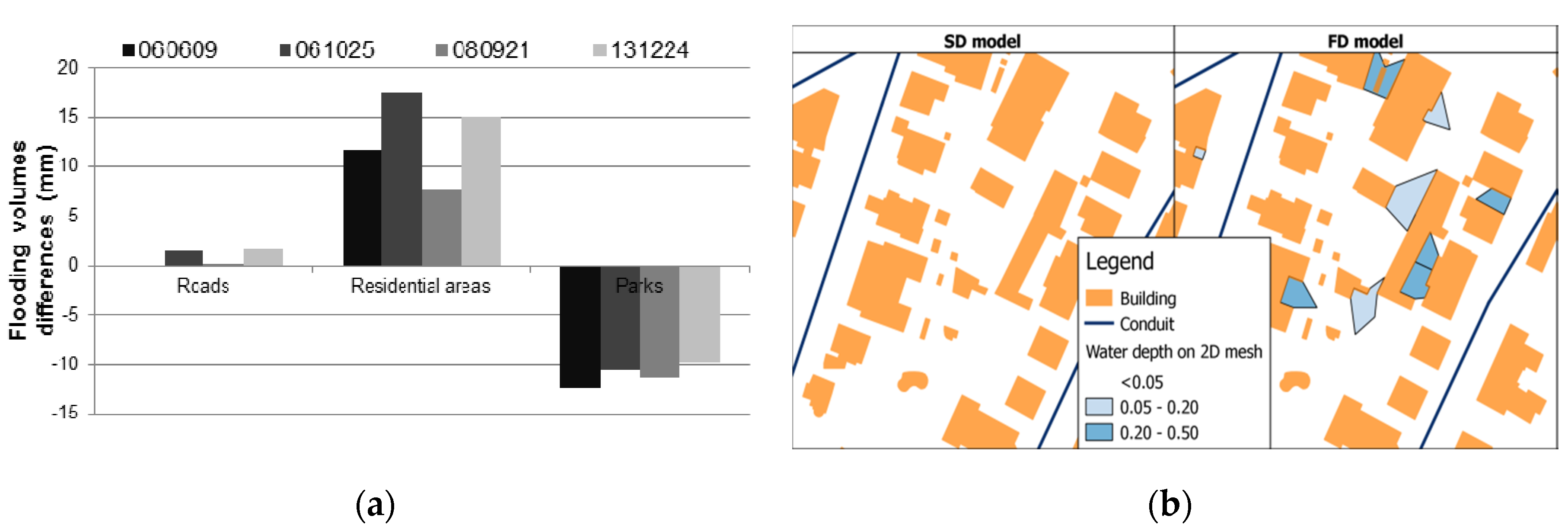
4.3. Assessing the Importance of Surface Storage as a Function of Rainfall Magnitude
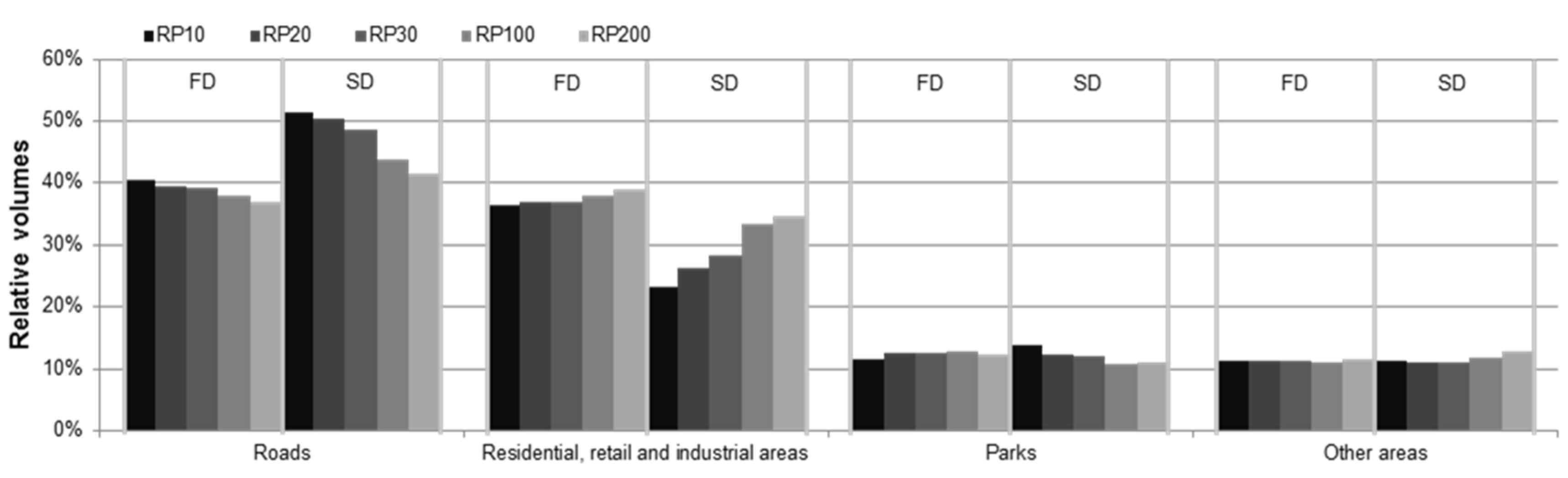

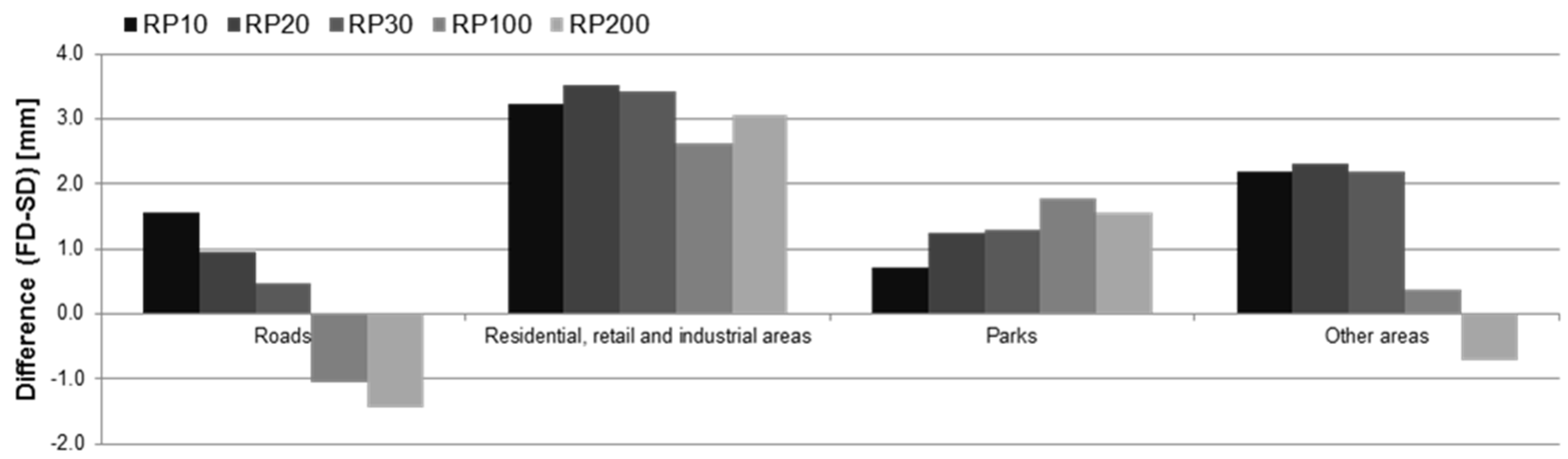
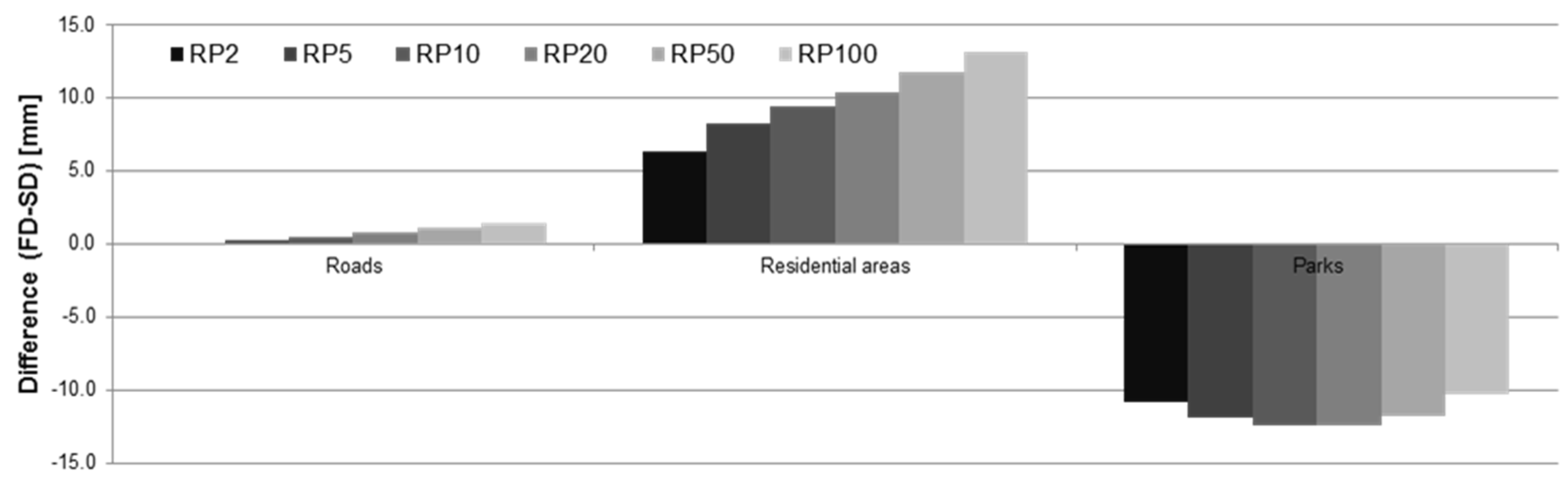
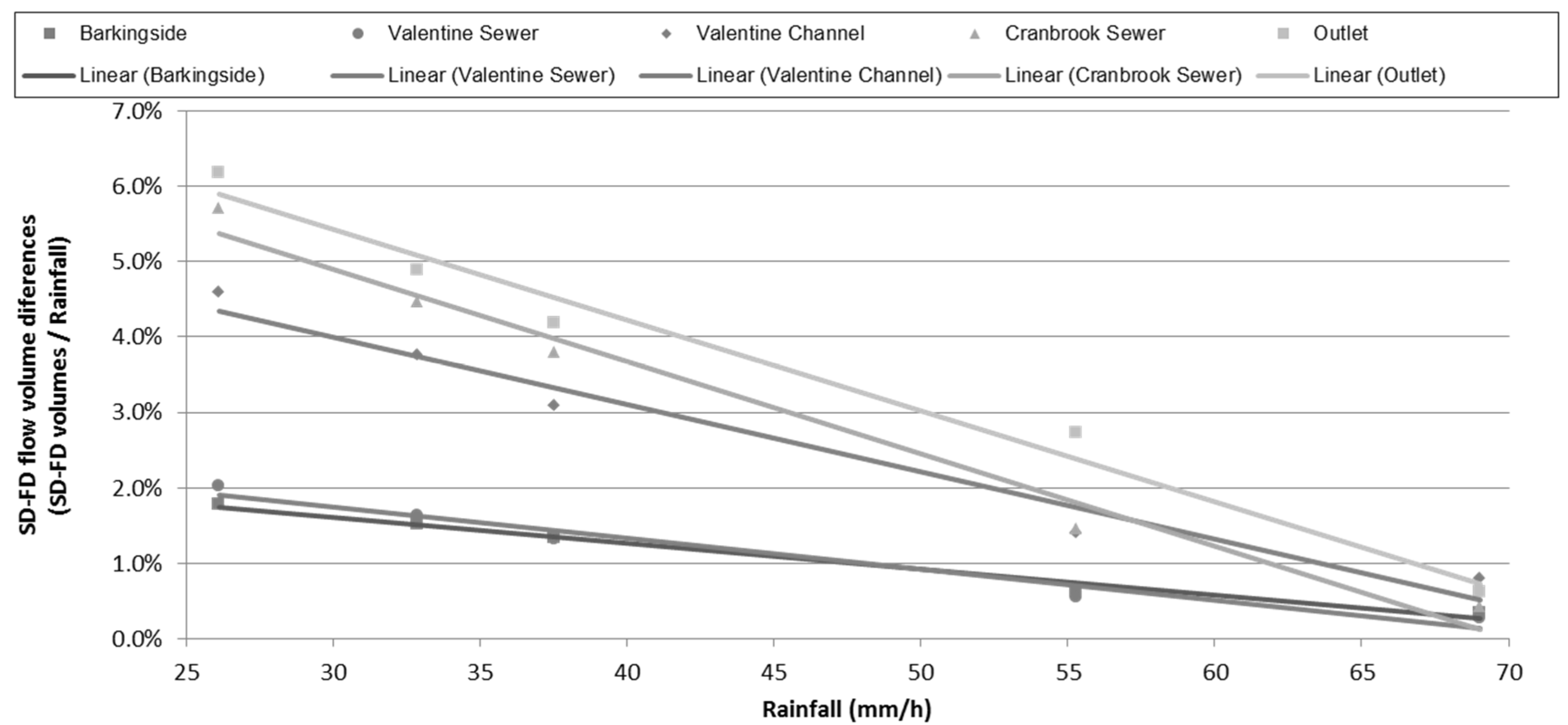
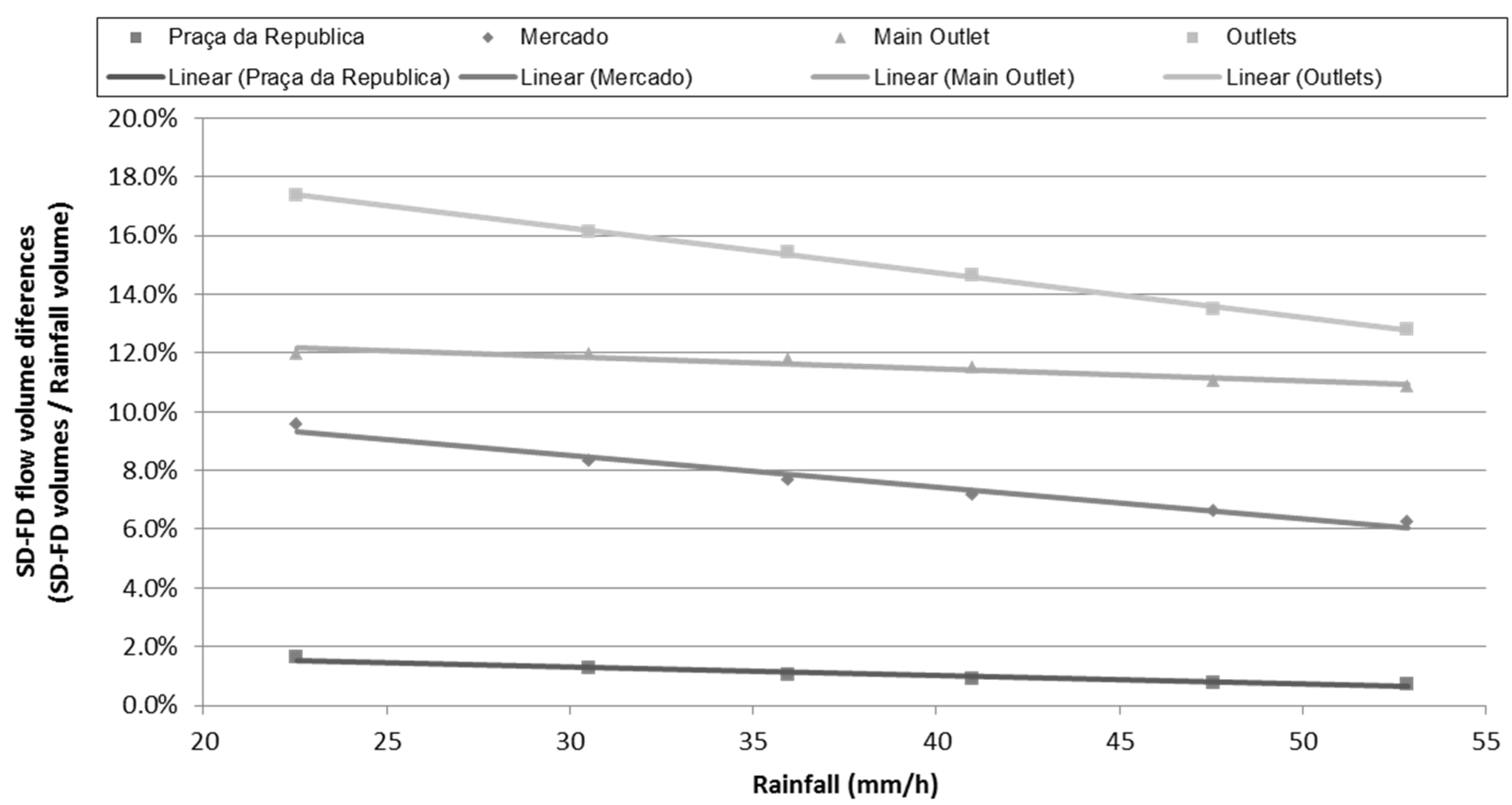
5. Discussion and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- United States Environmental Protection Agency (US EPA). Storm Water Management Model (SWMM). Available online: http://www.epa.gov/water-research/storm-water-management-model-swmm (accessed on 2 February 2016).
- Huber, W.; Roesner, L. The History and Evolution of the EPA SWMM. In Fifty Years of Watershed Modeling—Past, Present And Future; Available online: http://dc.engconfintl.org/watershed/29 (accessed on 2 February 2016).
- Ellis, J.H.; McBean, E.A.; Mulamoottil, G. Design of Dual Drainage Systems Using SWMM. J. Hydraul. Div. 1982, 108, 1222–1227. [Google Scholar]
- Abbott, M.B. The electronic encapsulation of knowledge in hydraulics, hydrology and water resources. Adv. Water Resour. 1993, 16, 21–39. [Google Scholar] [CrossRef]
- Djordjević, S.; Prodanović, D.; Maksimović, Č. An approach to simulation of dual drainage. Water Sci. Technol. 1999, 39, 95–103. [Google Scholar] [CrossRef]
- Mark, O.; Weesakul, S.; Apirumanekul, C.; Aroonnet, S.B.; Djordjević, S. Potential and limitations of 1D modelling of urban flooding. J. Hydrol. 2004, 299, 284–299. [Google Scholar] [CrossRef]
- Djordjević, S.; Prodanović, D.; Maksimović, C.; Ivetić, M.; Savić, D. SIPSON—Simulation of interaction between pipe flow and surface overland flow in networks. Water Sci. Technol. 2005, 52, 275–283. [Google Scholar] [PubMed]
- Maksimović, Č.; Prodanović, D.; Boonya-Aroonnet, S.; Leitão, J.P.; Djordjević, S.; Allitt, R. Overland flow and pathway analysis for modelling of urban pluvial flooding. J. Hydraul. Res. 2009, 47, 512–523. [Google Scholar] [CrossRef]
- Vojinovic, Z.; Tutulic, D. On the use of 1D and coupled 1D-2D modelling approaches for assessment of flood damage in urban areas. Urban Water J. 2009, 6, 183–199. [Google Scholar] [CrossRef]
- Chen, A.S.; Hsu, M.H.; Chen, T.S.; Chang, T.J. An integrated inundation model for highly developed urban areas. Water Sci. Technol. J. Int. Assoc. Water Pollut. Res. 2005, 51, 221–229. [Google Scholar]
- Carr, R.S.; Smith, G.P. Linking of 2D and Pipe Hydraulic Models at Fine Spatial Scales. Water Pract. Technol. 2007, 2. [Google Scholar] [CrossRef]
- Schmitt, T.G.; Thomas, M.; Ettrich, N. Analysis and modeling of flooding in urban drainage systems. J. Hydrol. 2004, 299, 300–311. [Google Scholar] [CrossRef]
- Seyoum, S.D.; Vojinovic, Z.; Price, R.K.; Weesakul, S. Coupled 1D and Noninertia 2D Flood Inundation Model for Simulation of Urban Flooding. J. Hydraul. Eng. 2012, 138, 23–34. [Google Scholar] [CrossRef]
- DHIgroup, MIKE SHE. Available online: http://www.mikepoweredbydhi.com/products/mike-she (accessed on 16 July 2015).
- Refsgaard, J.C.; Storm, B.; Clausen, T. Système Hydrologique Europeén (SHE): Review and perspectives after 30 years development in distributed physically-based hydrological modelling. Hydrol. Res. 2010, 41. [Google Scholar] [CrossRef]
- MOHID Water Modelling System. Available online: https://en.wikipedia.org/wiki/MOHID_water_modelling_system (accessed on 5 February 2016).
- Neves, R.; Brito, D.; Braunschweig, F.; Leitão, P.C.; Jauch, E.; Campuzano, F. Managing interfaces in catchment modelling. In Sustainable Watershed Management; CRC Press, Taylor & Francis Group: New York, NY, USA, 2014; pp. 19–24. [Google Scholar]
- Leitao, J.P.C. Enhancement of Digital Elevation Models and Overland Flow Path Delineation Methods for Advanced Urban Flood Modelling. Ph.D. Thesis, Imperial College London, London, UK, 2009. [Google Scholar]
- OpenStreetMap, OSM. Available online: http://www.openstreetmap.org/ (accessed on 20 October 2014).
- Wang, L.-P.; Ochoa-Rodríguez, S.; Simões, N.E.; Onof, C.; Maksimović, Č. Radar–raingauge data combination techniques: A revision and analysis of their suitability for urban hydrology. Water Sci. Technol. 2013, 68. [Google Scholar] [CrossRef] [PubMed]
- Fletcher, T.D.; Andrieu, H.; Hamel, P. Understanding, management and modelling of urban hydrology and its consequences for receiving waters: A state of the art. Adv. Water Resour. 2013, 51, 261–279. [Google Scholar] [CrossRef]
- Smith, L.S.; Liang, Q.; Quinn, P.F. A flexible hydrodynamic modelling framework for GPUs and CPUs: Application to the Carlisle 2005 floods. In Proceedings of the International Conference on Flood Resilience: Experiences in Asia and Europe, Exeter, UK, 5–7 September 2013.
- Stelling, G.S. Quadtree flood simulations with sub-grid digital elevation models. Proc. ICE Water Manag. 2012, 165, 567–580. [Google Scholar] [CrossRef]
- Ghimire, B.; Chen, A.S.; Guidolin, M.; Keedwell, E.C.; Djordjević, S.; Savić, D.A. Formulation of a fast 2D urban pluvial flood model using a cellular automata approach. J. Hydroinform. 2013, 15, 676–686. [Google Scholar] [CrossRef] [Green Version]
- Casulli, V.; Stelling, G.S. A semi-implicit numerical model for urban drainage systems. Int. J. Numer. Methods Fluids 2013, 73, 600–614. [Google Scholar] [CrossRef]
- Simões, N.; Leitão, J.P.; Pina, R.; Ochoa, S.; Sá Marques, A.; Maksimović, Č. Urban drainage models for flood forecasting: 1D/1D, 1D/2D and hybrid models. In Proceedings of the 12th International Conference on Urban Drainage, Porto Alegre, Brazil, 11–16 September 2011.
- Innovyze. InfoWorks ICM; Innovyze: Monrovia, CA, USA, 2013. [Google Scholar]
- Bailey, A.; Margetts, J. 2D Runoff Modelling—A Pipe Dream or the Future? In Proceedings of the WaPUG Autumn Conference, Blackpool, UK, 2008.
- Chang, T.-J.; Wang, C.-H.; Chen, A.S. A novel approach to model dynamic flow interactions between storm sewer system and overland surface for different land covers in urban areas. J. Hydrol. 2015, 524, 662–679. [Google Scholar] [CrossRef] [Green Version]
- Mansell, M. Rural and Urban Hydrology; ICE Publishing: London, UK, 2003. [Google Scholar]
- Butler, D.; Davies, J. Urban Drainage, 3rd ed.; CRC Press: New York, NY, USA, 2011. [Google Scholar]
- Pan, A.; Hou, A.; Tian, F.; Ni, G.; Hu, H. Hydrologically Enhanced Distributed Urban Drainage Model and Its Application in Beijing City. J. Hydrol. Eng. 2012, 17, 667–678. [Google Scholar] [CrossRef]
- Elliott, A.H.; Trowsdale, S.A. A review of models for low impact urban stormwater drainage. Environ. Model. Softw. 2007, 22, 394–405. [Google Scholar] [CrossRef]
- Pina, R.; Sousa, J.J.D.O.; Temido, J.L.S.S.; Sá Marques, A. O Novo Paradigma de Gestão dos Sistemas de Drenagem da Cidade de Coimbra—Causas das Inundações na Praça 8 de Maio, em Coimbra, e Propostas de Intervenção; APRH—Associação Portuguesa de Recursos Hídricos: Alvor, Portugal, 2010. (In Portuguese) [Google Scholar]
- Ally, M. Modelling Road Gullies; Richard Allitt Associates Ltd: West Sussex, UK, 2011. [Google Scholar]
- Simoes, N.E.D.C. Urban Pluvial Flood Forecasting. Ph.D. Thesis, Imperial College London, London, UK, 2012. [Google Scholar]
- WaPUG, Wastewater Planning Users Group. Code of Practice for the Hydraulic Modelling of Sewer Systems; Chartered Institution of Water and Environmental Management (CIWEM): London, UK, 2002. [Google Scholar]
- Leitão, J.P.; Simões, N.E.; Pina, R.D.; Sá Marques, A.; Maksimović, Č.; Gonçalves, G. Surface floods in Coimbra: Simple and dual-drainage studies. In Proceedings of the 11th Plinius Conference on Mediterranean Storms, Barcelona, Spain, 7–10 September 2009.
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pina, R.D.; Ochoa-Rodriguez, S.; Simões, N.E.; Mijic, A.; Marques, A.S.; Maksimović, Č. Semi- vs. Fully-Distributed Urban Stormwater Models: Model Set Up and Comparison with Two Real Case Studies. Water 2016, 8, 58. https://doi.org/10.3390/w8020058
Pina RD, Ochoa-Rodriguez S, Simões NE, Mijic A, Marques AS, Maksimović Č. Semi- vs. Fully-Distributed Urban Stormwater Models: Model Set Up and Comparison with Two Real Case Studies. Water. 2016; 8(2):58. https://doi.org/10.3390/w8020058
Chicago/Turabian StylePina, Rui Daniel, Susana Ochoa-Rodriguez, Nuno Eduardo Simões, Ana Mijic, Alfeu Sá Marques, and Čedo Maksimović. 2016. "Semi- vs. Fully-Distributed Urban Stormwater Models: Model Set Up and Comparison with Two Real Case Studies" Water 8, no. 2: 58. https://doi.org/10.3390/w8020058
APA StylePina, R. D., Ochoa-Rodriguez, S., Simões, N. E., Mijic, A., Marques, A. S., & Maksimović, Č. (2016). Semi- vs. Fully-Distributed Urban Stormwater Models: Model Set Up and Comparison with Two Real Case Studies. Water, 8(2), 58. https://doi.org/10.3390/w8020058





