Methodology for Selecting Best Management Practices Integrating Multiple Stakeholders and Criteria. Part 1: Methodology
Abstract
:1. Introduction
2. Methodology
2.1. Problem Definition
| Classification | Description | Examples |
|---|---|---|
| Complete or total aggregation (American school of thought) | Seeking to loosen all incomparability, a single, comprehensive and definitive answer is obtained when adding the performances of the alternatives. |
|
| Partial aggregation (French-speaking school of thought) | Accepting situations that are incomparable, it is based on “outranking relationships” between alternatives when adding the performances of the alternatives |
|
| Local or iterative aggregation | The situation is translated into local judgments, with a small number of analyzed alternatives and without an explicit rule for an answer. |
|
2.1.1. AHP
2.1.2. ELECTRE III
2.1.3. PROMETHEE II
| Type | Description | Function |
|---|---|---|
| I | Usual criterion | |
| II | Quasi criterion | |
| III | Linear criterion | |
| IV | Level criterion | |
| V | Linear with indifference | |
| VI | Gaussian criterion |
2.1.4. MTOPSIS
2.2. Preliminary Site Analysis
2.3. Analysis of Alternatives
- : Future cost analyzed at year ($)
- : Discount rate (expressed as a decimal)
- : Year associated with the future cost.
- : Current base value of the cost analyzed ($)
- : Inflation rate (expressed as a decimal)
2.4. Stakeholder Analysis
2.5. Application of the MCDA Methods
2.6. Analysis and Comparison
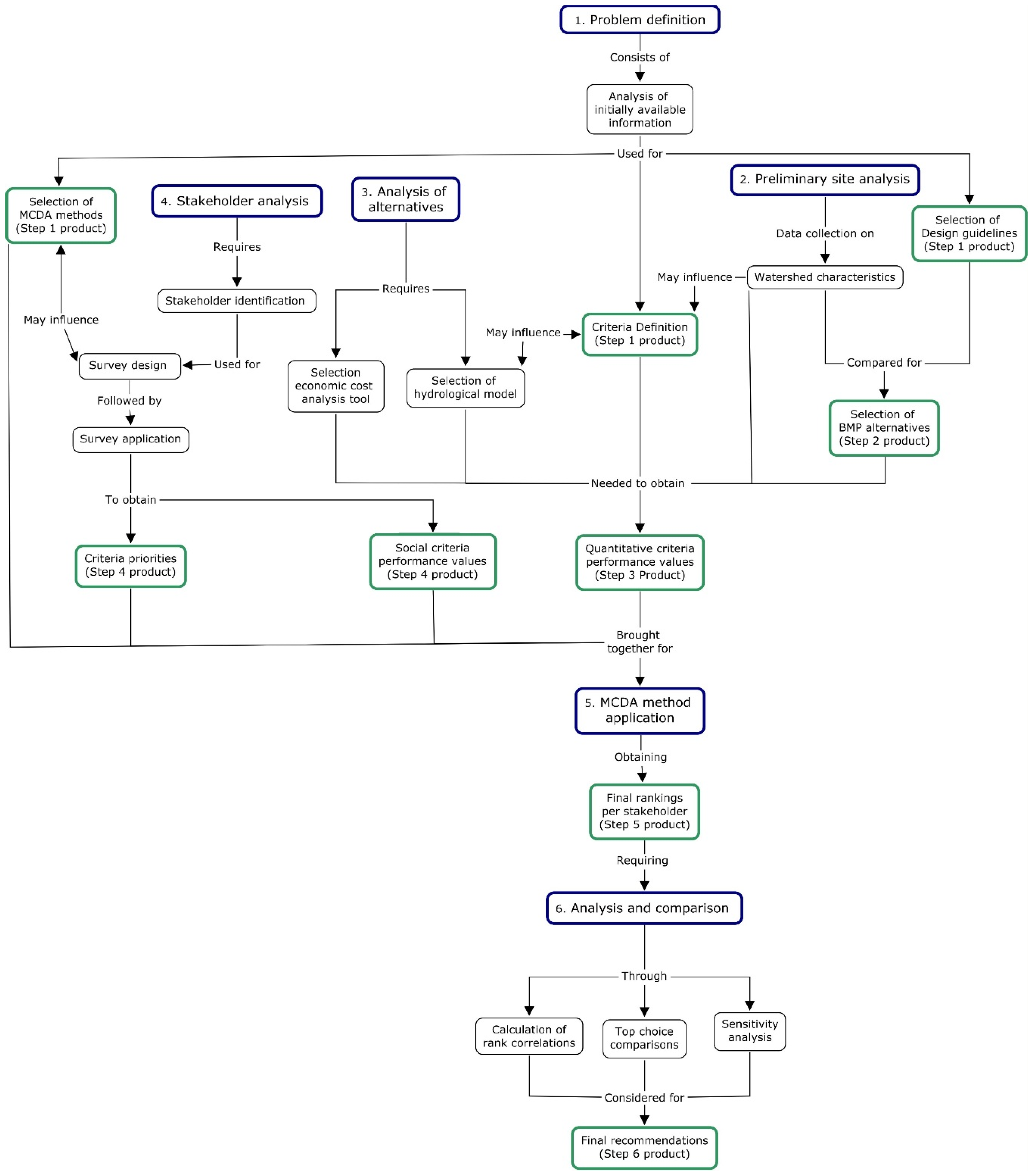
2.7. Sequence in the Methodology
| Step | Tasks | Product |
|---|---|---|
| 1. Problem definition |
|
|
| 2. Preliminary site analysis |
|
|
| 3. Analysis of alternatives |
|
|
| 4. Stakeholder Survey |
|
|
| 5. MCDA method applications |
|
|
| 6. Analysis and comparison |
|
|
3. Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| AHP | Analytical Hierarchy Process |
| BMPs | Best Management Practices |
| DHI | Danish Hydraulics Institute |
| ELECTRE | Elimination et Choix Traduisant la Réalité |
| GIS | Geographic information systems |
| MCDA | Multi-criteria decision aid |
| MTOPSIS | Modified Technique for Order Preference by Similarity to Ideal Solutions |
| NPV | Net Present Value |
| PROMETHEE | Preference Ranking Organization Method for Enrichment of Evaluation |
| STEP | Sustainable Technologies Program |
| SUSTAIN | System for Urban Stormwater Treatment and Analysis Integration |
| SWMM | Storm Water Management Model |
| USEPA | United States Environmental Protection Agency |
References
- Ahiablame, L.M.; Engel, B.A.; Chaubey, I. Effectiveness of low impact development practices: Literature review and suggestions for future research. Water Air Soil Pollut. 2012, 223, 4253–4273. [Google Scholar] [CrossRef]
- Rivard, G. Guide de Gestion des Eaux Pluviales; Ministère du Développement Durable Environnement et Lutte contre les Changements Climatiques: René-Lévesque, QC, Canada, 2011; p. 386. [Google Scholar]
- Linkov, I.; Moberg, E. Multi-Criteria Decision Analysis: Environmental Applications and Case Studies; CRC Press: Boca Raton, FL, USA, 2012; p. 204. [Google Scholar]
- Maystre, L.Y.; Pictet, J.; Simos, J.; Roy, B. Méthodes Multicritères ELECTRE: Description, Conseils Pratiques et Cas D'application à la Gestion Environnementale; Presse Polytehcniques et Universitaires Romandes: Laussane, Switzerland, 1994; p. 323. [Google Scholar]
- Chen, L.; Qiu, J.; Wei, G.; Shen, Z. A preference-based multi-objective model for the optimization of best management practices. J. Hydrol. 2015, 520, 356–366. [Google Scholar] [CrossRef]
- Zou, R.; Riverson, J.; Liu, Y.; Murphy, R.; Sim, Y. Enhanced nonlinearity interval mapping scheme for high-performance simulation-optimization of watershed-scale BMP placement. Water Resour. Res. 2015, 51, 1831–1845. [Google Scholar] [CrossRef]
- Efta, J.A.; Chung, W. Planning Best Management Practices to Reduce Sediment Delivery from Forest Roads Using WEPP: Road Erosion Modeling and Simulated Annealing Optimization. Croat. J. For. Eng. 2014, 35, 167–178. [Google Scholar]
- Fuamba, M.; Coulais, C.; Bertrand, H. An innovative method for selecting efficient Best Management Practices. In Proceedings of the 12th International Conference on Urban Drainage, Porto Alegre, Brazil, 11–16 September 2011; p. 8.
- Young, K.D.; Younos, T.; Dymond, R.L.; Kibler, D.F.; Lee, D.H. Application of the analytic hierarchy process for selecting and modeling stormwater best management practices. J. Contemp. Water Res. Educ. 2010, 146, 50–63. [Google Scholar] [CrossRef]
- Jia, H.; Yao, H.; Tang, Y.; Yu, S.L.; Zhen, J.X.; Lu, Y. Development of a multi-criteria index ranking system for urban runoff best management practices (BMPs) selection. Environ. Monit. Assess. 2013, 185, 7915–7933. [Google Scholar] [CrossRef] [PubMed]
- Martin, C.; Ruperd, Y.; Legret, M. Urban stormwater drainage management: The development of a multicriteria decision aid approach for best management practices. Eur. J. Oper. Res. 2007, 181, 338–349. [Google Scholar] [CrossRef]
- Chitsaz, N.; Banihabib, M.E. Comparison of Different Multi Criteria Decision-Making Models in Prioritizing Flood Management Alternatives. Water Resour. Manag. 2015, 29, 2503–2525. [Google Scholar] [CrossRef]
- Dyer, J.S. MAUT—Multiattribute Utility Theory. In Multiple Criteria Decision Analysis: State of the Art Surveys; Figueira, J., Greco, S., Ehrgott, M., Eds.; Springer Science & Business Media: Boston, MA, USA, 2005; pp. 265–296. [Google Scholar]
- Rogers, M.G.; Bruen, M.; Maystre, L.Y. ELECTRE and decision support: Methods and Applications in Engineering and Infrastructure Investment; Kluwer Academic Publishers: Boston, MA, USA, 2000; p. 208. [Google Scholar]
- Brans, J.P.; Mareschal, B. PROMETHEE Methods. In Multiple Criteria Decision Analysis: State of the Art Surveys; Figueira, J., Greco, S., Ehrgott, M., Eds.; Springer Science & Business Media: Boston, MA, USA, 2005; pp. 163–196. [Google Scholar]
- San Cristóbal, J.R. Multi Criteria Analysis in the Renewable Energy Industry; Springer Science & Business Media: London, UK, 2012; pp. 43–48. [Google Scholar]
- Saaty, T.L.; Vargas, L.G. Models, Methods, Concepts & Applications of the Analytic Hierarchy Process, 2nd ed.; Springer Science & Business Media: New York, NY, USA, 2012; p. 354. [Google Scholar]
- Ren, L.; Zhang, Y.; Wang, Y.; Sun, Z. Comparative analysis of a novel M-TOPSIS method and TOPSIS. Appl. Math. Res. Express 2007. [Google Scholar] [CrossRef]
- Zoppou, C. Review of urban storm water models. Environ. Model. Softw. 2001, 16, 195–231. [Google Scholar] [CrossRef]
- Global Sustainable Development Report, 2015 Edition ed; United Nations Deparment of Economic and Social Affairs (UN DESA): New York, NY, USA, 2015; p. 202.
- Chen, C.F.; Sheng, M.Y.; Chang, C.L.; Kang, S.F.; Lin, J.Y. Application of the SUSTAIN model to a watershed-scale case for water quality management. Water 2014, 6, 3575–3589. [Google Scholar] [CrossRef]
- Danish Hydraulics Institute. MIKE URBAN User’s Manual; DHI Water Environment Health: Hørsholm, Denmark, 2008. [Google Scholar]
- Cahill, T.H. Low Impact Development and Sustainable Stormwater Management; John Wiley & Sons: Hoboken, NJ, USA, 2012; p. 293. [Google Scholar]
- Reducing Stormwater Costs through Low Impact Development (LID) Strategies and Practices; EPA 841-F-07-006 Prepared under Contract No. 68-C-02-108; Environmental Protection Agency: Washington, DC, USA, 2007; p. 30.
- Uda, M.; Van Seters, T.; Graham, C.; Rocha, L. Assessment of Life Cycle Costs for Low Impact Development Stormwater Management Practices; Sustainable Technologies Evaluation Program, Toronto and Region Conservation Authority: Toronto, ON, Canada, 2013; p. 112. [Google Scholar]
- Sustainable Technologies Evaluation Program, Toronto and Region Conservation Authority. Low Impact Development Life Cycle Costs. Available online: http://www.sustainabletechnologies.ca/wp/home/urban-runoff-green-infrastructure/low-impact-development/low-impact-development-life-cycle-costs/ (accessed on 4 July 2015).
- Athawale, V.M.; Chakraborty, S. A comparative study on the ranking performance of some multi-criteria decision-making methods for industrial robot selection. Int. J. Ind. Eng. Comput. 2011, 2, 831–850. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aceves, M.C.; Fuamba, M. Methodology for Selecting Best Management Practices Integrating Multiple Stakeholders and Criteria. Part 1: Methodology. Water 2016, 8, 55. https://doi.org/10.3390/w8020055
Aceves MC, Fuamba M. Methodology for Selecting Best Management Practices Integrating Multiple Stakeholders and Criteria. Part 1: Methodology. Water. 2016; 8(2):55. https://doi.org/10.3390/w8020055
Chicago/Turabian StyleAceves, Mauricio Carvallo, and Musandji Fuamba. 2016. "Methodology for Selecting Best Management Practices Integrating Multiple Stakeholders and Criteria. Part 1: Methodology" Water 8, no. 2: 55. https://doi.org/10.3390/w8020055
APA StyleAceves, M. C., & Fuamba, M. (2016). Methodology for Selecting Best Management Practices Integrating Multiple Stakeholders and Criteria. Part 1: Methodology. Water, 8(2), 55. https://doi.org/10.3390/w8020055





