Assessing Community Resilience to Coastal Hazards in the Lower Mississippi River Basin

Abstract

This paper presents an assessment of community resilience to coastal hazards in the Lower Mississippi River Basin (LMRB) region in southeastern Louisiana. The assessment was conducted at the census block group scale. The specific purpose of this study was to provide a quantitative method to assess and validate the community resilience to coastal hazards, and to identify the relationships between a set of socio-environmental indicators and community resilience. The Resilience Inference Measurement (RIM) model was applied to assess the resilience of the block groups. The resilience index derived was empirically validated through two statistical procedures: K-means cluster analysis of exposure, damage, and recovery variables to derive the resilience groups, and discriminant analysis to identify the key indicators of resilience. The discriminant analysis yielded a classification accuracy of 73.1%. The results show that block groups with higher resilience were concentrated generally in the northern part of the study area, including those located north of Lake Pontchartrain and in East Baton Rouge, West Baton Rouge, and Lafayette parishes. The lower-resilience communities were located mostly along the coastline and lower elevation area including block groups in southern Plaquemines Parish and Terrebonne Parish. Regression analysis between the resilience scores and the indicators extracted from the discriminant analysis suggests that community resilience was significantly linked to multicomponent capacities. The findings could help develop adaptation strategies to reduce vulnerability, increase resilience, and improve long-term sustainability for the coastal region.

1. Introduction

Coastal communities around the world are especially vulnerable to multiple threats and hazards [1,2]. A major societal challenge is to ensure the safety and security of a population that is continually threatened by natural hazards and periodically subjected to catastrophic disasters. The Lower Mississippi River Basin (LMRB) in southeastern Louisiana is one of the most impacted and vulnerable coasts in the continental USA. This area has been facing recurring threats from coastal hazards, including large-scale, rapid-moving disasters such as hurricanes and storm surges and slow-moving disturbances such as land subsidence and sea level rise. These hazardous events have negatively impacted the communities in various degrees. The uneven responses and recovery behaviors of the communities may be due to their spatial variation of exposure to natural hazards, damage sustained, and social and environmental capacity [3,4,5,6,7,8]. Therefore, identifying the places that are resilient to disasters and understanding the underlying indicators are critical for pre-disaster preparation, post-disaster recovery, and establishment of mitigation plans.

It is increasingly recognized that designing and implementing adaptive and mitigation community management for coastal zone requires an integrated interdisciplinary approach. An important use of resilience assessment is the identification of key indicators and how these various indicators (e.g., social, economic, environmental) are connected to form resilience capacities [2,9]. This information will help decision-makers in formulating better strategies to enhance community resilience. Resilience assessment also deepens our understanding of which regions or communities have the lowest or the highest resilience, and how the indicators can be used to monitor the progress of communities in resilience building [9,10,11,12,13,14,15]. Resilience assessment can be used to provide guidelines for allocating resources and infrastructure development, as well as for strengthening zoning regulations, environmental sensitive area protection, and building codes to reduce vulnerability and risk [16]. However, a challenge remains in developing a framework that can empirically validate the resilience assessment results and identify the underlying driving factors.

This study applies a newly developed community resilience measurement framework, the Resilience Inference Measurement (RIM) model, to assess the community resilience to coastal hazards in the Lower Mississippi River Basin region [7,8,17]. The RIM framework considers community resilience as a broader concept and defines resilience as “the ability to prepare and plan for, absorb, recover from, and more successfully adapt to adverse events” [4,5,7,18,19]. The RIM framework provides a theoretically sound and practical approach to assess and validate the community resilience rankings and scores. It uses three dimensions (exposure, damage and recovery) to denote two relationships (vulnerability and adaptability). Both k-means clustering and discriminant analysis are employed to derive the a priori and posterior resilience rankings and identify the key social-environmental indicators to explain resilience. The method is based on the principle of empirical validation, and the derived statistical functions can be used to infer (predict) resiliency in other similar study regions.

This study assesses the community resilience in the LMRB region at a fine geographic scale, the census block group scale. The spatial variation of the resilience assessment in the study region is examined. A regression analysis is conducted to examine the relationship between community resilience and socio-environmental indicators. The results could serve as a useful tool for resilience planning and management.

2. Assessing Community Resilience to Natural Hazards

Recent studies have developed a number of theoretical frameworks and indices to analyze community resilience [4,7,8,18,20,21,22,23]. Some examples are described as follows. The Baseline Resilience Indicators for Communities (BRIC), developed by Cutter and her research team [4,24], are designed to be a comprehensive integration of all the components. The BRIC have six components, including social, economic, infrastructural, institutional, community, and environmental. Each of the components has several indicators that can be used to measure resilience at the community level. The selection of the variables is based on the literature, and the method of aggregation is easy to compute and could be applied for use in a policy context. The National Oceanic and Atmospheric Administration’s Coastal Resilience Index (CRI) [25] is targeted primarily at coastal storms. The CRI utilizes six components: critical facilities, transportation, community plans, mitigation measures, business plan, and social system. Sherrieb and others [18] identified an exhaustive list of 88 variables and then used correlation analysis to reduce the set into 17 variables representing two components, social capital and economic development, as indicators of capacities for community resilience. Additional resilience-related indices include the Predictive Indicator of Vulnerability [23], the Disaster Risk Index [26], the community assessment of resilience tool [5], the Resilience Inference Measurement (RIM) index [7], and the Climatic Hazard Resilience Indicator for Localities (CHRIL) [9].

The studies discussed above represent significant efforts in resilience index selection, model conceptualization, and model construction. Ostadtaghizadeh et al. [27], in a systematic review on community disaster resilience assessment models, concluded that existing community resilience indices generally include five important domains (social, economic, institutional, infrastructural and natural) and there is a need to use appropriate and effective methods to quantify their relative contribution to resilience.

However, validation of a resilience index with external reference data has posed a persistent challenge [28]. Effort has been made to validate indices either externally with real observable outcomes [29,30,31], or qualitatively with practitioners [32], or internally with sensitivity and uncertainty analysis [28]. Nonetheless, studies that focus on the validation of resilience indices, either qualitatively or quantitatively, are still uncommon. This is largely because community resilience is not a directly observable phenomenon and the validation of resilience index requires the use of proxies [28]. Currently, there are no commonly recognized independent proxy data used in the validation of resilience assessment. In many previous studies on resilience assessment, the lack of empirical validation of variable selection and the impact of variables on resilience are considered serious shortcomings [29].

3. Materials and Methods

3.1. Resilience Inference Measurement (RIM) Approach

This paper is based on a newly developed model, the Resilience Inference Measurement (RIM) model [7,17]. The RIM model offers a method for assessing the indirectly observable community resilience and validating the selection of capacity variables externally and internally. The method was first applied to quantify resilience to climate-related hazards for 52 counties along the northern Gulf of Mexico and yielded high classification accuracy (94.2%). The method has since been applied to evaluate the resilience of the Caribbean countries to coastal hazards and earthquake resilience in China [8,33].

As mentioned above, the RIM framework defines resilience as “the ability to prepare and plan for, absorb, recover from, and more successfully adapt to adverse events” [5,7]. Specifically, the RIM model uses three dimensions to denote two relationships (Figure 1). The three dimensions are the exposure of a community to hazards (such as hurricane frequency), the damage a community suffered from the exposure (such as property damage), and the recovery after disasters (such as population return). Vulnerability and adaptability are two latent relationships between the three dimensions, whereas resilience capacity, also a latent relationship, is indicated by both vulnerability and adaptability.

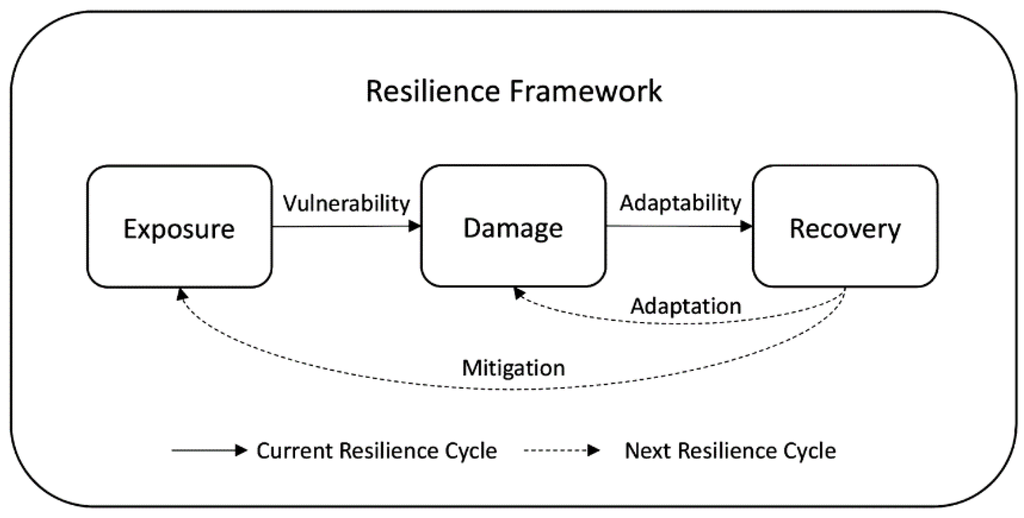
Figure 1. The Resilience Inference Measurement (RIM) framework [7].

Figure 1. The Resilience Inference Measurement (RIM) framework [7].

In the RIM model, vulnerability refers to the latent relationship between exposure and damage, whereas adaptability indicates the latent relationship between damage and recovery [7]. If a community (e.g., a block group) has high exposure to a hazard but sustains low damage, then the community is considered to have low vulnerability. Similarly, if a community sustains high damage but has a favorable recovery (e.g., return of population, infrastructure, or health status), then the community is considered to have high adaptability. Resilience is measured based on the two relationships. A high vulnerability/adaptability ratio is considered low resilience, whereas a low vulnerability/adaptability ratio is considered high resilience. The RIM model borrows the concept from the ecological resilience literature and classifies resilience into four states; from low to high resilience they are called susceptible, recovering, resistant, and usurper. These descriptive names used here to distinguish the four states of community resilience were slightly modified from the ecological resilience literature and adopted into the RIM framework to maintain consistency [17,34,35].

The actual process leading to these four states is more complex, which could involve two underlying processes—mitigation and adaptation. Mitigation refers to the actions or strategies taken to minimize the potential exposure. Adaptation refers to the measures applied to lessen the impacts that result from the disastrous events so that the community can recover, such as raising the housing structures above the flooding level to avoid serious damages from the next disaster [36]. The two processes are highly interrelated and together they indicate resilience. It is expected that a community that has capacity to generate effective mitigation strategies should also have the ability to adapt. In terms of resilience index development, however, this paper focuses only on evaluating the conditions of the three dimensions (exposure, damage, and recovery) and their relations with the underlying capacities as represented by a number of socioeconomic and environmental indicators [7]. Moreover, community resilience is a dynamic phenomenon, and vulnerability and adaptability change between resilience cycles due to the repetition of external disturbances. However, the dynamic resilience changes between disturbances are difficult to capture. For measurement purposes, the levels of community resilience are measured at certain time points so that the scores can be used to monitor the progress through time [4].

A major feature of the RIM model is empirical validation. The model uses real exposure, damage, and recovery data to derive the index and the relative contributions of resilience indicators. Two statistical techniques are involved when applying the RIM model. First, k-means clustering is conducted to derive the a priori resilience classification based upon the three dimensions (exposure, damage, recovery). Resilience groups are categorized into four states (susceptible, recovering, resistant, and usurper). Once the resilience memberships of the communities are identified, discriminant analysis is used to characterize the a priori resilience groups by a set of pre-disaster resilience capacity indicators. These pre-event indicators are extracted from the literature to serve as typical proxies for evaluating the community resilience spatially and temporally [20]. The posterior classification from discriminant analysis is then compared with the a priori classification from k-means clustering, thus providing a validation of the relative importance of the indicators.

The classification results from k-means clustering and the selected set of natural-human indicators are the input for discriminant analysis. In discriminant analysis, the Mahalanobis distances from each case (each community) to each of the resilience group centroids are calculated [37]. The probabilities of membership belonging to each group are converted based on the Mahalanobis distances. The shorter the Mahalanobis distance, the higher the probability this community belongs to the corresponding resilience group. Each case is assigned to the group that has the highest probability of group membership, which is also called the posterior group membership. To further explore the relationship between community resilience and indicators, the discrete resilience categories can be converted to continuous resilience scores based on the probabilities of group membership derived from discriminant analysis [7,38]. The continuous resilience score of each block group can be calculated using Equation (1).

$$ReScore={\displaystyle \sum }_{i=1}^{m}i\times Prob\left(i\right)$$

(1)

where m is the number of resilience groups from k-means clustering, $i$ is the ranking of resilience groups. $Prob\left(i\right)$ denotes the posterior probability of an individual case belonging to a particular resilience group $i$.

3.2. Study Area

This study focuses on southeastern coastal Louisiana, broadly recognized as the Lower Mississippi River Basin (LMRB) (Figure 2). This area includes 26 parishes and three major metropolitan areas (New Orleans, Baton Rouge, and Lafayette) in southern Louisiana. This region has been devastated by storm surges, floods, and hurricanes. At least five hurricanes (Katrina, Rita, Gustav, Ike, and Isaac) hit this region in the past decade (2005–2015), which caused significant loss of human lives and damages to properties [39,40,41,42,43,44,45]. The most destructive natural disaster in the U.S. history, Hurricane Katrina, crossed this region and caused severe destruction in August 2005. The most severe impact took place in New Orleans where the death toll was about 1600. From 2005 (pre-Katrina) to 2012, the population declined by 18.9% in Orleans Parish, 16.2% in Plaquemines Parish, and 35.9% in St. Bernard parish. In addition, the unemployment rate increased by 2.6% during this period. With the impending threats of climate change and sea level rise, this area is facing a serious challenge, which is how to develop adaptation strategies to reduce vulnerability, increase resilience, and achieve coastal sustainability.

The study area has experienced different extents of exposure to coastal hazards and behaved differently in different parts of the region after these disturbances. This makes the study area a test bed for exploring the disaster resilience of places. The resilience analysis was conducted at the census block group scale, with a total of 2086 block groups included in the study (24 block groups in the study area were not included due to no data).

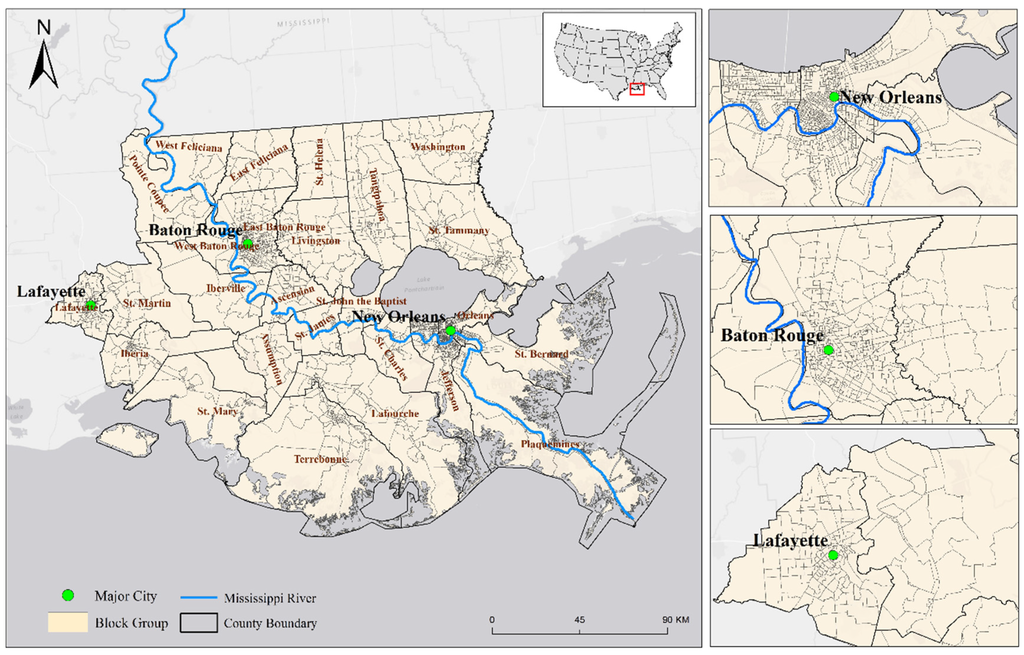
Figure 2. Study area at the block group level.

Figure 2. Study area at the block group level.

3.3. Data Collection and Processing

3.3.1. Exposure, Damage, Recovery

The three dimensions (exposure, damage, and recovery) in the RIM model were defined as: (1) the exposure to hazards, represented by the number of times a block group was hit by coastal hazards from 2000 to 2010, adjusted by the severity of the damage; (2) the damage from the exposure, represented by the property damage caused by these coastal hazards recorded in exposure; (3) the recovery, represented by population change from 2000 to 2010.

The exposure and damage data were derived from the Storm Event Database obtained from the National Oceanographic and Atmospheric Administration’s (NOAA) National Climate Center (NCDC) (https://www.ncdc.noaa.gov/). This data set contains a chronological listing of different types of hazards, such as hurricanes, tornadoes, snow, droughts, and others. Five major types of coastal hazards were considered in this study including storm surge, flood, hurricane, tropical storm, and tornado. In the NOAA raw dataset, each hazard event was recorded with its beginning and ending dates, event type, and property damages at one of the three geographic scales: point, city, or county scale. Data at the point level include the X-Y coordinates that an event hit. Data at the city and county levels list the cities or counties that an event affected.

To calculate the exposure and damage variables, the point data were tabulated according to the block groups they belong to. For city and county data, a volume-preserving areal interpolation method that distributes the value according to the developed land area was used to downscale the city- and county-level data into block groups [46,47,48].

The exposure to coastal hazards in this study is a cumulative value from 2000 to 2010. To more accurately represent exposure at the block group level, event duration, hazard frequency, and the weight of hazards were taken into account instead of simply event frequency (Equation (2)) [7,17]. For each block group x, the equation to calculate its exposure can be expressed as follows:

$$\mathit{\text{Exposure(x)}}={{\displaystyle \sum }}_{i=1}^5{{\displaystyle \sum }}_{j=1}^{N{x}_i}{w}_i(BeginDat{a}_{ij}-EndDat{a}_{ij})$$

(2)

where N_xi is the number of events of hazard type i occurred in block group x, j is the j^th event, event duration is derived from the difference of BeginDate_ij and EndDate_ij of event j of type i. Since this study focuses on five types of coastal hazards that have different magnitudes, it is necessary to evaluate the relative impacts $(w_i)$ of these five types of coastal hazards in order to integrate them into the exposure dimension. For example, Hurricane Katrina was far more severe than a flood. w_i is the weight of hazard type i, which is the ratio of the total damage caused by hazard type i and the total damage caused by all the five types of hazards (Equation (3)). Using the ratio between the total damage of an event type and the total damage of all events as the weight of that event to its relative severity would not create collinearity between the exposure and damage of each block group (Equation (4)). A correlation analysis between the exposure (as defined by Equation (2)) and the damage (as defined by Equation (4)) shows a low correlation (r = 0.142), given that some correlation between the two dimensions should be expected.

$$w_i=\frac{Total Damage of hazard i}{Total Damage of all hazards}$$

(3)

The damage for each block group was the cumulative property damage caused by the events from exposure divided by the population of the block group at the time of the event. Property damages caused by natural hazards always occur in developed land areas (e.g., asphalt, concrete, buildings), whereas barren land seldom has property damages. Based on this assumption, for each hazard event, the total value of property damage of a city/county was distributed to the block groups according to their developed land area. For example, if the developed land area of Block Group 1 in County A accounts for 5% of the total developed land area in County A, where County A suffered a total property damage of one million dollars from a hurricane event. Then, Block Group 1 is assigned 50 thousand (5% ×1 million) dollars damage from this hazard. The cumulative property damage for each block group is calculated by Equation (4).

$$Damage\left(x\right)={{\displaystyle \sum }}_{i=1}^N\raisebox{1ex}{$Damage\left(i\right)\times Dvlp\left(x\right)$}\!\left/ \!\raisebox{-1ex}{$\left(Dvlp\left(X\right)\times Pop\left(x\right)\right)$}\right.$$

(4)

where $Damage\left(x\right)$ = cumulative property damages of block group x during the ten year period; N is the number of hazard events this block group suffered; i is a particular event and $Damage\left(i\right)$ is the total property damage caused by this event as recorded in the raw data set; $Dvlp\left(x\right)$ is the developed land area of this block group; $Dvlp\left(X\right)$ is the developed land area of the city/county; $Pop\left(x\right)$ is the population of the block group x at the time of the event.

Studies have shown that recovery from a disastrous event takes an extensive amount of time, often measured in years [29]. A content analysis study of community recovery indicators found that population change/return was the most used recovery indicator in the disaster-focused journal articles from 2000 to 2010, and a following Delphi survey showed that experts reached consensus on its importance [49]. As stated in Lam et al. [7], population change over time reflects the wide range of decisions made by individuals and businesses to remain in or move away from an area after disturbances. It is a broad indicator of recovery that takes into account the rational behavior and choices of residents and organizations to locate to communities in the area, even those with higher levels of exposure to natural disturbances. Population change on its own may not necessarily indicate recovery, but it is meaningful when evaluated in the context of exposure and damages from storms and other natural disturbances over multiple years. Thus, population change between 2000 and 2010 at the block group level was used to indicate the recovery in this study. Population data were obtained from the U.S. Census Bureau.

3.3.2. Community Resilience Indicators

Identifying pre-disaster resilience indicators is a critical step in community resilience analysis [20]. This study gathered a list of representative resilience capacity variables that were previously discussed or utilized in the literature and also for data which are publicly accessible [4,5,26,50]. Twenty-five capacity indicators were selected, which cover multiple components of community resilience (social, economic, infrastructure, community, and environmental) (Table 1). The five components are the commonly acknowledged elements in grasping the multifaceted concept of community resilience [4,5,51]. Indicators from other dimensions could also be taken into consideration, such as those indicating social and cultural acceptability (organized beliefs of correctness, perceptions of level of participation and inclusiveness, etc.). However, these soft variables could not be included in this study due to their unavailability especially at such a geographical scale.

Table 1. Resilience Indicators.

Category	Variables	Justification
Social	% population over 65 years old	Morrow (2008) [52]
	Median age	Cutter et al. (2010) [4]
	Population density	Ryu et al. (2011) [53]
	% households without a vehicle	Cutter et al. (2010) [4]
	% housing units with telephone service available	Cutter et al. (2010) [4]
	% population over 25 but no schooling complete	Cutter et al. (2010) [4]
	% female householder	Cutter et al. (2010) [4]
Economic	employment population per 10,000 lab forces	Cutter et al. (2010) [4]
	% population living in poverty	Cutter et al. (2014) [24]
	Median household income	Sherrieb et al. (2010) [18]
	Median value of owner occupied housing	Cutter et al. (2014) [24]
	Per capita income	Lam et al. (2015) [7]
	% population employed in construction, transportation, material moving	NIST (2015) [51]
Infrastructure	% mobile homes	Cutter et al. (2010) [4]
	Total housing units per square mile	Cutter et al.(2010) [4]
	% housing units built after 2000	Cutter et al. (2010) [4]
	Total length of roads per sq. km	Cutter et al. (2010) [4]
	Health care facility per 1,000 population	Few (2007) [54]
	Number of schools per sq.km	Cutter et al. (2010) [4]
Community	% population that were native born and also live in the same house or same county	Cutter et al. (2010) [4]
Environmental	Mean elevation	Cutter et al. (2010) [4]
	% developed land area	Cutter et al. (2008) [20]
	Land loss area in sq.km from 2000 to 2010	The authors
	% area in an inundation zone	Cutter et al. (2008) [20]
	Mean subsidence rate	Zou et al. (2016) [55]

Table 1. Resilience Indicators.

Category	Variables	Justification
Social	% population over 65 years old	Morrow (2008) [52]
	Median age	Cutter et al. (2010) [4]
	Population density	Ryu et al. (2011) [53]
	% households without a vehicle	Cutter et al. (2010) [4]
	% housing units with telephone service available	Cutter et al. (2010) [4]
	% population over 25 but no schooling complete	Cutter et al. (2010) [4]
	% female householder	Cutter et al. (2010) [4]
Economic	employment population per 10,000 lab forces	Cutter et al. (2010) [4]
	% population living in poverty	Cutter et al. (2014) [24]
	Median household income	Sherrieb et al. (2010) [18]
	Median value of owner occupied housing	Cutter et al. (2014) [24]
	Per capita income	Lam et al. (2015) [7]
	% population employed in construction, transportation, material moving	NIST (2015) [51]
Infrastructure	% mobile homes	Cutter et al. (2010) [4]
	Total housing units per square mile	Cutter et al.(2010) [4]
	% housing units built after 2000	Cutter et al. (2010) [4]
	Total length of roads per sq. km	Cutter et al. (2010) [4]
	Health care facility per 1,000 population	Few (2007) [54]
	Number of schools per sq.km	Cutter et al. (2010) [4]
Community	% population that were native born and also live in the same house or same county	Cutter et al. (2010) [4]
Environmental	Mean elevation	Cutter et al. (2010) [4]
	% developed land area	Cutter et al. (2008) [20]
	Land loss area in sq.km from 2000 to 2010	The authors
	% area in an inundation zone	Cutter et al. (2008) [20]
	Mean subsidence rate	Zou et al. (2016) [55]

The census variables were collected from the U.S. Census Bureau (http://www.census.gov/) and the National Historical Geographic Information System (https://www.nhgis.org/). Land cover variables were obtained from the National Land Cover Database (http://www.mrlc.gov/). Elevation data were downloaded from the National Elevation Dataset (http://nationalmap.gov/elevation.html). The land subsidence data were obtained from the National Geodetic Survey (NGS) (http://www.ngs.noaa.gov/) database and then processed by the authors. Land loss rates were tabulated by the authors using the raw data from the National Wetlands Research Center (http://www.nwrc.usgs.gov/). Percent of area in an inundation zone was calculated using the raw data from FEMA National Flood Hazard Layer (http://catalog.data.gov/dataset).

3.4. Clustering Resilience Groups

K-means clustering is an unsupervised classification method. It aims to partition n observations into k (≤n) clusters such that the within-cluster sum of squares is minimized and each observation belonging to the cluster has the nearest distance to its centroid [56]. Based on the three dimensions (exposure, damage, recovery), k-means clustering was used to classify the block groups into different resilience states.

Before conducting the k-means clustering analysis, each dimension was standardized into z-scores (Equation (5)) to avoid the strong effect caused by different sizes of the three dimensions [57].

$$\mathrm{Z}(\mathrm{x})=\frac{x-\overline{x}}{{\sigma }_x}$$

(5)

where $\overline{x}$ and ${\sigma }_x$ are the mean and standard deviation, respectively, of variable x.

An important step in k-means clustering is to identify the optimal number of strong clusters. One efficient way is to identify from the scree plot where the sharpest drop of total within-cluster sum of squares occurs when the observations are divided into different number of clusters [58]. Figure 3 shows how the total within-cluster sum of square of all the block groups decreases as the number of clusters increases. The value of the total within-cluster sum of squares drops distinctly when moving from 1 to 4 clusters. After 4 clusters, there is no significant drop. This confirms that the 4-cluster solution defined in RIM model is reasonable for this study. Therefore a 4-cluster solution was used. The centroid values of each cluster on the three dimensions were used to identify the resilience state of the cluster.

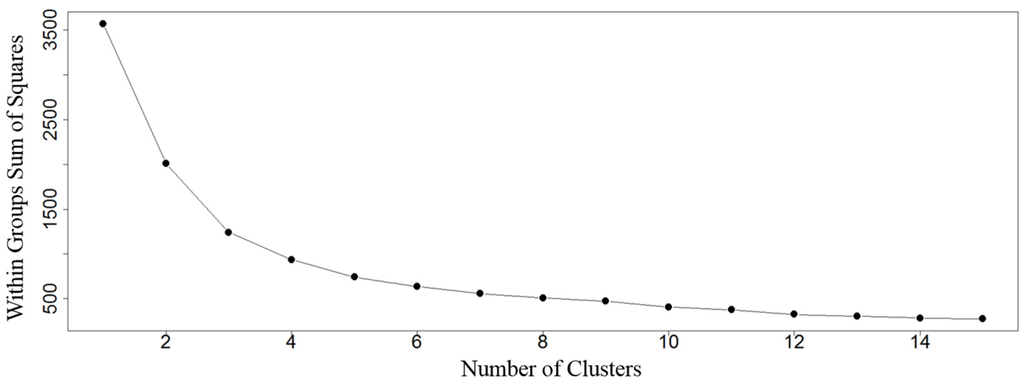
Figure 3. Plot of total within-cluster sum of squares against number of clusters.

Figure 3. Plot of total within-cluster sum of squares against number of clusters.

3.5. Discriminant Analysis of Resilience Indicators

K-means clustering classified the block groups into four resilience states. The next step is to identify the underlying socioeconomic and environmental characteristics that can predict the community resilience states. Discriminant analysis is an inferential statistical technique that is used when the dependent variable is categorical and the independent variables are interval or ratio. It involves deriving a linear combination of independent variables that can discriminate effectively between a priori defined groups [37,59].

Discriminant analysis requires the assumption of normality of the data set. In this study, normality was tested both quantitatively by the Kolmogorov-Smirnov normality test and qualitatively by visual inspection of the histograms. Although not all the variables were found to be strictly normally distributed, they are fairly symmetrically distributed with minor positive or negative skewness. It has been suggested that violation of the normality assumption is not fatal and that discriminant analysis is still robust and reliable to minor violation of the assumption, especially when a large sample of observations is used and the resultant classification accuracy is high [60].

Discriminant analysis with the stepwise option statistically reduces the number of variables from an exhaustive list, and picks as few variables as possible to explain as much variance as possible [61]. It selects variables based on a pre-defined criterion (F-value > 3.84 in this study). The F-value for a variable indicates its statistical significance in the discrimination between groups. In other words, it is a measure of the extent to which a variable makes a unique contribution to the prediction of group membership. Therefore, stepwise discriminant analysis also helps reduce the collinearity among the original set of variables. The selected variables from this step will serve as independent variables in the subsequent regression analysis.

To help explain the relationship between resilience scores computed from the discriminant analysis procedure and the indicator variables, an ordinary least squares (OLS) regression analysis was conducted. The continuous resilience score calculated from Equation (1) was used as the dependent variable and the socio-environmental indicators selected from the stepwise discriminant analysis were used as independent variables. Figure 4 explains the procedures employed in this study.

Figure 4. Flowchart of the procedure used in this study.

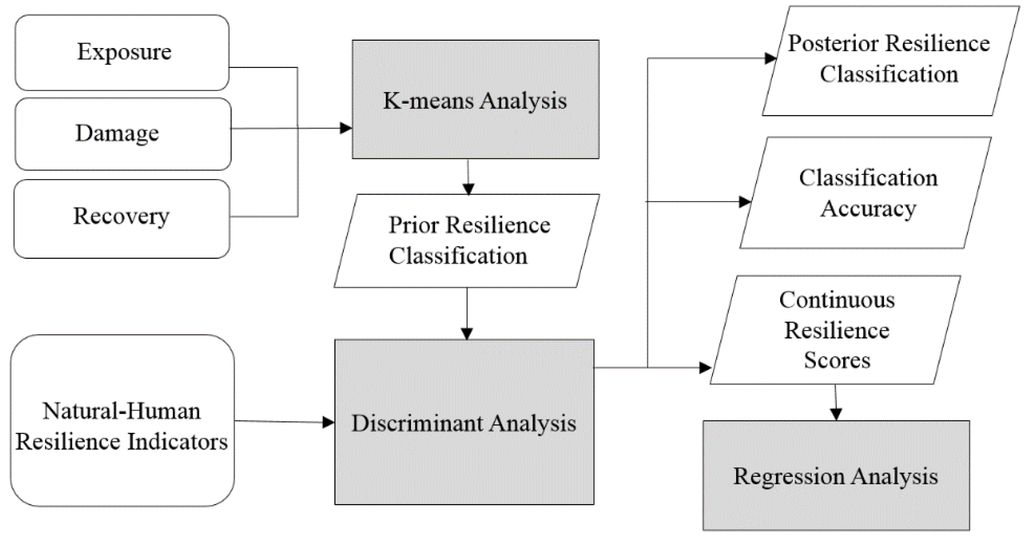
Figure 4. Flowchart of the procedure used in this study.

4. Results and Discussion

During the ten-year study period, a total of 420 coastal-related hazard events severely affected this study area, resulting in over 50 billion dollars of property damages. Figure 5 shows the spatial pattern of the three dimensions in standardized z-values. Of the 2086 block groups, the highest exposure values (>1.0 standard deviation) occurred in the parishes along the coastline (in the dark shade of brown), such as Jefferson, Plaquemines, St. Bernard, and Lafourche. High per capita damage block groups (>1.0 stand deviation) were found mostly along the Mississippi river in Plaquemines Parish and in some parts of Orleans and Lafourche parishes. Block groups with the highest population increase (>1.0 standard deviation) were scattered, with more of them located in the northern part of the study area. Several block groups in southern Plaquemines Parish along the coastline lost all the population in 2010 and became zero populated from 2000 to 2010. This area suffered the highest level of exposure and was where intense land subsidence and land loss occurred.

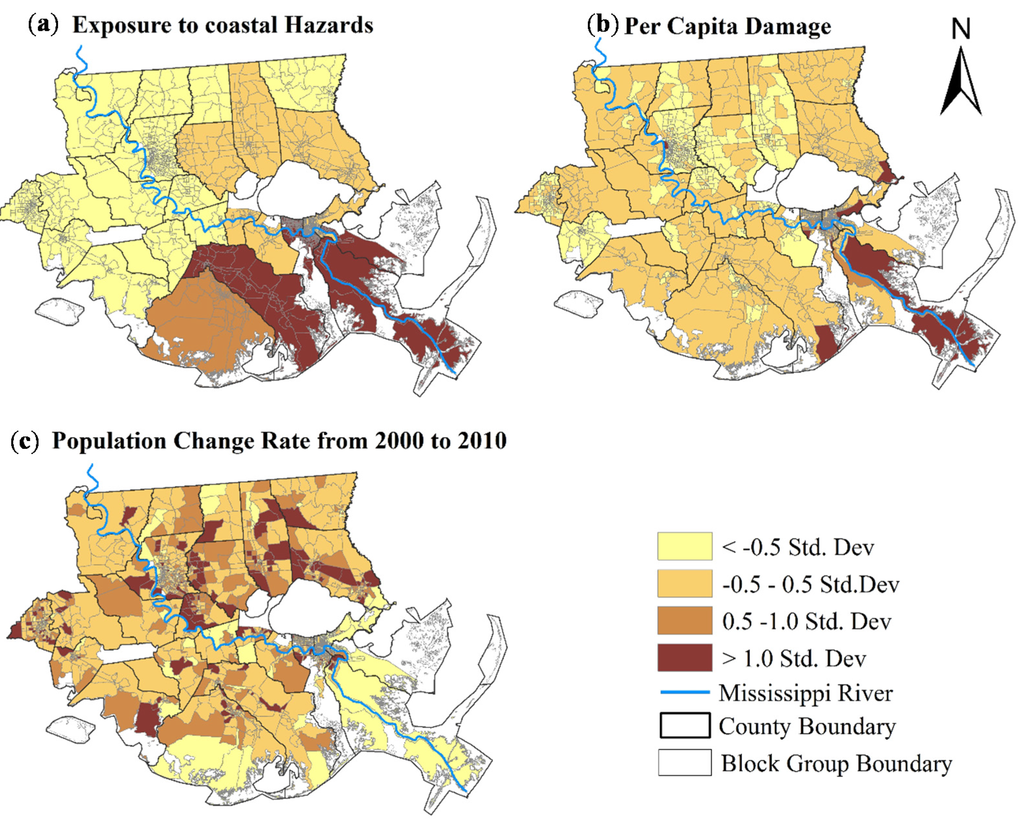
Figure 5. Z-scores of (a) exposure to natural hazards; (b) Per capita property damage; and (c) Population change rate from 2000 to 2010.

Figure 5. Z-scores of (a) exposure to natural hazards; (b) Per capita property damage; and (c) Population change rate from 2000 to 2010.

4.1. Spatial Variation of Community Resilience

As mentioned in Section 3.4 (k-means clustering), the block groups were clustered into four community resilience types. The centroid of each type was used to characterize each resilience state. The z-scores of the centroids in each type are shown in Table 2. Figure 6 is a 3-D plot of the four centroids. By analyzing the behavior of the centroids of each type on the three dimensions (exposure, damage, and recovery), we can rank them from 1 to 4 and name them from the lowest to highest resilience as “susceptible”, “recovering”, “resistant”, and “usurper”, as in the RIM model [7,17].

Table 2. Z-scores of centroids of the four resilience types on the three dimensions.

Dimension	Susceptible	Recovering	Resistant	Usurper
Exposure	−0.61	−1.02	2.61	0.06
Damage	0.95	−0.11	0.05	−0.09
Recovery	−0.27	−0.58	0.65	1.60

Table 2. Z-scores of centroids of the four resilience types on the three dimensions.

Dimension	Susceptible	Recovering	Resistant	Usurper
Exposure	−0.61	−1.02	2.61	0.06
Damage	0.95	−0.11	0.05	−0.09
Recovery	−0.27	−0.58	0.65	1.60

As seen in Figure 6, a “susceptible” community generally has below-average exposure, high damage, and the lowest z-score of recovery. This refers to a community that encounters severe damage and cannot fully recover after a disturbance, which is the lowest resilience state. A “recovering” community has below-average exposure, below-average damage, and average or slightly above-average recovery. “Resistant” implies that a block group only has low damage even when suffering high level of exposure and still recovers very well. A “usurper” block group not only can resist disturbances but also prosper afterwards. From susceptible to usurper, the z-scores of recovery increased steadily, indicating a positive relationship between community resilience and recovery (population change). From k-means clustering, 521 block groups were clustered into susceptible state; 1202 block groups were classified as recovering; 347 block groups were in resistant communities and 16 block groups were usurper (Table 3).

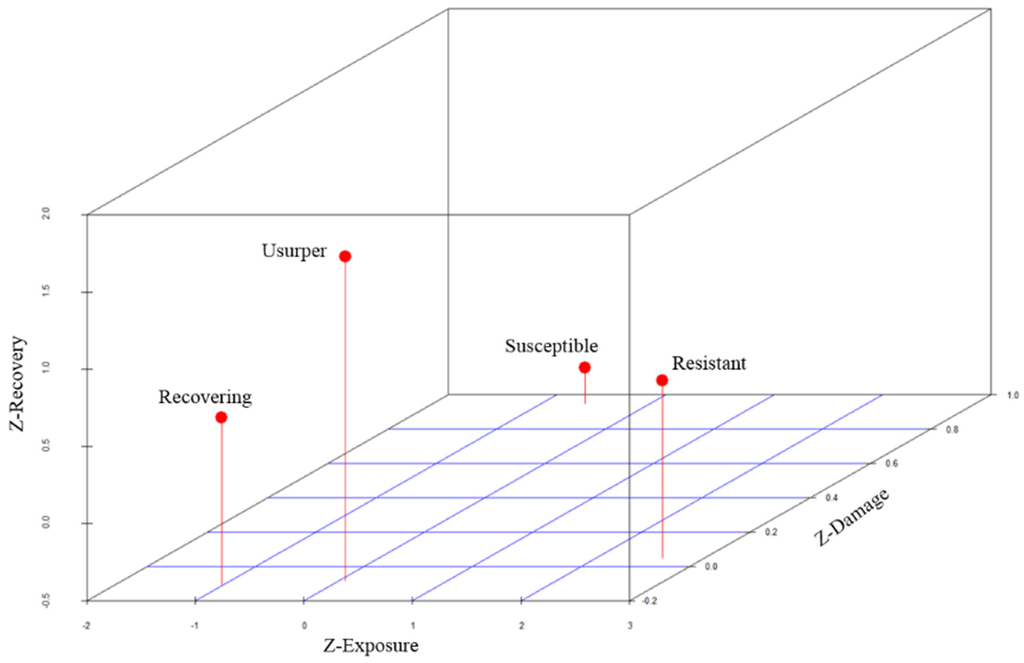
Figure 6. Three-dimensional plot of behaviors of the 4 community resilience states.

Figure 6. Three-dimensional plot of behaviors of the 4 community resilience states.

Table 3. Comparison between the two classifications

K-Means	Discriminant Analysis				Total
	Susceptible	Recovering	Resistant	Usurper
Susceptible	326	166	23	6	521
Recovering	34	1114	46	8	1202
Resistant	63	81	202	1	347
Usurper	1	7	3	5	16
Total	424	1489	155	18	2086

Table 3. Comparison between the two classifications

K-Means	Discriminant Analysis				Total
	Susceptible	Recovering	Resistant	Usurper
Susceptible	326	166	23	6	521
Recovering	34	1114	46	8	1202
Resistant	63	81	202	1	347
Usurper	1	7	3	5	16
Total	424	1489	155	18	2086

The results from the stepwise discriminant analysis show that 73.1% of block groups were correctly classified. The leave-one-out cross-validation was used to evaluate the robustness of the model in terms of predictive accuracy when the model is constructed with one case (block group) being left out [62]. Specifically, discriminant analysis was run 2086 times. In each run, 2085 block groups were used as the training set to develop the classification functions, and the functions were applied to predict the membership of the remaining one block group. The prediction results from the 2086 iterations were averaged to obtain the cross-validation accuracy (72.3%). The slight difference between classification accuracy and cross-validation accuracy suggests that the model is fairly robust.

The community resilience maps derived from both k-mean clustering and discriminant analysis are shown in Figure 7 and Figure 8. Table 3 compares the classifications from the two analyses. The misclassification means that a block group was classified by k-means into a resilience state based on its values of exposure, damage, and recovery, but its social-environmental indicators do not seem to suggest the same classification. Based on the discriminant analysis results (Figure 8), block groups with higher levels of community resilience (usurper and resistant) formed clusters in areas north of Lake Pontchartrain and along the Mississippi River in the area between Baton Rouge and New Orleans. Susceptible block groups were in the south, mostly directly adjacent to the coastline.

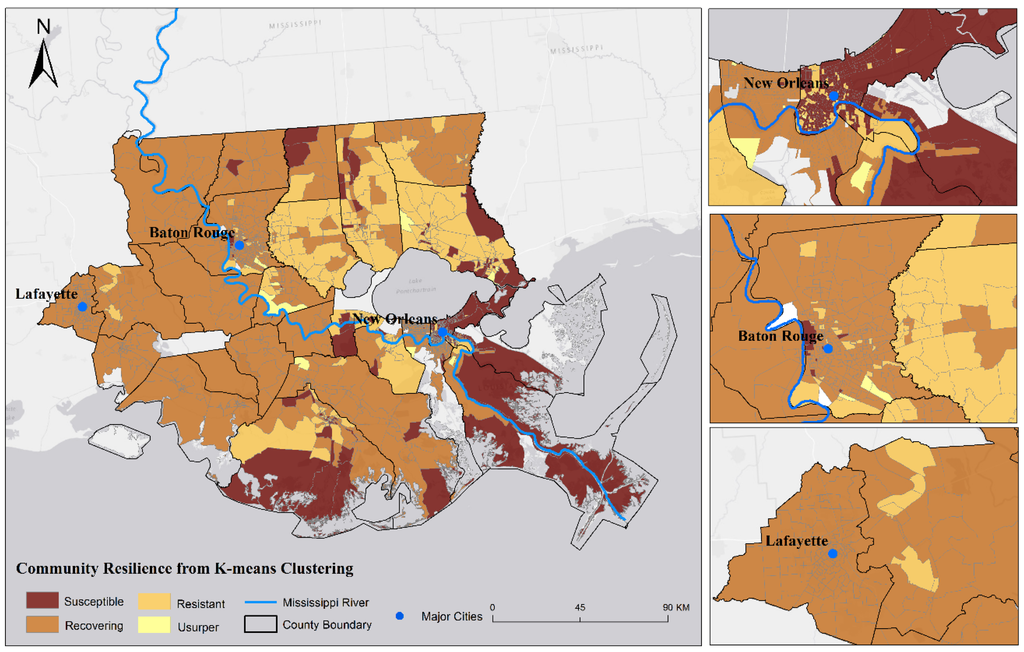
Figure 7. Community Resilience Classification from K-means Clustering.

Figure 7. Community Resilience Classification from K-means Clustering.

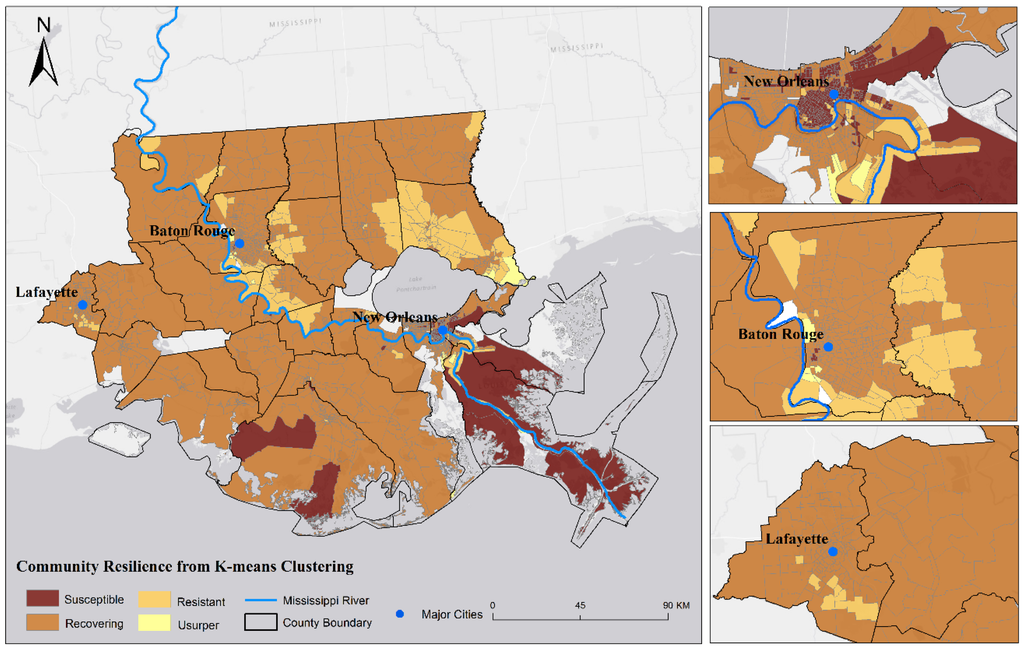
Figure 8. Community Resilience Classification from Discriminant Analysis.

Figure 8. Community Resilience Classification from Discriminant Analysis.

The four resilience states were denoted as 1 to 4 in discriminant analysis. Then, based on the probability of group membership, the continuous resilience score of each block group was calculated by Equation (1). The continuous resilience scores were divided into four levels, from 1.0–1.5, 1.6–2.5, 2.6–3.5, and 3.5–4.0 to denote low, medium low, medium high, and high resilience, respectively (Figure 9).

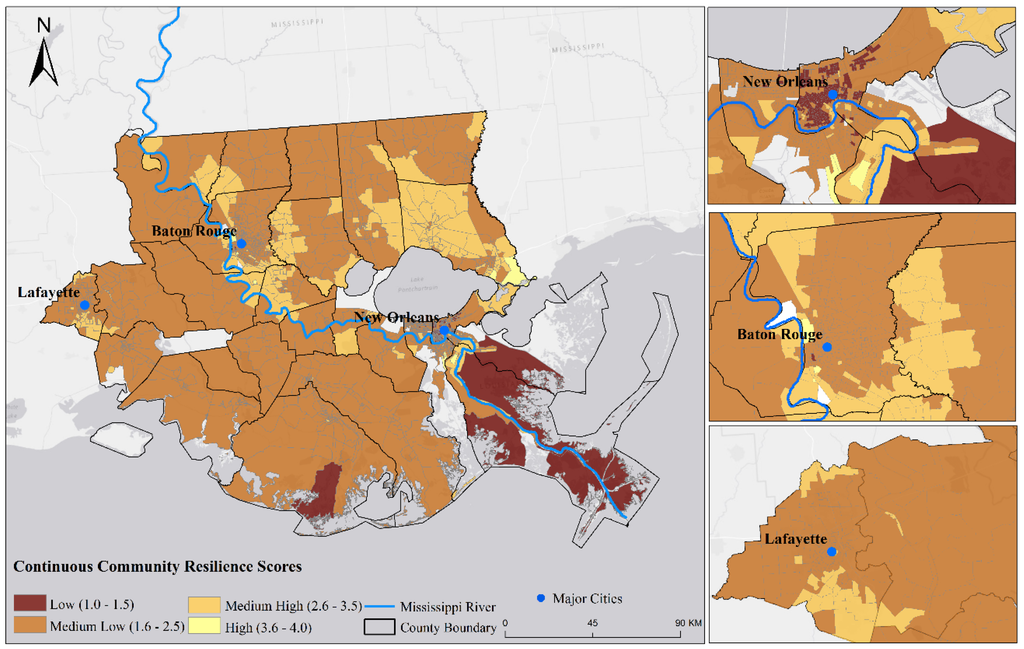
Figure 9. Continuous Community Resilience Scores Map.

Figure 9. Continuous Community Resilience Scores Map.

The continuous score map portrays a pattern that is less discrete than the discriminant analysis results, since the continuous scores were calculated based on a combination of group membership probabilities. This final resilience score map shows that high and medium-high block groups were concentrated north of Lake Pontchartrain and in areas surrounding the urban areas in East Baton Rouge, Ascension, and Lafayette parishes. The least resilience block groups were dominantly in the lower-elevation area proximate to the coastline.

4.2. Indicators of Community Resilience

Stepwise discriminant analysis selected 11 socio-environmental indicators out of the original 25. The 11 indicators cover all five components of community resilience discussed in this study (Table 4). The results from the OLS regression analysis allow us to examine the key indicators driving the community resilience pattern throughout the study area. The value of R (0.889) in this regression model indicates a significantly high correlation between the observed and predicted resilience scores (Table 4). This indicates that the overall model is effective in explaining the indicators of community resilience.

Socioeconomic conditions played an important role in shaping community resilience. The results in Table 4 suggest that increasing the percent of housing units with telephone service available would help increase the community resilience score. Telephone service access has been used as an indicator for communication capacity in several resilience indices [4,27,29]. It is essential for early warning and community cohesion enhancement. The percentage of housing units with telephone service available in this study area had a range from 0 to 100. Many block groups in the southern part had lower than 50% coverage of telephone services. Median household income is also a significant, positive predictor. In other words, communities with higher economic vitality can enhance their ability to respond and recover from disasters because these communities have funds and resources available to assist residents after disasters, thus increase its resilience [52]. Percent of female-headed households had a negative impact on resilience (standardized coefficient of −0.083). An anomaly is that the poverty variable (percent of population living in poverty) had a positive standardized coefficient, which is counter-intuitive. However, the coefficient is small (0.008) and not statistically significant. A closer look of the simple bivariate correlation between this variable and the resilience score shows a negative correlation (−0.35). This poverty variable is also highly positively correlated with percent of female-headed households (r = 0.74). Such an anomaly could occur in a multivariate analysis, when “independent” variables are interacting among themselves, and sometimes make the interpretation of the model results difficult [63]. We conducted an F-test to compare the two regression models (with and without the poverty variable) and confirmed that the poverty variable was not significant (p-value = 0.3457). Hence, removing the poverty variable or a variable highly correlated with poverty for planning purposes could be a solution.

Table 4. Regression results of all variables with continuous scores.

Category	Variable	Coefficient	Standardized Coefficient	Significance
Social	% housing units with telephone service available	0.003	0.072	0.0000
	% female-headed households	−0.002	−0.083	0.0001
Economic	% population living in poverty	0.001	0.008	0.6435
	Median household income	0.000	0.035	0.0318
Infrastructure	% population employed in construction, transportation, material moving	0.006	0.065	0.0000
	% housing units built after 2000	0.003	0.068	0.0000
	Total housing units per square mile	−0.121	−0.285	0.0000
	Total length of roads per sq. km	−0.031	−0.479	0.0000
Community	% population that was native born and also lives in the same house or same county	−0.011	−0.324	0.0000
Environmental	Mean subsidence rate % area in an inundation zone	−0.026 −0.002	−0.162 −0.165	0.0000 0.0000
	Constant	3.255	-	0.0000
	n	2086	-	-
	Significance	0.000	-	-
	R	0.889	-	-

Table 4. Regression results of all variables with continuous scores.

Category	Variable	Coefficient	Standardized Coefficient	Significance
Social	% housing units with telephone service available	0.003	0.072	0.0000
	% female-headed households	−0.002	−0.083	0.0001
Economic	% population living in poverty	0.001	0.008	0.6435
	Median household income	0.000	0.035	0.0318
Infrastructure	% population employed in construction, transportation, material moving	0.006	0.065	0.0000
	% housing units built after 2000	0.003	0.068	0.0000
	Total housing units per square mile	−0.121	−0.285	0.0000
	Total length of roads per sq. km	−0.031	−0.479	0.0000
Community	% population that was native born and also lives in the same house or same county	−0.011	−0.324	0.0000
Environmental	Mean subsidence rate % area in an inundation zone	−0.026 −0.002	−0.162 −0.165	0.0000 0.0000
	Constant	3.255	-	0.0000
	n	2086	-	-
	Significance	0.000	-	-
	R	0.889	-	-

Four significant predictors from the infrastructure component were derived; two (employment rate in construction, transportation, and material moving and percent of housing units built after 2000) contributed positively and the other two (housing density and road density) negatively to the resilience score. Employment rate in construction, transportation, and material moving may indicate the capacity of emergency preparedness and post-disaster debris removal, demolition, and reconstruction. Housing units built after 2000 may imply a strong recovery process resulting from disturbances during the study period. On the contrary, higher housing and road density could likely increase the damages from the hazards, thus leading to lower resilience [9].

The percent of the population that was native born and also live in the same house or same county, the only predictor extracted from the community component, was significantly negatively related to the resilience score. Higher value of the percent of native-born population means lower value of immigrant population. This variable may be both a cause and an effect. Higher immigrant population may mean that the place has already had high utility that attracted migration. At the same time, several studies have shown that immigrants strengthen community resilience with their diversity of education, livelihood, and personal experiences [64]. When disaster strikes, a community needs redundancy, alternatives, and backups in the system to recover. A diverse group of citizens that possesses various capabilities and kinds of technical expertise can facilitate the recovery process.

Within the environmental component, mean subsidence rate and percent of area in an inundation zone contributed negatively to resilience. Land subsidence would lead to widespread land loss along the coastline and deterioration of ecosystem services. Ongoing sinking land surface would continually cause more frequent floods and erode the ability of communities to recover from coastal hazards. When large segments of a community are within the inundation zone, this community is under high risk of coastal hazards such as flooding and storm surge, and is difficult to recover under frequent exposure.

5. Conclusions

This paper quantitatively assessed and validated the community resilience of the 2086 block groups in the Lower Mississippi River Basin using the Resilience Inference Measurement (RIM) framework. Social-environmental indicators associated with the community’s ability to reduce damage and recover from coastal hazards were identified. First, the block groups were clustered based on their values on the three dimensions (exposure, damage and recovery). Four strong clusters corresponding to the four states of resilience—susceptible, recovering, resistant, and usurper—were derived. Then, stepwise discriminant analysis was conducted using 25 pre-event capacity indicators to investigate the underlying factors associated with community resilience. A total of 11 indicators were extracted, and a classification accuracy of 73.1% was achieved. These 11 variables suggest that community resilience was shaped by multicomponent capacities (social, economic, infrastructure, community, and environmental). Also, the leave-one-out cross validation resulted in an accuracy of 72.3%, confirming the model robustness. The final continuous resilience score map shows that block groups with higher resilience were concentrated in the northern part of the study area whereas block groups with low resilience were dominantly proximate to the coast.

One major objective of this study was to provide the communities an easy-to-use resilience assessment tool that can also be used to identify key indicators for managing and promoting resilience. In order to further explore the relationships between the continuous resilience score and the selected 11 variables, a multiple regression was conducted, which led to a high R-value of 0.89. Of the ten variables that were significant, percent of housing units with telephone service available and median household income contributed positively to community resilience, whereas female-headed households with children had a negative impact on resilience. In the economic component, percent of population employed in construction, transportation, and material moving and percent of housing units built after 2000 promoted resilience by enhancing the ability of preparedness and post-disaster reconstruction. In the infrastructure component, high housing and road density in this vulnerable coastal region seemed to add more burdens to the community and increase the potential to suffer more property damages. In the community component, the percent of the population that was native born was found to be associated with resilience negatively. Finally, land subsidence and percent of inundation zone were two major environmental factors that put this area under high risk of coastal hazards and weaken the ability to recover.

The RIM model is one of the first empirically based approaches that aim at community resilience measurement with validation. This study advances the application of the RIM model from coarse-scale county level to fine-scale block group level so that important disparity within a county can be captured. While the results derived from this study may be context, scale, and place specific, this paper demonstrates that the RIM approach could be used as a tool to extract indicators to understand and ultimately promote community resilience. With more analyses at different study areas or using different time spans, it is possible to derive some common indicators that can be used to assess a wide range of places and regions to enable comparisons across different coastal regions in the world.