The Influence of Hydrologic Parameters on the Hydraulic Efficiency of an Extensive Green Roof in Mediterranean Area

Abstract

In an urban environment, green roofs represent a sustainable solution for mitigating stormwater volumes and hydrograph peaks. So far, many literature studies have investigated the hydraulic efficiency and the subsurface runoff coefficient of green roofs, showing their strong variability according to several factors, including the characteristics of storm events. Furthermore, only few studies have focused on the hydraulic efficiency of green roofs under Mediterranean climate conditions and defined the influencing hydrological parameters on the subsurface runoff coefficient. Nevertheless, for designing purposes, it is crucial to properly assess the subsurface runoff coefficient of a given green roof under specific climate conditions and its influencing factors. This study intends to, firstly, evaluate the subsurface runoff coefficient at daily and event-time scales for a given green roof, through a conceptual model implemented in SWMM. The model was loaded with both daily and 1-min rainfall data from two Mediterranean climate sites, one in Thessaloniki, Greece and one in Cosenza, Italy, respectively. Then, the most influencing hydrological parameters were examined through a statistical regression analysis. The findings show that the daily subsurface runoff coefficient is 0.70 for both sites, while the event-based one is 0.79 with a standard deviation of 0.23 for the site in Cosenza, Italy. The multiple linear regression analysis revealed that the influencing parameters are the rainfall intensity and antecedent dry weather period with a confidence level of 95%. This study demonstrated that, due to the high variability of the subsurface runoff coefficient, the use of a unique value for design purposes is inappropriate and that a preliminary estimation could be obtained as a function of the total rainfall depth and the antecedent dry weather period by using the validated multi-regression relationship which is site specific.

1. Introduction

In an urban environment, the ongoing surface sealing due to the development of built-up areas and motorways have produced a constant loss of natural areas. The drastic changes in the natural hydrological cycle, such as the reduction of infiltration and evapotranspiration, have increased the runoff volumes. During extreme rain events such volumes can overload urban drainage systems and cause local floods [1,2].

To restore the pre-development hydrologic cycle, green roofs can be implemented in urban areas. Such systems are structural facilities which are to capture, infiltrate, evaporate, and in combination with other measures, reuse stormwater. Green roofs also provide additional benefits, such as the mitigation of air quality and noise pollution and the enhancement of biodiversity [3,4,5]. From an energy prospective, green roofs also promote evaporative cooling, thereby offsetting the energy requirements associated with air conditioning systems and reducing urban heat island effects [6,7].

From a hydraulic perspective, several studies have shown that green roofs have significant effects on retaining rainfall volumes [8,9,10,11], delaying the peak flow rate [12,13] and reducing the runoff volume discharged into the combined sewer systems (CSSs) [14,15,16]. Many literature studies have, indeed, investigated the hydraulic efficiency of green roofs, but only few have focused on the performance of such systems under Mediterranean climate condition. The hydraulic efficiency of a green roof could be expressed with a lumped parameter, the subsurface runoff coefficient. This parameter, computed as the ratio between the total runoff depth delivered from the green roof and the total rainfall depth, is not only dependent on the geometrical features of the green roof, but it is strongly influenced by the characteristics of the storm events. The definition of such coefficient is crucial for designing purposes and, therefore, it has to be properly defined. Although many studies have analyzed the subsurface runoff coefficient for few selected events and shown its broad variability, a systematic statistical analysis has never been carried out in Mediterranean climate conditions [16,17,18,19,20].

In addition, literature studies have also never distinguished between daily and event-based runoff coefficients and verified whether their difference may be significant or not. This question may be of interest, when rainfall data with a low time resolution are only available.

The objectives of this study are three-fold. Firstly, the subsurface runoff coefficient of a given green roof is evaluated at both daily and event-time scales, through the conceptual model provided for an entire year of observations. To perform this analysis, a minimum inter-event time period was also defined for the specific green roof of interest, as opposed to use an inter-event time of about six hours, actually appropriate for urban catchments. Secondly, the influencing hydrological factors on the hydraulic efficiency of a given green roof were established through a systematic statistical analysis. Finally, the study aims at determining multi-regression equations, specific for the site of interest, which can be useful for preliminary design considerations, in the case a detailed model of the green roof is not available.

2. Literature Review

2.1. Factors Influencing the Hydrological—Hydraulic Behavior of a Green Roof

As previously mentioned, literature studies have shown that green roofs have a positive effect on the reduction of stormwater runoff [12,15,16,19,20,21,22,23]. The water retention capacity mainly depends on the physical features of the green roof (number of layers and materials, soil type and thickness, type of vegetation and percentage of roof covered, roof geometry), and the weather conditions (length of antecedent dry weather period, season/climate, characteristics of rain event like intensity and duration) [14].

Experimental sites in Germany have shown that the reduction of annual runoff from intensive green roofs is 65%–85% of the rainfall, while for extensive green roofs is around 27%–81% [17]. In Portland, Liptaň [21] has found that a tested green roof could reach a volume reduction of 10%–35% during the wet season and a reduction of 65%–100% in the dry season. Van Seters et al. [24] reported similar values for a large green roof in Toronto. Carter and Rasmussen [12], in Georgia, have shown that, for small rainfall events (<25.4 mm), the 88% of the stormwater volume was retained, for an average rainfall (25.4–76.2 mm) more than the 54%, and for the events higher than 76.2 mm, 48%. Similarly, Simmons et al. [23], in Texas, have demonstrated that, while small rainfall events (<10 mm) were totally retained by the green roof, rainfall events with a total depth of 49 mm and a duration of 140 min produced a retention efficiency up to 44%. Villareal and Bengtsson [25] (in Lund) have observed that the retention of a green roof largely depends on the intensity of rainfall; in fact, lower rain intensity events produce greater retention.

Many studies agree that the green roofs influence runoff hydrographs, especially by delaying the runoff peak. Locatelli et al. [20] have noted that the delay of the peak flow rate was up to 40 min, while Getter et al. [10] and Villarreal and Bengtsson [25] have found minimal delays. However, for the majority of studies the delay of the peak flow rate was found to be up to 30 min [12,23].

In literature, few studies investigated how the characteristics of the soil moisture affect the water retention capacity of the green roof [8,22,26]. The moisture content significantly influence the retention volume and in particular, when the substrate is close to saturation at the beginning of the rain event, only a small portion of water is absorbed [27,28]. Seasons with different weather conditions can influence the regime of humidity in the substrate. In fact, the moisture storage in green roofs is affected by extrinsic meteorological factors such as air temperature, humidity, wind speed, and solar radiation, which then influence the evaporation and transpiration [14,17].

Several studies have recognized that the type and the depth of the substrate have an impact on the stormwater retention, as well [14,16]. Carbone et al. [29] have analyzed the hydraulic/hydrologic behavior of a green roof changing the depth of the substrate for constant rainfall events. In particular, this study has shown that the subsurface runoff coefficient is influenced, with a linear law, by the depth of the substrate, in agreement with the results found in the literature. Indeed, previously, Mentes et al. [17] have observed that the relationship between annual precipitation and runoff was greatly influenced by the substrate depth.

Furthermore, different studies were conducted to evaluate the influence of slope on the retention capacity of a green roof. While some studies did not find a correlation between slope and runoff [17,22], others have observed that the retention of runoff may depend on the slope of the green roof [9,10,25]. However, the effect of the slope on the retention capacity is combined with the effect of other factors such as the physical properties of the soil, the duration and intensity of the precipitation, the flow conditions (saturated or unsaturated), the design of the layers and the choice of different kinds of materials for the drainage layer [14].

Many studies agree that the depth and the type of substrate have a greater influence on the water retention capacity of the green roof than the type of vegetation. However, it was also found that vegetation plays an important role in water retention during periods with high temperatures and small rainfall events [9,30,31,32]. Carbone et al. [33] evaluated the reduction of subsurface runoff coefficient on the experimental site at the University of Calabria, Italy. The results showed that for small rainfall events, the green roof was able to reduce the stormwater through the interception by the plants, while for the higher events there was an increasing runoff in the substrate, caused by the preferential flux paths generated by the root apparatus.

2.2. The Subsurface Runoff Coefficient of an Extensive Green Roof

The subsurface runoff coefficient, expressed as the ratio between the runoff from vegetated roof and the rainfall, is an extremely useful index to quantify the hydraulic efficiency of a green roof.

Uhl and Schiedt [18], in Muenster, DE, carried out a monitoring campaign on 18 green roofs with a surface of 12 m² and 24.5 m², with different slopes and stratigraphies (installed on a roof of 500 m²). The average annual runoff coefficient obtained from this study was 0.32. Stovin et al. [16] analyzed the hydrologic performance of a testbed in Sheffield, UK, under temperate weather conditions. The study involved the analysis of 22 significant rain events, in 29 months of observations, with rainfall depth greater than 5 mm and a minimum inter-event time of 6 h. Analyzing rainfall data was obtained a cumulative total retention of 50.2%, and, therefore, an average annual subsurface runoff coefficient equal to 0.48.

Palla et al. [34] explored the performance of a green roof installed at the University of Genoa, Italy, under Mediterranean climate conditions. The retained volumes, calculated as the percentage difference between the volume of rain and the discharged volume, ranged between 0% and 100%, with an average value of 51.5%. From this analysis an average value of the runoff coefficient 49.8% was achieved.

Voyde et al. [15] considered 91 events with a minimum rainfall depth of 2 mm and an inter-event time of 6 h, in an area with sub-tropical climate and found that the water retention efficiency of an extensive GR in Auckland, New Zealand, was about 66% on average, with a subsurface runoff coefficient of 0.34.

Gromaire et al. [19] have made a study of six different green roofs with an area of 35 m², installed on an experimental site in the town of Trappes, 30 km from Paris. From the analysis of 34 rain events, with a minimum rainfall depth of 1 mm and inter-event period of one hour, a coefficient of annual runoff less than 0.5 was obtained.

Locatelli et al. [20], by analyzing three different extensive green roofs in Denmark, have implemented a model to quantify the hydrological response of the green roofs based on 22 years of observations. The average subsurface runoff coefficient obtained was between 0.43 and 0.68.

Wong and Jim [35], in Hong Kong, obtained a cumulative total retention between 11% and 14%, depending on the substrate considered from the analysis of 63 rain events, with a minimum rainfall depth of 0.5 mm and the inter-event time of 6 h. Another study, in a humid sub-tropical climate, was carried out by Carter and Rasmussen [12], which obtained a total cumulative retention of 62% for 72 mm of substrate, for a green roof constructed at the University of Georgia.

In Table 1 is shown a summary of the subsurface runoff coefficient values on a yearly basis observed in the mentioned literature studies.

Table 1. Subsurface runoff coefficient found in the literature studies.

Reference	Climate Condition and Location	Subsurface Runoff Coefficient
Carter and Rasmussen (2006) [12]	Humid sub-tropical—Athens (GE)	0.38
Uhl and Schiedt (2008) [18]	Continental—Muenster (DE)	0.32
Palla et al. (2010) [34]	Mediterranean—Genova (IT)	0.48
Voyde et al. (2010) [15]	Sub-tropical—Auckland (NZ)	0.34
Stovin et al. (2012) [16]	Temperate—Sheffield (UK)	0.48
Gromaire et al. (2013) [19]	Temperate—Trappes (F)	0.36–0.50
Locatelli et al. (2014) [20]	Ocean—Odense and Copenaghen (DK)	0.43–0.68
Wong and Jim (2014) [35]	Humid sub-tropical—Hong Kong (CN)	0.86–0.89

Table 1. Subsurface runoff coefficient found in the literature studies.

Reference	Climate Condition and Location	Subsurface Runoff Coefficient
Carter and Rasmussen (2006) [12]	Humid sub-tropical—Athens (GE)	0.38
Uhl and Schiedt (2008) [18]	Continental—Muenster (DE)	0.32
Palla et al. (2010) [34]	Mediterranean—Genova (IT)	0.48
Voyde et al. (2010) [15]	Sub-tropical—Auckland (NZ)	0.34
Stovin et al. (2012) [16]	Temperate—Sheffield (UK)	0.48
Gromaire et al. (2013) [19]	Temperate—Trappes (F)	0.36–0.50
Locatelli et al. (2014) [20]	Ocean—Odense and Copenaghen (DK)	0.43–0.68
Wong and Jim (2014) [35]	Humid sub-tropical—Hong Kong (CN)	0.86–0.89

While many studies have analyzed the subsurface runoff coefficient at seasonal and annual scales, only few have evaluated it at event-scale [16,34]. This study will focus on the analysis of the influence of hydrological parameters on the subsurface runoff coefficient on daily and event-time scales, for a specific case study.

3. Materials and Methods

3.1. Experimental Site

The conceptual model, described in the following section, was built and validated with the measured data retrieved from an experimental green roof located at the University of Calabria, Italy. The test site, situated on a fifth-floor terrace of a campus’s building, is located in a Mediterranean climate region, characterized by hot-dry summers and cool-wet winters with an annual average of 850 mm. High temperatures during the summer average 27 °C.

The green roof, with an area of around 50 m² and a slope of 1%, is characterized by the following stratigraphy: (1) a soil substrate of 8 cm; (2) an “egg box” drainage and storage layer of 4 cm in pe-ad (with a storage capacity of 8.7 L/m²). A fine fibrous membrane was also placed between the substrate and the underlying drainage layer. The entire package is 12 cm.

The soil, consisting of volcanic lapillus, pumice, broken bricks and zeolites, enriched with organic matter, including peat and composted plant residues, is extremely draining and clay-free, with a good resistance to compaction and volume reduction. This mineral terrain substrate is built to: (1) anchor the root; (2) prevent standing water on the surface; (3) ensure water and nutritional supply; (4) guarantee the respiration of the root and the survival of micro-organisms.

Rainfall depth was measured every one minute using a 0.2 mm resolution tipping bucket rain gauge. With regard to the hydraulic parameters, flow meter devices, installed at the outlet of each compartment, were used to measure the effluent flow rates. The flow meter device was ad hoc, designed to measure a large range of flow rates (0.1–2 L/s), and was based on a stage-flow rate relationship through an opening. The water level was measured by a level sensor [36].

3.2. Data Analysis

The following study, as previously mentioned, was carried out in two phases. In the first phase, daily rainfall data from Thessaloniki (Greece) and Cosenza (Italy) were used; the two cities are both located in the Mediterranean area, characterized by similar meteorological conditions. The rainfall data relating to Cosenza where recorded from a rain gauge installed at the experimental green roof site at University of Calabria, with a resolution of 0.2 mm. The data set included 69 rainy days, collected between June 2013 and June 2014 (precisely from 21 June 2013 to 2 June 2014), with a total rainfall depth of 856.82 mm. The rainfall data from Thessaloniki were collected by the rain gauge at the Makedonia Airport for one year, in the period from 1 January 2014 to 31 December 2014; this period includes 66 rainy days, with a total rainfall of 726.70 mm.

In the second phase of the study the rainfall data with one minute time resolution, recorded only on the green roof experimental site for the whole period (21 June 2013 to 20 June 2014), were considered.

For both phases, only events with rainfall depth greater than 2 mm were selected, based on the assumption that events with rainfall depth < 2 mm unlikely produce runoff from a conventional roof [15]. Moreover, during the second phase, it was needed to estimate the specific inter-event time to define each independent rainfall event.

The study focused on the analysis of the following hydrological parameters: rainfall or precipitation depth (PD); rainfall duration (RD); rainfall intensity (i); and antecedent dry weather period (ADWP).

In particular, the antecedent dry weather period (ADWP) is the dry weather period between two independent rainfall events.

To isolate an individual storm event from a dataset, it is necessary to apply a suitable criterion to determine when an event begins and ends. A typical criterion used to distinguish between rainfall events is the definition of a minimum inter-event time. If the antecedent dry weather period between storm events (period with no rain) is higher than the minimum inter-event time, then two events can be considered independent.

In this study, the minimum inter-event period is hypothesized to be equal to the residence time that a fluid element spends in a given system. Residence time begins when a fluid element enters the system and ends when the same element leaves the system. The residence time strongly depends on the characteristics of the unit. In the case of a green roof, the residence time represents the time that a fluid particle spends to go across the surface, substrate and storage/aeration layers and finally to reach the outlet section. When the antecedent dry weather period between two storms is greater than the residence time, this means that the water volume from the first storm event is completely drained before that the consequent storm begins. If such a condition occurs, the two storm events can be considered independent.

3.3. Conceptual Model for the Hydraulic Design of a Green Roof

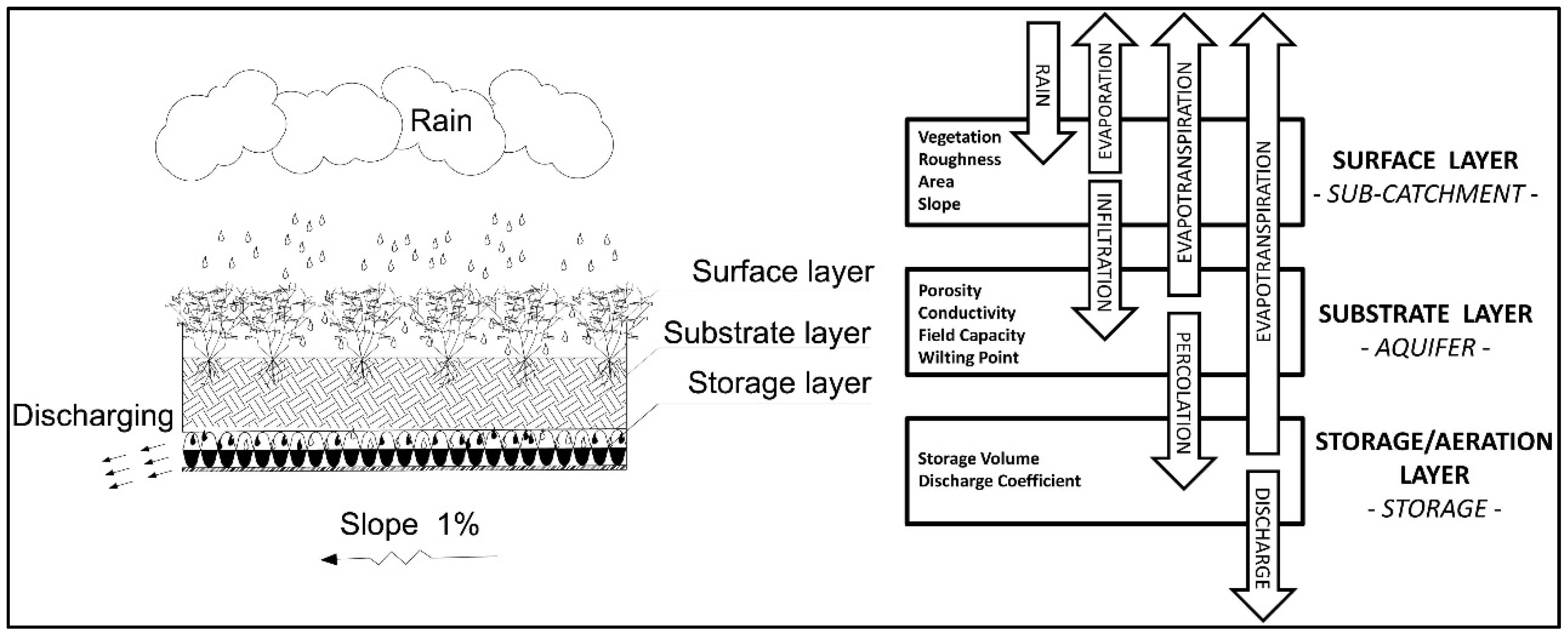
Few literature studies have developed models which accurately predict the hydraulic efficiency of green roofs [2,13,26]. In this study the conceptual model developed by Carbone et al. (2014) for the green roof described in the previous section was used [2]. This model conceptually represents a green roof into a series of three individual elements: (1) surface layer; (2) substrate layer; (3) storage/aeration; and storage layer (Figure 1). Each component of the model, which was built in order to exploit the basic elements of SWMM model (EPA, 2002), is subjected to a specific hydrologic and hydraulic process.

Figure 1. Vegetated roof stratigraphy and structure of the conceptual model.

Figure 1. Vegetated roof stratigraphy and structure of the conceptual model.

The top layer exposed to the atmosphere and covered by vegetation is modeled as sub-catchment, where infiltration, evaporation processes, and runoff generation occur. The sub-catchment is defined by the area and the slope of the vegetated roof, the roughness, and the typology of vegetation. Rainfall is the input of the surface layer, while the output are evapotranspiration and infiltration flow; the latter, in turn, becomes the only input of the substrate layer. Green–Ampt equations are used to describe the infiltration process.

The substrate layer is modeled as an aquifer. The flow from the substrate layer to the storage layer is controlled by a percolation equation, which was formulated from Darcy’s Law for unsaturated flow, in which the hydraulic conductivity (K) is a function of the moisture content (θ). For calculation of percolation, Carbone et al. assumed that the gradient, Δθ/Δz, is the difference between moisture content θ in the substrate and field capacity (FC) at the boundary with the storage layer, divided by the average depth of the substrate, dz/2. Thus:

$$\text{Percolation}=\mathrm{K}\left(\mathsf{\theta }\right)·\left[1+\left(\mathsf{\theta }-\text{FC}\right)·\frac{2}{\text{dz}}\right]·\frac{\Delta \mathsf{\Psi }}{\Delta \mathsf{\theta }}$$

(1)

The percolation rate is the input for the third module, relating to the storage/aeration layer, which is represented by a storage tank with geometrical characteristics dependent on the particular technology used. The relationships used to describe the hydraulic behavior of the storage tank are the balance Equation (2) and the discharging Equation (3), written as follows:

$$\frac{dW}{dt}=Q_e-Q_u$$

(2)

$$Q_u=\mathsf{\mu }·B·h·\sqrt{2·g·h}$$

(3)

where Q_u is the flow rate eluted from the vegetated roof; Q_e is the flow percolation rate; μ is the discharging coefficient; B is the width of the storage and h is the water level in the storage over the weir. In this model Carbone et al. assumed, for pe-ad drainage layer, a value of μ equal to 1.45.

Finally the output of the system is introduced into the last module represented by a conduit, governed by flow routing equations.

To take into account the influence of the initial moisture of the soil, Carbone et al. [2] considered a model parameter which varies according to the antecedent dry weather period. The calibration of this parameter was carried out in Carbone et al. [2]. The evapotranspiration process was modeled with the Thornthwaite’s equation based on daily temperature data.

In this study, the conceptual model, previously validated by Carbone et al. [2], was used with the aim of estimating the runoff from the experimental green roof. Specifically, through the conceptual model provided, the subsurface runoff coefficient is evaluated at both daily and event-time scales. The model was loaded with the daily rainfall data from Cosenza, Italy and Thessaloniki, Greece, to obtain the daily coefficient and the one-minute rainfall data from Cosenza, Italy to obtain the event-based coefficient.

3.4. Multiple Linear Regression Analysis

The multiple linear regression analysis is used to assess the correlation between two or more independent variables and a single continuous dependent variable. The multiple linear regression equation is:

$$Y={\mathsf{\beta }}_0+{\mathsf{\beta }}_1{X}_1+{\mathsf{\beta }}_2{X}_2+\dots +{\mathsf{\beta }}_{\mathrm{P}}{X}_{\mathrm{P}}+\mathsf{\epsilon }$$

(4)

where Y is the predicted or expected value of the dependent variable, X₁ through X_p are p distinct independent or predictor variables, β₀ is the value of Y when all of the independent variables (X₁ through X_p) are equal to zero, β₁ through β_P are the estimated regression coefficients, and ε is the residual term which translates the inability of the model to accurately reproduce the observed reality. In this study the independent variables are the hydrological parameters, such as precipitation depth, rainfall intensity, rainfall duration, and antecedent dry weather period, while the dependent variable is the runoff depth.

In order to evaluate the significance of each regression coefficient a t-test was used. A p-value of 0.05 was considered in this study. To define how closely the data are fit by the regression line, the R² coefficient is evaluated. In this study the multiple linear regression analysis was carried out to statistically define the most influencing hydrological factors on the hydraulic efficiency of a given green roof.

This analysis is carried out by firstly defining the subsurface runoff coefficient at a daily scale, by using daily rainfall data as input data in the conceptual model. The daily subsurface runoff coefficient is computed as the ratio between the total runoff depth and the total rainfall depth during a day. The data set from Cosenza, Italy is used to obtain the multi-regression relationships, which were, then, validated with the data set from Thessaloniki, Greece. Secondly, the subsurface runoff coefficient is evaluate at event-time scale by using one-minute data and the multi-regression analysis is carried out again for this dataset.

4. Results and Discussion

First of all, the minimum interevent time period specific for the green roof studied is defined. Based on the assumptions made in Section 3.2, the minimum interevent time period corresponds to the maximum residence time that occurs in the system. In this study, to obtain the maximum residence time of the green roof, the conceptual model, described in Section 3.2, is loaded with a series of constant rainfall depths, varying from 0.1 mm (corresponding to a rainfall intensity of 0.05 mm/h) to 25 mm (corresponding to a rainfall intensity of 12.5 mm/h). 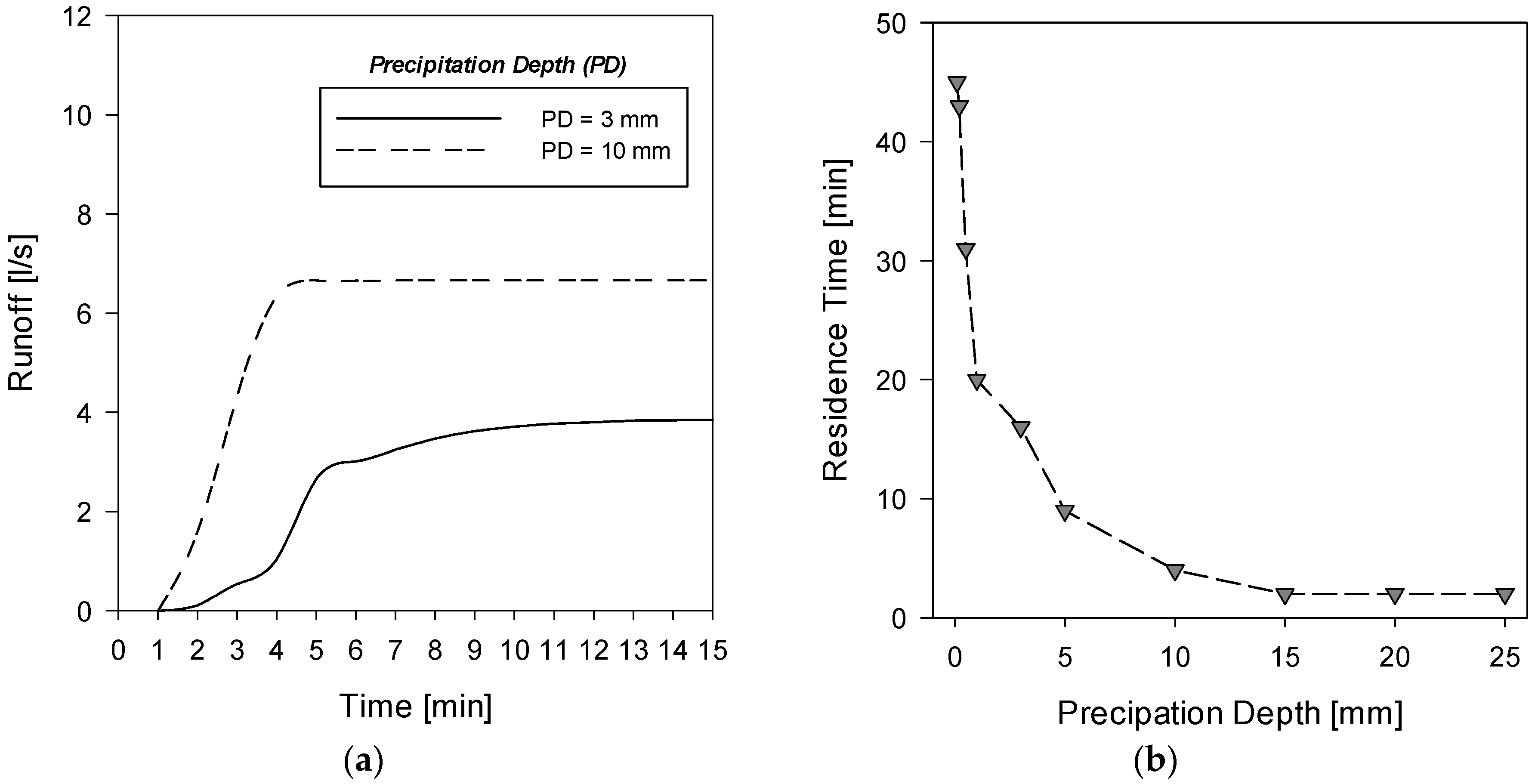In Figure 2a, the distributions of flow rate delivered at the outlet section of the green roof are reported for the different rainfall inputs. As can be observed, for each constant rainfall event, the flow rate increases, until it reaches an asymptotic value. The asymptotic value occurs when all the fluid particles reach the outlet section and represents the residence time of the system for the given rainfall input.

In Figure 2b the residence time values obtained for the different rainfall events are reported. It can be observed that the residence time decreases as the rainfall depth increases. While the residence time reaches a constant value of around 5 min for precipitation depth higher than 5 mm, the residence time varies from 8 min to 45 min, for low rainfall depths (<5 mm). Based on the assumption described in section 3.2, it is possible to establish that the minimum inter-event period of the green roof of interest is 40 min.

Figure 2. (a) Runoff from the green roof for two constant precipitation depths (3 mm, 10 mm); and (b) residence time of the system as a function of constant precipitation depth.

Figure 2. (a) Runoff from the green roof for two constant precipitation depths (3 mm, 10 mm); and (b) residence time of the system as a function of constant precipitation depth.

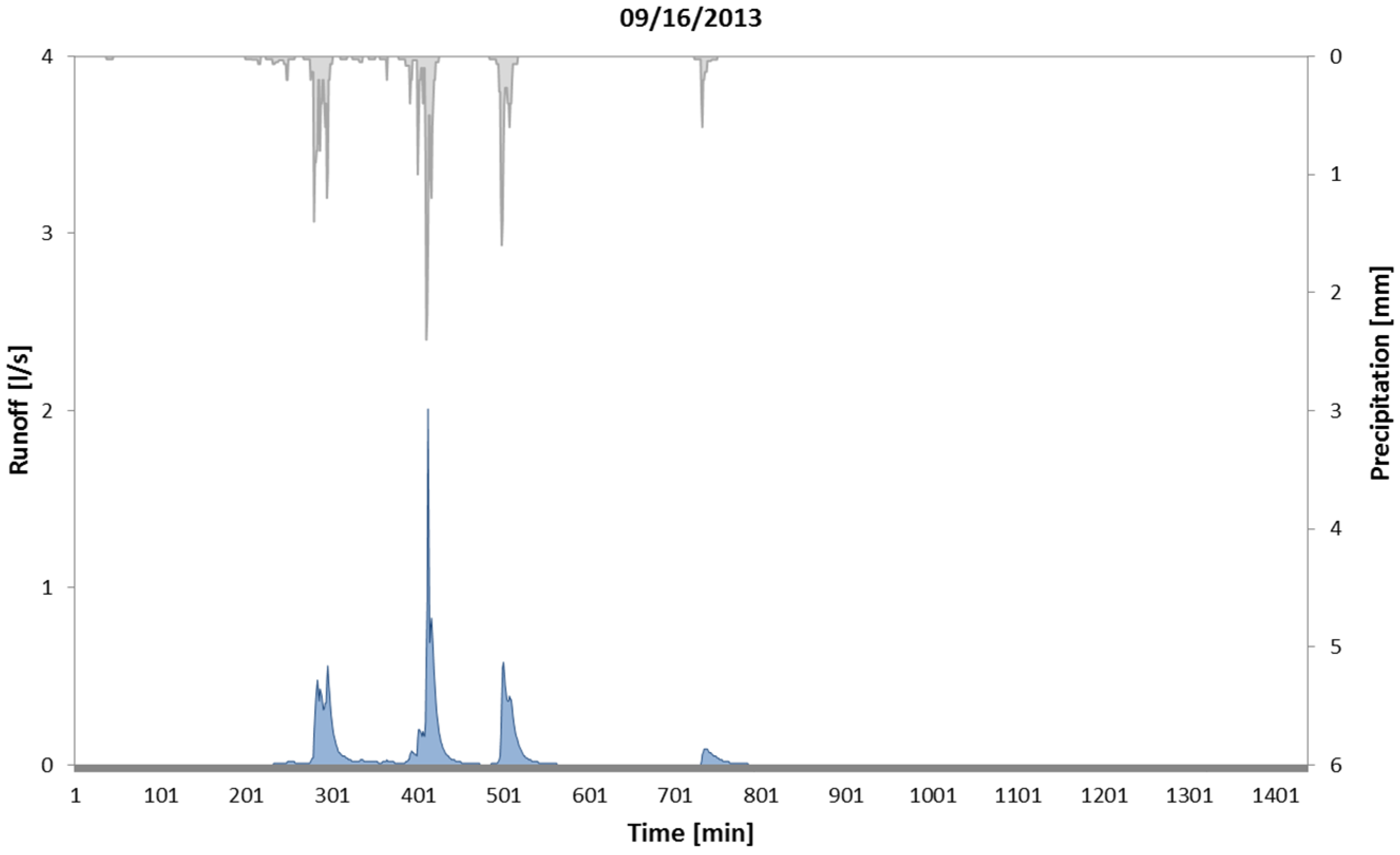
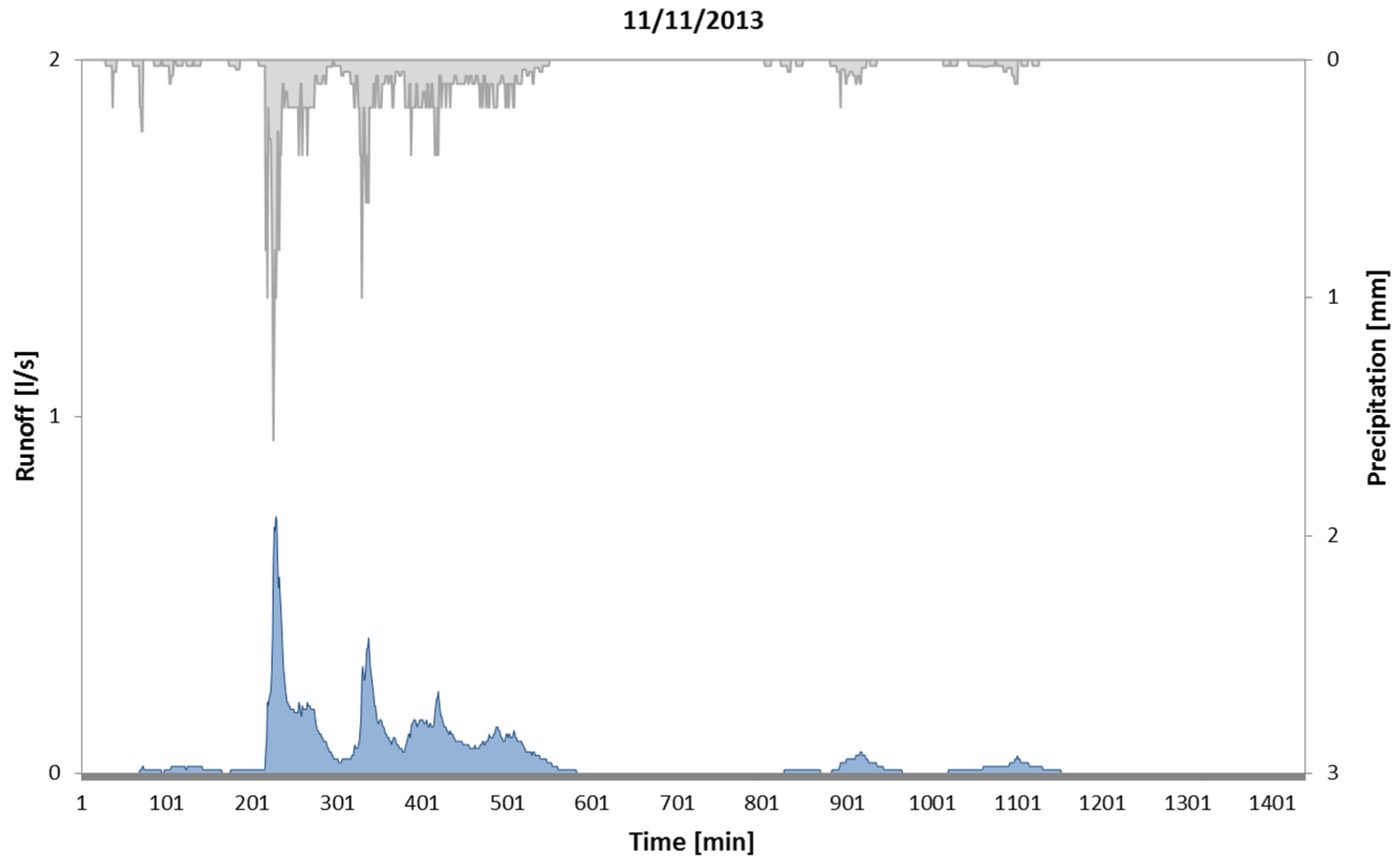
Through the conceptual model provided, the runoff volumes generated from the 69 rainfall events recorded in Cosenza (Italy) and the 66 rainfall events in Thessaloniki (Greece) were obtained. In the Figure A1 the hydrographs modeled for two selected rainfall-runoff events are reported. In Table 2 and Table 3 the results obtained in terms of total runoff volumes and subsurface runoff coefficients on daily basis are shown. As it can be observed the subsurface runoff coefficient exhibits a high variability. For example, two events with different rainfall depths, such as the event 12/09/2013, with a total rainfall depth of 2.40 mm, and the event 02/01/2014, with a total rainfall depth of 30.70 mm, produced runoff volumes of 0.85 mm and 29.15 mm, respectively. The subsurface runoff coefficient is equal to 0.35 for the first event and 0.95 for the second one. 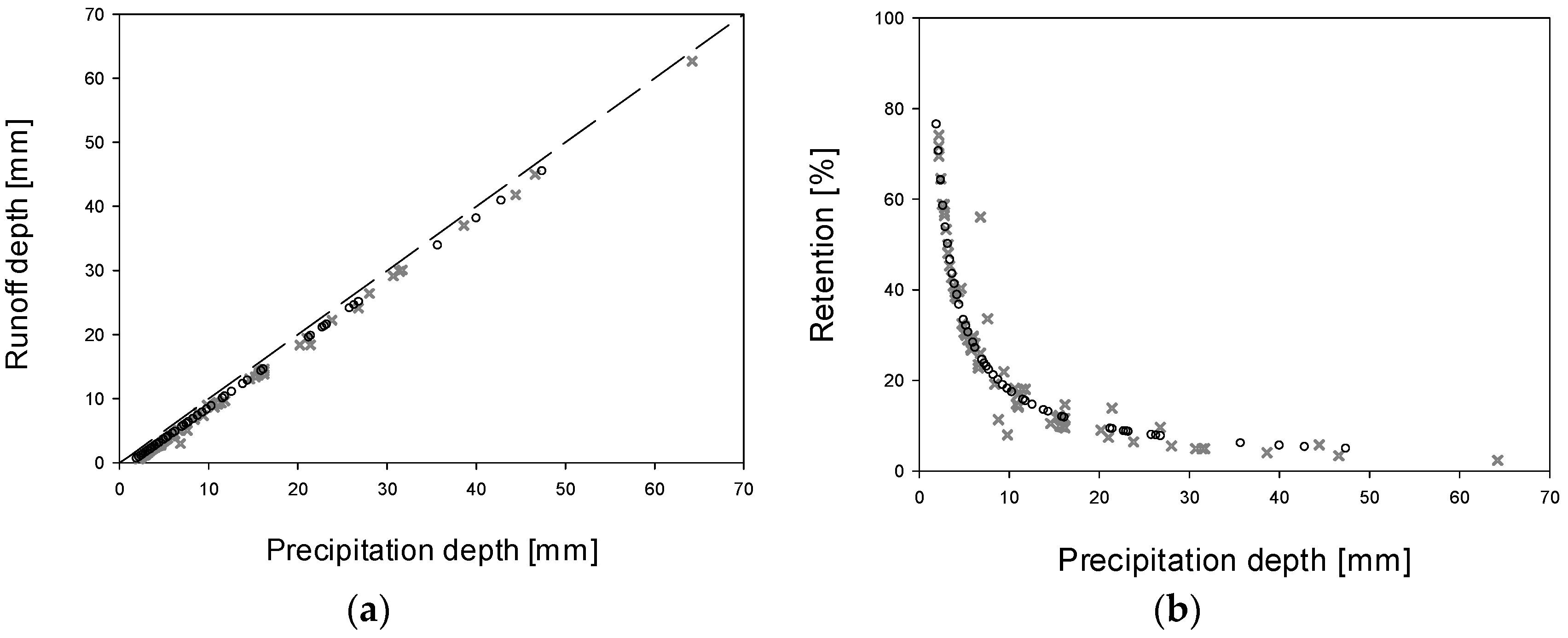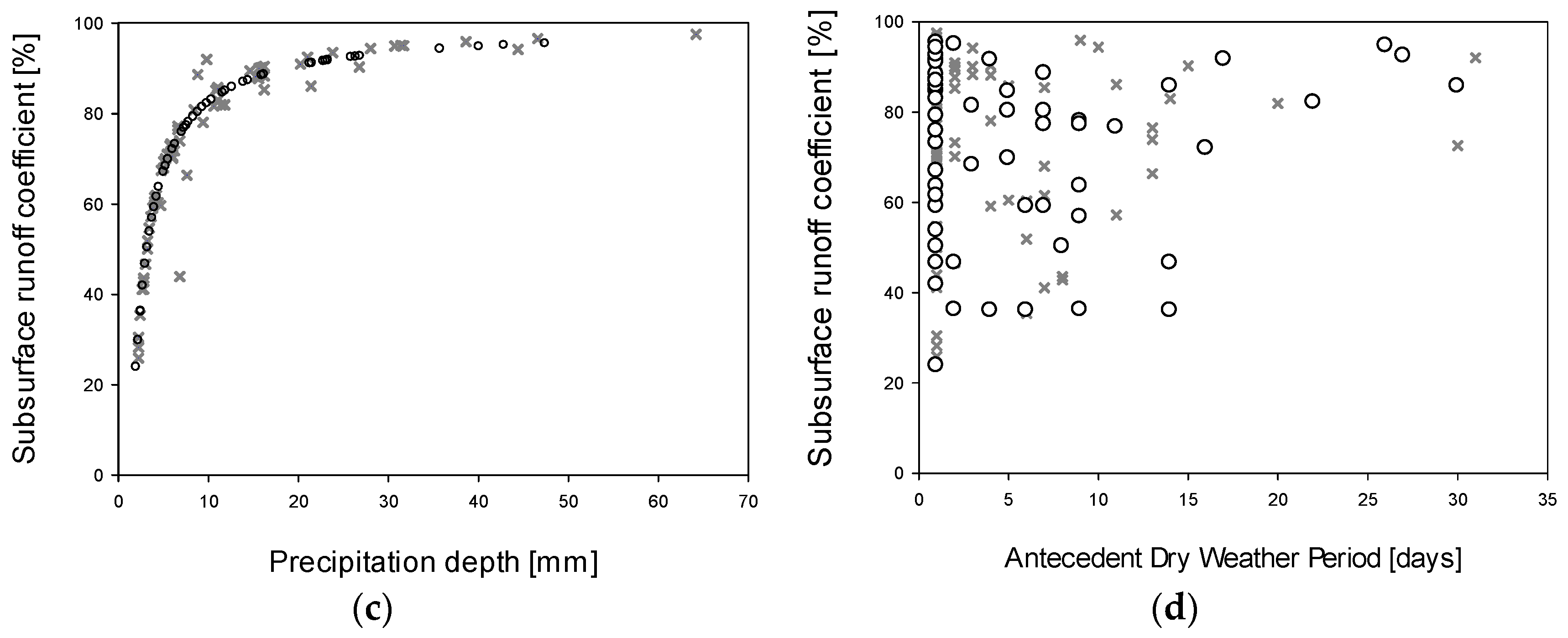In Figure 3a, the runoff depth is reported as a function of the precipitation depth for the two sites. The data closely lay on the bisector, thus demonstrating the strong relationship between rainfall and runoff values for both rainfall datasets. The same consideration can be drawn from Figure 3b, in which the retention percent is strongly related to the precipitation depth. In fact, the retention percent is the inverse of the subsurface runoff coefficient and it represents the amount of water that the green roof retains after a rainfall event. Specifically, Figure 3b shows that the retention percent exponentially drops as the rainfall depth increases. The maximum retention capacity is 80%. When the precipitation depth is greater than 10 mm, the retention capacity varies from 20% to 0%. In Figure 3c the subsurface runoff coefficient is reported as a function of the precipitation depth. As expected, the two parameters are strongly correlated and exhibit an opposite trend of the results in Figure 3b. Indeed, the surfurface runoff coefficient values rise as the rainfall increases, until an asymptotic value of around 95% is reached. This suggests that the hydraulic performance of the green roof is fairly high for small rainfall events; indeed, for precipitation lower than 5 mm, the green roof releases up to 60% of the rainfall volumes, while for precipitation higher than 5 mm, the system reatains at most 35%. In Figure 3d the subsurface runoff coefficient, as a function of the antecedent dry weather period, is reported. In this case, the results in terms of the subsurface runoff coefficient are scattered and seem to not be strongly related to the antecedent dry weather period. All of the plots in Figure 3 show that the results from the two sites in Mediterreanean area follow the same trend, suggesting that the climate condition impacts the hydraulic performance of a green roof.

Table 2. Precipitation depth (PD), runoff depth (RD), and subsurface runoff coefficient (SRC) for daily rainfall data of Cosenza, Italy.

Event Data	PD (mm)	RD (mm)	SRC (%)
07/07/2013	8.8	7.8	0.89
08/09/2013	9.8	9.02	0.92
08/10/2013	6.6	5.1	0.77
09/09/2013	6	4.36	0.73
09/12/2013	15.8	14.24	0.9
09/13/2013	3.4	1.86	0.55
09/16/2013	44.4	41.82	0.94
09/30/2013	11	9.13	0.83
10/01/2013	5.2	3.64	0.7
10/16/2013	16	14.44	0.9
11/05/2013	11.4	9.34	0.82
11/10/2013	4	2.42	0.61
11/11/2013	64.2	62.65	0.98
11/13/2013	6	4.21	0.7
11/15/2013	16.2	13.82	0.85
11/24/2013	46.6	45.02	0.97
11/25/2013	21	19.43	0.93
11/26/2013	6.81	2.99	0.44
11/27/2013	5.73	4.18	0.73
11/30/2013	16.2	14.31	0.88
12/01/2013	31.4	29.86	0.95
12/03/2013	15.6	14.05	0.9
12/09/2013	2.4	0.85	0.35
12/15/2013	3.2	1.66	0.52
12/26/2013	21.4	18.43	0.86
12/27/2013	4.75	3.21	0.67
12/31/2013	3.8	2.25	0.59
01/13/2014	6.6	5.05	0.77
01/14/2014	6.2	4.45	0.72
01/15/2014	3.2	1.6	0.5
01/19/2014	9.4	7.34	0.78
01/20/2014	11.8	9.67	0.82
01/21/2014	31.68	30.11	0.95
01/22/2014	5.4	3.83	0.71
01/28/2014	4.4	2.65	0.6
02/01/2014	30.7	29.16	0.95
02/02/2014	6	4.23	0.71
02/03/2014	23.8	22.26	0.94
02/04/2014	2.2	0.62	0.28
02/06/2014	5.8	4.25	0.73
02/08/2014	3	1.4	0.47
02/12/2014	26.76	24.17	0.9
02/13/2014	2.2	0.67	0.3
02/21/2014	2.8	1.22	0.44
03/01/2014	2.8	1.2	0.43
03/02/2014	5	3.47	0.69
03/04/2014	20.2	18.37	0.91
03/05/2014	4.68	2.79	0.6
03/06/2014	15.7	13.89	0.88
03/07/2014	2.2	0.57	0.26
03/08/2014	4.2	2.6	0.62
03/15/2014	5	3.4	0.68
03/24/2014	38.6	37.03	0.96
03/25/2014	2.8	1.15	0.41
03/27/2014	15.57	13.66	0.88
03/28/2014	16.2	14.65	0.9
04/04/2014	2.6	1.07	0.41
04/05/2014	10.6	8.66	0.82
04/06/2014	10.8	9.2	0.85
04/16/2014	28	26.44	0.94
04/23/2014	4	2.46	0.62
04/28/2014	11	9.44	0.86
04/29/2014	8.4	6.79	0.81
05/03/2014	15.23	13.43	0.88
05/16/2014	6.8	5.03	0.74
05/29/2014	7.61	5.05	0.66
06/01/2014	14.6	13.07	0.89
06/12/2014	3.6	2.06	0.57
06/19/2014	11	9.4	0.85
	856.82	737.64	0.73

Table 2. Precipitation depth (PD), runoff depth (RD), and subsurface runoff coefficient (SRC) for daily rainfall data of Cosenza, Italy.

Event Data	PD (mm)	RD (mm)	SRC (%)
07/07/2013	8.8	7.8	0.89
08/09/2013	9.8	9.02	0.92
08/10/2013	6.6	5.1	0.77
09/09/2013	6	4.36	0.73
09/12/2013	15.8	14.24	0.9
09/13/2013	3.4	1.86	0.55
09/16/2013	44.4	41.82	0.94
09/30/2013	11	9.13	0.83
10/01/2013	5.2	3.64	0.7
10/16/2013	16	14.44	0.9
11/05/2013	11.4	9.34	0.82
11/10/2013	4	2.42	0.61
11/11/2013	64.2	62.65	0.98
11/13/2013	6	4.21	0.7
11/15/2013	16.2	13.82	0.85
11/24/2013	46.6	45.02	0.97
11/25/2013	21	19.43	0.93
11/26/2013	6.81	2.99	0.44
11/27/2013	5.73	4.18	0.73
11/30/2013	16.2	14.31	0.88
12/01/2013	31.4	29.86	0.95
12/03/2013	15.6	14.05	0.9
12/09/2013	2.4	0.85	0.35
12/15/2013	3.2	1.66	0.52
12/26/2013	21.4	18.43	0.86
12/27/2013	4.75	3.21	0.67
12/31/2013	3.8	2.25	0.59
01/13/2014	6.6	5.05	0.77
01/14/2014	6.2	4.45	0.72
01/15/2014	3.2	1.6	0.5
01/19/2014	9.4	7.34	0.78
01/20/2014	11.8	9.67	0.82
01/21/2014	31.68	30.11	0.95
01/22/2014	5.4	3.83	0.71
01/28/2014	4.4	2.65	0.6
02/01/2014	30.7	29.16	0.95
02/02/2014	6	4.23	0.71
02/03/2014	23.8	22.26	0.94
02/04/2014	2.2	0.62	0.28
02/06/2014	5.8	4.25	0.73
02/08/2014	3	1.4	0.47
02/12/2014	26.76	24.17	0.9
02/13/2014	2.2	0.67	0.3
02/21/2014	2.8	1.22	0.44
03/01/2014	2.8	1.2	0.43
03/02/2014	5	3.47	0.69
03/04/2014	20.2	18.37	0.91
03/05/2014	4.68	2.79	0.6
03/06/2014	15.7	13.89	0.88
03/07/2014	2.2	0.57	0.26
03/08/2014	4.2	2.6	0.62
03/15/2014	5	3.4	0.68
03/24/2014	38.6	37.03	0.96
03/25/2014	2.8	1.15	0.41
03/27/2014	15.57	13.66	0.88
03/28/2014	16.2	14.65	0.9
04/04/2014	2.6	1.07	0.41
04/05/2014	10.6	8.66	0.82
04/06/2014	10.8	9.2	0.85
04/16/2014	28	26.44	0.94
04/23/2014	4	2.46	0.62
04/28/2014	11	9.44	0.86
04/29/2014	8.4	6.79	0.81
05/03/2014	15.23	13.43	0.88
05/16/2014	6.8	5.03	0.74
05/29/2014	7.61	5.05	0.66
06/01/2014	14.6	13.07	0.89
06/12/2014	3.6	2.06	0.57
06/19/2014	11	9.4	0.85
	856.82	737.64	0.73

Table 3. Precipitation depth (PD), runoff depth (RD), and subsurface runoff coefficient (SRC) for daily rainfall data of Thessaloniki, Greece.

Event Data	PD (mm)	RD (mm)	SRC (%)
01/02/2014	2.29	0.68	0.3
01/16/2014	3.05	1.42	0.46
01/25/2014	7.87	6.14	0.78
01/26/2014	4.32	2.65	0.61
01/29/2014	5.33	3.64	0.68
02/07/2014	7.62	5.88	0.77
02/13/2014	2.54	0.91	0.36
02/23/2014	11.68	9.87	0.84
02/24/2014	2.79	1.17	0.42
02/25/2014	6.35	4.64	0.73
03/02/2014	8.89	7.12	0.8
03/03/2014	11.68	9.87	0.84
03/04/2014	14.48	12.62	0.87
03/05/2014	8.38	6.63	0.79
03/06/2014	22.86	20.9	0.91
03/07/2014	3.05	1.42	0.46
03/11/2014	2.54	0.91	0.36
03/28/2014	23.37	21.4	0.92
04/08/2014	7.37	5.64	0.77
04/17/2014	4.57	2.91	0.64
04/18/2014	7.11	5.39	0.76
04/25/2014	8.89	7.12	0.8
04/26/2014	7.11	5.39	0.76
04/27/2014	5.08	3.4	0.67
04/28/2014	2.03	0.48	0.24
04/29/2014	11.94	10.13	0.85
04/30/2014	12.7	10.88	0.86
05/30/2014	12.7	10.88	0.86
06/04/2014	5.59	3.89	0.7
06/05/2014	4.06	2.4	0.59
06/19/2014	12.7	10.88	0.86
07/15/2014	40.13	37.98	0.95
07/16/2014	21.34	19.4	0.91
08/07/2014	9.91	8.13	0.82
09/03/2014	26.42	24.4	0.92
09/07/2014	23.11	21.15	0.91
09/08/2014	4.32	2.65	0.61
09/09/2014	4.57	2.91	0.64
09/16/2014	4.06	2.4	0.59
09/17/2014	16	14.13	0.88
09/18/2014	25.91	23.91	0.92
09/19/2014	13.97	12.13	0.87
09/26/2014	7.62	5.88	0.77
09/27/2014	3.3	1.66	0.5
10/06/2014	3.81	2.16	0.57
10/07/2014	3.56	1.91	0.54
10/23/2014	6.1	4.38	0.72
10/24/2014	8.38	6.63	0.79
10/25/2014	47.5	45.27	0.95
11/08/2014	2.54	0.91	0.36
11/09/2014	21.59	19.64	0.91
11/15/2014	4.06	2.4	0.59
11/17/2014	3.05	1.42	0.46
11/20/2014	9.4	7.63	0.81
11/28/2014	3.3	1.66	0.5
12/03/2014	11.68	9.87	0.84
12/04/2014	5.08	3.4	0.67
12/06/2014	42.93	40.74	0.95
12/07/2014	10.41	8.62	0.83
12/08/2014	3.3	1.66	0.5
12/09/2014	26.92	24.92	0.93
12/10/2014	35.81	33.7	0.94
12/17/2014	16.26	14.38	0.88
12/18/2014	4.32	2.65	0.61
12/27/2014	2.54	0.92	0.36
12/29/2014	2.54	0.92	0.36
	726.69	609.71	0.71

Table 3. Precipitation depth (PD), runoff depth (RD), and subsurface runoff coefficient (SRC) for daily rainfall data of Thessaloniki, Greece.

Event Data	PD (mm)	RD (mm)	SRC (%)
01/02/2014	2.29	0.68	0.3
01/16/2014	3.05	1.42	0.46
01/25/2014	7.87	6.14	0.78
01/26/2014	4.32	2.65	0.61
01/29/2014	5.33	3.64	0.68
02/07/2014	7.62	5.88	0.77
02/13/2014	2.54	0.91	0.36
02/23/2014	11.68	9.87	0.84
02/24/2014	2.79	1.17	0.42
02/25/2014	6.35	4.64	0.73
03/02/2014	8.89	7.12	0.8
03/03/2014	11.68	9.87	0.84
03/04/2014	14.48	12.62	0.87
03/05/2014	8.38	6.63	0.79
03/06/2014	22.86	20.9	0.91
03/07/2014	3.05	1.42	0.46
03/11/2014	2.54	0.91	0.36
03/28/2014	23.37	21.4	0.92
04/08/2014	7.37	5.64	0.77
04/17/2014	4.57	2.91	0.64
04/18/2014	7.11	5.39	0.76
04/25/2014	8.89	7.12	0.8
04/26/2014	7.11	5.39	0.76
04/27/2014	5.08	3.4	0.67
04/28/2014	2.03	0.48	0.24
04/29/2014	11.94	10.13	0.85
04/30/2014	12.7	10.88	0.86
05/30/2014	12.7	10.88	0.86
06/04/2014	5.59	3.89	0.7
06/05/2014	4.06	2.4	0.59
06/19/2014	12.7	10.88	0.86
07/15/2014	40.13	37.98	0.95
07/16/2014	21.34	19.4	0.91
08/07/2014	9.91	8.13	0.82
09/03/2014	26.42	24.4	0.92
09/07/2014	23.11	21.15	0.91
09/08/2014	4.32	2.65	0.61
09/09/2014	4.57	2.91	0.64
09/16/2014	4.06	2.4	0.59
09/17/2014	16	14.13	0.88
09/18/2014	25.91	23.91	0.92
09/19/2014	13.97	12.13	0.87
09/26/2014	7.62	5.88	0.77
09/27/2014	3.3	1.66	0.5
10/06/2014	3.81	2.16	0.57
10/07/2014	3.56	1.91	0.54
10/23/2014	6.1	4.38	0.72
10/24/2014	8.38	6.63	0.79
10/25/2014	47.5	45.27	0.95
11/08/2014	2.54	0.91	0.36
11/09/2014	21.59	19.64	0.91
11/15/2014	4.06	2.4	0.59
11/17/2014	3.05	1.42	0.46
11/20/2014	9.4	7.63	0.81
11/28/2014	3.3	1.66	0.5
12/03/2014	11.68	9.87	0.84
12/04/2014	5.08	3.4	0.67
12/06/2014	42.93	40.74	0.95
12/07/2014	10.41	8.62	0.83
12/08/2014	3.3	1.66	0.5
12/09/2014	26.92	24.92	0.93
12/10/2014	35.81	33.7	0.94
12/17/2014	16.26	14.38	0.88
12/18/2014	4.32	2.65	0.61
12/27/2014	2.54	0.92	0.36
12/29/2014	2.54	0.92	0.36
	726.69	609.71	0.71

Figure 3. Modeled results from Cosenza (Italy) and Thessaloniki (Greece) by using daily rainfall data: (a) runoff as a function of precipitation depth; (b) retention as a function of precipitation depth; (c) subsurface runoff coefficient as a function of precipitation depth; and (d) subsurface runoff coefficient as a function of antecedent dry weather period.

Figure 3. Modeled results from Cosenza (Italy) and Thessaloniki (Greece) by using daily rainfall data: (a) runoff as a function of precipitation depth; (b) retention as a function of precipitation depth; (c) subsurface runoff coefficient as a function of precipitation depth; and (d) subsurface runoff coefficient as a function of antecedent dry weather period.

In order to statistically investigate the significance of hydrological parameters, a multiple linear regression analysis was performed by using daily rainfall data collected in the city of Cosenza, Italy.

Based on the assumption that a longer antecedent dry period provides more time for the substrate to recharge its storage capacity [16], a relationship between runoff depth (RD), rainfall or precipitation depth (PD) and antecedent dry weather period (ADWP) was found.

The results of the multiple linear regression analysis are summarized in Table 4, where the t-statistics (significant at p = 0.05) are presented in the same order as the parameters in the equation. Equation (5) demonstrates a strong correlation between the runoff depth and the precipitation depth, showing a R² of 0.99. These findings are in agreement with the results previously obtained in Figure 3a, which shows the linear relationship between these parameters. However, to investigate the effect of the antecedent dry weather period on the hydraulic performance of the green roof, a forward regression analysis was carried out to verify its significance.

Table 4. Multiple linear regression analysis for daily rainfall data.

Regression Equation		ADWP (days)	R2	t-Statistic
RD = 0.06 + 1.16 PD	(5)	-	0.99	436.88
RD = −6.95 + 11.08 lnPD − 2.90 lnADWP	(6)	>4	0.86	11.06, −1.89 NS
RD = −4.33 + 11.52 lnPD − 4.24 lnADWP	(7)	>5	0.86	11.62, −2.59

Note: NS—not significant.

Table 4. Multiple linear regression analysis for daily rainfall data.

Regression Equation		ADWP (days)	R2	t-Statistic
RD = 0.06 + 1.16 PD	(5)	-	0.99	436.88
RD = −6.95 + 11.08 lnPD − 2.90 lnADWP	(6)	>4	0.86	11.06, −1.89 NS
RD = −4.33 + 11.52 lnPD − 4.24 lnADWP	(7)	>5	0.86	11.62, −2.59

Note: NS—not significant.

This investigation has led to Equations (6) and (7) reported in Table 4 with a good R² value of 0.86. However, the antecedent dry weather period (ADWP) turns out to be statistically significant, when it is longer than 5 days. In fact, when this parameter is less than five days (see Equation (6)), the t-statistic value is not significant.

Stovin et al. [16] identified the antecedent dry weather period as a significant determinant of hydrological performance. However, based on the results obtained from the multi-regression analysis, they concluded that it is not possible to predict the likely retention depth associated with a particular rainfall depth or return period, even when antecedent dry weather period and rainfall intensity or other antecedent weather parameters are taken into consideration. In the present study, instead, the correlation between the runoff depth and the parameters, precipitation depth, and antecedent dry weather period showed good R² values. This may be due to the differences in the rainfall data sets used, green roof features and the climate conditions, since Cosenza (Italy) and Sheffield (UK) are located in Mediterranean and temperate climates, respectively.

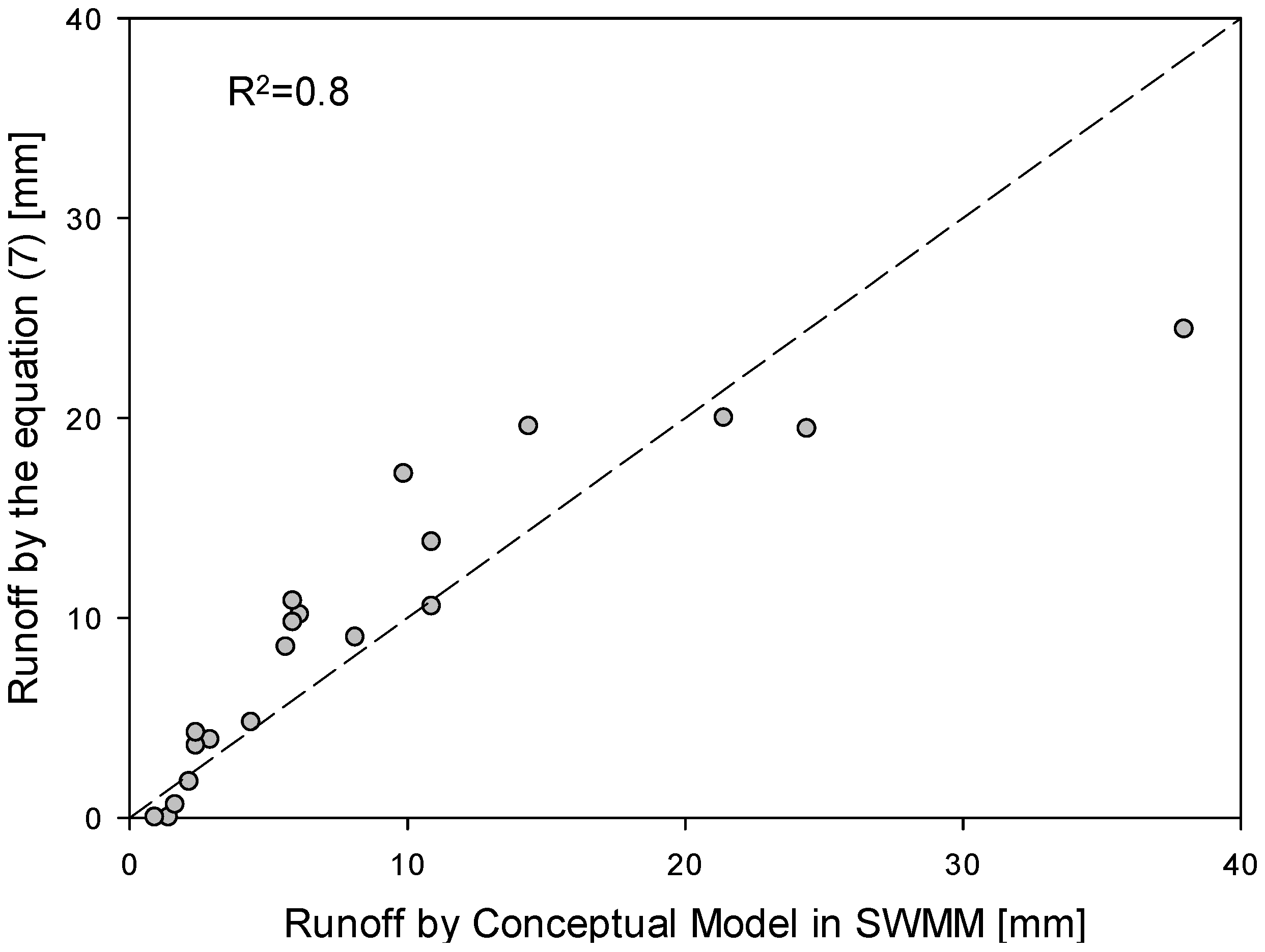
The multi-regression Equation (7) (IT > 5 days), reported in Table 4, is validated with the daily rainfall data from Thessaloniki, Greece. In the validation process, the SWMM model is used as a reference to verify the soundness of the data obtained from the statistical relationship. The runoff depth evaluated with the Equation (7) vs. the runoff depth obtained from the SWMM model are reported in Figure 4. The scattering of the data is closely on the bisector, shown in Figure 4, and a R² equal to 0.8 was obtained in the validation process, confirming how the Equation (7) is able to predict the hydrologic behavior of green roof in a Mediterranean climate for events with antecedent dry weather period greater than five days.

Figure 4. Runoff depth predicted by the Equation (7) vs. runoff modeled with the conceptual model in SWMM for all rainfall events from Thessaloniki (Greece).

Figure 4. Runoff depth predicted by the Equation (7) vs. runoff modeled with the conceptual model in SWMM for all rainfall events from Thessaloniki (Greece).

So far, the subsurface runoff coefficient based on a daily scale was obtained by using daily rainfall data as model input. The results, obtained in the previous phase, are then compared with the findings from the following analysis, which refers, instead, to the subsurface runoff coefficient evaluated on an event-time scale by using one-minute data.

Considering only the events with the rainfall depth higher than 2 mm and a minimum inter-event period of 40 min, 97 rainfall events (Table 5) were identified during the entire period.

Using the conceptual model developed in SWMM, for each rain event, the runoff depth from the green roof was modeled as well as the subsurface runoff coefficient and the retention.

Table 5. Rainfall events characteristics by using one-minute data from Cosenza.

Event Data	D (h)	PD (mm)	i (mm/h)	ADWP (h)	Event Data	D (h)	PD (mm)	i (mm/h)	ADWP (h)
07/07/2013	0.32	8.8	27.79	-	02/01/2014	9.9	15.4	1.56	3.85
08/10/2013	2.03	6.6	3.25	801	02/02/2014	2.23	3.8	1.7	24.32
09/09/2013	0.17	6	36	750.18	02/03/2014	6.07	12.6	2.08	3.33
09/12/2013	1.9	11.8	6.21	67.97	02/03/2014	2.35	2.6	1.11	0.82
09/13/2013	0.48	3.4	7.03	15.07	02/03/2014	6.03	8.4	1.39	1.77
09/16/2013	3.77	31.8	8.44	68.28	02/06/2014	2.42	3.8	1.57	59.75
09/16/2013	0.55	10	18.18	0.98	02/11/2014–02/12/2014	1.68	2.23	1.32	144.22
09/16/2013	0.45	2.4	5.33	3.43	02/12/2014–02/13/2014	1.88	4	2.12	11.18
09/30/2013	0.88	7.2	8.15	336.05	02/21/2014	1.07	2.6	2.44	200.82
10/01/2013	0.62	3.4	5.51	16.05	03/01/2014	2.47	2.2	0.89	196.1
10/16/2013	3.15	13.6	4.32	366.02	03/02/2014	5.3	5	0.94	7.25
10/16/2013	1.58	2.4	1.52	3.93	03/04/2014	5.27	10.6	2.01	45.95
11/05/2013	1.17	4.2	3.6	467.13	03/04/2014	2.95	7.8	2.64	6.35
11/05/2013	3.08	2.4	0.78	4.68	03/06/2014	3.38	11.8	3.49	48.93
11/05/2013	2.75	2.6	0.95	4.58	03/08/2014	1.33	2.2	1.65	39.12
11/11/2013	8.7	58	6.67	129.35	03/15/2014	1.27	2.8	2.21	157.42
11/11/2013	3.2	3.4	1.06	4.22	03/15/2014	1.83	2.2	1.2	1.25
11/11/2013	1.88	2.8	1.49	1.3	03/24/2014	7.88	21.6	2.74	210.18
11/13/2013	0.85	2.4	2.82	33.05	03/24/2014	1.6	8.4	5.25	3.02
11/15/2013	7.07	14.8	2.09	60.23	03/24/2014	1.17	3.4	2.91	1.52
11/22/2013–11/23/2013	3.65	15.8	4.33	167.57	03/24/2014	0.57	2.2	3.88	2.28
11/23/2013	2.78	11.2	4.02	1.05	03/27/2014	5.02	11.2	2.23	53.42
11/23/2013	2.4	9.6	4	1.1	03/28/2014	3.47	10.2	2.94	18.73
11/23/2013	3.27	4.6	1.41	2.23	03/28/2014	2.93	5.6	1.91	1.02
11/23/2013	1.52	5.6	3.69	4.27	04/04/2014	1.62	2.6	1.61	172.85
11/24/2013	2.9	15.4	5.31	11.25	04/05/2014	3.93	6.4	1.63	17.18
11/24/2013	0.82	36.2	44.33	2	04/05/2014	2.27	3.6	1.59	7.13
11/25/2013–11/26/2013	1.35	7.4	5.48	32.05	04/06/2014	4.78	8.2	1.71	3.53
11/26/2013	1.27	4	3.16	7.38	04/16/2014	3.23	22.2	6.87	232
11/30/2013–12/1/2013	21.27	38.4	1.81	98.17	04/16/2014	0.93	5.4	5.79	10.45
12/01/2013	3.3	7.2	2.18	1.52	04/23/2014	0.9	3.4	3.78	167.25
12/03/2013	3.37	9	2.67	38.85	04/28/2014	0.85	2.4	2.82	110.78
12/03/2013	4.47	6.6	1.48	0.72	04/28/2014	1.37	2.4	1.76	0.85
12/15/2013	2.03	3.2	1.57	292.72	04/28/2014	4.55	3.2	0.7	0.75
12/26/2013	3.57	8	2.24	257.35	04/29/2014	1.47	4.6	3.14	18.22
12/26/2013–12/27/2013	5.05	17	3.37	3.78	04/29/2014	1.25	2.2	1.76	6.65
12/31/2013	2.08	2.8	1.34	105.35	05/03/2014	3.32	11.2	3.38	85.67
01/13/2014	1.15	3.8	3.3	309.82	05/03/2014	0.8	3.6	4.5	7.38
01/13/2014	0.32	2.8	8.84	0.77	05/16/2014	0.97	2.6	2.69	297.07
01/14/2014	0.47	6	12.86	21.42	05/16/2014	3.22	4.2	1.31	16.42
01/19/2014	5.52	7.8	1.41	116.23	05/29/2014–05/30/2014	3.43	7.8	2.27	308.97
01/20/2014	1.33	2.4	1.8	29.2	06/01/2014	3.5	14.6	4.17	49.78
01/20/2014	0.75	3.8	5.07	1.67	06/12/2014	0.68	3.6	5.27	275.97
01/20/2014	1.13	5.4	4.76	1.18	06/19/2014	1.22	4.2	3.45	154.55
01/21/2014	0.45	3.6	8	0.73	06/19/2014	0.82	4.8	5.88	12.33
01/21/2014	3.77	8.4	2.23	0.83
01/21/2014	2.7	7.4	2.74	6.13
01/21/2014	2.15	2.2	1.02	1.05
01/21/2014	2.6	5.6	2.15	2.85
01/22/2014	4.12	4.6	1.12	1.37
01/28/2014	0.18	2.2	12	152.93
01/31/2014–02/01/2014	6.08	14.8	2.43	81.98

Table 5. Rainfall events characteristics by using one-minute data from Cosenza.

Event Data	D (h)	PD (mm)	i (mm/h)	ADWP (h)	Event Data	D (h)	PD (mm)	i (mm/h)	ADWP (h)
07/07/2013	0.32	8.8	27.79	-	02/01/2014	9.9	15.4	1.56	3.85
08/10/2013	2.03	6.6	3.25	801	02/02/2014	2.23	3.8	1.7	24.32
09/09/2013	0.17	6	36	750.18	02/03/2014	6.07	12.6	2.08	3.33
09/12/2013	1.9	11.8	6.21	67.97	02/03/2014	2.35	2.6	1.11	0.82
09/13/2013	0.48	3.4	7.03	15.07	02/03/2014	6.03	8.4	1.39	1.77
09/16/2013	3.77	31.8	8.44	68.28	02/06/2014	2.42	3.8	1.57	59.75
09/16/2013	0.55	10	18.18	0.98	02/11/2014–02/12/2014	1.68	2.23	1.32	144.22
09/16/2013	0.45	2.4	5.33	3.43	02/12/2014–02/13/2014	1.88	4	2.12	11.18
09/30/2013	0.88	7.2	8.15	336.05	02/21/2014	1.07	2.6	2.44	200.82
10/01/2013	0.62	3.4	5.51	16.05	03/01/2014	2.47	2.2	0.89	196.1
10/16/2013	3.15	13.6	4.32	366.02	03/02/2014	5.3	5	0.94	7.25
10/16/2013	1.58	2.4	1.52	3.93	03/04/2014	5.27	10.6	2.01	45.95
11/05/2013	1.17	4.2	3.6	467.13	03/04/2014	2.95	7.8	2.64	6.35
11/05/2013	3.08	2.4	0.78	4.68	03/06/2014	3.38	11.8	3.49	48.93
11/05/2013	2.75	2.6	0.95	4.58	03/08/2014	1.33	2.2	1.65	39.12
11/11/2013	8.7	58	6.67	129.35	03/15/2014	1.27	2.8	2.21	157.42
11/11/2013	3.2	3.4	1.06	4.22	03/15/2014	1.83	2.2	1.2	1.25
11/11/2013	1.88	2.8	1.49	1.3	03/24/2014	7.88	21.6	2.74	210.18
11/13/2013	0.85	2.4	2.82	33.05	03/24/2014	1.6	8.4	5.25	3.02
11/15/2013	7.07	14.8	2.09	60.23	03/24/2014	1.17	3.4	2.91	1.52
11/22/2013–11/23/2013	3.65	15.8	4.33	167.57	03/24/2014	0.57	2.2	3.88	2.28
11/23/2013	2.78	11.2	4.02	1.05	03/27/2014	5.02	11.2	2.23	53.42
11/23/2013	2.4	9.6	4	1.1	03/28/2014	3.47	10.2	2.94	18.73
11/23/2013	3.27	4.6	1.41	2.23	03/28/2014	2.93	5.6	1.91	1.02
11/23/2013	1.52	5.6	3.69	4.27	04/04/2014	1.62	2.6	1.61	172.85
11/24/2013	2.9	15.4	5.31	11.25	04/05/2014	3.93	6.4	1.63	17.18
11/24/2013	0.82	36.2	44.33	2	04/05/2014	2.27	3.6	1.59	7.13
11/25/2013–11/26/2013	1.35	7.4	5.48	32.05	04/06/2014	4.78	8.2	1.71	3.53
11/26/2013	1.27	4	3.16	7.38	04/16/2014	3.23	22.2	6.87	232
11/30/2013–12/1/2013	21.27	38.4	1.81	98.17	04/16/2014	0.93	5.4	5.79	10.45
12/01/2013	3.3	7.2	2.18	1.52	04/23/2014	0.9	3.4	3.78	167.25
12/03/2013	3.37	9	2.67	38.85	04/28/2014	0.85	2.4	2.82	110.78
12/03/2013	4.47	6.6	1.48	0.72	04/28/2014	1.37	2.4	1.76	0.85
12/15/2013	2.03	3.2	1.57	292.72	04/28/2014	4.55	3.2	0.7	0.75
12/26/2013	3.57	8	2.24	257.35	04/29/2014	1.47	4.6	3.14	18.22
12/26/2013–12/27/2013	5.05	17	3.37	3.78	04/29/2014	1.25	2.2	1.76	6.65
12/31/2013	2.08	2.8	1.34	105.35	05/03/2014	3.32	11.2	3.38	85.67
01/13/2014	1.15	3.8	3.3	309.82	05/03/2014	0.8	3.6	4.5	7.38
01/13/2014	0.32	2.8	8.84	0.77	05/16/2014	0.97	2.6	2.69	297.07
01/14/2014	0.47	6	12.86	21.42	05/16/2014	3.22	4.2	1.31	16.42
01/19/2014	5.52	7.8	1.41	116.23	05/29/2014–05/30/2014	3.43	7.8	2.27	308.97
01/20/2014	1.33	2.4	1.8	29.2	06/01/2014	3.5	14.6	4.17	49.78
01/20/2014	0.75	3.8	5.07	1.67	06/12/2014	0.68	3.6	5.27	275.97
01/20/2014	1.13	5.4	4.76	1.18	06/19/2014	1.22	4.2	3.45	154.55
01/21/2014	0.45	3.6	8	0.73	06/19/2014	0.82	4.8	5.88	12.33
01/21/2014	3.77	8.4	2.23	0.83
01/21/2014	2.7	7.4	2.74	6.13
01/21/2014	2.15	2.2	1.02	1.05
01/21/2014	2.6	5.6	2.15	2.85
01/22/2014	4.12	4.6	1.12	1.37
01/28/2014	0.18	2.2	12	152.93
01/31/2014–02/01/2014	6.08	14.8	2.43	81.98

In Table 6, the seasonal distribution of rainfall events and the results obtained from the conceptual model in terms of total runoff depth, retention, and subsurface runoff coefficient are shown. This analysis is carried out to highlight the seasonal variability of the hydraulic response of the green roof of interest. In particular, it is possible to observe that the retention coefficient ranges from 15% in Summer, when the total rainfall depth is equal to 80 mm, to 30% in Winter, with a total rainfall depth of 208.63 mm. These results show that the retention capacity of a green roof is lower in Summer than it is in Winter, unlike expected. This behavior can be explained considering the fact that the rainfall events during Summer are intense and very short in the Mediterranean climate conditions. Hence, despite the high temperatures, which should favor the storage of water, in the case of heavy rainfall with short duration, the green roof quickly reaches its field capacity, thus draining a large amount of the rainfall volumes.

Table 6. Seasonal distribution of rainfall events from Cosenza and the model results (RD, runoff depth; SRC, subsurface runoff coefficient; VR, retention).

Season	Number of Events	PD (mm)	RD (mm)	SRC (%)	VR (%)
Summer (06/21/2013–09/20/2013)	9	80.80	74.58	84.92	15.08
Autumn (09/21/2013–12/20/2013)	27	291.40	261.12	86.02	13.98
Winter (12/21/2013–03/20/2014)	35	208.63	170.22	71.78	28.22
Spring (03/21/2014–06/20/2014)	27	185.80	159.22	81.02	18.98

Table 6. Seasonal distribution of rainfall events from Cosenza and the model results (RD, runoff depth; SRC, subsurface runoff coefficient; VR, retention).

Season	Number of Events	PD (mm)	RD (mm)	SRC (%)	VR (%)
Summer (06/21/2013–09/20/2013)	9	80.80	74.58	84.92	15.08
Autumn (09/21/2013–12/20/2013)	27	291.40	261.12	86.02	13.98
Winter (12/21/2013–03/20/2014)	35	208.63	170.22	71.78	28.22
Spring (03/21/2014–06/20/2014)	27	185.80	159.22	81.02	18.98

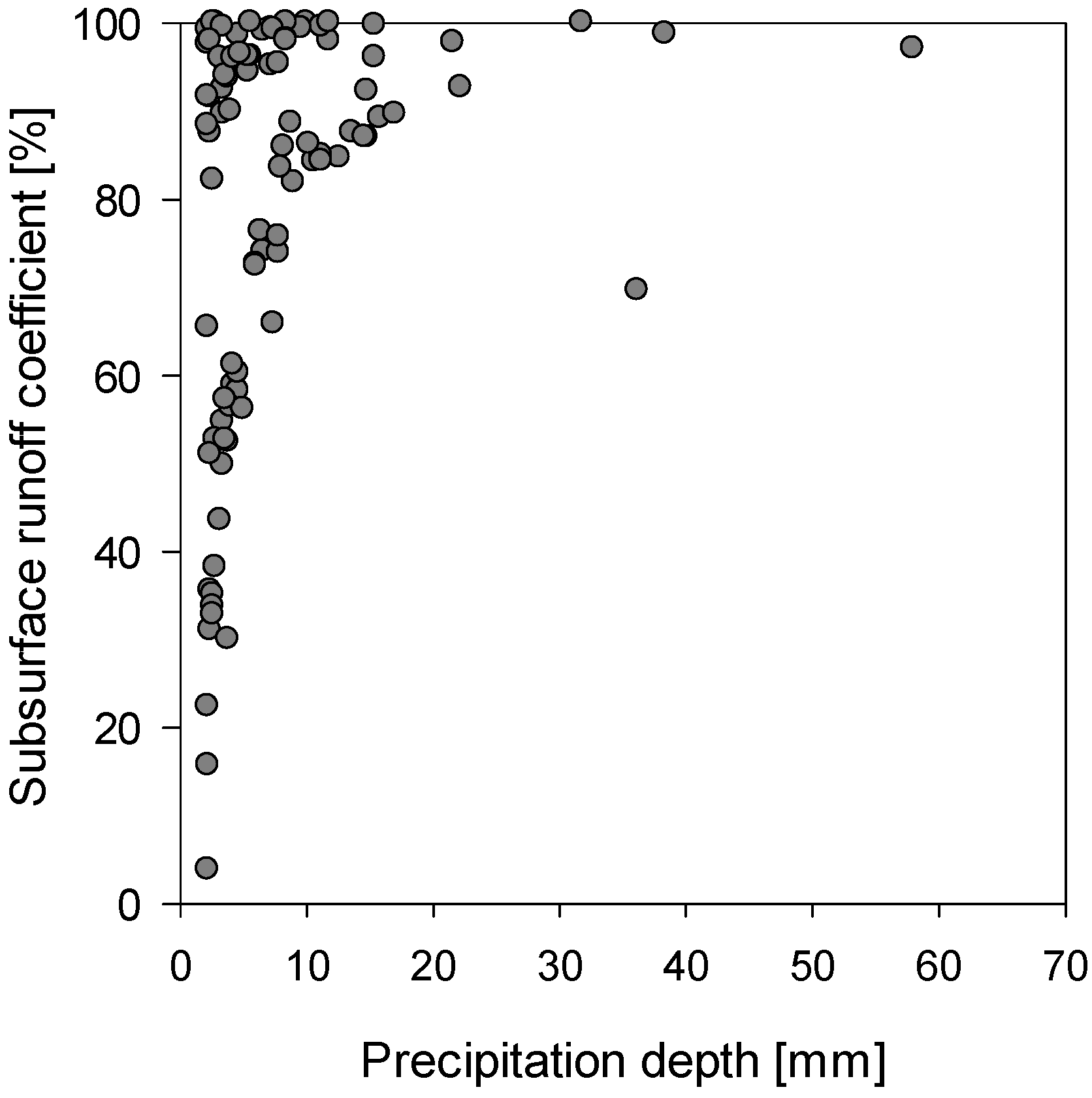
The results obtained for the entire year with 1-min time step, precipitation, and runoff exhibits the same proportionality, previously observed for daily data. From Figure 5, it is possible to notice how the subsurface runoff coefficient is close to 100% for events with high rainfall depths, while for rainfall depth <10 mm there is a significant variation depending on the antecedent dry weather period. For example, as shown in Table 5, for the two events of 01/21/2014 and 03/01/2014 with the same rainfall depth of 2.20 mm there are two different subsurface runoff: 99.24% and 35.08%; this can be explained by considering the antecedent dry weather period for the two events, 1.05 h and 196.10 h, respectively. A longer antecedent dry weather period between two rainfall events allows the substrate to completely dry out, so as to increase its retention capacity for the consequent storm.

Figure 5. Modeled subsurface runoff coefficient, on an event-time scale, as a function of precipitation depth, by using one-minute rainfall data from Cosenza.

Figure 5. Modeled subsurface runoff coefficient, on an event-time scale, as a function of precipitation depth, by using one-minute rainfall data from Cosenza.

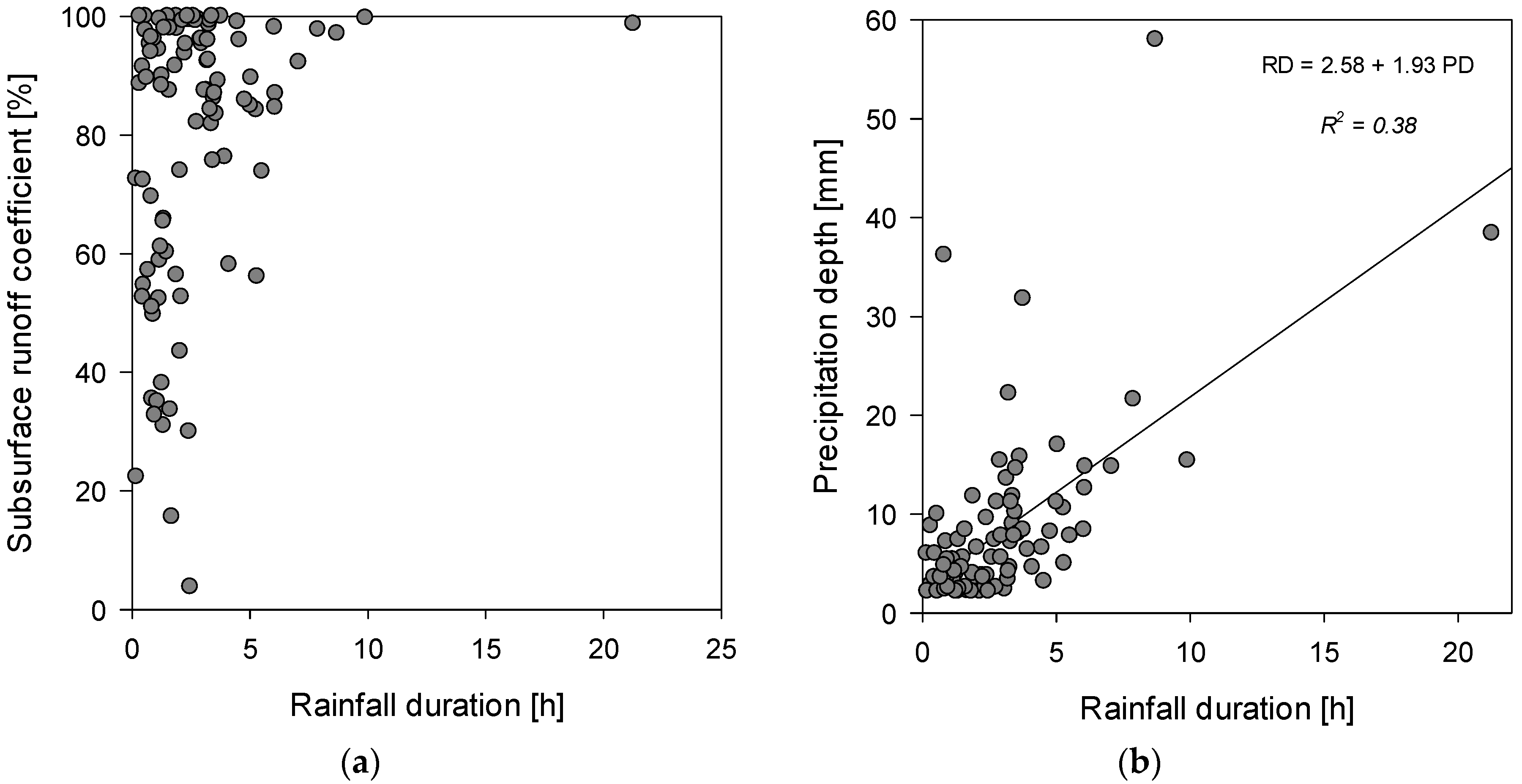
Additionally, in this part of the study the influence of the rainfall duration on the subsurface runoff coefficient was also investigated (Figure 6a). It is observed that for rainfall events with duration less than 5 h, the subsurface runoff coefficient is significantly variable, while for rainfall duration greater than 5 h, the runoff coefficient is consistently above 80%. The phenomenon that a longer precipitation generates a higher subsurface runoff coefficient is justified by the fact that under those circumstances the substrate, once it reaches the field capacity, will not retain the rainfall volume and will completely dry out. However, for high rainfall events with lower duration, the substrate behavior is mainly influenced by the initial moisture condition, suggesting that the antecedent dry weather period is an important influencing factor. Despite the fact that the duration may be considered a secondary variable, strongly related to rainfall volume, the two parameters are not statistically dependent, as shown in Figure 6b.

Figure 6. (a) Subsurface runoff coefficient as a function of rainfall duration for event-time data from Cosenza; and (b) the correlation between precipitation depth and rainfall duration.

Figure 6. (a) Subsurface runoff coefficient as a function of rainfall duration for event-time data from Cosenza; and (b) the correlation between precipitation depth and rainfall duration.

Furthermore, to statistically determine the significance of the hydrologic parameters on the event runoff coefficient, the multiple linear regression analysis is applied. Since six rainfall events were considered for the validation process and the first event was not take into account, because the information about its antecedent dry weather period is missing, only 90 rainfall events of the 97, were used.

Based on the observations previously made about the influence of antecedent dry weather periods, a relationship between runoff depth (RD), rainfall or precipitation depth (PD), antecedent dry weather period (ADWP), duration (D), and intensity (i) of rainfall, was obtained. The results of the multiple linear regression analysis are summarized in Table 7, where the t-statistics (significant at p = 0.05) are presented in the same order as the parameters in the equation.

Table 7. Multiple linear regression analysis, by using one-minute data from Cosenza.

Regression Equation		R2	t-Statistic
RD = −0.89 + PD	(8)	0.99	91.30
RD = −8.70 + 7.84 lnPD + 0.68 D	(9)	0.76	10.28, 3.89
RD = −0.24 + 1.01 PD – 0.27 lnADWP	(10)	0.99	120.62, −8.30
lnRD = −0.56 + 1.32 lnD − 0.13 lnIT + 1.40 lnADWP	(11)	0.88	23.13, −6.74, 20.10

Table 7. Multiple linear regression analysis, by using one-minute data from Cosenza.

Regression Equation		R2	t-Statistic
RD = −0.89 + PD	(8)	0.99	91.30
RD = −8.70 + 7.84 lnPD + 0.68 D	(9)	0.76	10.28, 3.89
RD = −0.24 + 1.01 PD – 0.27 lnADWP	(10)	0.99	120.62, −8.30
lnRD = −0.56 + 1.32 lnD − 0.13 lnIT + 1.40 lnADWP	(11)	0.88	23.13, −6.74, 20.10

Equation (8) correlates the runoff depth with the rainfall depth and exhibits a R² equal to 0.99. Equation (9) was defined by adding an additional parameter, the rainfall duration. Although Equation (9) exhibits a R² equal to 0.76, the t-statistic of the duration is characterized by a low significance level. In the regression Equations (10) and (11) in Table 7 the antecedent dry weather period is considered, as well. In particular, in Equation (10), the runoff is obtained by considering precipitation depth and antecedent dry weather period, with R² equal to 0.99 and all the parameters present a significant t-statistic. The Equation (11) correlates the runoff with rainfall event duration and intensity and the antecedent dry weather period with a R² equal to 0.88. From this analysis, Equation (10) seems to be the most significant one, since it provides a high R² value and a good statistic level for the antecedent dry weather period.

The multi-regression relationships, reported in Table 7, are validated by using a set of 1-min rainfall data from Cosenza, Italy. Six representative rainfall events, reported in Table 8, with varying total depth were selected from 97 rainfall events. The results from the statistical relationships are then compared with the runoff depth obtained from the SWMM model, loaded with the one-minute rainfall data as well. In the validation process, the SWMM model is used as a reference to verify the soundness of the data obtained from the statistical relationship.

Table 8. Selected rainfall events for validation process of Equations (8)–(11).

No.	Events	PD (mm)	RD (mm)	i (mm/h)	d (h)	ADWP (h)
1	09/13/2013	3.40	1.86	7.03	0.48	15.07
2	11/13/2013	2.40	0.85	2.82	0.85	33.05
3	11/24/2013	36.20	25.20	44.33	0.82	2.00
4	12/27/2013	17.00	15.24	3.37	5.05	3.73
5	01/10/2014	7.80	5.76	1.41	5.52	116.23
6	04/16/2014	22.20	20.57	6.87	3.23	232.00

Table 8. Selected rainfall events for validation process of Equations (8)–(11).

No.	Events	PD (mm)	RD (mm)	i (mm/h)	d (h)	ADWP (h)
1	09/13/2013	3.40	1.86	7.03	0.48	15.07
2	11/13/2013	2.40	0.85	2.82	0.85	33.05
3	11/24/2013	36.20	25.20	44.33	0.82	2.00
4	12/27/2013	17.00	15.24	3.37	5.05	3.73
5	01/10/2014	7.80	5.76	1.41	5.52	116.23
6	04/16/2014	22.20	20.57	6.87	3.23	232.00

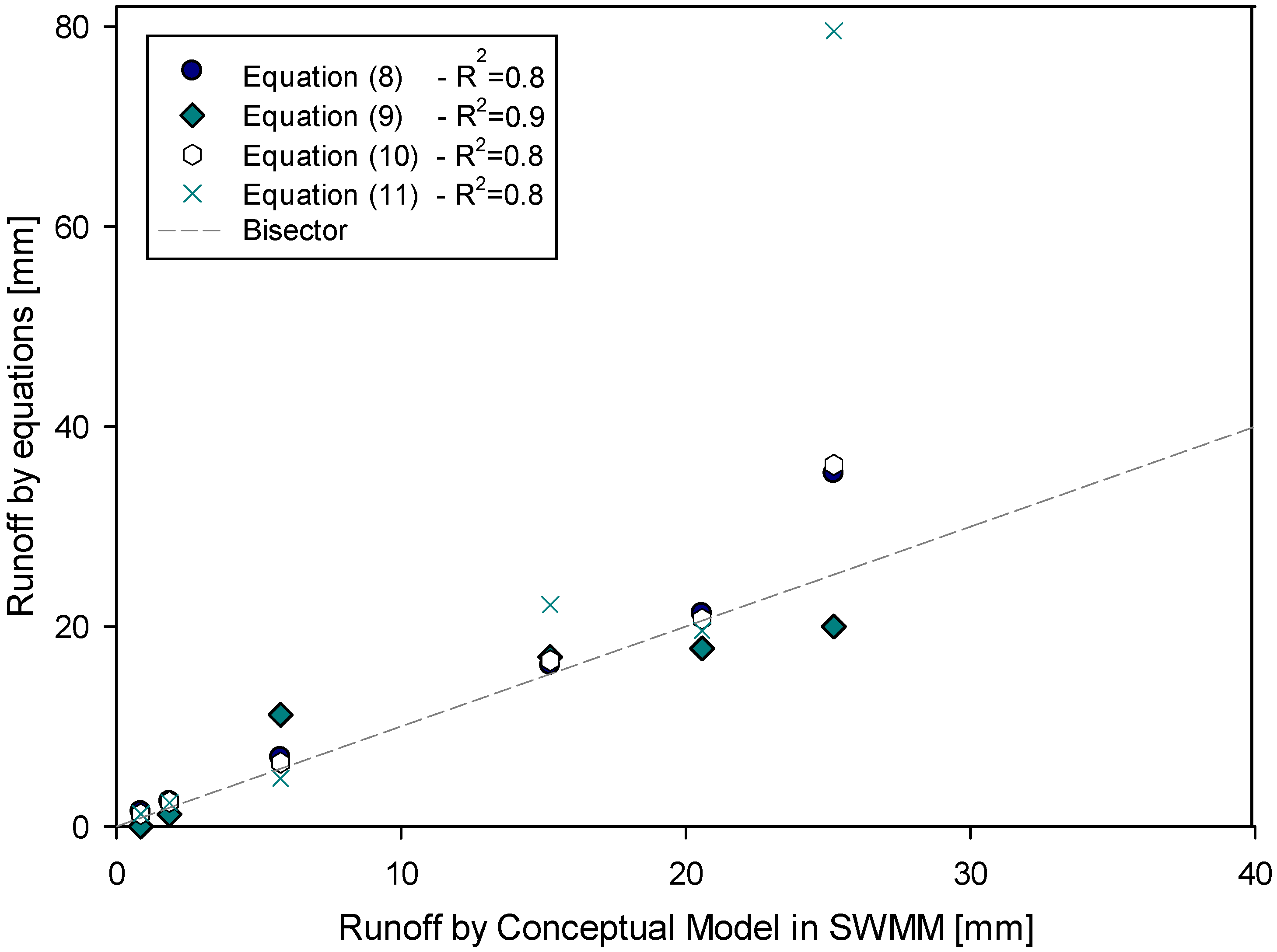
The results of the validation analysis, in which the runoff depth obtained with the regression equations is compared to the runoff depth modelled in SWMM, are reported in Figure 7. In this figure, for the entire datasets, a good scattering close to the bisector is shown. In particular, for Equation (9) a value of R² equal to 0.90 was obtained, while a value of 0.80 for the remaining regression Equations (8), (10), and (11). By observing each rainfall events in Figure 7, it is possible to see that Equations (8), (10), and (11) constantly overestimate the value of the runoff modeled in SWMM. More in detail, for the third rainy event (dated 24 November 2013) it is found an higher overestimation of runoff than the other events. This result can be explained by analyzing the rainfall event’s characteristics, as shown in Table 8, as well as the dataset used for regression analysis in Table 5. Indeed, the rainfall event No. 3 (on 24 November 2013) presents a precipitation depth of 36.20 mm and an intensity of 44.33 mm/h; instead, the regression equations were obtained from the dataset listed in Table 5, in which only two rainy events exhibit precipitation depth greater than 35 mm and only one event shows an intensity exceeding 30 mm/h.

Figure 7. Runoff depth predicted by the Equations (8)–(11) vs. the runoff depth with the conceptual model in SWMM for six rainfall events from Cosenza.

Figure 7. Runoff depth predicted by the Equations (8)–(11) vs. the runoff depth with the conceptual model in SWMM for six rainfall events from Cosenza.

The statistical analysis does not only allow the identification of the most influencing parameters on the hydraulic performance, but also to produce a series of validated multi-regression relationships for the specific green roof studied. Those equations can be used to preliminarily predict the runoff depth, for a given rainfall event, when more advanced model are not available.

5. Conclusions

Green roofs may represent a solution for minimizing the impact of urbanization on the hydrologic cycle and for sustainably managing water resources in urban environments. Several studies have shown that green roofs effectively control surface runoff in urban drainage systems reducing overall stormwater volumes and peak flow rates.

From the studies found in literature, the hydraulic efficiency of a green roof strongly depends on the hydrological parameters of the rainfall events, such as precipitation depth, antecedent dry weather period, duration, and intensity of the event. Most of the studies provided an annual or a seasonal subsurface runoff coefficient, varying from 0.32 to 0.89.

In this study, firstly, the subsurface runoff coefficient at daily and event-time scales for a given green roof, through a conceptual model implemented in SWMM, was evaluated. The model was loaded with both daily and 1-minute rainfall data from two Mediterranean-climate sites, one in Thessaloniki, Greece and one in Cosenza, Italy, respectively. Then, the most influencing hydrological parameters were examined through a statistical regression analysis. The findings show that the daily subsurface runoff coefficient is on average 0.70 for both sites, while the event-based one is on average 0.79 with a standard deviation of 0.23 for the site in Cosenza, Italy. A specific inter-event time of about 40 min, was defined for the green roof studied, as opposed to use an inappropriate value of 6–12 h used in previous scientific studies.

The modeled results, obtained with daily rainfall data recorded in Cosenza, Italy and in Thessaloniki, led to the following considerations: (1) there is a direct proportionality between precipitation and runoff; (2) the retention percent drops as the rainfall depth exponentially increases and the maximum retention capacity is 80%. When the precipitation depth is greater than 10 mm, the retention capacity varies from 20% to 0%. Through a multiple linear regression analysis, a relationship that correlates the runoff with precipitation and antecedent dry weather period was obtained and, consequently, validated.

The results, obtained in the previous phase, were then compared with an event-time scale analysis by using one-minute data. From this analysis precipitation and runoff exhibit the same proportionality, previously observed for daily data.

Furthermore, to statistically determine the significance of the hydrologic parameters on the event runoff coefficient, the multiple linear regression analysis was applied. Indeed, the investigation revealed that the influencing parameters are the rainfall depth and antecedent dry weather period with a confidence level of 95%. This study demonstrated that, due to the high variability of the subsurface runoff coefficient, the use of a unique value for design purposes is inappropriate. A preliminary estimation for designing purposes could be obtained as a function of the total rainfall depth and the antecedent dry weather period by using the validated multi-regression relationship which is site-specific.

To generalize the multi regression relationships found in this work and let them suitable for different typologies of green roofs, the influence of physical parameters will be further investigated in future research studies.