Probabilistic Forecasting of Drought Events Using Markov Chain- and Bayesian Network-Based Models: A Case Study of an Andean Regulated River Basin
Abstract
:1. Introduction
2. Materials and Methods
2.1. Case Study
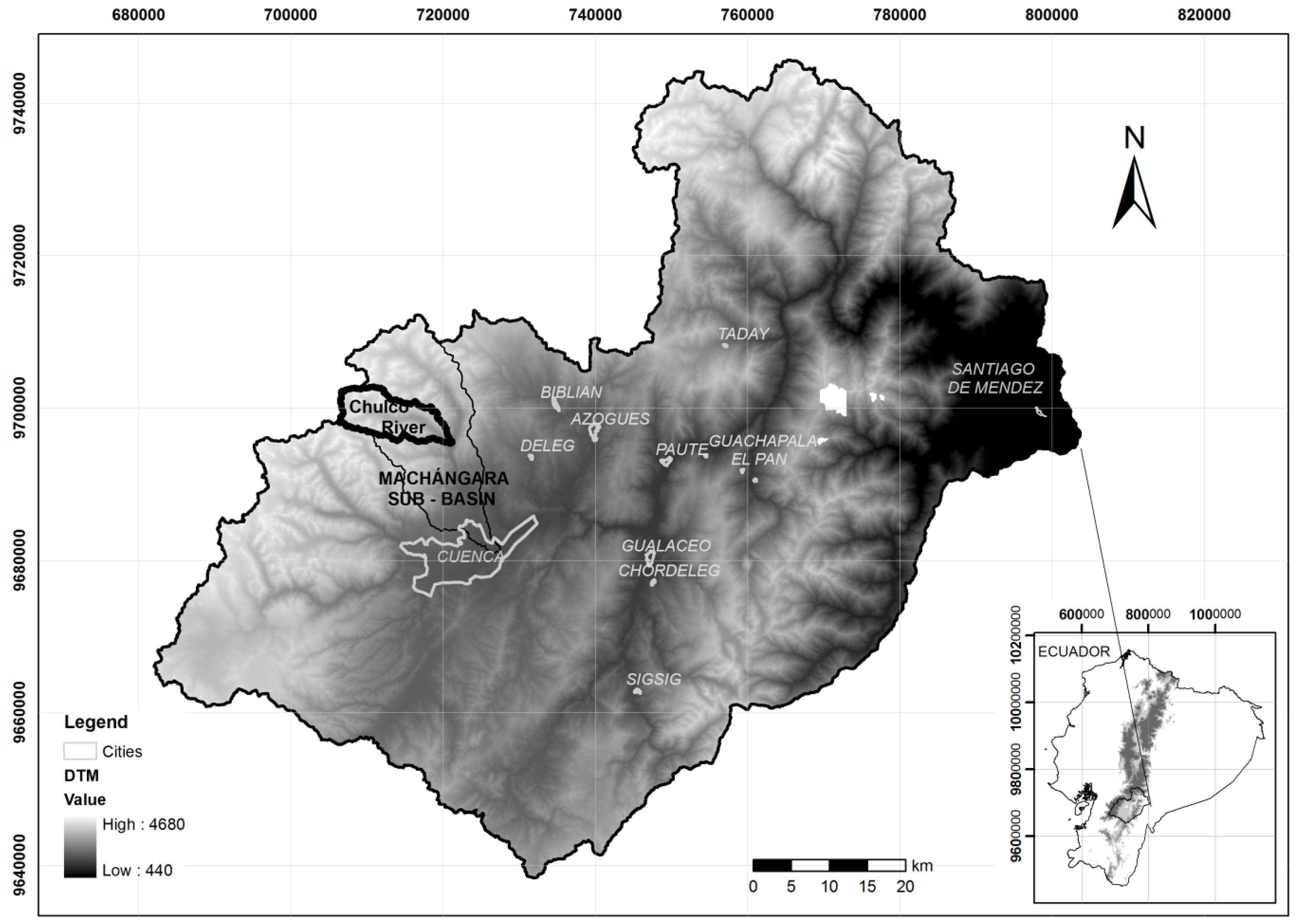
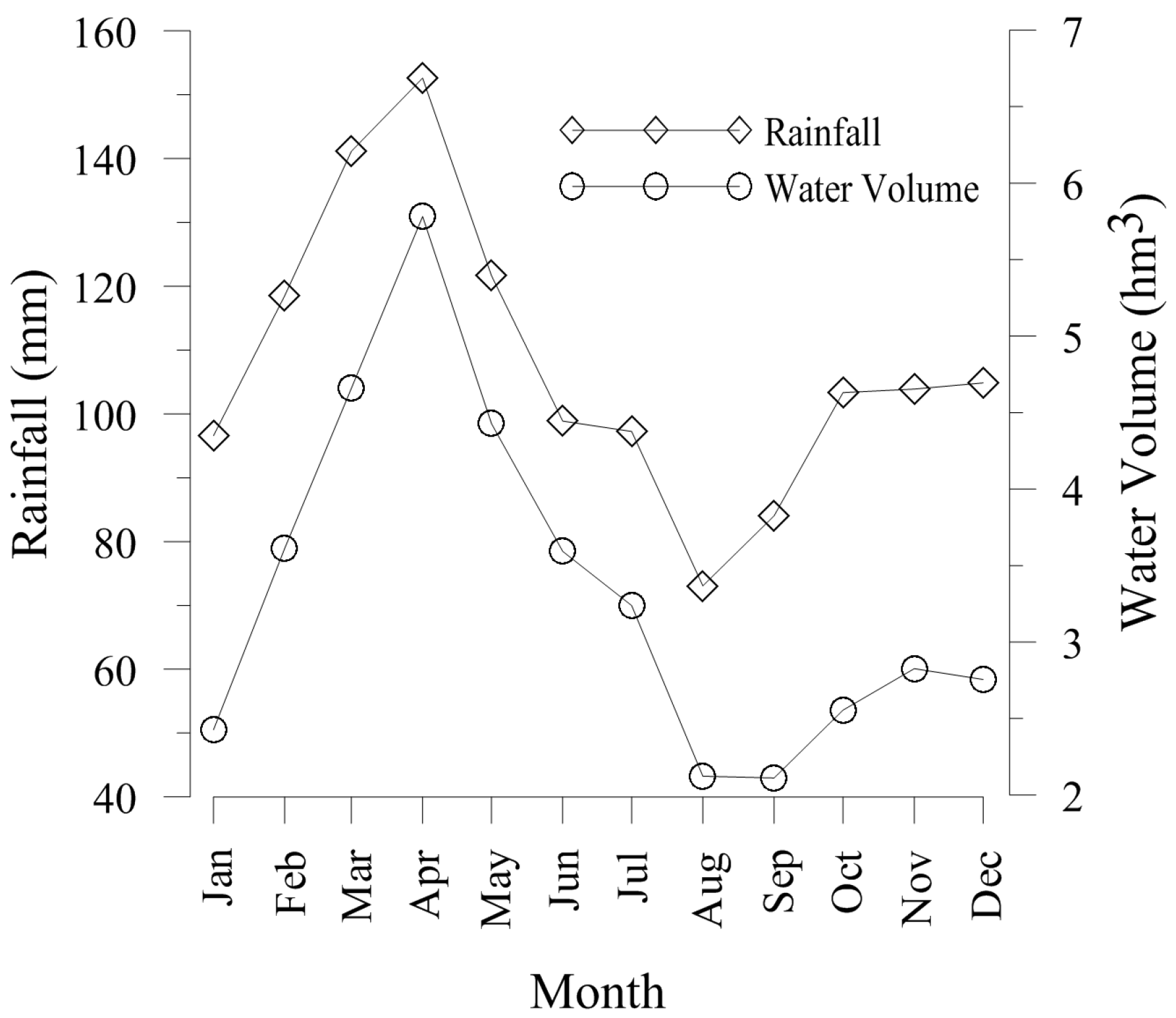
2.2. Drought Index
2.3. Markov Chain Models
2.4. Bayesian Network Models
2.5. Copulas
2.6. Copulas Fitting
2.7. Forecast Verification
3. Results and Discussion
3.1. Drought Index
| PC1 | January | February | March | April | May | June | July | August | September | October | November | December |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Eigenvalues | 6.21 | 7.26 | 7.89 | 7.13 | 7.64 | 7.08 | 7.10 | 7.16 | 7.08 | 6.77 | 5.86 | 5.71 |
| Explained variance | 62% | 73% | 79% | 71% | 76% | 71% | 71% | 72% | 71% | 68% | 59% | 57% |
| Category | Drought State | Frequency |
|---|---|---|
| 0 | no drought | 218 |
| 1 | mild drought | 185 |
| 2 | drought | 77 |
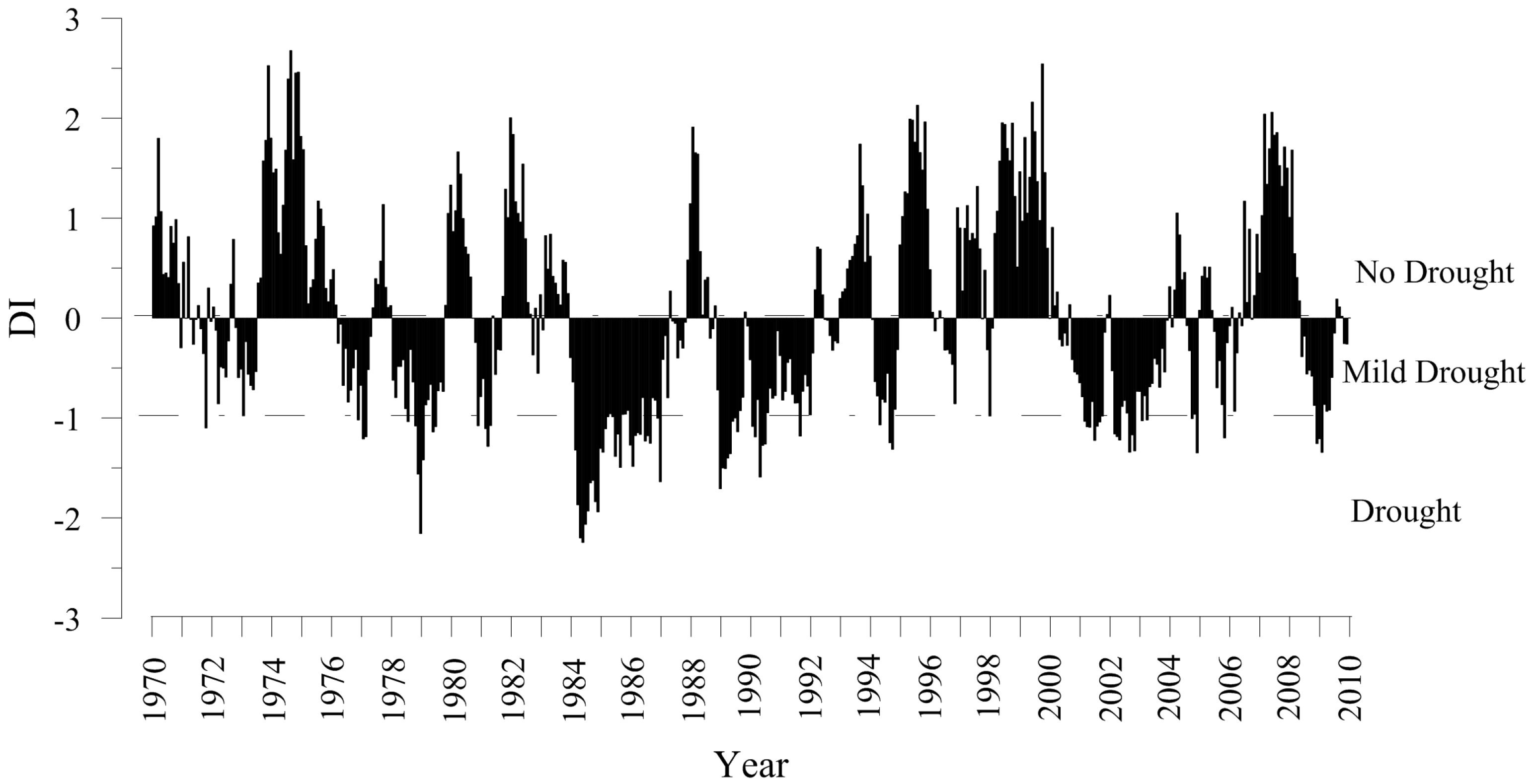

3.2. Markov Chain Models
| State i | State j | ||
|---|---|---|---|
| 0 | 1 | 2 | |
| 0 | 0.72 | 0.28 | 0.00 |
| 1 | 0.07 | 0.86 | 0.07 |
| 2 | 0.00 | 0.57 | 0.43 |
| States h-i | State j | ||
|---|---|---|---|
| 0 | 1 | 2 | |
| 0-0 | 0.75 | 0.25 | 0.00 |
| 0-1 | 0.00 | 1.00 | 0.00 |
| 0-2 | 0.33 | 0.33 | 0.33 |
| 1-0 | 0.50 | 0.50 | 0.00 |
| 1-1 | 0.09 | 0.82 | 0.09 |
| 1-2 | 0.00 | 0.33 | 0.67 |
| 2-0 | 0.33 | 0.33 | 0.33 |
| 2-1 | 0.00 | 1.00 | 0.00 |
| 2-2 | 0.00 | 0.75 | 0.25 |
3.3. Bayesian Network Models
| p Value | ||||||||||||
| Copulas | January | February | March | April | May | June | July | August | September | October | November | December |
| Normal | 0.292 | 0.233 | 0.077 | 0.329 | 0.368 | 0.527 | 0.369 | 0.727 | 0.189 | 0.222 | 0.524 | 0.664 |
| t | 0.057 | 0.108 | 0.066 | 0.358 | 0.338 | 0.313 | 0.464 | 0.432 | 0.127 | 0.322 | 0.326 | 0.326 |
| Clayton | 0.007 | 0.022 | 0.052 | 0.022 | 0.009 | 0.034 | 0.005 | 0.020 | 0.004 | 0.002 | 0.021 | 0.017 |
| Frank | 0.363 | 0.910 | 0.854 | 0.534 | 0.535 | 0.565 | 0.804 | 0.864 | 0.207 | 0.170 | 0.426 | 0.193 |
| S-statistic | ||||||||||||
| Copulas | January | February | March | April | May | June | July | August | September | October | November | December |
| Normal | 0.028 | 0.027 | 0.033 | 0.024 | 0.023 | 0.021 | 0.022 | 0.018 | 0.029 | 0.029 | 0.022 | 0.020 |
| t | 0.040 | 0.033 | 0.034 | 0.024 | 0.024 | 0.025 | 0.022 | 0.024 | 0.034 | 0.028 | 0.027 | 0.027 |
| Clayton | - | - | 0.049 | - | - | - | - | - | - | - | - | - |
| Frank | 0.027 | 0.018 | 0.018 | 0.023 | 0.022 | 0.023 | 0.019 | 0.019 | 0.030 | 0.034 | 0.026 | 0.031 |
| p Value | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Copulas | January | February | March | April | May | June | July | August | September | October | November | December |
| Normal | 0.083 | 0.164 | 0.103 | 0.582 | 0.698 | 0.651 | 0.400 | 0.276 | 0.459 | 0.542 | 0.433 | 0.437 |
| t | 0.007 | 0.079 | 0.087 | 0.406 | 0.523 | 0.254 | 0.236 | 0.110 | 0.305 | 0.294 | 0.064 | 0.088 |
| Clayton | 0.001 | 0.006 | 0.009 | 0.010 | 0.005 | 0.008 | 0.004 | 0.000 | 0.001 | 0.000 | 0.000 | 0.000 |
| Frank | 0.314 | 0.718 | 0.648 | 0.588 | 0.661 | 0.605 | 0.865 | 0.136 | 0.108 | 0.068 | 0.074 | 0.259 |
| S-statistic | ||||||||||||
| Copulas | January | February | March | April | May | June | July | August | September | October | November | December |
| Normal | 0.047 | 0.038 | 0.042 | 0.027 | 0.026 | 0.026 | 0.031 | 0.035 | 0.032 | 0.030 | 0.032 | 0.032 |
| t | - | 0.048 | 0.046 | 0.033 | 0.031 | 0.036 | 0.039 | 0.046 | 0.038 | 0.039 | 0.051 | 0.049 |
| Clayton | - | - | - | - | - | - | - | - | - | - | - | - |
| Frank | 0.045 | 0.032 | 0.034 | 0.035 | 0.033 | 0.034 | 0.028 | 0.055 | 0.061 | 0.064 | 0.063 | 0.049 |
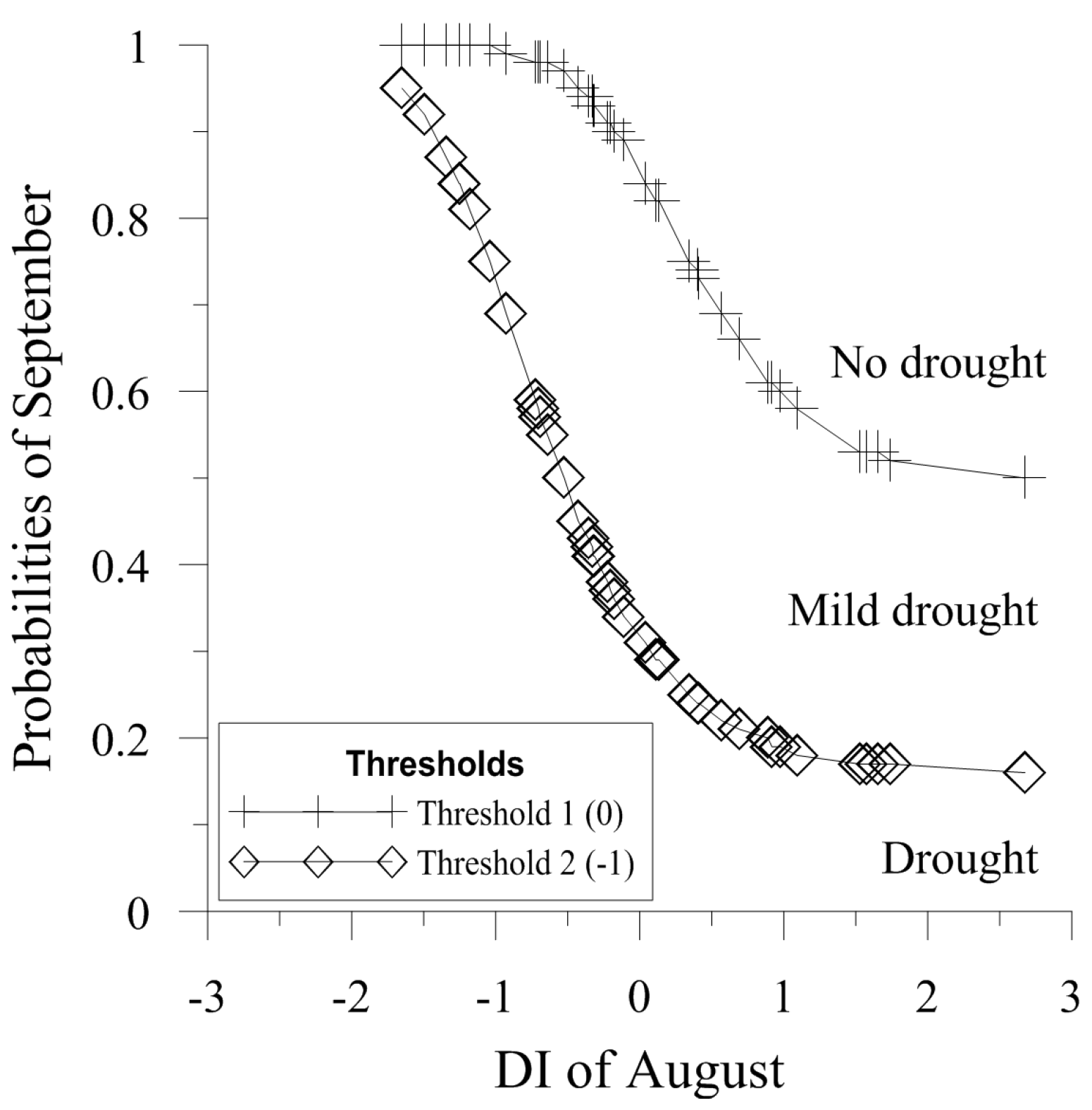
3.4. Forecast Verification
| Model | January | February | March | April | May | June | July | August | September | October | November | December |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (a) No Drought, Mild Drought and Drought | ||||||||||||
| MCFO | −0.40 | 0.27 | 0.63 | 0.52 | 0.37 | 0.41 | 0.48 | 0.45 | 0.33 | 0.20 | 0.15 | 0.15 |
| MCSO | −0.46 | −0.32 | 0.63 | 0.58 | 0.25 | 0.32 | 0.50 | 0.52 | 0.18 | 0.19 | 0.05 | 0.16 |
| BNFO | −0.50 | 0.13 | 0.09 | 0.06 | −0.20 | 0.08 | 0.04 | 0.00 | −0.11 | −0.15 | 0.02 | −0.09 |
| BNSO | −0.60 | −0.33 | −0.11 | −0.08 | −0.29 | −0.08 | −0.14 | −0.13 | −0.30 | −0.33 | −0.09 | −0.27 |
| (b) Mild Drought and Drought | ||||||||||||
| MCFO | −0.35 | 0.12 | 0.53 | 0.49 | 0.27 | 0.19 | 0.42 | 0.31 | 0.04 | 0.12 | 0.09 | 0.18 |
| MCSO | −0.28 | −0.28 | 0.53 | 0.53 | 0.15 | 0.07 | 0.48 | 0.47 | −0.14 | 0.10 | −0.03 | 0.16 |
| BNFO | 0.29 | 0.53 | 0.48 | 0.59 | 0.29 | 0.38 | 0.47 | 0.47 | −0.07 | 0.32 | 0.45 | 0.62 |
| BNSO | 0.28 | 0.50 | 0.37 | 0.53 | 0.23 | 0.20 | 0.38 | 0.39 | −0.27 | 0.18 | 0.42 | 0.53 |
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Mishra, A.K.; Singh, V.P. Review paper A review of drought concepts. J. Hydrol. 2010, 391, 202–216. [Google Scholar] [CrossRef]
- Zhong, S.; Shen, L.; Sha, J.; Okiyama, M.; Tokunaga, S.; Liu, L.; Yan, J. Assessing the water parallel pricing system against drought in China: A study based on a CGE model with multi-provincial irrigation water. Water 2015, 7, 3431–3465. [Google Scholar] [CrossRef]
- Karavitis, C.A.; Alexandris, S.; Tsesmelis, D.E.; Athanasopoulos, G. Application of the standardized precipitation index (SPI) in Greece. Water 2011, 3, 787–805. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Chura, O.; López-Moreno, J.I.; Azorin-Molina, C.; Sanchez-Lorenzo, A.; Aguilar, E.; Moran-Tejeda, E.; Trujillo, F.; Martínez, R.; Nieto, J.J. Spatio-temporal variability of droughts in Bolivia: 1955–2012. Int. J. Climatol. 2015, 35, 3024–3040. [Google Scholar] [CrossRef]
- Beniston, M. Climatic change in mountain regions: A review of possible impacts. Clim. Chang. 2003, 59, 5–31. [Google Scholar] [CrossRef]
- Buytaert, W.; Vuille, M.; Dewulf, A.; Urrutia, R.; Karmalkar, A.; Célleri, R. Uncertainties in climate change projections and regional downscaling in the tropical Andes: Implications for water resources management. Hydrol. Earth Syst. Sci. 2010, 14, 1247–1258. [Google Scholar] [CrossRef]
- Buytaert, W.; Célleri, R.; de Bièvre, B.; Cisneros, F.; Wyseure, G.; Deckers, J.; Hofstede, R. Human impact on the hydrology of the Andean páramos. Earth Sci. Rev. 2006, 79, 53–72. [Google Scholar] [CrossRef]
- Buytaert, W.; Celleri, R.; Willems, P. Spatial and temporal rainfall variability in mountainous areas: A case study from the south Ecuadorian Andes. J. Hydrol. 2006, 329, 413–421. [Google Scholar] [CrossRef]
- Al-Faraj, F.; Scholz, M.; Tigkas, D. Sensitivity of surface runoff to drought and climate change: Application for shared river basins. Water 2014, 6, 3033–3048. [Google Scholar] [CrossRef]
- Staudinger, M.; Stahl, K.; Seibert, J. A drought index accounting for snow. Water Resour. Res. 2014, 50, 7861–7872. [Google Scholar] [CrossRef]
- Celleri, R.; Willems, P.; Buytaert, W.; Feyen, J. Space-time rainfall variability in the Paute basin, Ecuadorian Andes. Hydrol. Process. 2007, 21, 3316–3327. [Google Scholar] [CrossRef]
- Steinemann, A. Drought indicators and triggers: A stochastic approach to evaluation. J. Am. Water Resour. Assoc. 2003, 39, 1217–1233. [Google Scholar] [CrossRef]
- Madadgar, S.; Moradkhani, H. A Bayesian framework for probabilistic seasonal drought forecasting. J. Hydrometeorol. 2013, 14, 1685–1706. [Google Scholar] [CrossRef]
- Kao, S.C.; Govindaraju, R.S. A copula-based joint deficit index for droughts. J. Hydrol. 2010, 380, 121–134. [Google Scholar] [CrossRef]
- Avilés, A.; Célleri, R.; Paredes, J.; Solera, A. Evaluation of markov chain based drought forecasts in an andean regulated river basin using the skill scores RPS and GMSS. Water Resour. Manag. 2015, 29, 1949–1963. [Google Scholar] [CrossRef]
- Viviroli, D.; Archer, D.R.; Buytaert, W.; Fowler, H.J.; Greenwood, G.B.; Hamlet, A.F.; Huang, Y.; Koboltschnig, G.; Litaor, M.I.; López-Moreno, J.I.; et al. Climate change and mountain water resources: Overview and recommendations for research, management and policy. Hydrol. Earth Syst. Sci. 2011, 15, 471–504. [Google Scholar] [CrossRef]
- Sánchez-Chóliz, J.; Sarasa, C. River flows in the Ebro basin: A century of evolution, 1913–2013. Water 2015, 7, 3072–3082. [Google Scholar] [CrossRef]
- Madadgar, S.; Moradkhani, H. Spatio-temporal drought forecasting within Bayesian networks. J. Hydrol. 2014, 512, 134–146. [Google Scholar] [CrossRef]
- Mishra, A.K.; Singh, V.P. Drought modeling—A review. J. Hydrol. 2011, 403, 157–175. [Google Scholar] [CrossRef]
- Kumar, V.; Panu, U. Predictive assessment of severity of agricultural droughts based on agro-climatic factors. J. Am. Water Resour. Assoc. 1997, 33, 1255–1264. [Google Scholar] [CrossRef]
- Leilah, A.A.; Al-Khateeb, S. Statistical analysis of wheat yield under drought conditions. J. Arid Environ. 2005, 61, 483–496. [Google Scholar] [CrossRef]
- Liu, W.T.; Juárez, R.I.N. ENSO drought onset prediction in northeast Brazil using NDVI. Int. J. Remote Sens. 2001, 22, 3483–3501. [Google Scholar] [CrossRef]
- Mishra, A.K.; Desai, V.R. Drought forecasting using stochastic models. Stoch. Environ. Res. Risk Assess. 2005, 19, 326–339. [Google Scholar] [CrossRef]
- Han, P.; Wang, P.X.; Zhang, S.Y.; Zhu, D.H. Drought forecasting based on the remote sensing data using ARIMA models. Math. Comput. Model. 2010, 51, 1398–1403. [Google Scholar] [CrossRef]
- Durdu, Ö.F. Application of linear stochastic models for drought forecasting in the Büyük Menderes river basin, western Turkey. Stoch. Environ. Res. Risk Assess. 2010, 24, 1145–1162. [Google Scholar] [CrossRef]
- Modarres, R. Streamflow drought time series forecasting. Stoch. Environ. Res. Risk Assess. 2007, 21, 223–233. [Google Scholar] [CrossRef]
- Fernández, C.; Vega, J.A.; Fonturbel, T.; Jiménez, E. Streamflow drought time series forecasting: A case study in a small watershed in North West Spain. Stoch. Environ. Res. Risk Assess. 2009, 23, 1063–1070. [Google Scholar] [CrossRef]
- Morid, S.; Smakhtin, V.; Bagherzadeh, K. Drought forecasting using artificial neural networks and time series of drought indices. Int. J. Climatol. 2007, 27, 2103–2111. [Google Scholar] [CrossRef]
- Mishra, A.K.; Desai, V.R.; Singh, V.P.; Asce, F. Drought forecasting using a hybrid stochastic and neural network model. J. Hydrol. Eng. 2007, 12, 626–638. [Google Scholar] [CrossRef]
- Mishra, A.K.; Desai, V.R. Drought forecasting using feed-forward recursive neural network. Ecol. Model. 2006, 198, 127–138. [Google Scholar] [CrossRef]
- Hwang, Y.; Carbone, G.J. Ensemble forecasts of drought indices using a conditional residual resampling technique. J. Appl. Meteorol. Climatol. 2009, 48, 1289–1301. [Google Scholar] [CrossRef]
- Murphy, A.H. The value of climatological, categorical and probabilistic forecasts in the cost-loss ratio situation. Mon. Weather Rev. 1977, 105, 803–816. [Google Scholar] [CrossRef]
- Lohani, V.K.; Loganathan, G.V. An early warning system for drought management using the Palmer drought index. J. Am. Water Resour. Assoc. 1997, 33, 1375–1386. [Google Scholar] [CrossRef]
- Paulo, A.A.; Pereira, L.S. Prediction of SPI drought class transitions using Markov chains. Water Resour. Manag. 2007, 21, 1813–1827. [Google Scholar] [CrossRef]
- Cancelliere, A.; Di Mauro, G.; Bonaccorso, B.; Rossi, G. Drought forecasting using the Standardized Precipitation Index. Water Resour. Manag. 2007, 21, 801–819. [Google Scholar] [CrossRef]
- Nalbantis, I.; Tsakiris, G. Assessment of hydrological drought revisited. Water Resour. Manag. 2009, 23, 881–897. [Google Scholar] [CrossRef]
- Yuan, X.; Wood, E.F.; Chaney, N.W.; Sheffield, J.; Kam, J.; Liang, M.; Guan, K. Probabilistic seasonal forecasting of African drought by dynamical models. J. Hydrometeorol. 2013, 14, 1706–1720. [Google Scholar] [CrossRef]
- Anderson, M.L.; Mierzwa, M.D.; Kavvas, M.L. Probabilistic seasonal forecasts of droughts with a simplified coupled hydrologic-atmospheric model for water resources planning. Stoch. Environ. Res. Risk Assess. 2000, 14, 263–274. [Google Scholar] [CrossRef]
- Chung, C.; Salas, J.D. Drought occurrence probabilities and risks of dependent hydrologic processes. J. Hydrol. Eng. 2000, 5, 259–268. [Google Scholar] [CrossRef]
- AghaKouchak, A. A baseline probabilistic drought forecasting framework using standardized soil moisture index: Application to the 2012 United States drought. Hydrol. Earth Syst. Sci. 2014, 18, 2485–2492. [Google Scholar] [CrossRef]
- Araghinejad, S. An approach for probabilistic hydrological drought forecasting. Water Resour. Manag. 2010, 25, 191–200. [Google Scholar] [CrossRef]
- Heckerman, D. A tutorial on learning with Bayesian networks. In Learning in Graphical Models; Springer: Dordrecht, The Netherlands, 1998; pp. 301–354. [Google Scholar]
- Pearl, J. Bayesian networks: A model of self-activated memory for evidential reasoning. In Proceedings of the 7th Conference of the Cognitive Science Society, Irvine, CA, USA, 15–17 August 1985; pp. 329–334.
- Yan, J. Enjoy the joy of copulas: With a Package copula. J. Stat. Softw. 2007, 21, 1–21. [Google Scholar] [CrossRef]
- Yan, J. Multivariate modeling with copulas and engineering applications. In Springer Handbook of Engineering Statistics; Pham, H., Ed.; Springer London: London, UK, 2006; pp. 973–990. [Google Scholar]
- Nelsen, R.B. An Introduction to Copulas, 2nd ed.; Springer: New York, NY, USA, 2006. [Google Scholar]
- Embrechts, P.; Lindskog, F.; McNeil, A. Modelling Dependence with Copulas and Applications to Risk Management; Département de mathématiques, Institut Fédéral de Technologie de Zurich: Zurich, Switzerland, 2001. [Google Scholar]
- Mason, S.J. On using “Climatology” as a reference strategy in the brier and ranked probability skill scores. Mon. Weather Rev. 2004, 132, 1891–1895. [Google Scholar] [CrossRef]
- Murphy, A. What is a good forecast? An essay on the nature of goodness in weather forecasting. Weather Forecast. 1993, 8, 281–293. [Google Scholar] [CrossRef]
- Kolmogorov, A. Sulla determinazione empirica di una legge di distribuzione. G. dell’Ist. Ital. degli Attuari 1933, 4, 83–91. [Google Scholar]
- World Meteorological Organization. Standardized Precipitation Index User Guide; World Meteorological Organization: Geneva, Switzerland, 2012. [Google Scholar]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences, 3rd ed.; Academic Press: Cambridge, MA, USA, 2011. [Google Scholar]
- Thulasiraman, K.; Swamy, M.N.S. Graphs: Theory and Algorithms; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Sklar, A. Fonctions de Répartition à n Dimensions et Leurs Marges; l’Institut de Statistique de l’Université de Paris: Paris, France, 1959; Volume 8, pp. 229–231. [Google Scholar]
- Joe, H. Multivariate Models and Multivariate Dependence Concepts; CRC Press: Boca Raton, FL, USA, 1997. [Google Scholar]
- Cherubini, U.; Luciano, E.; Vecchiato, W. Copula Methods in Finance; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Genest, C.; Rémillard, B. Validity of the parametric bootstrap for goodness-of-fit testing in semiparametric models. Ann. Inst. H. Poincaré Probab. Stat. 2008, 44, 1096–1127. [Google Scholar] [CrossRef]
- Anderson, T. On the distribution of the two-sample Cramer-von Mises criterion. Ann. Math. Stat. 1962, 22, 1148–1159. [Google Scholar] [CrossRef]
- Zhang, H.; Casey, T. Verification of categorical probability forecasts. Weather Forecast. 2000, 15, 80–89. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Avilés, A.; Célleri, R.; Solera, A.; Paredes, J. Probabilistic Forecasting of Drought Events Using Markov Chain- and Bayesian Network-Based Models: A Case Study of an Andean Regulated River Basin. Water 2016, 8, 37. https://doi.org/10.3390/w8020037
Avilés A, Célleri R, Solera A, Paredes J. Probabilistic Forecasting of Drought Events Using Markov Chain- and Bayesian Network-Based Models: A Case Study of an Andean Regulated River Basin. Water. 2016; 8(2):37. https://doi.org/10.3390/w8020037
Chicago/Turabian StyleAvilés, Alex, Rolando Célleri, Abel Solera, and Javier Paredes. 2016. "Probabilistic Forecasting of Drought Events Using Markov Chain- and Bayesian Network-Based Models: A Case Study of an Andean Regulated River Basin" Water 8, no. 2: 37. https://doi.org/10.3390/w8020037
APA StyleAvilés, A., Célleri, R., Solera, A., & Paredes, J. (2016). Probabilistic Forecasting of Drought Events Using Markov Chain- and Bayesian Network-Based Models: A Case Study of an Andean Regulated River Basin. Water, 8(2), 37. https://doi.org/10.3390/w8020037






