Abstract
The scarcity of water resources in mountain areas can distort normal water application patterns with among other effects, a negative impact on water supply and river ecosystems. Knowing the probability of droughts might help to optimize a priori the planning and management of the water resources in general and of the Andean watersheds in particular. This study compares Markov chain- (MC) and Bayesian network- (BN) based models in drought forecasting using a recently developed drought index with respect to their capability to characterize different drought severity states. The copula functions were used to solve the BNs and the ranked probability skill score (RPSS) to evaluate the performance of the models. Monthly rainfall and streamflow data of the Chulco River basin, located in Southern Ecuador, were used to assess the performance of both approaches. Global evaluation results revealed that the MC-based models predict better wet and dry periods, and BN-based models generate slightly more accurately forecasts of the most severe droughts. However, evaluation of monthly results reveals that, for each month of the hydrological year, either the MC- or BN-based model provides better forecasts. The presented approach could be of assistance to water managers to ensure that timely decision-making on drought response is undertaken.
1. Introduction
Droughts are recognized as an environmental disaster, the consequence of a reduction in precipitation over an extended period of time [1], negatively affecting agriculture, domestic water supply and economic growth [2], and in some cases even altering the functioning of natural ecosystems [3]. Droughts are especially important in regions where economic activities are highly dependent on water resources [4], such as in mountain regions which traditionally provide water resources and services to local communities and lowland residents [5]. For example, the Andean basins, which have been identified as excellent providers of water for multiple uses [6,7], could be affected by droughts and climate change, putting the water supply at risk and augmenting the vulnerability of the basin’s water resources systems and eco-services [8,9,10,11]. The increasing tendency of water shortage is a concern of water managers [11], wrestling with questions such as which drought indicator [12] and threshold of the indicators should be used to qualify the drought status. In fact, drought characterization requires indicators that are generally applicable, but specific enough to capture the type of drought relevant to the region and the variables of interest [10]. Droughts may occur at different moments in the hydrological year, with the consequence that hydrologic variables might experience quite different levels of drought, complicating the overall assessment of the drought status [13]. Furthermore, droughts can be the result of a succession of water shortages over different periods of time [14]. Consequently, there is a need to assess the drought status using indices based on multiple variables monitored during different time windows. The present study uses the drought index (DI) developed by Avilés et al. [15], which is based on water-related variables of different window-sizes in the hydrologic year, enabling the capturing of the drought status for short, medium and long periods. The main advantages of this index are its flexibility in aggregating basin water-related variables and capability of selectively using variables depending on the available hydro-meteorological data.
The characterization of droughts and its reliable prediction would help water managers to make the decisions that make water supplies safe and reliable, and that are risk-adverse. To this end water managers need the instruments that enable them to mimic the water supply and demand systems using adequate models that also address uncertainties and vulnerabilities, and help to prioritize risks [16]. A major restriction in the formulation of strategies addressing the availability of water is the forecast of droughts [17]. It is generally accepted that the reliable forecast of drought events plays an important role in the development of adequate strategies for the planning and distribution of water resources [13,18]. Several methodologies to forecast drought saw daylight in recent years, and Mishra and Singh [19] describe some of these approaches. Regression analysis [20,21,22] is a commonly used method; however, it has the limitation of assuming linearity between predictor and predictand, which makes the technique less suitable for long-lead forecasting [19]. Time series models [23,24,25,26,27] are advantageous since they provide a framework for the identification, estimation and the diagnostic check for model development [23], but they are also, as the regression models, linear. Neural networks [28,29,30] are nonlinear models having the capacity to discover patterns from data and estimate any complex functional relationship with high accuracy. However, major disadvantages of neural networks are their black-box nature and computational burden [19]. The above-listed models provide a deterministic prediction of the drought status, and does not consider the uncertainty associated with the forecast [31]. This aspect can be handled by probabilistic models, which forecast in a quantitative way droughts and the associated uncertainty [32]. A variety of probabilistic models for drought forecasting has been developed [13,15,18,31,33,34,35,36,37,38,39,40,41], but not that many calculate the conditional probability if there are multiple events, such as the Markov chains and Bayesian networks. Those approaches generate probabilistic forecasts of future droughts in function of earlier drought conditions. According to the probability conditional theory are the models based on MC most common for drought forecasting [15,33,34,35,36], while the BN-based models are more sophisticated. The latter have not been widely used for the probabilistic forecasting of drought events, notwithstanding they seem to have the ability of better forecasting droughts [13,18].
A BN is a graphical model that encodes the joint probability for a large set of random variables. They offer a natural way of describing the conditional dependencies of dependent variables in time, such as drought indices (DIs) with probabilities [42]. Since droughts are slowly evolving phenomena, strong temporal autocorrelation among DIs is expected [14], and, therefore, they can be expressed within a BN [18,43]. A considerable effort is required to solve BNs, a task that can be simplified using copula functions. Those functions are capable of combining several variables with different levels of correlation and dependence structures [13]. The two most frequently used copulas families are Elliptic and Archimedean copulas [44]; a commonly used list of copulas families can be found in the literature [45,46,47]. In this study, two types of each family, Elliptic and Archimedean are tested. To enhance the confidentiality of the forecasts, we used the RPSS for the verification of forecasts, which provides a measure of the accuracy of the forecast in terms of assigned probabilities [48,49].
This study uses the Drought Index (DI) developed on the basis of rainfall and streamflow data of the Chulco River basin in Southern Ecuador, as described in Aviles et al. [15]. In this study, the first-order Markov chain and the second-order Markov chain stochastic models were used to predict the frequency of monthly droughts. The aim of the present study is to compare MC-based models, a more classical approach, with BN-based models, a novel technique, for forecasting future droughts given knowledge of earlier droughts, and to assess the benefits of BNs over the first and second order MCs. Section 2 of the manuscript describes the methodology, including a brief description of the developed DI, the forecast models and the method used to verify forecasts. The third section of the paper gives a snapshot of the study area, while the fourth and fifth sections respectively present the results and conclusions.
2. Materials and Methods
2.1. Case Study
Data of the Andean Chulco mountain basin, which is situated in Southern Ecuador at an altitude of 3200–4300 m.a.s.l (Figure 1), were used to examine the performance of the MC and BN model approaches. Most of the basin area is covered by páramo (tussock grass). The Andean hilly páramo region consists of glacier-formed valleys and plains with a large variety of lakes, peat bogs and wet grasslands, intermingled with shrubland and low-statured montane forest patches [7]. The study basin is one of the few regulated basins in the region, with the El Labrado reservoir situated at the basin outlet. The reservoir stores water for urban, agricultural and industrial uses, and power generation. The basin is strategic because it is one of the few multi-purpose water resources systems in Southern Ecuador that benefits local and regional ecology and economies. From this point of view, research results might be useful for water managers working in similar environmental conditions.
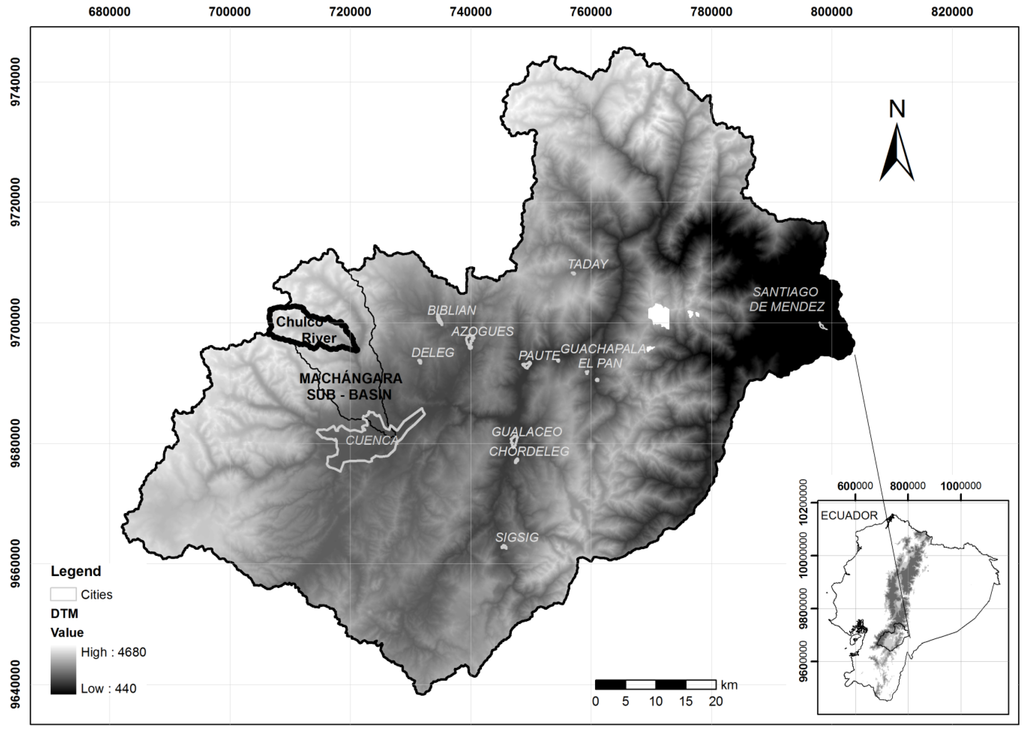
Figure 1.
Location of the Chulco river basin in the Paute river basin.
For development of the DI, monthly time series of basin average rainfall and stored volume in the El Labrado reservoir, for the period 1971 to 2010 were collected from the National Institute of Meteorology and Hydrology of Ecuador (INAMHI) and the Council Basin River Machangara (CBRM). Figure 2 shows the variation of the monthly average of rainfall and water volume, two time series of the variables. Similar to the study by Avilés et al. [15], to capture short, medium and large term droughts, time windows of 1, 3, 6, 9 and 12 months were selected for the generation of ten time series with varying time scales, respectively five time series of the total rainfall (PR1, PR3, PR6, PR9 and PR12) in mm, and five time series of the water volume entering the reservoir (VS1, VS3, VS6, VS9 and VS12) in hm3. The monthly seasonality is accounted by the division of the ten time series for each month. All data was standardized to jointly considered variables with different units.
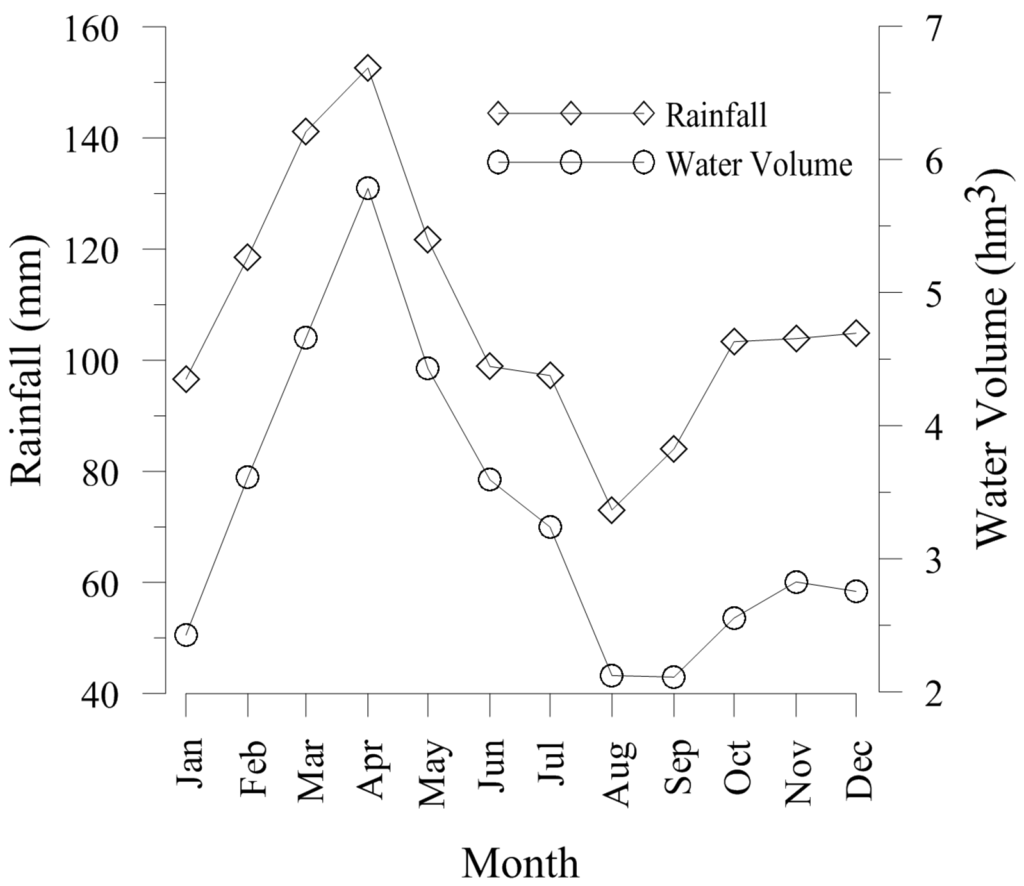
Figure 2.
Monthly average of the time series of rainfall and water volume for the period 1971–2010.
2.2. Drought Index
The DI used herein is derived subjecting available water-related variables of the study area to Principal Components Analysis (PCA), calculating the correlation matrices between time series of r available hydro-meteorological datasets, yielding the eigenvalues and eigenvectors. The eigenvectors establish the relationship between the principal components (PCs) and the original information, as expressed by Avilés et al. [15]:
where Z is the o x r matrix of PCs, o the number of observations, D the o x r matrix of the standardized original information, and E the r x r matrix of eigenvectors. DI is the first principal component (PC1), normalized by its standard deviation. Hence we have:
where DIi,k is the DI value for the kth month in the ith year, Zi,1,k the PC1 for the kth month in the ith year, and σk the sample standard deviation of Zi,1,k of all years. Once the DI values for each month and year were calculated, they were chronological rearranged into a single time series.
DI is a standardized index (SI) capable of capturing the anomalies from the average moisture condition of a basin as a function of the available information of water-related variables [13,14]. Any phenomenon that can be quantified continuously, such as the drought index, is likely treated as a discrete variable by categorizing the time series considering thresholds for each state of drought. Hence, DI, being a normal score satisfying the null hypothesis of the Kolmogorov-Smirnov test [50] for normality, was divided into categories to characterize the state of drought, using the same thresholds as the World Meteorological Organization [51]. Based on that, the following drought categories were derived: DI > 0 = category 0 (no drought); −1 < DI ≤ 0 = category 1 (mild drought); DI ≤ −1 = category 2 (moderate, severe and extreme drought). The three states of category 2 were taken as a single state called drought. This new time series of categorical values (variable Y) are the inputs of the Markov chain models, and the time series of cumulative normal distribution function of the DI values are the inputs of the Bayesian network models. The calibration and validation of the models was performed applying the leave-one-out cross-validation procedure.
2.3. Markov Chain Models
The behavior of a Markov chain (MC) is governed by a set of probabilities of transitions that specify probabilities for the system being in each of its possible states during the next time period [52]. A mth order Markov chain is one where the transition probabilities depend on the states in the previous m time periods. The Markovian property to the mth order Markov chain is (for more details see Wilks [52]):
Considering a first-order Markov chain (MCFO), i.e., m = 1, the transition probabilities provide the probabilistic forecast for the status of the next step based on the current status, applying the following equation:
where pij represents the transition probability that Ytn is equal to category j given Ytn−1 is equal to category i. The estimate of the transition probabilities () can be calculated to account for the conditional relative frequencies of transitions (fij):
where fij is the frequency that Y is equal to the category i at time tn−1 and equal to category j at the time tn. The value of s is the number of states of the system. The numerator represents the number of transitions of category i to category j, and the denominator stands for the sum of the number of transitions of category i to any other category.
If m = 2, we would have a second-order Markov chain (MCSO), where the transition probabilities depend on the states of the current and the previous time period, providing the probabilistic forecast of the status of the next time step. The transition probabilities are calculated as follows:
where phij represent the transition probability that Ytn is equal to category j, given that Ytn−1 is equal to the category i and Ytn−2 equal to the category h. The transition probability estimates () are obtained from conditional relative frequencies of transition counts (fhij):
where the numerator is the number of transitions of category h at time tn−2, category i at time tn−1, and category j at the time tn, and the denominator is the sum of the number of transitions categories h,i to any other category. For this condition, the probability of the drought status of the next time period depends on the status of the two previous time periods.
2.4. Bayesian Network Models
Heckerman [42] claims that a Bayesian network for a set of variables X = {X1, ..., Xn} consists of: (1) a network structure (NS) that encodes a set of conditional independence assertions about variables in X; and (2) a set P of local probability distributions associated with each variable. Together, these components define the joint probability distribution for X. The NS is a directed acyclic graph (DAG), consisting of the sequence of events or random variables with direct ordering, such as time evolving events [18,53]. Given the NS, the joint probability distribution for X, is given by:
where Xi is both the variable and its corresponding node, and Pai are the parents of node Xi in NS. The probabilistic information on the nodes stands for the influence of their parents in the graph on the node. For further details, the reader is referred to Heckerman [42].
Following a similar mathematical formulation as in Madadgar and Moradkhani [13,18], and given the set of variables X is a unique time-evolving random variable (e.g., drought index), X = {Xt1, ..., Xtn}, where the dependency ordering follows the temporal sequence and the parents of Xti is the set of all prior variables (Xt1, …, Xti−1), then Equation (8) can be expressed as:
Equation (9) represents the chain rule in probability theory, which can be solved as:
Reordering Equation (10), we obtain:
Equation (11) represents a BN-based model, where the conditional probabilities of the forecast variable (Xtn) are calculated given the predictor variables (Xt1, …, Xtn−1). The calculation of the joint probability distributions in the right-hand side of Equation (11) is a relatively cumbersome task, which can be considerably simplified using copula functions.
2.5. Copulas
Copulas are functions that join multivariate distribution functions whose one-dimensional margins are uniform on the interval [0,1] [46]. Accepting the mathematical definition of copulas in Yan [45], one obtains a random vector (U1, …, Un)T, where each margin Ui, i = 1, …, n, is a uniform random variable over the unit interval. Suppose the joint cumulative distribution function (CDF) of (U1, …, Un)T, is as follows:
where the function C is called a n-dimensional copula and CDF specifies the probabilities that the random quantity X will not exceed particular values [52], i.e., U(X) = U(X ≤ x). On the other hand, Sklar’s theorem [54] explains the role that copulas play in the relationship between multivariate distribution functions and their univariate margins [46]. The theorem states that a joint multivariate distribution functions F(X1, …, Xn), for all x in the domain of F, can be expressed by a n-dimensional copula, as follows [13,44]:
where Ui(Xi) represents the ith univariate marginal distribution on the unit interval [0,1] and C is the cumulative copula distribution function that represents the multivariate dependence structure [55]. If U1, ..., Un are all continuous and C is unique [45], Equation (11) can be expressed as:
If n = 2 (dependence of first order), the conditional probabilities of the forecast variable (Xt2) are calculated given the predictor variable (Xt1), i.e., the next drought status is conditional to the current status. Similarly, if n = 3 (dependence of second order), the conditional probabilities of the forecast variable (Xt3) are calculated given the predictor variables (Xt1,Xt2), i.e., the next drought status is conditional to the current status and the status of a previous step. These cases could be called Bayesian networks of the first order (BNFO) and second order (BNSO), respectively. Thus, replacing n = 2 and n = 3 in Equation (14) leads to the following expressions:
To calculate the probability that DI in the next time step does not exceed the thresholds defined in Section 2.2, in which drought states are categorized as drought, mild drought, and non-drought, given the availability of the information for the current status for the BNFO model and the states of the current and previous time steps for the BNSO model, Equations (15) and (16) can be rewritten as:
where xds is the drought index that causes a drought status according to the threshold defined in Section 2.2 (xd0 = 0 and xd1 = −1). Applying Equations (17) and (18), the probabilities of having a category 0 (no drought), i.e., DI > 0, will be equal to:
Analogously, the probabilities of having a category 1 (mild drought), i.e., −1 < DI ≤ 0, can be formulated as:
Finally, the probabilities of having a category 2 (drought), i.e., DI ≤ −1, can be expressed as:
2.6. Copulas Fitting
The procedure for constructing joint distributions includes: (1) identifying marginal distributions on the unit interval [0,1]; (2) selecting suitable dependence structures; and (3) forming joint distributions [14]. The marginal distributions (Ui) of step 1 can be derived when the DI values are transformed to a cumulative normal distribution function, in accordance with Section 2.2. Since droughts are slowly evolving phenomena, strong temporal autocorrelation among DI is expected [14]. Steps 2 and 3 consist in modeling the temporal dependence structure by fitting the copula functions given the marginal distribution.
Two elliptical copulas (normal and t) and two Archimedean copulas (Clayton and Frank) were tested in this study, as to define the most appropriate function for the joint distributions. The canonical maximum likelihood (CML) [56] method was applied for the estimation of the parameters in the copula functions, using the empirical cumulative distribution function of each marginal distribution (Ui) to transform the observations into pseudo-observations on the unit interval [0,1] [44]. The best fitted copula function was identified by the parametric bootstrap-based goodness-of-fit test [57], which consists in comparing a distance (ΔC) between the empirical copula (CE) and the estimated parametric copula (Cθ) function under the null hypothesis that CE ∈ Cθ. The latter is evaluated by the p value; if the p value is greater than the significance level α the null hypothesis is accepted, conversely, the null hypothesis is rejected. P values can be obtained via the Monte Carlo method embedded in a parametric bootstrapping procedure.
The Cramér-von-Mises statistic (S) [58] was applied on the group of copulas that are in agreement with the null hypothesis, as to derive the best alternative among the fitted copulas. In the group of copulas that are greater than the significance level, the smallest S is chosen as the best copula function [13]. The expression of the statistic is as follows, where d is the sample size:
2.7. Forecast Verification
The quality of the forecasts was assessed using the cross-validation procedure, whereby RPSS, despite being a skill score appropriate for the evaluation of probabilistic forecasts of categorical variables, was applied to verify the overall quality of the forecasts of both models. It is noticed here that the results of the Bayesian network model were divided by the categories before the forecast verification.
The ranked probability score (RPS) is a skill measurement that penalizes forecast errors in terms of the probability assigned to the events [59], and is based on the square error between the cumulative probabilities of forecasts and observations. This score is sensitive to distance, i.e., it includes a penalty for the forecasts that are further away of the observations. According to Wilks [52], RPS is defined as:
where Ym is the cumulative probabilities of forecasts, Om is the cumulative probabilities of observations (Om) and s the number of event categories or states of the system. As RPS is seen as the probabilistic extension of the square error, a perfect forecast would have an RPS value equal to 0 and the worst forecasts would be very much different from zero.
For the assessment of the usefulness of forecasts, RPSS could be used, which refers to the relative accuracy of a set of forecasts with respect to some set of reference forecasts. In fact, RPSS can be interpreted as the percentage improvement over the reference forecast [52], and is computed as:
where is the average of the RPS values for each forecast-observation record and the average of the RPS values computed with respectively the reference forecasts and observations. In this study, the reference forecast is the climatological relative frequencies of the predictand. RPSS = 1 means a 100% improvement over the reference forecasts, while, if RPSS is equal to 0 or less, there is no improvement over the reference forecast.
3. Results and Discussion
3.1. Drought Index
Applying PCA for each month of the year, using information of the correlation matrices of the ten time series (PR1, PR3, PR6, PR9, PR12, VS1, VS3, VS6, VS9 and VS12), the eigenvalues and eigenvectors were obtained. Table 1 shows the eigenvalues and the explained variance of the PC1 for each month.

Table 1.
Eigenvalues and explained variance of the PC1.
| PC1 | January | February | March | April | May | June | July | August | September | October | November | December |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Eigenvalues | 6.21 | 7.26 | 7.89 | 7.13 | 7.64 | 7.08 | 7.10 | 7.16 | 7.08 | 6.77 | 5.86 | 5.71 |
| Explained variance | 62% | 73% | 79% | 71% | 76% | 71% | 71% | 72% | 71% | 68% | 59% | 57% |
By means of Equations (1) and (2), and using information from the eigenvectors and the standardized original data, the DI values were derived for each month and rearranged in chronological order, forming the DI time series for the period 1971 to 2010. The DI values were converted into a cumulative normal distribution function that served as input for the Bayesian network models, while the Markov chain models require categorized time series of the DI according to the thresholds listed in Section 2.2. Table 2 lists the frequencies of each category (drought states) for the 480 months of the categorical time series, Figure 3 shows the time series of the DI, and Figure 4 depicts an example of the correlation between the time series of the DI of the months of July, August and September. The models were fitted using leave-one-out cross-validation, a procedure allowing an assessment of the accuracy of the forecast with respect to all events in the period 1971–2010.

Table 2.
Frequency of drought state categories.
| Category | Drought State | Frequency |
|---|---|---|
| 0 | no drought | 218 |
| 1 | mild drought | 185 |
| 2 | drought | 77 |
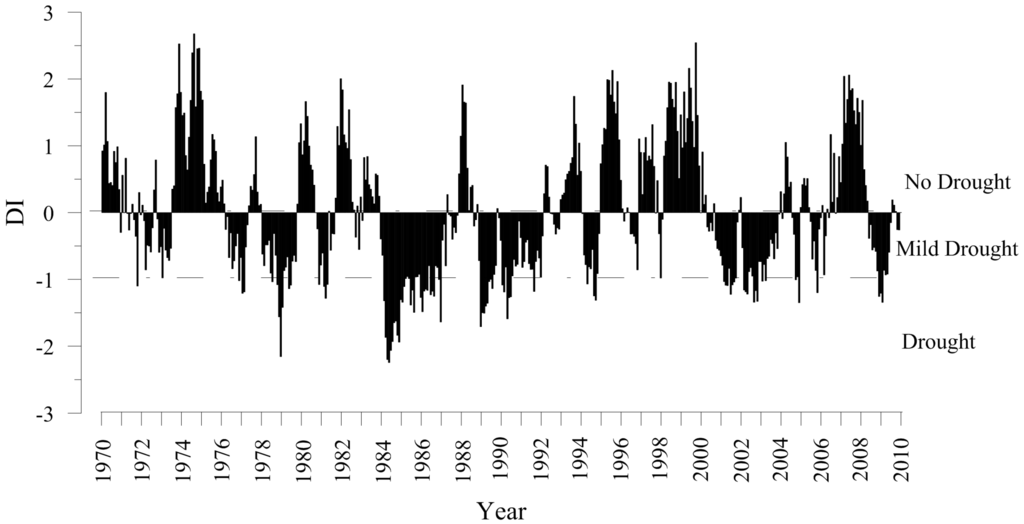
Figure 3.
Time series of the DI (1971–2010).
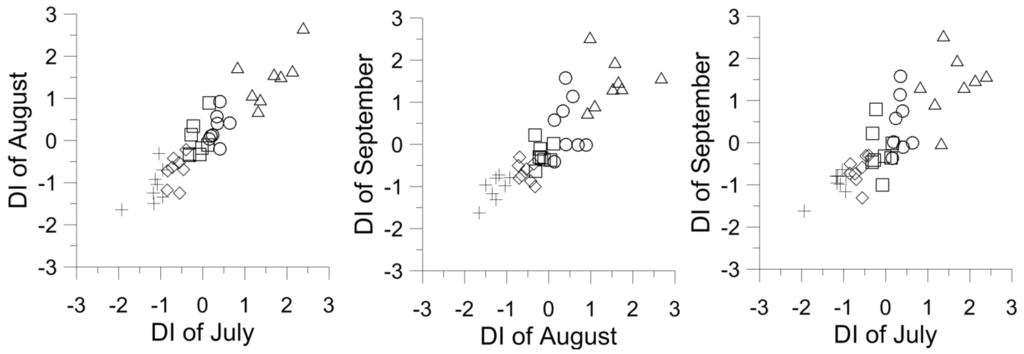
Figure 4.
Scatter plots of DI respectively between the months July–August, August–September and July–September for the period 1971–2010.
3.2. Markov Chain Models
To take seasonality into account, the non-homogeneous model version of MC was used, i.e., transition probabilities were calculated for each month of the year, yielding twelve matrices of transition probabilities estimates for each model (MCFO and MCSO). These matrices enabled the derivation of probabilistic forecasts of the status of next month j, given the current status in month i by applying the MCFO model, and given the states in the current month i and previous month h applying the MCSO model. The transition probability matrix leaving the third year out in the cross-validation procedure for August (month with least rain) using the MCFO model is shown in Table 3, and the transition probability matrix for July-August applying the MCSO model is listed in Table 4. For example, if in August the drought status corresponds to category 1 (mild drought), then according to Table 3 the drought forecasting probabilities for the month of September are: 7% for category 0 (no drought), 86% for category 1 (mild drought) and 7% for category 2 (drought), the adding to 100%. Similarly, the drought forecasting probabilities for September using the information in Table 4 when the states of July and August are category 0 (no-drought) are: 75% for category 0 (no drought), 25% for category 1 (mild drought), and 0% for category 2 (drought), adding to 100%. In the absence of transitions between states, the transition probability for each state is likely equal to one divided by the number of categories, e.g., the states 0-2 and 2-0 in Table 4 have a probability of 33.33% for each category.

Table 3.
Transition probability matrix of the MCFO model leaving the third year out in cross-validation for the month August.
| State i | State j | ||
|---|---|---|---|
| 0 | 1 | 2 | |
| 0 | 0.72 | 0.28 | 0.00 |
| 1 | 0.07 | 0.86 | 0.07 |
| 2 | 0.00 | 0.57 | 0.43 |

Table 4.
Transition probability matrix of the MCSO model leaving the third year out in cross-validation for the period July–August.
| States h-i | State j | ||
|---|---|---|---|
| 0 | 1 | 2 | |
| 0-0 | 0.75 | 0.25 | 0.00 |
| 0-1 | 0.00 | 1.00 | 0.00 |
| 0-2 | 0.33 | 0.33 | 0.33 |
| 1-0 | 0.50 | 0.50 | 0.00 |
| 1-1 | 0.09 | 0.82 | 0.09 |
| 1-2 | 0.00 | 0.33 | 0.67 |
| 2-0 | 0.33 | 0.33 | 0.33 |
| 2-1 | 0.00 | 1.00 | 0.00 |
| 2-2 | 0.00 | 0.75 | 0.25 |
3.3. Bayesian Network Models
The BN models consider seasonality, and copula fittings were developed for each month. For testing the null hypothesis, the significance level α was made equal to 0.05, and the number of the bootstrap in the Monte Carlo method equal to 1000. For example, Table 5 and Table 6 depict the p values and the S-statistic of the BNFO and BNSO models for each month and the four types of copulas (normal, t, Clayton and Frank), leaving the third year out in the cross-validation. The four copula types were tested because of the symmetrical dependence between most monthly DI time series and the stronger dependence in the lower tail between few monthly time series of DI, as shown in Figure 4.

Table 5.
p value and S-statistic leaving the third year out in cross-validation for the BNFO model.
| p Value | ||||||||||||
| Copulas | January | February | March | April | May | June | July | August | September | October | November | December |
| Normal | 0.292 | 0.233 | 0.077 | 0.329 | 0.368 | 0.527 | 0.369 | 0.727 | 0.189 | 0.222 | 0.524 | 0.664 |
| t | 0.057 | 0.108 | 0.066 | 0.358 | 0.338 | 0.313 | 0.464 | 0.432 | 0.127 | 0.322 | 0.326 | 0.326 |
| Clayton | 0.007 | 0.022 | 0.052 | 0.022 | 0.009 | 0.034 | 0.005 | 0.020 | 0.004 | 0.002 | 0.021 | 0.017 |
| Frank | 0.363 | 0.910 | 0.854 | 0.534 | 0.535 | 0.565 | 0.804 | 0.864 | 0.207 | 0.170 | 0.426 | 0.193 |
| S-statistic | ||||||||||||
| Copulas | January | February | March | April | May | June | July | August | September | October | November | December |
| Normal | 0.028 | 0.027 | 0.033 | 0.024 | 0.023 | 0.021 | 0.022 | 0.018 | 0.029 | 0.029 | 0.022 | 0.020 |
| t | 0.040 | 0.033 | 0.034 | 0.024 | 0.024 | 0.025 | 0.022 | 0.024 | 0.034 | 0.028 | 0.027 | 0.027 |
| Clayton | - | - | 0.049 | - | - | - | - | - | - | - | - | - |
| Frank | 0.027 | 0.018 | 0.018 | 0.023 | 0.022 | 0.023 | 0.019 | 0.019 | 0.030 | 0.034 | 0.026 | 0.031 |

Table 6.
p value and S-statistic leaving the third year out in cross-validation for the BNSO model.
| p Value | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Copulas | January | February | March | April | May | June | July | August | September | October | November | December |
| Normal | 0.083 | 0.164 | 0.103 | 0.582 | 0.698 | 0.651 | 0.400 | 0.276 | 0.459 | 0.542 | 0.433 | 0.437 |
| t | 0.007 | 0.079 | 0.087 | 0.406 | 0.523 | 0.254 | 0.236 | 0.110 | 0.305 | 0.294 | 0.064 | 0.088 |
| Clayton | 0.001 | 0.006 | 0.009 | 0.010 | 0.005 | 0.008 | 0.004 | 0.000 | 0.001 | 0.000 | 0.000 | 0.000 |
| Frank | 0.314 | 0.718 | 0.648 | 0.588 | 0.661 | 0.605 | 0.865 | 0.136 | 0.108 | 0.068 | 0.074 | 0.259 |
| S-statistic | ||||||||||||
| Copulas | January | February | March | April | May | June | July | August | September | October | November | December |
| Normal | 0.047 | 0.038 | 0.042 | 0.027 | 0.026 | 0.026 | 0.031 | 0.035 | 0.032 | 0.030 | 0.032 | 0.032 |
| t | - | 0.048 | 0.046 | 0.033 | 0.031 | 0.036 | 0.039 | 0.046 | 0.038 | 0.039 | 0.051 | 0.049 |
| Clayton | - | - | - | - | - | - | - | - | - | - | - | - |
| Frank | 0.045 | 0.032 | 0.034 | 0.035 | 0.033 | 0.034 | 0.028 | 0.055 | 0.061 | 0.064 | 0.063 | 0.049 |
The shaded p values represent the copulas that reject the null hypothesis and the shaded S-statistics highlight the copulas with the best fit for each month. The latter copulas were chosen to calculate the conditional probabilities of the drought status for next month given the drought status of the current month for the BNFO model and the current and previous drought states for the BNSO model, applying Equations (19)–(24). Equations (18), (20), (22) and (24) have bivariate copulas as a denominator; these are the same copulas with the best fit shown in Table 5. Figure 5 shows the probability distributions of the drought forecasting for the month of September given the drought index of the month of August for the BNFO model, leaving the third year out in the cross-validation. For example, if there is a DI of −1.65 in August corresponding to category 2 (drought), the probabilities drought forecasting for the month of September are: 0% for category 0 (no drought), 5% for category 1 (mild drought) and 95% for category 2 (drought). In a similar way, if there is a DI of 2.68 in August corresponding to a category 0 (no drought), the probabilities drought forecasting for the month September are: 50% for category 0 (no drought), 34% for category 1 (mild drought), and 16% for category 2 (drought). In brief, a low DI value in August leads to higher probabilities of severe droughts in September; conversely, high values of DI in August lead to low probabilities of drought in September.
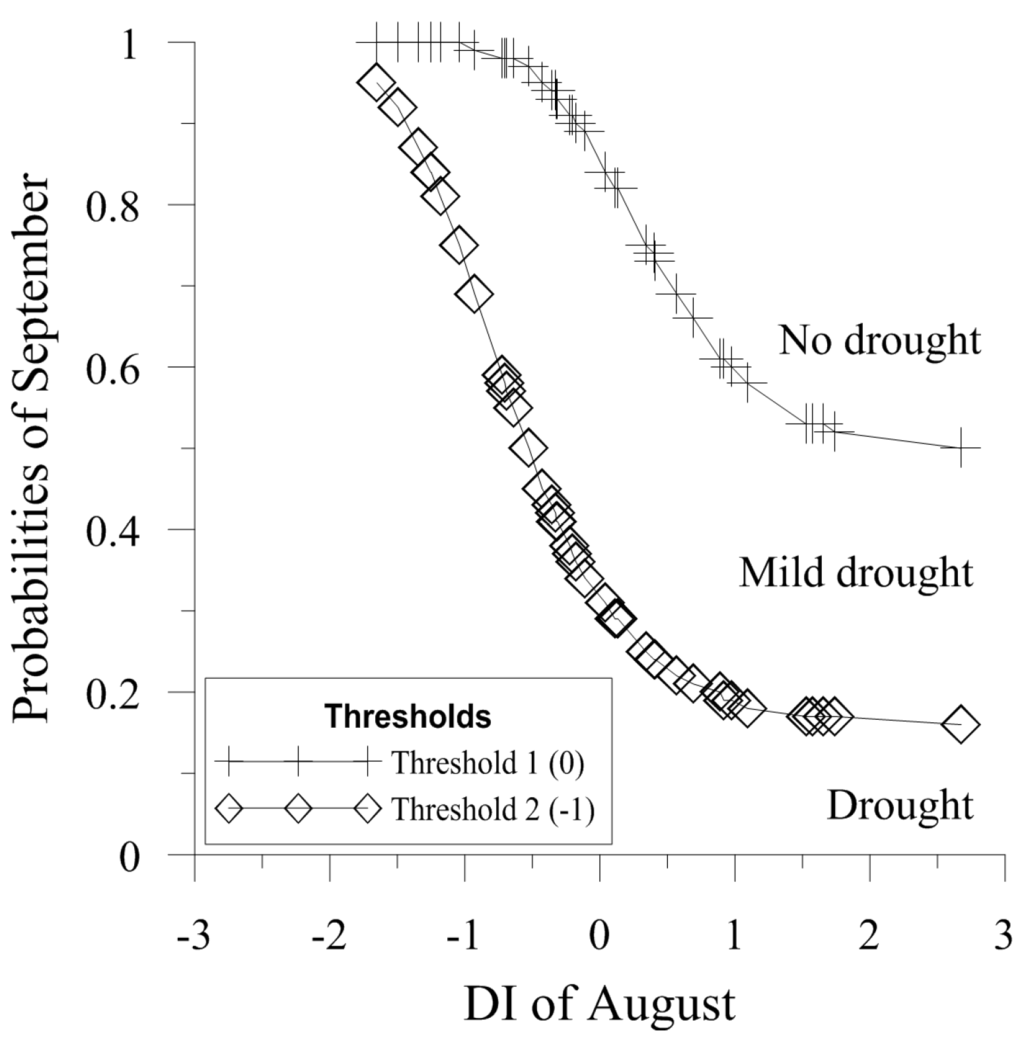
Figure 5.
Probabilities of drought forecasts leaving the third year out in cross-validation using the BNFO model for the month of September given the DI of August corresponding respectively to the drought threshold values 0 and −1.
A similar analysis can be performed for the BNSO model, with the difference that for the forecast of next month one has to take into consideration the information of the current and the previous month. Though the results of the BN models are continuous variables, the division of the resulting time series by the categories results in discrete time series, comparable with the forecast results of the MC models.
3.4. Forecast Verification
Cross-validation was used to evaluate the probabilistic forecasts. Forty RPS values were derived for each month, and each model applying the leave-one-out procedure and RPSClim was calculated on the basis of reference forecasts equal to climatological relative frequencies of the time series of categorical values of the DI. Considering the average of the RPS and RPSClim values for the entire time series, i.e., taking into account all states of drought (drought, mild drought and no-drought) and all months, and, using Equation (27) to calculate the RPSS values, the MCFO model performed better compared to the other models with the greatest value of improvement over the reference forecast equal to 0.29, followed by the MCSO and BNFO models with values of RPSS equal to 0.21 and −0.05 (negative RPSS values mean that the reference forecasts are better that the tested model). Considering only the observed drought states (drought and mild drought), the BNFO model performed better with the greatest values of RPSS equal to 0.40, followed by the BNSO and MCFO models with RPSS values equal to 0.33 and 0.19, respectively. Even considering only the most severe drought status, the BNFO model yielded better results, with the greatest RPSS value equal to 0.44, followed by the MCSO and BNSO models with RPSS values equal to 0.37 and 0.35. These results indicate that, for the given case study, the MCFO model performed better for the probabilistic forecast of dry and wet periods, while, for the probabilistic forecast of dry periods, the BN-based models are a better option.
Table 7 depicts the assessment of the monthly drought forecasts, with, in the top section of the table, (a) the RPSS values of all observed states (drought, mild drought and no-drought), and, in the bottom section, (b) the RPSS values for mild drought and drought states. On the basis of the RPSS values in the top section (a) of Table 7, it can be concluded that the MCFO model produces better forecasts than the reference forecasts in the months January, February, March, May, June, September, October and November, while in the months of April, July and August the MCSO performed better. The RPSS values in the bottom section (b) of Table 7 reveal that the BNFO model produces better forecasts than the reference forecasts in the months January, February, April, May, June, October, November and December; the MCFO model performed better in March and September; and the MCSO model performs best in July and August.

Table 7.
RPSS values of the monthly assessment of drought forecasts.
| Model | January | February | March | April | May | June | July | August | September | October | November | December |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (a) No Drought, Mild Drought and Drought | ||||||||||||
| MCFO | −0.40 | 0.27 | 0.63 | 0.52 | 0.37 | 0.41 | 0.48 | 0.45 | 0.33 | 0.20 | 0.15 | 0.15 |
| MCSO | −0.46 | −0.32 | 0.63 | 0.58 | 0.25 | 0.32 | 0.50 | 0.52 | 0.18 | 0.19 | 0.05 | 0.16 |
| BNFO | −0.50 | 0.13 | 0.09 | 0.06 | −0.20 | 0.08 | 0.04 | 0.00 | −0.11 | −0.15 | 0.02 | −0.09 |
| BNSO | −0.60 | −0.33 | −0.11 | −0.08 | −0.29 | −0.08 | −0.14 | −0.13 | −0.30 | −0.33 | −0.09 | −0.27 |
| (b) Mild Drought and Drought | ||||||||||||
| MCFO | −0.35 | 0.12 | 0.53 | 0.49 | 0.27 | 0.19 | 0.42 | 0.31 | 0.04 | 0.12 | 0.09 | 0.18 |
| MCSO | −0.28 | −0.28 | 0.53 | 0.53 | 0.15 | 0.07 | 0.48 | 0.47 | −0.14 | 0.10 | −0.03 | 0.16 |
| BNFO | 0.29 | 0.53 | 0.48 | 0.59 | 0.29 | 0.38 | 0.47 | 0.47 | −0.07 | 0.32 | 0.45 | 0.62 |
| BNSO | 0.28 | 0.50 | 0.37 | 0.53 | 0.23 | 0.20 | 0.38 | 0.39 | −0.27 | 0.18 | 0.42 | 0.53 |
Whereas global assessment of drought forecasts permits evaluation of the overall performance of the models, the assessment of drought forecasts on a monthly basis might reveal which of the models perform best for a given month of the hydrologic year. For example, our study disclosed that the MC-based models perform better in predicting dry periods in specific months. Although a monthly scale was used for drought forecasting, findings are in agreement with the results obtained by Madadgar and Moradkhani [13]; drought forecasts using the BN-based models did not significantly differ from the forecast generated of other models. Those authors [18] also stated that the BN model in combination with copula functions is a useful procedure in the probabilistic forecasting of drought events.
4. Conclusions
The performance of the MC- and BN-based models in drought forecasting was tested. Both conditional-based approaches offer the ability to derive probabilistic forecasts based on information of previous droughts. Copula functions were used to simplify the solution of the mathematical formulation of the Bayesian network, enabling the derivation of joint distribution functions. Employing a recently developed drought index, both modeling approaches were applied and tested using 40-year rainfall and streamflow data of the Chulco River basin, an Andean regulated river basin in Southern Ecuador. The leave-one-out cross-validation procedure was used for forecast verification. Results revealed that BN-based models were slightly better in forecasting severe drought events than the MC-based models; however, the monthly verification of forecasts suggests that the four models distinctively perform better for given drought categories in given months of the hydrological year. The tested approaches can be applied to other spatial and temporal scales, and serve other purposes such as simulation, characterization, classification and evaluation of drought events for decision-making. It is evident that monthly probabilistic forecasting will be instructive water managers in the development of appropriate mitigation measures.
Acknowledgments
This research was financially supported by the University of Cuenca through its Dirección de Investigación (DIUC) and the Empresa pública municipal de telecomunicaciones, agua potable, alcantarillado y saneamiento de Cuenca (ETAPA-Parque Nacional Cajas) via the projects “Meteorological Cycles and Evapotranspiration along the Altitudinal Gradient of the Cajas National Park” and “Identification of hydro-meteorological processes that trigger extreme floods in the city of Cuenca using precipitation radar”. The authors are grateful to INAMHI and CBRM for providing the data. Thanks are due to Jan Feyen for his valuable comments and suggestions, and the revision of the manuscript. We are grateful to Lenin Campozano, who programmed the cross-validation procedure. The helpful comments of two anonymous reviewers are specially acknowledged.
Author Contributions
Alex Avilés conceived the initial idea of the study, constructed the models and prepared the manuscript. Rolando Célleri participated in the design of the study, and provided a critical revision of manuscript. Abel Solera and Javier Paredes provided many useful suggestions to improve the analysis of the results and supervised the research.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Mishra, A.K.; Singh, V.P. Review paper A review of drought concepts. J. Hydrol. 2010, 391, 202–216. [Google Scholar] [CrossRef]
- Zhong, S.; Shen, L.; Sha, J.; Okiyama, M.; Tokunaga, S.; Liu, L.; Yan, J. Assessing the water parallel pricing system against drought in China: A study based on a CGE model with multi-provincial irrigation water. Water 2015, 7, 3431–3465. [Google Scholar] [CrossRef]
- Karavitis, C.A.; Alexandris, S.; Tsesmelis, D.E.; Athanasopoulos, G. Application of the standardized precipitation index (SPI) in Greece. Water 2011, 3, 787–805. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Chura, O.; López-Moreno, J.I.; Azorin-Molina, C.; Sanchez-Lorenzo, A.; Aguilar, E.; Moran-Tejeda, E.; Trujillo, F.; Martínez, R.; Nieto, J.J. Spatio-temporal variability of droughts in Bolivia: 1955–2012. Int. J. Climatol. 2015, 35, 3024–3040. [Google Scholar] [CrossRef]
- Beniston, M. Climatic change in mountain regions: A review of possible impacts. Clim. Chang. 2003, 59, 5–31. [Google Scholar] [CrossRef]
- Buytaert, W.; Vuille, M.; Dewulf, A.; Urrutia, R.; Karmalkar, A.; Célleri, R. Uncertainties in climate change projections and regional downscaling in the tropical Andes: Implications for water resources management. Hydrol. Earth Syst. Sci. 2010, 14, 1247–1258. [Google Scholar] [CrossRef]
- Buytaert, W.; Célleri, R.; de Bièvre, B.; Cisneros, F.; Wyseure, G.; Deckers, J.; Hofstede, R. Human impact on the hydrology of the Andean páramos. Earth Sci. Rev. 2006, 79, 53–72. [Google Scholar] [CrossRef]
- Buytaert, W.; Celleri, R.; Willems, P. Spatial and temporal rainfall variability in mountainous areas: A case study from the south Ecuadorian Andes. J. Hydrol. 2006, 329, 413–421. [Google Scholar] [CrossRef]
- Al-Faraj, F.; Scholz, M.; Tigkas, D. Sensitivity of surface runoff to drought and climate change: Application for shared river basins. Water 2014, 6, 3033–3048. [Google Scholar] [CrossRef]
- Staudinger, M.; Stahl, K.; Seibert, J. A drought index accounting for snow. Water Resour. Res. 2014, 50, 7861–7872. [Google Scholar] [CrossRef]
- Celleri, R.; Willems, P.; Buytaert, W.; Feyen, J. Space-time rainfall variability in the Paute basin, Ecuadorian Andes. Hydrol. Process. 2007, 21, 3316–3327. [Google Scholar] [CrossRef]
- Steinemann, A. Drought indicators and triggers: A stochastic approach to evaluation. J. Am. Water Resour. Assoc. 2003, 39, 1217–1233. [Google Scholar] [CrossRef]
- Madadgar, S.; Moradkhani, H. A Bayesian framework for probabilistic seasonal drought forecasting. J. Hydrometeorol. 2013, 14, 1685–1706. [Google Scholar] [CrossRef]
- Kao, S.C.; Govindaraju, R.S. A copula-based joint deficit index for droughts. J. Hydrol. 2010, 380, 121–134. [Google Scholar] [CrossRef]
- Avilés, A.; Célleri, R.; Paredes, J.; Solera, A. Evaluation of markov chain based drought forecasts in an andean regulated river basin using the skill scores RPS and GMSS. Water Resour. Manag. 2015, 29, 1949–1963. [Google Scholar] [CrossRef]
- Viviroli, D.; Archer, D.R.; Buytaert, W.; Fowler, H.J.; Greenwood, G.B.; Hamlet, A.F.; Huang, Y.; Koboltschnig, G.; Litaor, M.I.; López-Moreno, J.I.; et al. Climate change and mountain water resources: Overview and recommendations for research, management and policy. Hydrol. Earth Syst. Sci. 2011, 15, 471–504. [Google Scholar] [CrossRef]
- Sánchez-Chóliz, J.; Sarasa, C. River flows in the Ebro basin: A century of evolution, 1913–2013. Water 2015, 7, 3072–3082. [Google Scholar] [CrossRef]
- Madadgar, S.; Moradkhani, H. Spatio-temporal drought forecasting within Bayesian networks. J. Hydrol. 2014, 512, 134–146. [Google Scholar] [CrossRef]
- Mishra, A.K.; Singh, V.P. Drought modeling—A review. J. Hydrol. 2011, 403, 157–175. [Google Scholar] [CrossRef]
- Kumar, V.; Panu, U. Predictive assessment of severity of agricultural droughts based on agro-climatic factors. J. Am. Water Resour. Assoc. 1997, 33, 1255–1264. [Google Scholar] [CrossRef]
- Leilah, A.A.; Al-Khateeb, S. Statistical analysis of wheat yield under drought conditions. J. Arid Environ. 2005, 61, 483–496. [Google Scholar] [CrossRef]
- Liu, W.T.; Juárez, R.I.N. ENSO drought onset prediction in northeast Brazil using NDVI. Int. J. Remote Sens. 2001, 22, 3483–3501. [Google Scholar] [CrossRef]
- Mishra, A.K.; Desai, V.R. Drought forecasting using stochastic models. Stoch. Environ. Res. Risk Assess. 2005, 19, 326–339. [Google Scholar] [CrossRef]
- Han, P.; Wang, P.X.; Zhang, S.Y.; Zhu, D.H. Drought forecasting based on the remote sensing data using ARIMA models. Math. Comput. Model. 2010, 51, 1398–1403. [Google Scholar] [CrossRef]
- Durdu, Ö.F. Application of linear stochastic models for drought forecasting in the Büyük Menderes river basin, western Turkey. Stoch. Environ. Res. Risk Assess. 2010, 24, 1145–1162. [Google Scholar] [CrossRef]
- Modarres, R. Streamflow drought time series forecasting. Stoch. Environ. Res. Risk Assess. 2007, 21, 223–233. [Google Scholar] [CrossRef]
- Fernández, C.; Vega, J.A.; Fonturbel, T.; Jiménez, E. Streamflow drought time series forecasting: A case study in a small watershed in North West Spain. Stoch. Environ. Res. Risk Assess. 2009, 23, 1063–1070. [Google Scholar] [CrossRef]
- Morid, S.; Smakhtin, V.; Bagherzadeh, K. Drought forecasting using artificial neural networks and time series of drought indices. Int. J. Climatol. 2007, 27, 2103–2111. [Google Scholar] [CrossRef]
- Mishra, A.K.; Desai, V.R.; Singh, V.P.; Asce, F. Drought forecasting using a hybrid stochastic and neural network model. J. Hydrol. Eng. 2007, 12, 626–638. [Google Scholar] [CrossRef]
- Mishra, A.K.; Desai, V.R. Drought forecasting using feed-forward recursive neural network. Ecol. Model. 2006, 198, 127–138. [Google Scholar] [CrossRef]
- Hwang, Y.; Carbone, G.J. Ensemble forecasts of drought indices using a conditional residual resampling technique. J. Appl. Meteorol. Climatol. 2009, 48, 1289–1301. [Google Scholar] [CrossRef]
- Murphy, A.H. The value of climatological, categorical and probabilistic forecasts in the cost-loss ratio situation. Mon. Weather Rev. 1977, 105, 803–816. [Google Scholar] [CrossRef]
- Lohani, V.K.; Loganathan, G.V. An early warning system for drought management using the Palmer drought index. J. Am. Water Resour. Assoc. 1997, 33, 1375–1386. [Google Scholar] [CrossRef]
- Paulo, A.A.; Pereira, L.S. Prediction of SPI drought class transitions using Markov chains. Water Resour. Manag. 2007, 21, 1813–1827. [Google Scholar] [CrossRef]
- Cancelliere, A.; Di Mauro, G.; Bonaccorso, B.; Rossi, G. Drought forecasting using the Standardized Precipitation Index. Water Resour. Manag. 2007, 21, 801–819. [Google Scholar] [CrossRef]
- Nalbantis, I.; Tsakiris, G. Assessment of hydrological drought revisited. Water Resour. Manag. 2009, 23, 881–897. [Google Scholar] [CrossRef]
- Yuan, X.; Wood, E.F.; Chaney, N.W.; Sheffield, J.; Kam, J.; Liang, M.; Guan, K. Probabilistic seasonal forecasting of African drought by dynamical models. J. Hydrometeorol. 2013, 14, 1706–1720. [Google Scholar] [CrossRef]
- Anderson, M.L.; Mierzwa, M.D.; Kavvas, M.L. Probabilistic seasonal forecasts of droughts with a simplified coupled hydrologic-atmospheric model for water resources planning. Stoch. Environ. Res. Risk Assess. 2000, 14, 263–274. [Google Scholar] [CrossRef]
- Chung, C.; Salas, J.D. Drought occurrence probabilities and risks of dependent hydrologic processes. J. Hydrol. Eng. 2000, 5, 259–268. [Google Scholar] [CrossRef]
- AghaKouchak, A. A baseline probabilistic drought forecasting framework using standardized soil moisture index: Application to the 2012 United States drought. Hydrol. Earth Syst. Sci. 2014, 18, 2485–2492. [Google Scholar] [CrossRef]
- Araghinejad, S. An approach for probabilistic hydrological drought forecasting. Water Resour. Manag. 2010, 25, 191–200. [Google Scholar] [CrossRef]
- Heckerman, D. A tutorial on learning with Bayesian networks. In Learning in Graphical Models; Springer: Dordrecht, The Netherlands, 1998; pp. 301–354. [Google Scholar]
- Pearl, J. Bayesian networks: A model of self-activated memory for evidential reasoning. In Proceedings of the 7th Conference of the Cognitive Science Society, Irvine, CA, USA, 15–17 August 1985; pp. 329–334.
- Yan, J. Enjoy the joy of copulas: With a Package copula. J. Stat. Softw. 2007, 21, 1–21. [Google Scholar] [CrossRef]
- Yan, J. Multivariate modeling with copulas and engineering applications. In Springer Handbook of Engineering Statistics; Pham, H., Ed.; Springer London: London, UK, 2006; pp. 973–990. [Google Scholar]
- Nelsen, R.B. An Introduction to Copulas, 2nd ed.; Springer: New York, NY, USA, 2006. [Google Scholar]
- Embrechts, P.; Lindskog, F.; McNeil, A. Modelling Dependence with Copulas and Applications to Risk Management; Département de mathématiques, Institut Fédéral de Technologie de Zurich: Zurich, Switzerland, 2001. [Google Scholar]
- Mason, S.J. On using “Climatology” as a reference strategy in the brier and ranked probability skill scores. Mon. Weather Rev. 2004, 132, 1891–1895. [Google Scholar] [CrossRef]
- Murphy, A. What is a good forecast? An essay on the nature of goodness in weather forecasting. Weather Forecast. 1993, 8, 281–293. [Google Scholar] [CrossRef]
- Kolmogorov, A. Sulla determinazione empirica di una legge di distribuzione. G. dell’Ist. Ital. degli Attuari 1933, 4, 83–91. [Google Scholar]
- World Meteorological Organization. Standardized Precipitation Index User Guide; World Meteorological Organization: Geneva, Switzerland, 2012. [Google Scholar]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences, 3rd ed.; Academic Press: Cambridge, MA, USA, 2011. [Google Scholar]
- Thulasiraman, K.; Swamy, M.N.S. Graphs: Theory and Algorithms; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Sklar, A. Fonctions de Répartition à n Dimensions et Leurs Marges; l’Institut de Statistique de l’Université de Paris: Paris, France, 1959; Volume 8, pp. 229–231. [Google Scholar]
- Joe, H. Multivariate Models and Multivariate Dependence Concepts; CRC Press: Boca Raton, FL, USA, 1997. [Google Scholar]
- Cherubini, U.; Luciano, E.; Vecchiato, W. Copula Methods in Finance; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Genest, C.; Rémillard, B. Validity of the parametric bootstrap for goodness-of-fit testing in semiparametric models. Ann. Inst. H. Poincaré Probab. Stat. 2008, 44, 1096–1127. [Google Scholar] [CrossRef]
- Anderson, T. On the distribution of the two-sample Cramer-von Mises criterion. Ann. Math. Stat. 1962, 22, 1148–1159. [Google Scholar] [CrossRef]
- Zhang, H.; Casey, T. Verification of categorical probability forecasts. Weather Forecast. 2000, 15, 80–89. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).