Efficiency Criteria as a Solution to the Uncertainty in the Choice of Population Size in Population-Based Algorithms Applied to Water Network Optimization
Abstract
:1. Introduction
2. Materials and Methods
2.1. Problem Formulation and Selected Algorithms
2.2. Specific Operators and Calibration
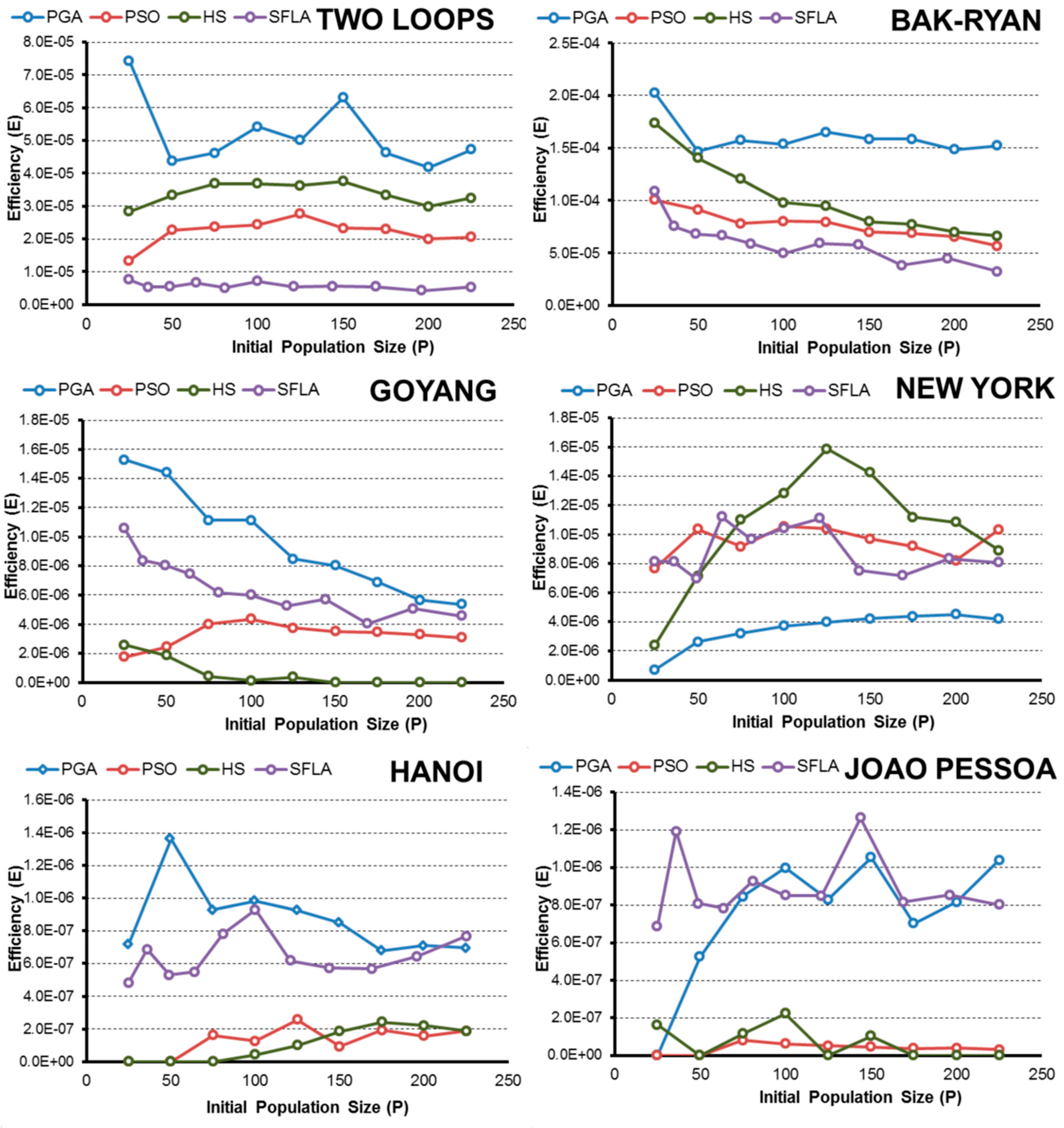
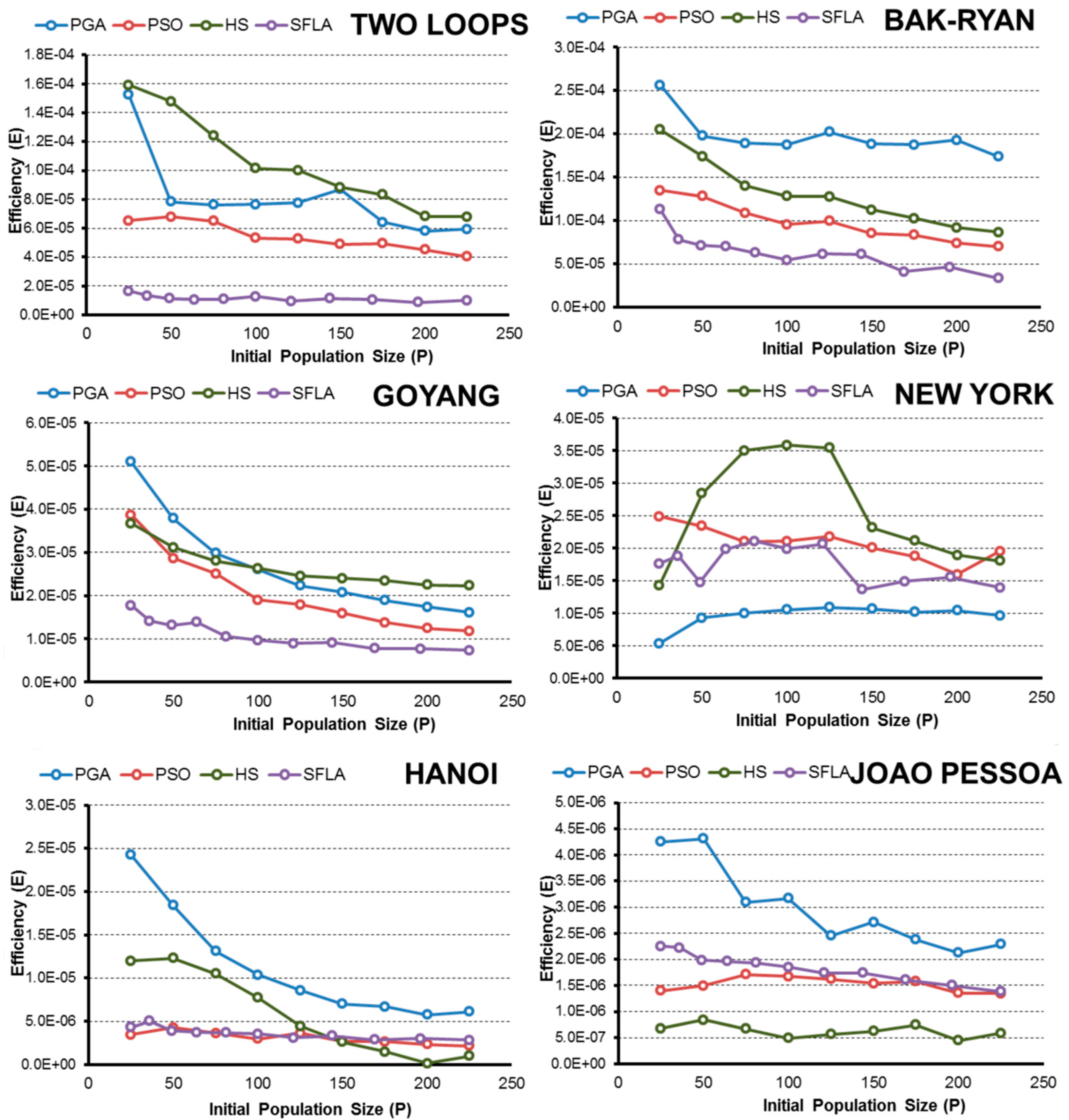
2.3. Efficiency Criteria
2.4. Programming Environment
3. Test Problems and Results
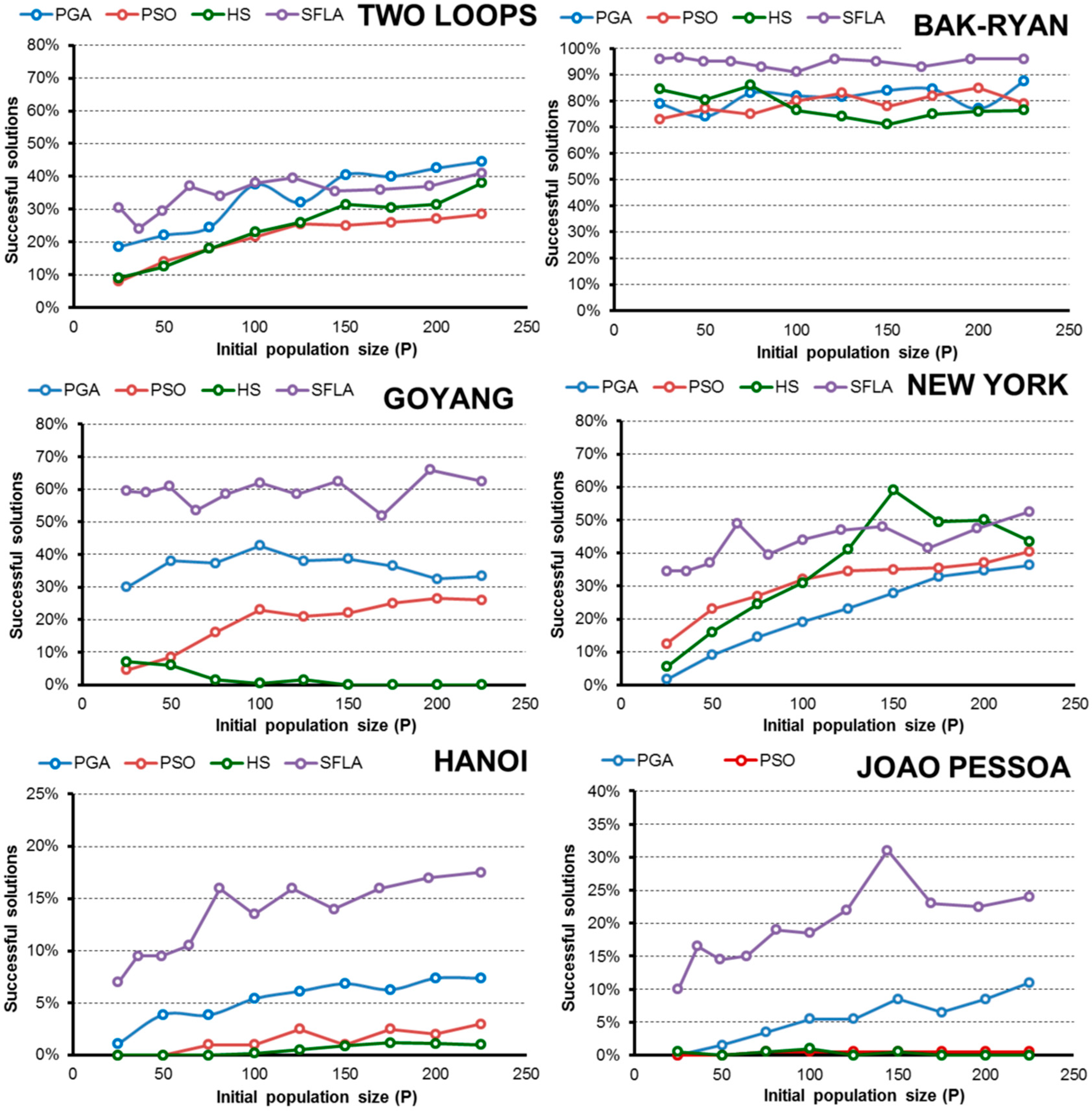
4. Analysis of Results
5. Conclusions
- In terms of efficiency E and considering the complexity of the pipe-sizing problem, the PGA and SFLA are better for complex networks, such as Hanoi or Joao Pessoa, when the goal is to obtain the global minimum. These algorithms are more likely to identify the lowest-cost solution. Meanwhile, the HS and PSO algorithms hardly found global minimums, which severely decrease their efficiency.
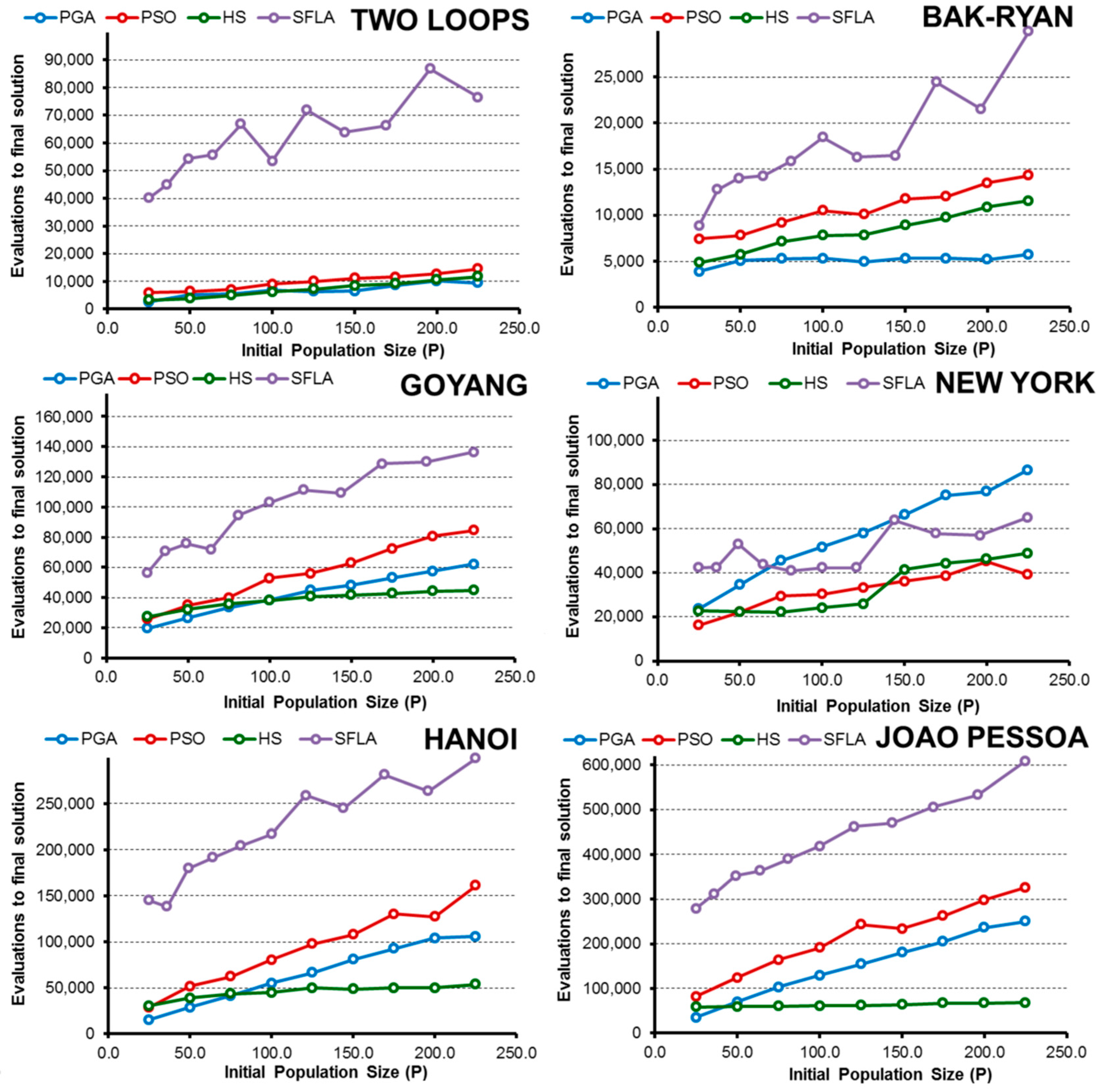
- The HS algorithm exhibited improved performance in less complex water networks such as small problems, in which all algorithms are able to find minimal solutions easily. In addition, if we extend the range of solutions that is considered successful to include good solutions (3% above the global minimum), the HS algorithm is the best in the New York network and the second most efficient for the rest of networks (except in the Joao Pessoa network). In this case, the algorithms that require fewer OF evaluations to reach the final solution benefit, and HS is the fastest algorithm.
- The PGA is the most robust technique for finding low-cost solutions because it has a high value of E in all networks, which is similar to the values obtained by the best algorithm in each case.
- SFL algorithm efficiency E is close to the PGA in complex networks (Hanoi and Joao Pessoa) when the goal is to obtain the low-cost solution. However, if the optimization goal is based on obtaining “good solutions”, other techniques are better because the algorithm SFL is penalized due to the high number of evaluations of the objective function performed in the optimization process.
- Regarding the initial random population size, normally the efficiency improves as P increases to a certain limit, beyond which the performance no longer improves or worsens. This size “limit” depends on the complexity of the problem and the problem goal, but larger populations are generally less efficient than small populations when finding a global known.
- In addition, expanding the optimization goal to include a set of “good solutions” close to the global minimum (3% above) confirms the hypothesis, and in the range considered, the smallest population is the most efficient in almost all algorithms and networks.
- Numerically, all algorithms exhibit their highest values of E when finding good solutions near the minimum for 25 < P < 50. To obtain low-cost solutions, the tested algorithms need larger populations (except in the simplest problems), with the highest values of E observed for approximately 75 < P < 125. These values vary slightly for each algorithm and network, but they are a good starting point, regardless of the complexity of the network in the studied cases.
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| PbA | Population-based algorithm |
| WDN | water distribution network |
| OF | Objective Function |
| PGA | Pseudo-Genetic Algorithm |
| PSO | Particle Swarm Optimization |
| SFLA | Shuffled Frog Leaping Algorithm |
| HS | Harmony Search |
| HAWaNet | Heuristic Algorithms Water Networks |
| NP | Nondeterministic, polynomial time |
| BMP | Best Management Practice |
| GA | Genetic Algorithm |
References
- Yates, D.F.; Templeman, A.B.; Boffey, T.B. The computational complexity of the problem of determining least capital cost designs for water supply networks. Eng. Optim. 1984, 7, 143–155. [Google Scholar] [CrossRef]
- Alperovits, E.; Shamir, U. Design of optimal water distribution systems. Water Resour. Res. 1977, 13, 885–900. [Google Scholar] [CrossRef]
- Su, Y.; Mays, L.W.; Duan, N.; Lansey, K.E. Reliability-Based Optimization Model for Water Distribution Systems. J. Hydraul. Eng. 1987, 113, 1539–1556. [Google Scholar] [CrossRef]
- Haddad, O.B.; Tabari, M.M.R.; Fallah-Mehdipour, E.; Mariño, M.A. Groundwater Model Calibration by Meta-Heuristic Algorithms. Water Resour. Manag. 2013, 27, 2515–2529. [Google Scholar] [CrossRef]
- Ostadrahimi, L.; Mariño, M.A.; Afshar, A. Multi-reservoir Operation Rules: Multi-swarm PSO-based Optimization Approach. Water Resour. Manag. 2011, 26, 407–427. [Google Scholar] [CrossRef]
- Afshar, A.; Massoumi, F.; Afshar, A.; Mariño, M.A. State of the Art Review of Ant Colony Optimization Applications in Water Resource Management. Water Resour. Manag. 2015, 29, 3891–3904. [Google Scholar] [CrossRef]
- Artita, K.S.; Kaini, P.; Nicklow, J.W. Examining the Possibilities: Generating Alternative Watershed-Scale BMP Designs with Evolutionary Algorithms. Water Resour. Manag. 2013, 27, 3849–3863. [Google Scholar] [CrossRef]
- Silver, E.A. An overview of heuristic solution methods. J. Oper. Res. Soc. 2004, 55, 936–956. [Google Scholar] [CrossRef]
- Bäck, T.; Fogel, D.B.; Michalewics, Z. Handbook of Evolutionary Computation; Oxford University Press: Oxford, UK, 1997. [Google Scholar]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization, and Machine Learning; Addison-Wesley Longman Publishing Co., Inc.: Boston, MA, USA, 1989. [Google Scholar]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by Simulated Annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Glover, F. Tabu Search—Part I. ORSA J. Comput. 1989, 1, 190–206. [Google Scholar] [CrossRef]
- Iglesias, P.; Mora, D.; Martinez, F.; Fuertes, V.S. Study of sensitivity of the parameters of a genetic algorithm for design of water distribution networks. J. Urban Environ. Eng. 2007, 1, 61–69. [Google Scholar] [CrossRef]
- Reca, J.; Martínez, J. Genetic algorithms for the design of looped irrigation water distribution networks. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Baños, R.; Gil, C.; Agulleiro, J.I.; Reca, J. A Memetic Algorithm for Water Distribution Network Design. In Soft Computing in Industrial Applications; Saad, A., Dahal, K., Sarfaz, M., Roy, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 279–289. [Google Scholar]
- Geem, Z. Multiobjective Optimization of Water Distribution Networks Using Fuzzy Theory and Harmony Search. Water 2015, 7, 3613–3625. [Google Scholar] [CrossRef]
- Geem, Z.W. Optimal cost design of water distribution networks using harmony search. Eng. Optim. 2006, 38, 259–277. [Google Scholar] [CrossRef]
- Eusuff, M.M.; Lansey, K.E. Optimization of Water Distribution Network Design Using the Shuffled Frog Leaping Algorithm. J. Water Resour. Plan. Manag. 2003, 129, 210–225. [Google Scholar] [CrossRef]
- Geem, Z.W. Particle-swarm harmony search for water network design. Eng. Optim. 2009, 41, 297–311. [Google Scholar] [CrossRef]
- Mora-Melia, D.; Iglesias-Rey, P.L.; Martinez-Solano, F.J.; Fuertes-Miquel, V.S. Design of Water Distribution Networks using a Pseudo-Genetic Algorithm and Sensitivity of Genetic Operators. Water Resour. Manag. 2013, 27, 4149–4162. [Google Scholar] [CrossRef]
- Mora-Melia, D.; Iglesias-Rey, P.; Fuertes-Miquel, V.; Martinez-Solano, F. Application of the Harmony Search Algorithm to Water Distribution Networks Design. In Proceeedings of the International Workshop on Environmental Hydraulics, IWEH09, Valencia, Spain, 29–30 October 2009; Lopez-Jimenez, P., Fuertes-Miquel, V., Iglesias-Rey, P., Lopez Patiño, G., Martinez-Solano, F., Palau-Salvador, G., Eds.; Taylor & Francis Group: Abingdon, UK, 2010. [Google Scholar]
- Maier, H.R.; Kapelan, Z.; Kasprzyk, J.; Kollat, J.; Matott, L.S.; Cunha, M.C.; Dandy, G.C.; Gibbs, M.S.; Keedwell, E.; Marchi, A.; et al. Evolutionary algorithms and other metaheuristics in water resources: Current status, research challenges and future directions. Environ. Model. Softw. 2014, 62, 271–299. [Google Scholar] [CrossRef]
- Zhu, K.Q.; Liu, Z. Population Diversity in Permutation-Based Genetic Algorithm; Springer: Berlin/Heidelberg, Germany, 2004; pp. 537–547. [Google Scholar]
- Liu, W.; Yan, F. On the population diversity control of evolutionary algorithms for production scheduling problems. In Proceedings of the IEEE Fifth International Conference on Advanced Computational Intelligence (ICACI), Nanjing, China, 18–20 October 2012; pp. 468–473.
- Witt, C. Population size versus runtime of a simple evolutionary algorithm. Theor. Comput. Sci. 2008, 403, 104–120. [Google Scholar] [CrossRef]
- Schonemann, L. The impact of population sizes and diversity on the adaptability of evolution strategies in dynamic environments. In Proceedings of the 2004 Congress on Evolutionary Computation (IEEE Cat. No.04TH8753), Portland, OR, USA, 19–23 June 2004; pp. 1270–1277.
- Simões, A.; Costa, E. The Influence of Population and Memory Sizes on the Evolutionary Algorithm’s Performance for Dynamic Environments; Springer: Berlin/Heidelberg, Germany, 2009; pp. 705–714. [Google Scholar]
- Richter, H.; Yang, S. Memory Based on Abstraction for Dynamic Fitness Functions; Springer: Berlin/Heidelberg, Germany, 2008; pp. 596–605. [Google Scholar]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
- Dandy, G.; Wilkins, A.; Rohrlach, H. A Methodology for Comparing Evolutionary Algorithms for Optimising Water Distribution Systems. In Water Distribution Systems Analysis 2010; American Society of Civil Engineers: Reston, VA, USA, 2011; pp. 786–798. [Google Scholar]
- Marchi, A.; Dandy, G.; Wilkins, A.; Rohrlach, H. Methodology for Comparing Evolutionary Algorithms for Optimization of Water Distribution Systems. J. Water Resour. Plan. Manag. 2014, 140, 22–31. [Google Scholar] [CrossRef]
- Mora-Melia, D.; Iglesias-Rey, P.L.; Martinez-Solano, F.J.; Ballesteros-Pérez, P. Efficiency of Evolutionary Algorithms in Water Network Pipe Sizing. Water Resour. Manag. 2015, 29, 4817–4831. [Google Scholar] [CrossRef]
- McClymont, K.; Keedwell, E.; Savic, D. An analysis of the interface between evolutionary algorithm operators and problem features for water resources problems. A case study in water distribution network design. Environ. Model. Softw. 2015, 69, 414–424. [Google Scholar] [CrossRef]
- Savic, D.A.; Walters, G.A. Genetic Algorithms for Least-Cost Design of Water Distribution Networks. J. Water Resour. Plan. Manag. 1997, 123, 67–77. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, Australia, 21 November–1 December 1995; Volume 4, pp. 1942–1948.
- Elbeltagi, E.; Hegazy, T.; Grierson, D. A modified shuffled frog-leaping optimization algorithm: Applications to project management. Struct. Infrastruct. Eng. 2007, 3, 53–60. [Google Scholar] [CrossRef]
- Mora-Melia, D.; Iglesias-Rey, P.; Martínez-Solano, F.; Muñoz-Velasco, P. The Efficiency of Setting Parameters in a Modified Shuffled Frog Leaping Algorithm Applied to Optimizing Water Distribution Networks. Water 2016, 8, 182. [Google Scholar] [CrossRef]
- Eiben, A.E.; Hinterding, R.; Michalewicz, Z. Parameter control in evolutionary algorithms. IEEE Trans. Evol. Comput. 1999, 3, 124–141. [Google Scholar] [CrossRef]
- Mora-Melia, D.; Iglesias-Rey, P.; Fuertes-Miquel, V.; Martinez-Solano, F. Comparison of Evolutionary Algorithms for Design of Sewer Systems; Lopez-Jimenez, P., Fuertes-Miquel, V., Iglesias-Rey, P., Lopez Patiño, G., Martinez-Solano, F., Palau-Salvador, G., Eds.; Taylor & Francis Group: Abingdon, UK, 2010; Volume 1. [Google Scholar]
- Rossman, L.A. EPANET 2.0 User’s Manual; EPA/600/R-00/057, Water Supply and Water Resources Div.; National Risk Management Research Laboratory: Cincinnatti, OH, USA, 2000. [Google Scholar]
- Wang, Q.; Guidolin, M.; Savic, D.; Kapelan, Z. Two-Objective Design of Benchmark Problems of a Water Distribution System via MOEAs: Towards the Best-Known Approximation of the True Pareto Front. J. Water Resour. Plan. Manag. 2015, 141, 04014060. [Google Scholar] [CrossRef]
- Fujiwara, O.; Khang, D.B. A two-phase decomposition method for optimal design of looped water distribution networks. Water Resour. Res. 1990, 26, 539–549. [Google Scholar] [CrossRef]
- Schaake, J.; Lai, F.H. Linear Programming and Dynamic Programming Application to Water Distribution Network Design; M.I.T. Hydrodynamics Laboratory, Ed.; M.I.T. Hydrodynamics Laboratory: Cambridge, MA, USA, 1969. [Google Scholar]
- Kim, J.H.; Kim, T.G.; Kim, J.H.; Yoon, Y.N. A study on the pipe network system design using non-linear programming. J. Korean Water Resour. Assoc. 1994, 27, 59–67. [Google Scholar]
- Gomes, H.; de Tarso Marques Bezerra, S.; de Carvalho, P.S.O.; Salvino, M.M. Optimal dimensioning model of water distribution systems. Water SA 2009, 35, 421–431. [Google Scholar] [CrossRef]
| Algorithm/Network | Two Loops | Bak-Ryan | Hanoi | Joao Pessoa | New York | GoYang |
|---|---|---|---|---|---|---|
| PGA | ||||||
| Pc | 10%–90% | 10%–90% | 10%–90% | 10%–90% | >60% | 10%–90% |
| * Pm | 4% | 3% | 3% | 2% | 4% | 3% |
| PSO | ||||||
| * Vlim | 10% | 10% | 20% | 20% | 30% | 10% |
| * Pconf | 10%–20% | 10%–20% | 10%–20% | 10%–20% | 10% | 10%–20% |
| C1 | 2 | 2 | 2 | 2 | 2 | 2 |
| C2 | 2 | 2 | 2 | 2 | 2 | 2 |
| HS | ||||||
| * HMCR | 90% | 90% | 95% | 95% | 90% | 90% |
| * PAR | 15% | 15% | 10% | 10% | 15% | 15% |
| SFLA | ||||||
| * C | 2 | 2 | 2 | 2 | 2 | 1.5 |
| Q | 50% | 50% | 50% | 50% | 50% | 50% |
| Ns | 30 | 30 | 30 | 30 | 30 | 30 |
| Network | Number of Pipes | Number of Possible Diameters | Search Space | Minimum Pressure Requirements (mca) | Best Known Solution ($) | Number of Different Solutions |
|---|---|---|---|---|---|---|
| Two Loops | 8 | 14 | 1.48 × 109 | 30 | 419,000 | 60 |
| BakRyan | 9 | 11 | 2.36 × 109 | 15 | 903,620 | 10 |
| New York | 21 | 16 | 1.93 × 1025 | 30 | 38.642 × 106 | 2163 |
| GoYang | 30 | 8 | 1.24 × 1027 | 15 | 177.010 × 106 a | 303 |
| Hanoi | 34 | 14 | 2.87 × 1026 | 30 | 6.081 × 106 | 5553 |
| Joao Pessoa | 72 | 10 | 1 × 1072 | 15 | 192.366 × 106 | 16,101 |
| Algorithm/Network | Two Loops | BakRyan | Hanoi | Joao Pessoa | New York | GoYang |
|---|---|---|---|---|---|---|
| Pseudo-Genetic algorithm (PGA) | ||||||
| Low cost solution | 25 | 25 | P = 50 | P = 100 | P = 100 | P = 25 |
| Good solution (3% above) | 25 | 25 | P = 25 | P = 25–50 | P = 50 | P = 25 |
| Particle Swarm Optimization algorithm (PSO) | ||||||
| Low cost solution | 125 | 25 | P = 125 | P = 75 | P = 50 | P = 75 |
| Good solution (3% above) | 25 | 25 | P = 50 | P = 75 | P = 25 | P = 25 |
| Harmony Search algorithm (HS) | ||||||
| Low cost solution | 75 | 25 | P = 175 | P = 100 | P = 125 | P = 25 |
| Good solution (3% above) | 25 | 25 | P = 25–50 | P = 50 | P = 75 | P = 25 |
| Shuffled Frog Leaping algorithm (SFLA) | ||||||
| Low cost solution | 25 | 25 | P = 100 | P = 150 | P = 75 | P = 25 |
| Good solution (3% above) | 25 | 25 | P = 25 | P = 25 | P = 75 | P = 25 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mora-Melià, D.; Gutiérrez-Bahamondes, J.H.; Iglesias-Rey, P.L.; Martínez-Solano, F.J. Efficiency Criteria as a Solution to the Uncertainty in the Choice of Population Size in Population-Based Algorithms Applied to Water Network Optimization. Water 2016, 8, 583. https://doi.org/10.3390/w8120583
Mora-Melià D, Gutiérrez-Bahamondes JH, Iglesias-Rey PL, Martínez-Solano FJ. Efficiency Criteria as a Solution to the Uncertainty in the Choice of Population Size in Population-Based Algorithms Applied to Water Network Optimization. Water. 2016; 8(12):583. https://doi.org/10.3390/w8120583
Chicago/Turabian StyleMora-Melià, Daniel, Jimmy H. Gutiérrez-Bahamondes, Pedro L. Iglesias-Rey, and F. Javier Martínez-Solano. 2016. "Efficiency Criteria as a Solution to the Uncertainty in the Choice of Population Size in Population-Based Algorithms Applied to Water Network Optimization" Water 8, no. 12: 583. https://doi.org/10.3390/w8120583
APA StyleMora-Melià, D., Gutiérrez-Bahamondes, J. H., Iglesias-Rey, P. L., & Martínez-Solano, F. J. (2016). Efficiency Criteria as a Solution to the Uncertainty in the Choice of Population Size in Population-Based Algorithms Applied to Water Network Optimization. Water, 8(12), 583. https://doi.org/10.3390/w8120583







