Global Sea Surface Temperature and Sea Level Rise Estimation with Optimal Historical Time Lag Data
Abstract
:1. Introduction
2. Dynamic Systems Model with Time Lag
3. Calibration of DSM with Time Lag
4. Determination of Optimal Time Lag
5. Numerical Results and Discussion
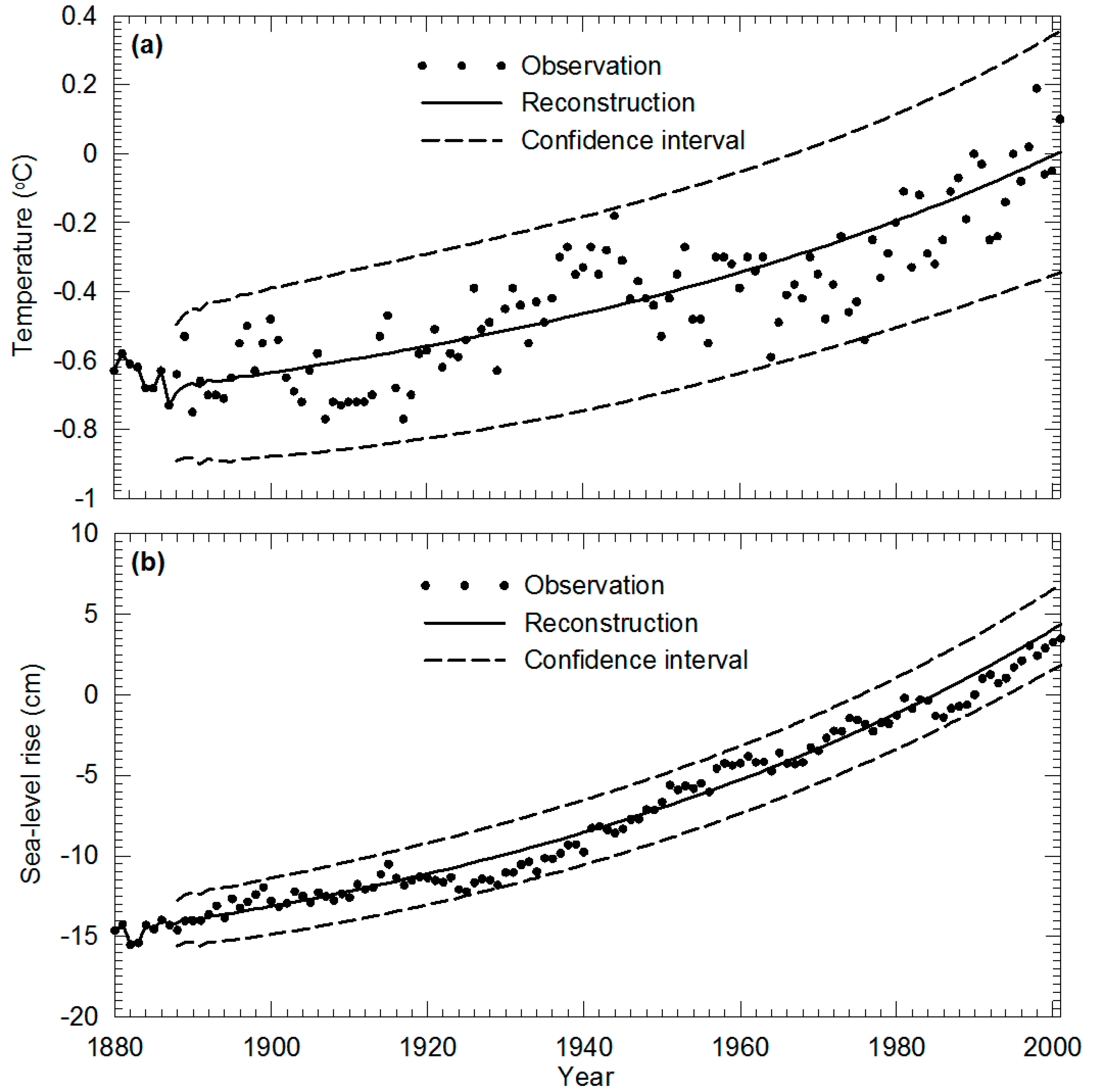
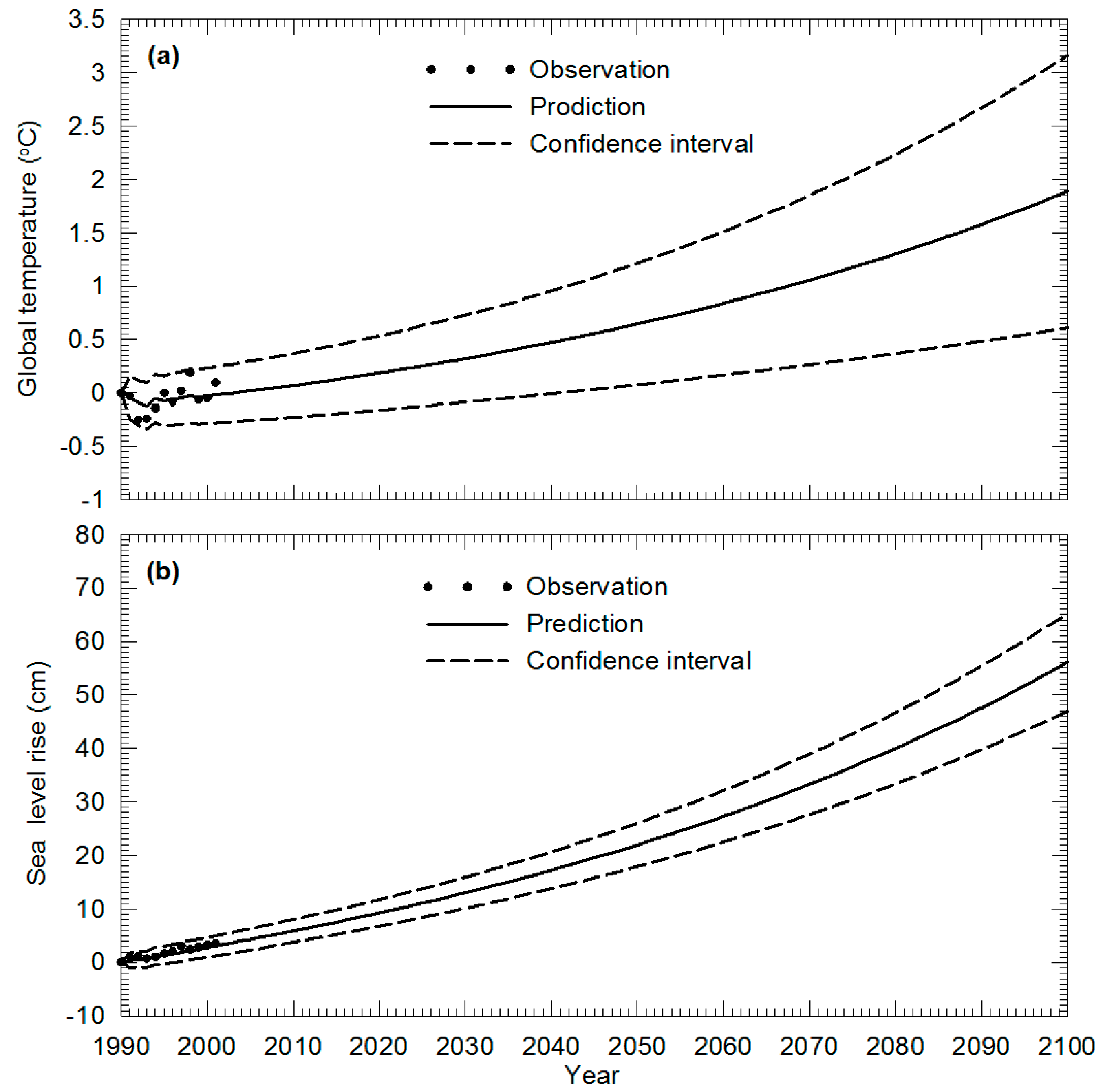
5.1. Time-Invariant DSM (TI-DSM) Application
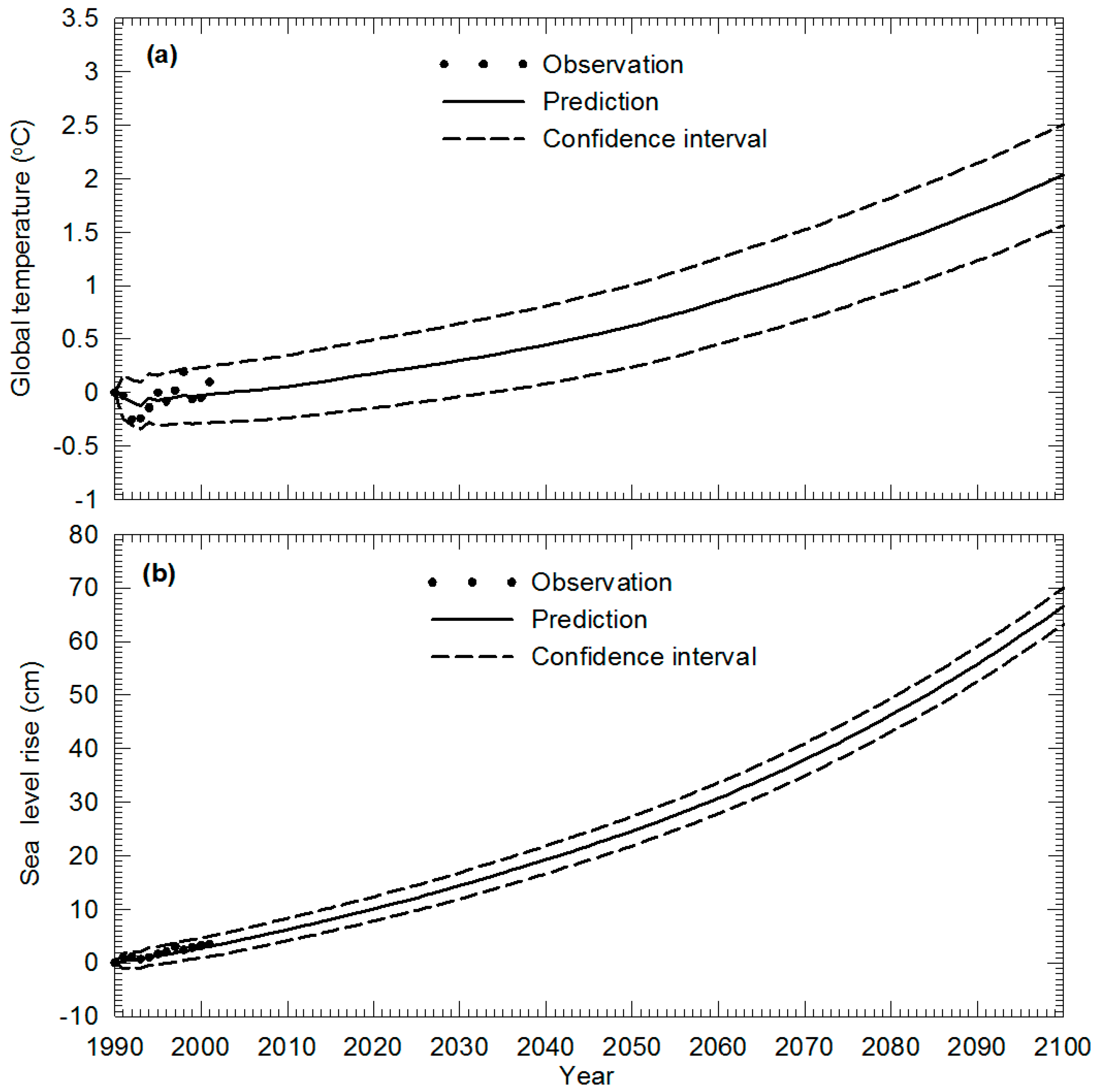
5.2. Time-Variant DSM (TV-DSM) Application
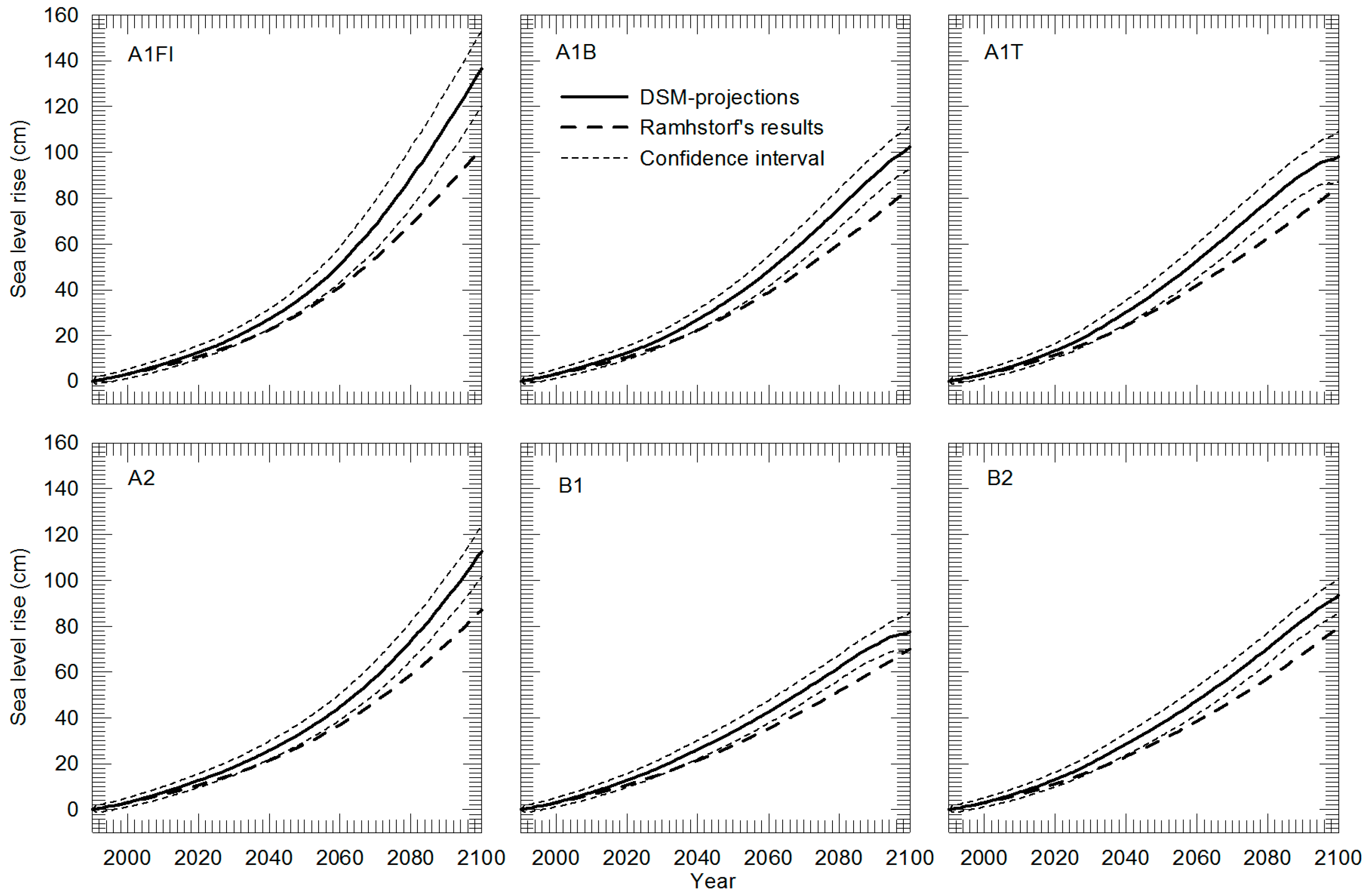
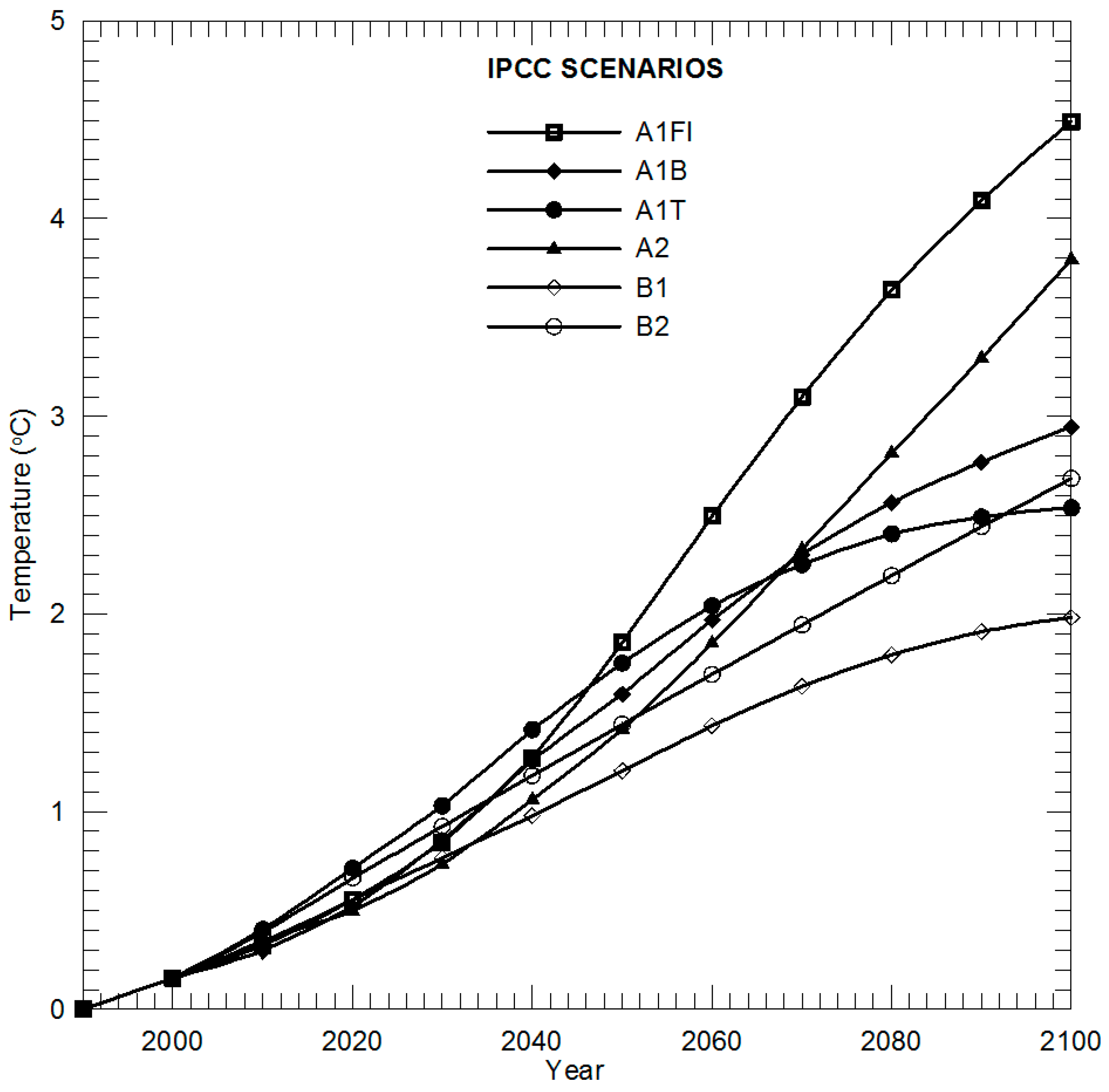
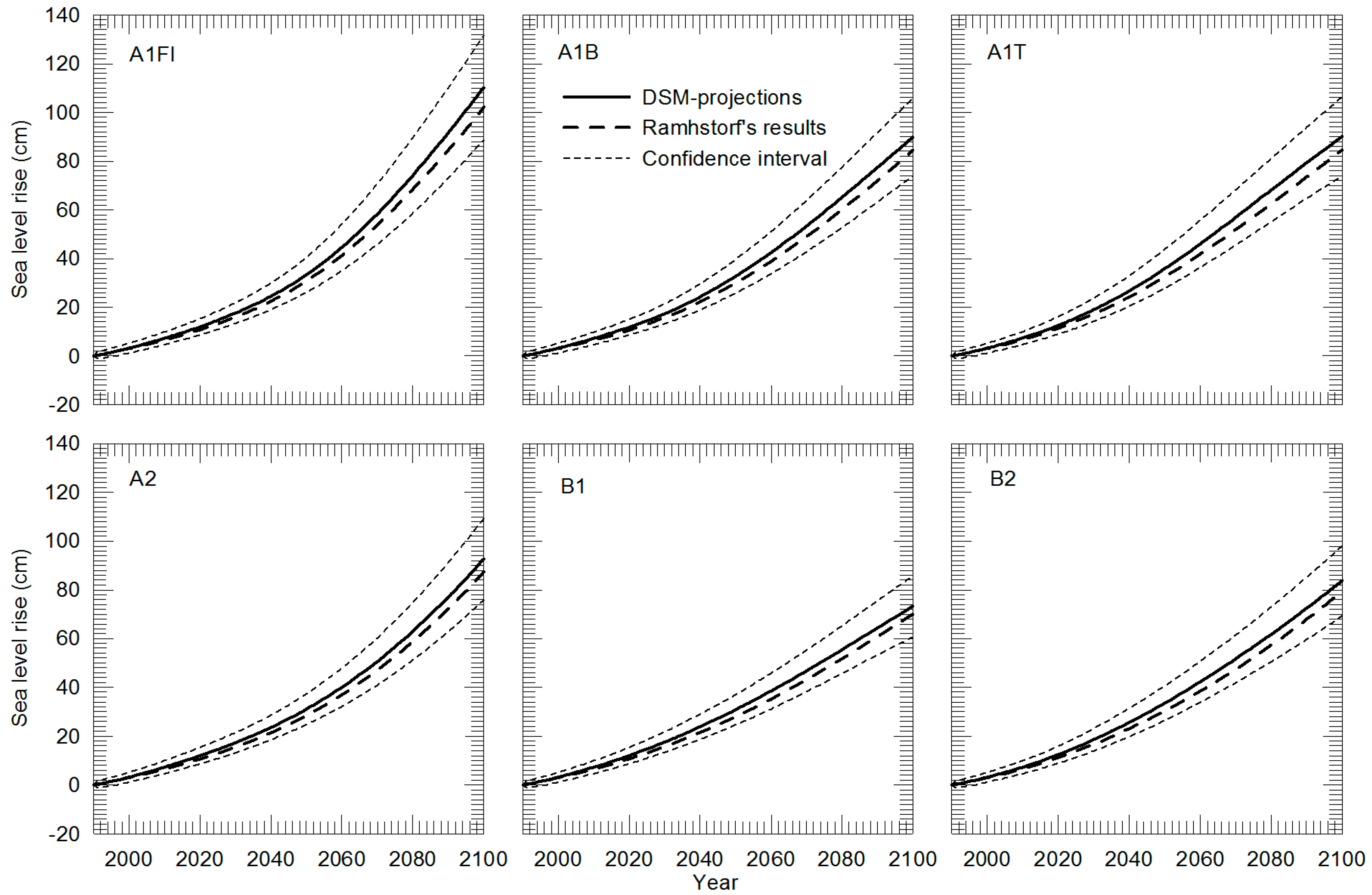
5.3. Applications Using IPCC Scenarios
6. Conclusions
Author Contributions
Conflicts of Interest
References
- National Research Council. America’s Climate Choices; The National Academies Press: Washington, DC, USA, 2011; p. 135. [Google Scholar]
- Intergovernmental Panel on Climate Change. Climate Change 2001: The Scientific Basis. Contribution of Working Group I to the Third Assessment Report of the Intergovernmental Panel on Climate Change; Houghton, J.T., Ding, Y., Griggs, D.J., Noguer, M., van der Linden, P.J., Dai, X., Maskell, K., Johnson, C.A., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2001. [Google Scholar]
- Intergovernmental Panel on Climate Change. Climate Change 2007: The Physical Science Basis. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Solomon, S., Qin, D., Manning, M., Chen, Z., Marquis, M., Averyt, K.B., Tignor, M., Miller, H.L., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2007. [Google Scholar]
- Intergovernmental Panel on Climate Change. Summary for Policymakers. Available online: http://www.ipcc.ch/report/ar5/wg1/ (accessed on 26 November 2013).
- Douglas, B.C. Global sea rise: A redetermination. Surv. Geophys. 1997, 18, 279–292. [Google Scholar] [CrossRef]
- Church, J.A.; White, N.J. A 20th century acceleration in global sea-level rise. Geophys. Res. Lett. 2006, 33, L01602. [Google Scholar] [CrossRef]
- Meehl, G.A.; Stocker, T.F.; Friedlingstein, W.D.; Collins, P.; Gaye, A.T.; Gregory, J.M.; Kitoh, A.; Knutti, R.; Murphy, J.M.; Noda, A.; et al. Projections of global average sea level change for the 21st century. In Climate Change 2007: The Physical Science Basis. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Solomon, S., Qin, D., Manning, M., Chen, Z., Marquis, M., Averyt, K.B., Tignor, M., Miller, H.L., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2007. [Google Scholar]
- Etkins, R.; Epstein, E.S. The rise of global mean sea-level as an indication of climate change. Science 1982, 215, 287–289. [Google Scholar] [CrossRef] [PubMed]
- Gornitz, V.L.; Lebedeff, S.; Hansen, J. Global sea-level trend in the past century. Science 1982, 215, 1611–1614. [Google Scholar] [CrossRef] [PubMed]
- Rahmstorf, S. A semi-empirical approach to projecting future sea-level rise. Science 2007, 315, 368–370. [Google Scholar] [CrossRef] [PubMed]
- Holgate, S.; Jevrejeva, S.; Woodworth, P.; Brewer, S. Comment on “A semi-emprical approach to projecting future sea-level rise”. Science 2007, 317, 1866. [Google Scholar] [CrossRef] [PubMed]
- Vermeer, M.; Rahmstorf, S. Global sea level linked to global temperature. Proc. Natl. Acad. Sci. USA 2009, 106, 21527–21532. [Google Scholar] [CrossRef] [PubMed]
- Grinsted, A.; Moore, J.C.; Jevrejeva, S. Reconstructing sea level from paleo and projected temperatures 200 to 2100 AD. Clim. Dyn. 2010, 34, 461–472. [Google Scholar] [CrossRef]
- Jevrejeva, S.; Grinsted, A.; Moore, J.C. Anthropogenic forcing dominates sea level rise since 1850. Geophys. Res. Lett. 2009, 36, L20706. [Google Scholar] [CrossRef]
- Jevrejeva, S.; Moore, J.C.; Grinsted, A. How will sea level response to changes in natural and anthropogenic forcings by 2100? Geophy. Res. Lett. 2010, 37, L07703. [Google Scholar]
- Aral, M.M.; Guan, J.; Chang, B. A dynamic system model to predict global sea-level rise and temperature change. J. Hydrol. Eng. 2012, 17, 237–242. [Google Scholar] [CrossRef]
- Schmith, T.; Johansen, S.; Thejll, P. Statistical analysis of global surface temperature and sea level using cointegration methods. J. Clim. 2012, 25, 7822–7833. [Google Scholar] [CrossRef]
- Guan, J.; Chang, B.; Aral, M.M. A Dynamic Control System Model for Global Temperature Change and Sea level Rise in Response to CO2 Emissions. Clim. Res. 2013, 58, 55–66. [Google Scholar] [CrossRef]
- Chang, B.; Guan, J.; Aral, M.M. Modeling spatial variations of sea level rise and corresponding inundation impacts: A case study for Florida, USA. J. Water Qual. Expo. Health 2013, 6, 39–51. [Google Scholar] [CrossRef]
- Chang, B.; Guan, J.; Aral, M.M. A scientific discourse: Climate change and sea-level rise. ASCE J. Hydrol. Eng. 2013, 20. [Google Scholar] [CrossRef]
- Wadsworth, H.M. Handbook of Statistical Methods for Engineers and Scientists, 2nd ed.; McGraw-Hill: New York, NY, USA, 1998. [Google Scholar]
- Hyndman, R.J.; Koehler, A.B. Another look at measures of forecast accuracy. Int. J. For. 2006, 22, 679–688. [Google Scholar] [CrossRef]
- Draper, N.R.; Smith, H. Applied regression analysis. In Wiley Series in Probability and Statistics; Wiley: New York, NY, USA, 1998. [Google Scholar]
- McLachlan, G.J.; Do, K.-A.; Ambroise, C. Analyzing Microarray Gene Expression Data; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Pfeffer, W.T.; Harper, J.T.; O’Neel, S. Kinematic constraints on glacier contributions to 21st-century sea-level rise. Science 2008, 321, 1340–1343. [Google Scholar] [CrossRef] [PubMed]
- Rahmstorf, S. A new view on sea level rise. Nat. Rep. Clim. Chang. 2010, 4, 44–45. [Google Scholar] [CrossRef]
| Time Lag | Matrix |
|---|---|
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| Time Lag | Matrix |
|---|---|
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| Scenario | Sea Level Rise (cm in 2100 Relative to 1990) | |||
|---|---|---|---|---|
| Best Estimate | 90% Confidence Interval | Rahmstorf’s Projections [10] | IPCC Projections [2,3] | |
| A1FI | 110.2 | [88.7, 131.7] | 102.1 | [26, 59] |
| A1B | 89.9 | [73.9, 106.0] | 84.4 | [21, 48] |
| A1T | 90.1 | [73.8, 106.4] | 84.7 | [20, 45] |
| A2 | 92.6 | [75.9, 109.3] | 87.2 | [23, 51] |
| B1 | 73.2 | [60.6, 85.8] | 70.0 | [18, 38] |
| B2 | 83.7 | [69.2, 98.1] | 79.5 | [20, 43] |
| Scenario | Sea Level Rise (cm in 2100 Relative to 1990) | |||
|---|---|---|---|---|
| Best Estimate | 90% Confidence Interval | Rahmstorf’s Projections [10] | IPCC Projections [2,3] | |
| A1FI | 136.4 | [119.9, 152.9] | 102.1 | [26, 59] |
| A1B | 102.4 | [93.0, 111.7] | 84.4 | [21, 48] |
| A1T | 98.1 | [87.0, 109.1] | 84.7 | [20, 45] |
| A2 | 112.7 | [101.5, 123.7] | 87.2 | [23, 51] |
| B1 | 77.7 | [69.6, 85.7] | 70.0 | [18, 38] |
| B2 | 93.3 | [85.7, 100.9] | 79.5 | [20, 43] |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aral, M.M.; Guan, J. Global Sea Surface Temperature and Sea Level Rise Estimation with Optimal Historical Time Lag Data. Water 2016, 8, 519. https://doi.org/10.3390/w8110519
Aral MM, Guan J. Global Sea Surface Temperature and Sea Level Rise Estimation with Optimal Historical Time Lag Data. Water. 2016; 8(11):519. https://doi.org/10.3390/w8110519
Chicago/Turabian StyleAral, Mustafa M., and Jiabao Guan. 2016. "Global Sea Surface Temperature and Sea Level Rise Estimation with Optimal Historical Time Lag Data" Water 8, no. 11: 519. https://doi.org/10.3390/w8110519
APA StyleAral, M. M., & Guan, J. (2016). Global Sea Surface Temperature and Sea Level Rise Estimation with Optimal Historical Time Lag Data. Water, 8(11), 519. https://doi.org/10.3390/w8110519