Novel Slope Source Term Treatment for Preservation of Quiescent Steady States in Shallow Water Flows
Abstract
:1. Introduction
2. Governing Equations and Numerical Model
2.1. Variable Reconstruction and Limiting
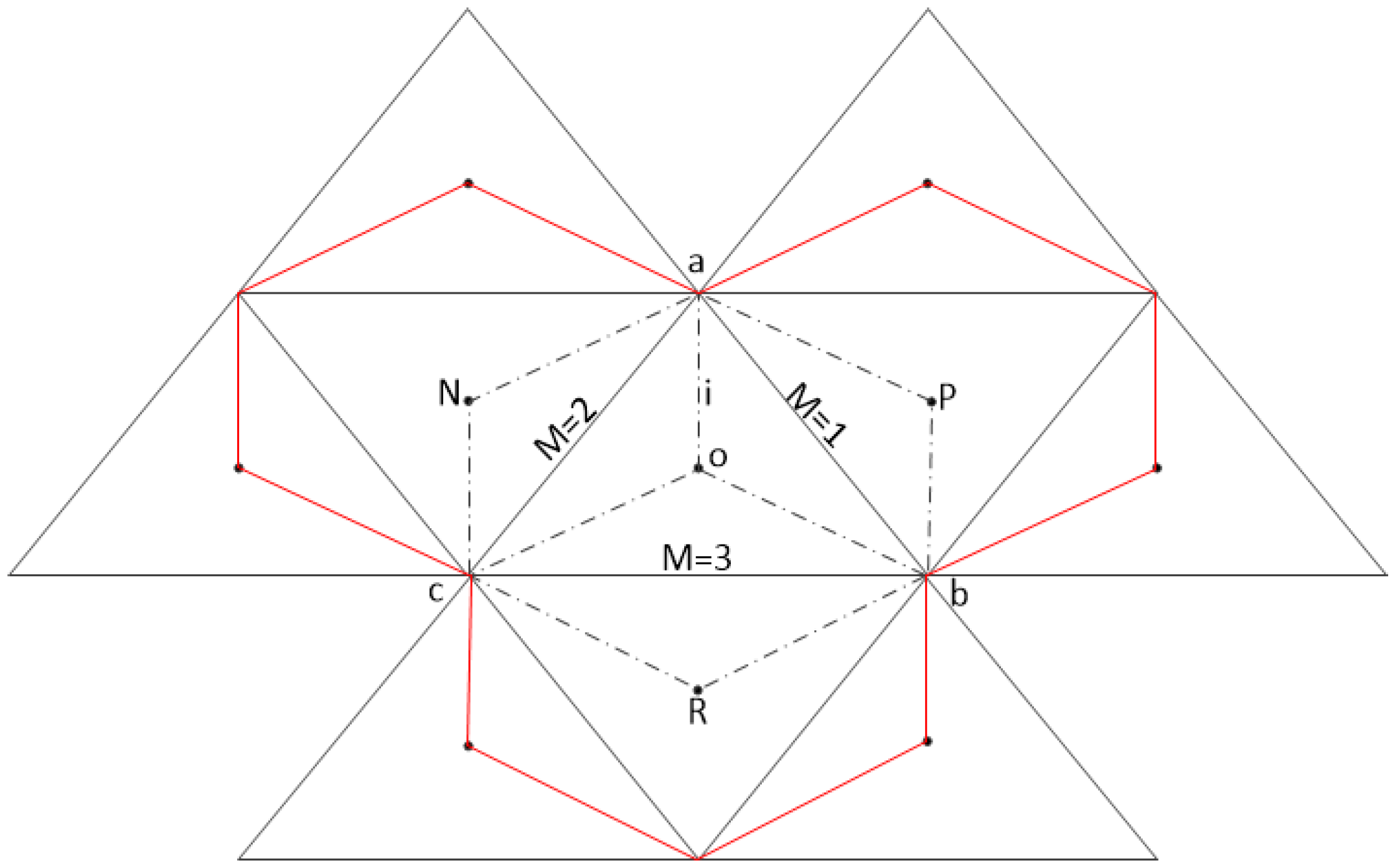
2.2. Slope Term Treatment and Preservation of C-Property
2.3. Wet–Dry Front Treatment
2.4. Boundary Conditions
3. Model Applications
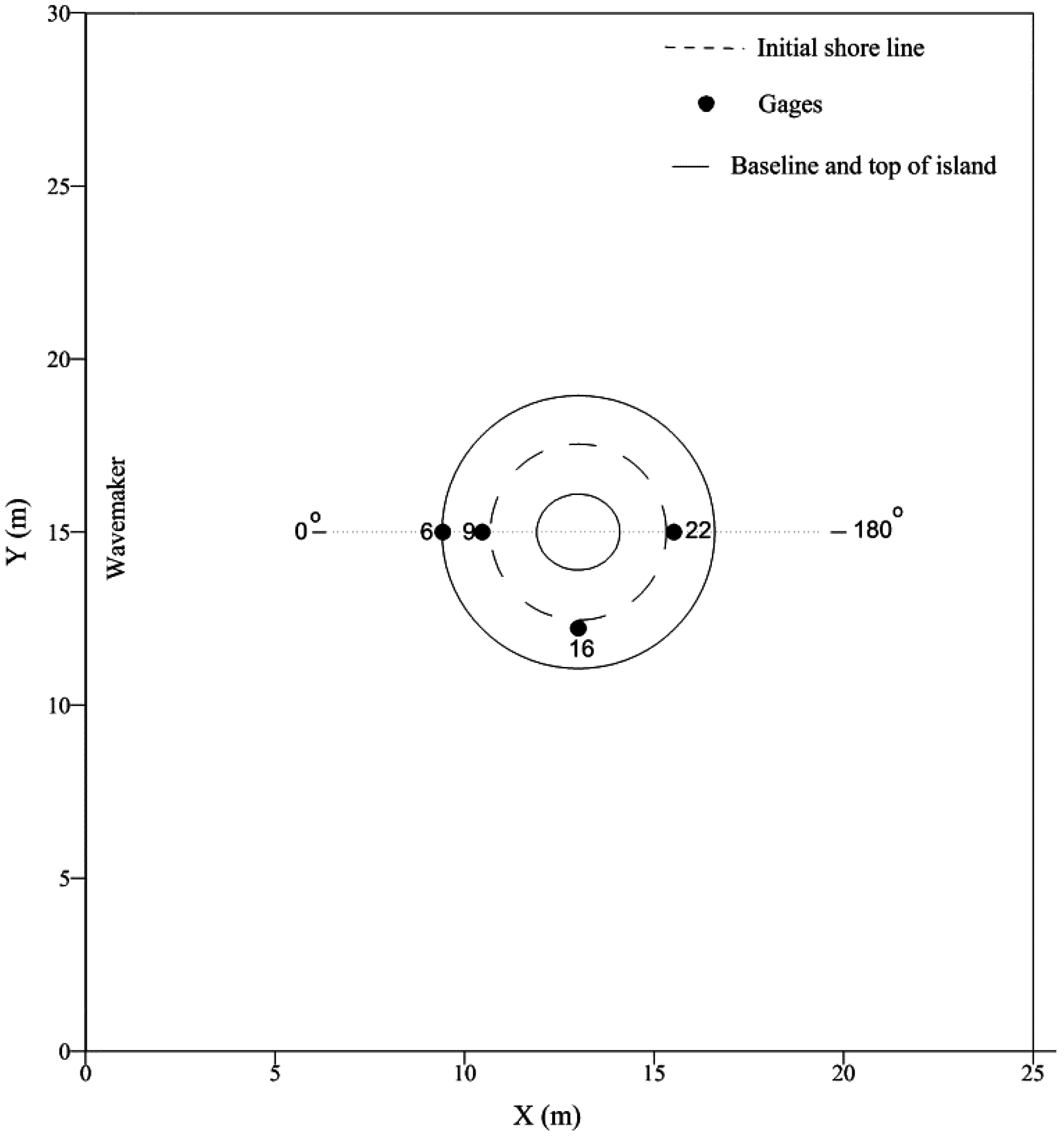
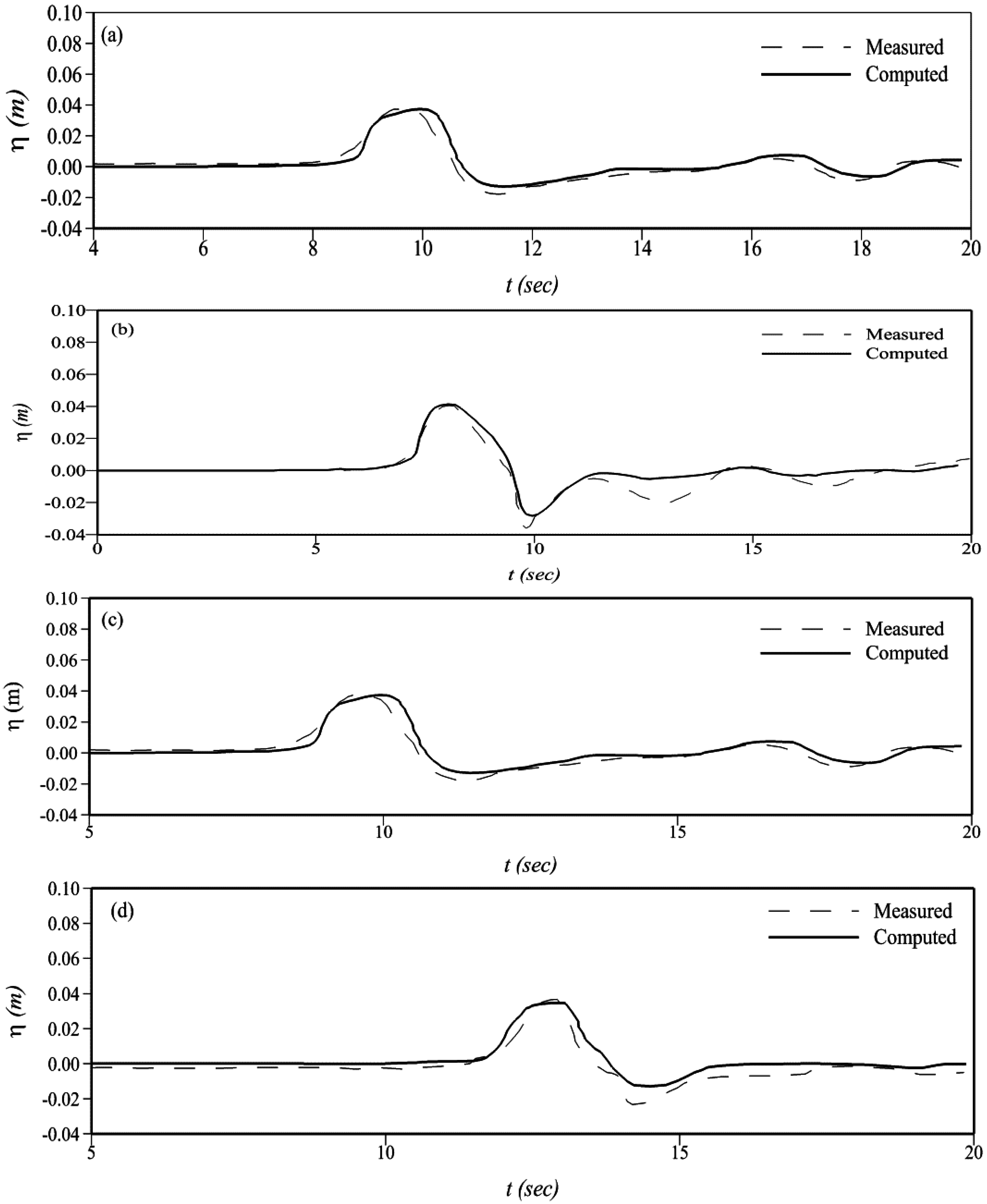
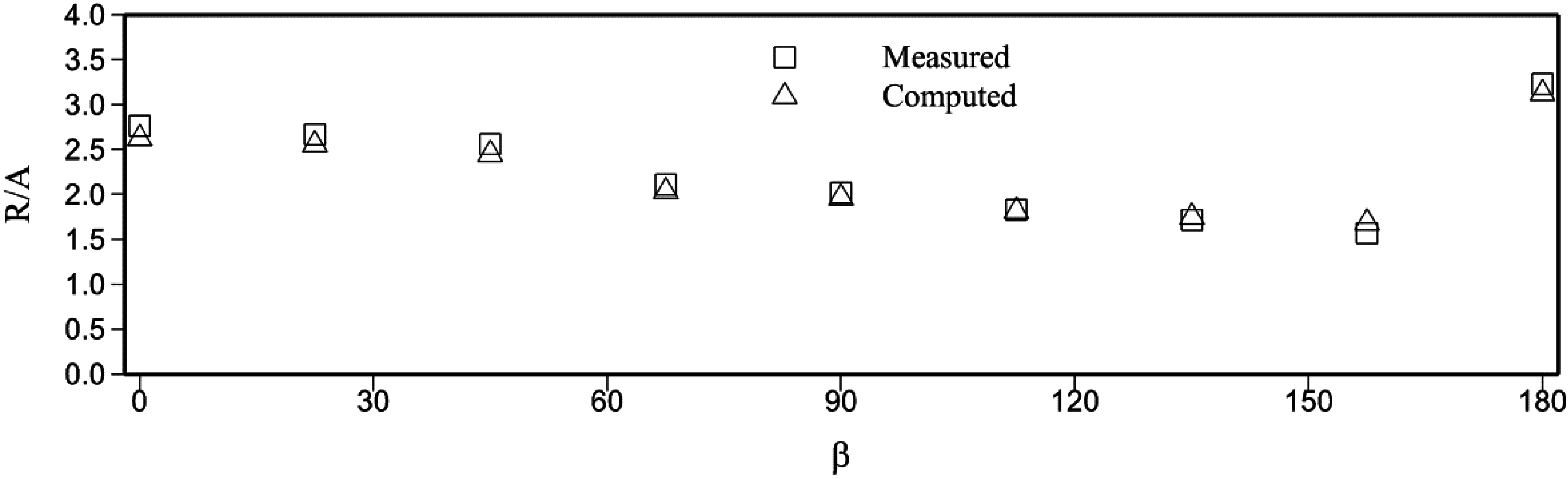
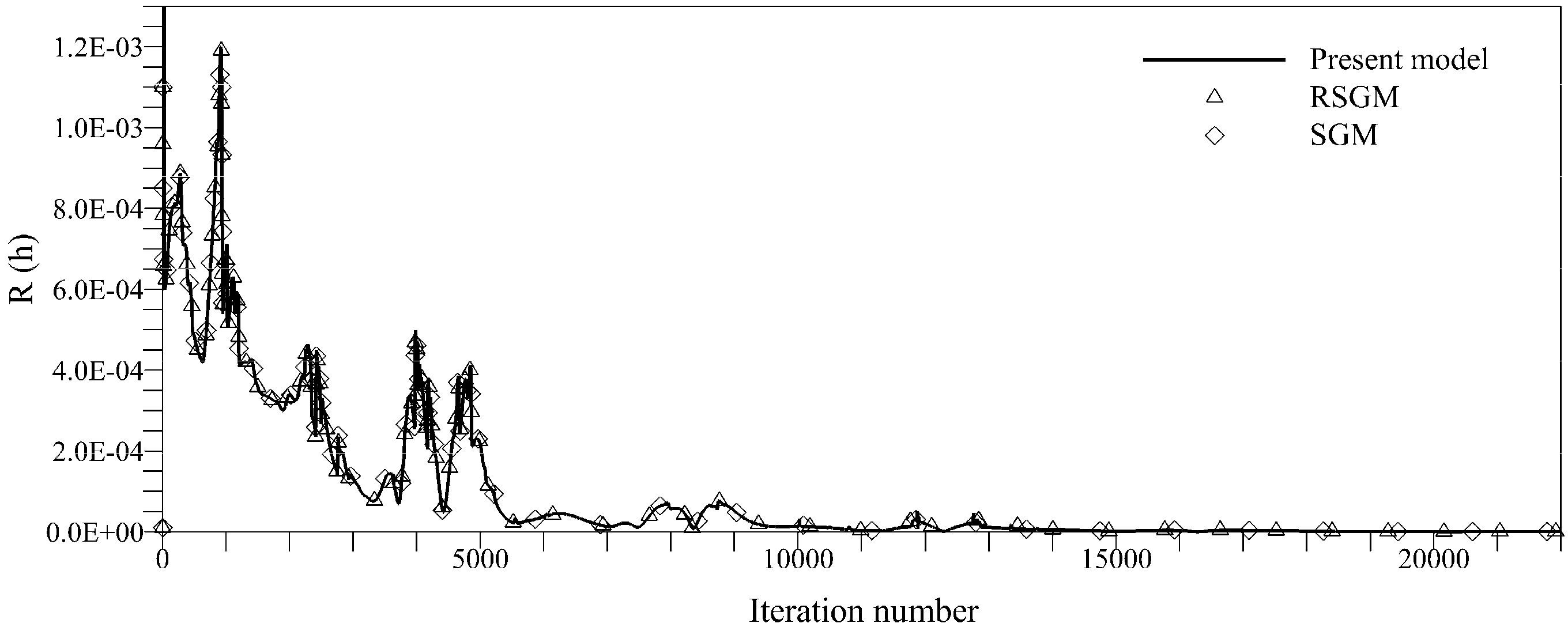
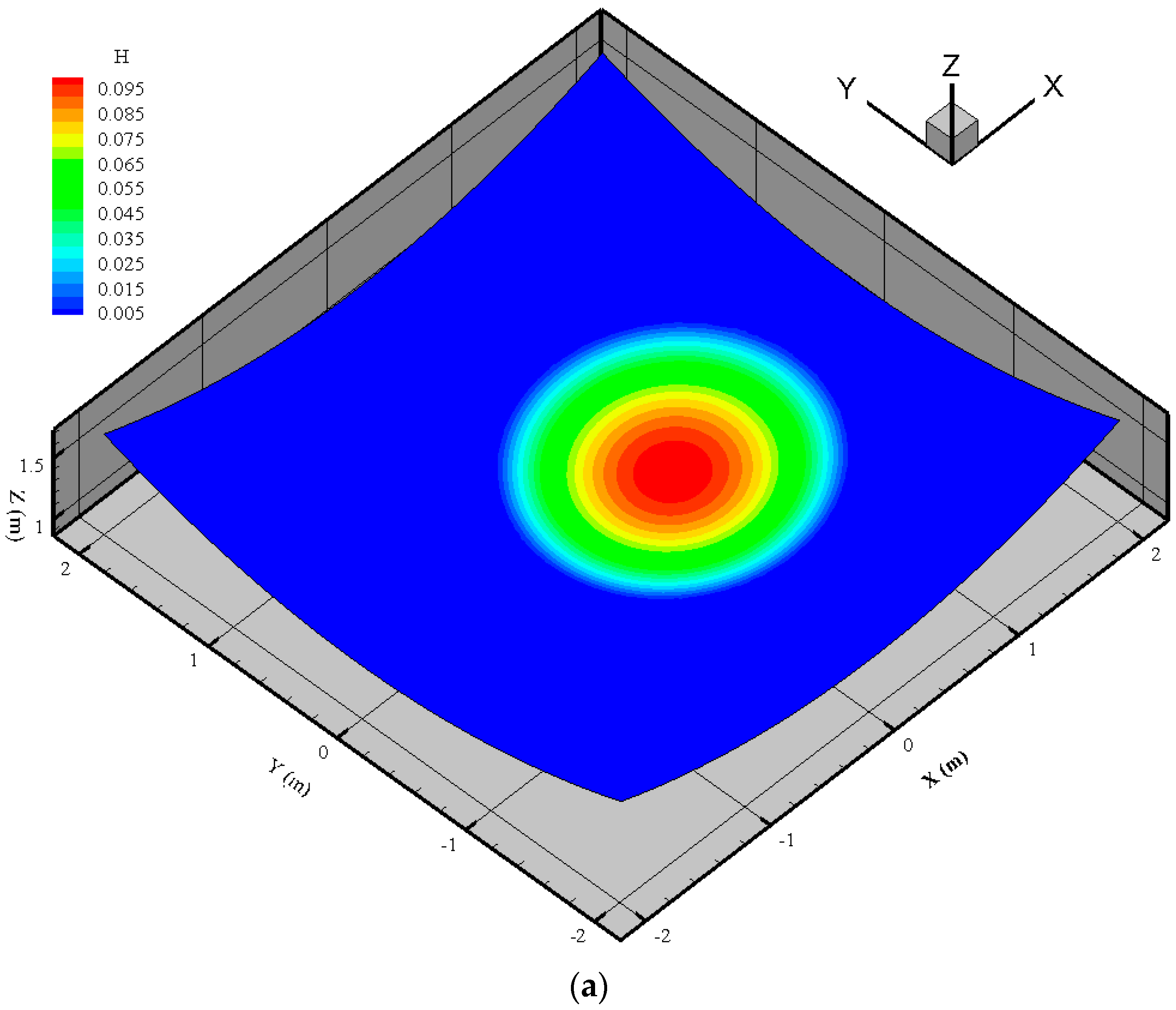
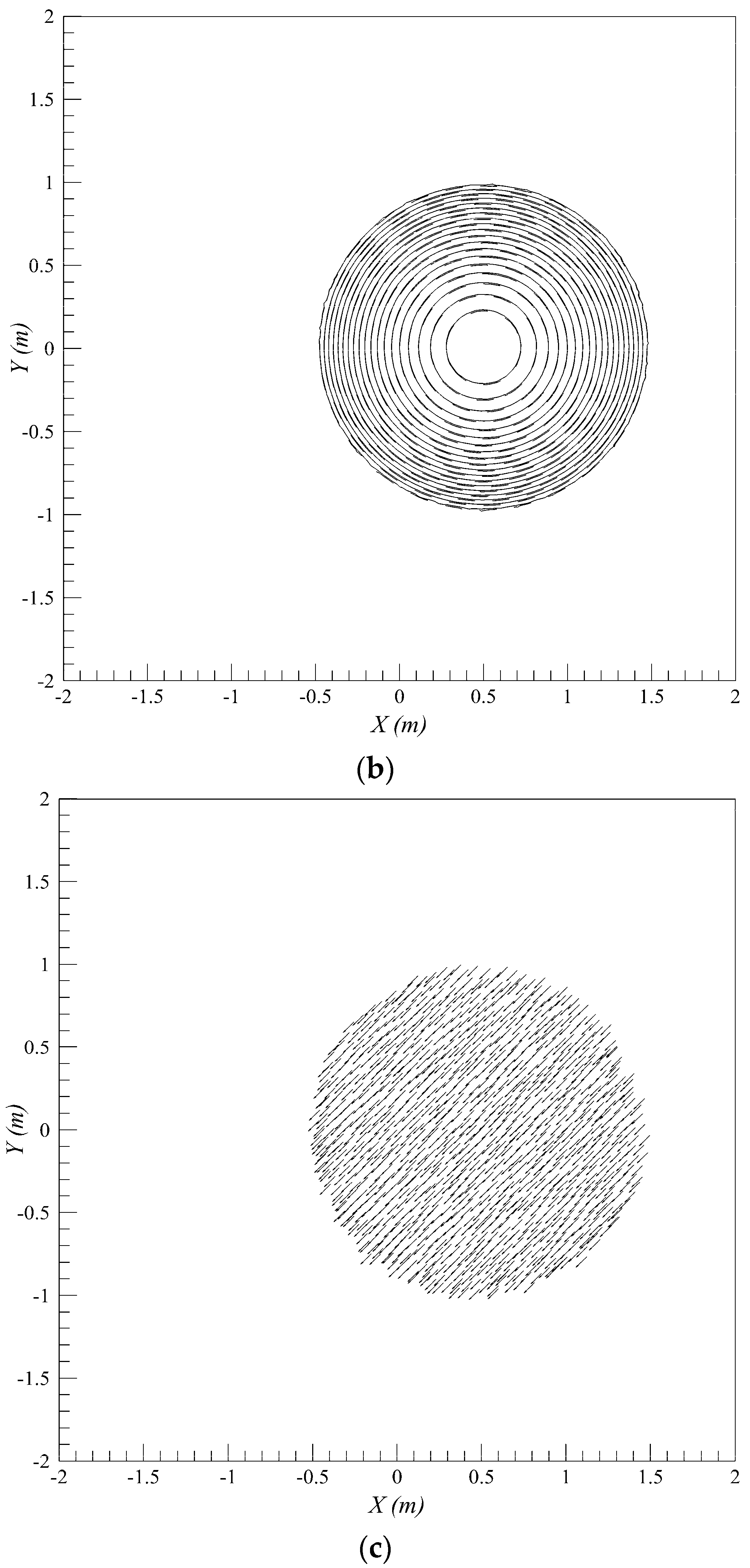
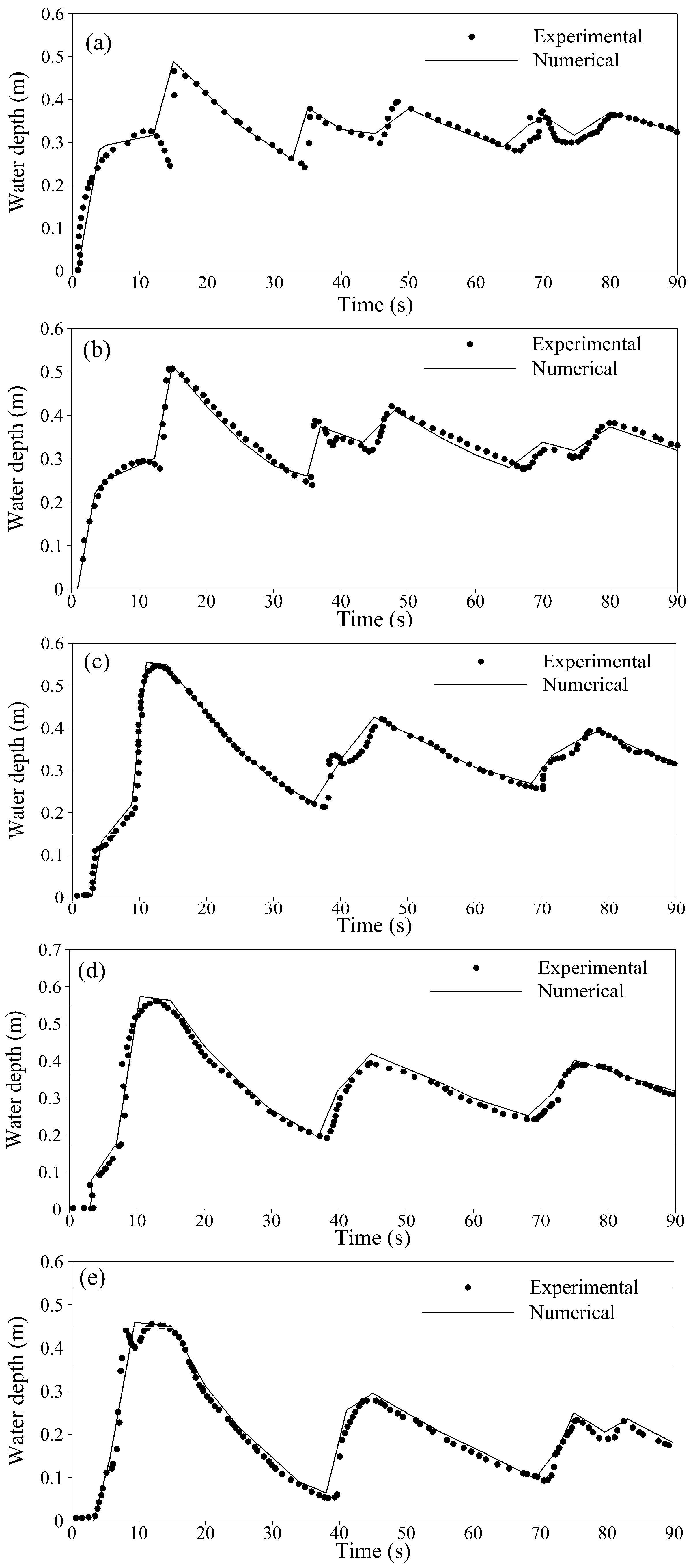
3.1. Solitary Wave Interaction with Conical Island
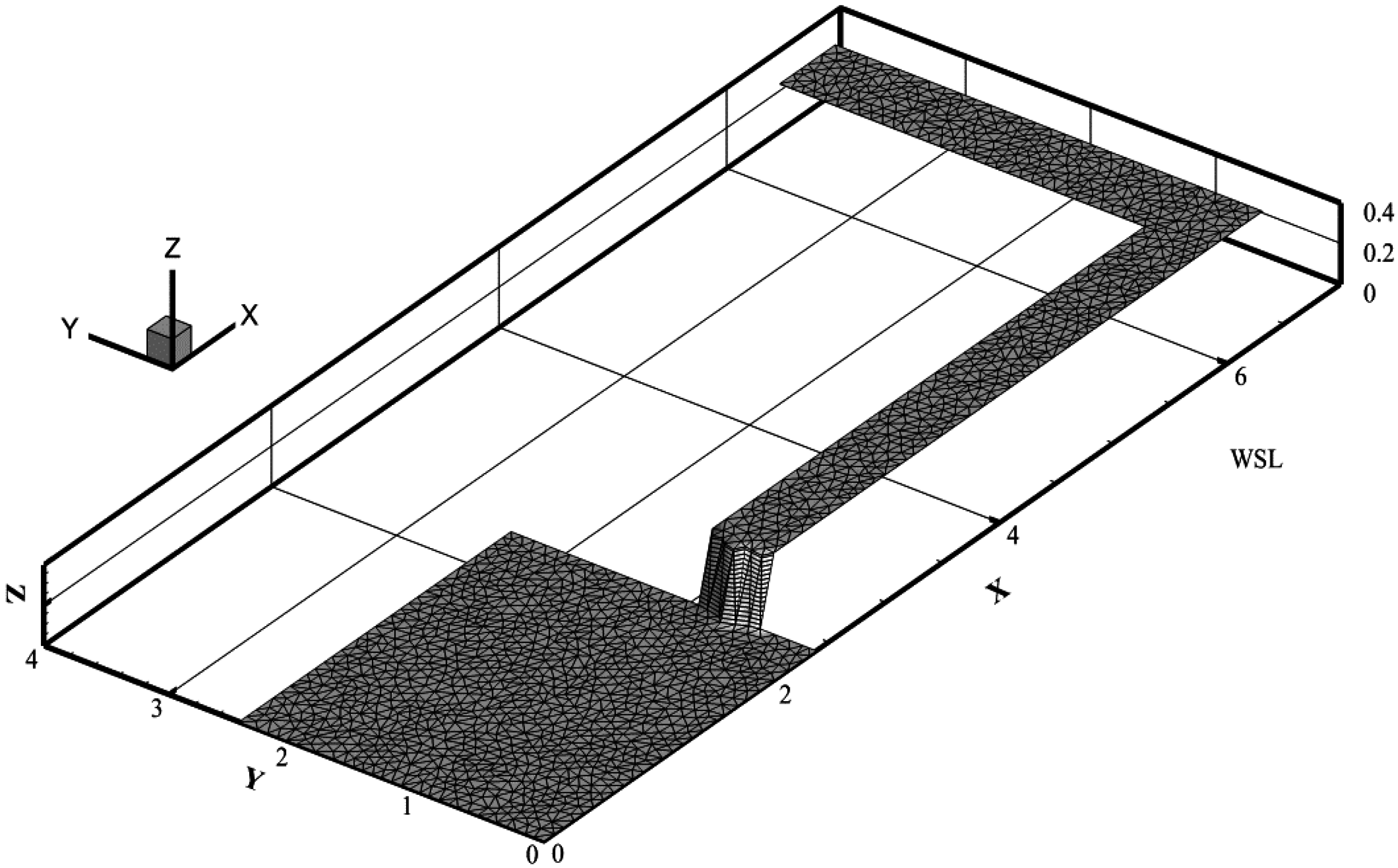
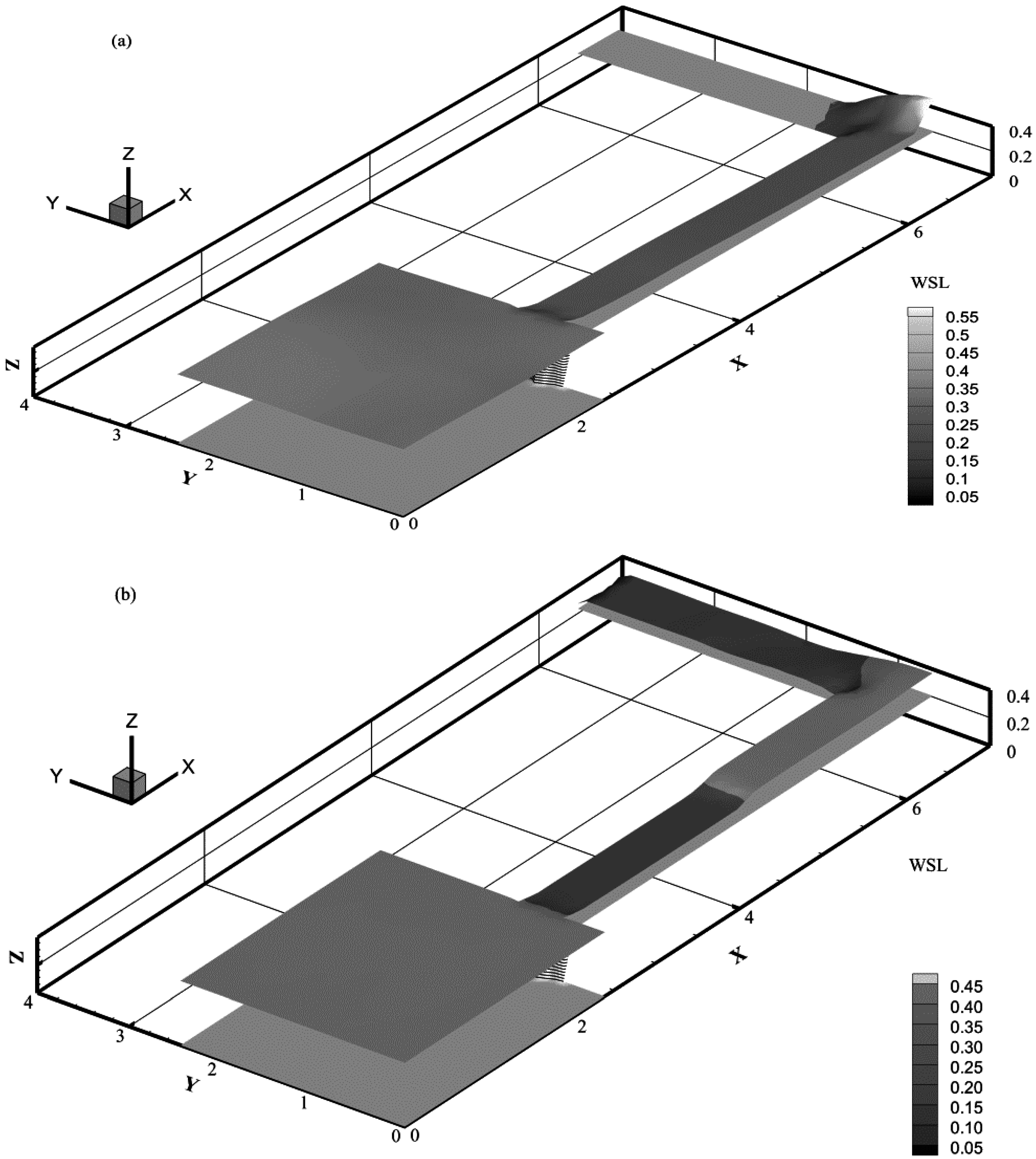
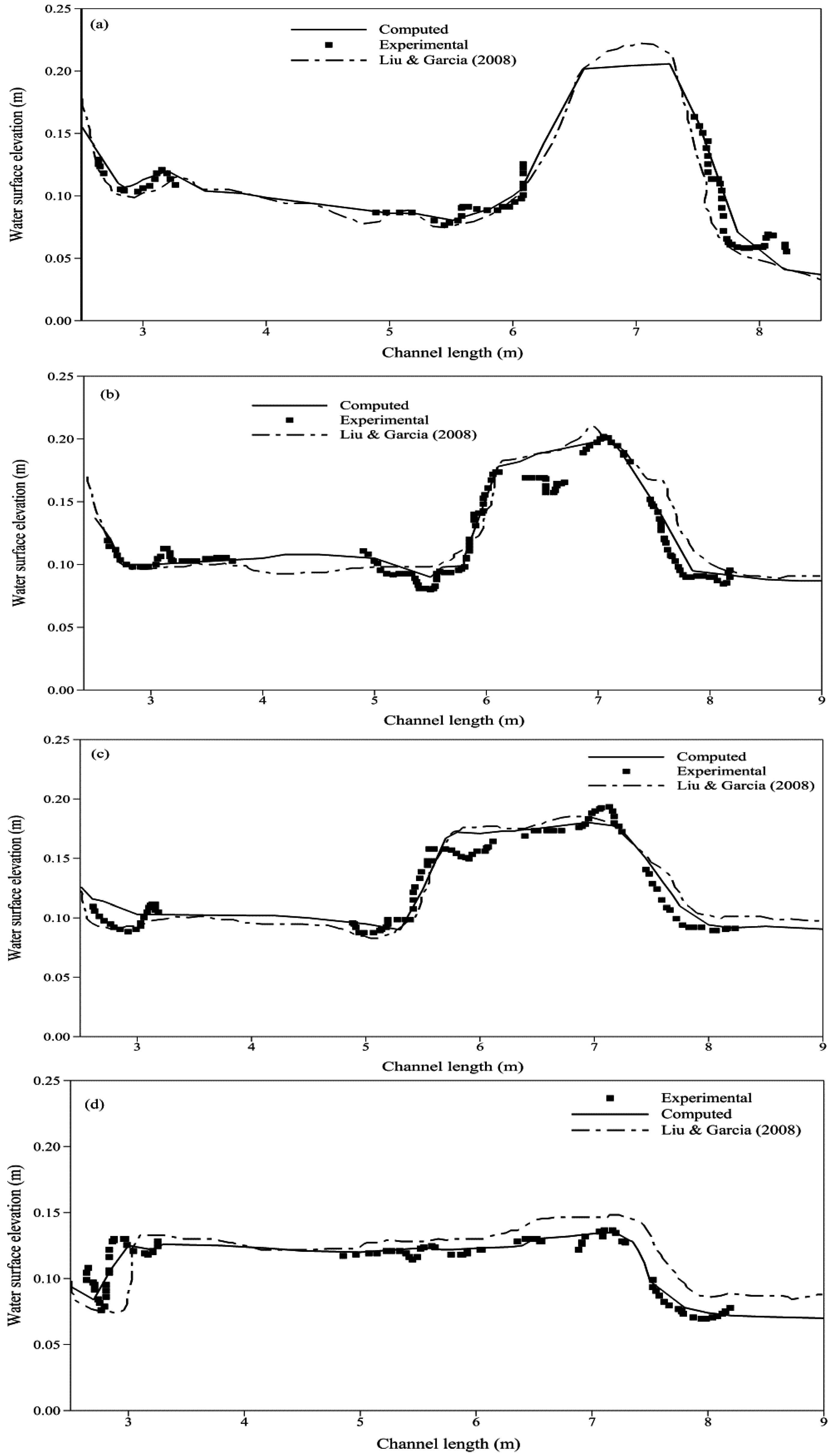
3.2. Dam-Break Flow in an L-Shaped Channel
3.3. Flow over a Hump
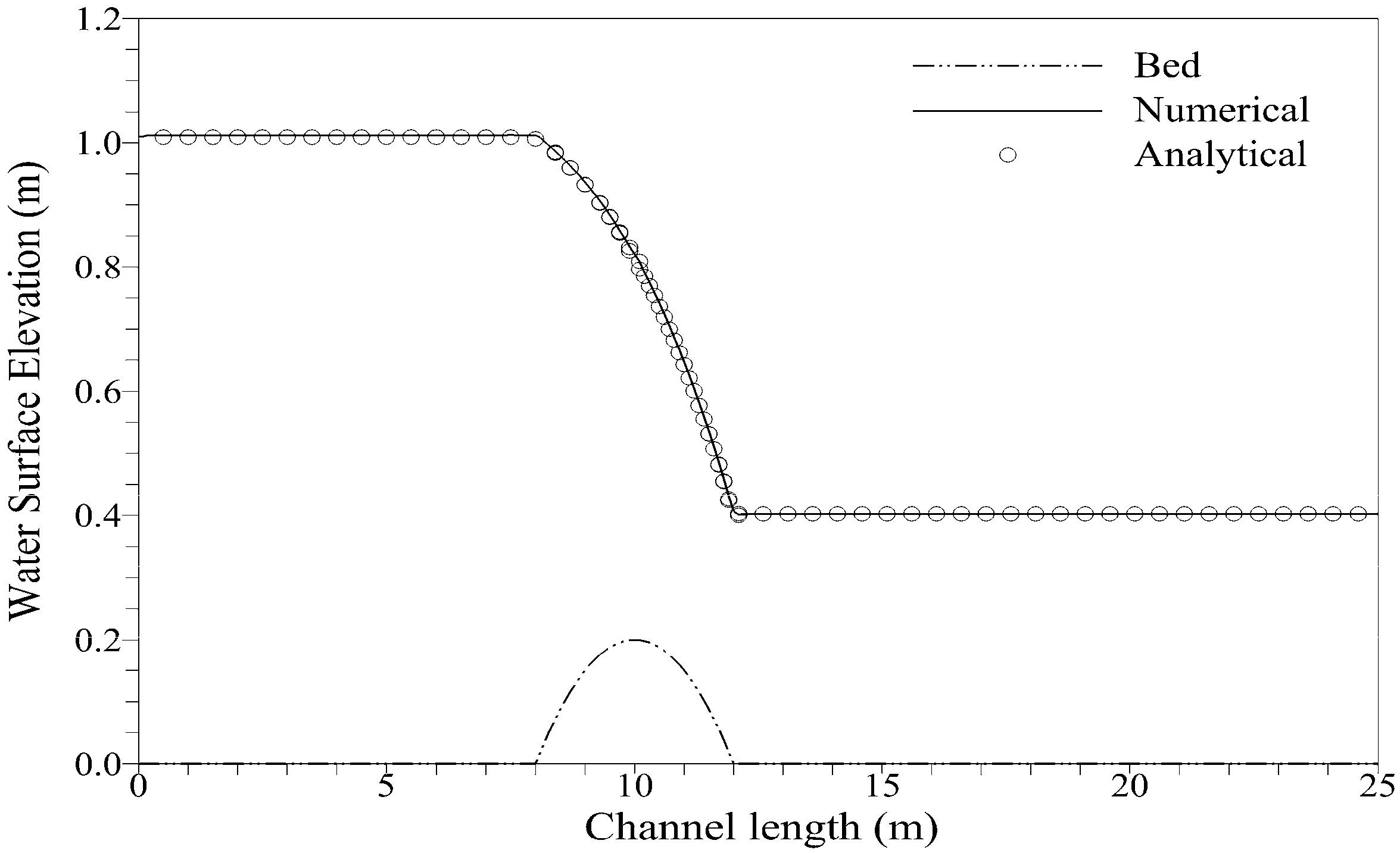
3.3.1. Transcritical Flow with a Shock
3.3.2. Transcritical Flow without a Shock
3.3.3. Subcritical Flow
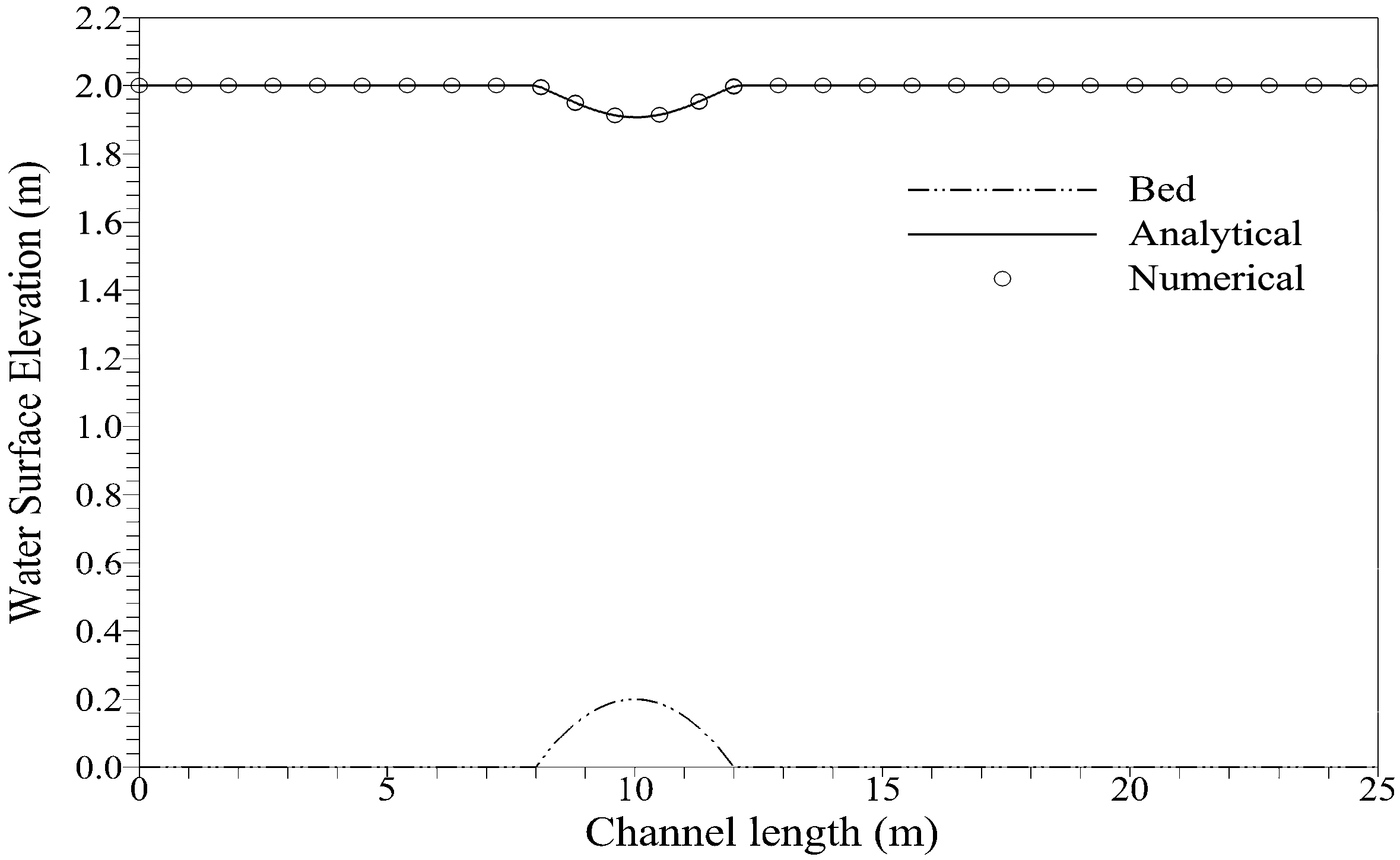
3.4. Thacker’s Planar Solution
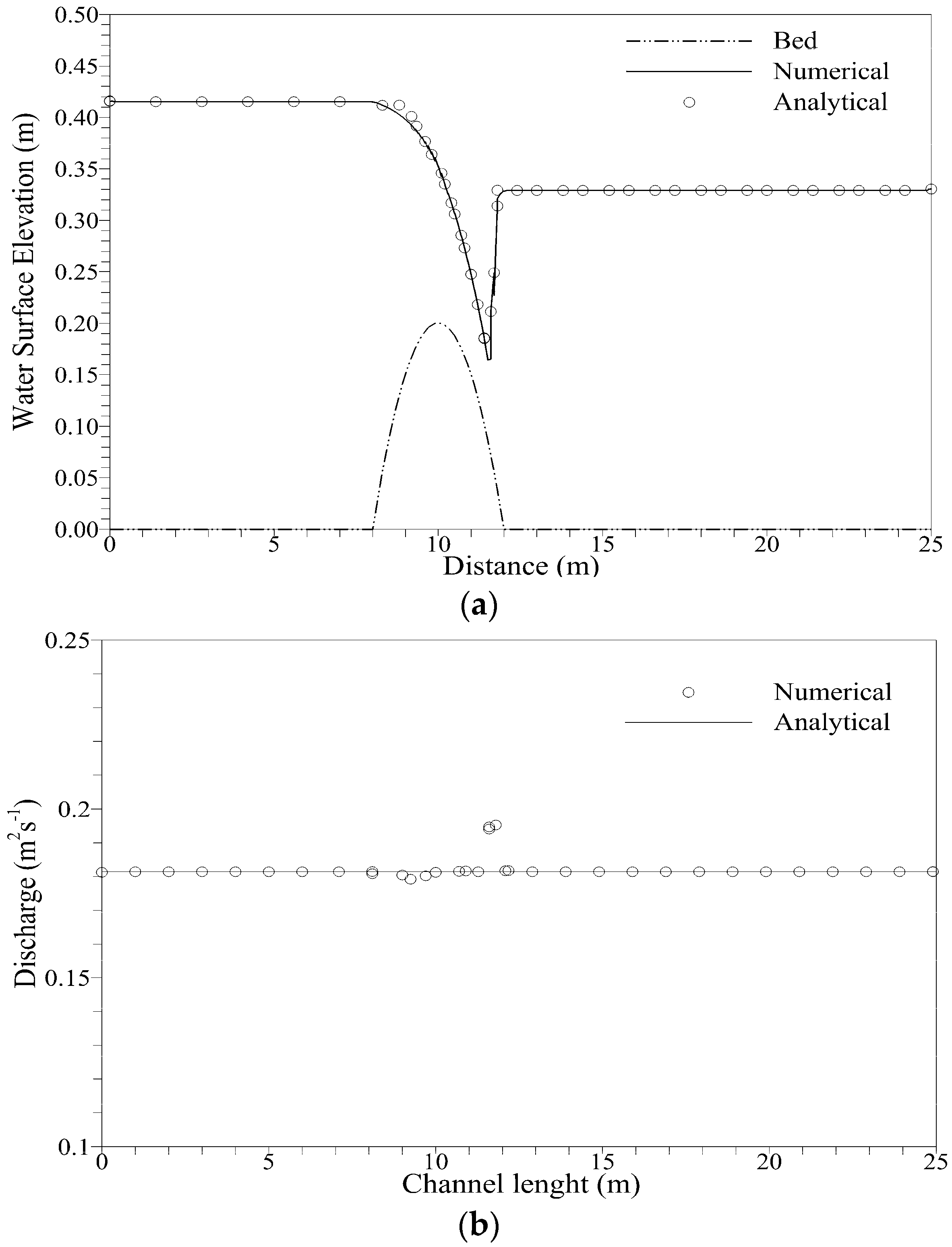
3.5. Dam-Break over a Triangular Obstacle
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Liang, Q.; Marche, F. Numerical resolution of well-balanced shallow water equations with complex source terms. Adv. Water Resour. 2009, 32, 873–884. [Google Scholar] [CrossRef]
- Audusse, E.; Bristeau, M.-O. A well-balanced positivity preserving “second-order” scheme for shallow water flows on unstructured meshes. J. Comput. Phys. 2005, 206, 311–333. [Google Scholar] [CrossRef]
- Mohammadian, A.; Le Roux, D.Y. Simulation of shallow flows over variable topographies using unstructured grids. Int. J. Numer. Methods Fluids 2006, 52, 473–498. [Google Scholar] [CrossRef]
- Hubbard, M.E.; Dodd, N. A 2D numerical model of wave run-up and overtopping. Coast. Eng. 2002, 47, 1–26. [Google Scholar] [CrossRef]
- Rehman, K.; Cho, Y.-S. Bed evolution under rapidly varying flows by a new method for wave speed estimation. Water 2016, 8, 212. [Google Scholar] [CrossRef]
- Hou, J.; Simons, F.; Liang, Q.; Hinkelmann, R. An improved hydrostatic reconstruction method for shallow water model. J. Hydraul. Res. 2014, 52, 432–439. [Google Scholar] [CrossRef]
- Kim, D.-H.; Cho, Y.-S.; Kim, H.-J. Well-balanced scheme between flux and source terms for computation of shallow-water equations over irregular bathymetry. J. Eng. Mech. 2008, 134, 277–290. [Google Scholar] [CrossRef]
- Hou, J.; Liang, Q.; Zhang, H.; Hinkelmann, R. An efficient unstructured MUSCL scheme for solving the 2D shallow water equations. Environ. Model. Softw. 2015, 66, 131–152. [Google Scholar] [CrossRef]
- Duran, A.; Liang, Q.; Marche, F. On the well-balanced numerical discretization of shallow water equations on unstructured meshes. J. Comput. Phys. 2013, 235, 565–586. [Google Scholar] [CrossRef]
- Capdeville, G. A central WENO scheme for solving hyperbolic conservation laws on non-uniform meshes. J. Comput. Phys. 2008, 227, 2977–3014. [Google Scholar] [CrossRef]
- Xing, Y.; Shu, C.-W. High order finite difference WENO schemes with the exact conservation property for the shallow water equations. J. Comput. Phys. 2005, 208, 206–227. [Google Scholar] [CrossRef]
- Noelle, S.; Xing, Y.; Shu, C.-W. High-order well-balanced finite volume WENO schemes for shallow water equation with moving water. J. Comput. Phys. 2007, 226, 29–58. [Google Scholar] [CrossRef]
- Jawahar, P.; Kamath, H. A high-resolution procedure for Euler and Navier–Stokes Computations on unstructured grids. J. Comput. Phys. 2000, 164, 165–203. [Google Scholar] [CrossRef]
- Yoon, T.; Kang, S. Finite volume model for two-dimensional shallow water flows on unstructured grids. J. Hydraul. Eng. 2004, 130, 678–688. [Google Scholar] [CrossRef]
- Li, S.; Duffy, C.J. Fully coupled approach to modeling shallow water flow, sediment transport, and bed evolution in rivers. Water Resour. Res. 2011, 47, W03508. [Google Scholar] [CrossRef]
- Hou, J.; Simons, F.; Mahgoub, M.; Hinkelmann, R. A robust well-balanced model on unstructured grids for shallow water flows with wetting and drying over complex topography. Comput. Meth. Appl. Mech. Eng. 2013, 257, 126–149. [Google Scholar] [CrossRef]
- Bermudez, A.; Vazquez, M.E. Upwind methods for hyperbolic conservation laws with source terms. Comput. Fluids 1994, 23, 1049–1071. [Google Scholar] [CrossRef]
- Brufau, P.; Garcıa-Navarro, P. Unsteady free surface flow simulation over complex topography with a multidimensional upwind technique. J. Comput. Phys. 2003, 186, 503–526. [Google Scholar] [CrossRef]
- Bladé, E.; Valentín, M.G.; Sánchez-Juny, M.; Dolz, J. Source term treatment of SWEs using the surface gradient upwind method. J. Hydraul. Res. 2012, 50, 447–448. [Google Scholar] [CrossRef]
- Zhou, J.G.; Causon, D.M.; Mingham, C.G.; Ingram, D.M. The surface gradient method for the treatment of source terms in the shallow-water equations. J. Comput. Phys. 2001, 168, 1–25. [Google Scholar] [CrossRef]
- Kim, H.-J.; Cho, Y.-S. Numerical model for flood routing with a Cartesian cut-cell domain. J. Hydraul. Res. 2011, 49, 205–212. [Google Scholar] [CrossRef]
- Audusse, E.; Bouchut, F.; Bristeau, M.-O.; Klein, R.; Perthame, B. A fast and stable well-balanced scheme with hydrostatic reconstruction for shallow water flows. SIAM J. Sci. Comput. 2004, 25, 2050–2065. [Google Scholar] [CrossRef]
- Kesserwani, G.; Liang, Q. Well-balanced RKDG2 solutions to the shallow water equations over irregular domains with wetting and drying. Comput. Fluids 2010, 39, 2040–2050. [Google Scholar] [CrossRef]
- Marche, F. A simple well-balanced model for two-dimensional coastal engineering applications. In Hyperbolic Problems: Theory, Numerics, Applications; Benzoni-Gavage, S., Serre, D., Eds.; Springer: Berlin, Germany, 2008; pp. 271–283. [Google Scholar]
- Xing, Y. Exactly well-balanced discontinuous Galerkin methods for the shallow water equations with moving water equilibrium. J. Comput. Phys. 2014, 257, 536–553. [Google Scholar] [CrossRef]
- Hou, J.; Liang, Q.; Simons, F.; Hinkelmann, R. A 2D well-balanced shallow flow model for unstructured grids with novel slope source term treatment. Adv. Water Resour. 2013, 52, 107–131. [Google Scholar] [CrossRef]
- Murillo, J.; García-Navarro, P.; Burguete, J.; Brufau, P. The influence of source terms on stability, accuracy and conservation in two-dimensional shallow flow simulation using triangular finite volumes. Int. J. Numer. Methods Fluids 2007, 54, 543–590. [Google Scholar] [CrossRef]
- Begnudelli, L.; Sanders, B.F. Unstructured grid finite-volume algorithm for shallow-water flow and scalar transport with wetting and drying. J. Hydraul. Eng. 2006, 132, 371–384. [Google Scholar] [CrossRef]
- Toro, E.F. Riemann Solvers and Numerical Methods for Fluid Dynamics: A Practical Introduction; Springer Science & Business Media: Berlin, Germany, 2009. [Google Scholar]
- Holmes, D.; Connell, S. Solution of the 2D Navier-Stokes equations on unstructured adaptive grids. In Proceedings of the 9th Computational Fluid Dynamics Conference, Buffalo, NY, USA, 13–15 June 1989; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1989. [Google Scholar]
- Cho, Y.-S. Numerical Simulations of Tsunami Propagation and Run-up. Ph.D. Thesis, Cornell University, Ithaca, NY, USA, Janunary 1995. [Google Scholar]
- Wei, Y.; Mao, X.-Z.; Cheung, K.F. Well-balanced finite-volume model for long-wave runup. J. Waterw. Port Coast. Ocean Eng. 2006, 132, 114–124. [Google Scholar] [CrossRef]
- Briggs, M.J.; Synolakis, C.E.; Harkins, G.S.; Green, D.R. Laboratory experiments of tsunami runup on a circular island. In Tsunamis: 1992–1994; Imamura, F., Satake, K., Eds.; Birkhäuser Basel: Basel, Switzerland, 1995; pp. 569–593. [Google Scholar]
- Choi, B.H.; Kim, D.C.; Pelinovsky, E.; Woo, S.B. Three-dimensional simulation of tsunami run-up around conical island. Coast. Eng. 2007, 54, 618–629. [Google Scholar] [CrossRef]
- Lynett, P.J.; Wu, T.-R.; Liu, P.L.-F. Modeling wave runup with depth-integrated equations. Coast. Eng. 2002, 46, 89–107. [Google Scholar] [CrossRef]
- Frazão, S.S.; Zech, Y. Dam break in channels with 90 bend. J. Hydraul. Eng. 2002, 128, 956–968. [Google Scholar] [CrossRef]
- Liu, X.; Landry, B.; García, M. Two-dimensional scour simulations based on coupled model of shallow water equations and sediment transport on unstructured meshes. Coast. Eng. 2008, 55, 800–810. [Google Scholar] [CrossRef]
- Kuiry, S.N.; Pramanik, K.; Sen, D. Finite volume model for shallow water equations with improved treatment of source terms. J. Hydraul. Eng. 2008, 134, 231–242. [Google Scholar] [CrossRef]
- Thacker, W.C. Some exact solutions to the nonlinear shallow-water wave equations. J. Fluid Mech. 1981, 107, 499–508. [Google Scholar] [CrossRef]


| Flow Type | h | |
|---|---|---|
| Transcritical flow with a shock | ||
| Transcritical flow without a shock | ||
| Subcritical flow |
| Line Segments in x- and y-Directions | Total Number Grid Points | Characteristic Length for Each Grid | Norm | Norm | ||
|---|---|---|---|---|---|---|
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rehman, K.; Cho, Y.-S. Novel Slope Source Term Treatment for Preservation of Quiescent Steady States in Shallow Water Flows. Water 2016, 8, 488. https://doi.org/10.3390/w8110488
Rehman K, Cho Y-S. Novel Slope Source Term Treatment for Preservation of Quiescent Steady States in Shallow Water Flows. Water. 2016; 8(11):488. https://doi.org/10.3390/w8110488
Chicago/Turabian StyleRehman, Khawar, and Yong-Sik Cho. 2016. "Novel Slope Source Term Treatment for Preservation of Quiescent Steady States in Shallow Water Flows" Water 8, no. 11: 488. https://doi.org/10.3390/w8110488
APA StyleRehman, K., & Cho, Y.-S. (2016). Novel Slope Source Term Treatment for Preservation of Quiescent Steady States in Shallow Water Flows. Water, 8(11), 488. https://doi.org/10.3390/w8110488






