Case Study: A Real-Time Flood Forecasting System with Predictive Uncertainty Estimation for the Godavari River, India
Abstract
:1. Introduction
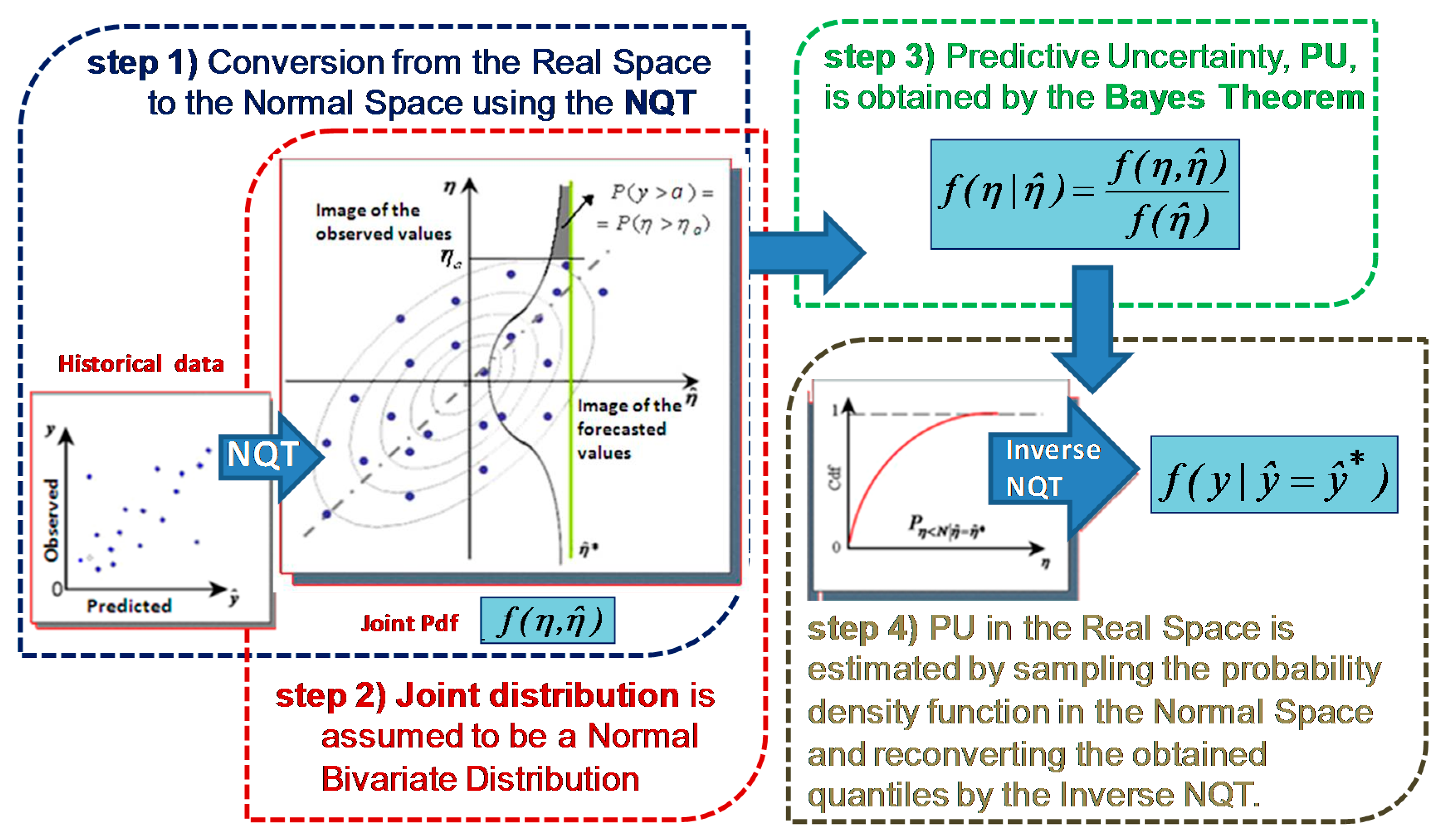
2. Predictive Uncertainty Assessment: The Model Conditional Processor in the Multi-Temporal Approach
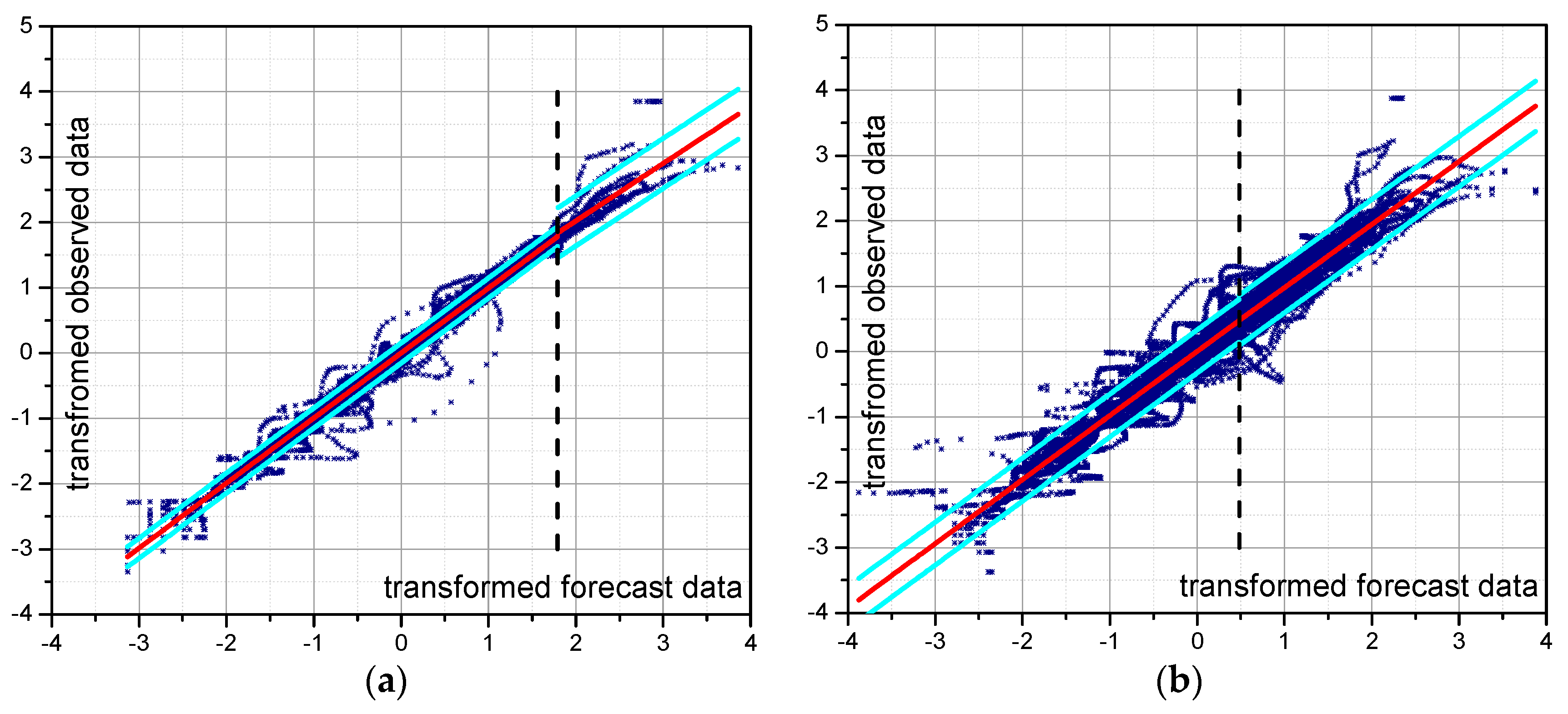
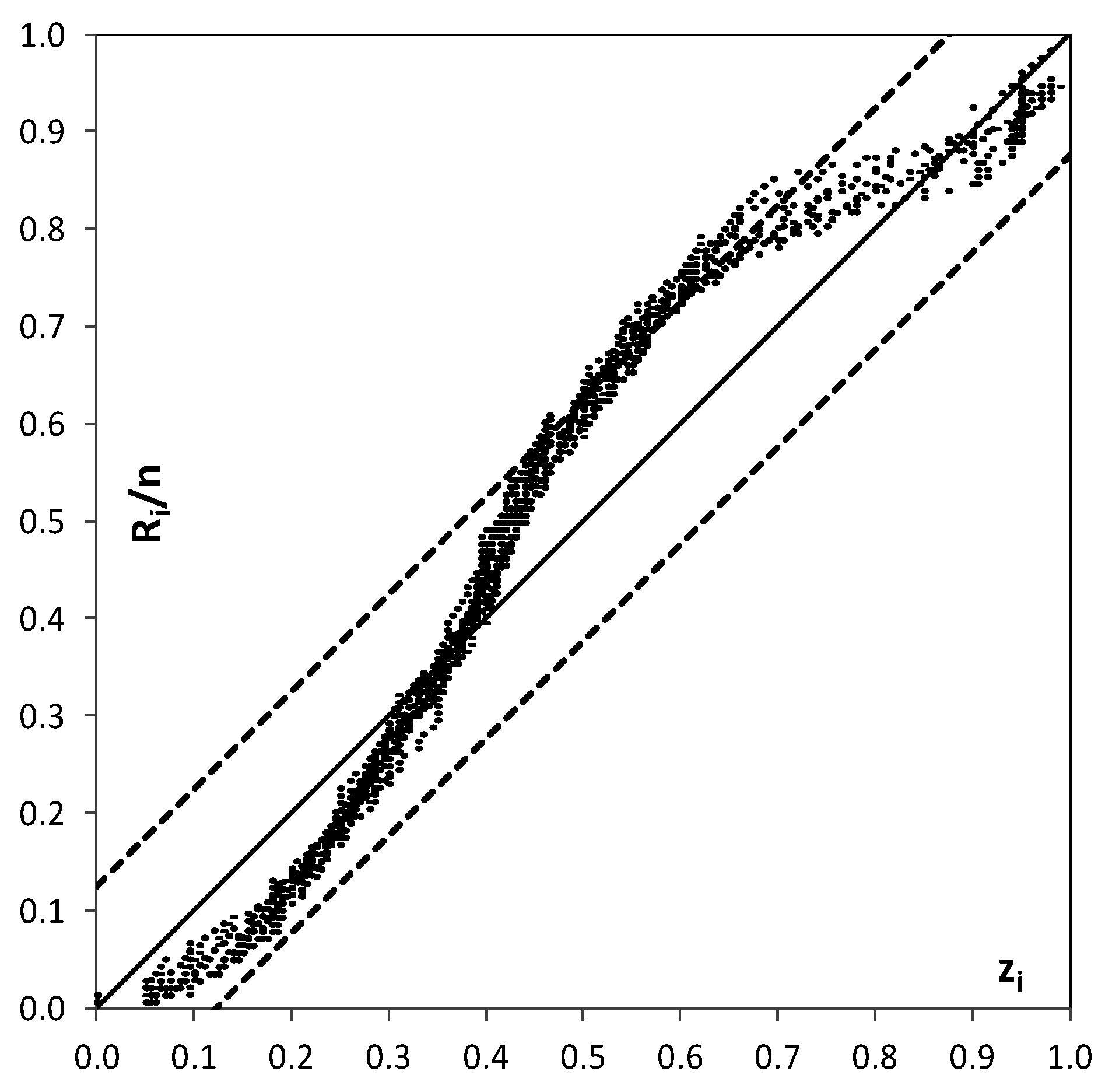
- First, the observations, , and the forecasts, (k = 1, …, M, M = number of available forecasts provided by M different forecasting models), are converted into the normal space using the NQT (Figure 1, blue box on the left side). The original variables, and , whose empirical cumulative distribution functions are computed using the Weibull plotting position (see Equations (1) and (2)), are converted to their transformed values and , respectively, which are normally distributed with zero mean and unit variance. According to the NQT definition, the probability of each element of and is the same as its original corresponding value in and . Thus, the relation between the original variables and their transformed values is:with i = 1, …, n, n is the number of the historical available data, and i is the plotting position order.
- In the normal space, the joint probability distribution of observed and predicted variables, , is assumed to be a Normal Multivariate Distribution in the first formulation [19] (Figure 1, red box on the left side) or composed by two Truncated Normal Multivariate Distributions as proposed by Coccia and Todini [16].
- The predictive density is obtained applying the Bayes Theorem (Figure 1, green box on the right side):It is normally distributed with mean, , and variance, , defined as:
- The PU in the normal space is finally reconverted to the real space by applying the Inverse NQT (Figure 1, grey box on the right side).
3. Forecasting Model: STAFOM-RCM
- STAFOM provides a first estimate of the forecast stage (preliminary forecast) at the downstream end, , computed as:where is the stage observed at the downstream end at , is the forecast lead-time (typically assumed equal to the mean observed wave travel time, TL, of the reach), is the observed upstream discharge at , L is the river reach length, and and are parameters of the downstream rating curve (). and refer to the Muskingum parameters K and θ respecting the constraint :qfor is the lateral flow contribution for unit channel length estimated as [27]:where and are the upstream and downstream flow areas, respectively, computed by using the relationship between the stage and the flow area estimated from the knowledge of the section geometry; TL is the flood wave travel time assumed equal to the lead-time, , for forecasting purposes. The lateral flow is assumed uniformly distributed along the branch and, hence, the total lateral discharge entering in the reach in the time interval , , is equal to .
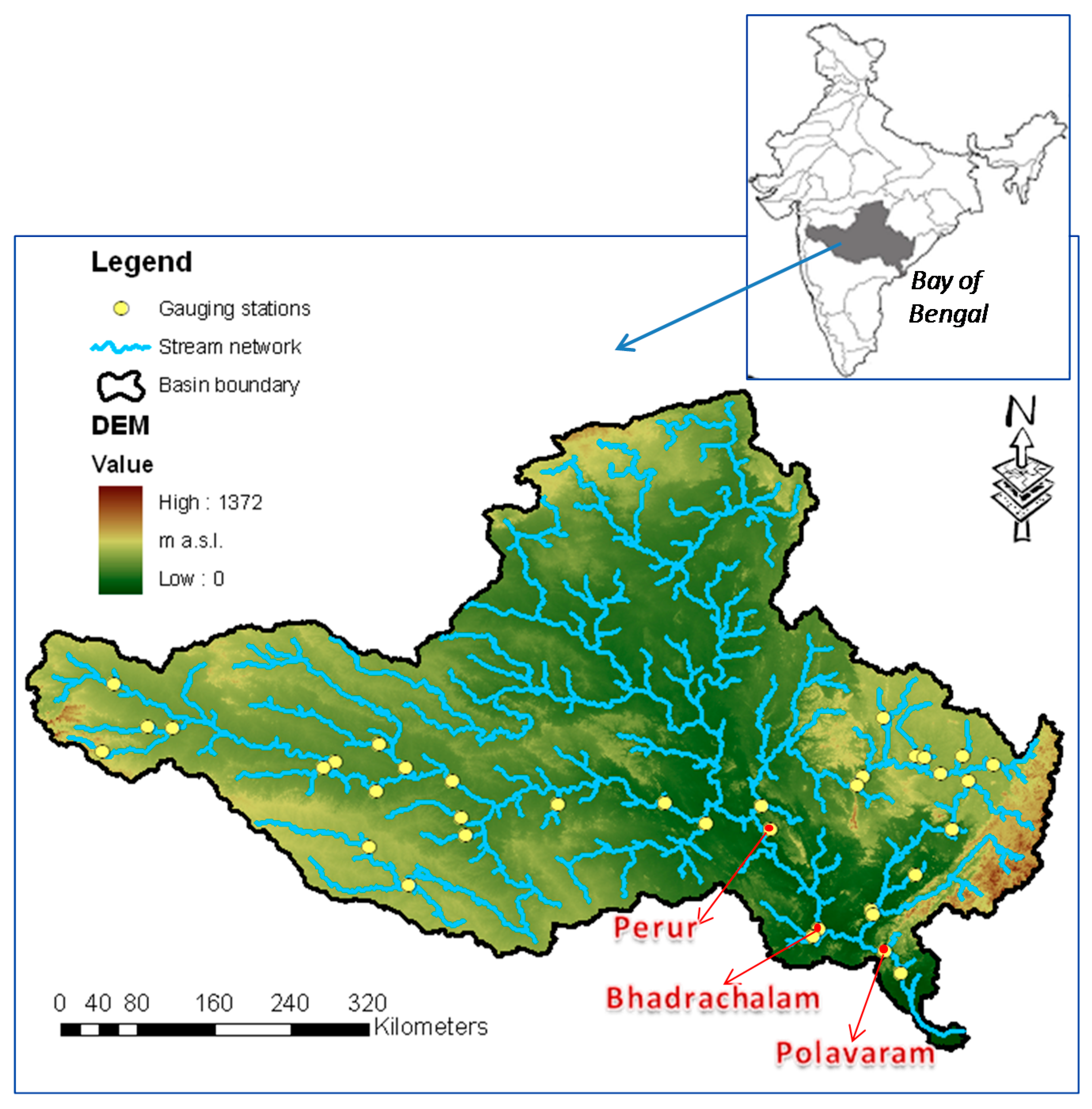
4. Study Area, Model Setting and Dataset
5. Results and Discussion
5.1. Performance Evaluation Measures
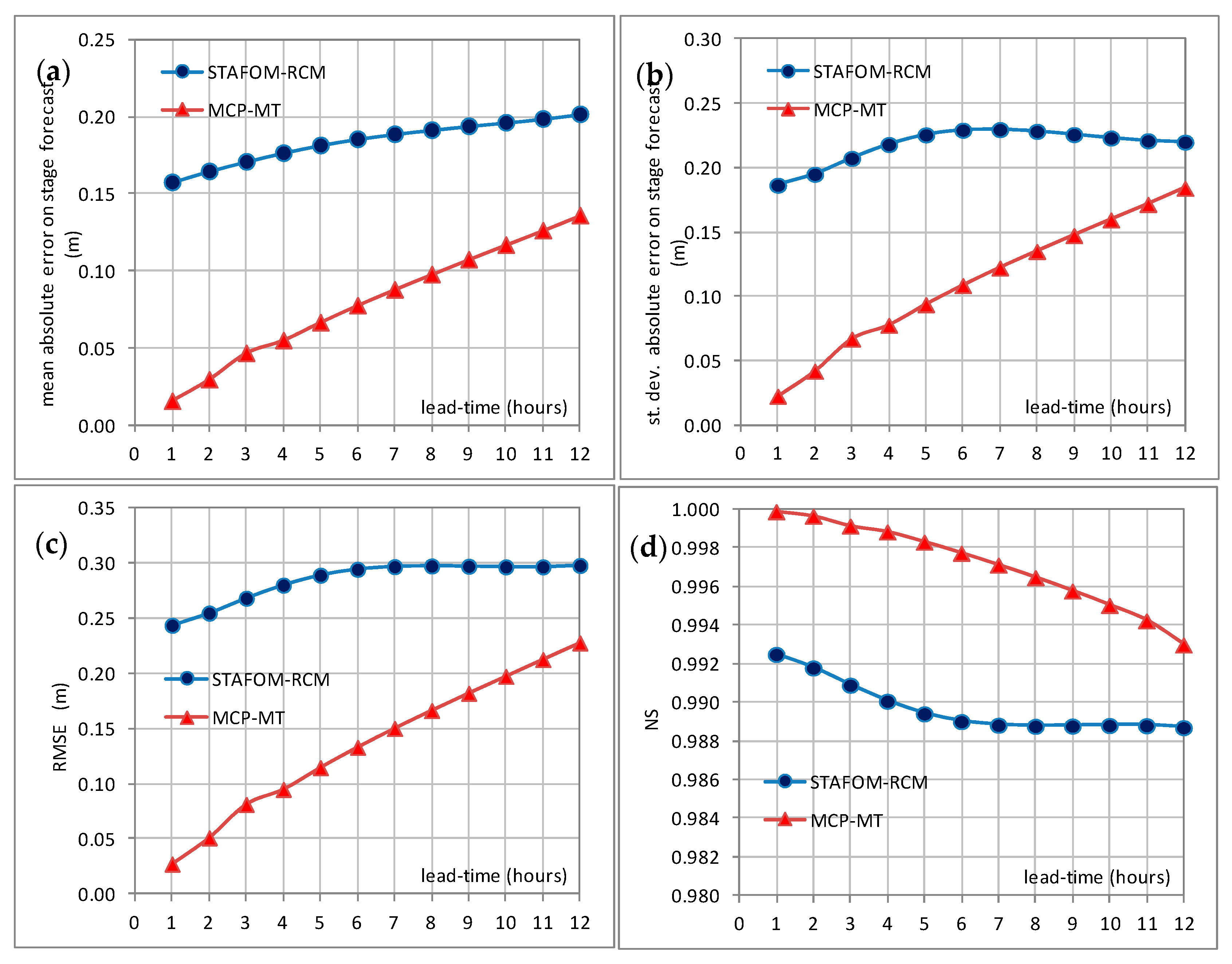
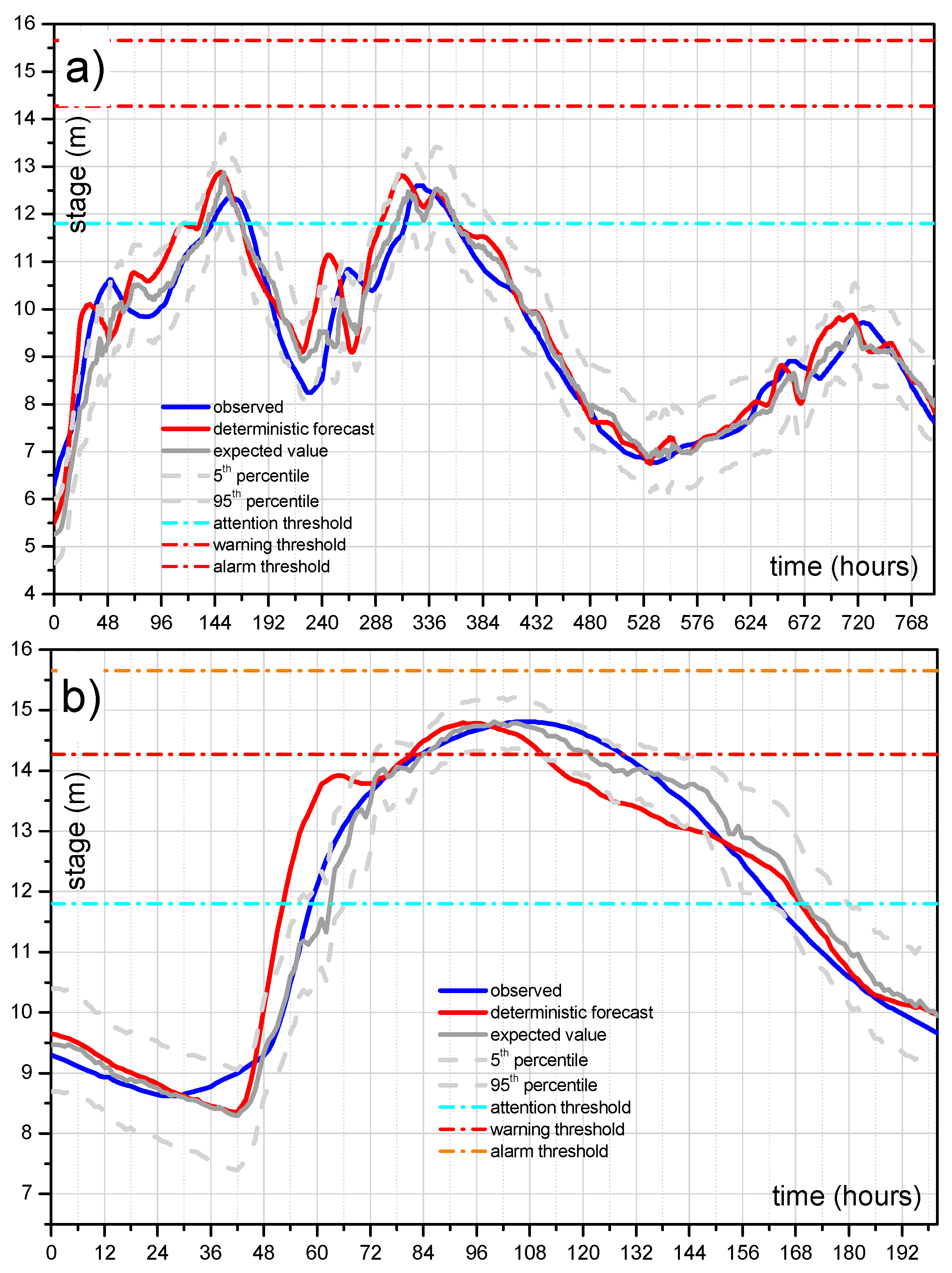
5.2. Forecasting Model
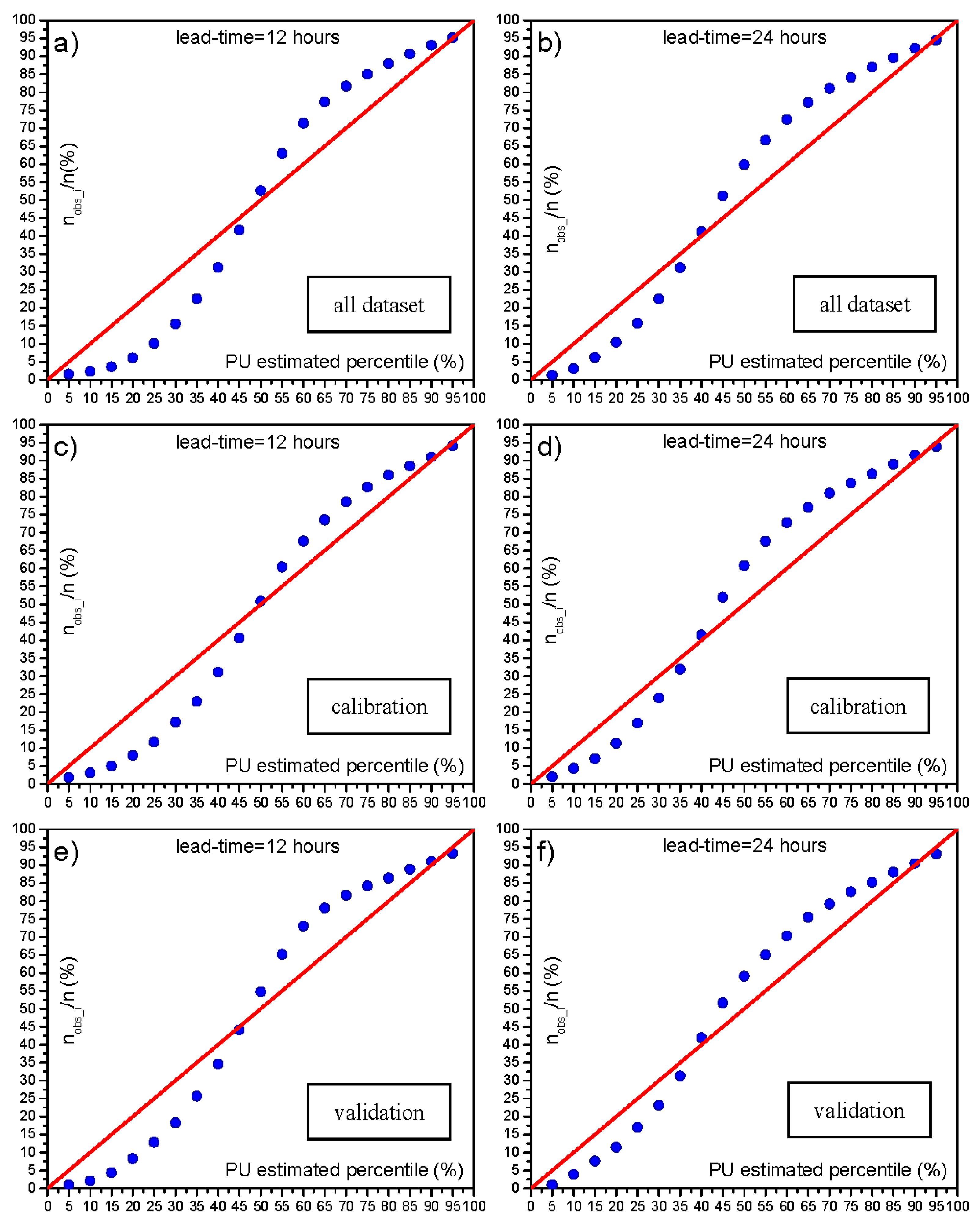
5.3. Predictive Uncertainty Estimate Using MCP-MT
5.3.1. Calibration and Validation
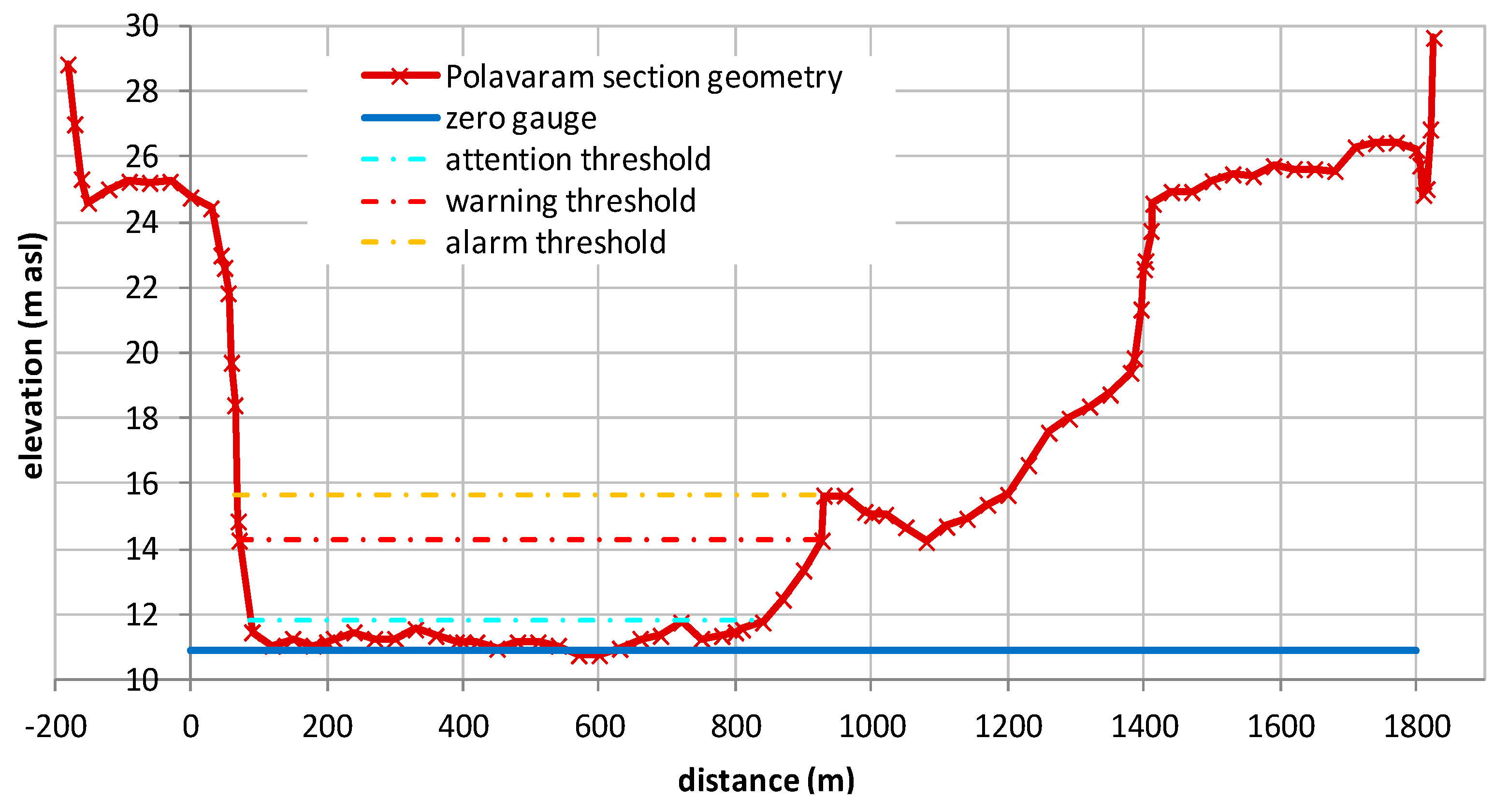
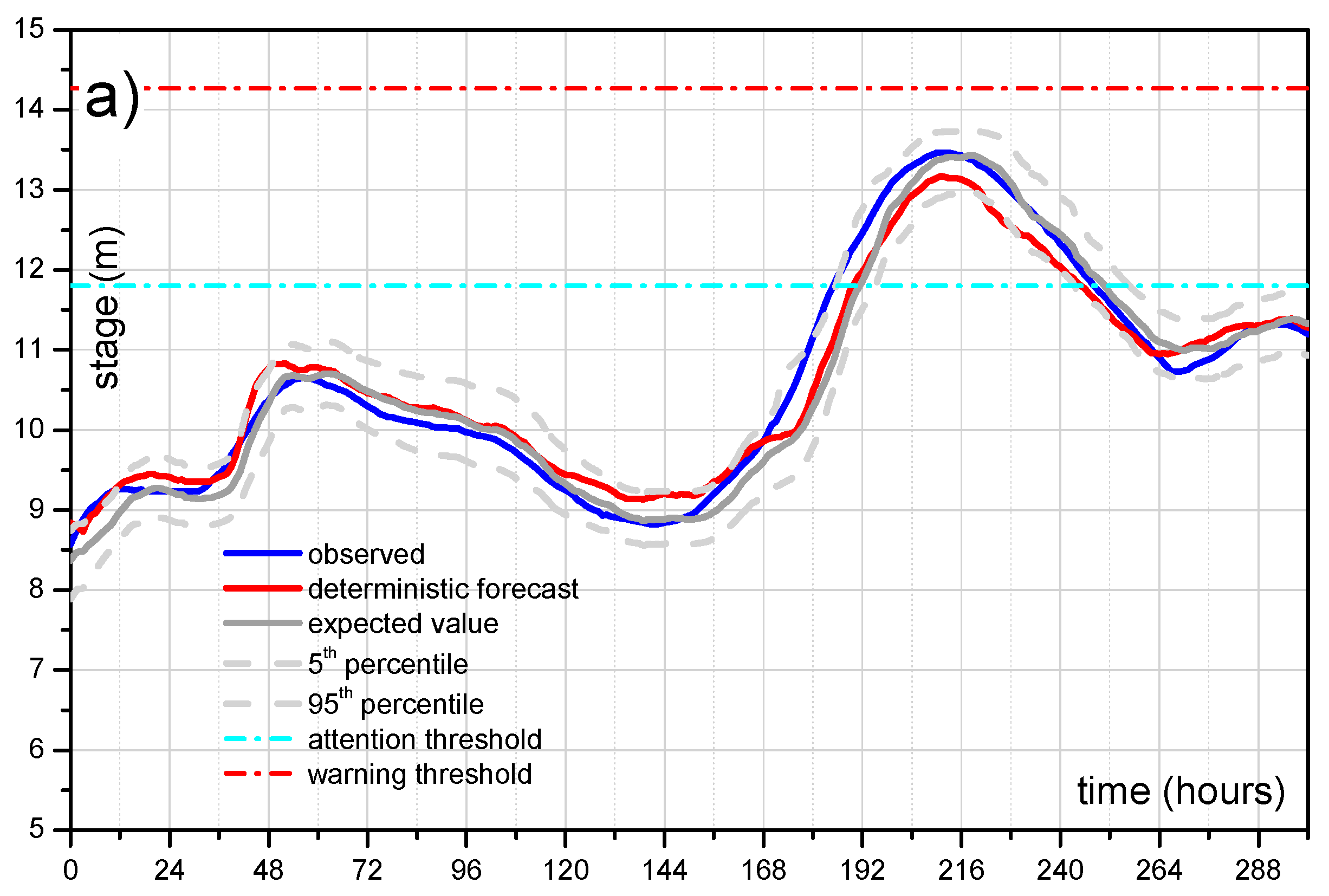
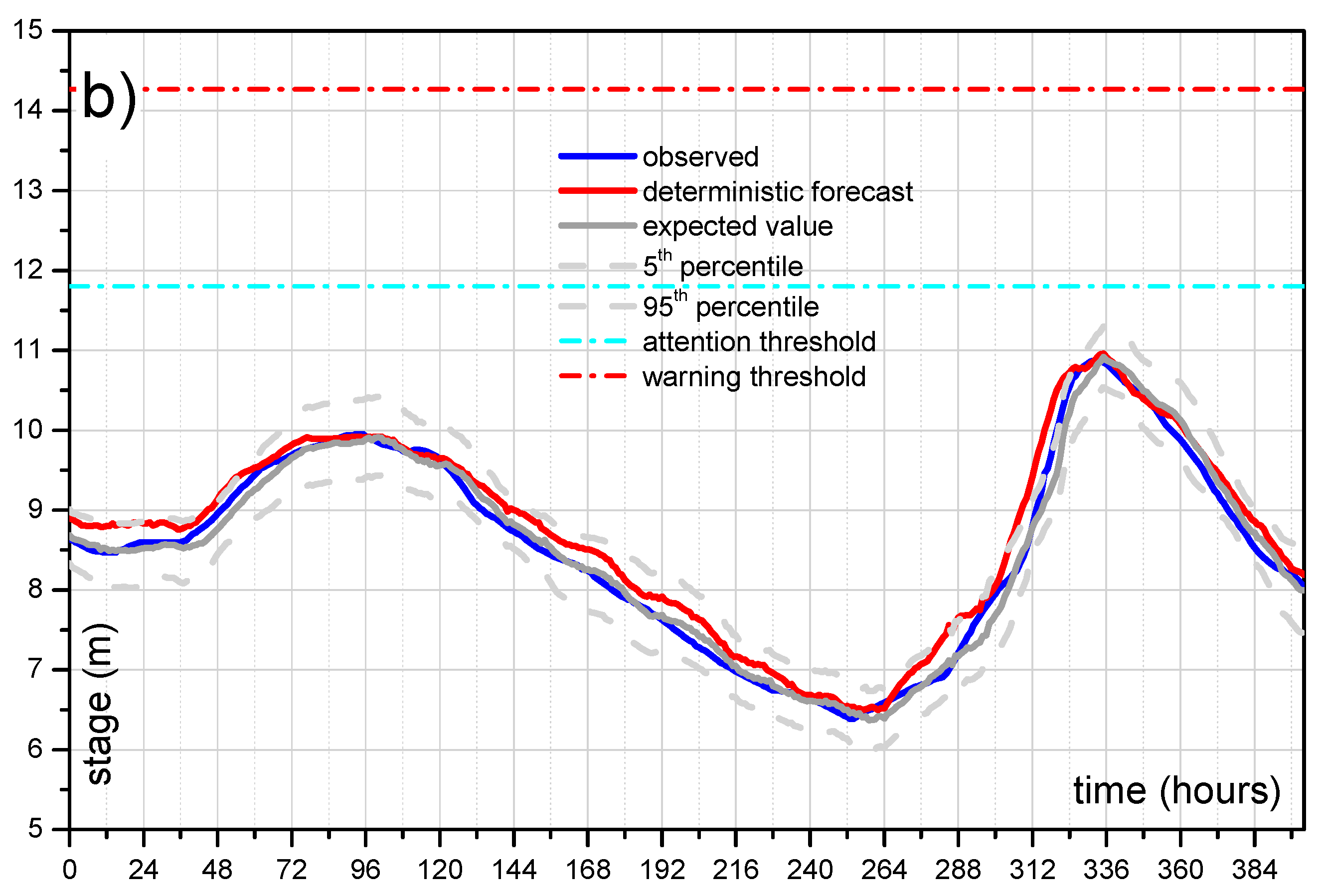
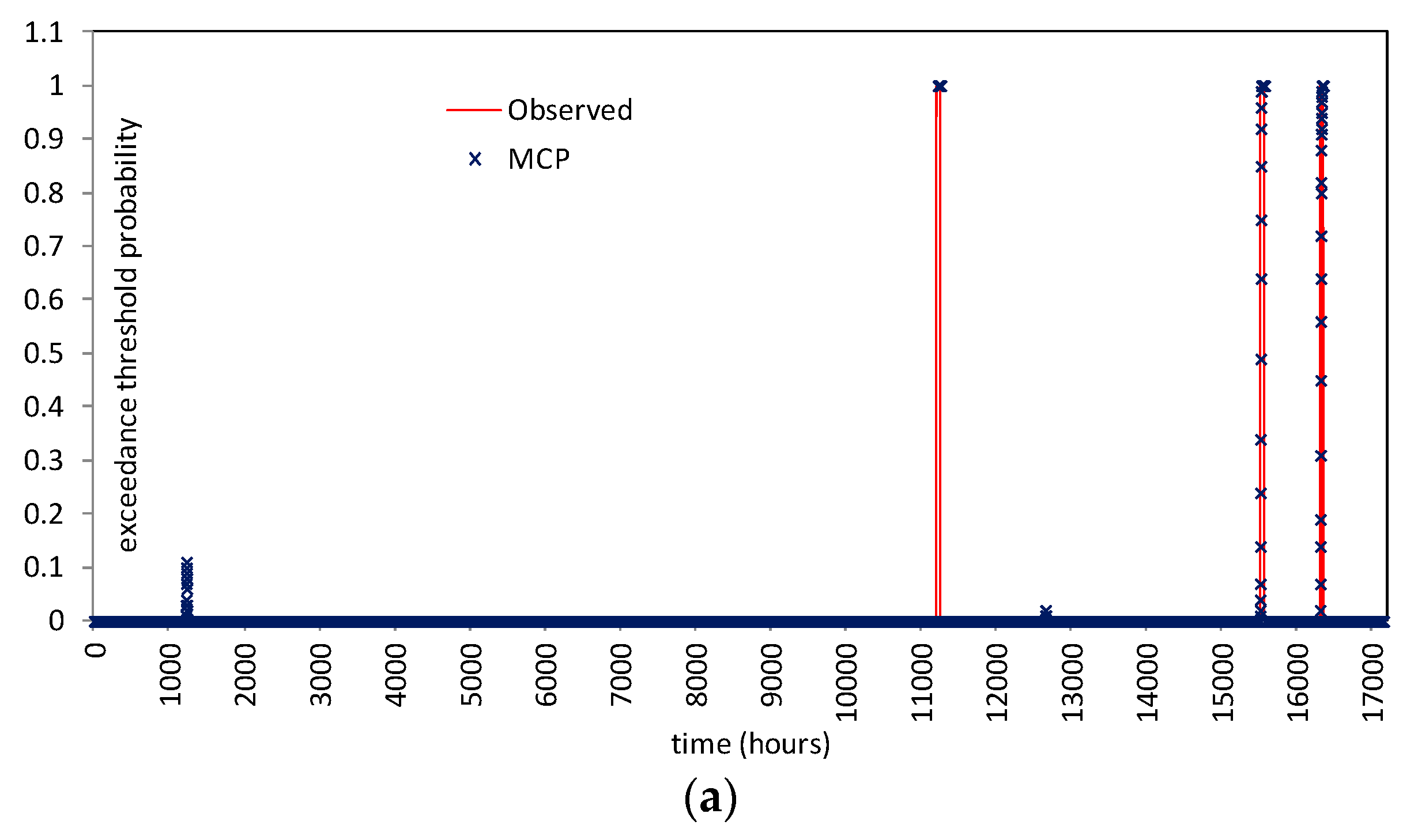
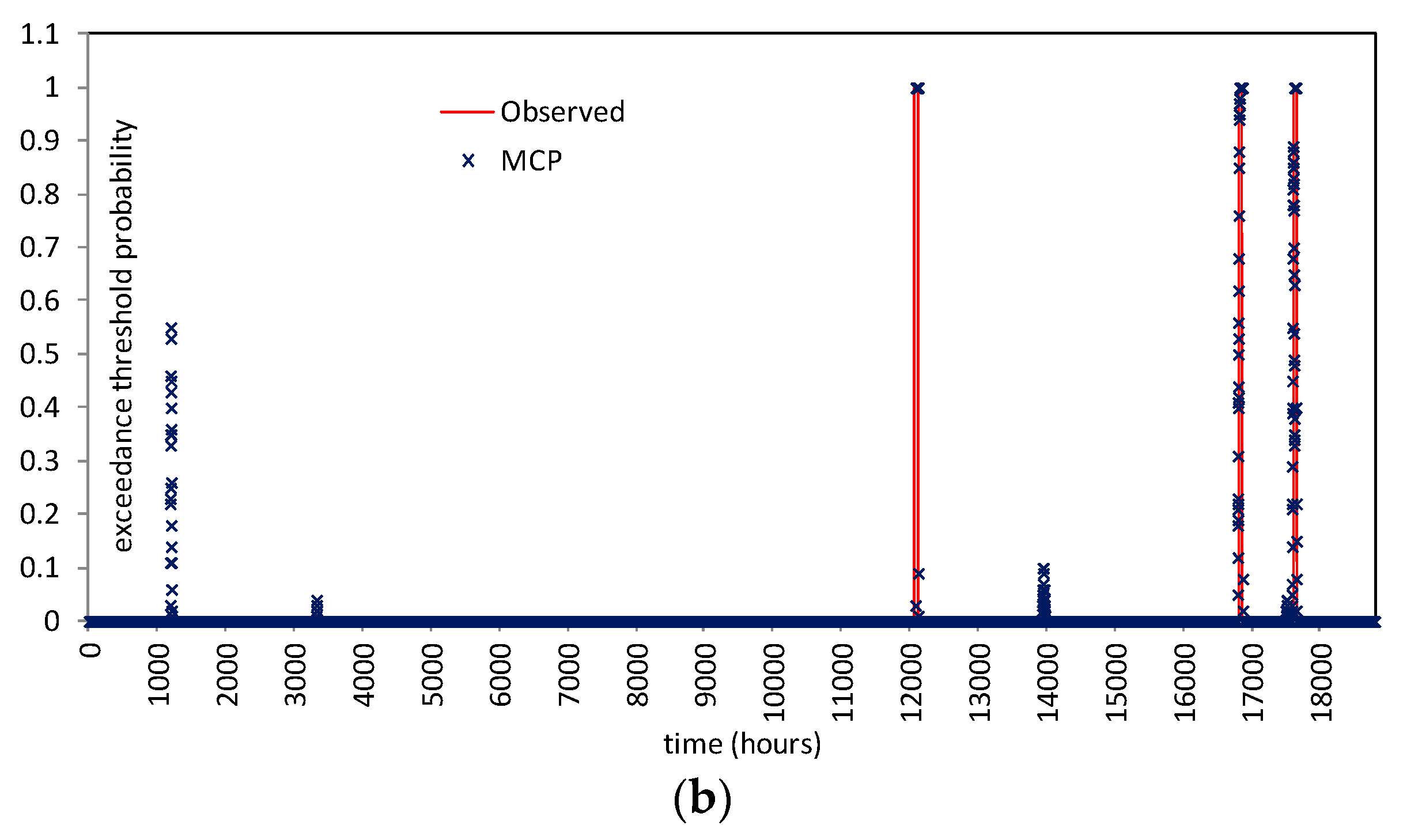
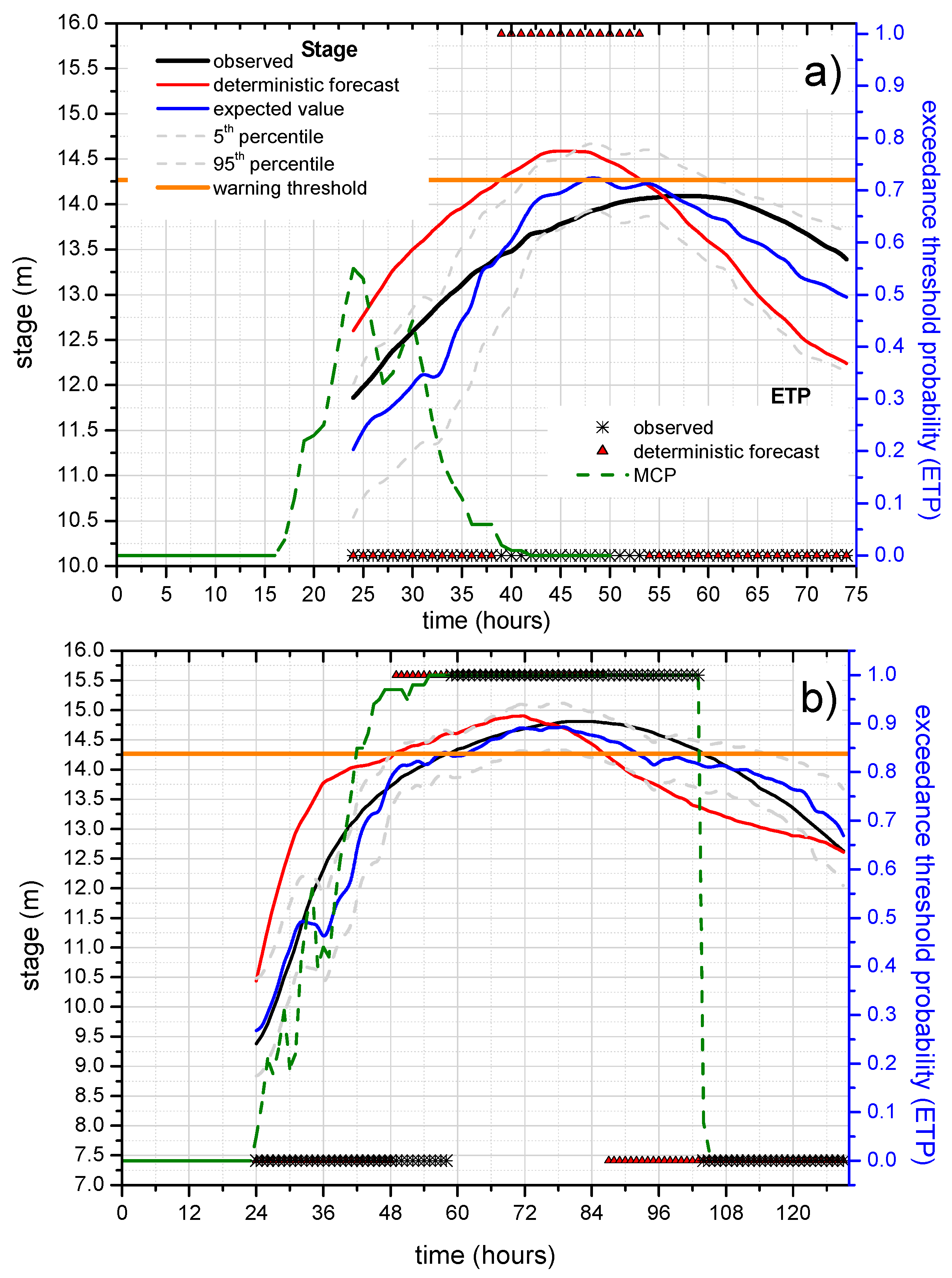
5.3.2. Probability of Hydrometric Thresholds Exceedance: Flooding Probability within a Time Horizon and Contingency Table
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Pappenberger, F.; Cloke, H.L.; Parker, D.J.; Wetterhall, F.; Richardson, D.S.; Thielen, J. The monetary benefit of early flood warnings in Europe. Environ. Sci. Policy 2015, 51, 278–291. [Google Scholar] [CrossRef]
- Krzysztofowicz, R. Bayesian system for probabilistic river stage forecasting. J. Hydrol. 2002, 268, 16–40. [Google Scholar] [CrossRef]
- Todini, E. Role and treatment of uncertainty in real-time flood forecasting. Hydrol. Process. 2004, 18, 2743–2746. [Google Scholar] [CrossRef]
- Clark, M.P.; Slater, A.G. Probabilistic quantitative precipitation estimation in complex terrain. J. Hydrometeorol. 2006, 7, 3–22. [Google Scholar] [CrossRef]
- Vrugt, J.A.; Robinson, B.A. Treatment of uncertainty using ensemble methods: Comparison of sequential data assimilation and Bayesian model averaging. Water Resour. Res. 2007, 43, W01411. [Google Scholar] [CrossRef]
- Ebtehaj, M.; Moradkhani, H.; Gupta, H.V. Improving robustness of hydrologic parameter estimation by the use of moving block bootstrap resampling. Water Resour. Res. 2010, 46, W07515. [Google Scholar] [CrossRef]
- He, X.; Refsgaard, J.C.; Sonnenborg, T.O.; Vejen, F.; Jensen, K.H. Statistical analysis of the impact of radar rainfall uncertainties on water resources modeling. Water Resour. Res. 2011, 47, W09526. [Google Scholar] [CrossRef]
- Legleiter, C.J.; Kyriakidis, P.C.; McDonald, R.R.; Nelson, J.M. Effects of uncertain topographic input data on twodimensional flow modeling in a gravel-bed river. Water Resour. Res. 2011, 47, W03518. [Google Scholar] [CrossRef]
- Sikorska, A.E.; Scheidegger, A.; Banasik, K.; Rieckermann, J. Bayesian uncertainty assessment of flood predictions in ungauged urban basins for conceptual rainfall-runoff models. Hydrol. Earth Syst. Sci. 2012, 16, 1221–1236. [Google Scholar] [CrossRef]
- Montanari, A.; Koutsoyiannis, D. A blueprint for process-based modeling of uncertain hydrological systems. Water Resour. Res. 2012, 48, W09555. [Google Scholar] [CrossRef]
- Montanari, A.; Grossi, G. Estimating the uncertainty of hydrological forecasts: A statistical approach. Water Resour. Res. 2008, 44, W00B08. [Google Scholar] [CrossRef]
- Smith, P.J.; Beven, K.J.; Weerts, A.H.; Leedal, D. Adaptive correction of deterministic models to produce accurate probabilistic forecasts. Hydrol. Earth Syst. Sci. 2012, 16, 2783–2799. [Google Scholar] [CrossRef] [Green Version]
- Hoss, F.; Fischbeck, P.S. Performance and robustness of probabilistic river forecasts computed with quantile regression based on multiple independent variables. Hydrol. Earth Syst. Sci. 2015, 19, 3969–3990. [Google Scholar] [CrossRef]
- Krzysztofowicz, R. Bayesian theory of probabilistic forecasting via deterministic hydrologic model. Water Resour. Res. 1999, 35, 2739–2750. [Google Scholar] [CrossRef]
- Krzysztofowicz, R.; Kelly, K.S. Hydrologic uncertainty processor for probabilistic river stage forecasting. Water Resour. Res. 2000, 36, 3265–3277. [Google Scholar] [CrossRef]
- Coccia, G.; Todini, E. Recent development in predictive uncertainty assessment based on the model conditional processor approach. Hydrol. Earth Syst. Sci. 2011, 15, 3253–3274. [Google Scholar] [CrossRef]
- Raftery, A.E. Bayesian model selection in structural equation models. In Testing Structural Equation Models; Bollen, K.A., Long, J.S., Eds.; Sage: Beverly Hills, CA, USA, 1993; pp. 163–180. [Google Scholar]
- Raftery, A.E.; Balabdaoui, F.; Gneiting, T.; Polakowski, M. Using Bayesian model averaging to calibrate forecast ensembles. Mon. Weather Rev. 2005, 133, 1155–1174. [Google Scholar] [CrossRef]
- Todini, E. A model conditional processor to assess predictive uncertainty in flood forecasting. Int. J. River Basin Manag. 2008, 6, 123–137. [Google Scholar] [CrossRef]
- Plate, E.J.; Shahzad, K.M. Uncertainty Analysis of Multi-Model Flood Forecasts. Water 2015, 7, 6788–6809. [Google Scholar] [CrossRef]
- Coccia, G. Analysis and Developments of Uncertainty Processors for Real Time Flood Forecasting. Ph.D. Thesis, Alma Mater Studiorum University of Bologna, Bologna, Italy, 2011. [Google Scholar]
- Barbetta, S.; Moramarco, T.; Franchini, M.; Melone, F.; Brocca, L.; Singh, V.P. Case Study: Improving real-time stage forecasting Muskingum model by incorporating the Rating Curve Model. J. Hydrol. Eng. 2011, 16, 540–557. [Google Scholar] [CrossRef]
- Van der Waerden, B.L. Order tests for two-sample problem and their power I. Indag. Math. 1952, 14, 453–458. [Google Scholar] [CrossRef]
- Van der Waerden, B.L. Order tests for two-sample problem and their power II. Indag. Math. 1953, 15, 303–310. [Google Scholar] [CrossRef]
- Van der Waerden, B.L. Order tests for two-sample problem and their power III. Indag. Math. 1953, 15, 311–316. [Google Scholar] [CrossRef]
- Barbetta, S.; Moramarco, T.; Brocca, L.; Franchini, M.; Melone, F. Confidence interval of real-time forecast stages provided by the STAFOM-RCM model: The case study of the Tiber River (Italy). Hydrol. Process. 2014, 28, 729–743. [Google Scholar] [CrossRef]
- Moramarco, T.; Barbetta, S.; Melone, F.; Singh, V.P. Relating local stage and remote discharge with significant lateral inflow. J. Hydrol. Eng. 2005, 10, 58–69. [Google Scholar] [CrossRef]
- Barbetta, S.; Franchini, M.; Melone, F.; Moramarco, T. Enhancement and comprehensive evaluation of the Rating Curve Model for different river sites. J. Hydrol. 2012, 464–465, 376–387. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models, Part I: A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Kitanidis, P.K.; Bras, R. Real time forecasting with a conceptual hydrologic model. 2. Applications and results. Water Resour. Res. 1980, 16, 1034–1044. [Google Scholar] [CrossRef]
- Laio, F.; Tamea, S. Verification tools for probabilistic forecasts of continuous hydrological variables. Hydrol. Earth Syst. Sci. 2007, 11, 1267–1277. [Google Scholar] [CrossRef]
- Wilks, D.S. Statistical Methods in Atmospheric Sciences, 2nd ed.; Academic Press: San Diego, CA, USA, 2006. [Google Scholar]
| River Reach | L (km) | Aup (km2) | Adown (km2) | Aint (km2) | S0 | B (m) | TL (h) | |
|---|---|---|---|---|---|---|---|---|
| reach 1 | Bhadrachalam-Polavaram | 73 | 280,505 | 307,800 | 27,295 (9%) | 0.00025 | 1300 | 10–12 |
| reach 2 | Perur-Polavaram | 206 | 268,200 | 39,600 (13%) | 0.0003 | 20–24 |
| River Reach | Lead-Time (h) | STAFOM-RCM | MCP-MT Expected Value | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| er_h (m) | NS | RMSE (m) | PC | er_h (m) | NS | RMSE (m) | PC | ||||
| m | σ | m | σ | ||||||||
| reach 1 | 10 | 0.196 | 0.223 | 0.989 | 0.297 | 0.56 | 0.117 | 0.159 | 0.995 | 0.198 | 0.81 |
| 12 | 0.202 | 0.220 | 0.989 | 0.298 | 0.67 | 0.136 | 0.184 | 0.993 | 0.228 | 0.81 | |
| reach 2 | 20 | 0.344 | 0.403 | 0.960 | 0.530 | 0.34 | 0.283 | 0.328 | 0.973 | 0.433 | 0.56 |
| 24 | 0.353 | 0.413 | 0.958 | 0.543 | 0.48 | 0.269 | 0.317 | 0.975 | 0.416 | 0.70 | |
| River Reach | Lead-Time (h) | Perc90% | Width of the 90% Uncertainty Band | |
|---|---|---|---|---|
| Mean (m) | Standard Deviation (m) | |||
| reach 1 | 10 | 93.7 | 0.73 | 0.20 |
| 12 | 93.6 | 0.84 | 0.23 | |
| reach 2 | 20 | 93.1 | 1.42 | 0.32 |
| 24 | 93.2 | 1.40 | 0.30 | |
| River Reach | Lead-Time (h) | STAFOM-RCM | MCP-MT Expected Value | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| er_h (m) | NS | RMSE (m) | PC | er_h (m) | NS | RMSE (m) | PC | ||||
| m | σ | m | σ | ||||||||
| Calibration (2001–2004) | |||||||||||
| reach 1 | 12 | 0.184 | 0.194 | 0.99 | 0.267 | 0.73 | 0.115 | 0.137 | 0.996 | 0.178 | 0.88 |
| reach 2 | 24 | 0.343 | 0.400 | 0.958 | 0.527 | 0.4 | 0.263 | 0.306 | 0.975 | 0.403 | 0.74 |
| Validation (2005, 2007, 2010) | |||||||||||
| reach 1 | 12 | 0.221 | 0.243 | 0.987 | 0.328 | 0.58 | 0.142 | 0.212 | 0.992 | 0.255 | 0.75 |
| reach 2 | 24 | 0.362 | 0.426 | 0.958 | 0.56 | 0.55 | 0.292 | 0.348 | 0.973 | 0.455 | 0.71 |
| River Reach | Lead-Time (h) | Perc90% | Width of the 90% Uncertainty Band | |
|---|---|---|---|---|
| Mean (m) | Standard Deviation (m) | |||
| Calibration (2001–2004) | ||||
| reach 1 | 12 | 92.3 | 0.68 | 0.22 |
| reach 2 | 24 | 92.3 | 1.33 | 0.33 |
| Validation (2005, 2007, 2010) | ||||
| reach 1 | 12 | 92.0 | 0.74 | 0.20 |
| reach 2 | 24 | 92.2 | 1.4 | 0.29 |
| River Reach | Warning Threshold (14.27 m) | Attention Threshold (11.80 m) | |||||
|---|---|---|---|---|---|---|---|
| Hits | False Alarms | Misses | Hits | False Alarms | Misses | ||
| All Dataset (2001–2010) | |||||||
| reach 1 (12 h) | STAFOM-RCM | 3 | 2 | 0 | 14 | 1 | 0 |
| Exp. value | 3 | 0 | 0 | 14 | 1 | 0 | |
| 95th perc. | 3 | 2 | 0 | 14 | 1 | 0 | |
| reach 2 (24 h) | STAFOM-RCM | 2 | 1 | 1 | 15 | 2 | 0 |
| Exp. value | 2 | 1 | 1 | 14 | 1 | 1 | |
| 95th perc. | 3 | 2 | 0 | 15 | 2 | 0 | |
| Calibration (2001–2004) | |||||||
| reach 1 (12 h) | STAFOM-RCM | 0 | 1 | 0 | 5 | 0 | 0 |
| Exp. value | 0 | 0 | 0 | 5 | 0 | 0 | |
| 95th perc. | 0 | 1 | 0 | 5 | 0 | 0 | |
| reach 2 (24 h) | STAFOM-RCM | 0 | 1 | 0 | 6 | 1 | 0 |
| Exp. value | 0 | 0 | 0 | 6 | 0 | 0 | |
| 95th perc. | 0 | 0 | 0 | 6 | 1 | 0 | |
| Validation (2005, 2007, 2010) | |||||||
| reach 1 (12 h) | STAFOM-RCM | 3 | 1 | 0 | 9 | 1 | 0 |
| Exp. value | 3 | 0 | 0 | 9 | 1 | 0 | |
| 95th perc. | 3 | 1 | 0 | 9 | 1 | 0 | |
| reach 2 (24 h) | STAFOM-RCM | 2 | 0 | 1 | 9 | 1 | 0 |
| Exp. value | 2 | 0 | 1 | 8 | 1 | 1 | |
| 95th perc. | 2 | 0 | 1 | 9 | 1 | 0 | |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barbetta, S.; Coccia, G.; Moramarco, T.; Todini, E. Case Study: A Real-Time Flood Forecasting System with Predictive Uncertainty Estimation for the Godavari River, India. Water 2016, 8, 463. https://doi.org/10.3390/w8100463
Barbetta S, Coccia G, Moramarco T, Todini E. Case Study: A Real-Time Flood Forecasting System with Predictive Uncertainty Estimation for the Godavari River, India. Water. 2016; 8(10):463. https://doi.org/10.3390/w8100463
Chicago/Turabian StyleBarbetta, Silvia, Gabriele Coccia, Tommaso Moramarco, and Ezio Todini. 2016. "Case Study: A Real-Time Flood Forecasting System with Predictive Uncertainty Estimation for the Godavari River, India" Water 8, no. 10: 463. https://doi.org/10.3390/w8100463
APA StyleBarbetta, S., Coccia, G., Moramarco, T., & Todini, E. (2016). Case Study: A Real-Time Flood Forecasting System with Predictive Uncertainty Estimation for the Godavari River, India. Water, 8(10), 463. https://doi.org/10.3390/w8100463









