Nonlinear Relationship of Near-Bed Velocity and Growth of Riverbed Periphyton
Abstract
:1. Introduction
2. Materials and Methods
2.1. Periphyton Collection and Processing
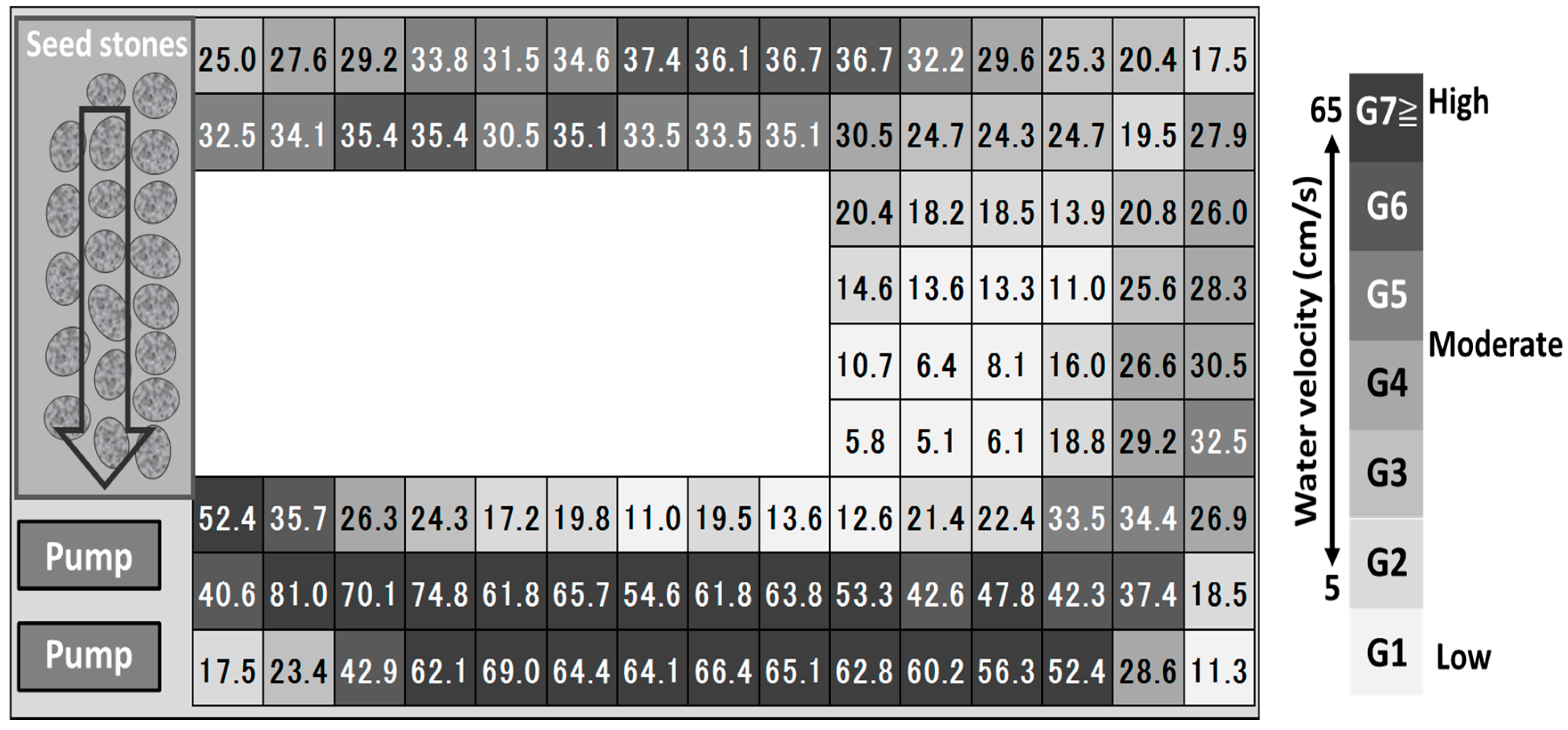
2.2. Experimental Setup
2.3. Analysis
2.4. Model Application
3. Results and Discussion
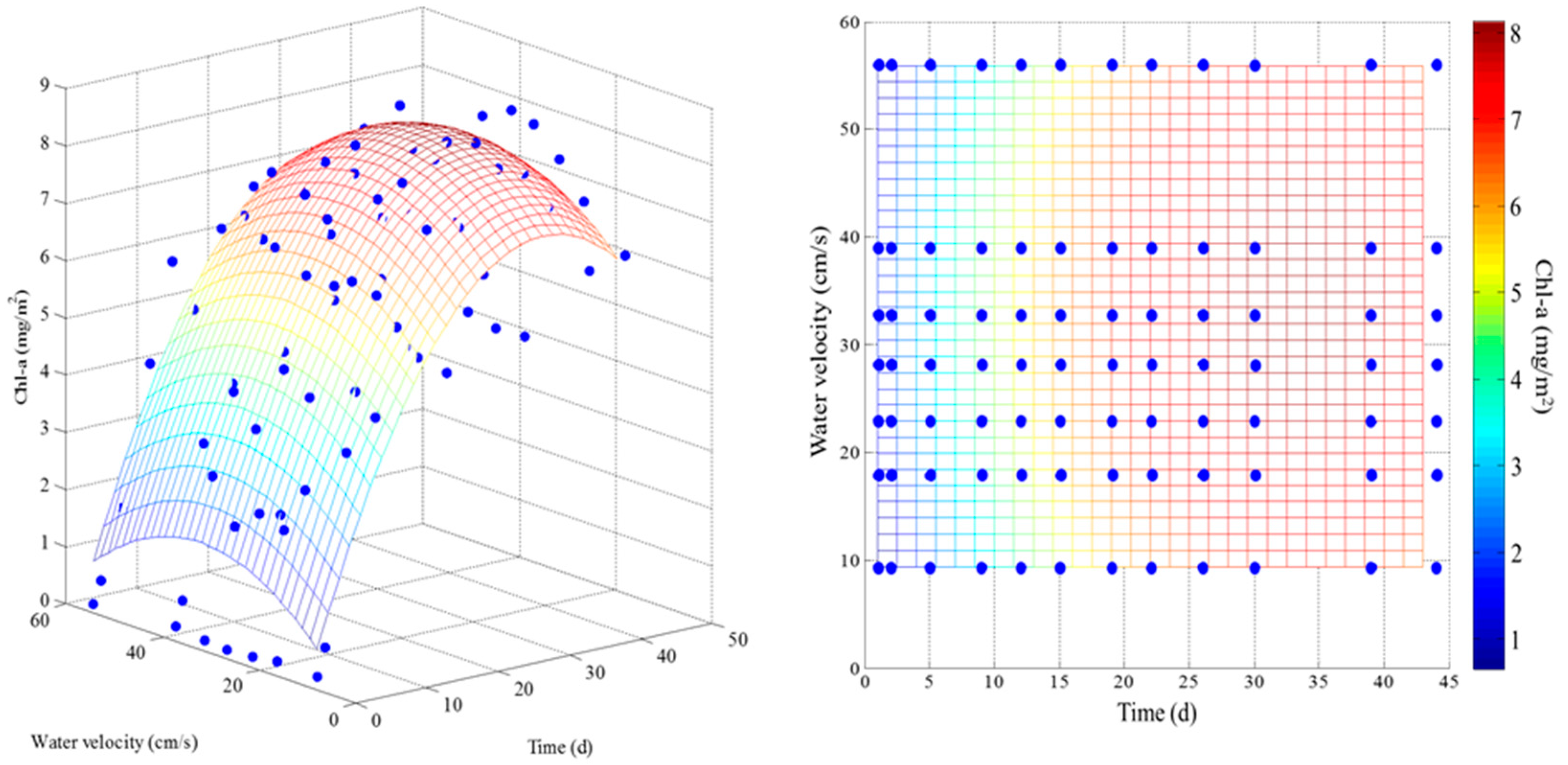
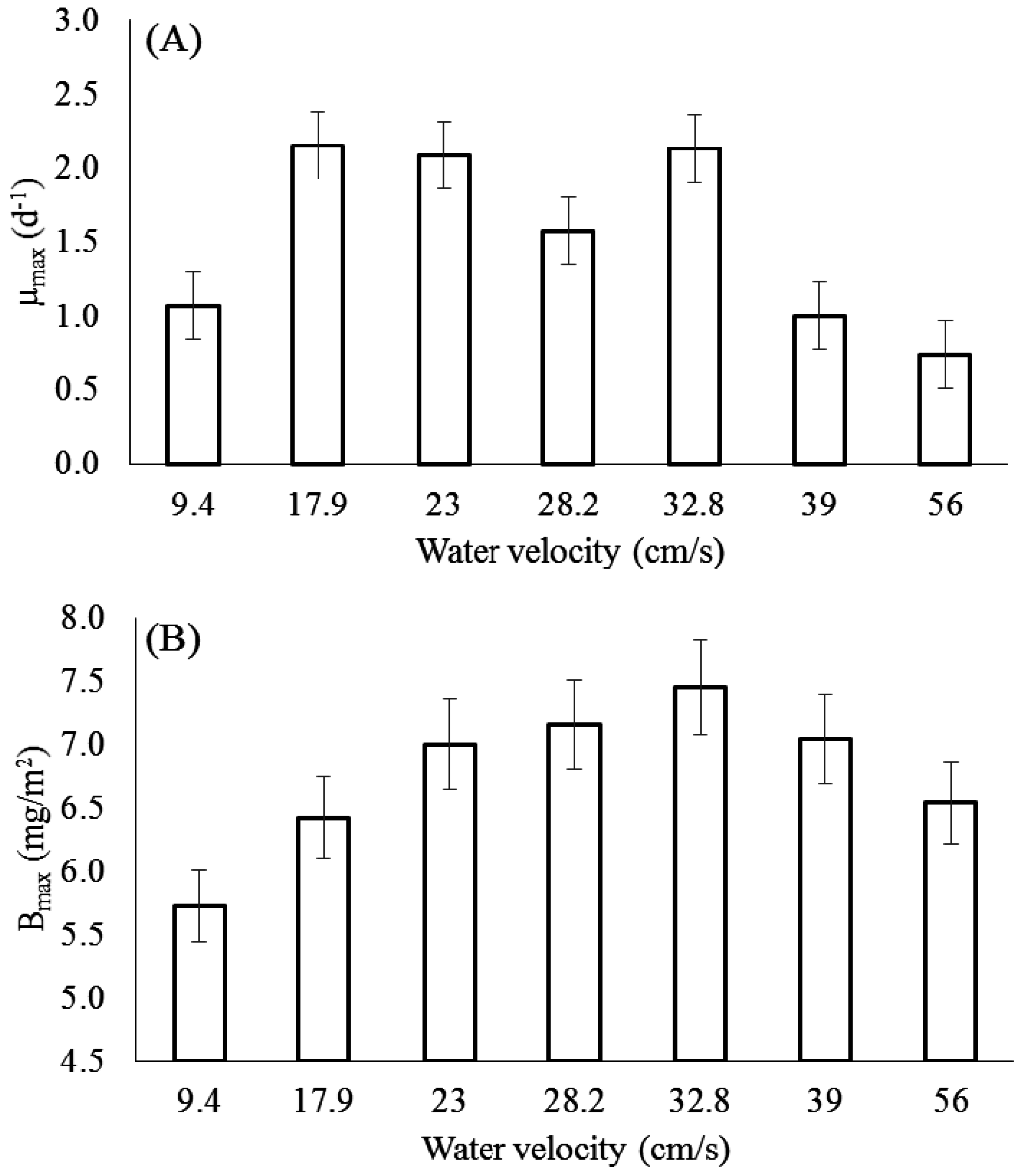
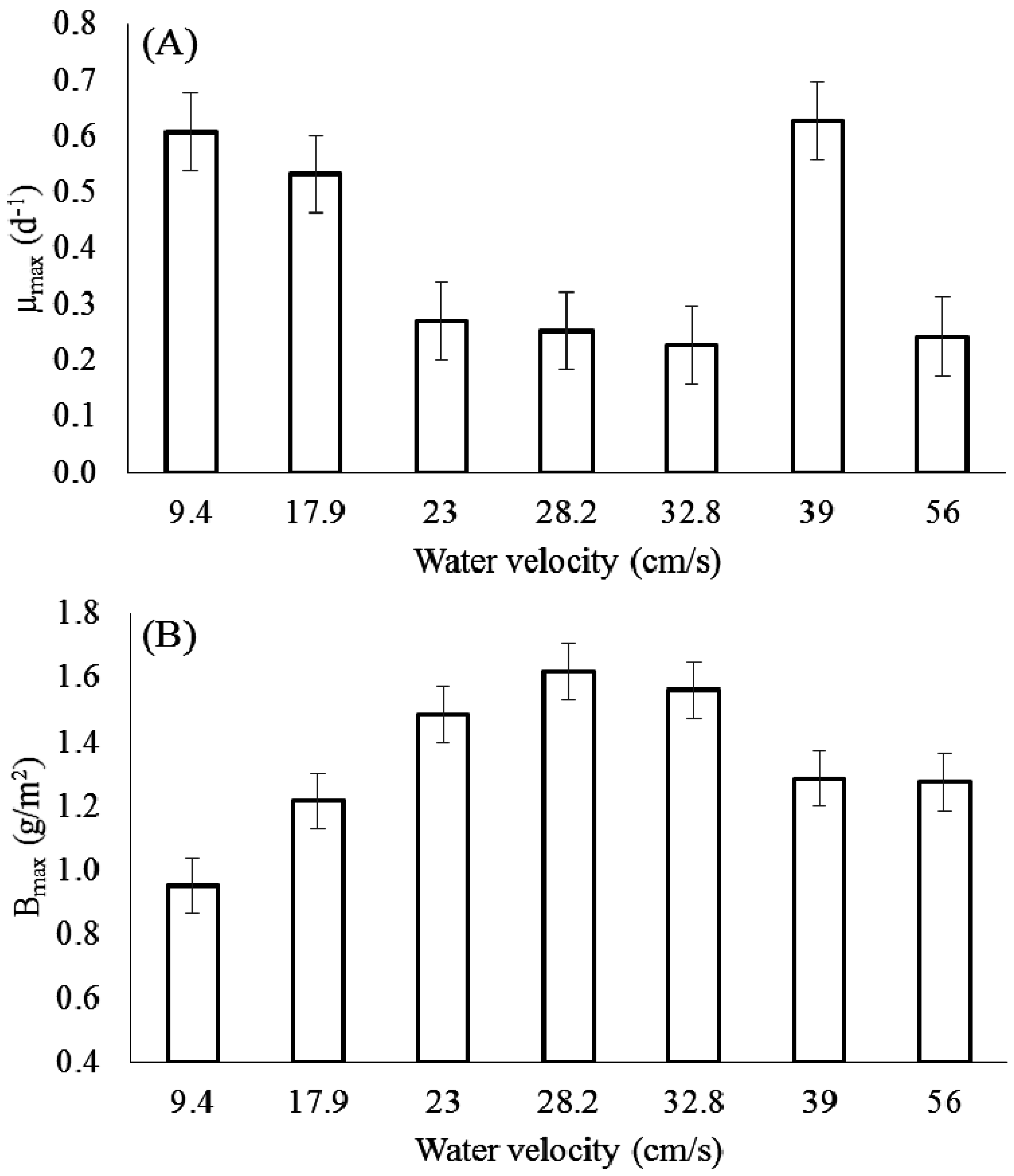
3.1. Effect of Velocity on Chlorophyll-a
3.2. Effect of Velocity on Biomass
3.3. Effect of Velocity on the Autotrophic Index
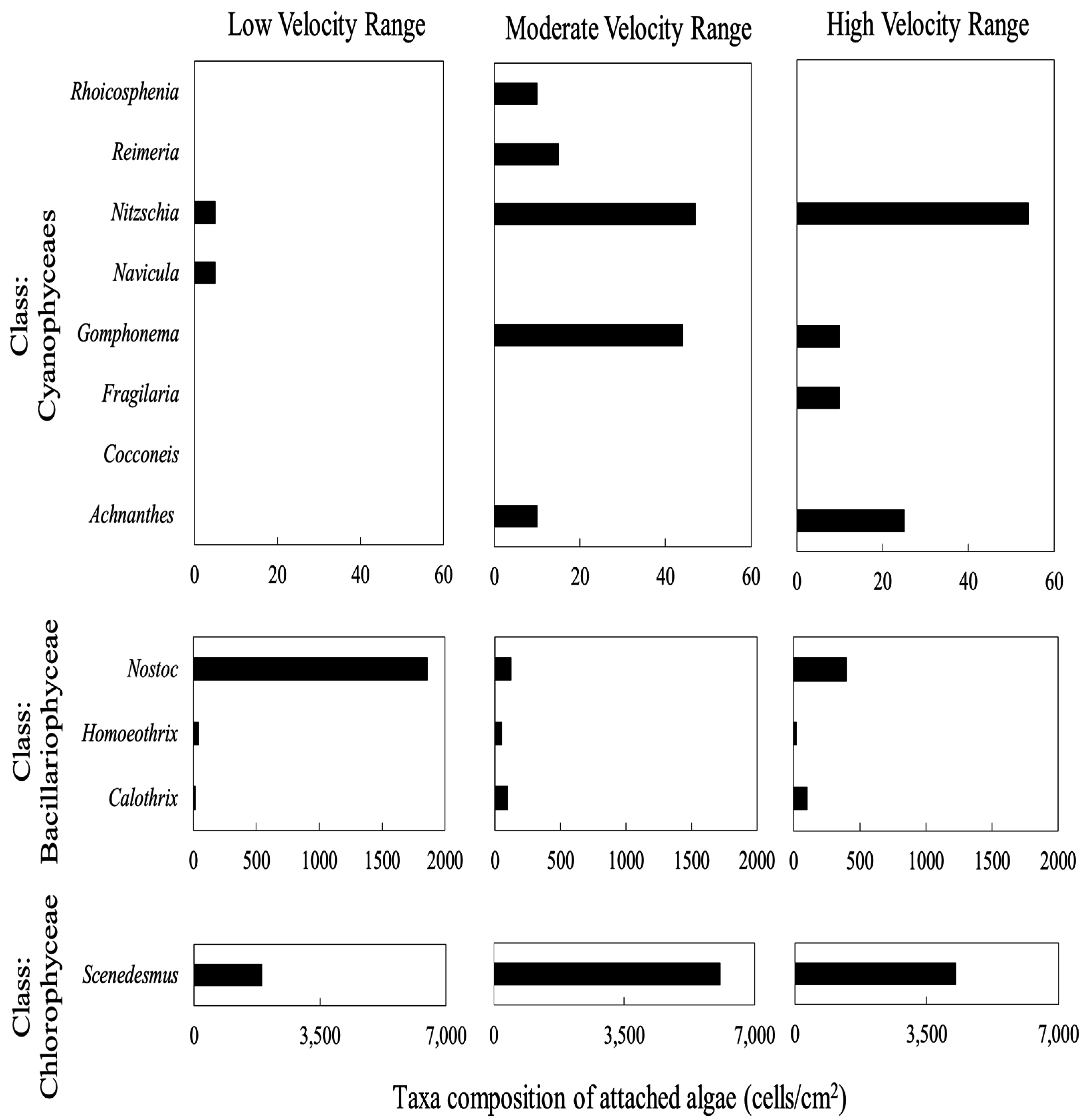
3.4. Periphyton Species Composition
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Weitzel, R.L. Methods and Measurements of Periphyton Communities: A Review; ASTM International: Philadelphia, PA, USA, 1979. [Google Scholar]
- Aizaki, M. Growth rates of microorganisms in a periphyton community. Jpn. J. Limnol. 1979, 40, 10–19. (In Japanese) [Google Scholar] [CrossRef]
- Lau, Y.; Liu, D. Effect of flow rate on biofilm accumulation in open channels. Water Res. 1993, 27, 355–360. [Google Scholar] [CrossRef]
- Fovet, O.; Litrico, X.; Belaud, G. Turbidity management during flushing-flows: A model for open-loop control. Adv. Water Resour. 2012, 39, 7–17. [Google Scholar] [CrossRef]
- Labiod, C.; Godillot, R.; Caussade, B. The relationship between stream periphyton dynamics and near-bed turbulence in rough open-channel flow. Ecol. Model. 2007, 209, 78–96. [Google Scholar] [CrossRef]
- Feminella, W.; Hawkins, P. Interactions between stream herbivores and periphyton: A quantitative analysis of past experiments. J. N. Am. Benthol. Soc. 1995, 14, 465–509. [Google Scholar] [CrossRef]
- Opsahl, W.; Wellnitz, T.; Poff, N. Current velocity and invertebrate grazing regulate stream algae: Results of an in situ electrical exclusion. Hydrobiologia 2003, 499, 135–145. [Google Scholar] [CrossRef]
- Hintz, D.; Wellnitz, T. Current velocity influences the facilitation and removal of algae by stream grazers. Aquat. Ecol. 2013, 47, 235–244. [Google Scholar] [CrossRef]
- Jakob, C.; Robinson, C.T.; Uehlinger, U. Longitudinal effects of experimental floods on stream benthos downstream from a large dam. Aquat. Sci. 2003, 65, 223–231. [Google Scholar] [CrossRef]
- Vonshak, A.; Torzillo, G. 4 environmental stress physiology. In Handbook of Microalgal Culture: Biotechnology and Applied Phycology; John Wiley & Sons: Ames, IA, USA, 2004. [Google Scholar]
- Dodds, W.K. Micro-environmental characteristics of filamentous algal communities in flowing freshwaters. Freshw. Biol. 1991, 25, 199–209. [Google Scholar] [CrossRef]
- Fuller, R.L.; Dennison, J.; Doyle, S.; Levy, L.; Owen, J.; Shope, E.; Swarr, G.; Vo, L.; Weichert, K.; DiCesare, E. Influence of flood history and hydrology on transport of organic matter in a frequently flooded river. J. Freshw. Ecol. 2014, 29, 37–51. [Google Scholar] [CrossRef]
- Uehlinger, U.; Kawecka, B.; Robinson, C. Effects of experimental floods on periphyton and stream metabolism below a high dam in the Swiss Alps (River Spöl). Aquat. Sci. 2003, 65, 199–209. [Google Scholar] [CrossRef]
- Gillespie, B.R.; Desmet, S.; Kay, P.; Tillotson, M.R.; Brown, L.E. A critical analysis of regulated river ecosystem responses to managed environmental flows from reservoirs. Freshw. Biol. 2015, 60, 410–425. [Google Scholar] [CrossRef]
- Franchi, E.; Carosi, A.; Ghetti, L.; Giannetto, D.; Pedicillo, G.; Pompei, L.; Lorenzoni, M. Changes in the fish community of the upper tiber river after construction of a hydro-dam. J. Limnol. 2014, 73, 203–210. [Google Scholar] [CrossRef]
- Graba, M.; Kettab, A.; Sauvage, S.; Sanchez-Pérez, J.M. On modeling chronic detachment of periphyton in artificial rough, open channel flow. Desalin. Water Treat. 2012, 41, 79–87. [Google Scholar] [CrossRef]
- Godillot, R.; Caussade, B.; Ameziane, T.; Capblancq, J. Interplay between turbulence and periphyton in rough open-channel flow. J. Hydraul. Res. 2001, 39, 227–239. [Google Scholar] [CrossRef]
- Arnon, S.; Packman, A.I.; Peterson, C.G.; Gray, K.A. Effects of overlying velocity on periphyton structure and denitrification. J. Geophys. Res. Biogeosci. 2007, 112, 1–10. [Google Scholar] [CrossRef]
- Dodds, W.K.; Biggs, B.J. Water velocity attenuation by stream periphyton and macrophytes in relation to growth form and architecture. J. N. Am. Benthol. Soc. 2002, 21, 2–15. [Google Scholar] [CrossRef]
- Mebane, C.A.; Simon, N.S.; Maret, T.R. Linking nutrient enrichment and streamflow to macrophytes in agricultural streams. Hydrobiologia 2014, 722, 143–158. [Google Scholar] [CrossRef]
- Biggs, B.J.; Hickey, C.W. Periphyton responses to a hydraulic gradient in a regulated river in New Zealand. Freshw. Biol. 1994, 32, 49–59. [Google Scholar] [CrossRef]
- Nikora, V.; Goring, D.; Biggs, B. On stream periphyton-turbulence interactions. N. Z. J. Mar. Freshw. Res. 1997, 31, 435–448. [Google Scholar] [CrossRef]
- Nikora, V.; Goring, D.; Biggs, B. A simple model of stream periphyton-flow interactions. Oikos 1998, 607–611. [Google Scholar] [CrossRef]
- Moulin, F.Y.; Peltier, Y.; Bercovitz, Y.; Eiff, O.; Beer, A.; Pen, C.; Boulêtreau, S.; Garabétian, F.; Sellali, M.; Sànchez-Pérez, J. Experimental study of the interaction between a turbulent flow and a river biofilm growing on macrorugosities. Freshw. Biol. 2008, 36, 249–263. [Google Scholar]
- Zhang, H.; Chen, R.; Li, F.; Chen, L. Effect of flow rate on environmental variables and phytoplankton dynamics: Results from field enclosures. Chin. J. Oceanol. Limnol. 2015, 33, 430–438. [Google Scholar] [CrossRef]
- McIntire, C.D. Some effects of current velocity on periphyton communities in laboratory streams. Hydrobiologia 1966, 27, 559–570. [Google Scholar] [CrossRef]
- Ahn, C.H.; Song, H.M.; Lee, S.; Oh, J.H.; Ahn, H.; Park, J.-R.; Lee, J.M.; Joo, J.C. Effects of water velocity and specific surface area on filamentous periphyton biomass in an artificial stream mesocosm. Water 2013, 5, 1723–1740. [Google Scholar] [CrossRef]
- Poff, N.L.; Voelz, N.J.; Ward, J.; Lee, R. Algal colonization under four experimentally-controlled current regimes in high mountain stream. J. N. Am. Benthol. Soc. 1990, 303–318. [Google Scholar] [CrossRef]
- Jowett, I.G.; Biggs, B.J. Flood and velocity effects on periphyton and silt accumulation in two New Zealand rivers. N. Z. J. Mar. Freshw. Res. 1997, 31, 287–300. [Google Scholar] [CrossRef]
- Filstrup, C.T.; Wagner, T.; Soranno, P.A.; Stanley, E.H.; Stow, C.A.; Webster, K.E.; Downing, J.A. Regional variability among nonlinear chlorophyll–phosphorus relationships in lakes. Limnol. Oceanogr. 2014, 59, 1691–1703. [Google Scholar] [CrossRef]
- Uehlinger, U.; Bührer, H.; Reichert, P. Periphyton dynamics in a floodprone prealpine river: Evaluation of significant processes by modelling. Freshw. Biol. 1996, 36, 249–263. [Google Scholar] [CrossRef]
- Karemore, A.; Pal, R.; Sen, R. Strategic enhancement of algal biomass and lipid in chlorococcum infusionum as bioenergy feedstock. Algal Res. 2013, 2, 113–121. [Google Scholar] [CrossRef]
- Pan, C.; Fan, Y.; Xing, Y.; Hou, H.; Zhang, M. Statistical optimization of process parameters on biohydrogen production from glucose by Clostridium sp. Fanp2. Bioresour. Technol. 2008, 99, 3146–3154. [Google Scholar] [CrossRef] [PubMed]
- Reddy, L.; Wee, Y.-J.; Yun, J.-S.; Ryu, H.-W. Optimization of alkaline protease production by batch culture of bacillus sp. Rky3 through plackett–burman and response surface methodological approaches. Bioresour. Technol. 2008, 99, 2242–2249. [Google Scholar] [CrossRef] [PubMed]
- Şahan, T.; Ceylan, H.; Şahiner, N.; Aktaş, N. Optimization of removal conditions of copper ions from aqueous solutions by trametes versicolor. Bioresour. Technol. 2010, 101, 4520–4526. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Zhang, Y.; Zhuang, B.; Zhou, X. Strategic enhancement of algal biomass, nutrient uptake and lipid through statistical optimization of nutrient supplementation in coupling scenedesmus obliquus-like microalgae cultivation and municipal wastewater treatment. Bioresour. Technol. 2014, 171, 71–79. [Google Scholar] [CrossRef] [PubMed]
- Wani, T.A.; Ahmad, A.; Zargar, S.; Khalil, N.Y.; Darwish, I.A. Use of response surface methodology for development of new microwell-based spectrophotometric method for determination of atrovastatin calcium in tablets. Chem. Cent. J. 2012, 6, 134. [Google Scholar] [CrossRef] [PubMed]
- Kobayashi, S. The Effect of Exfoliated Periphyton on Pollution of River Water. Jpn. J. Water Pollut. Res. 1982, 5, 6. [Google Scholar] [CrossRef]
- Akamatsu, Y.; Ikeda, S.; Kanai, S.; Osawa, S.; Osawa, K. Phytoremediation of endocrine disrupting chemicals in urban river water. Doboku Gakkai Ronbunshuu G/JSCE J. Environ. Syst. Eng. 2010, 66, 201–210. [Google Scholar] [CrossRef]
- Holm-Hansen, O.; Lorenzen, C.J.; Holmes, R.W.; Strickland, J.D. Fluorometric determination of chlorophyll. J. Du Cons. 1965, 30, 3–15. [Google Scholar] [CrossRef]
- Apha, A. Standard Methods for The Examination of Water and Wastewater; American Public Health Association/American Water Works Association/Water Environment Federation: Washington, WA, USA, 1995. [Google Scholar]
- Akiyama, M.; Ioriya, T.; Imahori, K.; Kasaki, H.; Kumamoto, S.; Kobayashi, H.; Takahashi, E.; Tsumura, K.; Hirano, M.; Hirose, H. Illustrations of the Japanese Fresh-Water Algae; Uchidarokakuho Publishing Company, Limited: Tokyo, Japan, 1977. [Google Scholar]
- Watanabe, T.; Ohtsuka, T.; Tuji, A.; Houki, A. Picture Book and Ecology of the Freshwater Diatoms; Uchida-Rokakuho: Tokyo, Japan, 2005. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. ACM SIGMOBILE Mob. Comput. Commun. Rev. 2001, 5, 3–55. [Google Scholar] [CrossRef]
- Simkins, S.; Alexander, M. Models for mineralization kinetics with the variables of substrate concentration and population density. Appl. Environ. Microbiol. 1984, 47, 1299–1306. [Google Scholar] [PubMed]
- Flinders, C.A.; Hart, D.D. Effects of pulsed flows on nuisance periphyton growths in rivers: A mesocosm study. River Res. Appl. 2009, 25, 1320–1330. [Google Scholar] [CrossRef]
- Biggs, B.; Kilroy, C.; Mulcock, C.; Scarsbrook, M. New Zealand stream monitoring and assessment kit. Stream Monit. Man. Version 1998, 1, 50–150. [Google Scholar]
- Horner, R.R.; Welch, E.B.; Seeley, M.R.; Jacoby, J.M. Responses of periphyton to changes in current velocity, suspended sediment and phosphorus concentration. Freshw. Biol. 1990, 24, 215–232. [Google Scholar] [CrossRef]
- Majdi, N.; Traunspurger, W.; Boyer, S.; Mialet, B.; Tackx, M.; Fernandez, R.; Gehner, S.; Ten-Hage, L.; Buffan-Dubau, E. Response of biofilm-dwelling nematodes to habitat changes in the garonne river, France: Influence of hydrodynamics and microalgal availability. Hydrobiologia 2011, 673, 229–244. [Google Scholar] [CrossRef]
- Bothwell, M.L. Phosphorus-limited growth dynamics of lotic periphytic diatom communities: Areal biomass and cellular growth rate responses. Can. J. Fish. Aquat. Sci. 1989, 46, 1293–1301. [Google Scholar] [CrossRef]
- Luce, J.J.; Cattaneo, A.; Lapointe, M.F. Spatial patterns in periphyton biomass after low-magnitude flow spates: Geomorphic factors affecting patchiness across gravel-cobble riffles. J. N. Am. Benthol. Soc. 2010, 29, 614–626. [Google Scholar] [CrossRef]
- Hondzo, M.; Wang, H. Effects of turbulence on growth and metabolism of periphyton in a laboratory flume. Water Resour. Res. 2002, 38, 13-1–13-9. [Google Scholar] [CrossRef]
- Tonkin, J.D.; Death, R.G.; Barquín, J. Periphyton control on stream invertebrate diversity: Is periphyton architecture more important than biomass? Mar. Freshw. Res. 2014, 65, 818–829. [Google Scholar] [CrossRef]
- Juneja, A.; Ceballos, R.M.; Murthy, G.S. Effects of environmental factors and nutrient availability on the biochemical composition of algae for biofuels production: A review. Energies 2013, 6, 4607–4638. [Google Scholar] [CrossRef]
- Weber, I.; McFarland, H. Periphyton biomass-chlorophyll ratio as an index of water quality. In Proceedings of the 17th Meeting of Midwest Benthological Society, Gilbertsville, KY, USA, 9–11 April 1969.
- Tuji, A. Observation of developmental processes in loosely attached diatom (Bacillariophyceae) communities. Phycol. Res. 2000, 48, 75–84. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ateia, M.; Nasr, M.; Ikeda, A.; Okada, H.; Fujii, M.; Natsuike, M.; Yoshimura, C. Nonlinear Relationship of Near-Bed Velocity and Growth of Riverbed Periphyton. Water 2016, 8, 461. https://doi.org/10.3390/w8100461
Ateia M, Nasr M, Ikeda A, Okada H, Fujii M, Natsuike M, Yoshimura C. Nonlinear Relationship of Near-Bed Velocity and Growth of Riverbed Periphyton. Water. 2016; 8(10):461. https://doi.org/10.3390/w8100461
Chicago/Turabian StyleAteia, Mohamed, Mahmoud Nasr, Akira Ikeda, Hisako Okada, Manabu Fujii, Masafumi Natsuike, and Chihiro Yoshimura. 2016. "Nonlinear Relationship of Near-Bed Velocity and Growth of Riverbed Periphyton" Water 8, no. 10: 461. https://doi.org/10.3390/w8100461
APA StyleAteia, M., Nasr, M., Ikeda, A., Okada, H., Fujii, M., Natsuike, M., & Yoshimura, C. (2016). Nonlinear Relationship of Near-Bed Velocity and Growth of Riverbed Periphyton. Water, 8(10), 461. https://doi.org/10.3390/w8100461







