The Acoustic Properties of Suspended Sediment in Large Rivers: Consequences on ADCP Methods Applicability
Abstract
:1. Introduction
2. Materials and Methods
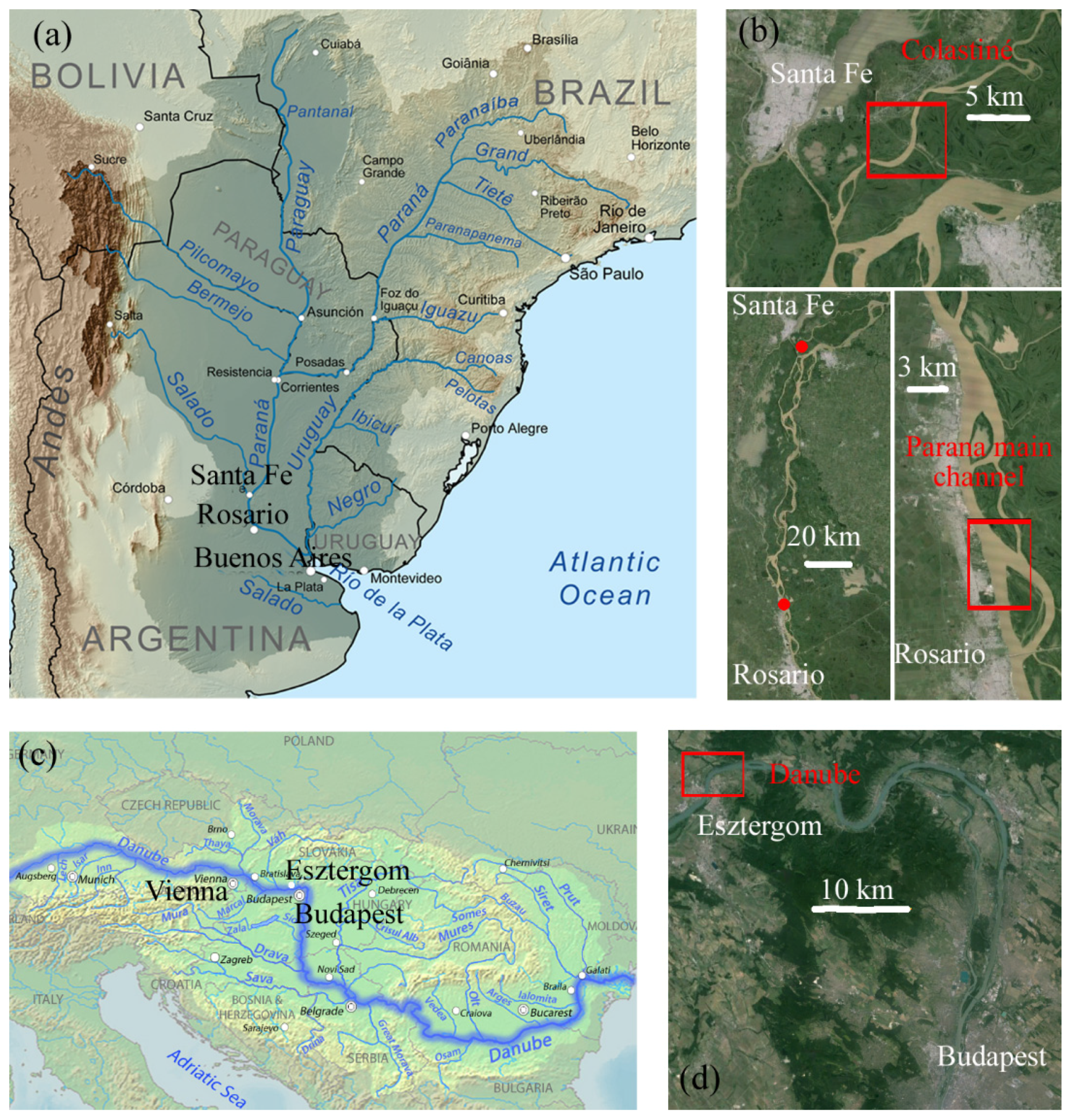
2.1. Study Areas and Sampling Campaigns of Water-Sediment Mixture

2.2. Acoustic Theory

3. Results
3.1. Results from Samples
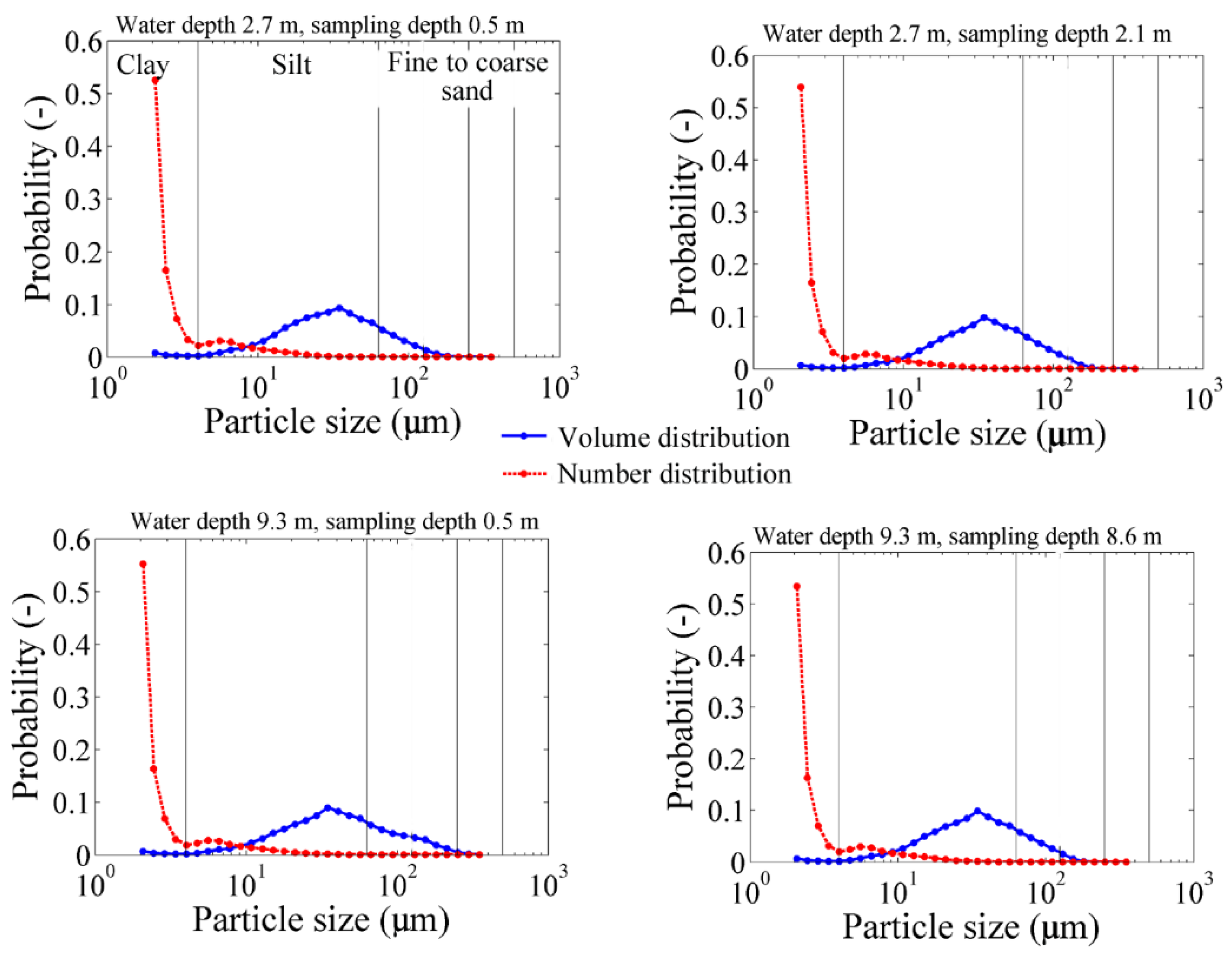

| Dataset | Particle Size Number Distribution, p(a) | Particle Size Volume Distribution | |||
|---|---|---|---|---|---|
| Mean Size, D (μm) | Standard dev., std (μm) | std/D (-) | Geometric Mean (μm) | Geometric std (-) | |
| Danube | 3.7 | 4.0 | 1.1 | 28.0 | 2.2 |
| Colastiné (Parana): wash-load | 1.0 | 0.8 | 0.8 | 6.7 | 2.8 |
| Colastiné (Parana): suspended-load | 92.1 | 31.5 | 0.3 | 117.4 | 1.3 |
| Parana main channel: suspended-load | 82.5 | 26.3 | 0.3 | 105.7 | 1.4 |
| Dataset | Minimum | Mean | Maximum |
|---|---|---|---|
| Danube | 256 | 326 | 401 |
| Colastiné (Parana): wash-load | 389 | 426 | 449 |
| Colastiné (Parana): suspended-load | 6.5 | 34.8 | 92.4 |
| Parana main channel: suspended-load | 10.3 | 19.3 | 32.2 |
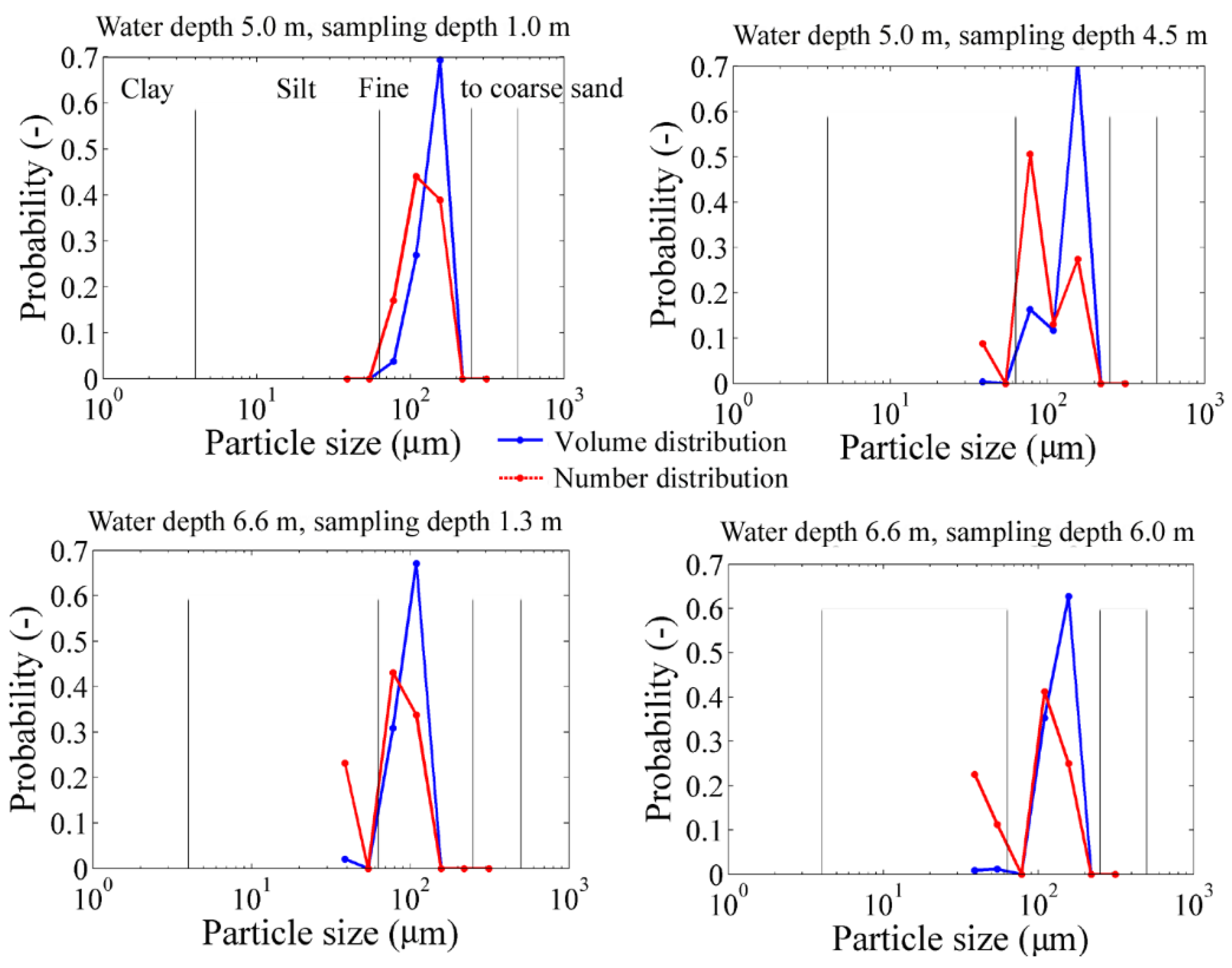
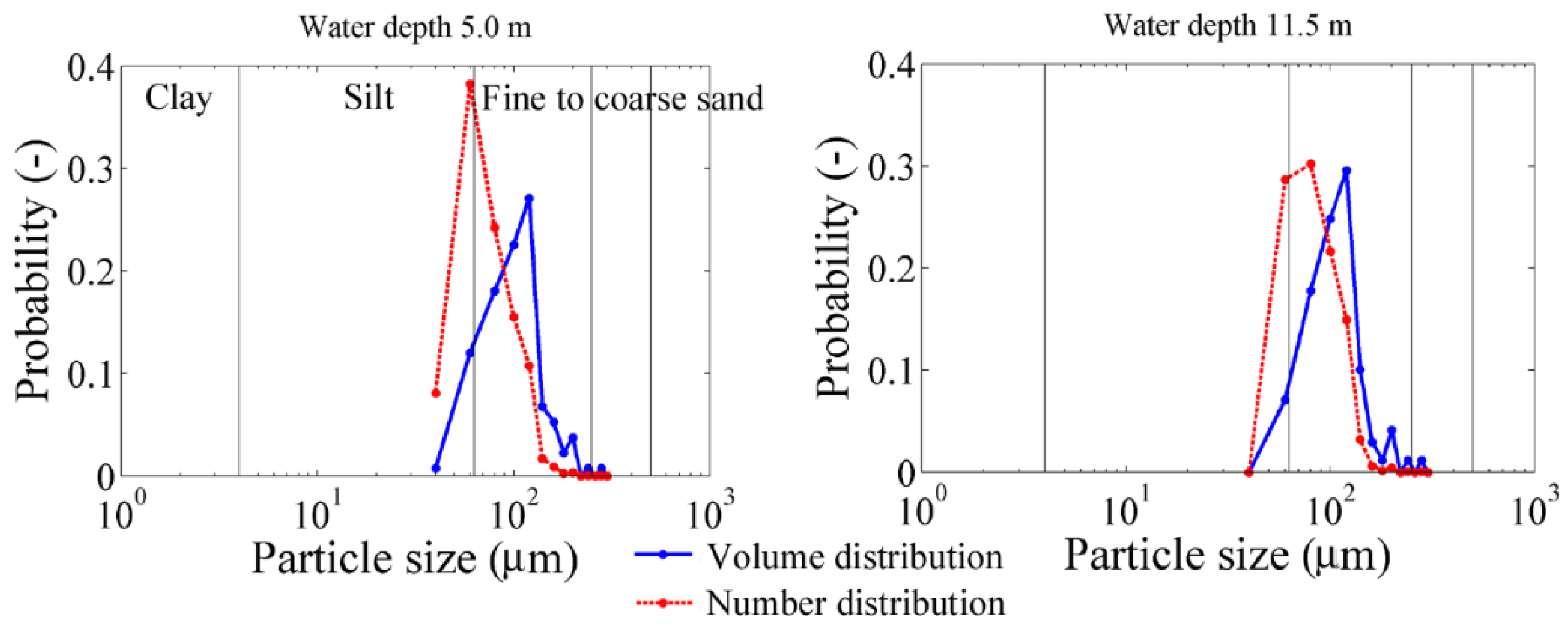
3.2. Backscattering Coefficient and Viscous-Scattering Attenuation Normalized Coefficients
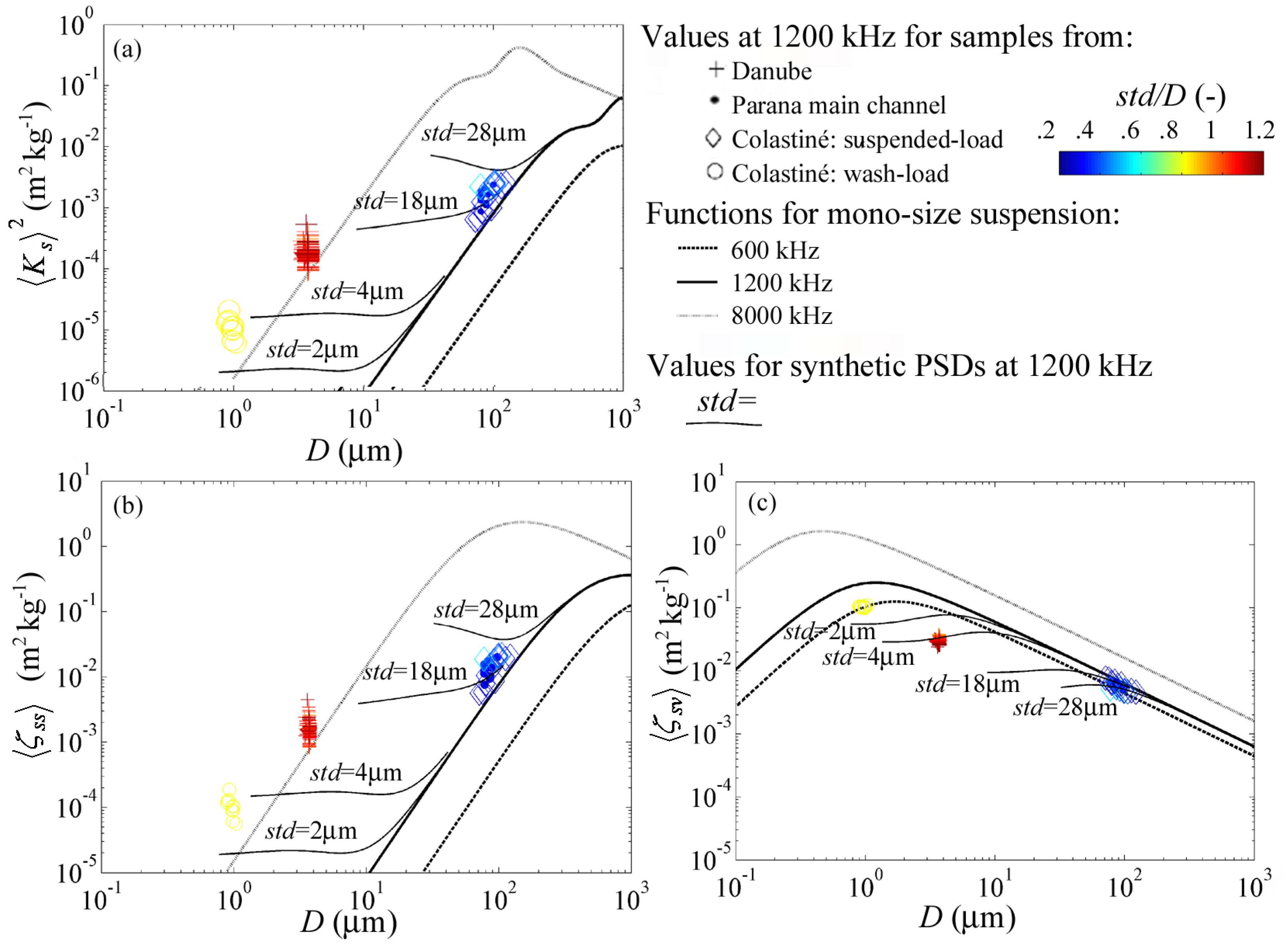

3.3. Backscattering Strength and Viscous-Scattering Attenuation Coefficients
| Dataset | Backscattering Strength | Scattering Attenuation Coefficient | Viscous Attenuation Coefficient | |
|---|---|---|---|---|
| Danube | 0.69 | 0.63 | 0.49 | Concentration |
| −0.20 | −0.21 | −0.11 | D | |
| 0.17 | 0.16 | −0.64 | std/D | |
| Colastiné (Parana): wash-load | 0.10 | 0.19 | 0.80 | Concentration |
| −0.73 | −0.67 | 0.30 | D | |
| 0.10 | 0.17 | 0.08 | std/D | |
| Colastiné (Parana): suspended-load | 0.86 | 0.91 | 0.96 | Concentration |
| 0.36 | 0.27 | −0.11 | D | |
| 0.46 | 0.44 | 0.14 | std/D | |
| Parana main channel: suspended-load | 0.87 | 0.86 | 0.97 | Concentration |
| 0.64 | 0.70 | 0.48 | D | |
| 0.36 | 0.34 | −0.17 | std/D |
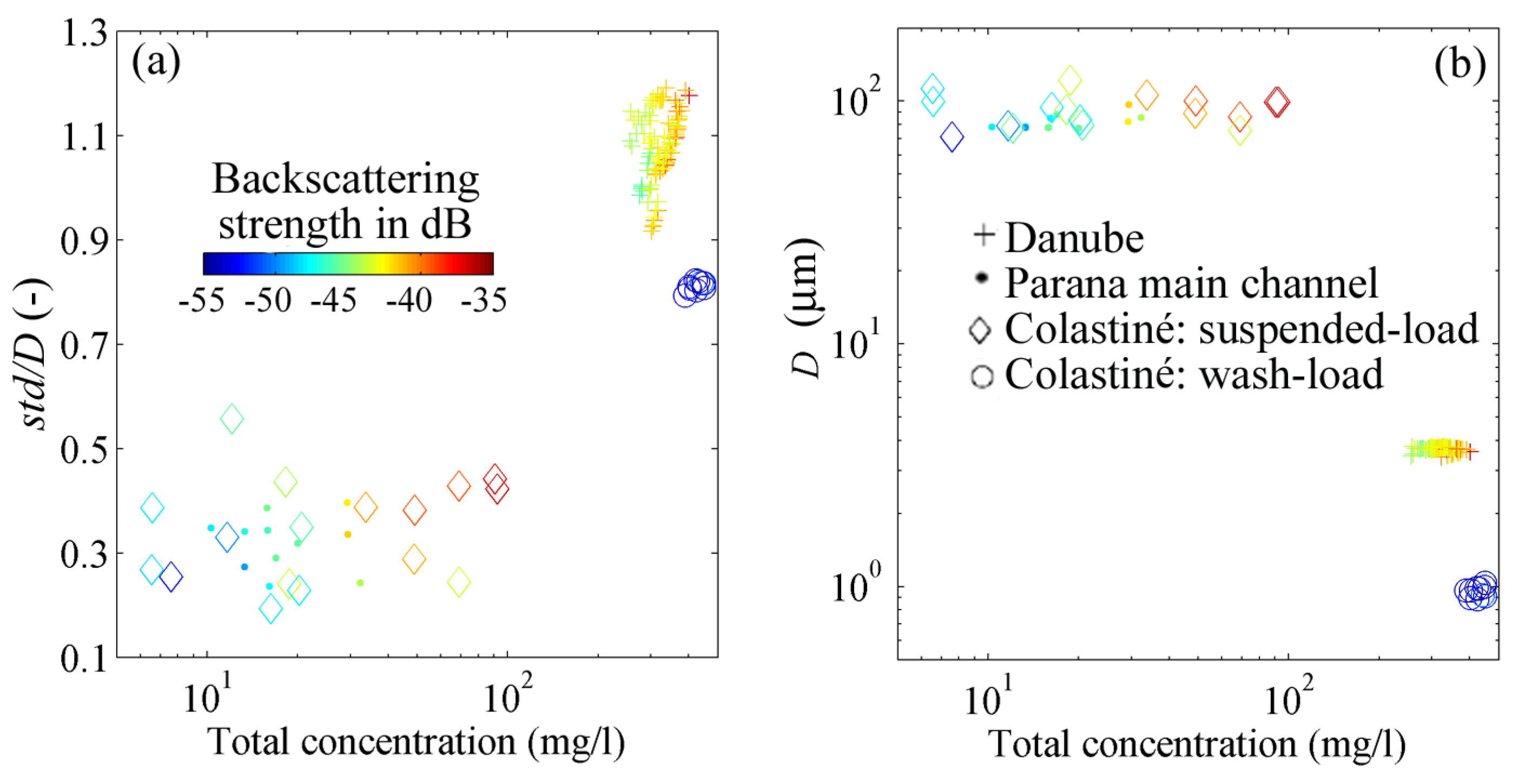

4. Discussion
4.1. Implications of the Acoustic Features Assessed from the Observed PSDs
4.2. Recommendations
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Guerrero, M.; Re, M.; Kazimierski, L.D.D.; Menéndez, A.N.; Ugarelli, R. Effect of climate change on navigation channel dredging of the Parana River. Int. J. River Basin Manag. 2013, 11, 439–448. [Google Scholar] [CrossRef]
- Paarlberg, A.J.; Guerrero, M.; Huthoff, F.; Re, M. Optimizing Dredge-and-Dump Activities for River Navigability Using a Hydro-Morphodynamic Model. Water 2015, 7, 3943–3962. [Google Scholar] [CrossRef]
- Archetti, R.; Romagnoli, C. Analysis of the effects of different storm events on shoreline dynamics of an artificially embayed beach. Earth Surf. Process. Landforms 2011, 36, 1449–1463. [Google Scholar] [CrossRef]
- Carniel, S.; Sclavo, M.; Archetti, R. Oceanological and Hydrobiological Studies Towards validating a last generation, integrated wave-current-sediment numerical model in coastal regions using video measurements. Oceanol. Hydrobiol. Stud. 2011, 40, 1897–3191. [Google Scholar] [CrossRef]
- Domeneghetti, A.; Gandolfi, S.; Castellarin, A.; Brandimarte, L.; Di Baldassarre, G.; Barbarella, M.; Brath, A. Flood risk mitigation in developing countries: Deriving accurate topographic data for remote areas under severe time and economic constraints. J. Flood Risk Manag. 2014, 8, 301–314. [Google Scholar] [CrossRef]
- Guerrero, M. The investigation of sediment processes in rivers by means of the Acoustic Doppler Profiler. In Proceedings of the Bologna IAHS 2014—6th IAHS-EGU International Symposium on Integrated Water Resources Management, Bologna, Italy, 4–6 June 2014.
- Ceola, S.; Hödl, I.; Adlboller, M.; Singer, G.; Bertuzzo, E.; Mari, L.; Botter, G.; Waringer, J.; Battin, T.J.; Rinaldo, A. Hydrologic Variability Affects Invertebrate Grazing on Phototrophic Biofilms in Stream Microcosms. PLoS ONE 2013, 8. [Google Scholar] [CrossRef]
- Wild, T.B.; Loucks, D.P. Managing flow, sediment, and hydropower regimes in the Sre Pok, Se San, and Se Kong Rivers of the Mekong basin. Water Resour. Res. 2014, 50, 5141–5157. [Google Scholar] [CrossRef]
- Guerrero, M.; Nones, M.; Saurral, R.; Montroull, N.; Szupiany, R.N. Parana river sediment dynamics in the context of climate change. Int. J. River Basin Manag. 2013, 11, 423–437. [Google Scholar] [CrossRef]
- Guerrero, M.; Latosinski, F.; Nones, M.; Szupiany, R.N.; Re, M.; Gaeta, M.G. Sediment fluxes investigation for 2-D modelling of large rivers morphodynamics. Adv. Water Resour. 2015, 81, 186–198. [Google Scholar] [CrossRef]
- Simmons, S.M.; Parsons, D.R.; Best, J.L.; Orfeo, O.; Lane, S.N.; Kostaschuk, R.; Hardy, R.J.; West, G.; Malzone, C.; Marcus, J.; Pocwiardowski, P. Monitoring suspended sediment dynamics using MBES. J. Hydraul. Eng. 2010, 136, 45–49. [Google Scholar] [CrossRef]
- Guerrero, M.; Szupiany, R.N.; Amsler, M.L. Comparison of acoustic backscattering techniques for suspended sediments investigations. Flow Meas. Instrum. 2011, 22, 392–401. [Google Scholar] [CrossRef]
- Guerrero, M.; Szupiany, R.N.; Latosinski, F. Multi-frequency acoustic for suspended sediment studies: An application in the Parana River. J. Hydraul. Res. 2013, 51, 696–707. [Google Scholar] [CrossRef]
- Sassi, M.G.; Hoitink, A.J.F.; Vermeulen, B. Impact of sound attenuation by suspended sediment on ADCP backscatter calibrations. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Latosinski, F.; Szupiany, R.N.; García, C.M.; Guerrero, M.; Amsler, M.L. Estimation of Concentration and Load of Suspended Sediment in a Large River by Means of Doppler Technology. J. Hydraul. Eng. 2014, 140. [Google Scholar] [CrossRef]
- Rennie, C.D.; Millar, R.G.; Church, M.A. Measurement of bedload velocity using an acoustic Doppler current profiler. J. Hydraul. Eng. 2002, 128, 473–483. [Google Scholar] [CrossRef]
- Rennie, C.D.; Villard, P.V. Site specificity of bedload measurement using an acoustic Doppler current profiler. J. Geophys. Res. Earth Surf. 2004, 109. [Google Scholar] [CrossRef]
- Moore, S.A.; Le Coz, J.; Hurther, D.; Paquier, A. On the application of horizontal ADCPs to suspended sediment transport surveys in rivers. Cont. Shelf Res. 2012, 46, 50–63. [Google Scholar] [CrossRef]
- Moate, B.D.; Thorne, P.D. Measurement and inversion of acoustic scattering from suspension having broad size distributions. J. Acoust. Soc. Am. 2009, 126, 2905–2917. [Google Scholar] [CrossRef] [PubMed]
- Thorne, P.D.; Meral, R. Formulations for the scattering properties of suspended sandy sediments for the use in the application of acoustics to sediment transport processes. Cont. Shelf Res. 2008, 28, 309–317. [Google Scholar] [CrossRef]
- Hay, A.E.; Sheng, J. Vertical profiles of suspended sand concentration and size from multifrequency acoustic backscatter. J. Geophys. Res. 1992, 97, 15661–15677. [Google Scholar] [CrossRef]
- Wright, S.A.; Topping, D.T.; Williams, C.A. Discriminating silt and clay from suspended sand in rivers using side-looking profilers. In Proceedings of the 2nd Joint Federal Interagency Sedimentation Conference, LasVegas, NV, USA, 27 June–1 July 2010.
- Hanes, D.M. On the possibility of single-frequency acoustic measurement of sand and clay concentrations in uniform suspensions. Cont. Shelf Res. 2012, 46, 64–66. [Google Scholar] [CrossRef]
- Thorne, P.D.; Hanes, D.M. A review of acoustic measurement of small scale sediment processes. Cont. Shelf Res. 2002, 22, 603–632. [Google Scholar] [CrossRef]
- Thorne, P.D.; Hurther, D. An overview on the use of backscattered sound for measuring suspended particle size and concentration profiles in non-cohesive inorganic sediment transport studies. Cont. Shelf Res. 2013, 73, 97–118. [Google Scholar] [CrossRef]
- Latrubese, E. Patterns of anabranching channels: The ultimate end-member adjustment of mega rivers. Geomorphology 2008, 101, 130–145. [Google Scholar] [CrossRef]
- Drago, E.C.; Amsler, M.L. Bed sediment characteristics in the Paraná and Paraguay Rivers. Water Int. 1998, 23, 174–183. [Google Scholar] [CrossRef]
- Montagnini, M.D.; Prendes, H.H.; Schreider, M.I.; Amsler, M.L.; Martinez, H.L. Desarrollo de un muestreador de sedimentos en suspension integrador en profundidad. In Proceedings of the XVII Congreso Nacional del Agua, Santa Fe, Argentina, 3–7 August 1998; Volume 3, pp. 535–537.
- Guy, H.P.; Norman, V.W. Fluvial Sediment Concepts. In Techniques for Water Resources Investigations of the U.S. Geological Survey; USGS: Arlington, VA, USA, 1970. [Google Scholar]
- Gray, J.R.; Gartner, J.W. Technological advances in suspended-sediment surrogate monitoring. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Kumar, R.; Strom, K.; Keyvani, A. Floc properties and settling velocity of San Jacinto estuary mud under variable shear and salinity conditions. Cont. Shelf Res. 2010, 30, 2067–2081. [Google Scholar] [CrossRef]
- Baranya, S.; Józsa, J.; Török, G.T.; Rüther, N. A comprehensive field analysis of a river confluence. In River Flow 2012, In Proceedings of the International Conference on Fluvial Hydraulics, San José, Costa Rica, 5–7 September 2012; Munoz, R.M., Ed.; Taylor & Francis Group: London, UK, 2012; pp. 565–571. [Google Scholar]
- Baranya, S.; Józsa, J. Estimation of suspended sediment concentrations with ADCP in Danube river. J. Hydrol. Hydromech. 2013, 61, 232–240. [Google Scholar] [CrossRef]
- Gray, J.R.; Agrawal, Y.C.; Pottsmith, H.C. The LISST-SL streamlined isokinetic suspended-sediment profiler. In Proceedings of the Ninth International Symposium on River Sedimentation, Yichang, China, 18–21 October 2004; pp. 2549–2555.
- Agrawal, Y.C.; Mikkelsen, O.A.; Pottsmith, H.C. Grain Size Distribution and Sediment Flux Structure in a River Profile, Measured with a LISST-SL Instrument. Sequoia Scientific, Inc. Report 2012. Available online: http://www.sequoiasci.com (accessed on 30 October 2015).
- Guerrero, M.; Rüther, N.; Archetti, R. Comparison under controlled conditions between multi-frequency ADCPs and LISST-SL for investigating suspended sand in rivers. Flow Meas. Instrum. 2014, 37, 73–82. [Google Scholar] [CrossRef]
- Haun, S.; Rüther, N.; Baranya, S.; Guerrero, M. Comparison of real time suspended sediment transport measurements in river environment by LISST instruments in stationary and moving operation mode. Flow Meas. Instrum. 2015, 41, 10–17. [Google Scholar] [CrossRef]
- Medwin, H.; Clay, C.S. Fundamentals of Acoustical Oceanography; Academic Press: London, UK, 1998. [Google Scholar]
- Urick, R.J. Principles of Underwater Sound; Peninsula Publishing: Los Altos, CA, USA, 1997. [Google Scholar]
- Urick, R.J. The absorption of sound in suspensions of irregular particles. J. Acoust. Soc. Am. 1948, 20, 283–289. [Google Scholar] [CrossRef]
- Downing, A.; Thorne, P.D.; Vincent, C.E. Backscattering from a suspension in the near-field of a piston transducer. J. Acoust. Soc. Am. 1995, 97, 1614–1620. [Google Scholar] [CrossRef]
- RD Instruments. Using the 305A4205 Hydrophone to Identify the RSSI Scale Factors for Calibrating the Echo Strength Output of an ADCP, Technical note, FST-004 (August 1999). San Diego, CA, USA, 1999. Available online: http://www.comm-tec.com/Library (accessed on 30 October 2015).
- Rouse, H. Fluid Mechanics for Hydraulic Engineers; Dover Publications: New York, NY, USA, 1961. [Google Scholar]
- Czuba, J.A.; Straub, T.D.; Curran, C.A.; Landers, M.N.; Domanski, M.M. Comparison of fluvial suspended-sediment concentrations and particle-size distributions measured with in-stream laser diffraction and in physical samples. Water Resour. Res. 2015, 51, 320–340. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guerrero, M.; Rüther, N.; Szupiany, R.; Haun, S.; Baranya, S.; Latosinski, F. The Acoustic Properties of Suspended Sediment in Large Rivers: Consequences on ADCP Methods Applicability. Water 2016, 8, 13. https://doi.org/10.3390/w8010013
Guerrero M, Rüther N, Szupiany R, Haun S, Baranya S, Latosinski F. The Acoustic Properties of Suspended Sediment in Large Rivers: Consequences on ADCP Methods Applicability. Water. 2016; 8(1):13. https://doi.org/10.3390/w8010013
Chicago/Turabian StyleGuerrero, Massimo, Nils Rüther, Ricardo Szupiany, Stefan Haun, Sandor Baranya, and Francisco Latosinski. 2016. "The Acoustic Properties of Suspended Sediment in Large Rivers: Consequences on ADCP Methods Applicability" Water 8, no. 1: 13. https://doi.org/10.3390/w8010013
APA StyleGuerrero, M., Rüther, N., Szupiany, R., Haun, S., Baranya, S., & Latosinski, F. (2016). The Acoustic Properties of Suspended Sediment in Large Rivers: Consequences on ADCP Methods Applicability. Water, 8(1), 13. https://doi.org/10.3390/w8010013








