1. Introduction
Water, H
2O, undergoes self-ionization giving origin to the hydronium ion, H
3O
+ (or H
+ for simplicity of writing) and hydroxide ion, OH
−, in equal concentrations of the order of 10
−7 mol·dm
−3, depending on temperature,
T, pressure,
p, and ionic strength,
I; H
+ confers free acidity to the system, commonly expressed in terms of pH = −lg
aH+, where
aH+ =
mH+γ
H+ stands for activity of the indicated chemical species, H
+,
mH+ and γ
H+ being its molality and activity coefficient respectively. For simplicity of writing, when calculating logarithms,
ai, and
mi, are used instead of the mathematically correct forms
ai/
and
mi/
, where the quantities with superscript “
0” represent the standard state for the chemical species
i under concern and equal the value 1 mol·kg
−1. Since, in general terms, water is likely to come in contact with almost every other substance and materials, chemical reactions tend to take place in aqueous solutions, therefore affecting and being affected by H
+ concentration, e.g.,
mH+/mol·kg
−1, hence its activity,
aH+. Activity,
aH+, and concentration,
mH+, of chemical species are equivalent quantities,
i.e., the activity coefficient, γ
H+= 1 in the limiting condition of ideal dilute solutions, as it is the case of pure water [
1]. Aqueous systems range from simple dilute solutions, e.g., distilled water, to complex mixtures of high ionic strength, e.g., seawater [
2]. In the very dilute solutions, the concentration of chemical species, molecules or ions, is very small and the approximation γ
H+ = 1 may be acceptable for some intended uses. Solutions of high complexity, both in terms of species concentration and diversity, introduce interactions that reflect upon deviations from ideality, with activity coefficients becoming significantly different from 1.
Mean values for activity coefficients,
can be measured for solutions where the concentrations of the respective ions,
mH+ and
mCl−, are known. Nevertheless owing to the inevitable presence of both anions and cations in solution, experimental assessment of the activity coefficients of individual ions, γ
+ or γ
− cannot be done. It can only be achieved through model approaches [
3]. Experimentally assessed mean values,
, or modeled mean, γ
±, or single values γ
H+ or γ
Cl− introduce uncertainty to pH values assigned to the reference buffer solutions subject to measurement. Particularly complex mixtures of high ionic strength, as is the case of seawater,
I ≈ 0.7 mol·kg
−1, present major deviations from ideality as well as problems of chemical interferences, e.g., due to the presence of sulphate.
Under these various circumstances, covering a wide range of concentrations and matrices, calibration of the measuring setup requires calibration standards of compositions similar to those of the sample solutions. Nevertheless, the common situation is that commercial pH meters come with two or three pH reference buffer solutions (pH (S) = 4,7 and 10) from the list of NIST (ex-NBS) buffers,
I ≤ 0.1 mol·kg
−1 [
4], which are used by the great majority of practitioners who are not fully aware of this potential source of uncertainty. This may eventually bring the result to an unacceptably low level of quality, not fit for its intended purpose. The use of other more appropriate pH buffer solutions, when available, is advisable and is becoming more common practice among experts.
Although the conceptual definition of any chemical quantity is error free, its value obtained from a measurement, or calculated from a model equation, is affected by an uncertainty which is the result of added contributions from the various steps, propagating through the traceability chain [
5].
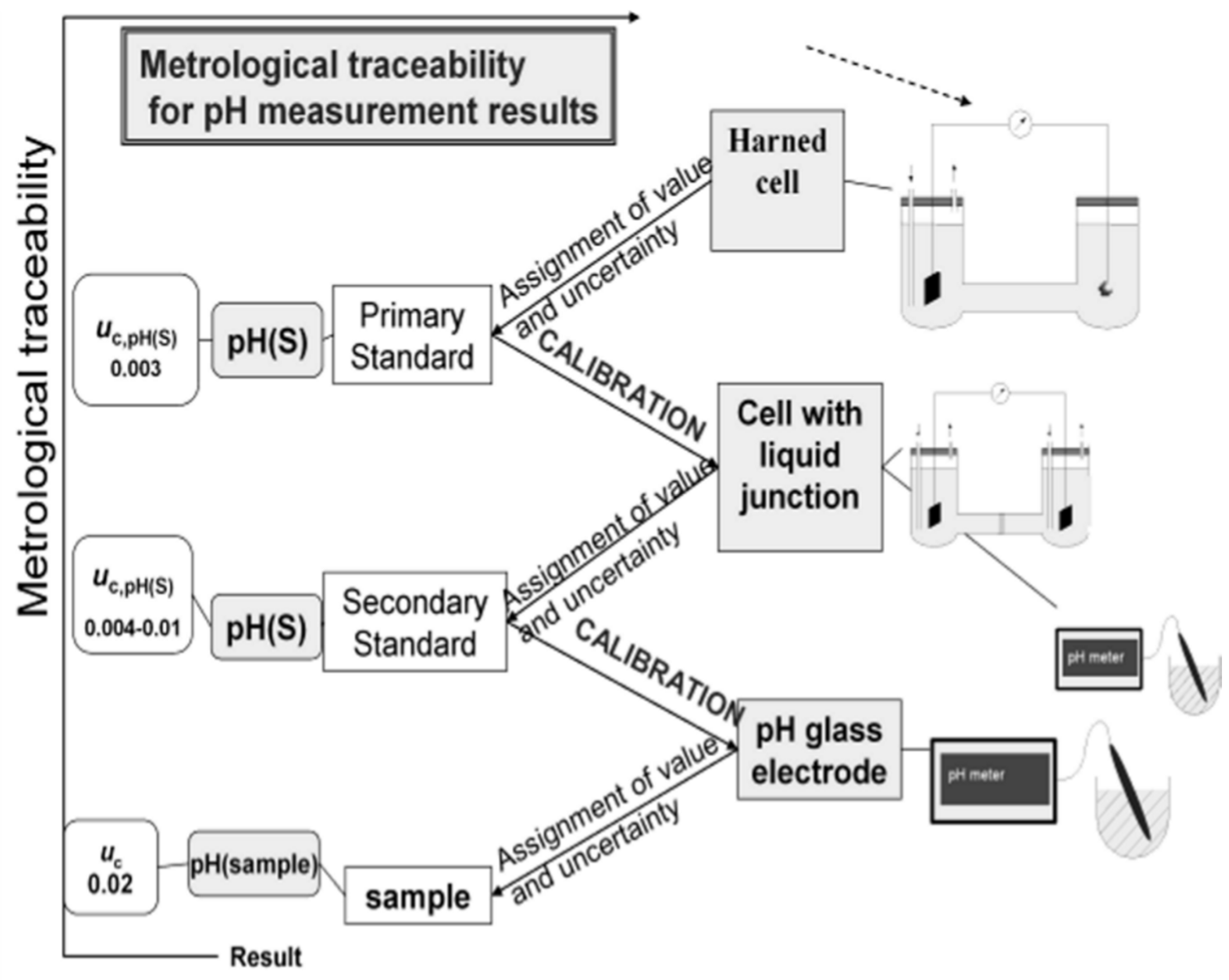
Figure 1 schematically represents the unbroken chain that links the various levels of metrological quality for pH, below the Primary Level, with the corresponding uncertainty target values [
6,
7] for aqueous solutions up to an ionic strength of 0.1 mol·kg
−1. Above this metrological level an additional source of uncertainty, 0.01, is introduced by the purely electrostatic Debye-Hückel model with the Bates-Guggenheim convention for the distance of closest approach of chloride ions, adopted for the assessment of the individual activity coefficient, γ
Cl− [
2].
Figure 1.
Metrological traceability scheme for pH.
Uc denotes the expanded measurement uncertainty (coverage factor
k = 2; the value of the measurand lies with a probability of approximately 95% within the interval of values) assigned to the pH values obtained for aqueous solutions up to an ionic strength of 0.1 mol·kg
−1 [
7].
Figure 1.
Metrological traceability scheme for pH.
Uc denotes the expanded measurement uncertainty (coverage factor
k = 2; the value of the measurand lies with a probability of approximately 95% within the interval of values) assigned to the pH values obtained for aqueous solutions up to an ionic strength of 0.1 mol·kg
−1 [
7].
For higher ionic strength aqueous solutions, e.g., seawater,
I ≈ 0.7 mol·kg
−1, a more elaborate model, as it is the Pitzer model, accounting for electrostatic and specific interactions [
8], is bound to match reality more closely.
In this work, aiming at addressing seawater, a strategy is presented for the adoption of experimentally assessed mean activity coefficients,
. Primary potentiometric measurements were performed in a series of acidic aqueous solutions of known concentrat
ion, consistently approaching a seawater matrix, ASW, for the assessment of experimental values of the acidity function, p(
aH+γ
Cl−) and mean activity coefficients,
. This allows evaluation of p
mH+, with the corresponding uncertainty, without extra-thermodynamic assumptions, thus establishing full traceability to the mole. Mean activity coefficients can also be calculated,
, upon taking into account a value of
mH+ derived from the literature value for the acidity constant of the hydrogen sulphate ion, Ka (HSO
4−) [
9]. Compatibility with mean activity coefficients calculated from the semi empirical Pitzer model equations
, validates the use of the model [
10], also available for single ion activity coefficients.
2. Method
Primary pH = p
aH+ values, are conventionally assigned [
2] to primary standard pH buffer solutions (S) of ionic strength,
I ≤ 0.1 mol·kg
−1, through a primary method, pH (S). This includes measurement of Harned cell (H+ sensitive hydrogen gas electrode and Cl
− sensitive silver, silver chloride electrode, without transference) potentials,
E, calculations with the Nernst equation (Equation (1)) and adoption of extra-thermodynamic assumptions concerning models of electrolyte solutions, for the assignment of mean or single activity coefficients:
where
E0 is the standard cell potential, assessed from measurement in 0.01 mol·kg
−1 HCl,
R is the gas constant,
T is the absolute temperature and
F is the Faraday constant.
This equation can be rearranged to give the acidity function, p(
aH+γ
Cl−), (Equation (2)):
solely expressed in terms of experimentally available quantities:
pH (S) values can be calculated from the acidity function by adoption of a conventional value to the activity coefficient of the chloride ion, γCl−.
By adopting the purely electrostatic Debye-Hückel model with the Bates–Guggenheim convention for the chloride ion, γ
Cl−, valid to ionic strengths,
I, below 0.1 mol·kg
−1, and assuming the value 0.01 in pH for the respective uncertainty, pH becomes traceable to the internationally accepted SI [
2]. Above this value, the model is no longer valid and the use of the Pitzer model [
8] has been debated.
The experimental procedure is, nevertheless, the basis for the assessment of the mean activity coefficient,
, for solutions of known
mCl− and
mH+, independent of model assumptions:
Since it is:
the standard uncertainty of the acidity function,
u[p(
aH+γ
Cl−)], can be calculated [
11] by Equation (10).
where
pH
2 is the partial pressure of hydrogen in the cell and ∆
E is the bias potential of the Ag/AgCl electrodes.
The uncertainty of p
mH (S) is assessed through Equations (11)–(13).
where
Through the application of this methodology to proper selected standard pH buffer solutions (S), for which chloride concentration, mCl−, and valid γ± values have been assessed, it is possible to obtain pmH(S). Making the reference buffers further available for the calibration of measuring devices, allows evaluation of pmH+ values for unknown aqueous samples, based on experimental values, hence fully traceable to the mole. This is of particular relevance for speciation studies, in environmental sciences and toxicological studies.
The two quantities, paH+ and pmH+, are related through the activity coefficient of the single hydrogen ion, γH+.
Activity coefficients, γ
±, γ
H+ and γ
Cl− can also be calculated by means of Pitzer electrolyte solutions model equations [
8,
12,
13,
14], thus enabling assessment of the consistency between experimental and model approaches.
Assessed by either potentiometry with the glass combination pH electrode, or by other recommended instrumental method for evaluation of hydrogen ion signal, measured pH or pmH+ values will always be affected by an uncertainty equal or bigger than the one respectively associated to the reference pH (S), or pmH(S) values assigned to the calibrating solutions, S.
In the particular case of seawater, the methodology can be applied to, e.g., a Tris-TrisHCl reference buffer prepared in a matrix of artificial seawater, ASW [
15,
16] which is becoming widely adopted by the oceanographic community. UV-Vis spectrophotometry, with m-cresol purple indicator, has gained support as an alternative to potentiometry with pH electrodes [
17].
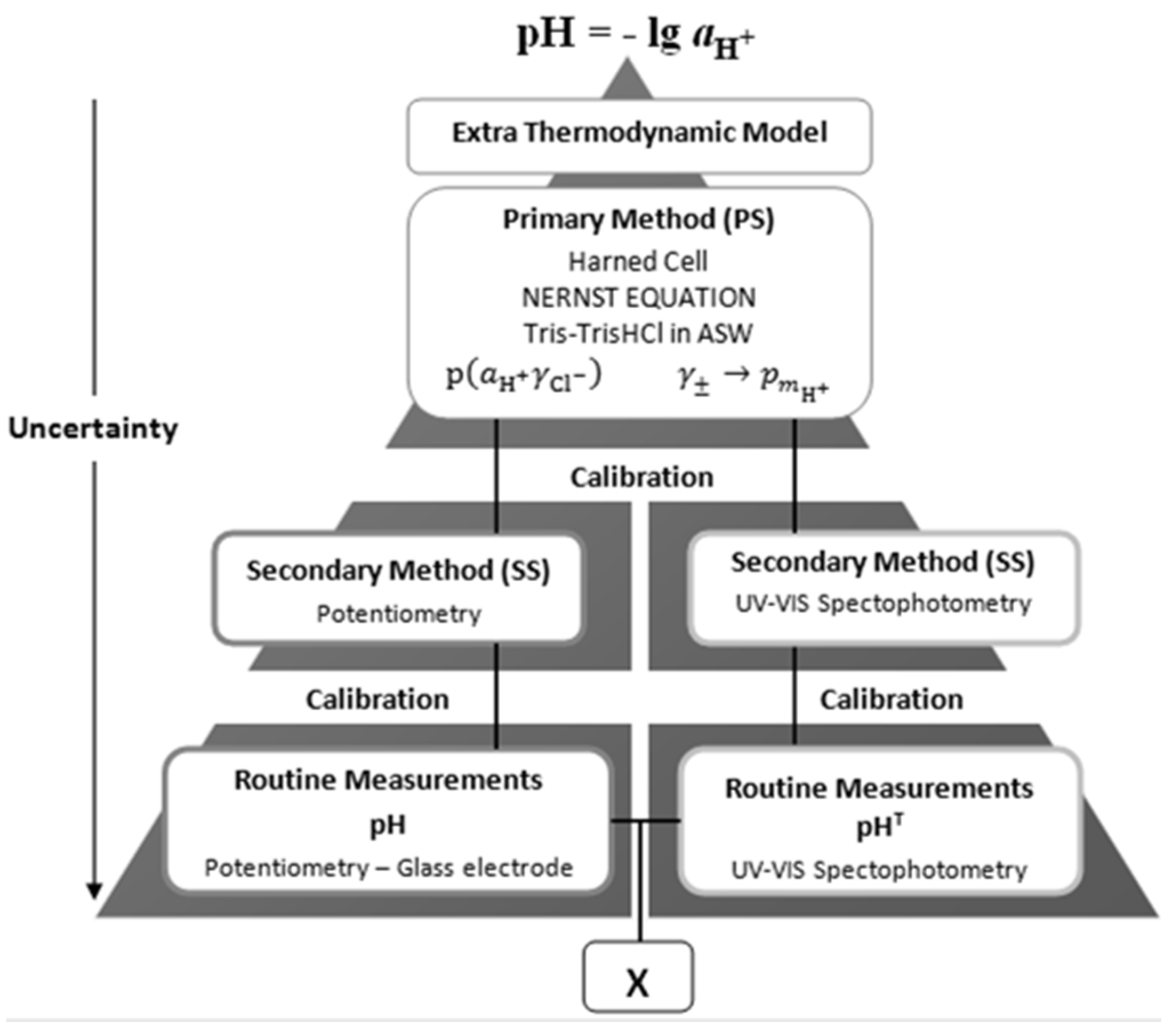
Traceability of results to common references is a key issue for ensuring their comparability and enabling interpretation in terms of the physical-chemical meaning of the quantities, pH or p
mH+, hence on the properties of the aquatic systems under study. This is illustrated by a double traceability chain, represented schematically by
Figure 2, which enables assessment of compatibility of measured results [
18].
Figure 2.
Schematic representation of a double traceability chain, showing traceability of two different types of analytical signals pertaining to hydrogen ion, H+, to common references of pH or pmH+, and higher up to the conceptually defined pH value.
Figure 2.
Schematic representation of a double traceability chain, showing traceability of two different types of analytical signals pertaining to hydrogen ion, H+, to common references of pH or pmH+, and higher up to the conceptually defined pH value.
3. Results and Discussion
Harned cell potentials were measured in acidic saline solutions approaching seawater composition, 0.01 mol·kg
−1 HCl + (NaCl + KCl + Na
2SO
4 + CaCl
2 + MgCl
2), at
I = 0.67 mol·kg
−1 [
19]. All measurements were performed at 25 °C [
10].
Solid reagents were of the highest purity grade (≥99.99%). Hydrochloric acid stock solutions were prepared from Merck Suprapur
® 30% HCl solution and were reassessed by titration against tris(hydroxymethyl) methylamine (Sigma-Aldrich ≥99.8% purity, supplied by Química, S.L., Sintra, Portugal) according to reference procedures [
20]. All solutions were prepared using high purity Millipore
® Milli-Q Advantage water, with resistivity higher than 18.2 MΩ·cm.
Recommended procedures have been followed [
2] ensuring experimentally assessed values of acidity function, p(
aH+γ
Cl−), mean activity coefficients,
, hence also p(
mH+). Mean activity coefficients calculated from experimental data,
, for sulphate-free solutions were co-opted for solutions of the same ionic strength where sodium sulphate substituted an equivalent amount of sodium chloride. Mean activity coefficients can also be calculated,
, upon taking into account a value of
mH+ based on the literature value for the acidity constant of the hydrogen sulphate ion, Ka (HSO
4−).
Mean activity coefficients have also been calculated by means of Pitzer model equations, at 25 °C.
Assessment of compatibility between
,
and
, for approximately 95% confidence level, supports consistency of the Pitzer model for the different involved interactions [
10].
The standard uncertainties for
were obtained for three different background solutions of different complexity approaching seawater composition,
Table 1, respectively:
Solution A—0.01 mol·kg−1 HCl + NaCl
Solution B—0.01 mol·kg−1 HCl + (NaCl + KCl + CaCl2 + MgCl2)
Solution C—0.01 mol·kg−1 HCl + (NaCl + KCl + Na2SO4 + CaCl2 + MgCl2)
The value of
for solution B has been imported into solution C, which allowed calculation of the corresponding
mH+. In parallel, as an alternative procedure for this later, Ka = 1.2 × 10
−2 [
8], was used to calculate
mH+, which on its turn led to
.
Values obtained for the uncertainty components of p
mH(S), (Equation (12)), for HCl in saline background, are also presented in
Table 1. These values lead to estimation of the combined uncertainty
u(p
mH+).
Table 1.
Acidity function p(aH+γCl−) and pmH+ values with their respective uncertainty, u, budgets assessed in different background solutions: A, B and C.
Table 1.
Acidity function p(aH+γCl−) and pmH+ values with their respective uncertainty, u, budgets assessed in different background solutions: A, B and C.
| Solution | γ± | u(γ±) | u(2lgγ±) | p(aH+γCl−) | u(paH+γCl−) | pmH+ | u(pmH+) |
|---|
| A * | 0.7440 | 0.0085 | 0.010 | 2.2939 | 0.0038 | 2.037 | 0.011 |
| B * | 0.7284 | 0.020 | 0.024 | 2.2919 | 0.0038 | 2.017 | 0.024 |
| C * | 0.7284 | 0.020 | 0.024 | 2.2628 | 0.0038 | 1.988 | 0.024 |
| C ** | 0.7249 | 0.046 | 0.056 | 2.2628 | 0.0038 | 1.983 | 0.056 |
The considerably higher uncertainty value u(2lgγ±) for the sulphate containing solution (C**) is due to the high impact of the acidity constant, Ka(HSO4−), on the calculation of the uncertainty of .
The contribution of the uncertainty introduced by γ
± to p
mH+ has been calculated for the two values of mean activity coefficient,
and
, and for the possible scenario of an order of magnitude lower uncertainty level, C′,
Table 2.
Table 2.
Uncertainty introduced by γ± to the calculation of pmH+ for acidic solutions in seawater background, function of its uncertainty level.
Table 2.
Uncertainty introduced by γ± to the calculation of pmH+ for acidic solutions in seawater background, function of its uncertainty level.
| Solution | γ± | uγ± | u(2lgγ±) | u(pmH+) | UpmH+ (Expanded, k = 2) |
|---|
| CExp | 0.7284 | 0.020 | 0.024 | 0.024 | 0.048 |
| C′Exp | 0.7284 | 0.0020 | 0.0024 | 0.0024 | 0.0048 |
| CCalc | 0.7249 | 0.046 | 0.056 | 0.056 | 0.12 |
| C′Calc | 0.7249 | 0.0046 | 0.0056 | 0.0056 | 0.012 |
| CPtz | 0.76998 | 0.00518 | 0.0058 | 0.0058 | 0.012 |
The major influence on the estimation of u(pmH+) comes from the uncertainty of the mean activity coefficient, uγ±. As shown, its effect, u(2lgγ±), can be lowered upon improvement of the quality of the raw data .
4. Conclusions
A series of acidic aqueous solutions in single and complex chloride media of known concentration, consistently approaching a seawater matrix, ASW, were prepared and subject to primary potentiometric measurements for the assessment of experimental values of the acidity function, p(aH+γCl−) and mean activity coefficients, .
Assessment of the mean activity coefficient, γ±, for reference pH buffer standards, S, allows further calculation of their respective concentrations, mH+, hence −lgmH+ = pmH+ = pmH(S).
Compatibility of experimental values, , and model assessed, , enables adoption of either approach with equivalent quality.
Adding to the uncertainty of the acidity function, (paH+γCl−) the major uncertainty component largely contributing to the combined uncertainty of pmH+, u(pmH+), comes from (γ±).
Application of the developed methodology to adequately chosen reference buffer solutions, S, leads to assignment of pmH(S) values with their respective uncertainties. This enables calibration of measuring devices in terms of pmH+, thus ensuring fully traceable sample pmH+values.