Simulation of Summer Hourly Stream Flow by Applying TOPMODEL and Two Routing Algorithms to the Sparsely Gauged Lhasa River Basin in China
Abstract
:1. Introduction
| Basin | Country | Area (km2) | Elevation (m) | Annual Precipitation (mm/year) | Number of Rain Gauges | Number of Stream Station | Reference |
|---|---|---|---|---|---|---|---|
| Bukmoon | South Korea | 0.15 | 120–341 | 1487 | 1 | 1 | [6] |
| Can Vila | Spain | 0.56 | -- | 925 | 2 | 1 | [7] |
| Slapton Wood | UK | 0.94 | -- | 1050 | -- | -- | [8] |
| Hafren | UK | 3.5 | -- | 2400 | 1 | 1 | [9] |
| Peacheater Creek | USA | 64 | 248.1–432.5 | -- | -- | -- | [10] |
| Lossie | UK | 216 | -- | 830 | 1 | 1 | [11] |
| Yasu River | Japan | 387 | -- | -- | 4 | 1 | [12] |
| Ardeche at Sauze St Martin | France | 2240 | 571 | 1430 | -- | -- | [13] |
| G1 ROOF | Sweden | 6300 | 123–143 | 1020 | -- | -- | [14] |
2. Study Area and Related Literature
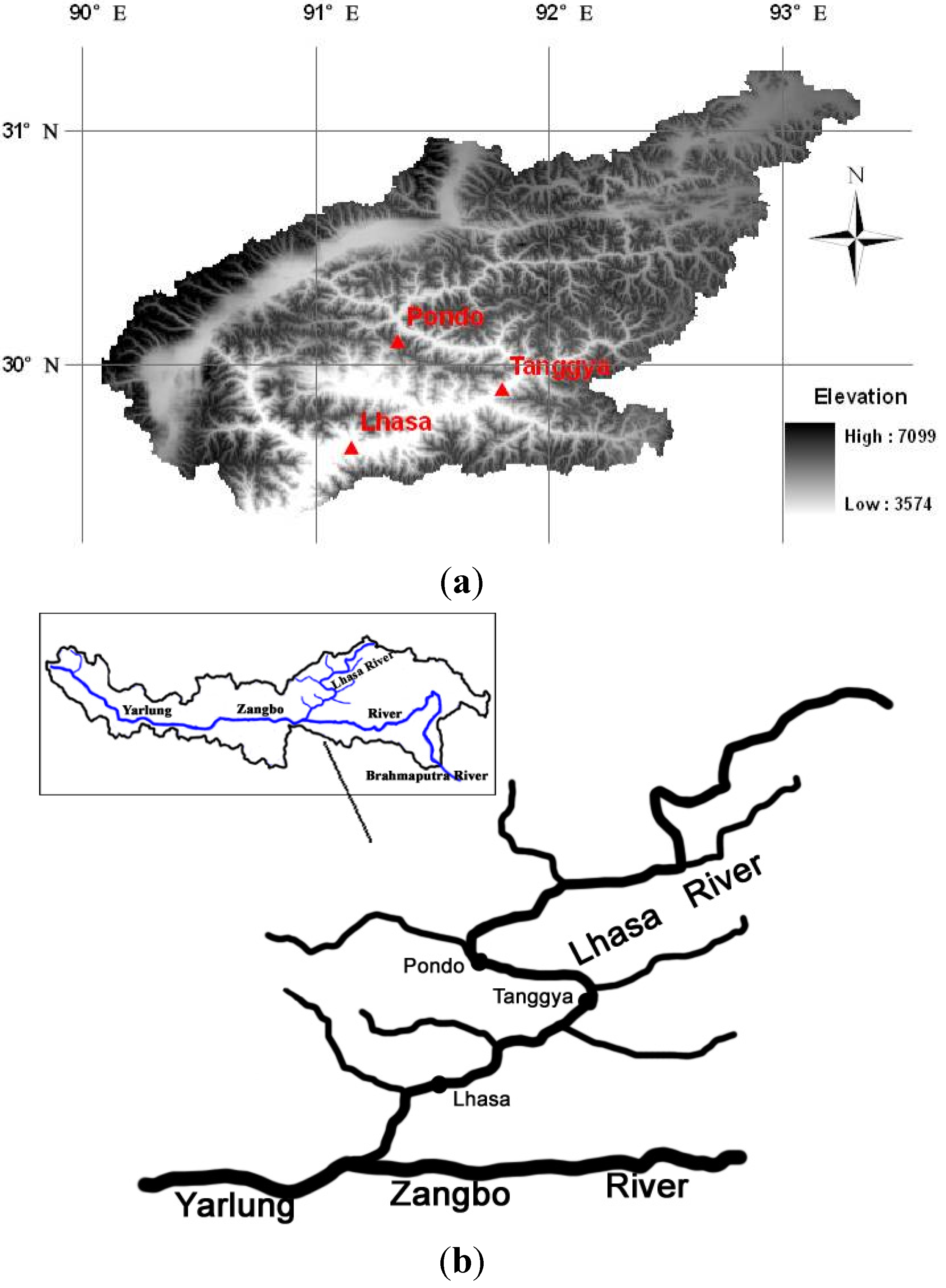
| Hydrological Station | Location | Elevation (m) | Watershed Area (km2) | Mean Annual Precipitation (mm) |
|---|---|---|---|---|
| Pondo | 30°06′ N, 91°21′ E | 4050 | 16,370 | 530 |
| Tanggya | 29°54′ N, 91°48′ E | 3850 | 20,367 | 520 |
| Lhasa | 29°39′ N, 91°09′ E | 3670 | 26,225 | 447 |
3. Data and Methodology
3.1. Research Data
3.2. TOPographic Model (TOPMODEL)
3.3. Original Routing Algorithm
3.4. New Routing Algorithm
3.5. Criteria for Evaluating Model Performance
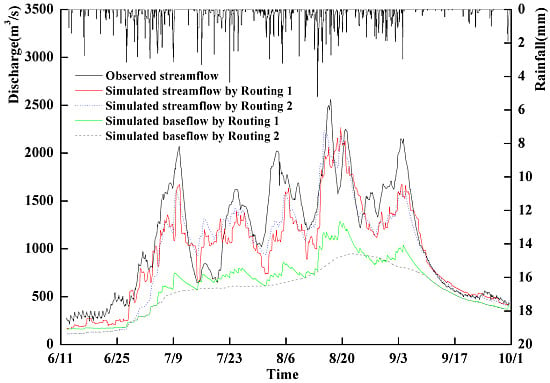
4. Results and Discussion
| Period | Year | Routing 1 | Routing 2 | ||||
|---|---|---|---|---|---|---|---|
| NE | RE (%) | r | NE | RE (%) | r | ||
| Calibration | 1999 | 0.76 | 5 | 0.89 | 0.73 | 9 | 0.87 |
| 2000 | 0.70 | −6 | 0.85 | 0.77 | −5 | 0.90 | |
| Verification | 1998 | 0.77 | −12 | 0.91 | 0.78 | −12 | 0.91 |
| Period | Year | Observed Peak Flow | Simulated Peak Flow by Routing 1 | Simulated Peak Flow by Routing 2 | |||||
|---|---|---|---|---|---|---|---|---|---|
| Time (MM-DD h) | Discharge (m3/s) | Time (MM-DD h) | Discharge (m3/s) | Relative Error (%) | Time (MM-DD h) | Discharge (m3/s) | Relative Error (%) | ||
| Verification | 1998 | 07-10 10:00 | 2070 | 07-10 11:00 | 1671 | −19 | 07-09 17:00 | 1608 | −22 |
| 1998 | 08-17 02:00 | 2560 | 08-19 15:00 | 2267 | −11 | 08-15 14:00 | 2236 | −13 | |
| Calibration | 1999 | 06-30 20:00 | 1190 | 07-02 19:00 | 1140 | −4 | 07-03 08:00 | 1014 | −15 |
| 1999 | 09-02 00:00 | 1590 | 08-31 16:00 | 1659 | 4 | 08-31 16:00 | 1715 | 8 | |
| 2000 | 08-03 10:00 | 1610 | 08-03 15:00 | 1915 | 19 | 08-03 10:00 | 1774 | 10 | |
| 2000 | 08-24 00:00 | 1930 | 08-22 22:00 | 1836 | −5 | 08-22 17:00 | 1828 | −5 | |
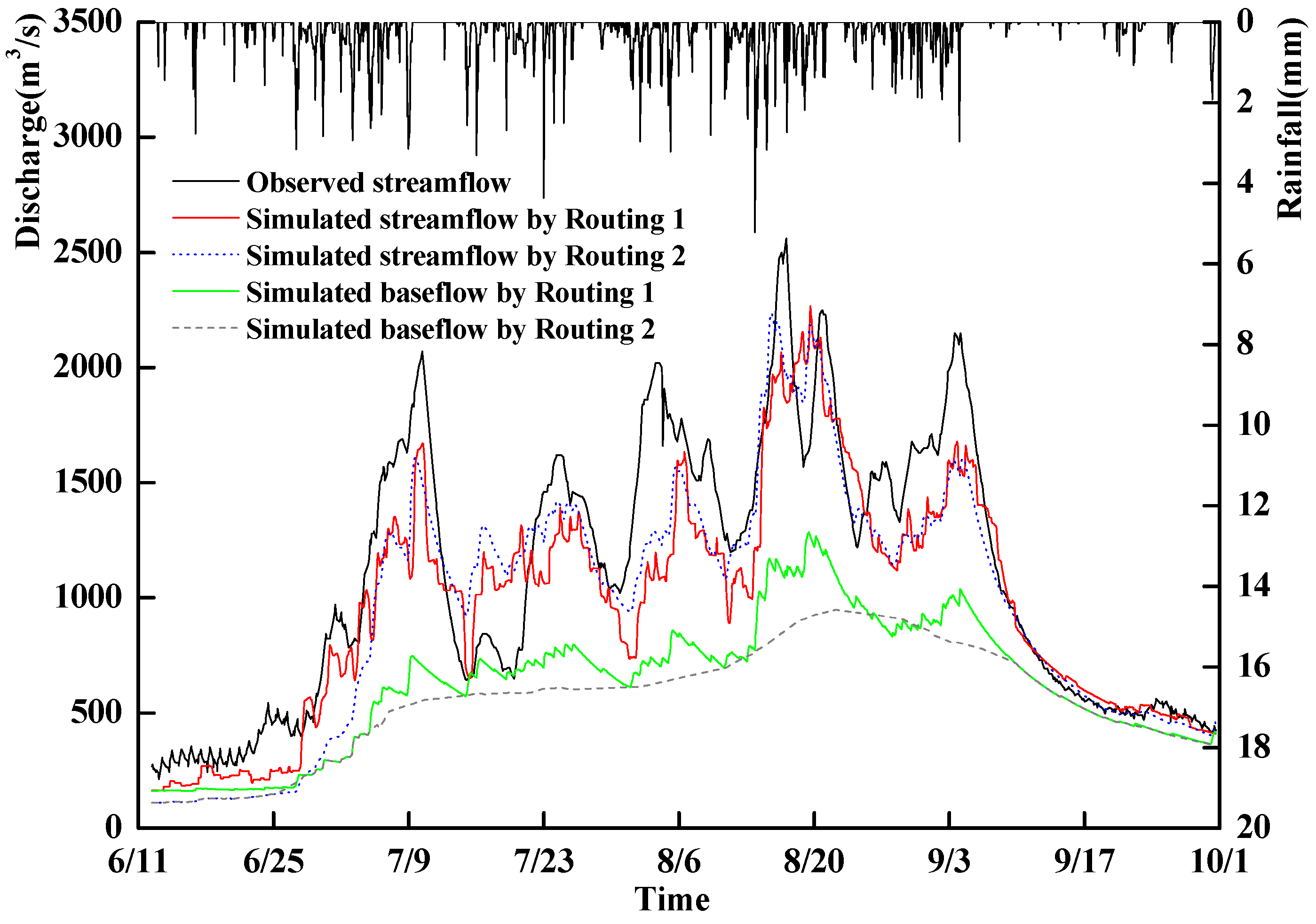
| Time | Correlation Coefficient | |
|---|---|---|
| Routing 1 | Routing 2 | |
| 5 July 1998 04:00 to 12 July 1998 16:00 | 0.81 | 0.83 |
| 21 July 1998 10:00 to 28 July 1998 18:00 | 0.62 | 0.73 |
| 31 July 1998 13:00 to 10 August 1998 00:00 | 0.60 | 0.72 |
| 15 August 1998 20:00 to 17 August 1998 18:00 | 0.59 | 0.71 |
| 24 August 1998 20:00 to 7 September 1998 17:00 | 0.69 | 0.89 |
| 22 August 1999 05:00 to 26 August 1999 15:00 | 0.63 | 0.70 |
| 28 August 1999 02:00 to 7 September 1999 04:00 | 0.84 | 0.84 |
| 12 September 1999 11:00 to 20 September 1999 01:00 | 0.65 | 0.68 |
| 1 August 2000 10:00 to 9 August 2000 00:00 | 0.82 | 0.83 |
| 19 August 2000 00:00 to 31 August 2000 06:00 | 0.86 | 0.88 |
| 12 September 2000 11:00 to 20 September 2000 01:00 | 0.72 | 0.75 |
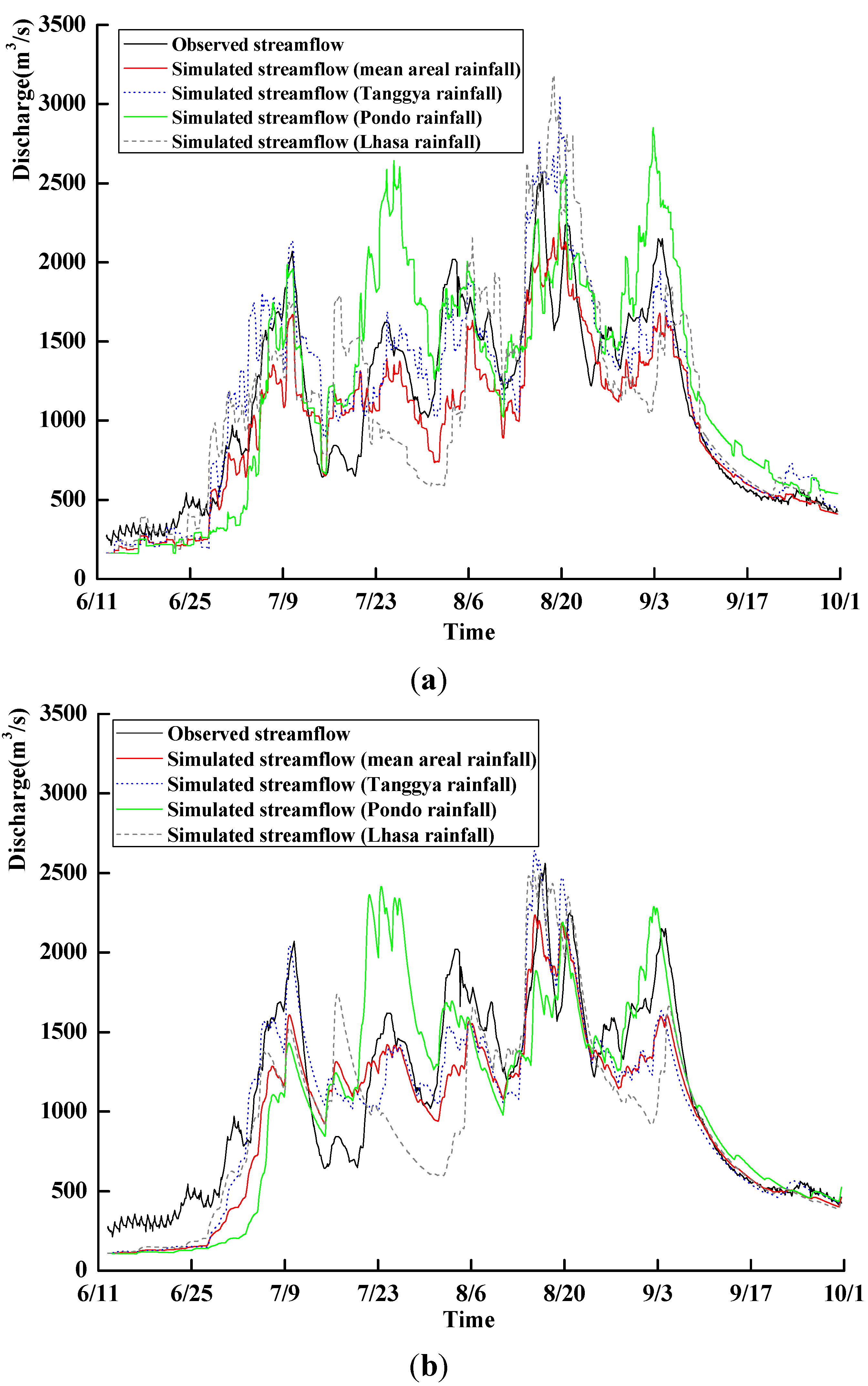
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Beven, K.J.; Kirkby, M.J. A physically based variable contributing area model of basin hydrology. Hydrol. Sci. Bull. 1979, 24, 43–69. [Google Scholar] [CrossRef]
- Beven, K.J.; Lamb, R.; Quinn, P.F.; Romanowicz, R.; Freer, J. TOPMODEL. In Computer Models of Watershed Hydrology; Singh, V.P., Ed.; Water Resources Publications: Highlands Ranch, CO, USA, 1995; pp. 627–668. [Google Scholar]
- Murphy, J.C.; Knight, R.R.; Wolfe, W.J.; Gain, W.S. Predicting ecological flow regime at ungaged sites: A comparison of methods. River Res. Appl. 2013, 29, 660–669. [Google Scholar] [CrossRef]
- Zhu, D.; Peng, D.Z.; Cluckie, I.D. Statistical analysis of error propagation from radar rainfall to hydrological models. Hydrol. Earth Syst. Sci. 2013, 17, 1445–1453. [Google Scholar] [CrossRef]
- Peng, D.Z.; Xu, Z.X.; Qiu, L.H.; Zhao, W.M. Distributed rainfall-runoff simulation for an unclosed river basin with complex river system: A case study of lower reach of the Wei River, China. J. Flood Risk Manag. 2014, 2014. [Google Scholar] [CrossRef]
- Choi, H.T.; Beven, K.J. Multi-Period and multi-criteria model conditioning to reduce prediction uncertainty in an application of TOPMODEL within the GLUE framework. J. Hydrol. 2007, 332, 316–336. [Google Scholar] [CrossRef]
- Gallart, F.; Latron, J.; Llorens, P.; Beven, K.J. Using internal catchment information to reduce the uncertainty of discharge and baseflow predictions. Adv. Water Resour. 2007, 30, 808–823. [Google Scholar] [CrossRef]
- Beven, K.J.; Freer, J. A dynamic TOPMODEL. Hydrol. Process. 2001, 15, 1993–2011. [Google Scholar] [CrossRef]
- Page, T.; Beven, K.J.; Freer, J.; Neal, C. Modelling the chloride signal at Plynlimon, Wales, using a modified dynamic TOPMODEL incorporating conservative chemical mixing (with uncertainty). Hydrol. Process. 2007, 21, 292–307. [Google Scholar] [CrossRef]
- Wu, S.; Li, J.; Huang, G.H. Modeling the effects of elevation data resolution on the performance of topography-based watershed runoff simulation. Environ. Model. Softw. 2007, 22, 1250–1260. [Google Scholar] [CrossRef]
- Cameron, D. An application of the UKCIP02 climate change scenarios to flood estimation by continuous simulation for a gauged catchment in the northeast of Scotland, UK (with uncertainty). J. Hydrol. 2006, 328, 212–226. [Google Scholar] [CrossRef]
- Chiang, S.; Tachikawa, Y.; Takara, K. Hydrological model performance comparison through uncertainty recognition and quantification. Hydrol. Process. 2007, 21, 1179–1195. [Google Scholar] [CrossRef]
- Clark, D.B.; Gedney, N. Representing the effects of subgrid variability of soil moisture on runoff generation in a land surface model. J. Geophys. Res. 2008, 113. [Google Scholar] [CrossRef]
- Seibert, J.; Bishop, K.H.; Nyberg, L. A test of TOPMODEL’s ability to predict spatially distributed groundwater levels. Hydrol. Process. 1997, 11, 1131–1144. [Google Scholar] [CrossRef]
- Huang, X.; Sillanpaa, M.; Gjessing, E.T.; Peraniemi, S.; Vogt, R.D. Water quality in the southern Tibetan Plateau: Chemical evaluation of the Yarlung Tsangpo (Brahmaputra). River Res. Appl. 2011, 27, 113–121. [Google Scholar] [CrossRef]
- Peng, D.Z.; Du, Y. Comparative analysis of several Lhasa River basin flood forecast models in Yarlung Zangbo River. In Proceedings of the 4th International Conference on Bioinformatics and Biomedical Engineering (iCBBE), Chengdu, China, 18–20 June 2010.
- Qiu, L.H.; You, J.J.; Qiao, F.; Peng, D.Z. Simulation of snowmelt runoff in the ungauged basin based on MODIS: A case study in Lhasa River basin. Stoch. Environ. Res. Risk Assess. 2014, 28, 1577–1585. [Google Scholar] [CrossRef]
- Wu, T.; Yuan, P.; Dai, L.; Ding, Y.; Xie, S. Research on the stream flow forecast methods of Tibet Lhasa River. Water Conserv. Sci. Technol. Econ. 2005, 11, 77–79. (In Chinese) [Google Scholar]
- Zhang, X.Y.; Dong, Z.C.; Wang, J.Q.; Zhao, J.X. Method of flood forecasting for Niyang River Basin of Yarlung Zangbo River. J. Hohai Univ. (Nat. Sci.) 2005, 33, 530–533. (In Chinese) [Google Scholar]
- Zhang, Z.G.; Xu, Z.X.; Gong, T.L. Cascade-correlation algorithm and its application in monthly stream flow forecasting. Adv. Water Sci. 2007, 18, 114–117. (In Chinese) [Google Scholar]
- Chen, J.; Kumar, P. Topographic influence on the seasonal and inter-annual variation of water and energy balance of basins in North America. J. Clim. 2001, 14, 1989–2014. [Google Scholar] [CrossRef]
- Chen, J.; Sun, L. Using MODIS EVI to detect vegetation damage caused by the 2008 ice and snow storms in south China. J. Geophys. Res.-Biogeosci. 2010, 115. [Google Scholar] [CrossRef]
- Beven, K.J. Rainfall-Runoff Modelling; John Wiley & Sons Ltd.: Chichester, UK, 2001. [Google Scholar]
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied Hydrology; McGraw-Hill Inc.: New York, NY, USA, 1988; pp. 211–213. [Google Scholar]
- Nash, J.E. The form of the instantaneous unit hydrograph. Int. Assoc. Sci. Hydrol. 1957, 45, 114–121. [Google Scholar]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Murty, K.G. Linear Programming; John Wiley & Sons Inc.: New York, NY, USA, 1983. [Google Scholar]
- McDonnell, J.J. A rationale for old water discharge through macropores in a steep, humid catchment. Water Resour. Res. 1990, 26, 2821–2832. [Google Scholar] [CrossRef]
- Kendall, C.; McDonnell, J.J. Isotope Tracers in Catchment Hydrology; Elsevier Science B.V.: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Tibetan Bureau of Hydrology. Handbook of Hydrological Forecasting; Tibet Water Resources Department: Lhasa, China, 2000. (In Chinese) [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, D.; Chen, J.; Fang, J. Simulation of Summer Hourly Stream Flow by Applying TOPMODEL and Two Routing Algorithms to the Sparsely Gauged Lhasa River Basin in China. Water 2015, 7, 4041-4053. https://doi.org/10.3390/w7084041
Peng D, Chen J, Fang J. Simulation of Summer Hourly Stream Flow by Applying TOPMODEL and Two Routing Algorithms to the Sparsely Gauged Lhasa River Basin in China. Water. 2015; 7(8):4041-4053. https://doi.org/10.3390/w7084041
Chicago/Turabian StylePeng, Dingzhi, Ji Chen, and Jing Fang. 2015. "Simulation of Summer Hourly Stream Flow by Applying TOPMODEL and Two Routing Algorithms to the Sparsely Gauged Lhasa River Basin in China" Water 7, no. 8: 4041-4053. https://doi.org/10.3390/w7084041
APA StylePeng, D., Chen, J., & Fang, J. (2015). Simulation of Summer Hourly Stream Flow by Applying TOPMODEL and Two Routing Algorithms to the Sparsely Gauged Lhasa River Basin in China. Water, 7(8), 4041-4053. https://doi.org/10.3390/w7084041