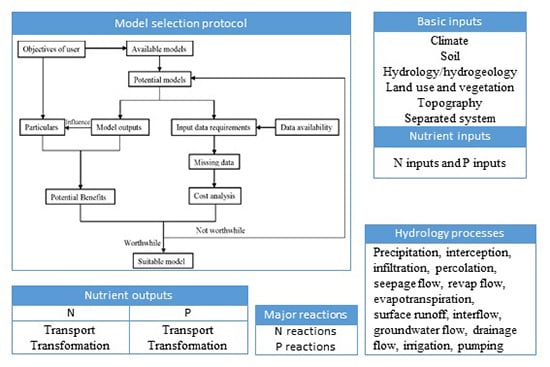
A Multi-Criteria Model Selection Protocol for Practical Applications to Nutrient Transport at the Catchment Scale
Abstract
:1. Introduction
2. Model Description
2.1. SWAT
2.2. SWIM
2.3. GWLF
2.4. AnnAGNPS
2.5. HSPF
3. Model Components Analysis
3.1. Surface and Subsurface Hydrological Components
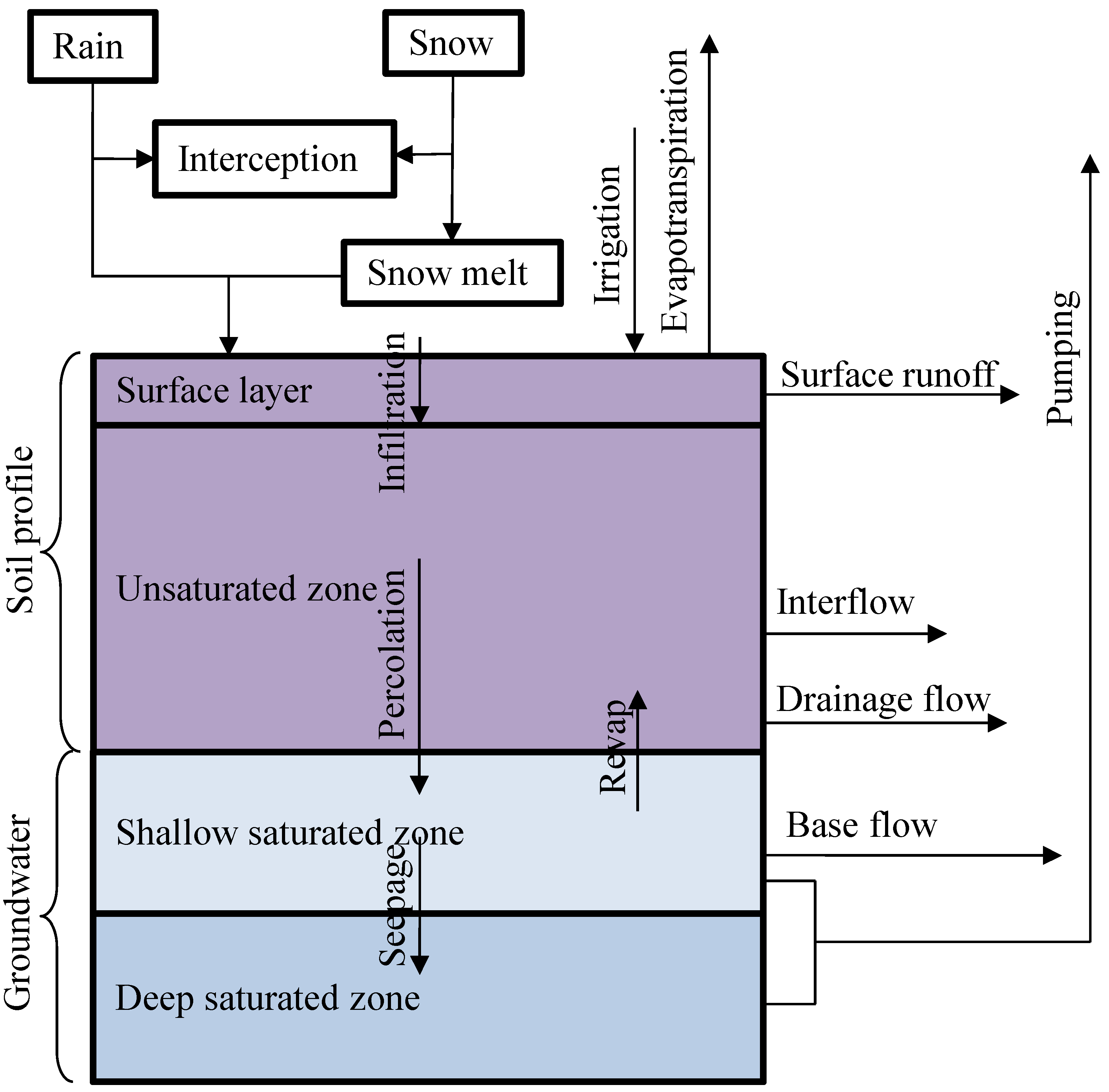
| SWAT | SWIM | GWLF | AnnAGNPS | HSPF |
|---|---|---|---|---|
| Surface Runoff | Surface runoff | Surface runoff | Surface runoff | Surface runoff |
| Infiltration | Infiltration | Infiltration | Infiltration | Infiltration |
| Evapotranspiration | Evapotranspiration | Evapotranspiration | Evapotranspiration | Evapotranspiration |
| Interflow | Interflow | Percolation flow | Interflow | Interflow |
| Percolation flow | Percolation flow | Base flow | Percolation flow | Percolation flow |
| Base flow | Base flow | Seepage flow | Drainage flow | Base flow |
| Revap flow | Revap flow | - | - | Interception |
| Pumping flow | Seepage flow | - | - | - |
| Interception | - | - | - | - |
| Drainage flow | - | - | - | - |
| Seepage flow | - | - | - | - |
3.2. Reactions
3.3. Input Requirements
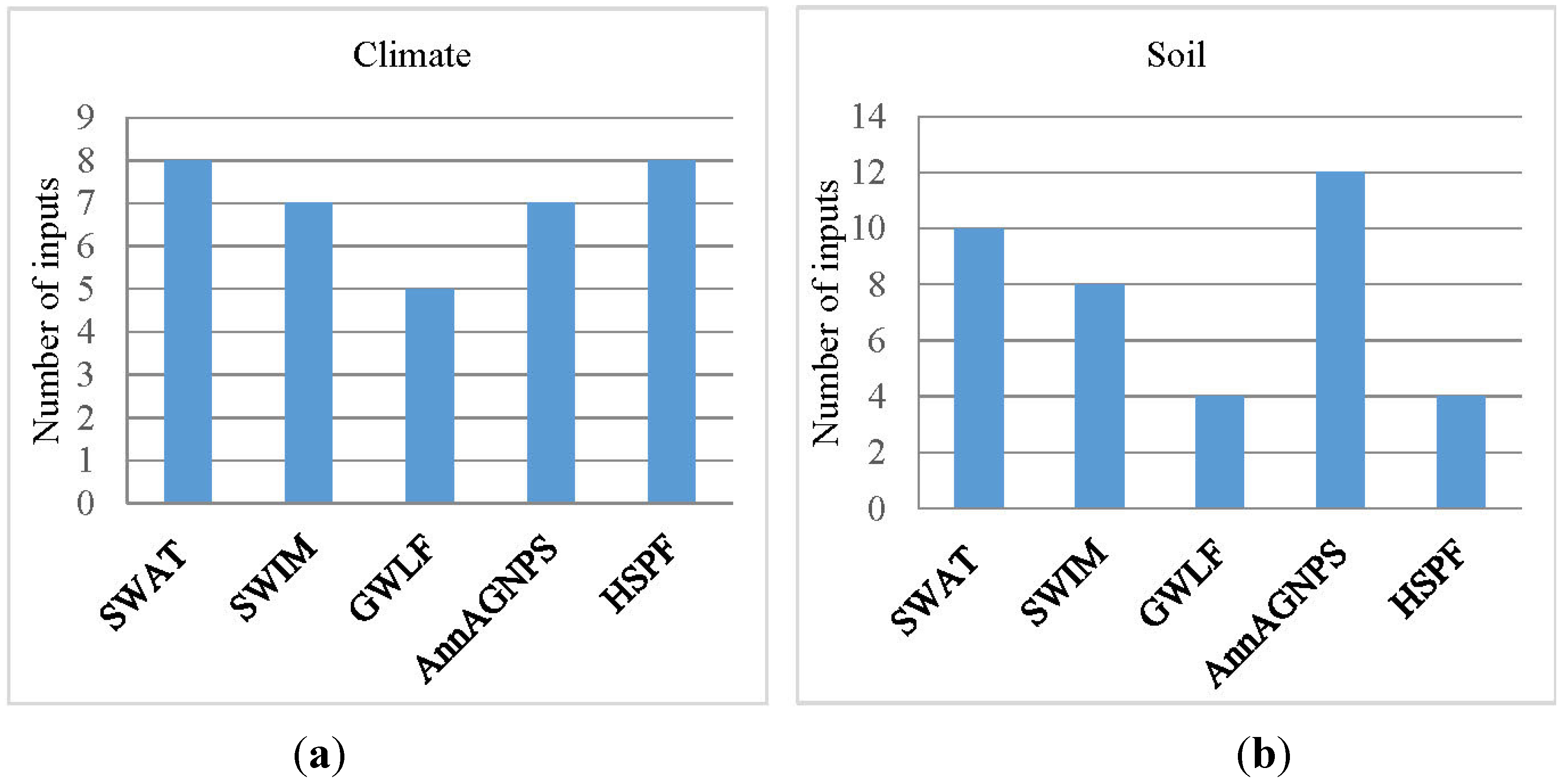
3.3.1. Basic Input Data
| Climate | SWAT | SWIM | GWLF | AnnAGNPS | HSPF |
| Rainfall | √ | √ | √ | √ | √ |
| Snow | √ | √ | √ | √ | √ |
| Air temperature | √ | √ | √ | √ | √ |
| Solar radiation | √ | √ | √ | √ | |
| Humidity/dew point | √ | (√) | √ | √ | |
| Wind speed | √ | (√) | √ | √ | |
| Carbon dioxide concentration | √ | ||||
| Evapotranspiration | √ | √ | √ | √ | √ |
| Daily daylight hours | √ | ||||
| Vapor pressure | √ | ||||
| Soil | SWAT | SWIM | GWLF | AnnAGNPS | HSPF |
| Depth/thickness | √ | √ | √ | √ | |
| Texture | √ | √ | √ | √ | |
| Temperature | √ | ||||
| Bulk density | √ | √ | √ | √ | |
| Initial soil water content/moisture | √ | √ | √ | √ | √ |
| Field capacity | (√) | √ | √ | ||
| Wilting point | (√) | √ | √ | ||
| Hydraulic conductivity | √ | √ | √ | ||
| Porosity | √ | √ | √ | ||
| Available water capacity | √ | √ | |||
| Organic matter | √ | ||||
| pH | √ | ||||
| Organic carbon content % | √ | √ | √ | ||
| CaCO3 content % | √ | ||||
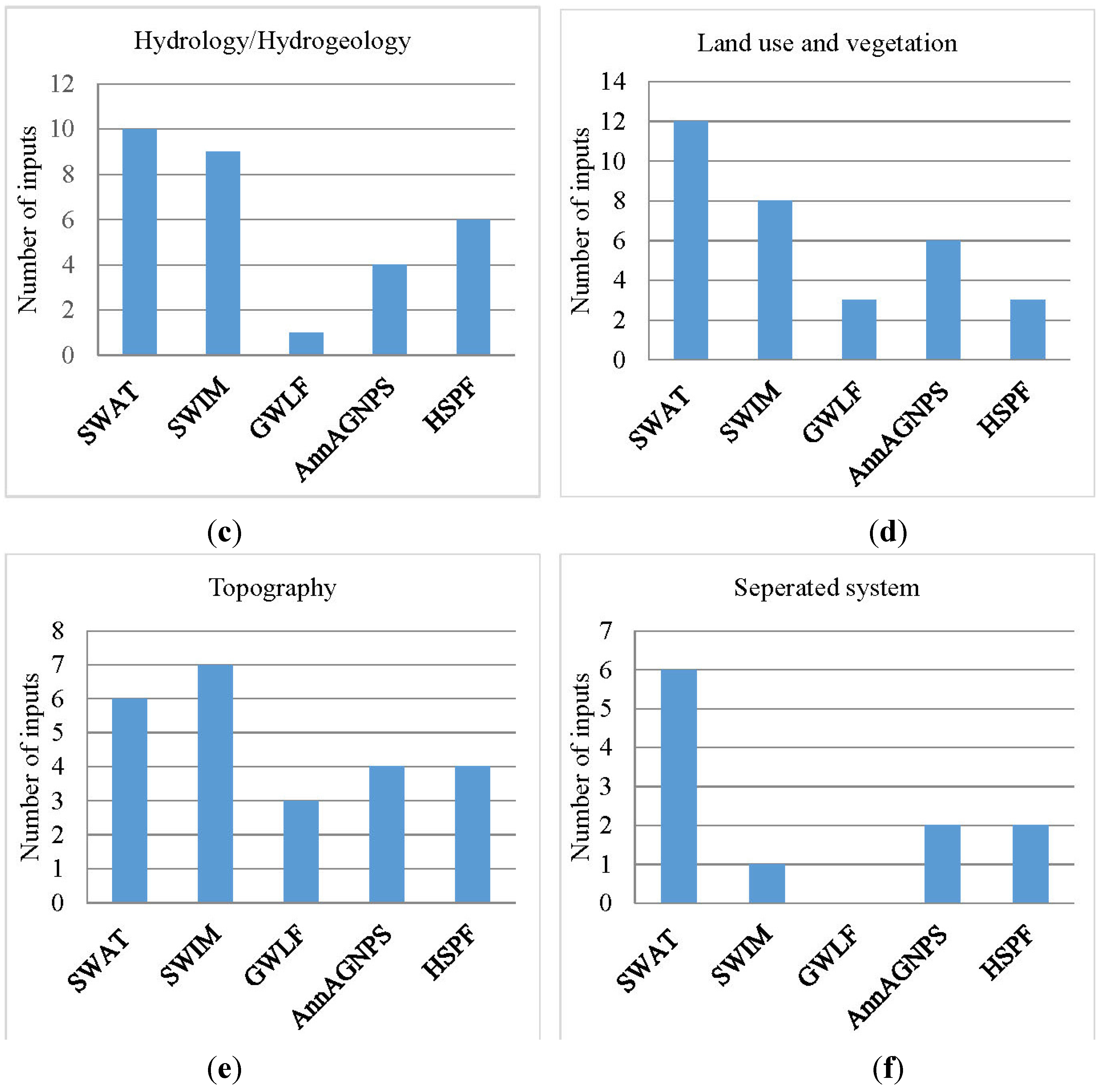
| Hydrology/Hydrogeology | |||||
| Water table height | √ | √ | √ | ||
| Hydraulic conductivity | √ | √ | √ | ||
| Specific yield of shallow aquifer | √ | √ | |||
| Groundwater extraction | √ | ||||
| Snow water content/snow melt | √ | √ | √ | √ | |
| Initial shallow aquifer storage | √ | √ | |||
| Revap storage | √ | √ | |||
| Recharge water | √ | √ | |||
| Drain spacing | √ | √ | |||
| Irrigation | √ | √ | |||
| Drainable volume of water stored in the saturated zone | √ | ||||
| Saturated depth from the imperious layer | √ | ||||
| Surface water storage | √ | ||||
| Active groundwater storage | √ | ||||
| Interflow storage | √ | ||||
| Lower zone storage | √ | ||||
| pH (water) | √ | ||||
| Land Use and Vegetation | SWAT | SWIM | GWLF | AnnAGNPS | HSPF |
| Land use | √ | √ | √ | √ | √ |
| Land cover | √ | √ | √ | √ | √ |
| Vegetation type | √ | √ | √ | √ | √ |
| Vegetation height | √ | ||||
| Leaf area index | √ | √ | |||
| Plant canopy height | √ | ||||
| Residue | √ | √ | √ | ||
| Total biomass | √ | √ | |||
| Base temperature for plant growth | √ | √ | |||
| Root depth | √ | √ | |||
| Fertilizing rate/amount | √ | √ | √ | ||
| Crop management/tillage operation | √ | √ | |||
| Topography | |||||
| Area | √ | √ | √ | √ | √ |
| Elevation | √ | √ | √ | √ | |
| Hillslope length | √ | √ | |||
| Hillslope steepness | √ | √ | |||
| Hillslope width | √ | ||||
| Land surface slope length | √ | √ | √ | √ | √ |
| Land surface slope steepness | √ | √ | √ | √ | √ |
| Separated System | |||||
| Channel system/in-stream system | √ | √ | √ | √ | |
| Tile drainage system | √ | √ | |||
| Pond system | √ | ||||
| Wetland system | √ | ||||
| Reservoir system | √ | √ | |||
| Pothole system | √ |
3.3.2. Nutrient Input Data
| Initial Soil Nitrogen | SWAT | SWIM | GWLF | AnnAGNPS | HSPF |
| Organic N | (√) | √ | √ | √ | |
| NO3 | (√) | √ | √ | √ | |
| NH4 | √ | √ | |||
| Fresh organic N | √ | ||||
| Normal fraction of N in plant biomass (crop-specific) | √ | √ | |||
| Nitrogen in runoff | |||||
| Dissolved N | √ | ||||
| Nitrogen in groundwater | |||||
| Dissolved N | √ | ||||
| Nitrogen in sediment | |||||
| Total N | √ | ||||
| Plant uptake nitrogen | |||||
| Total N | √ | ||||
| Urban sources | |||||
| Total N | √ | √ | √ | ||
| NO3 | √ | ||||
| Point sources | |||||
| Organic n | √ | ||||
| NO3 | √ | ||||
| NO2 | √ | ||||
| NH4 | √ | ||||
| Dissolved N | √ | ||||
| Fertilizer nitrogen (crop-specific) | |||||
| Organic N | √ | √ | |||
| Active organic N | √ | ||||
| Inorganic N | √ | √ | |||
| NH4 | √ | ||||
| Septic system | |||||
| Dissolved N in outflow | √ | ||||
| Dissolved N from ponded system | √ | ||||
| Total N | √ | ||||
| NO3 | √ | ||||
| NO2 | √ | ||||
| Organic N | √ | ||||
| NH4 | √ | ||||
| Initial nitrogen in pond | |||||
| Organic N | √ | ||||
| NO3 | √ | ||||
| Initial nitrogen in wetland | |||||
| Organic N | √ | ||||
| NO3 | √ | ||||
| Initial nitrogen in reservoir | SWAT | SWIM | GWLF | AnnAGNPS | HSPF |
| Organic N | √ | ||||
| NO3 | √ | √ | |||
| NO2 | √ | √ | |||
| NH4 | √ | ||||
| NH4 + NH3 | √ | ||||
| In-stream nitrogen | |||||
| Organic N | √ | ||||
| NO3 | √ | √ | |||
| NO2 | √ | √ | |||
| NH4 | √ | ||||
| NH4 + NH3 | √ | ||||
| Atmospheric deposition | |||||
| NO3 in rain | √ | √ | |||
| NH4 in rain | √ | ||||
| NO3 in dry deposition | √ | ||||
| NH4 in dry deposition | √ |
| Initial Soil Phosphorus | SWAT | SWIM | GWLF | AnnAGNPS | HSPF |
| Organic P | (√) | √ | √ | √ | |
| PO4 | √ | ||||
| Fresh organic P | √ | ||||
| Soluble P | (√) | ||||
| Labile inorganic P | √ | √ | |||
| Active inorganic P | √ | √ | |||
| Stable inorganic P | √ | √ | |||
| Normal fraction of P in plant biomass (crop-specific) | √ | √ | |||
| Phosphorus in runoff | |||||
| Dissolved P | √ | ||||
| Phosphorus in groundwater | |||||
| Dissolved P | √ | ||||
| Phosphorus in sediment | |||||
| Total P | √ | ||||
| Plant uptake Phosphorus | |||||
| Total P | √ | ||||
| Urban Sources | |||||
| Total P | √ | √ | √ | ||
| Point sources | |||||
| Organic P | √ | ||||
| Soluble P | √ | ||||
| Dissolved P | √ | ||||
| Fertilizer phosphorus (crop-specific) | |||||
| Organic P | √ | √ | |||
| Active organic P | √ | ||||
| Inorganic P | √ | √ | |||
| Septic system | |||||
| Dissolved P in outflow | √ | ||||
| Dissolved P from ponded system | √ | ||||
| Total P | √ | ||||
| PO4 | √ | ||||
| Organic P | √ | ||||
| Initial phosphorus in pond | |||||
| Organic P | √ | ||||
| Soluble P | √ | ||||
| Initial phosphorus in wetland | |||||
| Organic P | √ | ||||
| Soluble P | √ | ||||
| Initial phosphorus in reservoir | |||||
| Organic P | √ | ||||
| Soluble P | √ | ||||
| PO4 | √ | ||||
| In-stream phosphorus | |||||
| Organic P | √ | ||||
| PO4 | √ |
3.4. Nutrient Output
| Soil Nitrogen | SWAT | SWIM | GWLF | AnnAGNPS | HSPF | |
| Organic N | √ | |||||
| NO3 | √ | |||||
| NH4 | √ | |||||
| Add in | ||||||
| Organic N from residue | √ | √ | ||||
| Nitrogen applied in fertilizer | √ | √ | ||||
| NO3 added to soil profile by rain | √ | √ | ||||
| Transport | ||||||
| Surface Runoff | ||||||
| Total N in sediment | √ | √ | ||||
| Organic N in sediment | √ | √ | √ | √ | ||
| NH4 in sediment | √ | |||||
| NO3 in water | √ | √ | ||||
| NH4 in water | √ | |||||
| Inorganic N in water | √ | |||||
| Dissolved N in water | √ | |||||
| Nitrogen from Urban area by wash off | ||||||
| Total N | √ | √ | √ | |||
| Nitrogen from septic system | ||||||
| Dissolved N | √ | |||||
| Total N | √ | |||||
| Nitrogen from point source | ||||||
| Dissolved N | √ | |||||
| Interflow | ||||||
| NO3 | √ | √ | √ | |||
| NH4 | √ | |||||
| Inorganic N | √ | |||||
| Subsurface drainage flow | ||||||
| Inorganic N | √ | |||||
| Leaching by percolation | ||||||
| NO3 | √ | √ | √ | |||
| NH4 | √ | |||||
| Inorganic N | √ | |||||
| Groundwater Flow | ||||||
| NO3 | √ | √ | ||||
| NH4 | √ | |||||
| Dissolved N | √ | |||||
| Infiltration | ||||||
| Inorganic N | √ | |||||
| From first soil layer to surface by evaporation | ||||||
| NO3 | √ | |||||
| Surface Water Body Systems | SWAT | SWIM | GWLF | AnnAGNPS | HSPF | |
| Organic N transported with water into reach | √ | |||||
| Organic N transported with water out of reach | √ | |||||
| NO3 transported with water into reach | √ | √ | ||||
| NO3 transported with water out of reach | √ | √ | ||||
| NH4 transported with water into reach | √ | √ | ||||
| NH4 transported with water out of reach | √ | √ | ||||
| NO2 transported with water into reach | √ | √ | ||||
| NO2 transported with water out of reach | √ | √ | ||||
| Concentration of organic N in pond | √ | |||||
| Concentration of NO3 in pond | √ | |||||
| Concentration of organic N in wetland | √ | |||||
| Concentration of NO3 in wetland | √ | |||||
| Organic N transported into reservoir | √ | |||||
| Organic N transported out of reservoir | √ | |||||
| NO3 transported into reservoir | √ | √ | ||||
| NO3 transported out of reservoir | √ | √ | ||||
| NO2 transported into reservoir | √ | √ | ||||
| NO2 transported out of reservoir | √ | √ | ||||
| NH4 transported into reservoir | √ | √ | ||||
| NH4 transported out of reservoir | √ | √ | ||||
| Transformation | ||||||
| Fixation | √ | |||||
| Nitrification | √ | √ | ||||
| Ammonia volatilization | √ | √ | ||||
| Denitrification | √ | √ | √ | √ | ||
| Ionization | √ | |||||
| Mineralization/immobilization | ||||||
| Fresh organic N to mineral N | √ | √ | √ | |||
| Active organic N to mineral N | √ | √ | √ | |||
| N transferred between active organic N and stable organic N | √ | √ | ||||
| NO3 to Organic N | √ | |||||
| NH4 to Organic N | √ | |||||
| Organic N to NH4 | √ | |||||
| Decomposition | √ | √ | √ | √ | ||
| Plant uptake | ||||||
| Inorganic N | √ | √ | √ | |||
| NH4 | √ | |||||
| NO3 | √ | |||||
| In-stream reaction (related to Algae or plankton) | ||||||
| organic N | √ | √ | ||||
| NH4 | √ | |||||
| NH4 + NH3 | √ | |||||
| NO3 | √ | √ | ||||
| NO2 | √ | √ | ||||
| Adsorption/Desorption | SWAT | SWIM | GWLF | AnnAGNPS | HSPF | |
| NH4 | √ | |||||
| Nitrogen settling/sinking in ponds, wetland and reservoir | ||||||
| Total N | √ | √ | ||||
| Reservoir system chemical and biochemical transformation | √ | |||||

| Soil Phosphorus | SWAT | SWIM | GWLF | AnnAGNPS | HSPF |
| Organic P | √ | ||||
| PO4 | √ | ||||
| Soluble P | √ | ||||
| Labile inorganic P | √ | ||||
| Active inorganic P | √ | ||||
| Stable inorganic P | √ | ||||
| Add in | |||||
| Phosphorus (mineral and organic) applied in fertilizer | √ | √ | |||
| Organic P from residue | √ | √ | |||
| Transport | |||||
| Surface Runoff | SWAT | SWIM | GWLF | AnnAGNPS | HSPF |
| Total P in sediment | √ | √ | √ | ||
| Organic P in sediment | √ | √ | √ | ||
| Mineral P in sediment | √ | ||||
| Inorganic P in sediment | √ | ||||
| PO4 in sediment | √ | ||||
| Soluble P in water | √ | √ | |||
| Inorganic P in water | √ | ||||
| PO4 in water | √ | ||||
| Dissolved P in water | √ | ||||
| Phosphorus from Urban area by wash off | |||||
| Total P | √ | √ | √ | ||
| Phosphorus from septic system | |||||
| Dissolved P | √ | ||||
| Total P | √ | ||||
| Phosphorus from point source | |||||
| Dissolved P | √ | ||||
| Interflow | |||||
| PO4 | √ | ||||
| Leaching by percolation | |||||
| Soluble P | √ | ||||
| PO4 | √ | ||||
| Groundwater flow | |||||
| Soluble P | √ | ||||
| PO4 | √ | ||||
| Dissolved P | √ | ||||
| Infiltration | |||||
| Inorganic P | √ | ||||
| Surface Water Body Systems | |||||
| Organic P transported with water into reach | √ | ||||
| Organic P transported with water out of reach | √ | ||||
| Mineral P transported with water into reach | √ | ||||
| Mineral P transported with water out of reach | √ | ||||
| Inflow PO4 to reach | √ | ||||
| Outflow PO4 from reach | √ | ||||
| Concentration of organic P in pond | √ | ||||
| Concentration of mineral P in pond | √ | ||||
| Concentration of organic P in wetland | √ | ||||
| Concentration of mineral p in wetland | √ | ||||
| Organic p transported into reservoir | √ | ||||
| Organic p transported out of reservoir | √ | ||||
| Mineral P transported into reservoir | √ | ||||
| Mineral P transported out of reservoir | √ | ||||
| Inflow PO4 to reservoir | √ | ||||
| Outflow PO4 from reservoir | √ | ||||
| Transformation | |||||
| Decomposition | √ | √ | √ | √ | |
| Mineralization/ Immobilization | SWAT | SWIM | GWLF | AnnAGNPS | HSPF |
| Fresh organic to mineral P | √ | √ | √ | ||
| Organic to labile mineral P | √ | √ | √ | ||
| PO4 to Organic P | √ | ||||
| Organic P to PO4 | √ | ||||
| Sorption | |||||
| P transferred between Labile and active mineral P | √ | √ | √ | ||
| P transferred between Active and stable mineral P | √ | √ | |||
| Plant uptake | |||||
| Inorganic P | √ | √ | |||
| PO4 | √ | ||||
| In-stream reaction(related to Algae or plankton) | |||||
| Organic P | √ | √ | |||
| Soluble P | √ | ||||
| PO4 | √ | ||||
| Adsorption/desorption | |||||
| PO4 | √ | ||||
| Phosphorus settling/sinking in ponds, wetland and reservoir | |||||
| Total P | √ | √ | |||
| Reservoir system chemical and biochemical transformation | √ |
3.5. Model Complexity
- (1)
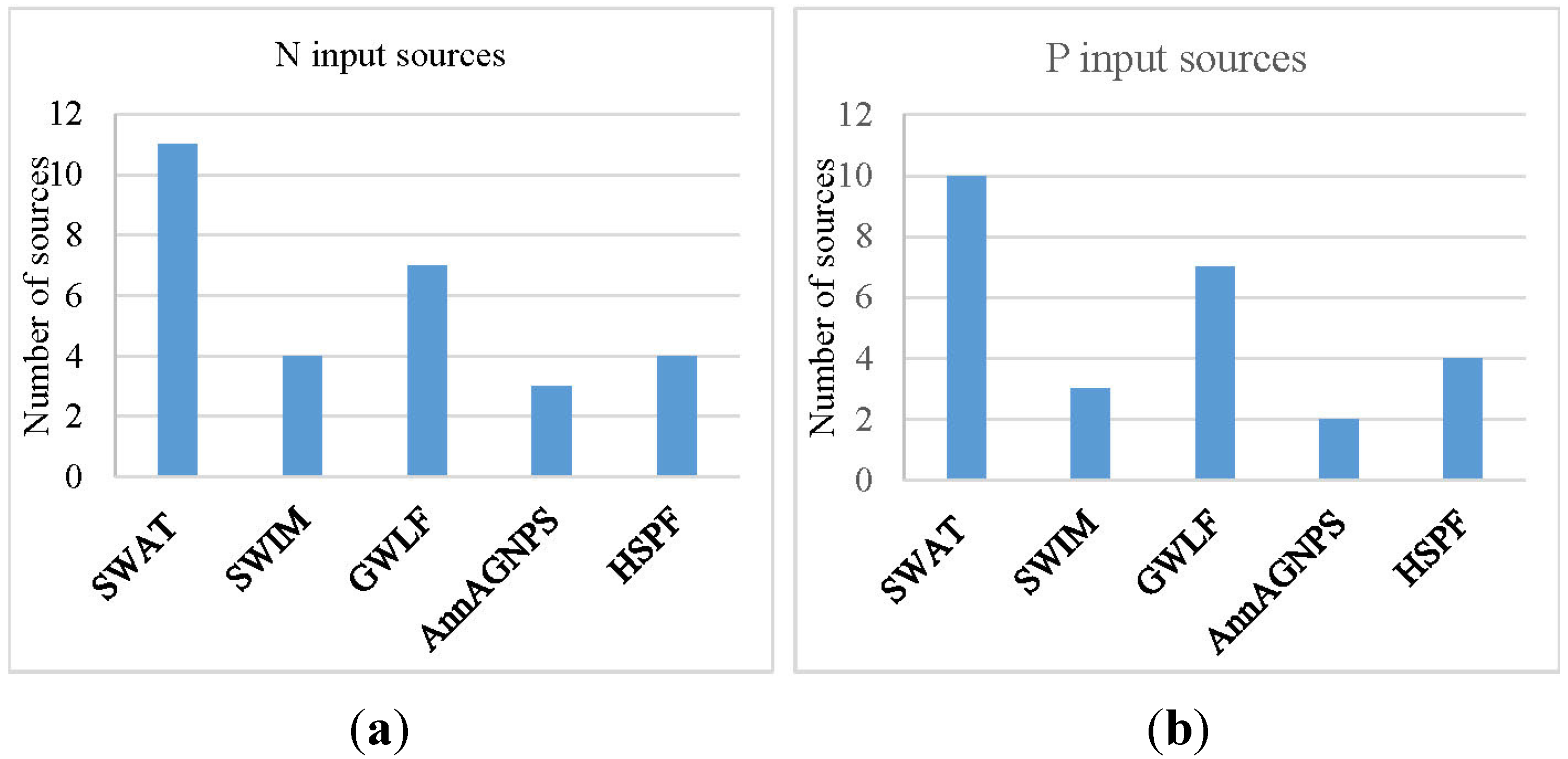
- Not all nutrient sources are considered by all five models, e.g., nutrient from septic system can be simulated by SWAT and GWLF, but are not considered yet by the others.
- (2)
- Despite the models contain the same hydrological process, only some models predict reactive transport in a given hydrological compartment, e.g., groundwater flow/base flow is simulated by SWAT, SWIM, GWLF and HSPF, but only SWAT and HSPF predict nutrient transport in this compartment.
- (3)
- Not all possible transformation reactions are modeled by all the models, e.g., nitrification is simulated only by SWAT and HSPF.
- (4)
- Some models contain the same process or reaction and all can simulate the nutrient fate of the process or reaction, but the nutrient forms may be different, e.g. four models compute N in interflow, but the form is NO3 for SWAT and SWIM, inorganic N for AnnAGNPS, and NO3 and NH4 for HSPF.
4. Set up a Model Selection Protocol
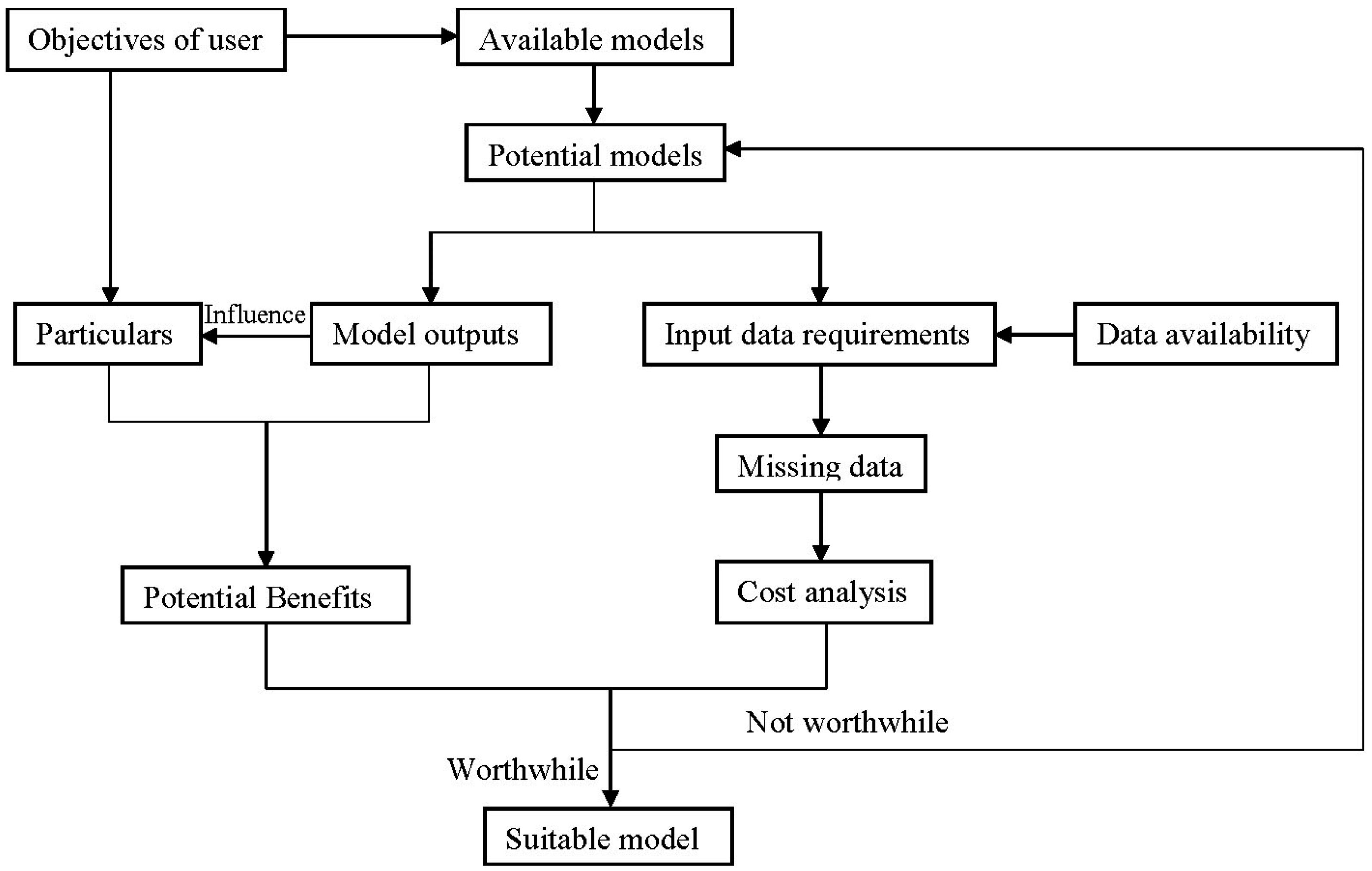
4.1. A Model Selection Protocol
- (1)
- Define the objectives of the user.
- (2)
- Make a list about the models at hand and the models that can be available.
- (3)
- Select the potential models that are capable of simulating the general user’s objectives.
- (4)
- Make a list about the corresponding outputs and input requirements of the potential models.
- (5)
- Investigate data availability.
- (6)
- Specify the objectives in more details, considering the potential outputs.
- (7)
- Specify the missing data, comparing the input requirements with the available data.
- (8)
- Analyze the time and financial cost for additional data measurements.
- (9)
- Analyze the potential benefits associated with the use of additional data and eventually a more complex model in terms of model predictions and outputs.
- (10)
- Select the model by evaluating the benefits and cost.
4.2. Objectives of the User
4.3. Input Data Availability
4.4. Model Complexity
4.5. Cost and Benefit Analysis
4.6. Model Selection Protocol: Some Applications
- (1)
- HSPF is complex enough to solve and further explain the problems of this practical case;
- (2)
- HSPF’s easier representation of hydrological processes is easier to be handled by the modelers;
- (3)
- An easier understanding of the model will lead to a faster achievement of the project objective.
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Lindim, C.; Pinho, J.L.; Vieira, J.M.P. Analysis of spatial and temporal patterns in a large reservoir using water quality and hydrodynamic modeling. Ecol. Model. 2011, 222, 2485–2494. [Google Scholar] [CrossRef]
- Krysanova, V.; Haberlandt, U. Assessment of nitrogen leaching from arable land in large river basins: Part I. Simulation experiments using a process-based model. Ecol. Model. 2002, 150, 255–275. [Google Scholar] [CrossRef]
- Huang, S.; Hesse, C.; Krysanova, V.; Hattermann, F. From meso- to macro-scale dynamic water quality modelling for the assessment of land use change scenarios. Ecol. Model. 2009, 220, 2543–2558. [Google Scholar] [CrossRef]
- Niraula, R.; Kalin, L.; Srivastava, P.; Anderson, C.J. Identifying critical source areas of nonpoint source pollution with SWAT and GWLF. Ecol. Model. 2013, 268, 123–133. [Google Scholar] [CrossRef]
- Xu, Y. Transport and retention of nitrogen, phosphorus and carbon in North America’s largest river swamp basin, the Atchafalaya river basin. Water 2013, 5, 379–393. [Google Scholar] [CrossRef]
- Pease, L.M.; Oduor, P.; Padmanabhan, G. Estimating sediment, nitrogen, and phosphorous loads from the Pipestem Creek watershed, North Dakota, using AnnAGNPS. Comput. Geosci. 2010, 36, 282–291. [Google Scholar] [CrossRef]
- Hesse, C.; Krysanova, V.; Päzolt, J.; Hattermann, F.F. Eco-Hydrological modelling in a highly regulated lowland catchment to find measures for improving water quality. Ecol. Model. 2008, 218, 135–148. [Google Scholar] [CrossRef]
- Mayzelle, M.; Viers, J.; Medellín-Azuara, J.; Harter, T. Economic feasibility of irrigated agricultural land use buffers to reduce groundwater nitrate in rural drinking water sources. Water 2014, 7, 12–37. [Google Scholar] [CrossRef]
- Shen, Z.; Liao, Q.; Hong, Q.; Gong, Y. An overview of research on agricultural non-point source pollution modelling in China. Sep. Purif. Technol. 2012, 84, 104–111. [Google Scholar] [CrossRef]
- Hunter, H.M.; Walton, R.S. Land-Use effects on fluxes of suspended sediment, nitrogen and phosphorus from a river catchment of the Great Barrier Reef, Australia. J. Hydrol. 2008, 356, 131–146. [Google Scholar] [CrossRef]
- Küstermann, B.; Christen, O.; Hülsbergen, K.J. Modelling nitrogen cycles of farming systems as basis of site- and farm-specific nitrogen management. Agric. Ecosyst. Environ. 2010, 135, 70–80. [Google Scholar] [CrossRef]
- Panagopoulos, Y.; Makropoulos, C.; Baltas, E.; Mimikou, M. SWAT parameterization for the identification of critical diffuse pollution source areas under data limitations. Ecol. Model. 2011, 222, 3500–3512. [Google Scholar] [CrossRef]
- Chen, Y.; Shuai, J.; Zhang, Z.; Shi, P.; Tao, F. Simulating the impact of watershed management for surface water quality protection: A case study on reducing inorganic nitrogen load at a watershed scale. Ecol. Eng. 2014, 62, 61–70. [Google Scholar] [CrossRef]
- Shen, Z.; Chen, L.; Hong, Q.; Qiu, J.; Xie, H.; Liu, R. Assessment of nitrogen and phosphorus loads and causal factors from different land use and soil types in the Three Gorges Reservoir Area. Sci. Total Environ. 2013, 454–455, 383–392. [Google Scholar] [CrossRef] [PubMed]
- Volf, G.; Atanasova, N.; Kompare, B.; Ožanić, N. Modeling nutrient loads to the northern Adriatic. J. Hydrol. 2013, 504, 182–193. [Google Scholar] [CrossRef]
- Nasr, A.; Bruen, M.; Jordan, P.; Moles, R.; Kiely, G.; Byrne, P. A comparison of SWAT, HSPF and SHETRAN/GOPC for modelling phosphorus export from three catchments in Ireland. Water Res. 2007, 41, 1065–1073. [Google Scholar] [CrossRef] [PubMed]
- Thorsen, M.; Refsgaard, J.C.; Hansen, S.; Pebesma, E.; Jensen, J.B.; Kleeschulte, S. Assessment of uncertainty in simulation of nitrate leaching to aquifers at catchment scale. J. Hydrol. 2001, 242, 210–227. [Google Scholar] [CrossRef]
- Ranatunga, K.; Nation, E.R.; Barratt, D.G. Review of soil water models and their applications in Australia. Environ. Model. Softw. 2008, 23, 1182–1206. [Google Scholar] [CrossRef]
- Robson, B.J. State of the art in modelling of phosphorus in aquatic systems: Review, criticisms and commentary. Environ. Model. Softw. 2014, 61, 339–359. [Google Scholar] [CrossRef]
- CRC Catchment Hydrology. General Approach to Modelling and Practical Issues to Model Choice; CRC Catchment Hydrology: Melbourne, Australia, 2000. [Google Scholar]
- Xie, H.; Lian, Y. Uncertainty-Based evaluation and comparison of SWAT and HSPF applications to the Illinois River Basin. J. Hydrol. 2013, 481, 119–131. [Google Scholar] [CrossRef]
- Saloranta, T.M.; Kämäri, J.; Rekolainen, S.; Malve, O. Benchmark criteria: A tool for selecting appropriate models in the field of water management. Environ. Manag. 2003, 32, 322–333. [Google Scholar]
- Boorman, D.B.; Williams, R.J.; Hutchins, M.G.; Penning, E.; Groot, S.; Icke, J. A model selection protocol to support the use of models for water management. Hydrol. Earth Syst. Sci. 2007, 11, 634–646. [Google Scholar] [CrossRef]
- Beven, K.J. Rainfall-Runoff Modelling: The Primer, 2nd ed.; John Wiley & Sons: Chichester, UK, 2012; pp. 16–18. [Google Scholar]
- Galioto, F.; Marconi, V.; Raggi, M.; Viaggi, D. An assessment of disproportionate costs in WFD: The experience of Emilia-Romagna. Water 2013, 5, 1967–1995. [Google Scholar] [CrossRef]
- Rahman, M.; Rusteberg, B.; Uddin, M.; Saada, M.; Rabi, A.; Sauter, M. Impact assessment and multicriteria decision analysis of alternative managed aquifer recharge strategies based on treated wastewater in northern Gaza. Water 2014, 6, 3807–3827. [Google Scholar] [CrossRef]
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Williams, J.R. Soil and Water Assessment Tool Theoretical Documentation Version 2009; Texas Water Resources Institute: College Station, TX, USA, 2011; pp. 1–618. [Google Scholar]
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large area hydrologic modeling and assessment part I: model development1. J. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Shen, Z.; Zhong, Y.; Huang, Q.; Chen, L. Identifying non-point source priority management areas in watersheds with multiple functional zones. Water Res. 2015, 68, 563–571. [Google Scholar] [CrossRef] [PubMed]
- Krysanova, V.; Wechsung, F.; Arnold, J.; Srinivasan, R.; Williams, J. PIK Report No. 69 “SWIM (Soil and Water Integrated Model), User Manual”; Potsdam Institute for Climate Impact Research: Potsdam, Germany, 2000; pp. 1–239. [Google Scholar]
- Krysanova, V.; Meiner, A.; Roosaare, J.; Vasilyev, A. Simulation modelling of the coastal waters pollution from agricultural watershed. Ecol. Model. 1989, 49, 7–29. [Google Scholar] [CrossRef]
- Haith, D.A.; Mandel, R.; Wu, R.S. GWLF—Generalized Watershed Loading Functions. Version 2.0. User’s Manual; Department of Agricultural & Biological Engineering, Cornell University: Ithaca, NY, USA, 1992; pp. 1–63. [Google Scholar]
- Bingner, R.L.; Theurer, F.D.; Yuan, Y.P. AnnAGNPS Technical Processes Documentation, Version 5.2; U.S. Department of Agriculture: Washington, DC, USA, 2011; pp. 1–143.
- Young, R.A.; Onstad, C.A.; Bosch, D.D.; Anderson, W.P. AGNPS: A non-point source pollution model for evaluating agricultural watersheds. J. Soil Water Conserv. 1989, 44, 168–173. [Google Scholar]
- Bicknell, B.R.; Imhoff, J.C.; Kittle, J.L., Jr.; Donigian, A.S., Jr.; Johanson, R.C. Hydrological Simulation Program—FORTRAN: User’s Manual for version 11; U.S. Environmental Protection Agency, National Exposure Research Laboratory: Athens, GA, USA, 1997; pp. 1–755.
- Jeon, J.H.; Yoon, C.G.; Donigian, A.S., Jr.; Jung, K.W. Development of the HSPF-Paddy model to estimate watershed pollutant loads in paddy farming regions. Agric. Water Manag. 2007, 90, 75–86. [Google Scholar] [CrossRef]
- Wrede, S.; Seibert, J.; Uhlenbrook, S. Distributed conceptual modelling in a Swedish lowland catchment: A multi-criteria model assessment. Hydrol. Res. 2013, 44, 318–333. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tuo, Y.; Chiogna, G.; Disse, M. A Multi-Criteria Model Selection Protocol for Practical Applications to Nutrient Transport at the Catchment Scale. Water 2015, 7, 2851-2880. https://doi.org/10.3390/w7062851
Tuo Y, Chiogna G, Disse M. A Multi-Criteria Model Selection Protocol for Practical Applications to Nutrient Transport at the Catchment Scale. Water. 2015; 7(6):2851-2880. https://doi.org/10.3390/w7062851
Chicago/Turabian StyleTuo, Ye, Gabriele Chiogna, and Markus Disse. 2015. "A Multi-Criteria Model Selection Protocol for Practical Applications to Nutrient Transport at the Catchment Scale" Water 7, no. 6: 2851-2880. https://doi.org/10.3390/w7062851
APA StyleTuo, Y., Chiogna, G., & Disse, M. (2015). A Multi-Criteria Model Selection Protocol for Practical Applications to Nutrient Transport at the Catchment Scale. Water, 7(6), 2851-2880. https://doi.org/10.3390/w7062851