Modeling of Soil Water and Salt Dynamics and Its Effects on Root Water Uptake in Heihe Arid Wetland, Gansu, China
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
| Soil Layer (cm) | 0–15 | 15–25 | 25–55 | 55–65 | 65–100 | 100–150 |
|---|---|---|---|---|---|---|
| Texture | Silt Loam | Silt Loam | Silt Loam | Silt Loam | Silt Loam | Coarse Sand |
| Clay (%) | 11 | 10 | 11 | 13 | 16 | - |
| Silt (%) | 54 | 65 | 66 | 64 | 56 | - |
| Sand (%) | 35 | 25 | 23 | 23 | 28 | 100 |
| Bulk density(g·cm−3) | 1.2 | 1.35 | 1.42 | 1.44 | 1.44 | 1.42 |
| θr (cm3·cm−3) | 0.093 | 0.08 | 0.075 | 0.071 | 0.079 | 0.051 |
| θs(cm3·cm−3) | 0.543 | 0.493 | 0.502 | 0.462 | 0.534 | 0.376 |
| α (cm−1) | 0.019 | 0.028 | 0.032 | 0.033 | 0.035 | 0.034 |
| n | 2.06 | 1.70 | 1.50 | 1.36 | 1.71 | 4.43 |
| l | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 |
| Ks (cm·d−1) | 2.5 | 10.6 | 24.7 | 6.7 | 34.0 | 1428.0 |
| λ (cm) | 16.8 | 19.5 | 48.2 | 29.1 | 10.8 | 124.0 |
2.2. Measurements
2.3. Model Simulation
2.3.1. Soil Water Flow and Solute Transport
2.3.2. Solute Transport
2.3.3. Root Water Uptake
2.4. Initial and Boundary Condition
2.5. Model Calibration and Validation
2.6. Simulation Scenarios
| Main Scenarios | Scenarios in Detail |
|---|---|
| Root water uptake predictions | Depth to water table raise 15% of the 2012 reference depth, DWT+15% |
| Depth to water table raise 30% of the 2012 reference depth, DWT+30% | |
| Depth to water table raise 45% of the 2012 reference depth, DWT+45% | |
| Depth to water table raise 60% of the 2012 reference depth, DWT+60% | |
| Depth to water table drop 15% of the 2012 reference depth, DWT-15% | |
| Depth to water table drop 30% of the 2012 reference depth, DWT-30% | |
| Depth to water table drop 45% of the 2012 reference depth, DWT-45% | |
| Depth to water table drop 60% of the 2012 reference depth, DWT-60% | |
| Groundwater electrical conductivity increase 15% of the 2012 reference value, ECgw+ 15% | |
| Groundwater electrical conductivity increase 30% of the 2012 reference value, ECgw+ 30% | |
| Groundwater electrical conductivity increase 45% of the 2012 reference value, ECgw+ 45% | |
| Groundwater electrical conductivity increase 60% of the 2012 reference value, ECgw+ 60% | |
| Groundwater electrical conductivity decrease 15% of the 2012 reference value, ECgw− 15% | |
| Groundwater electrical conductivity decrease 30% of the 2012 reference value, ECgw− 30% | |
| Groundwater electrical conductivity decrease 45% of the 2012 reference value, ECgw− 45% | |
| Groundwater electrical conductivity decrease 60% of the 2012 reference value, ECgw− 60% | |
| Long term (30 years) salinity trends | Depth to water table is 60 cm, DWT = 60 cm |
| Depth to water table is 100 cm, DWT = 100 cm | |
| Depth to water table is 140 cm, DWT = 140 cm | |
| Groundwater electrical conductivity is 1.75 dS/m, ECgw = 1.75 dS/m | |
| Groundwater electrical conductivity is 3.75 dS/m, ECgw = 3.75 dS/m | |
| Groundwater electrical conductivity is 5.75 dS/m, ECgw = 5.75 dS/m | |
| Preseason irrigation strategy | A human irrigation (irrigation amount range from 1 to 80 cm) applied at the initial stages of plant growth (2 May 2012). |
3. Results and Discussion
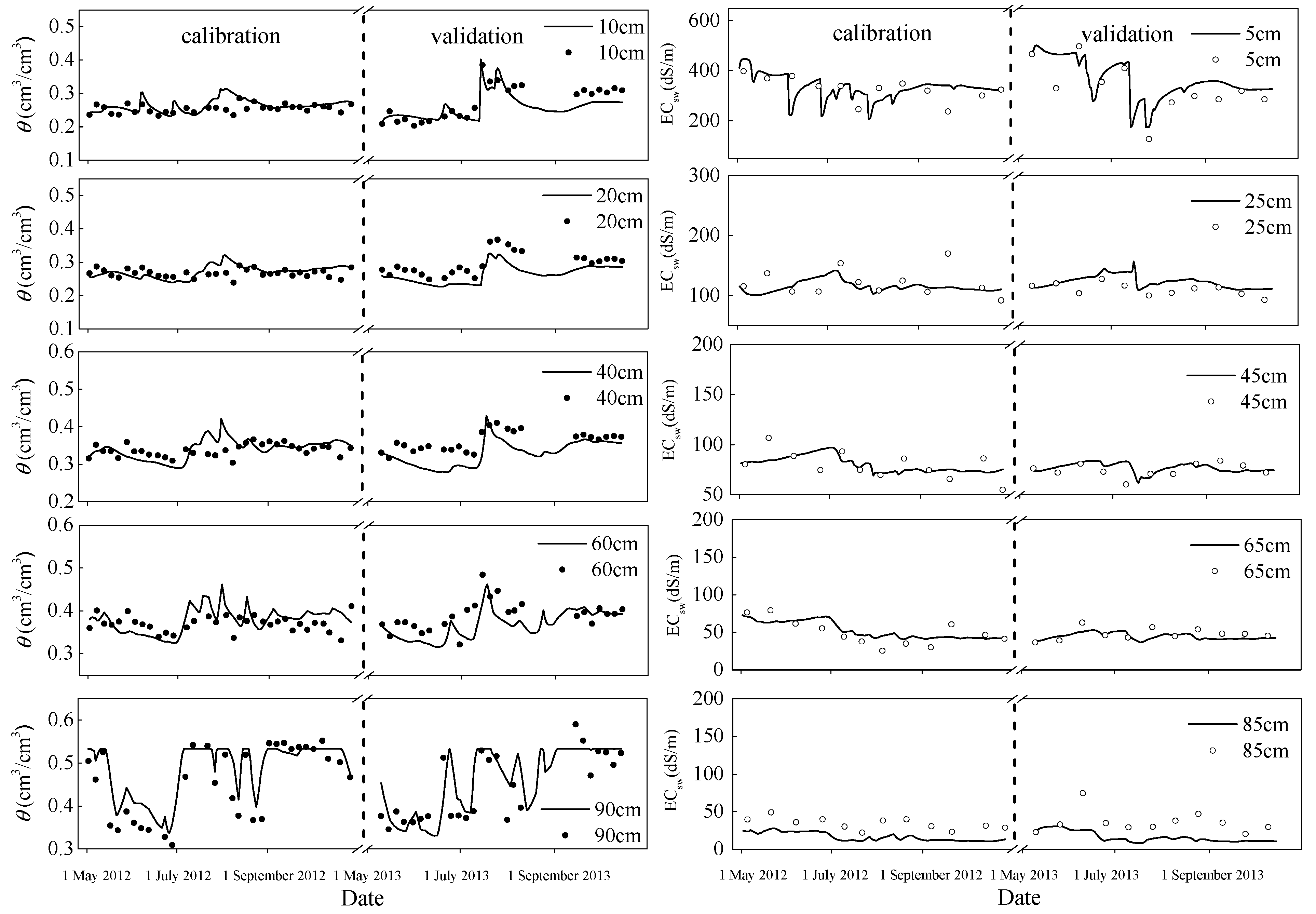
3.1. Model Calibration and Validation
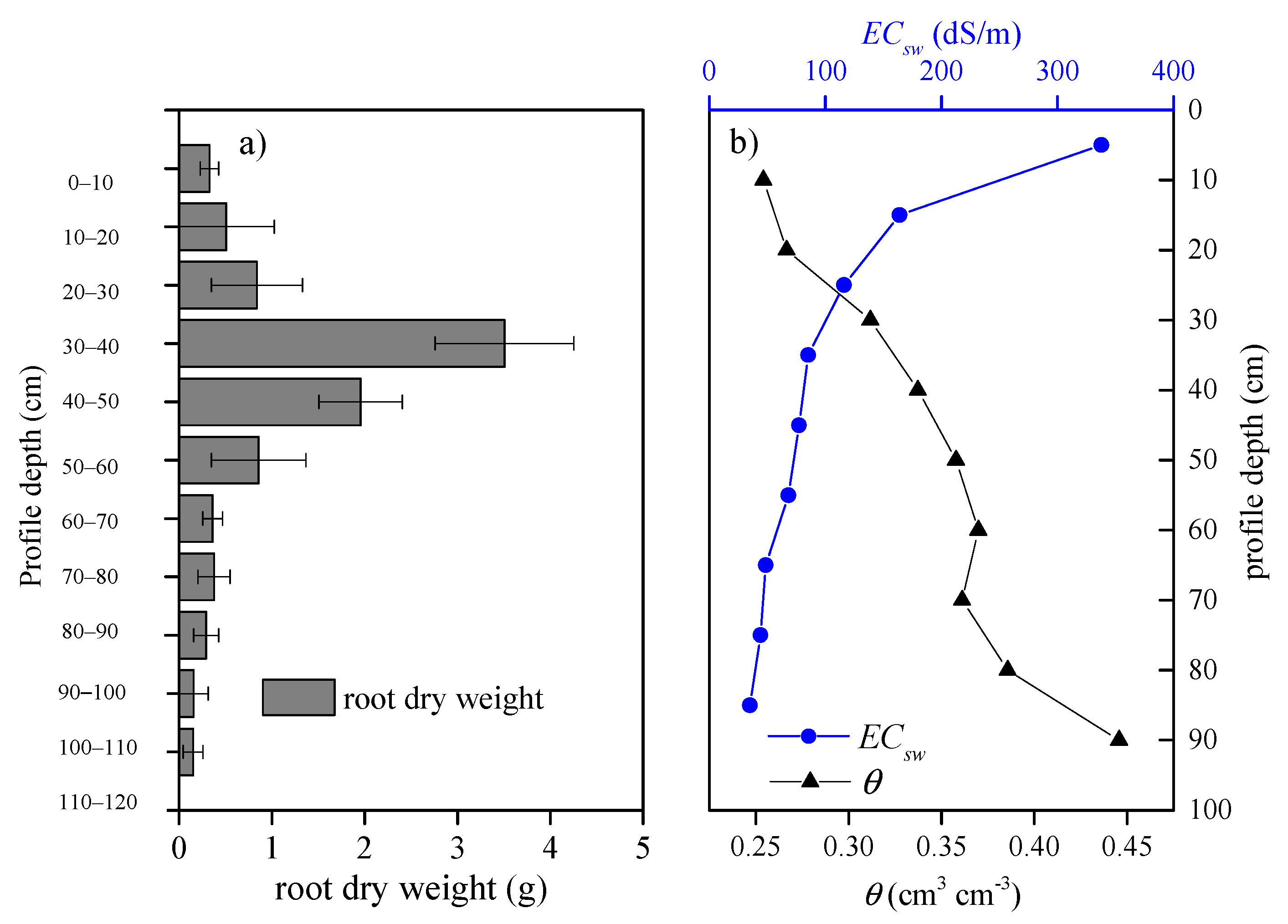
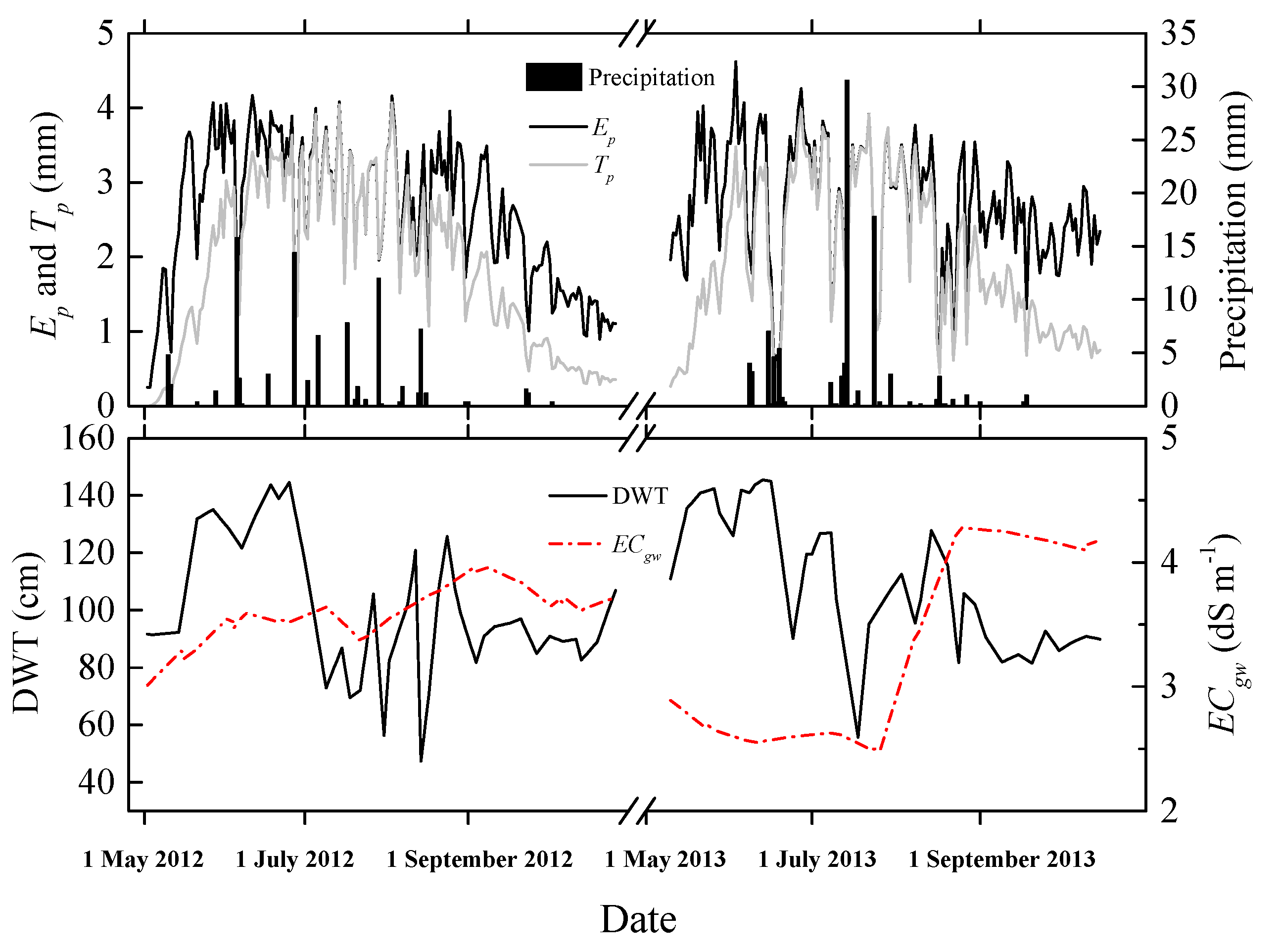
3.2. Soil Water and Salt Dynamics and Their Effects on Root Water Uptake of Tamarisk
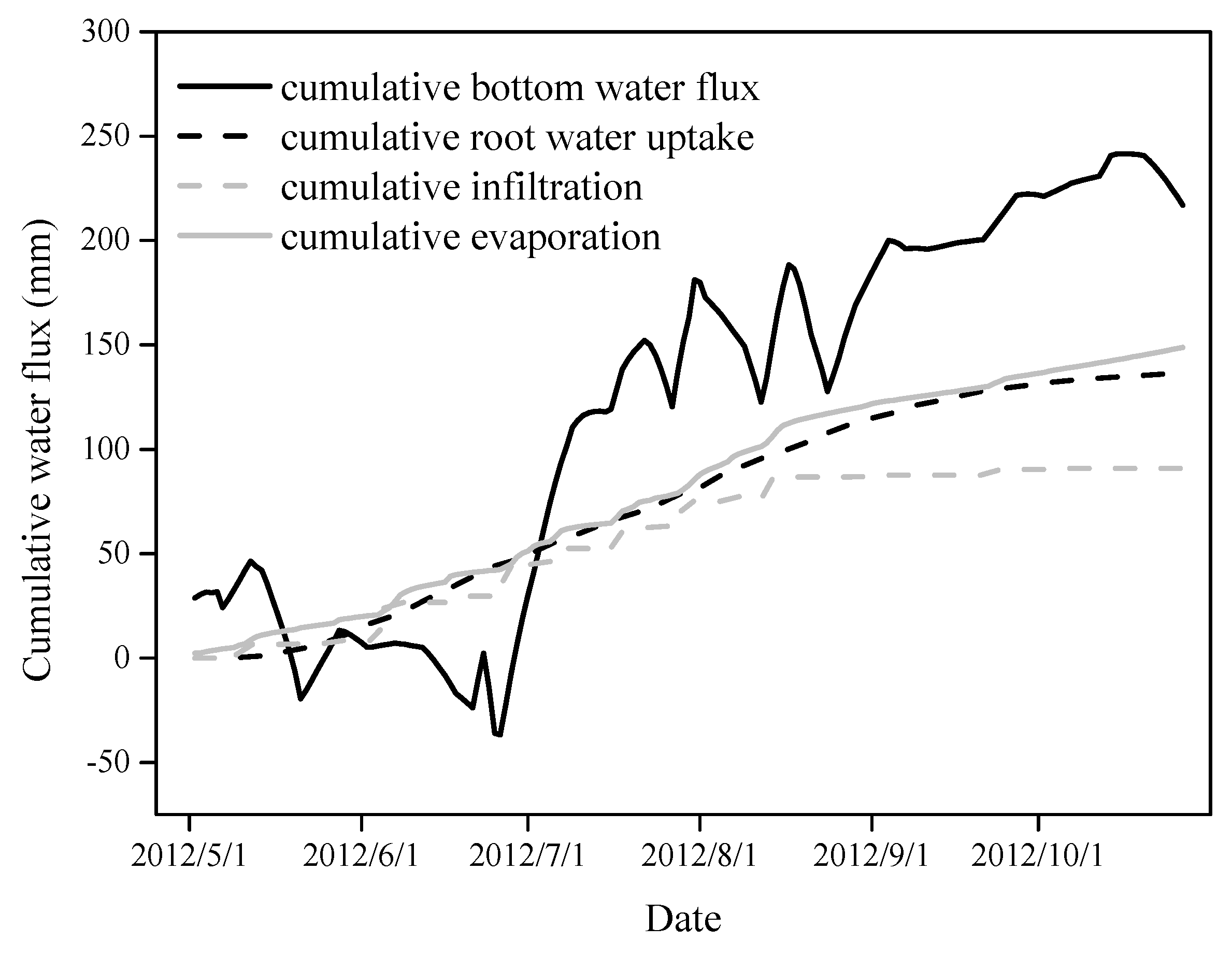
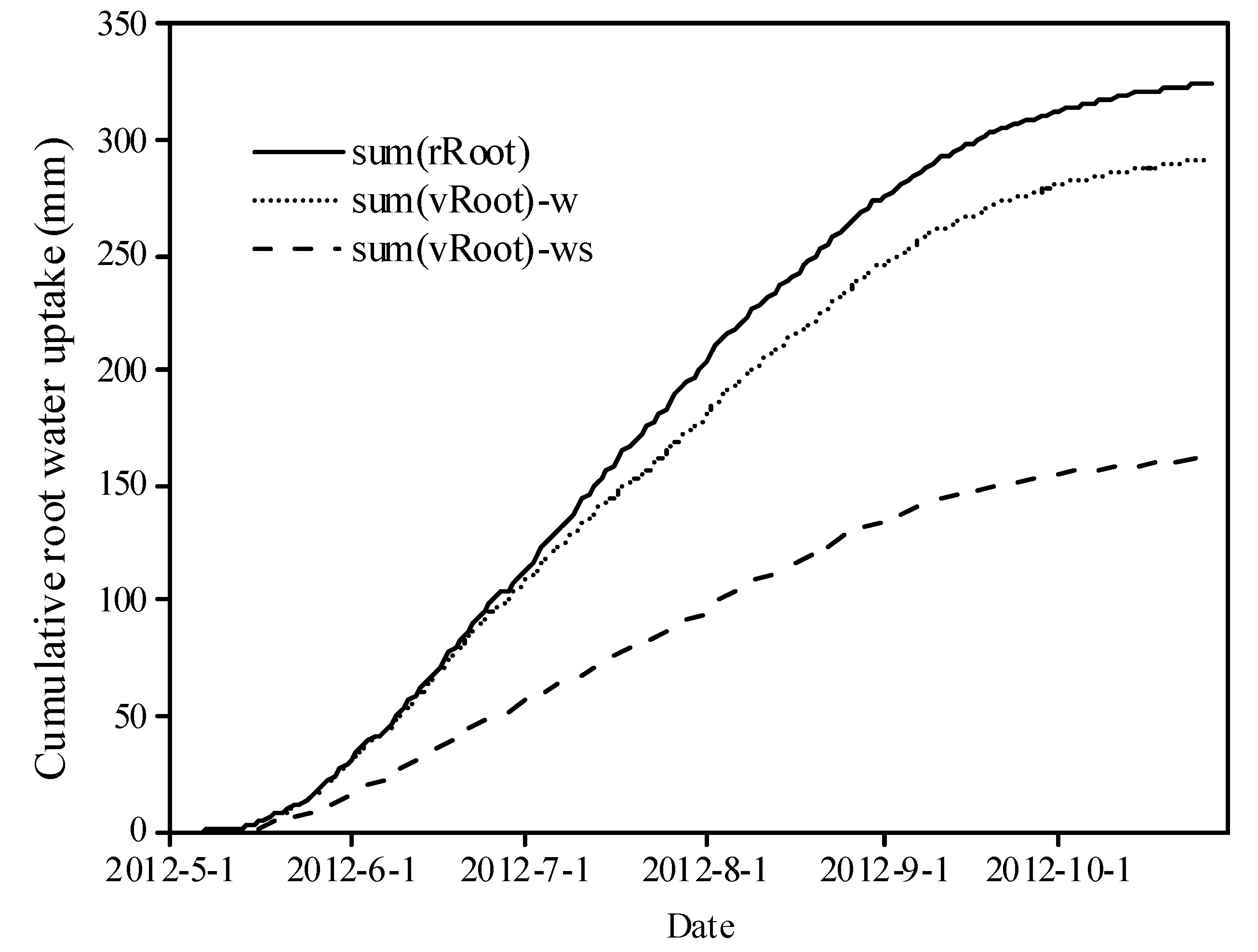
3.3. Scenario Simulations
3.3.1. Root Water Uptake Predictions

3.3.2. The Long-Term Salinization Trends
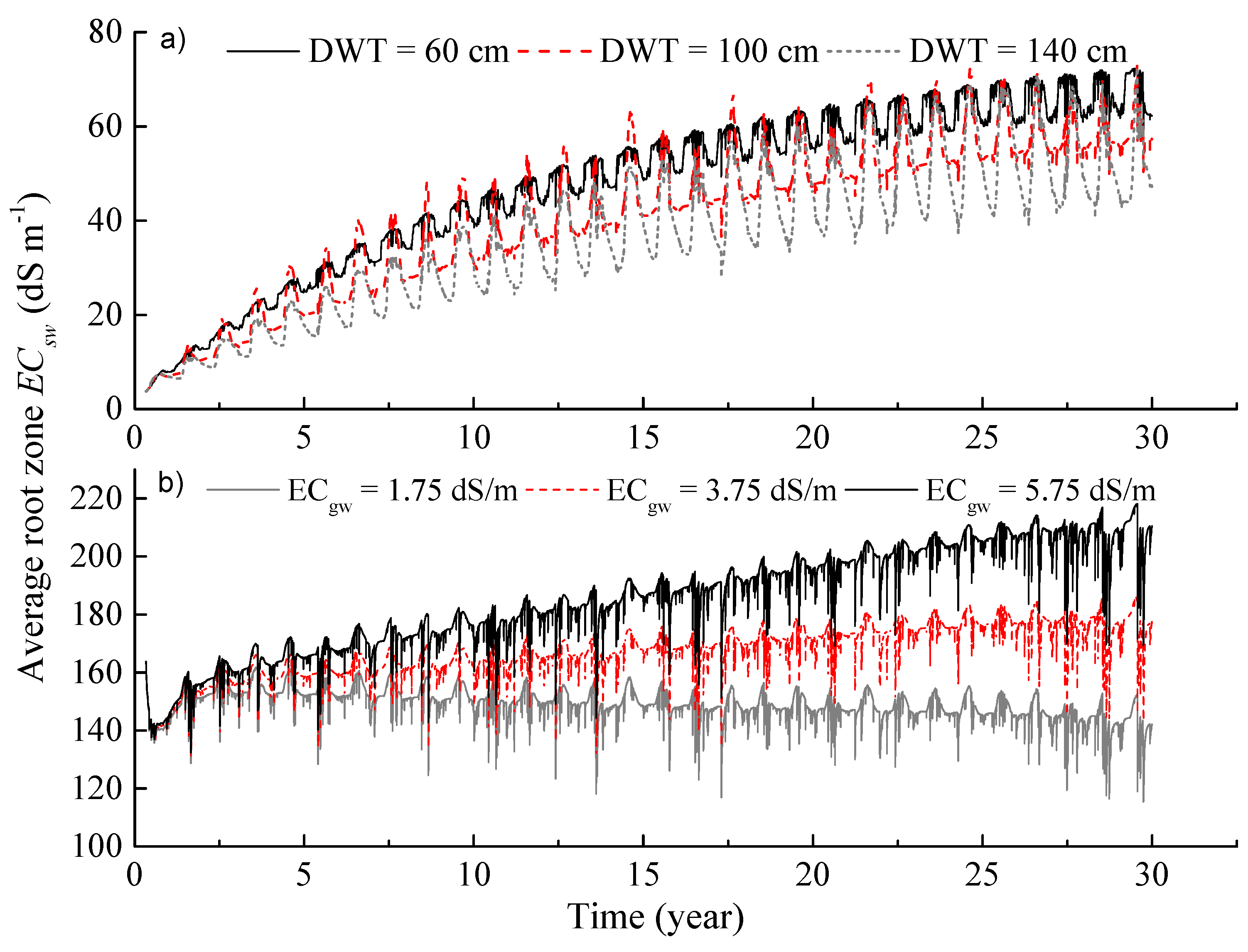
3.3.3. Preseason Irrigation Strategy
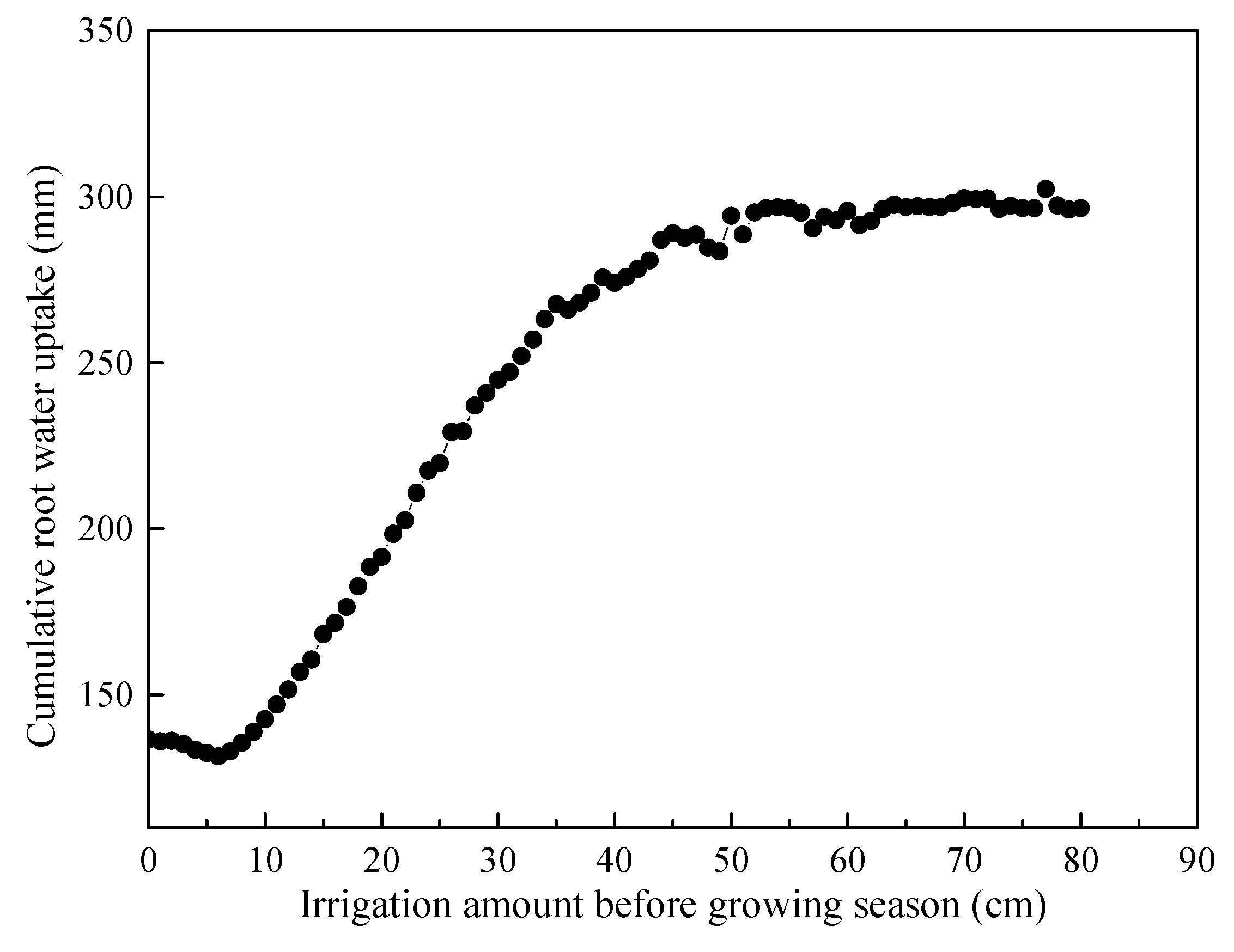
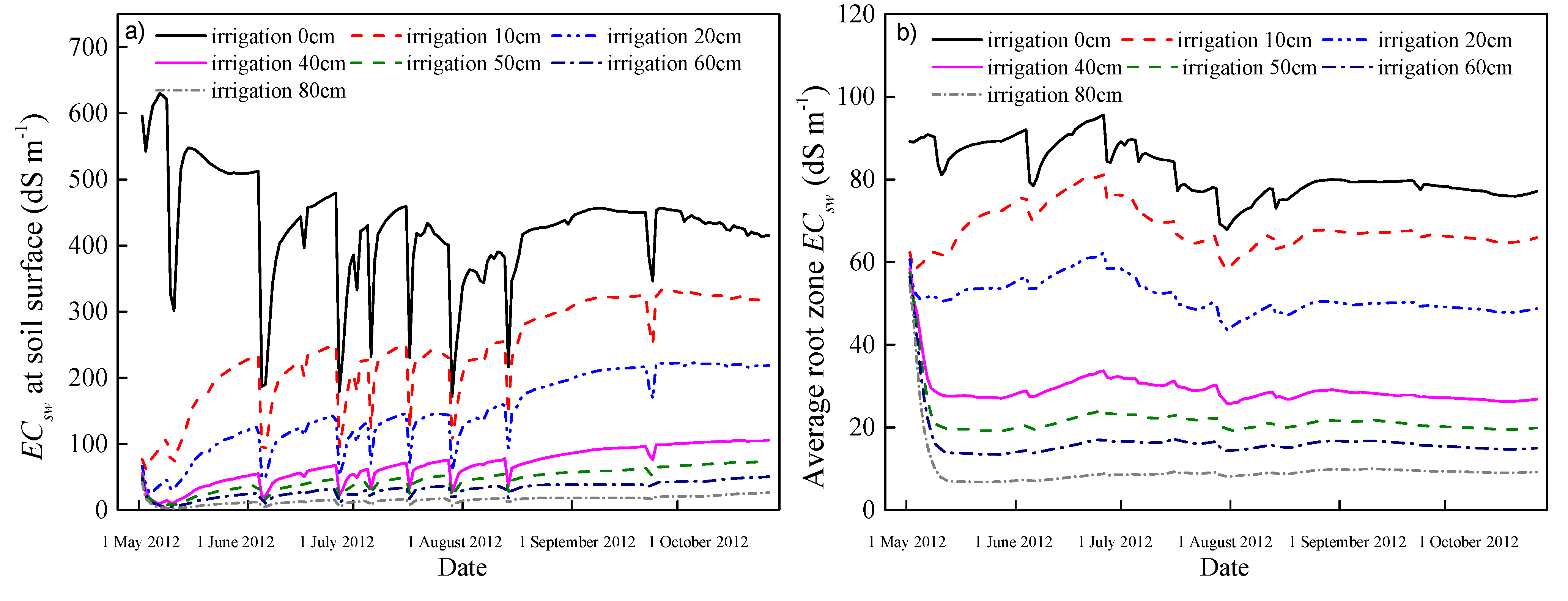
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Jolly, I.D.; McEwan, K.L.; Holland, K.L. A review of groundwater-surface water interactions in arid/semi-arid wetlands and the consequences of salinity for wetland ecology. Ecohydrology 2008, 1, 43–58. [Google Scholar] [CrossRef]
- Niu, Y.; Liu, X.D.; Zhang, H.B.; Meng, H.J. The ecological function evaluation of wetland in upper and middle reaches of heihe basin. Wetl. Sci. 2007, 3, 215–220. (In Chinese) [Google Scholar]
- Lei, K.; Zhang, M.X. The wetland resources in china and the conservation advices. Wetl. Sci. 2005, 3, 81–86. (In Chinese) [Google Scholar]
- Xie, T.; Liu, X.; Sun, T. The effects of groundwater table and flood irrigation strategies on soil water and salt dynamics and reed water use in the yellow river delta, china. Ecol. Model. 2011, 222, 241–252. [Google Scholar] [CrossRef]
- Ahmad, M.U.D.; Bastiaanssen, W.G.M.; Feddes, R.A. Sustainable use of groundwater for irrigation: A numerical analysis of the subsoil water fluxes. Irrig. Drain. 2002, 51, 227–241. [Google Scholar] [CrossRef]
- Gowing, J.W.; Rose, D.A.; Ghamarnia, H. The effect of salinity on water productivity of wheat under deficit irrigation above shallow groundwater. Agric. Water Manag. 2009, 96, 517–524. [Google Scholar] [CrossRef]
- Jiang, P.H.; Zhao, R.F.; Zhao, H.L.; Lu, L.P.; Xie, Z.L. Relationships of wetland landscape fragmentation with climate change in middle reaches of heihe river, China. J. Appl. Ecol. 2013, 24, 1661–1668. (In Chinese) [Google Scholar]
- Zhang, H.B.; Meng, H.J.; Liu, X.D.; Zhao, W.J.; Wang, X.P. Vegetation characteristics and ecological restoration technology of typical degradation wetlands in the middle of heihe river basin, zhangye city of gansu province. Wetl. Sci. 2012, 10, 194–199. (In Chinese) [Google Scholar]
- Feng, Q.; Liu, W.; Su, Y.H.; Zhang, Y.W.; Si, J.H. Distribution and evolution of water chemistry in heihe river basin. Environ. Geol. 2004, 45, 947–956. [Google Scholar] [CrossRef]
- Tedeschi, A.; Dell’Aquila, R. Effects of irrigation with saline waters, at different concentrations, on soil physical and chemical characteristics. Agric. Water Manag. 2005, 77, 308–322. [Google Scholar] [CrossRef]
- Ayars, J.E.; Shouse, P.; Lesch, S.M. In situ use of groundwater by alfalfa. Agric. Water Manag. 2009, 96, 1579–1586. [Google Scholar] [CrossRef]
- Ayars, J.E.; Christen, E.W.; Soppe, R.W.; Meyer, W.S. The resource potential of in-situ shallow ground water use in irrigated agriculture: A review. Irrig. Sci. 2005, 24, 147–160. [Google Scholar] [CrossRef]
- Singh, R.; Singh, J. Irrigation planning in cotton through simulation modeling. Irrig. Sci. 1996, 17, 31–36. [Google Scholar] [CrossRef]
- Feddes, R.A.; Kabat, P.; van Bakel, P.; Bronswijk, J.J.B.; Halbertsma, J. Modelling soil water dynamics in the unsaturated zone—State of the art. J. Hydrol. 1988, 100, 69–111. [Google Scholar] [CrossRef]
- de Jong, R.; Bootsma, A. Review of recent developments in soil water simulation models. Can. J. Soil Sci. 1996, 76, 263–273. [Google Scholar] [CrossRef]
- Saito, H.; Šimůnek, J.; Mohanty, B.P. Numerical analysis of coupled water, vapor, and heat transport in the vadose zone. Vadose Zone J. 2006, 5, 784–800. [Google Scholar] [CrossRef]
- Jacques, D.; Šimůnek, J.; Timmerman, A.; Feyen, J. Calibration of richards’ and convection-dispersion equations to field-scale water flow and solute transport under rainfall conditions. J. Hydrol. 2002, 259, 15–31. [Google Scholar] [CrossRef]
- Wang, T.; Franz, T.E.; Zlotnik, V.A. Controls of soil hydraulic characteristics on modeling groundwater recharge under different climatic conditions. J. Hydrol. 2015, 521, 470–481. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Mualem, Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 1976, 12, 513–522. [Google Scholar] [CrossRef]
- Šimůnek, J.; van Genuchten, M.T.; Šejna, M. Hydrus: Model use, calibration, and validation. Tansac Asabe 2012, 55, 1261–1274. [Google Scholar]
- Šimůnek, J.; van Genuchten, M.T.; Sejna, M. The hydrus-1d software package for simulating the one-dimensional movement of water, heat, and multiple solutes in variably-saturated media. Univ. Calif. -Riverside Res. Rep. 2005, 3, 1–240. [Google Scholar]
- Zhao, W.; Liu, B.; Zhang, Z. Water requirements of maize in the middle heihe river basin, china. Agric. Water Manag. 2010, 97, 215–223. [Google Scholar] [CrossRef]
- Gee, G.W.; Or, D. 2.4 particle-size analysis. Methods Soil Anal. Part 2002, 4, 255–293. [Google Scholar]
- Klute, A.; Dirksen, C. Hydraulic conductivity and diffusivity: Laboratory methods. In Methods of Soil Analysis: Part 1—Physical and Mineralogical Methods; American Society of Agronomy: Madison, WI, USA, 1986; pp. 687–734. [Google Scholar]
- Feddes, R.A.; Kowalik, P.J.; Zaradny, H.X. Simulation of Field Water Use and Crop Yield; Centre for Agricultural Publishing and Documentation: Wageningen, The Netherlands, 1978. [Google Scholar]
- Šimůnek, J.; Hopmans, J.W. Modeling compensated root water and nutrient uptake. Ecol. Model. 2009, 220, 505–521. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A Numerical Model for Water and Solute Movement in and below the Root Zone; United States Department of Agriculture Agricultural Research Service U.S. Salinity Laboratory: Riverside, CA, USA, 1987.
- Slavich, P.G.; Petterson, G.H. Estimating the electrical conductivity of saturated paste extracts from 1: 5 soil, water suspensions and texture. Soil Res. 1993, 31, 73–81. [Google Scholar] [CrossRef]
- Corwin, D.L.; Lesch, S.M. Application of soil electrical conductivity to precision agriculture. Agron. J. 2003, 95, 455–471. [Google Scholar] [CrossRef]
- Richards, L.A. U.S. salinity laboratory staff. In USDA Handbook No. 60. Diagnosis and Improvement of Saline and Alkali Soils; USDA: Washington, DC, USA, 1954; p. 13. [Google Scholar]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements-FAO Irrigation and Drainage Paper 56; FAO: Rome, Italy, 1998; Volume 300, p. 6541. [Google Scholar]
- Allen, R.G.; Pereira, L.S. Estimating crop coefficients from fraction of ground cover and height. Irrig. Sci. 2009, 28, 17–34. [Google Scholar] [CrossRef]
- Schaap, M.G.; Leij, F.J.; van Genuchten, M.T. Rosetta: A computer program for estimating soil hydraulic parameters with hierarchical pedotransfer functions. J. Hydrol. 2001, 251, 163–176. [Google Scholar] [CrossRef]
- Vanderborght, J.; Vereecken, H. Review of dispersivities for transport modeling in soils. Vadose Zone J. 2007, 6, 29–52. [Google Scholar] [CrossRef]
- Gelhar, L.W.; Welty, C.; Rehfeldt, R.K. A critical review of data on field-scale dispersion in aquifers. Water Resour. Res. 1992, 28, 1955–1974. [Google Scholar] [CrossRef]
- Moayyad, B. Importance of Groundwater Depth, Soil Texture and Rooting Depth on Arid Riparian Evapotranspiration; New Mexico Institute of Mining and Technology: Socorro, NM, USA, 2001. [Google Scholar]
- Grinevskii, S.O. Modeling root water uptake when calculating unsaturated flow in the vadose zone and groundwater recharge. Mosc. Univ. Geol. Bull. 2011, 66, 189–201. [Google Scholar] [CrossRef]
- Marquardt, D.W. An algorithm for least-squares estimation of nonlinear parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Semenov, M.A.; Barrow, E.M.; Lars-Wg, A. A Stochastic Weather Generator for Use in Climate Impact Studies; User Manual: Hertfordshire, UK, 2002. [Google Scholar]
- Kandelous, M.M.; Kamai, T.; Vrugt, J.A.; Šimůnek, J.; Hanson, B.; Hopmans, J.W. Evaluation of subsurface drip irrigation design and management parameters for alfalfa. Agric. Water Manag. 2012, 109, 81–93. [Google Scholar] [CrossRef]
- Ramos, T.B.; Šimůnek, J.; Gonçalves, M.C.; Martins, J.C.; Prazeres, A.; Pereira, L.S. Two-dimensional modeling of water and nitrogen fate from sweet sorghum irrigated with fresh and blended saline waters. Agric. Water Manag. 2012, 111, 87–104. [Google Scholar] [CrossRef]
- Siyal, A.A.; Bristow, K.L.; Šimůnek, J. Minimizing nitrogen leaching from furrow irrigation through novel fertilizer placement and soil surface management strategies. Agric. Water Manag. 2012, 115, 242–251. [Google Scholar] [CrossRef]
- Garg, K.K.; Das, B.S.; Safeeq, M.; Bhadoria, P.B.S. Measurement and modeling of soil water regime in a lowland paddy field showing preferential transport. Agric. Water Manag. 2009, 96, 1705–1714. [Google Scholar] [CrossRef]
- Patil, M.D.; Das, B.S.; Bhadoria, P.B.S. A simple bund plugging technique for improving water productivity in wetland rice. Soil Tillage Res. 2011, 112, 66–75. [Google Scholar] [CrossRef]
- Vazifedoust, M.; van Dam, J.C.; Feddes, R.A.; Feizi, M. Increasing water productivity of irrigated crops under limited water supply at field scale. Agric. Water Manag. 2008, 95, 89–102. [Google Scholar] [CrossRef]
- Robarge, W.P. Precipitation/Dissolution Reactions in Soils; CRC Press: Boca Raton, FL, USA, 1999; p. 2. [Google Scholar]
- Herczeg, A.L.; Dogramaci, S.S.; Leaney, F.W.J. Origin of dissolved salts in a large, semi-arid groundwater system: Murray basin, australia. Mar. Freshw. Res. 2001, 52, 41–52. [Google Scholar] [CrossRef]
- Li, C.; Lei, J.; Zhao, Y.; Xu, X.; Li, S. Effect of saline water irrigation on soil development and plant growth in the taklimakan desert highway shelterbelt. Soil Tillage Res. 2015, 146, 99–107. [Google Scholar] [CrossRef]
- Morris, J.D.; Collopy, J.J. Water use and salt accumulation by Eucalyptus camaldulensis and Casuarina cunninghamiana on a site with shallow saline groundwater. Agric. Water Manag. 1999, 39, 205–227. [Google Scholar] [CrossRef]
- Satchithanantham, S.; Krahn, V.; Sri Ranjan, R.; Sager, S. Shallow groundwater uptake and irrigation water redistribution within the potato root zone. Agric. Water Manag. 2014, 132, 101–110. [Google Scholar] [CrossRef]
- Bastias, E.; Alcaraz-Lopez, C.; Bonilla, I.; Martinez-Ballesta, M.C.; Bolanos, L.; Carvajal, M. Interactions between salinity and boron toxicity in tomato plants involve apoplastic calcium. J. Plant Physiol. 2010, 167, 54–60. [Google Scholar] [CrossRef] [PubMed]
- Brotherson, J.D.; Field, D. Tamarix: Impacts of a successful weed. Ra ngelands 1987, 9, 110–112. [Google Scholar]
- Sala, A.; Smith, S.D.; Devitt, D.A. Water use by tamarix ramosissima and associated phreatophytes in a mojave desert floodplain. Ecol. Appl. 1996, 888–898. [Google Scholar] [CrossRef]
- Ibrakhimov, M.; Khamzina, A.; Forkutsa, I.; Paluasheva, G.; Lamers, J.P.A.; Tischbein, B.; Vlek, P.L.G.; Martius, C. Groundwater table and salinity: Spatial and temporal distribution and influence on soil salinization in khorezm region (uzbekistan, aral sea basin). Irrig. Drain. Syst. 2007, 21, 219–236. [Google Scholar] [CrossRef]
- Holland, K.L.; Charles, A.H.; Jolly, I.D.; Overton, I.C.; Gehrig, S.; Simmons, C.T. Effectiveness of artificial watering of a semi-arid saline wetland for managing riparian vegetation health. Hydrol. Process. 2009, 23, 3474–3484. [Google Scholar] [CrossRef]
- Askri, B.; Ahmed, A.T.; Abichou, T.; Bouhlila, R. Effects of shallow water table, salinity and frequency of irrigation water on the date palm water use. J. Hydrol. 2014, 513, 81–90. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Yi, J.; Zhang, J.; Zhao, Y.; Si, B.; Hill, R.L.; Cui, L.; Liu, X. Modeling of Soil Water and Salt Dynamics and Its Effects on Root Water Uptake in Heihe Arid Wetland, Gansu, China. Water 2015, 7, 2382-2401. https://doi.org/10.3390/w7052382
Li H, Yi J, Zhang J, Zhao Y, Si B, Hill RL, Cui L, Liu X. Modeling of Soil Water and Salt Dynamics and Its Effects on Root Water Uptake in Heihe Arid Wetland, Gansu, China. Water. 2015; 7(5):2382-2401. https://doi.org/10.3390/w7052382
Chicago/Turabian StyleLi, Huijie, Jun Yi, Jianguo Zhang, Ying Zhao, Bingcheng Si, Robert Lee Hill, Lele Cui, and Xiaoyu Liu. 2015. "Modeling of Soil Water and Salt Dynamics and Its Effects on Root Water Uptake in Heihe Arid Wetland, Gansu, China" Water 7, no. 5: 2382-2401. https://doi.org/10.3390/w7052382
APA StyleLi, H., Yi, J., Zhang, J., Zhao, Y., Si, B., Hill, R. L., Cui, L., & Liu, X. (2015). Modeling of Soil Water and Salt Dynamics and Its Effects on Root Water Uptake in Heihe Arid Wetland, Gansu, China. Water, 7(5), 2382-2401. https://doi.org/10.3390/w7052382







