Quantification of Water and Salt Exchanges in a Tidal Estuary
Abstract
:1. Introduction


2. Materials and Methods
2.1. Study Area
| Statistical Parameters | Discharges (m3·s−1) | Water Surface Elevation (m) | |||
|---|---|---|---|---|---|
| Wolf-Bay Rivers | Perdido-Bay Rivers | GIWW | Gulf of Mexico | Big Lagoon | |
| Minimum | 0.95 | 11.05 | −0.29 | −0.31 | −0.19 |
| Maximum | 15.37 | 762.45 | 0.58 | 0.56 | 0.54 |
| Mean | 1.95 | 38.81 | 0.10 | 0.10 | 0.14 |
| Standard Deviation | 1.97 | 66.05 | 0.14 | 0.15 | 0.17 |
| 1st Quartile | 1.11 | 14.61 | 0.019 | 0.01 | 0.00 |
| Median | 1.24 | 16.56 | 0.11 | 0.11 | 0.13 |
| 3rd Quartile | 1.74 | 32.83 | 0.20 | 0.20 | 0.25 |
2.2. Hydrodynamic Model
2.3. Theoretical Formulation for Eulerian Decomposition Method
3. Results and Discussions
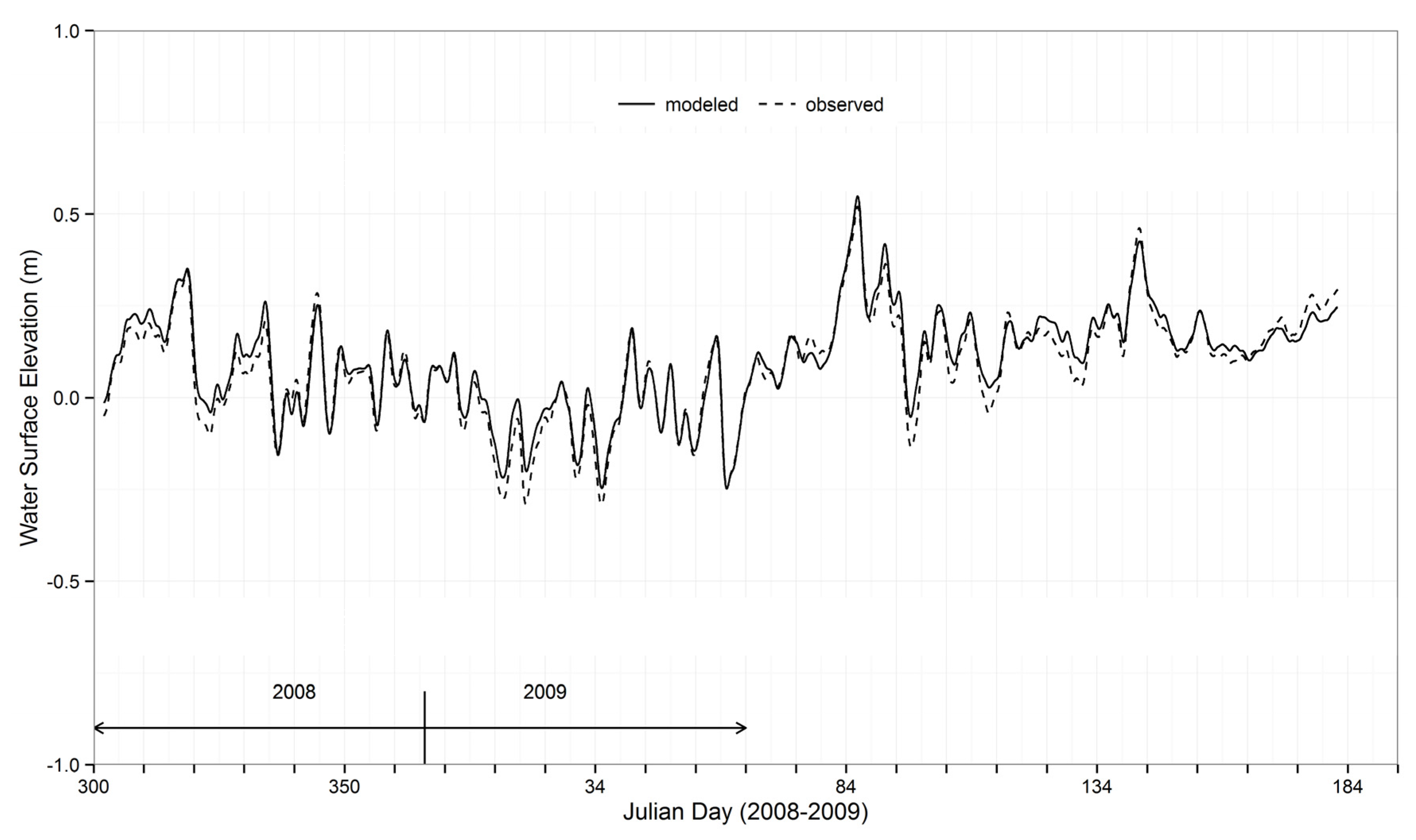
3.1. Comparison of Subtidal Water Surface Elevations
| Statistical Parameters | Blue Angels Park | Terry Cove | ||
|---|---|---|---|---|
| Observed − Modeled | |Observed − Modeled| | Observed − Modeled | |Observed − Modeled| | |
| Minimum | −0.13 | 0.00 | −0.1 | 0.00 |
| Maximum | 0.18 | 0.18 | 0.05 | 0.10 |
| Mean | 0.00 | 0.03 | −0.02 | 0.02 |
| Standard Deviation | 0.04 | 0.03 | 0.03 | 0.02 |
| 1st Quartile | −0.02 | 0.01 | −0.04 | 0.01 |
| Median | 0.00 | 0.02 | −0.02 | 0.02 |
| 3rd Quartile | 0.02 | 0.04 | 0.00 | 0.04 |
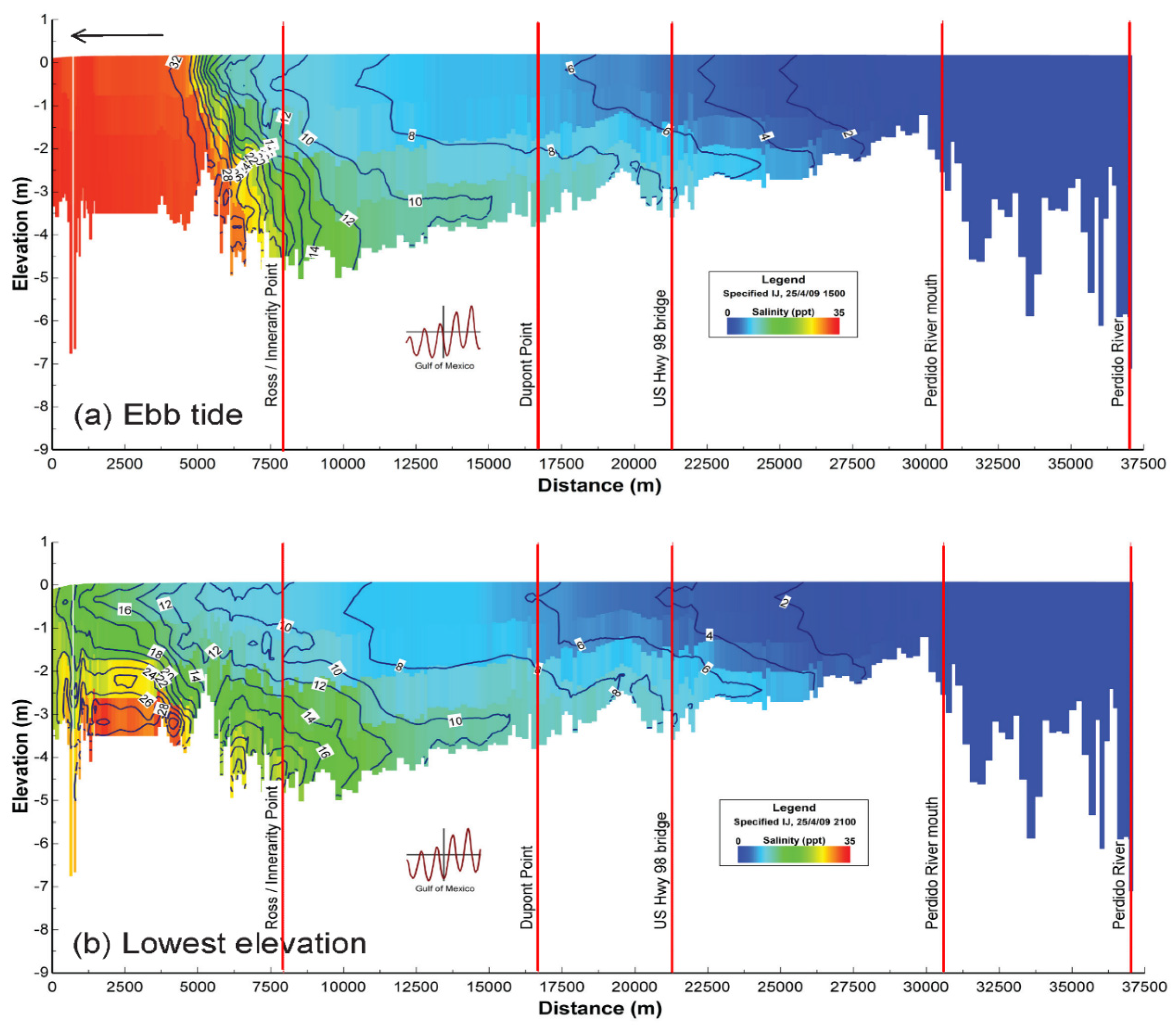
3.2. Salinity Distributions in Perdido Bay
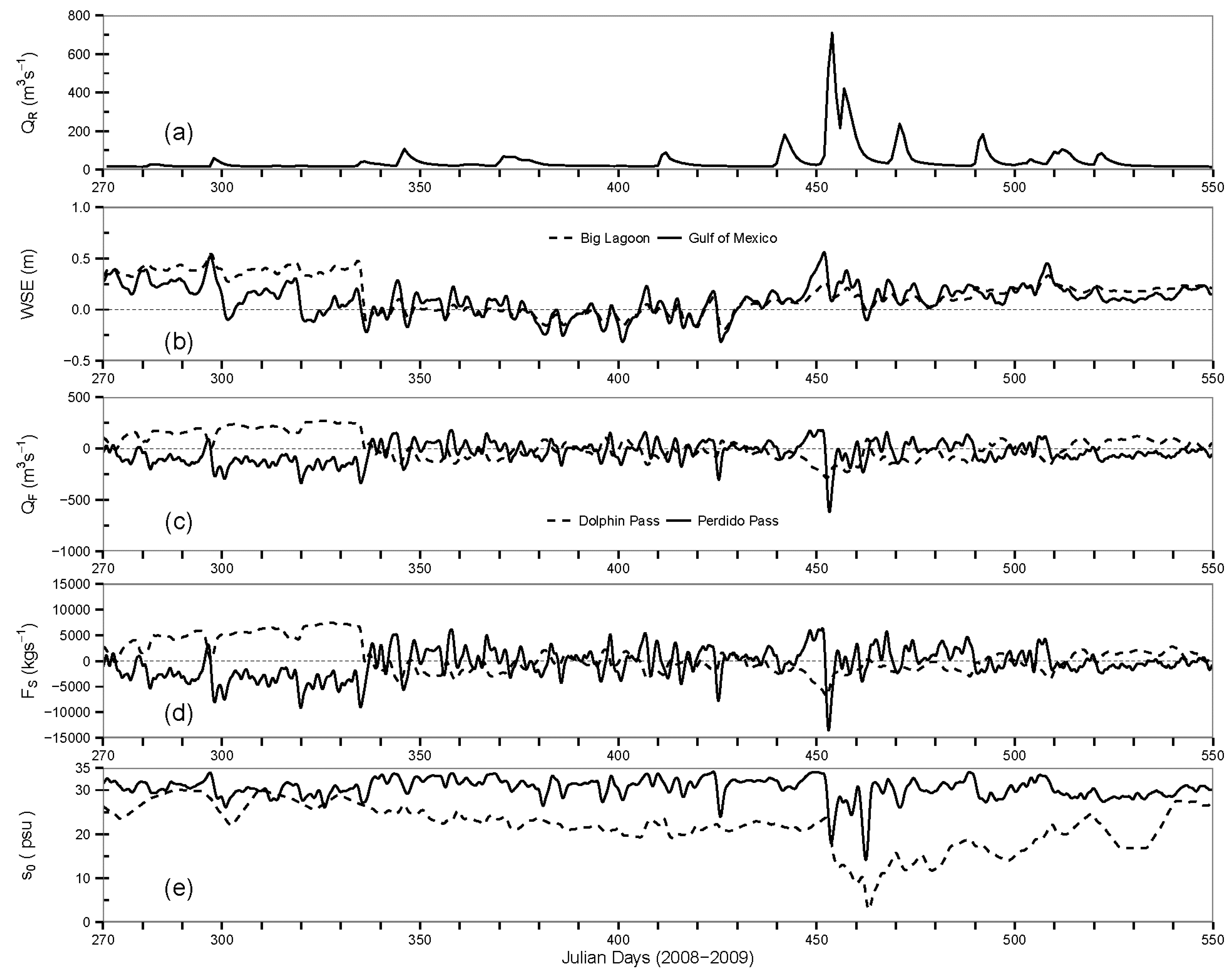
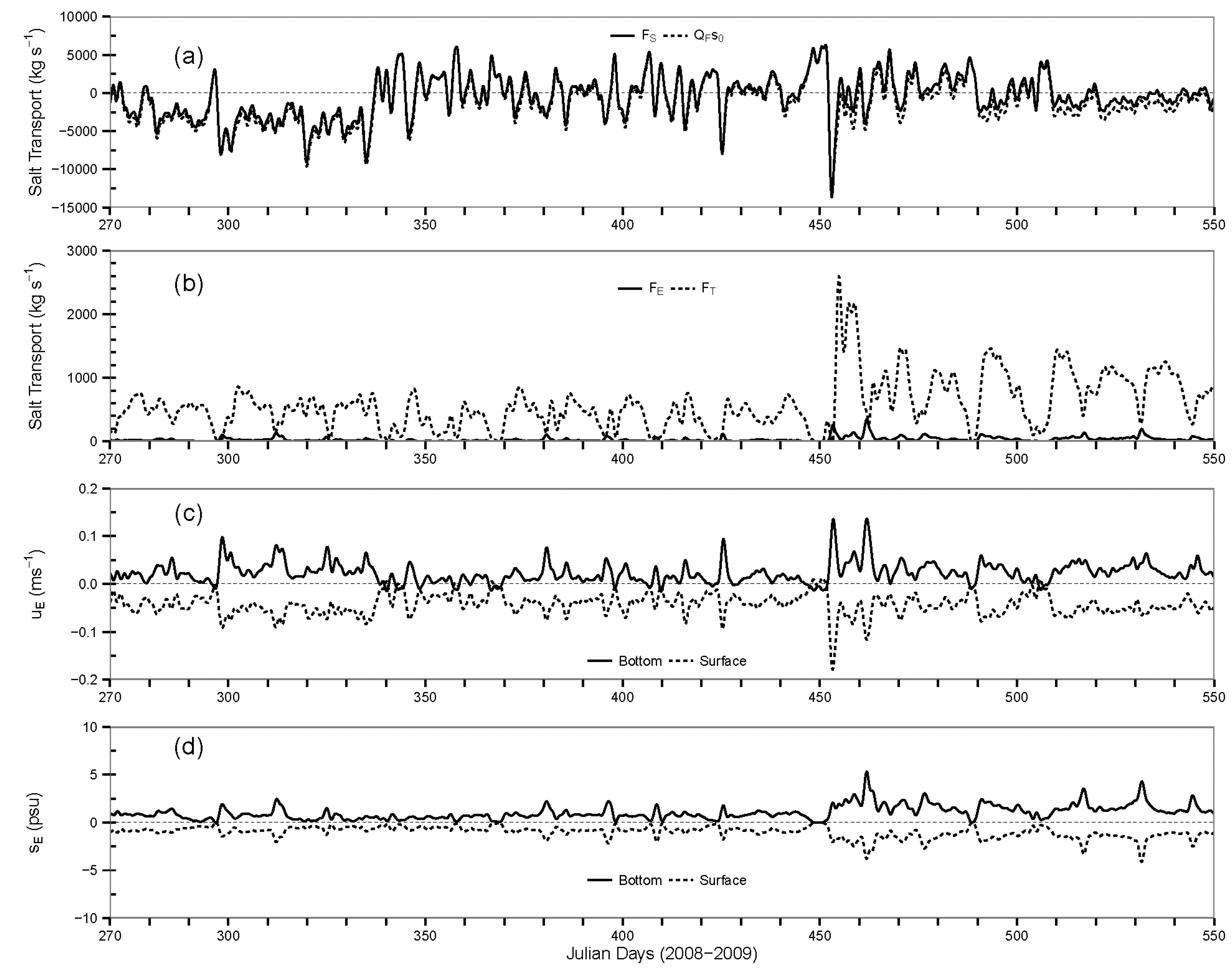
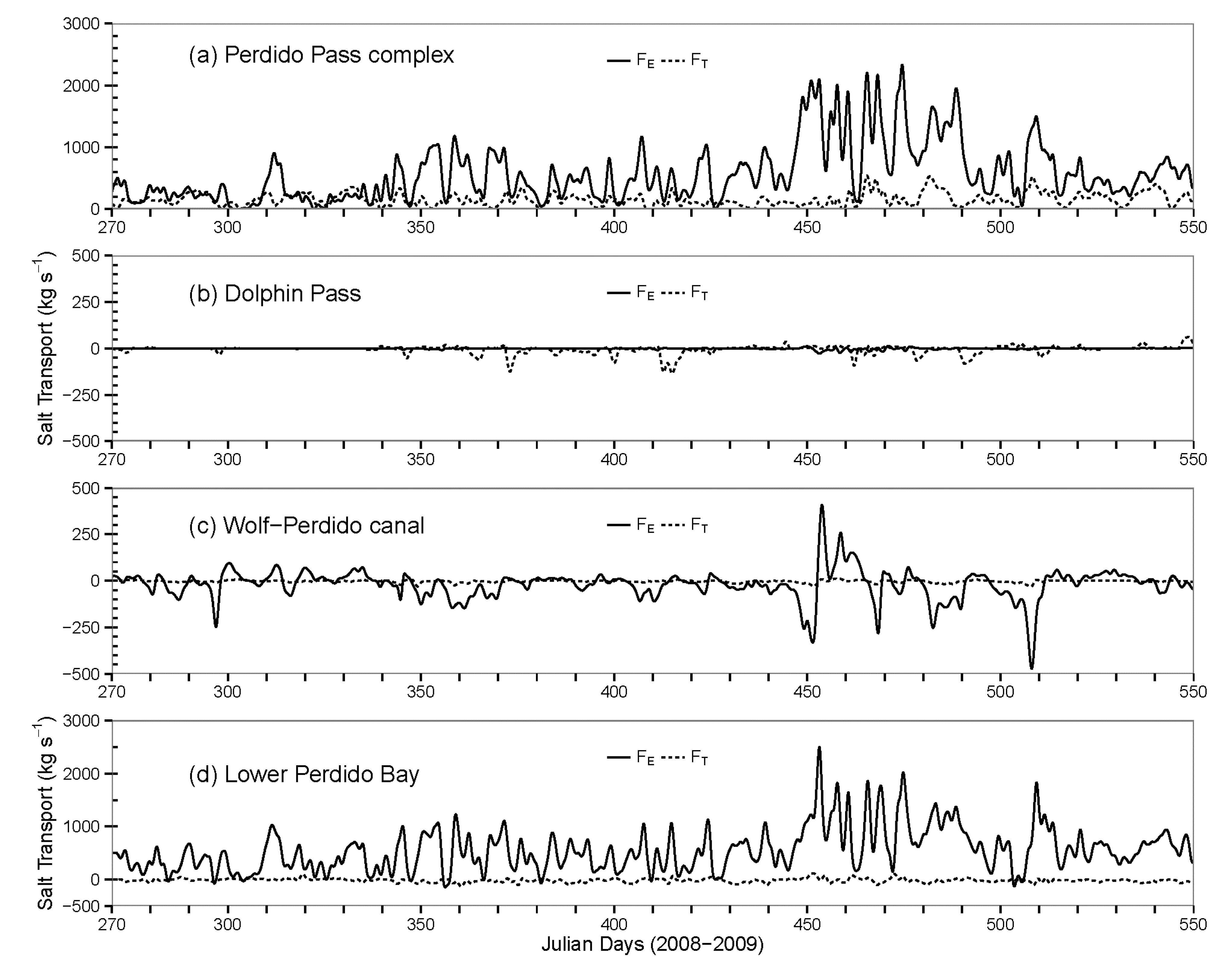
3.3. Eulerian Flux Decomposition in the PBWB System
| Statistical Parameters | Perdido Pass | Perdido Pass Complex | Dolphin Pass | Wolf-Perdido Canal | Lower Perdido Bay | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| QF | FS | QF | FS | QF | FS | QF | FS | QF | FS | |
| Minimum | −619 | −13,480 | −873 | −14,810 | −286 | −6,789 | −127 | −2,181 | −777 | −11,430 |
| Maximum | 180 | 6,289 | 139 | 4,020 | 272 | 7,393 | 51 | 804 | 94 | 2,198 |
| Mean | −42 | −527 | −34 | 113 | 16 | 648 | −14 | −309 | −50 | −360 |
| Standard Deviation | 98 | 2787 | 95 | 1,862 | 121 | 2,924 | 25 | 472 | 76 | 1,302 |
| 1st Quartile | −101 | −2,114 | −66 | −713 | −75 | −1,474 | −29 | −570 | −71 | −921 |
| Median | −40 | −506 | −15 | 430 | 3 | 44 | −12 | −231 | −36 | −125 |
| 3rd Quartile | 18 | 1,118 | 21 | 1,153 | 89 | 1,852 | 2 | 11 | −10 | 327 |
| Cross SectionsVariables | FE | FS | QF |
|---|---|---|---|
| Combined through Sections A-A and C-C versus through Section B-B | 0.06 | 0.95 | 0.97 |
| Combined through Sections B-B and D-D versus through Section E-E | 0.91 | 0.98 | 0.99 |
| Parameter/Location | Perdido Pass | Perdido Pass Complex | Wolf-Perdido Canal | |||
|---|---|---|---|---|---|---|
| +50% Q | −50% Q | +50% Q | −50% Q | +50% Q | −50% Q | |
| FE | −34% | −10% | 41% | −6% | −288% | 3576% |
| (20.2 1) | (18.6) | (180.4) | (121.2) | (42.6) | (87.6) | |
| FT | 20% | −22% | 4% | −19% | 1560% | −1317% |
| (130.7) | (175.8) | (39.5) | (51.6) | (4.0) | (6.1) | |
| FS | −25% | 22% | −1% | 19% | −4% | 10% |
| (223.5) | (301.8) | (218.8) | (282.8) | (61.6) | (95.5) | |
| QF | −44% | 38% | 4% | −8% | −2% | 13% |
| (18.3 2) | (19.0) | (27.0) | (27.2) | (6.9) | (6.5) | |
3.4. Exchange through Perdido Pass
3.5. Exchange through the Perdido Pass Complex and Dolphin Pass
3.6. Exchange through the Wolf-Perdido Canal and Lower Perdido Bay
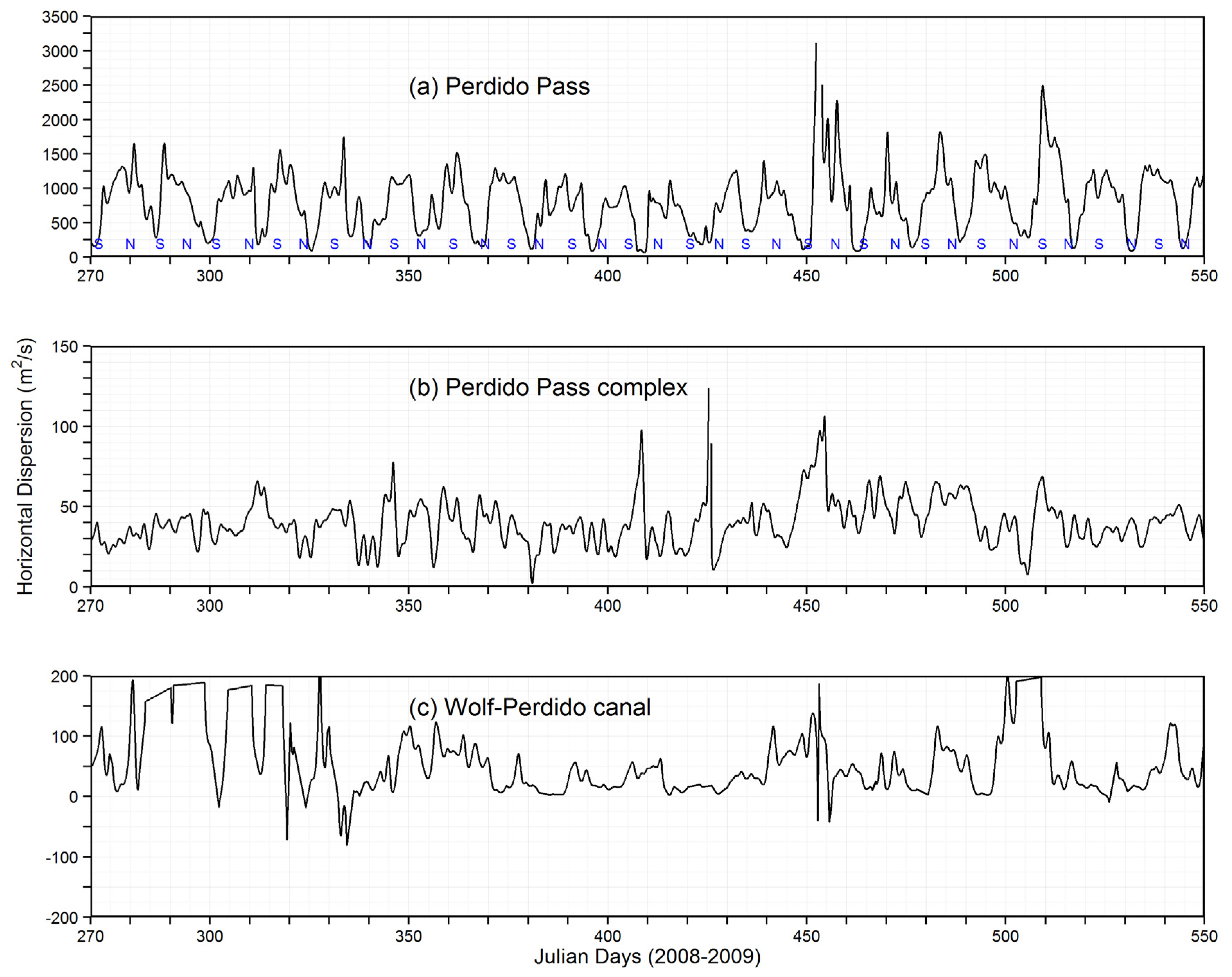
3.7. Horizontal Dispersion
3.8. Sensitivity Experiments

4. Summary and Conclusions
- The salinity at Perdido Bay varied largely with upstream inflows (low and high inflows) and tides at open boundaries (ebb and flood tides). Inflow of highly saline water at the bottom layers and outflow of relative low salinity water at the surface layers resulted from the interaction of flood tide at the Gulf of Mexico and inflows from upstream. Salinity was always small from the US Hwy 98 Bridge towards Perdido River. During low inflows from upstream and flood tides from the Gulf of Mexico, maximum salinity up to 32 psu reached Ross/Innerarity Point (lower Perdido Bay).
- Eulerian analysis concluded that tidal oscillatory fluxes (FT) at Perdido Pass (Section A-A) and Dolphin Pass (Section C-C) were dominant compared to exchange flow component FE, whereas at Sections B-B (Perdido Pass complex), D-D (Wolf-Perdido canal), and E-E (lower Perdido Bay) the exchange flows FE were dominant.
- During the simulation period, it was found that a small amount of flow exchange occurred between Wolf Bay and Perdido Bay. During the high inflows from rivers in Perdido Bay and higher tides from the Gulf and Big Lagoon, the water from Perdido Bay moved towards Wolf Bay, however, during normal flows and gentle tides the water from Wolf Bay moved towards Perdido Bay. It means the influences from Perdido Bay and the Gulf of Mexico was relatively small in Wolf Bay under normal inflows.
- Horizontal dispersion coefficient was computed at three locations for the calibration run and it was found that the magnitude of horizontal dispersion at Perdido Pass (a relatively narrow channel which directly connects to the Gulf) was approximately 10 times larger than horizontal dispersion coefficient at Perdido Pass complex (wide cross section).
- Sensitivity runs with 50% increase and 50% decrease in freshwater inflow relative to the calibration run were performed. At Perdido Pass, total salt flux FS would decrease on average by 25% for 50% Q increase while it would increase by 22% for 50% Q decrease, because tidal boundary at the Gulf is fixed for the calibration and sensitivity runs.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Neilson, B.J.; Cronin, L.E. Estuaries and Nutrients; Humana Press: Clifton, NJ, USA, 1981. [Google Scholar]
- Kennish, M.J. Ecology of Estuaries, Volume i: Physical and Chemical Aspects; CRC Press, Inc.: Boca Raton, FL, USA, 1986; p. 254. [Google Scholar]
- Bilgili, A.; Proehl, J.A.; Lynch, D.R.; Smith, K.W.; Swift, M.R. Estuary/ocean exchange and tidal mixing in a gulf of maine estuary: A lagrangian modeling study. Estuar. Coast. Shelf Sci. 2005, 65, 607–624. [Google Scholar] [CrossRef]
- Ketchum, B.H. The exchanges of fresh and salt waters in tidal estuaries. J. Marine Res. 1951, 10, 18–38. [Google Scholar]
- MacCready, P. Calculating estuarine exchange flow using isohaline coordinates. J. Phys. Oceanogr. 2011, 41, 1116–1124. [Google Scholar] [CrossRef]
- Lewis, R.E.; Lewis, J.O. The principal factors contributing to the flux of salt in a narrow, partially stratified estuary. Estuar. Coast. Shelf Sci. 1983, 16, 599–626. [Google Scholar] [CrossRef]
- Jay, D.A.; Musiak, J.D. Internal tidal asymmetry in channel flows: Origins and consequences. Coast. Estuar. Stud. 1996, 211–249. [Google Scholar] [CrossRef]
- Fischer, H.B. Mixing and dispersion in estuaries. Annu. Rev. Fluid Mech. 1976, 8, 107–133. [Google Scholar] [CrossRef]
- Hansen, D.V.; Rattray, M., Jr. New dimensions in estuary classification. Limnol. Oceanogr. 1966, 319–326. [Google Scholar] [CrossRef]
- Smith, R. Buoyancy effects upon longitudinal dispersion in wide well-mixed estuaries. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. 1980, 296, 467–496. [Google Scholar] [CrossRef]
- Uncles, R.J.; Stephens, J.A. Salt intrusion in the tweed estuary. Estuar. Coast. Shelf Sci. 1996, 43, 271–293. [Google Scholar] [CrossRef]
- Fischer, H.B.; List, E.J.; Koh, R.C.Y.; Imberger, J.; Brooks, N.H. Mixing in Inland and Coastal Waters; Academic Press: San Diego, CA, USA, 1979. [Google Scholar]
- MacDonald, D.G. Estimating an estuarine mixing and exchange ratio from boundary data with application to mt. Hope bay (massachusetts/rhode island). Estuar. Coast. Shelf Sci. 2006, 70, 326–332. [Google Scholar] [CrossRef]
- Gilcoto, M.; Pardo, P.C.; Alvarez-Salgado, X.A.; Perez, F.F. Exchange fluxes between the ria de vigo and the shelf: A bidirectional flow forced by remote wind. J. Geophys. Res.-Oceans 2007, 112. [Google Scholar] [CrossRef]
- Traynum, S.; Styles, R. Exchange flow between two estuaries connected by a shallow tidal channel. J. Coast. Res. 2008, 24, 1260–1268. [Google Scholar] [CrossRef]
- Engqvist, A.; Stenstrom, P. Flow regimes and long-term water exchange of the himmerfjarden estuary. Estuar. Coast. Shelf Sci. 2009, 83, 159–174. [Google Scholar] [CrossRef]
- Valle-Levinson, A.; Gutierrez de Velasco, G.; Trasviña, A.; Souza, A.; Durazo, R.; Mehta, A. Residual exchange flows in subtropical estuaries. Estuar. Coasts 2009, 32, 54–67. [Google Scholar] [CrossRef]
- Chen, S.N.; Geyer, W.R.; Ralston, D.K.; Lerczak, J.A. Estuarine exchange flow quantified with isohaline coordinates: Contrasting long and short estuaries. J. Phys. Oceanogr. 2012, 42, 748–763. [Google Scholar] [CrossRef]
- Devkota, J.; Fang, X.; Fang, V.Z. Response characteristics of perdido and wolf bay system to inflows and sea level rise. Br. J. Environ. Clim. Chang. 2013, 3, 229–256. [Google Scholar] [CrossRef]
- Xia, M.; Craig, P.M.; Wallen, C.M.; Stoddard, A.; Mandrup-Poulsen, J.; Peng, M.; Schaeffer, B.; Liu, Z. Numerical simulation of salinity and dissolved oxygen at perdido bay and adjacent coastal ocean. J. Coast. Res. 2011, 27, 73–86. [Google Scholar] [CrossRef]
- Xia, M.; Xie, L.; Pietrafesa, L.J.; Whitney, M.M. The ideal response of a gulf of mexico estuary plume to wind forcing: Its connection with salt flux and a lagrangian view. J. Geophys. Res. 2011, 116, C08035. [Google Scholar]
- Lerczak, J.A.; Geyer, W.R.; Chant, R.J. Mechanisms driving the time-dependent salt flux in a partially stratified estuary. J. Phys. Oceanogr. 2006, 36, 2296–2311. [Google Scholar] [CrossRef]
- Kim, C.-K.; Park, K. A modeling study of water and salt exchange for a micro-tidal, stratified northern gulf of mexico estuary. J. Marine Syst. 2012, 96–97, 103–115. [Google Scholar] [CrossRef]
- Livingston, R.J. Trophic Organization in Coastal Systems; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Duchon, C.E. Lanczos filtering in one and two dimensions. J. Appl. Meteorol. 1979, 18, 1016–1022. [Google Scholar] [CrossRef]
- Wang, R.; Kalin, L. Modelling effects of land use/cover changes under limited data. Ecohydrology 2011, 4, 265–276. [Google Scholar] [CrossRef]
- Beasley, L.R. Interaction of Groundwater,Surface Water and Seawater in Wolf Bay, Weeks Bay, and Dauphin Island Coastal Watersheds, Alabama; Auburn University: Auburn, AL, USA, 2010. [Google Scholar]
- Hamrick, J.M. A Three-Dimensional Environmental Fluid Dynamics Computer Code: Theoretical and Computational Aspects; Special Report 317; Virginia Institute of Marine Science, College of William and Mary: Gloucester Point, VA, USA, 1992. [Google Scholar]
- Hamrick, J.M.; Mills, W.B. Analysis of water temperatures in conowingo pond as influenced by the peach bottom atomic power plant thermal discharge. Environ. Sci. Policy 2000, 3, 197–209. [Google Scholar] [CrossRef]
- Park, K.; Jung, H.-S.; Kim, H.-S.; Ahn, S.-M. Three-dimensional hydrodynamic-eutrophication model (hem-3d): Application to kwang-yang bay, korea. Marine Environ. Res. 2005, 60, 171–193. [Google Scholar] [CrossRef]
- Mellor, G.L.; Yamada, T. Development of a turbulence closure model for geophysical fluid problems. Rev. Geophys. Space Phys. 1982, 20, 851–875. [Google Scholar] [CrossRef]
- Galperin, B.; Kantha, L.H.; Hassid, S.; Rosati, A. A quasi-equilibrium turbulent energy model for geophysical flows. J. Atmos. Sci. 1988, 45, 55–62. [Google Scholar] [CrossRef]
- Gong, W.; Shen, J.; Hong, B. The influence of wind on the water age in the tidal rappahannock river. Marine Environ. Res. 2009, 68, 203–216. [Google Scholar] [CrossRef]
- Godin, G. The Analysis of Tides; University of Toronto Press: Toronto, ON, Canada, 1972; p. 264. [Google Scholar]
- Processing and Publication of Discharge and State Data Collected in Tidally-Influenced Areas. Available online: http://water.usgs.gov/admin/memo/SW/sw10.08-final_tidal_policy_memo.pdf (accessed on 1 March 2014).
- Sterling, M.; Beaman, F.; Morvan, H.; Wright, N. Bed-shear stress characteristics of a simple, prismatic, rectangular channel. J. Eng. Mech. 2008, 134, 1085–1094. [Google Scholar] [CrossRef]
- Dronkers, J.; van de Kreeke, J. Experimental determination of salt intrusion mechanisms in the volkerak estuary. Neth. J. Sea Res. 1986, 20, 1–19. [Google Scholar] [CrossRef]
- Fischer, H.B. Mass transport mechanisms in partially stratified estuaries. J. Fluid Mech. 1972, 53, 671–687. [Google Scholar] [CrossRef]
- Scott, C.F. A numerical study of the interaction of tidal oscillations and non-linearities in an estuary. Estuar. Coast. Shelf Sci. 1994, 39, 477–496. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Devkota, J.; Fang, X. Quantification of Water and Salt Exchanges in a Tidal Estuary. Water 2015, 7, 1769-1791. https://doi.org/10.3390/w7051769
Devkota J, Fang X. Quantification of Water and Salt Exchanges in a Tidal Estuary. Water. 2015; 7(5):1769-1791. https://doi.org/10.3390/w7051769
Chicago/Turabian StyleDevkota, Janesh, and Xing Fang. 2015. "Quantification of Water and Salt Exchanges in a Tidal Estuary" Water 7, no. 5: 1769-1791. https://doi.org/10.3390/w7051769
APA StyleDevkota, J., & Fang, X. (2015). Quantification of Water and Salt Exchanges in a Tidal Estuary. Water, 7(5), 1769-1791. https://doi.org/10.3390/w7051769







