Assessing the Influences of a Flood Diversion Project on Mitigating River Stage, Inundation Extent and Economic Loss
Abstract
:1. Introduction
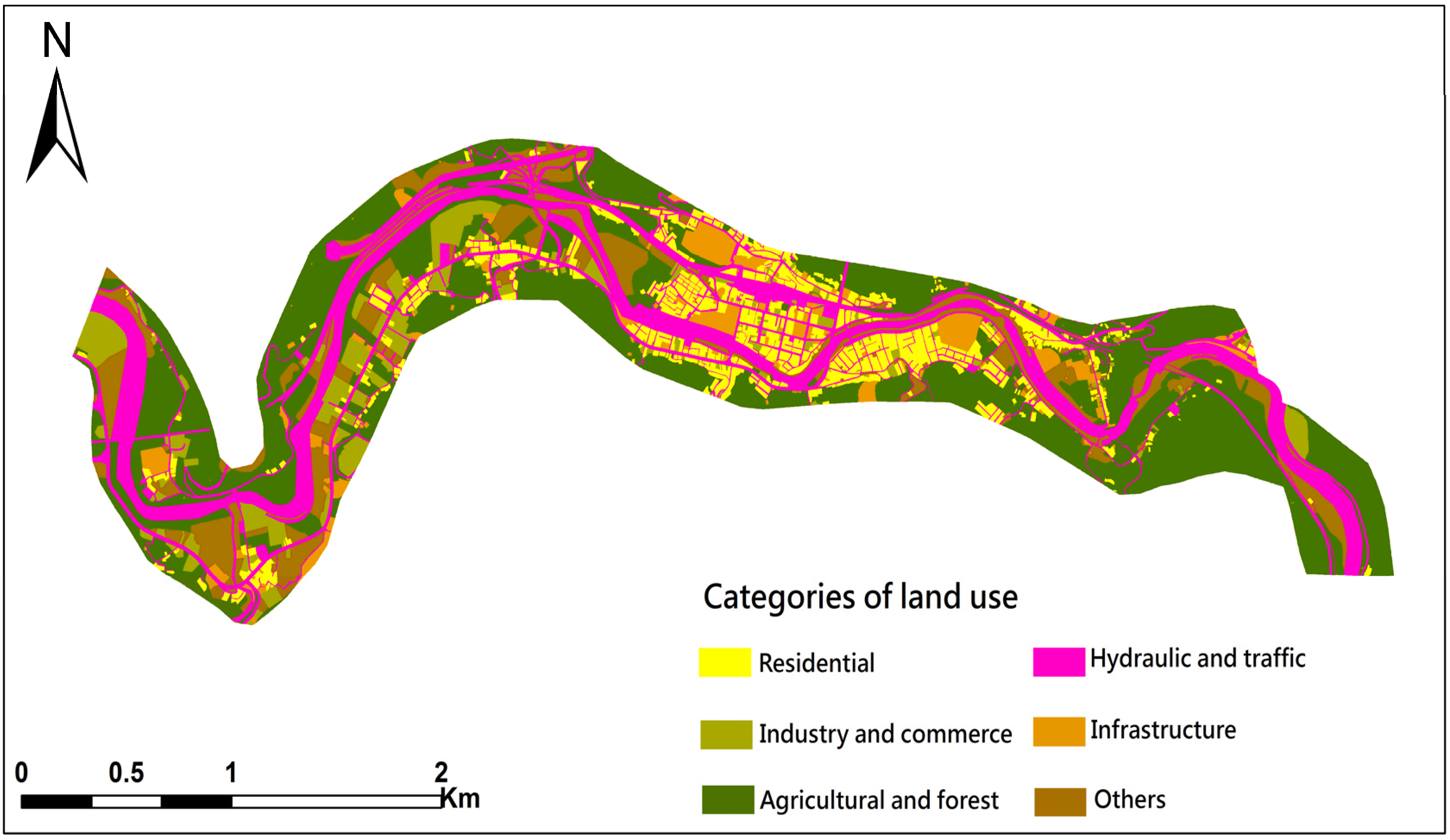
2. Description of the Study Area
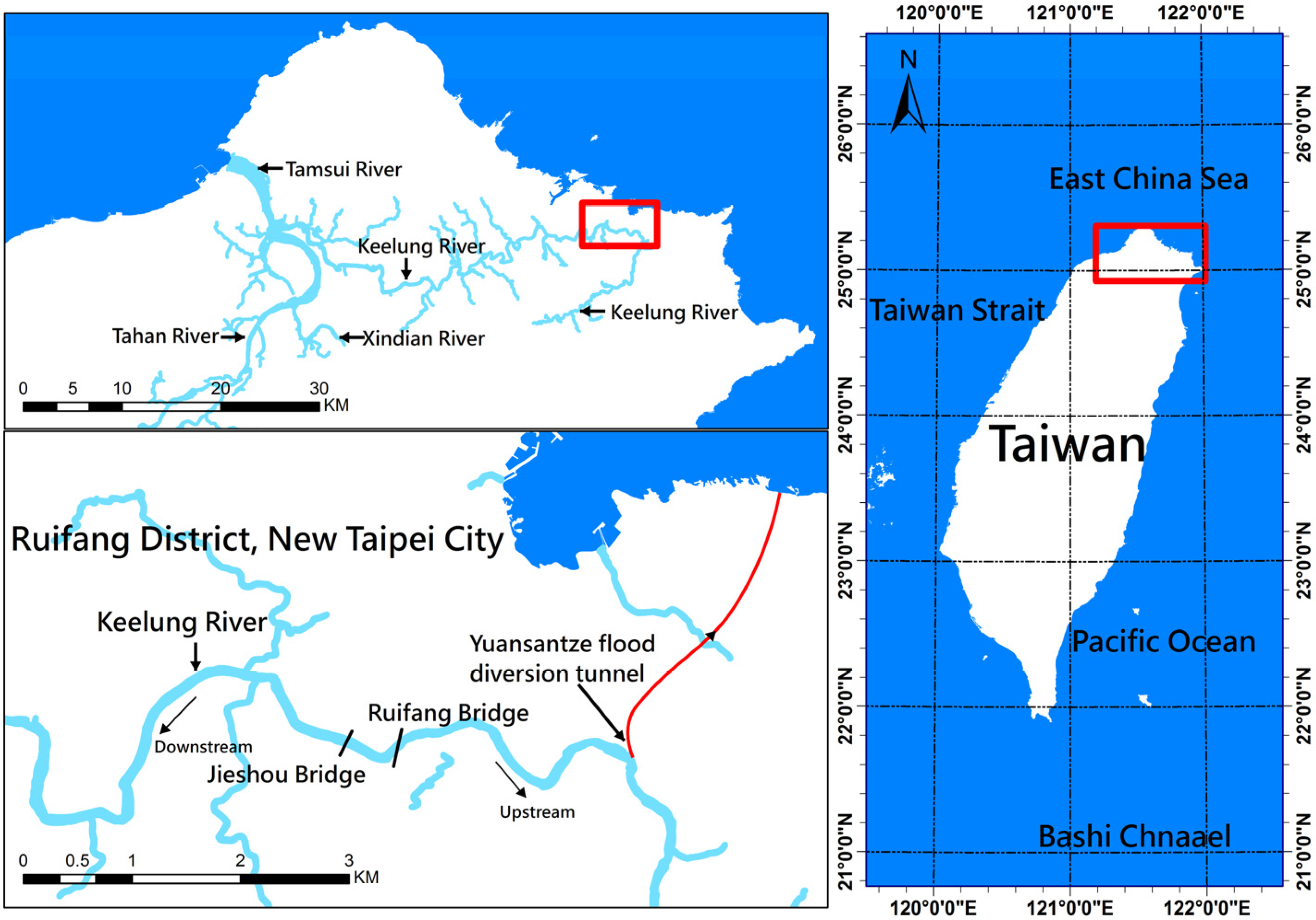
3. Materials and Methods
3.1. Data
3.2. Hydrodynamic Model
3.3. Estimation of Economic Loss
3.4. Model Implementation
3.5. Indices of Model Performance
4. Model Validation
| Typhoon Event | Maximum Diversion Discharge from the Keelung River (m3/s) | Total Diversion Water Volume from the Keelung River (m3) |
|---|---|---|
| Typhoon Sinlaku (2008) | 247 | 1065 × 103 |
| Typhoon Megi (2010) | 455 | 1792 × 103 |
| Typhoon Saola (2012) | 773 | 1879 × 103 |
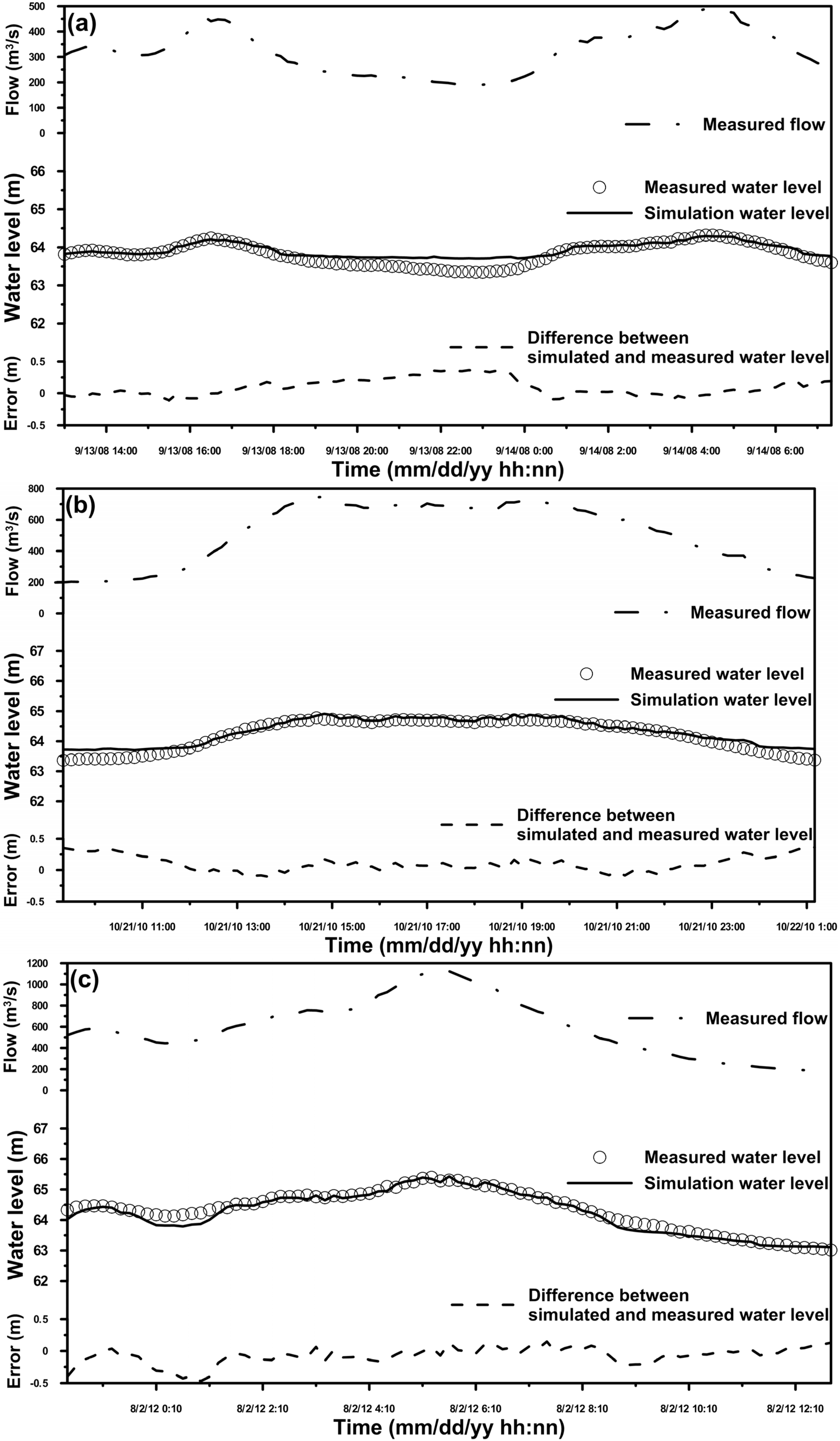
| Typhoon Event | Model | MAE (m) | RMSE (m) | R2 | PBIAS (%) |
|---|---|---|---|---|---|
| Typhoon Sinlaku (2008) | Two-dimensional model | 0.19 | 0.20 | 0.86 | 0.29 |
| Three-dimensional model | 0.12 | 0.16 | 0.87 | 0.15 | |
| Typhoon Megi (2010) | Two-dimensional model | 0.23 | 0.24 | 0.95 | 0.35 |
| Three-dimensional model | 0.12 | 0.16 | 0.96 | 0.16 | |
| Typhoon Saola (2012) | Two-dimensional model | 0.34 | 0.36 | 0.96 | 0.52 |
| Three-dimensional model | 0.11 | 0.15 | 0.96 | −0.11 |
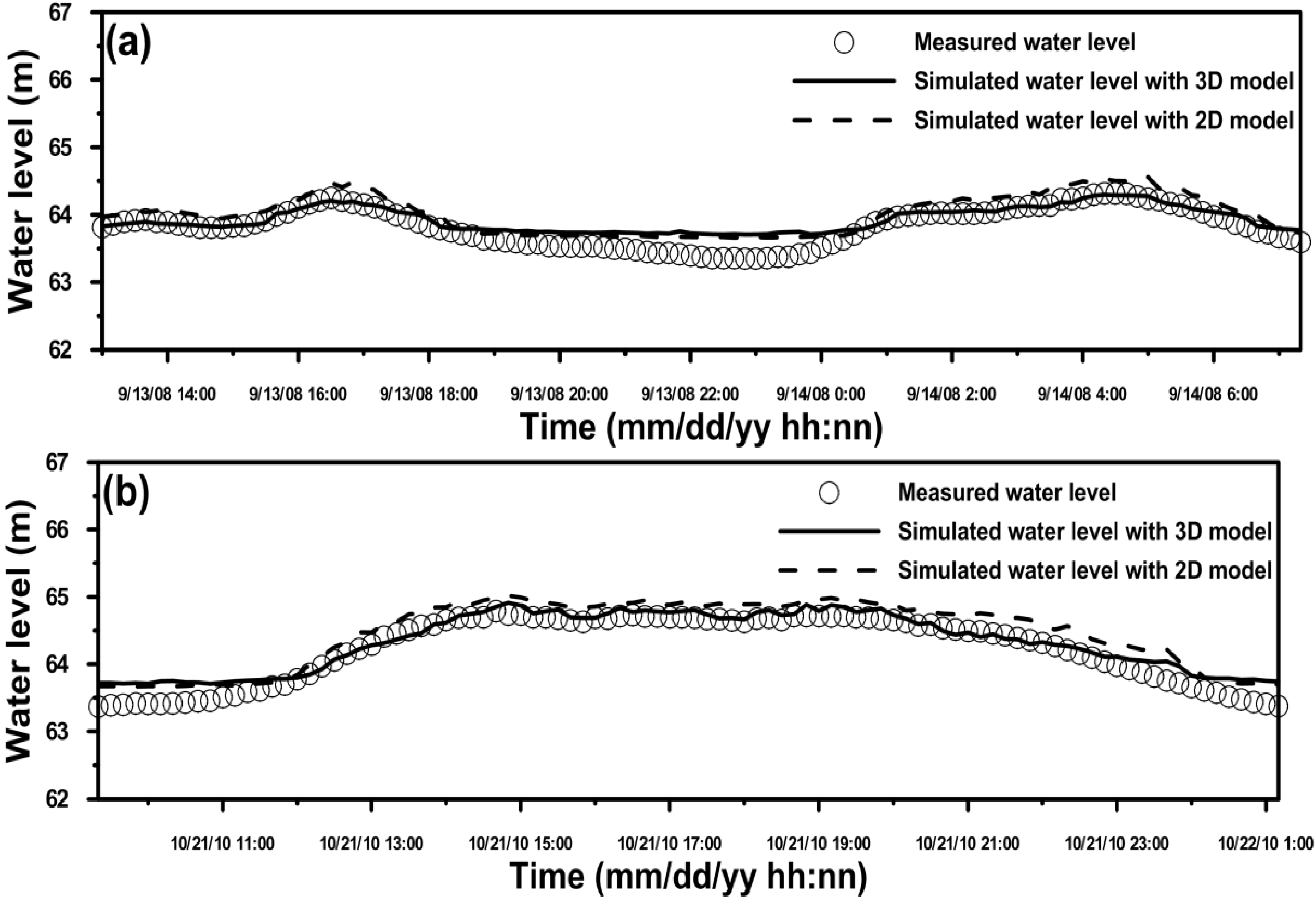
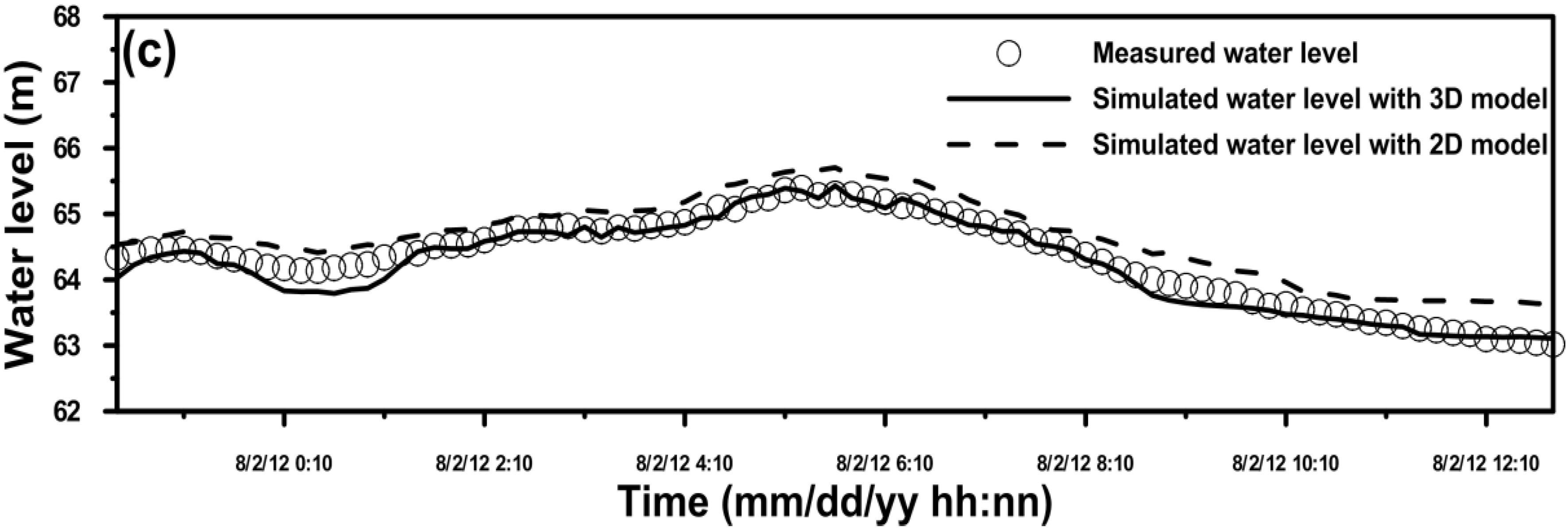
5. Model Application and Discussion
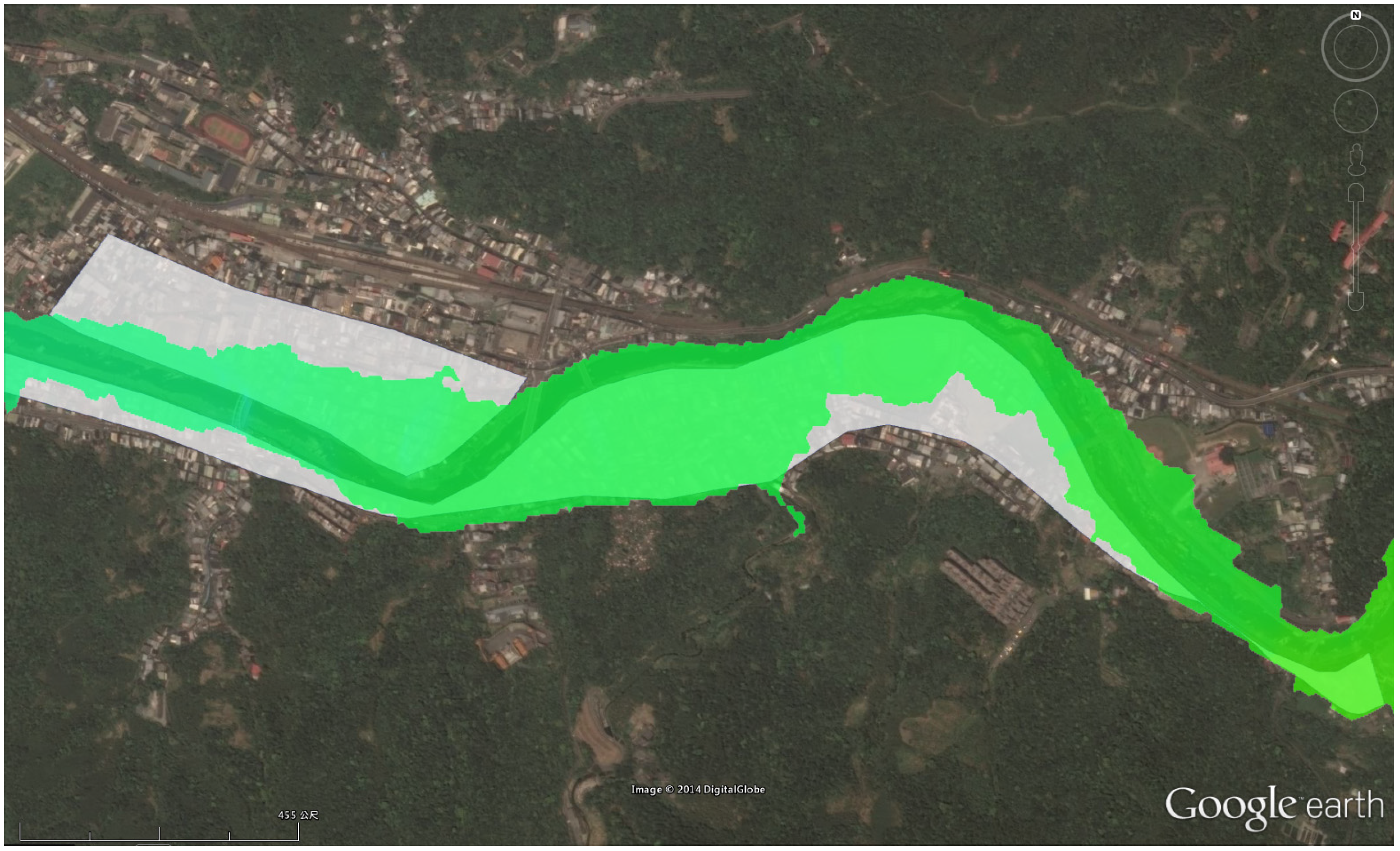
5.1. Influence of the YFDT on River Level and Inundation Extent
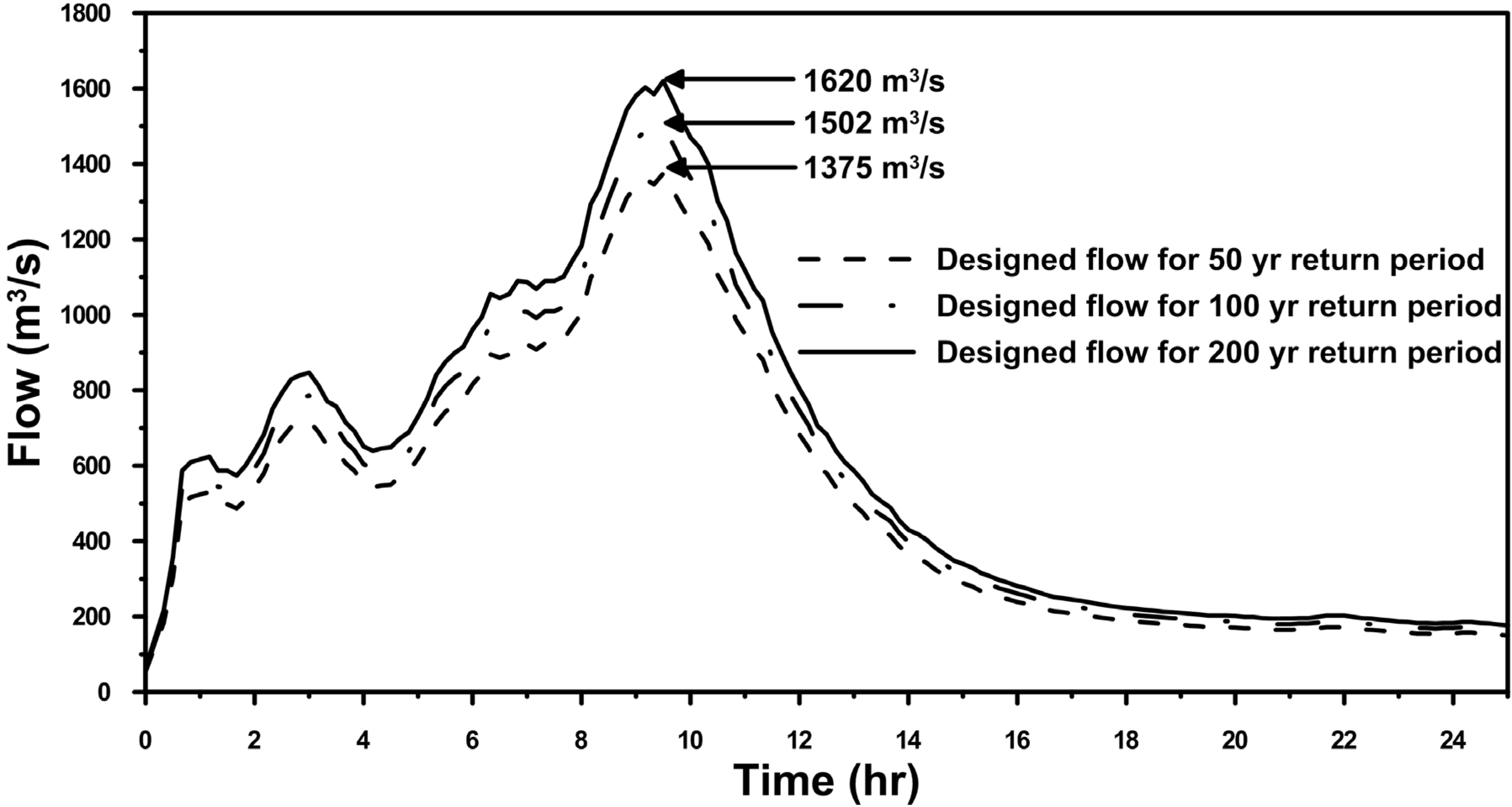
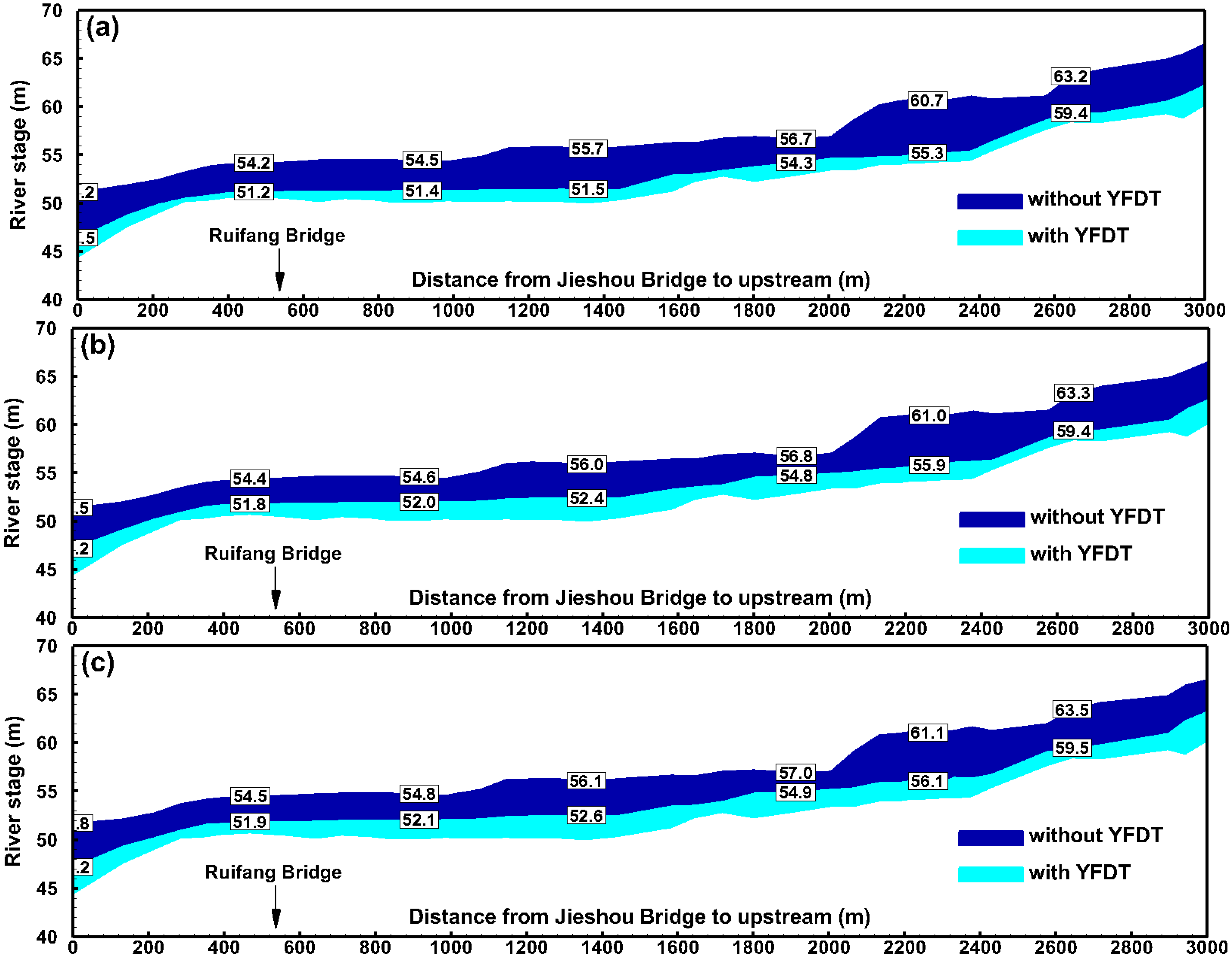
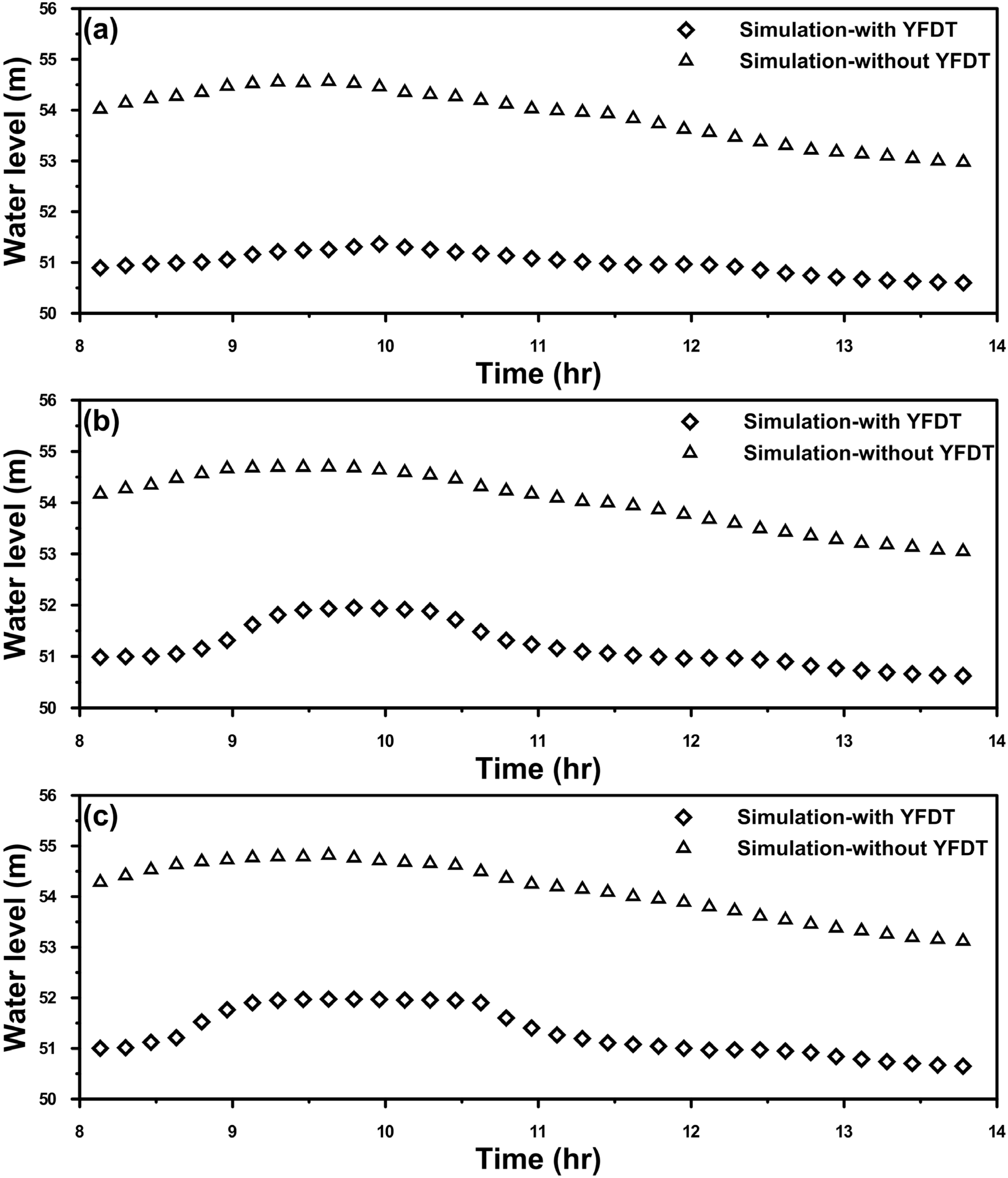
| Return Period | With YFDT | Without YFDT | ||
|---|---|---|---|---|
| Inundation Area (km2) | Inundation Depth (m) | Inundation Area (km2) | Inundation Depth (m) | |
| 2-year | -- | -- | 0.71 | 3.16 |
| 5-year | -- | -- | 0.87 | 3.84 |
| 10-year | 0.28 | 0.56 | 0.99 | 4.15 |
| 20-year | 0.29 | 0.57 | 1.05 | 4.33 |
| 50-year | 0.39 | 1.23 | 1.13 | 4.52 |
| 100-year | 0.50 | 1.89 | 1.20 | 4.63 |
| 200-year | 0.52 | 1.96 | 1.23 | 4.82 |
5.2. Influence of the YFDT on Economic Loss
| Return Period | Pr (a) | Economic Loss (NTD, in Millions) | Pi (d) | Expected Benefits (EB) (NTD, in Millions) (e) = (c − b) × d | |
|---|---|---|---|---|---|
| With YFDT (b) | Without YFDT (c) | ||||
| 2-year | 0.5 | - | 246 | 0.150 | 36.90 |
| 5-year | 0.2 | - | 379 | 0.200 | 75.80 |
| 10-year | 0.1 | 13 | 456 | 0.075 | 33.23 |
| 20-year | 0.05 | 14 | 502 | 0.040 | 19.52 |
| 50-year | 0.02 | 45 | 558 | 0.020 | 10.26 |
| 100-year | 0.01 | 90 | 622 | 0.0075 | 3.99 |
| 200-year | 0.005 | 98 | 666 | 0.0075 | 4.26 |
| Average annual expected benefit (AAEBdis, summation of column (e)) | 183.61 | ||||
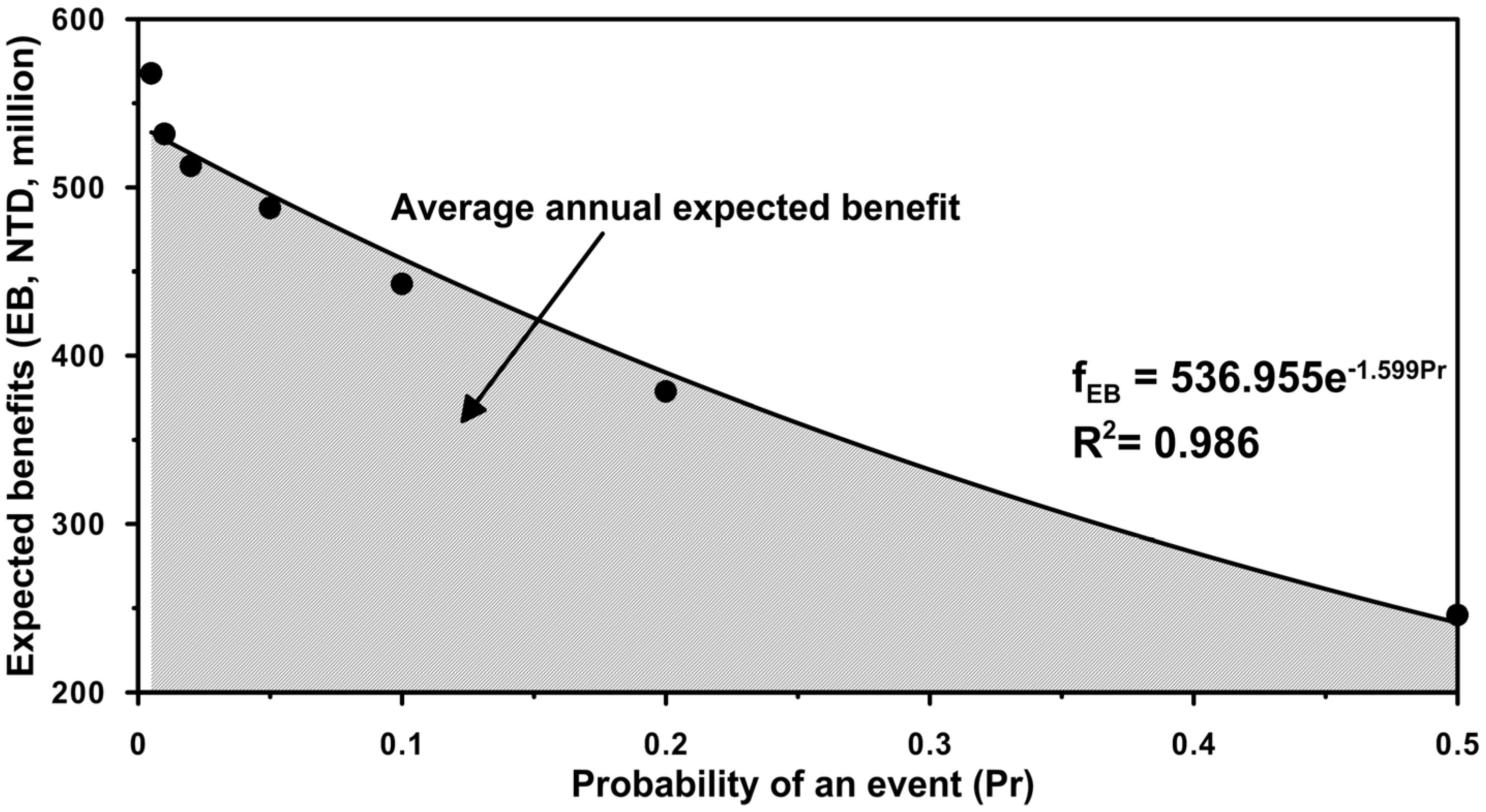
5.3. Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Valdiya, K.S. Coping with Natural Hazards: Indian Context; Orient BlackSwan: Andhra Pradesh, India, 2004; p. 284. [Google Scholar]
- Liu, W.C.; Wu, C.Y. Flash flood routing modeling for levee-breaks and overbank flows due to typhoon events in a complicated river system. Nat. Hazards 2011, 58, 2057–1076. [Google Scholar] [CrossRef]
- Hsieh, L.S.; Hsu, M.H.; Li, M.H. An assessment of structural measures for flood-prone lowlands with high population density along the Keelung River in Taiwan. Nat. Hazards 2006, 37, 133–152. [Google Scholar] [CrossRef]
- The 10th River Management Office. Hydrological Measurements and Hydraulic Analyses for the Yuanshantz Flood Diversion Works; Technical Report; Water Resources Agency: Taipei, Taiwan, 2013. (In Chinese)
- Yang, Z.; Wang, T.; Khangaonkar, T.; Breithaupt, S. Integrated modeling of flood flows and tidal hydrodynamics over a coastal floodplain. Environ. Fluid Mech. 2012, 12, 63–80. [Google Scholar] [CrossRef]
- Condon, A.J.; Sheng, Y.P. Evaluation of coastal inundation hazard for present and future climates. Nat. Hazards 2012, 62, 345–373. [Google Scholar] [CrossRef]
- Allison, M.A.; Vosburg, B.M.; Ramirez, M.T.; Meselhe, E.A. Mississippi River channel response to the Bonnet Carre Spillway opening in the 2011 flood and it implications for the design and operation of river diversions. J. Hydrol. 2013, 477, 104–118. [Google Scholar] [CrossRef]
- Chen, C.N.; Tsai, C.H.; Wu, M.H.; Tsai, C.T. Numerical simulation of potential inundation in a coastal zone. J. Flood Risk Manag. 2015, in press. [Google Scholar]
- Chen, W.B.; Liu, W.C. Modeling flood inundation induced by river flow and storm surges over a river basin. Water 2014, 6, 3182–3199. [Google Scholar] [CrossRef]
- Merwade, V.; Cook, A.; Coonrod, J. GIS techniques for creating river terrain models for hydrodynamic modeling and flood inundation mapping. Environ. Model. Softw. 2008, 23, 1300–1311. [Google Scholar] [CrossRef]
- Water Resource Planning Institute. Physical Model Studies for Detailed Design of the Yuanshantz Flood Diversion Works; Technical Report; Water Resources Agency: Taichung, Taiwan, 2005. (In Chinese)
- Chen, C.; Liu, H.; Beardsley, R.C. An unstructured grid, finite-volume, three-dimensional, primitive equations ocean model: Application to coastal ocean and estuaries. J. Atmos. Ocean. Technol. 2003, 20, 159–186. [Google Scholar] [CrossRef]
- Chen, C.; Beardsley, R.; Cowles, G. An unstructured grid, finite-volume coastal ocean model (FVCOM) system. Oceanography 2006, 19, 78–89. [Google Scholar] [CrossRef]
- Mellor, G.L.; Yamada, T. Development of a turbulence closure model for geophysical fluid problems. Rev. Geophys. Space Phys. 1982, 20, 851–875. [Google Scholar] [CrossRef]
- Smagorinsky, J. General circulation experiments with the primitive equations. Part I. The basic experiment. Mon. Weather Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- Blumberg, A.F.; Mellor, G.L. A description of a three-dimensional coastal ocean circulation model. In Three-Dimensional Coastal Ocean Models; Heaps, N., Ed.; American Geophysical Union: Washington, DC, USA, 1987; Volume 4, pp. 1–16. [Google Scholar]
- Helweg, O.J. Water Resources Planning and Management; John Wiley & Sons: Hoboken, NJ, USA, 1985. [Google Scholar]
- Arnell, N.W. Expected annual damages and uncertainties in flood frequency estimation. J. Water Resour. Plan. Manag. 1989, 115, 94–107. [Google Scholar] [CrossRef]
- Gupta, H.V.; Sorooshian, S.; Yapo, P.O. Status of automatic calibration for hydrologic models: Comparison with multilevel expert calibration. J. Hydrol. Eng. 1999, 4, 135–143. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Am. Soc. Agric. Biol. Eng. 2007, 50, 885–900. [Google Scholar]
- Domeneghetti, A.; Castellarin, A.; Brath, A. Assessing rating-curve uncertainty and its effects on hydraulic calibration. Hydrol. Earth Syst. Sci. 2012, 16, 1191–1202. [Google Scholar] [CrossRef]
- Sasaki, J.; Komatsu, Y.; Matsumaru, R.; Wiyono, R.U.A. Unstructured model investigation of 2004 Indian Ocean tsunami inundation in Banda Aceh, Indonesia. J. Coast. Res. 2011, 64, 941–945. [Google Scholar]
- Ghimire, S. Application of a 2D hydrodynamic model for assessing flood risk from extreme storm events. Climate 2013, 1, 148–162. [Google Scholar] [CrossRef]
- Water Resource Agency (WRA). Hydrology Measurements and Hydraulic Analyses for Inflow Region of the Yuanshantze Flood Diversion (1/3); Technical Report; WRA: Taipei, Taiwan, 2009. (In Chinese)
- Li, H.C.; Chen, Y.C.; Guo, M.J. The development and application of Taiwan loss assessment system (TALS). J. Taiwan Agric. Eng. 2013, 59, 42–55. (In Chinese) [Google Scholar]
- Cerco, C.F.; Bunch, B.; Letter, J. Impact of flood-diversion tunnel on Newark Bay and adjacent waters. J. Hydraul. Eng. 1999, 125, 328–338. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, W.-B.; Liu, W.-C.; Fu, H.-S.; Jang, J.-H. Assessing the Influences of a Flood Diversion Project on Mitigating River Stage, Inundation Extent and Economic Loss. Water 2015, 7, 1731-1750. https://doi.org/10.3390/w7041731
Chen W-B, Liu W-C, Fu H-S, Jang J-H. Assessing the Influences of a Flood Diversion Project on Mitigating River Stage, Inundation Extent and Economic Loss. Water. 2015; 7(4):1731-1750. https://doi.org/10.3390/w7041731
Chicago/Turabian StyleChen, Wei-Bo, Wen-Cheng Liu, Huei-Shuin Fu, and Jiun-Huei Jang. 2015. "Assessing the Influences of a Flood Diversion Project on Mitigating River Stage, Inundation Extent and Economic Loss" Water 7, no. 4: 1731-1750. https://doi.org/10.3390/w7041731
APA StyleChen, W.-B., Liu, W.-C., Fu, H.-S., & Jang, J.-H. (2015). Assessing the Influences of a Flood Diversion Project on Mitigating River Stage, Inundation Extent and Economic Loss. Water, 7(4), 1731-1750. https://doi.org/10.3390/w7041731








