Unlike in transmission mains, WDN are topologically complex and have service connections, making water loss control a difficult task. If the water lost is not visible or the consumers do not report service anomalies, such as low pressure or lack of water, leaks can be very difficult to locate. Leak location activity is usually supported by acoustic equipment, but this approach is expensive, requires specialized human labour and can be very time consuming. An automatic, quick and accurate leak location methodology or technique is the aspiration of every water company.
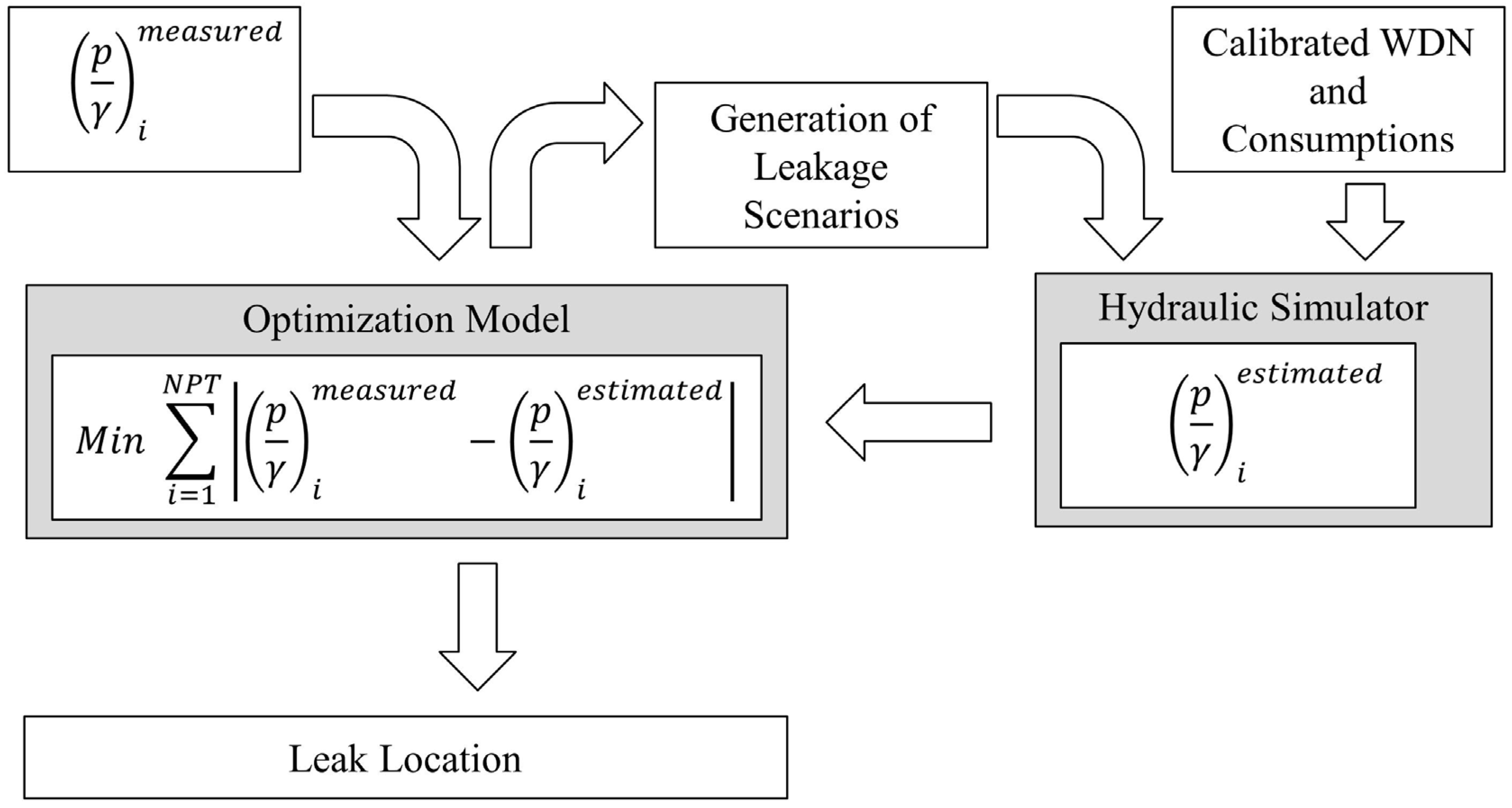
Although manufacturers continue developing new and better equipment, leak location in plastic pipes or in pipes with large diameters is still a problem. To contribute towards the mitigation of this problem, a new computational methodology was developed to help locating unreported leaks and estimating its flow (water loss assessment). This methodology results from linking a hydraulic simulation model to an optimization model. The hydraulic simulation model performs steady state analysis to estimate the water distribution network behaviour. The optimization model aims to minimize the difference between measured and estimated pressures, and its decision variables are the locations and flows from unreported leaks.
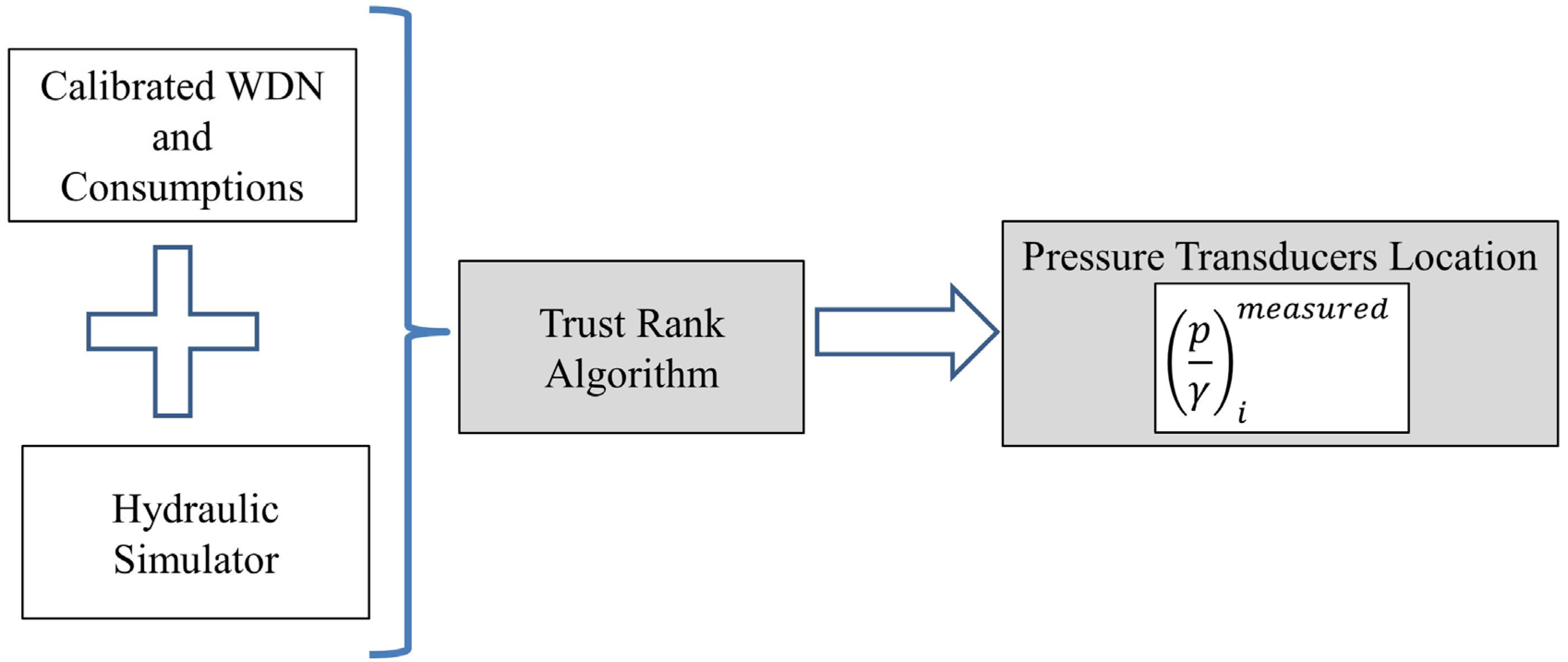
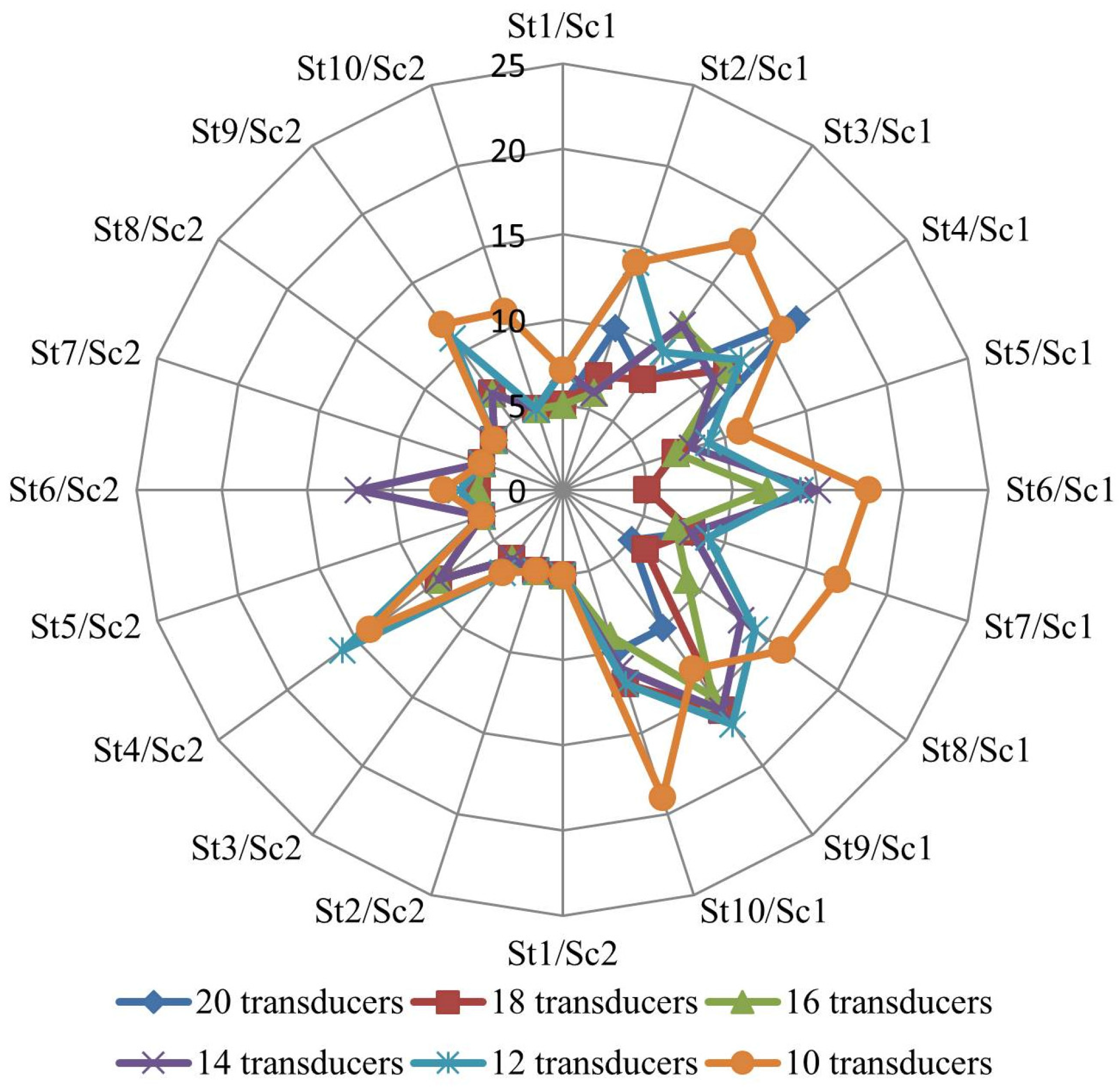
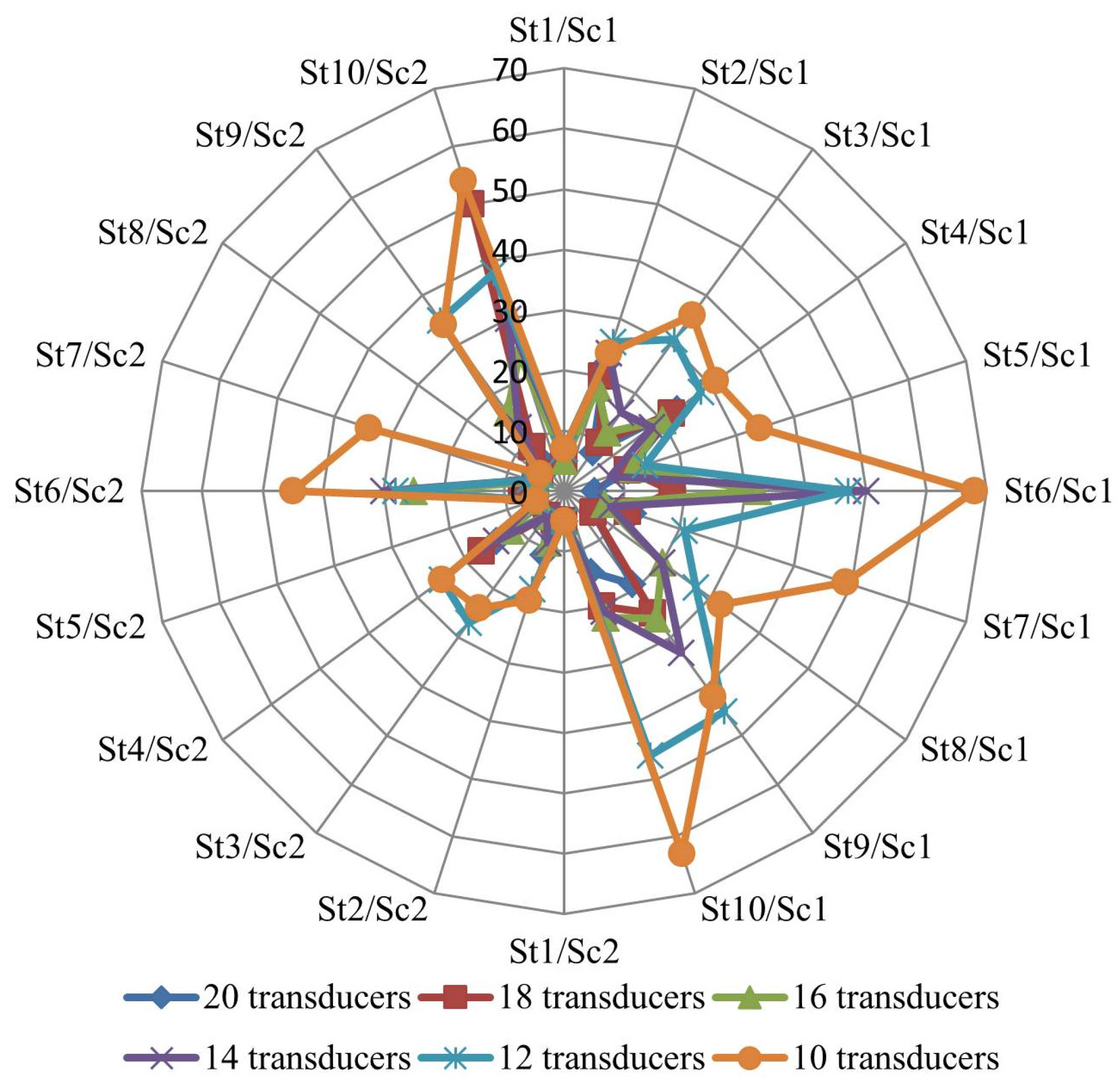
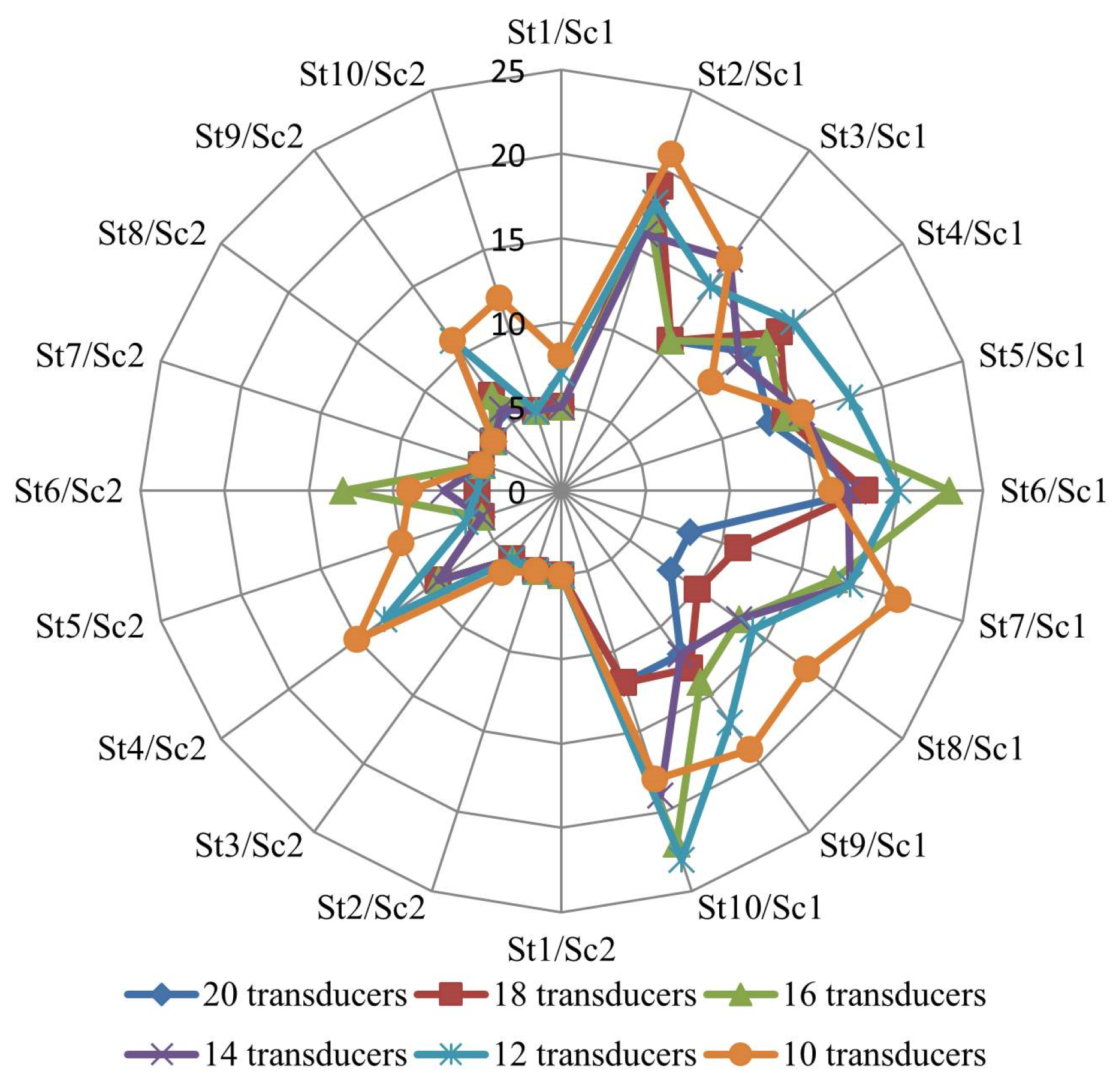
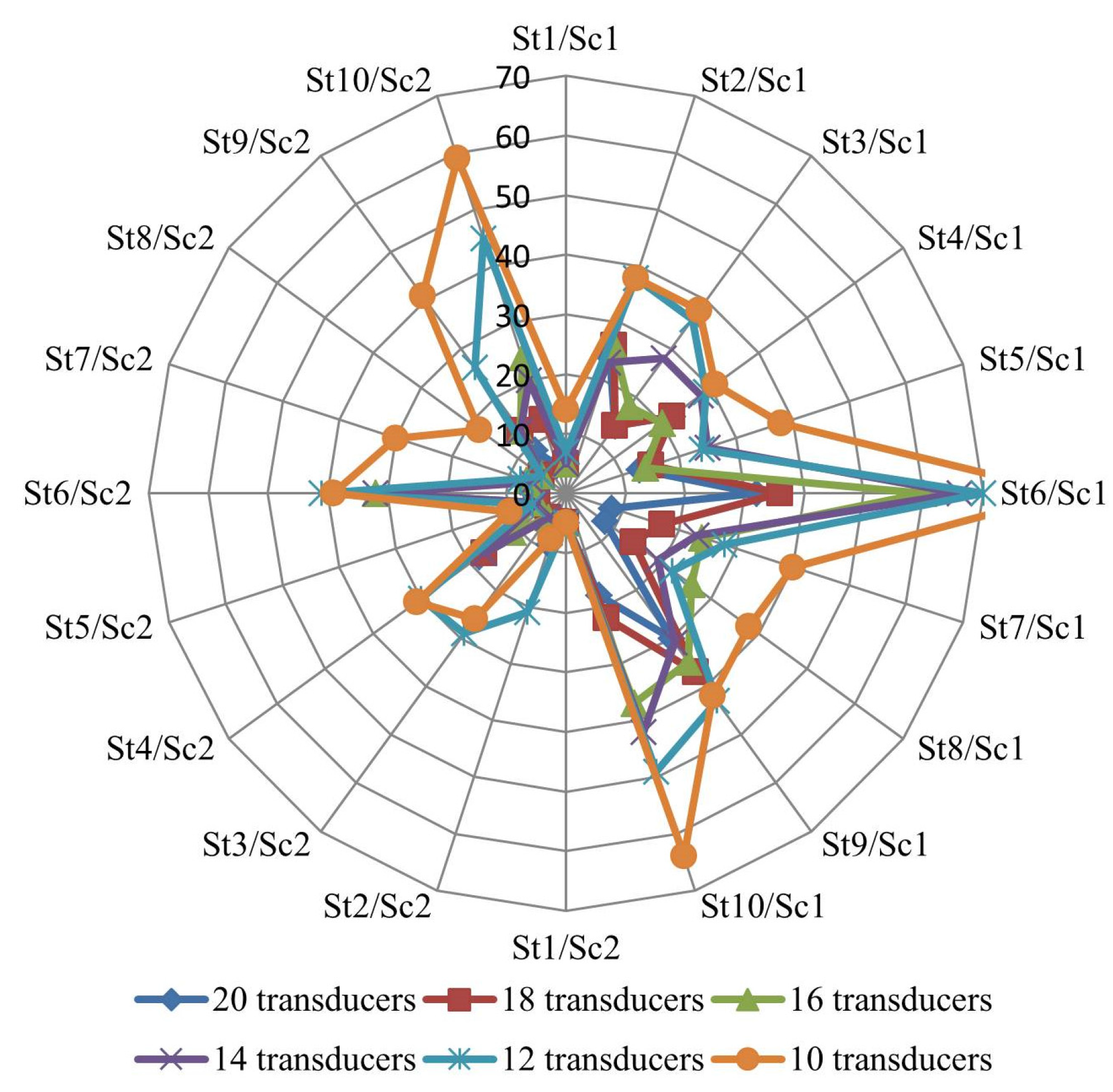
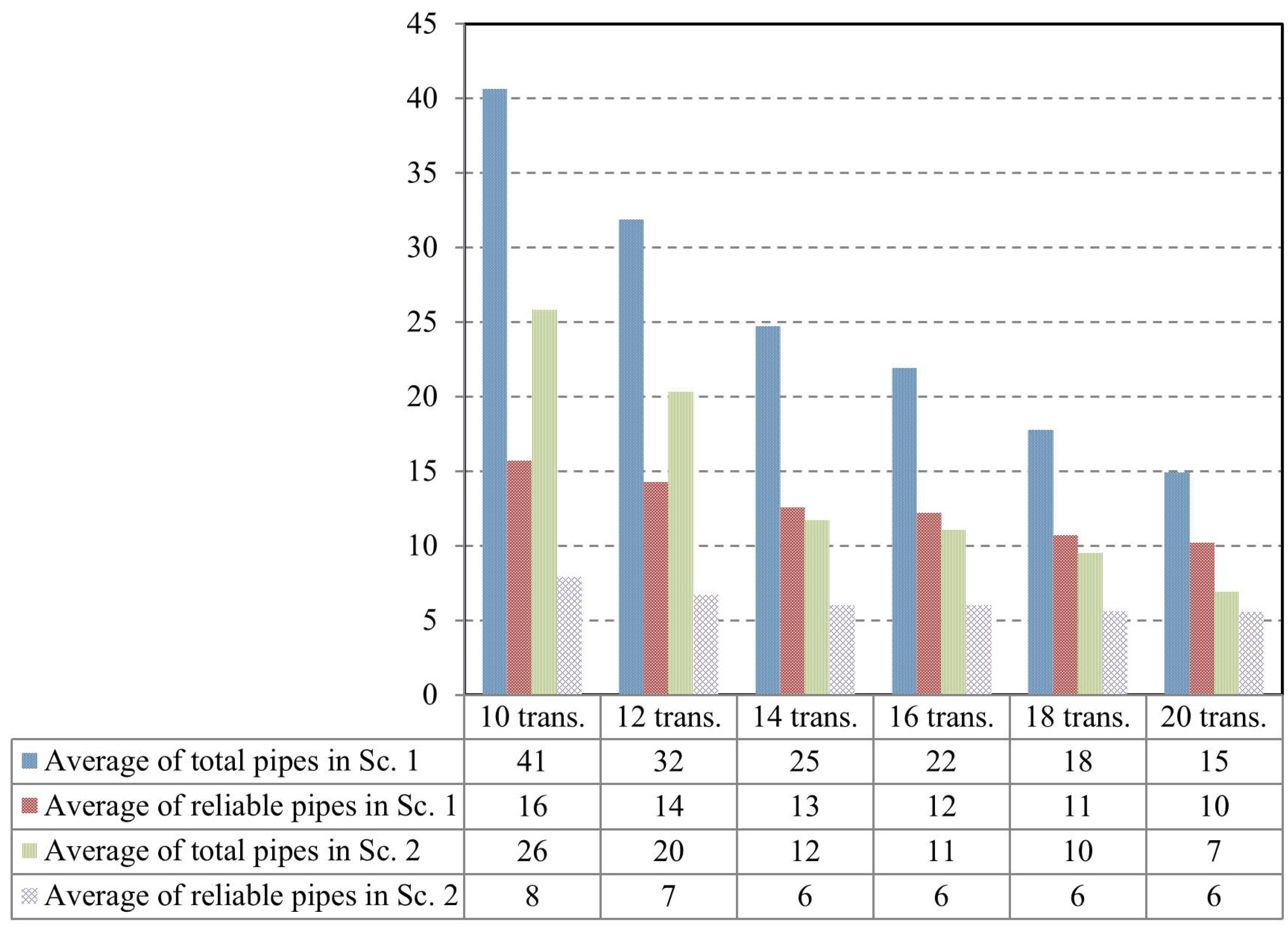
This paper presents a methodology to quantify and to locate leaks. The original contribution is the use of a tool based on the TrustRank algorithm for the selection of nodes for pressure monitoring. The results from these methodologies presented here are: (I) A sensitivity analysis of the number of pressure transducers on the quality of the final solution; (II) A reduction of the number of pipes to be inspected; and (III) A focus on the problematic pipes which allows a better office planning of the inspection works to perform atthe field. To obtain these results, a methodology for the identification of probable leaky pipes and an estimate of their leakage flows is also presented.
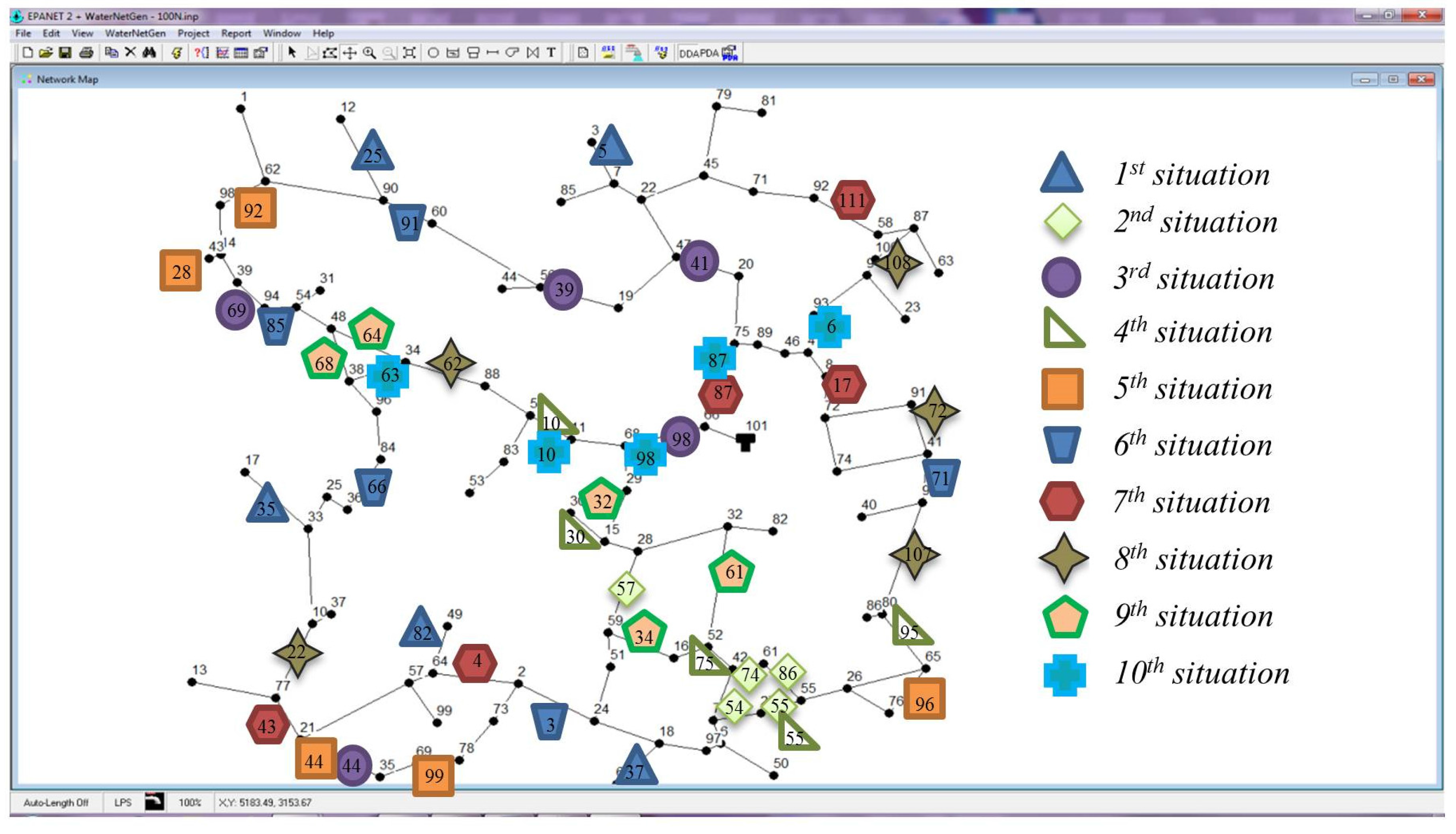
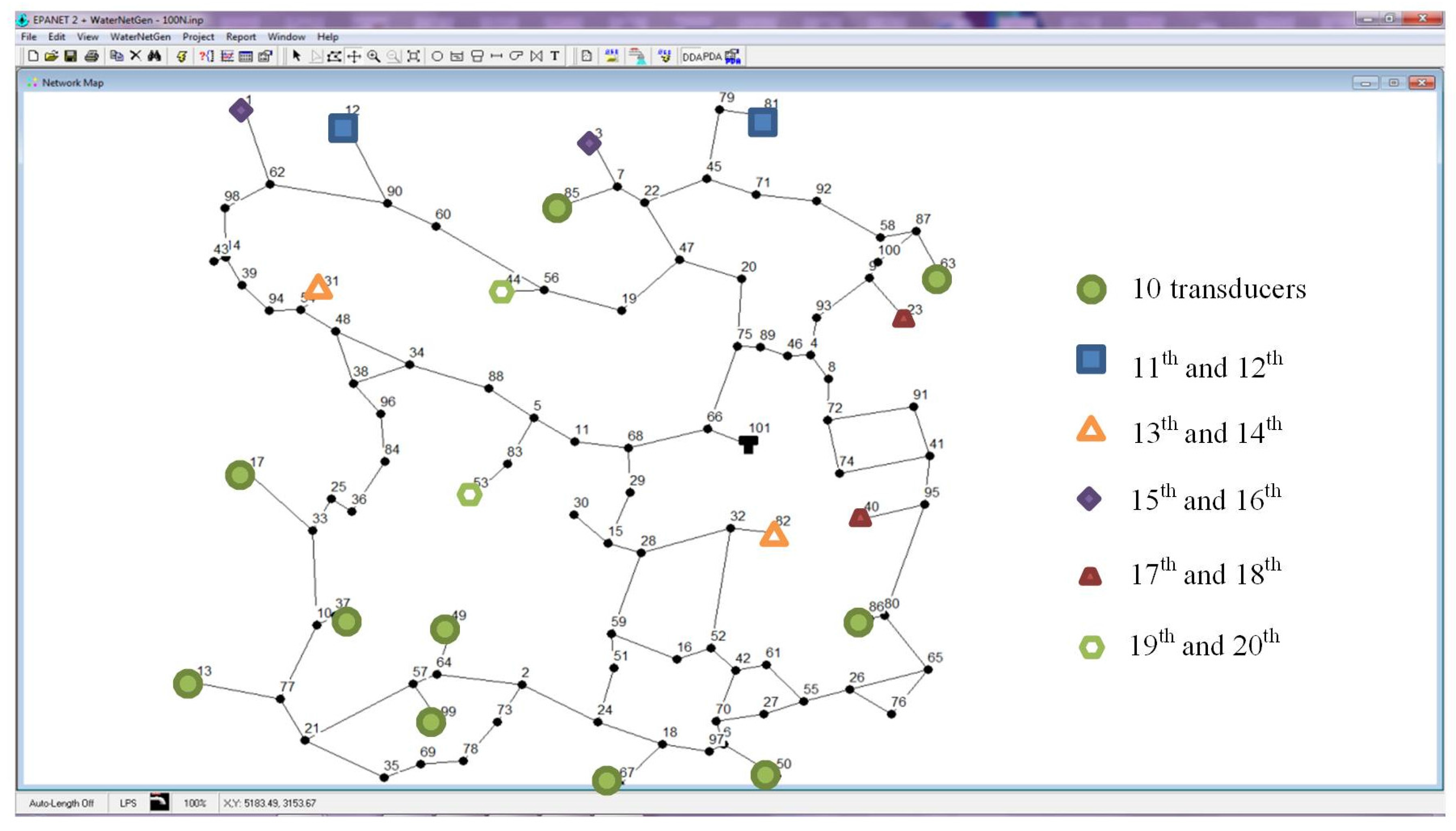
The potential of the methodology is illustrated with several case studies, considering different levels of water losses and different sets of pressure monitoring nodes. The results are discussed and the solutions obtained show the benefits of the developed methodologies.
State of the Art
According to Pilcher [
6], in the 1850s water loss control in WDN was already a concern. Although these are fundamental infrastructures to communities, being buried, they often pass unnoticed to the public, and this distracts people’s awareness away from the water loss problem.
Water loss has several negative impacts, for both the water companies and the society itself, namely: operational (lower service level), economic (lower income and higher operating and capital costs), environmental (higher amount of water and energy usage, and consequent higher water and carbon footprints), public health (potential focus of contamination) and social (service disruptions, traffic disturbances and damage to people and their belongings). These impacts will be more severe with the increase of water demand, the climate change and water scarcity.
Water loss includes apparent losses (unauthorized consumption and customer meter inaccuracies) and real losses (leakage on transmission and/or distribution mains, leakage and overflows at utility’s storage tanks and leakage on service connections up to the point of customer metering). Real losses are an operational problem and correspond to the annual volume of water lost through leakage and overflows at tanks and leaks and bursts in pipes and service connections up to the point of customer metering [
7].
The reduction of real losses in WDN can be attained by adopting active leakage control (ALC) policies. But ALC is not a simple task because unreported leaks can be very difficult to locate, in particular if the water lost is not visible or the customers do not report service anomalies (low pressure or lack of water). The leak location activity is usually supported by acoustic equipment, but it has some drawbacks: is quite expensive, requires specialized human labour, can be very time consuming and is not very effective in plastic pipes and pipes with large diameters. An automatic, quick and accurate leak location methodology or technique is the aspiration of every water company.
Monitoring is important in the water loss control context. Tank monitoring is the most common and usually comprises: water level (to avoid overflows and test for leakage) and flow, particularly during the night when consumption is at its minimum—minimum night flow (for real losses estimation and to support ALC activities). However, measurements in other parts of the WDN is also common, like flow measurement at the entrance of each district metered area (DMA) or pressure measurement at the entrance of each pressure management area (PMA) and at critical points [
8]. Nevertheless, the opportunity to monitor pressure in other spots can play an important role in the context of WDN operation.
In the last few years the monitoring technology has undergone a remarkable evolution. Nowadays equipment is easily achievable, smaller, accurate and precise, can be battery powered and last for years, and can communicate through wireless networks. These new features contributed to widespread monitoring in WDN. Data collected through monitoring has been used for years to calibrate hydraulic models, and it is helpful in planning and operation activities, including leak location. But the location of the flow and pressure sensors plays an important role, and the optimal sensor placement is still an open research subject. For example, for leak location purposes, Candelieri
et al. [
9] selected the best locations by identifying the best trade-off between reliability and deployment costs, Bort
et al. [
10] compared two alternatives using pressure sensitivity; Blesa [
11] used robustness analysis and clustering and Steffelbauer [
12] investigated the use of Monte Carlo simulation.
Some of the existing methodologies developed for leak detection/location are based solely on the analysis of flow and/or pressure measurements: Artificial Neural Networks have been used for leak detection [
13,
14,
15] and also for leak location [
16]; Poulakis
et al. [
17] and Qi [
18] proposed a Bayesian system identification methodology for leak location; Fuzzy Inference Systems, which are computational techniques from the field of Artificial Intelligence, were used by Mounce
et al. [
19] to detect leaks in WDN, and Fuzzy set theory was also used by Islam
et al. [
20] for leak detection and location; Aksela
et al. [
21] used self-organizing maps, combining flow data with a leak function to model leakages, to solve the leakage detection problem; Gertler
et al. [
22] applied principal component analysis to locate leaks; Jung
et al. [
23] used nonlinear Kalman filter; Okeya
et al. used a modified Kalman filter [
24]; Kang
et al. [
25] used control limit analysis to detect bursts; and Goulet
et al. [
5] used a model-falsification methodology for leak-detection.
Flow and/or pressure sensors data, combined with the energy and mass conservation laws, provide the necessary conditions to build state-estimation (or inverse) problems. This methodology was traditionally used to calibrate WDN models [
26], given a set of flow and/or pressure measurements. Pudar and Liggett [
27] presented a methodology based on this idea considering equivalent orifice areas of possible leaks as the unknowns. Andersen and Powell [
28] presented an implicit formulation of the standard weighted least squares state-estimation problem, solved using an implicit Lagrangian approach. Poulakis
et al. [
17] used a Bayesian probabilistic framework to handle the unavoidable uncertainties in measurement and modeling errors, while Puust
et al. [
29] used the Shuffled Complex Evolution Metropolis (SCEM-UA) algorithm to estimate the probability density functions of unknown leak areas.
The same data combined with hydraulic simulation models can also be used to locate leaks in WDN. These hydraulic models can be based on steady state or unsteady state (transient) conditions. The arising of hydraulic transient based techniques to locate leaks occurred in the 1990s [
30] and they consist inartificially introduce transients in the WDN and analyse the pressure data to locate the leaks. Despite that leak location with transients can be excellent for tank-pipe-tank systems, in real WDN its application can be much compromised. Due to the transients behaviour, the pressure data must be recorded with very short time steps and the accuracy of the procedure is very dependent on the celerity (pressure wave velocity), which can be difficult to estimate accurately in real world conditions. Notwithstanding, transient test-based techniques have proved to be effective in locating leaks in transmission mains. The pioneering work from Liggett and Chen [
30] opened a new field of research. The main advances observed in the following two decades can be found in Colombo
et al. [
31] and Puust
et al. [
32] present extensive reviews of these methodologies. More recently signal processing has demonstrated its capabilities to help in this problem [
33,
34], the impedance method was used [
35], wavelet analysis has improved [
36,
37], a portable pressure wave-maker has been designed [
38] and experiments were carried out in real pipe systems to demonstrate the reliability of this approach [
39,
40].
Even knowing that true steady state conditions do not occur, leak location with steady state models seems to be a suitable approach for real world WDN [
41]. The steady state based techniques simulate different hypothetical leakage scenarios, corresponding to different leak locations and severities (leak flows), trying to match the flow and/or pressure data obtained from transducers installed in the WDN. The implementation of this approach requires a calibrated model of the WDN and its accuracy depends on the pressure measurements and the head loss estimation. Leakage modelling can be performed using Demand-Driven-Analysis (DDA)—leak flows are pressure independent [
42,
43] or Pressure-Driven-Analysis (PDA)—leak flows depend on the pressure values [
44,
45], however, due to the pressure/leakage relationship, the latter approach is theoretically more sound. Wu and Sage [
46] used DDA while Wu
et al. [
47] used PDA, but in both works the optimization problem to identify the leak locations was solved with genetic algorithms. Based on previous work [
27,
46], Ribeiro
et al. [
48] used a calibrated model and a simulated annealing algorithm to locate leaks during the minimum night flow period. The hydraulic simulations were performed assigning leak flows to pipes and these were equally distributed among the pipe endpoints. Solutions from this methodology helped to identify the most probable leak locations and estimate the respective leak flows.
As location and number of pressure transducers contribute to the success of methodologies to locate and quantify leaks, this paper presents an innovative tool based on the TrustRank algorithm to help in selecting the nodes for pressure monitoring.