Can Low-Resolution Airborne Laser Scanning Data Be Used to Model Stream Rating Curves?
Abstract
:1. Introduction
2. Materials and Methods
2.1. Test Site and Datasets
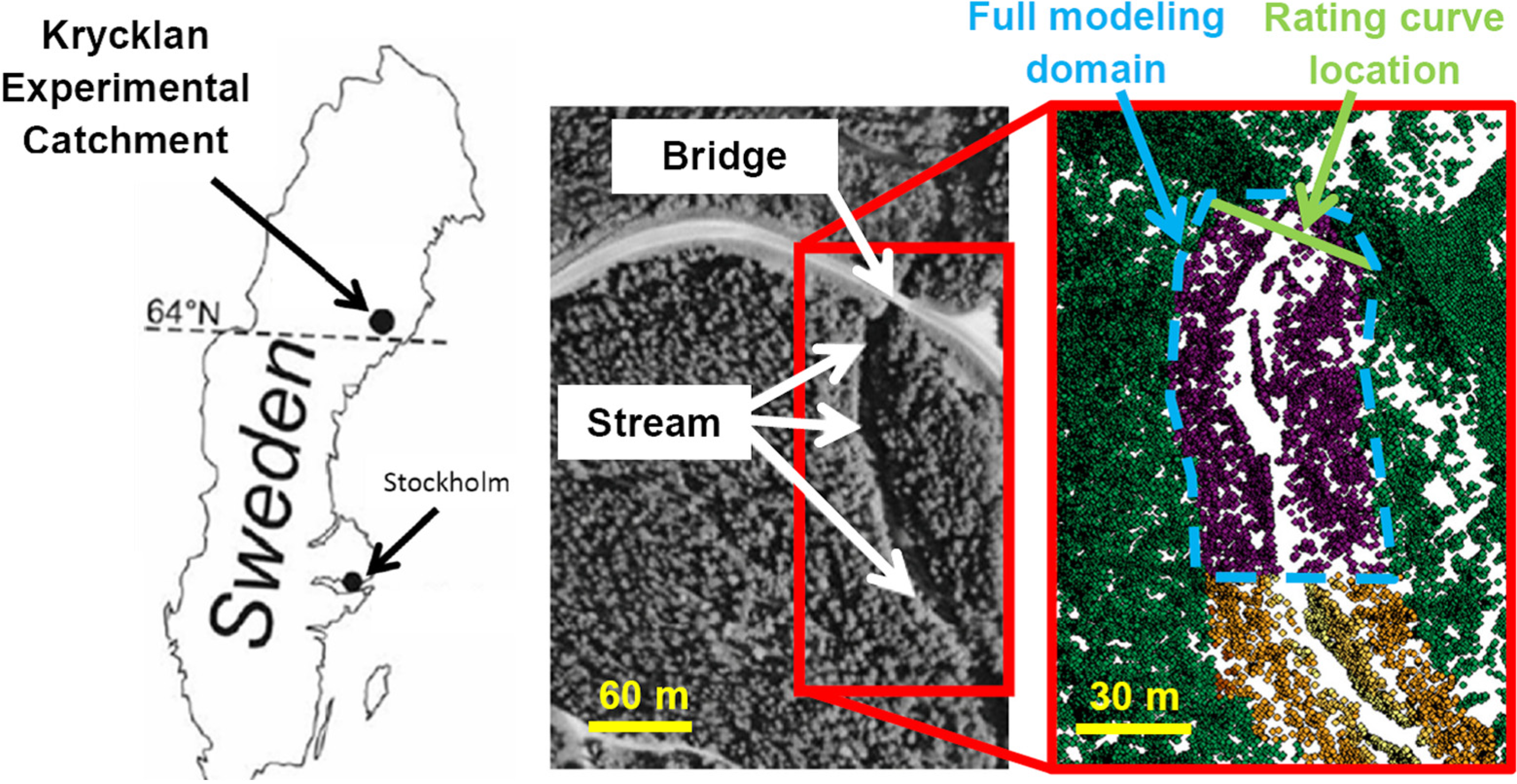
2.2. Methods
2.2.1. Step 1: 3D Point Cloud Thinning of Airborne Laser Scanning Data

2.2.2. Step 2: Hydraulic Modeling of Rating Curves
3. Results
3.1. Estimation of Rating Curves and Channel Geometry

| Property | Distance (m) | Non-Thinned | Thinned (Survey) | Thinned (Flat Bottom) | Non-Thinned | Thinned (Survey) | Thinned (Flat Bottom) |
|---|---|---|---|---|---|---|---|
| Streamflow (m3/s) | 1.0 | 1.0 | 1.0 | 8.0 | 8.0 | 8.0 | |
| Reference Stage (m) | 0.6 | 0.6 | 0.6 | 1.4 | 1.4 | 1.4 | |
| Area (m2) | 0 | 3.7 | 4.0 | 2.8 | 11.7 | 12.3 | 8.8 |
| Wetted Perimeter (m) | 0 | 7.9 | 7.8 | 5.8 | 12.2 | 13.2 | 10.4 |
| Hydraulic Radius (m) | 0 | 0.5 | 0.5 | 0.5 | 1.0 | 0.9 | 0.8 |
| Top width (m) | 0 | 7.6 | 7.5 | 7.5 | 11.0 | 12.1 | 10.2 |
| Area (m2) | 45 | 2.9 | 3.5 | 3.8 | 10.3 | 11.3 | 10.9 |
| Wetted Perimeter (m) | 45 | 8.4 | 9.1 | 8.5 | 11.1 | 11.6 | 11.1 |
| Hydraulic Radius (m) | 45 | 0.3 | 0.4 | 0.4 | 0.9 | 1.0 | 1.0 |
| Top width (m) | 45 | 8.2 | 8.8 | 8.2 | 10.2 | 10.5 | 9.9 |
| Area (m2) | 90 | 1.8 | 2.2 | 4.3 | 9.5 | 10.9 | 11.6 |
| Wetted Perimeter (m) | 90 | 7.8 | 7.9 | 9.2 | 12.0 | 14.1 | 10.9 |
| Hydraulic Radius (m) | 90 | 0.2 | 0.3 | 0.5 | 0.8 | 0.8 | 1.1 |
| Top width (m) | 90 | 7.5 | 7.6 | 8.8 | 11.2 | 12.8 | 9.3 |
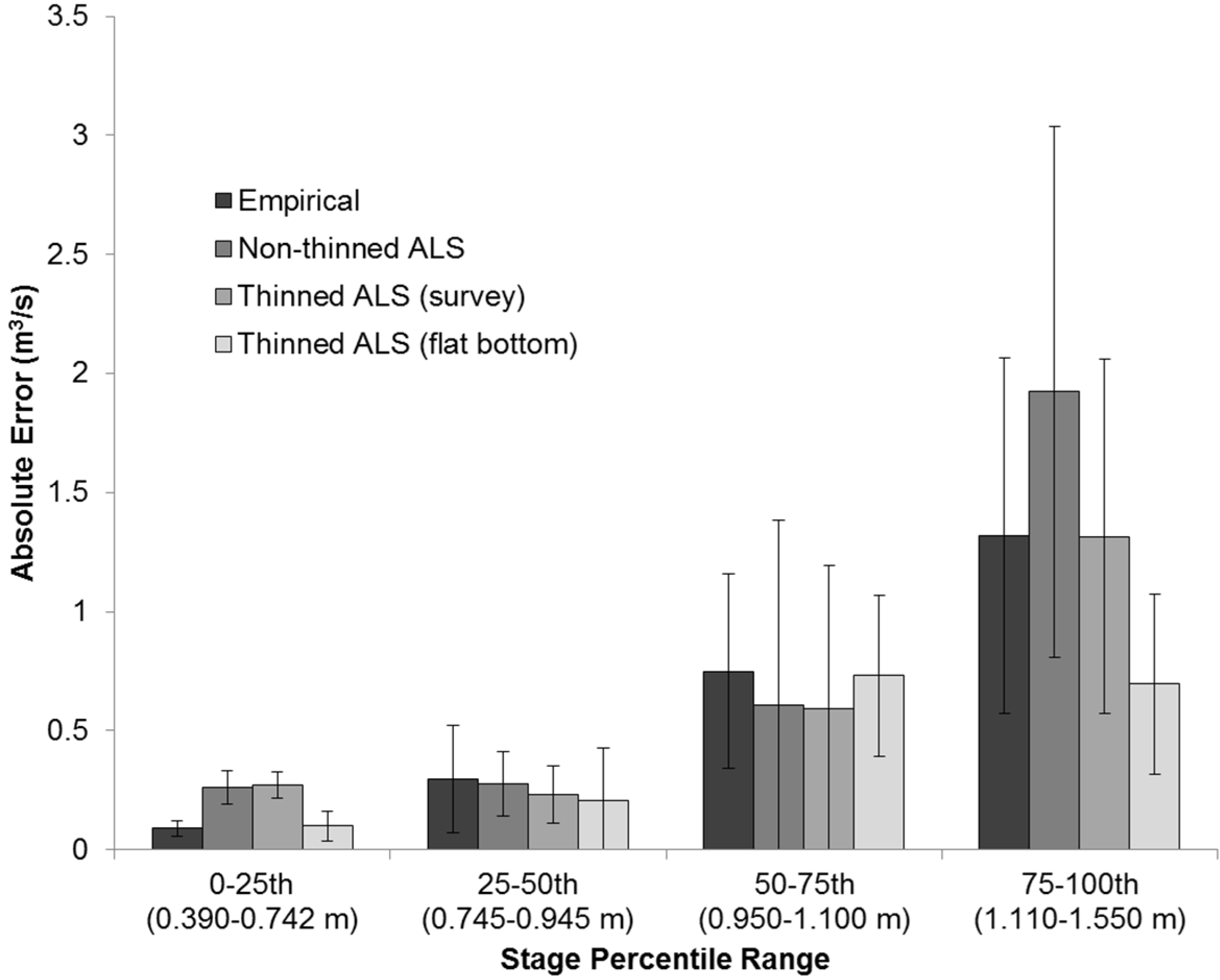
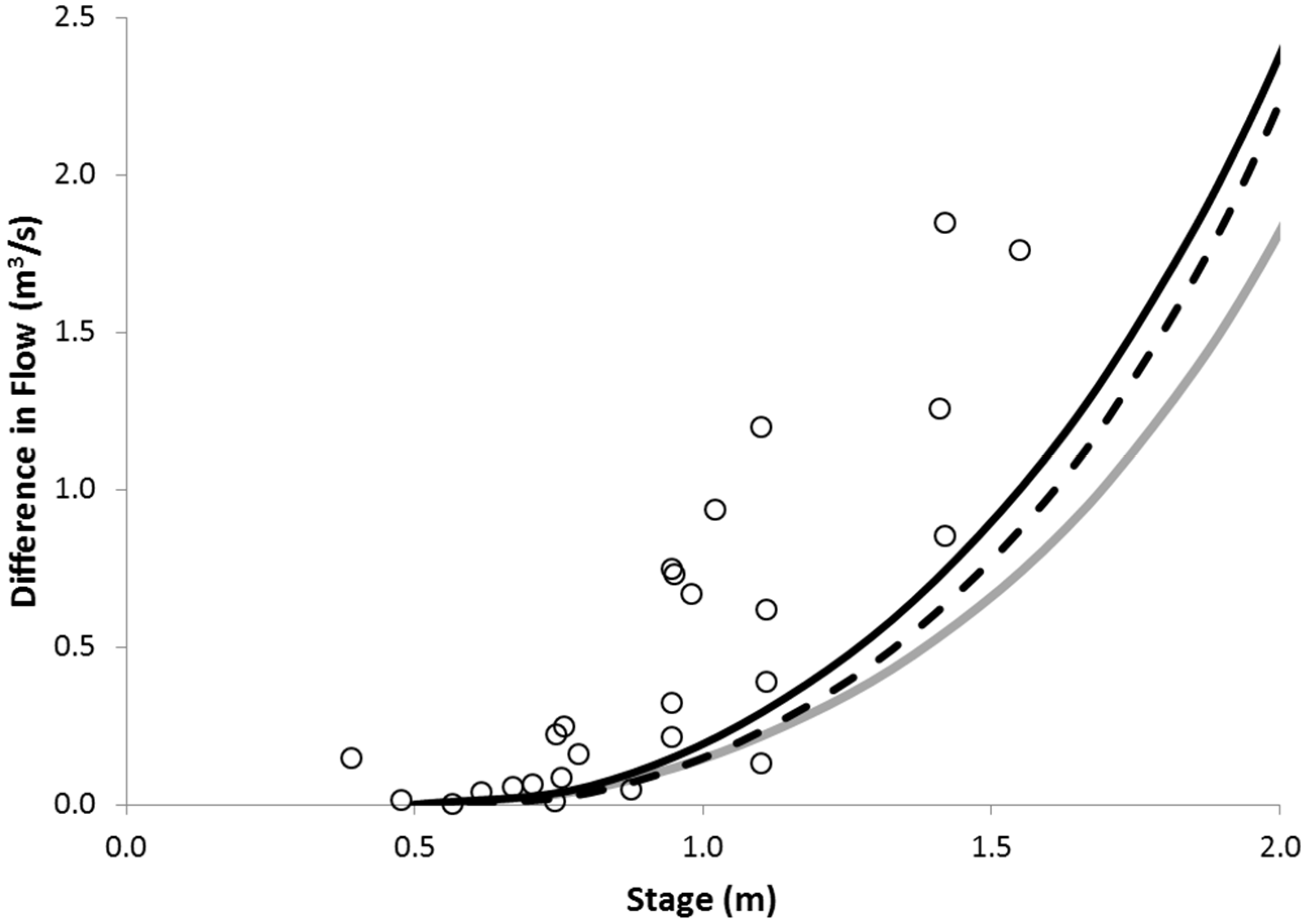
3.2. Potential Errors Introduced through Using Low-Resolution LiDAR
| Empirical | Non-Thinned | Thinned (Survey) | Thinned (Flat Bottom) | |
|---|---|---|---|---|
| Maximum (m3/s) | 9.12 | 9.96 | 9.11 | 8.18 |
| Minimum (m3/s) | 0.19 | 0.30 | 0.32 | 0.28 |
| Median (m3/s) | 0.55 | 0.77 | 0.80 | 0.69 |
| Interquartile Range (IQR) (m3/s) | 0.50 | 0.63 | 0.62 | 0.54 |
| IQR/Median (-) | 0.90 | 0.82 | 0.77 | 0.78 |
4. Discussion and Concluding Remarks
Acknowledgments
Conflicts of Interest
References
- Ackermann, F. Airborne Laser Scanning—Present status and future expectations. ISPRS J. Photogramm. Remote Sens. 1999, 54, 64–67. [Google Scholar] [CrossRef]
- Vosselman, G.; Maas, H.-G. Airborne and Terrestrial Laser Scanning; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Kraus, K.; Pfeifer, N. Determination of terrain models in wooded areas with airborne laser scanner data. ISPRS J. Photogramm. Remote Sens. 1998, 53, 193–203. [Google Scholar] [CrossRef]
- Höfle, B.; Vetter, M.; Pfeifer, N.; Mandlburger, G.; Stötter, J. Water surface mapping from airborne laser scanning using signal intensity and elevation data. Earth Surf. Process. Landf. 2009, 34, 1635–1649. [Google Scholar] [CrossRef]
- Krishnan, S.; Crosby, C.; Nandigam, V.; Phan, M.; Cowart, C.; Baru, C.; Arrowsmith, R. OpenTopography: A service oriented architecture for community access to LIDAR topography. In Proceedings of the 2nd International Conference on Computing for Geospatial Research and Applications, Washington, DC, USA, 23–25 May 2011.
- Heerd, R.M.; Kuijlaars, E.A.C.; Zeeuw, M.P.; van't Zand, R.J. Productspecificatie AHN 2000; Rijkswaterstaat AGI: Delft, The Netherlands, 2000. [Google Scholar]
- Artuso, R.; Bovet, S.; Streilein, A. Practical methods for the verification of countrywide terrain and surface models. Available online: http://www.isprs.org/proceedings/xxxiv/3-w13/papers/Artuso_ALSDD2003.pdf (accessed on 18 March 2015).
- Morville Petersen, Y.; Burman Rost, H. Swedish LiDAR Project. GIM Int. 2011, 2, 21–23. [Google Scholar]
- Stoker, J.; Harding, D.; Parrish, J. The need for a national lidar dataset. Photogramm. Eng. Remote Sens. 2008, 74, 1065–1067. [Google Scholar]
- Höfle, B.; Rutzinger, M. Topographic airborne LiDAR in geomorphology: A technological perspective. Ann. Geomorphol. 2011, 55, 1–29. [Google Scholar] [CrossRef]
- Mandlburger, G.; Hauer, C.; Höfle, B.; Habersack, H.; Pfeifer, N. Optimisation of LiDAR derived terrain models for river flow modelling. Hydrol. Earth Syst. Sci. 2009, 13, 1453–1466. [Google Scholar] [CrossRef]
- Harpold, A.; Lyon, S.W.; Marshall, J. Using LiDAR to Advance Critical Zone Science. Eos Trans. AGU 2014, 95, 364. [Google Scholar] [CrossRef]
- Marks, K.; Bates, P. Integration of high-resolution topographic data with floodplain flow models. Hydrol. Process. 2000, 14, 2109–2122. [Google Scholar] [CrossRef]
- Vetter, M. Airborne Laser Scanning Terrain and Land Cover Models as Basis for Hydrological and Hydraulic Studies. PhD Thesis, Vienna Doctoral Programme on Water Resource Systems, Centre for Water Resource Systems, Vienna University of Technology, Vienna University of Technology, Wien, Austria, 15 May 2013. [Google Scholar]
- Mackey, B.H.; Roering, J.J.; McKean, J.A. Long-term kinematics and sediment flux of an active earthflow, Eel River, California. Geology 2009, 37, 803–806. [Google Scholar] [CrossRef]
- Kinzel, P.J.; Wright, C.W.; Nelson, J.M.; Burman, A.R. Evaluation of an experimental LiDAR for surveying a shallow, braided, sand-bedded river. J. Hydraul. Eng. ASCE 2007, 133, 838–842. [Google Scholar] [CrossRef]
- Snyder, N.P. Studying stream morphology with airborne laser elevation data. Eos 2009, 90, 45–46. [Google Scholar] [CrossRef]
- French, J.R. Airborne LiDAR in support of geomorphological and hydraulic modelling. Earth Surf. Process. Landf. 2003, 28, 321–335. [Google Scholar] [CrossRef]
- Brügelmann, R.; Bollweg, A. Laser altimetry for river management. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2004, 35, 234–239. [Google Scholar]
- Hollaus, M.; Wagner, W.; Kraus, K. Airborne laser scanning and usefulness for hydrological models. Adv. Geosci. 2005, 5, 57–63. [Google Scholar] [CrossRef]
- Thoma, D.P.; Gupta, S.C.; Bauer, M.E.; Kirchoff, C.E. Airborne laser scanning for riverbank erosion assessment. Remote Sens. Environ. 2005, 95, 493–501. [Google Scholar] [CrossRef]
- Jones, A.F.; Brewer, P.A.; Johnstone, E.; Macklin, M.G. High resolution interpretative geomorphological mapping of river valley environments using airborne LiDAR data. Earth Surf. Process. Landf. 2007, 32, 1574–1592. [Google Scholar] [CrossRef]
- Hyyppä, J.; Holopeinen, M.; Olsson, H. Laser scanning in forests. Remote Sens. 2012, 4, 2919–2922. [Google Scholar] [CrossRef]
- Maas, H.-G. Forestry Applications. In Airborne and Terrestrial Laser Scanning; Vosselman, G., Maas, H.-G., Eds.; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Palminteri, S.; Powell, G.V.N.; Asner, G.P.; Peres, C.A. LiDAR measurements of canopy structure predict spatial distribution of a tropical mature forest primate. Remote Sens. Environ. 2012, 127, 98–105. [Google Scholar] [CrossRef]
- Hunter, N.; Bates, P.; Neelz, S.; Pender, G.; Villanueva, I.; Wright, N.; Liang, D.; Falconer, R.; Lin, B.; Waller, S.; et al. Benchmarking 2D hydraulic models for urban flooding. Water Manag. 2008, 161, 13–30. [Google Scholar]
- Turner, A.B.; Colby, J.D.; Csontos, R.M.; Batten, M. Flood Modeling Using a Synthesis of Multi-Platform LiDAR Data. Water 2013, 5, 1533–1560. [Google Scholar] [CrossRef]
- Asner, G.P.; Mascaro, J.; Muller-Landau, H.C.; Vieilledent, G.; Vaudry, R.; Rasamoelina, M.; van Breugel, M. A universal airborne LiDAR approach for tropical forest carbon mapping. Oecologia 2012, 168, 1147–1160. [Google Scholar] [CrossRef] [PubMed]
- Bremer, M.; Rutzinger, M.; Wichmann, V. Derivation of tree skeletons and error assessment using LiDAR point cloud data of varying quality. ISPRS J. Photogramm. Remote Sens. 2013, 80, 39–50. [Google Scholar] [CrossRef]
- Maas, H.-G.; Bienert, A.; Scheller, S.; Keane, E. Automatic forest inventory parameter determination from terrestrial laser scanner data. Int. J. Remote Sens. 2008, 29, 1579–1593. [Google Scholar] [CrossRef]
- Cobby, D.M.; Mason, D.C.; Horritt, M.S.; Bates, P.D. Two-dimensional hydraulic flood modelling using a finite-element mesh decomposed according to vegetation and topographic features derived from airborne scanning laser altimetry. Hydrol. Process. 2003, 17, 1979–2000. [Google Scholar] [CrossRef]
- Mason, D.C.; Cobby, D.M.; Horritt, M.S.; Bates, P.D. Floodplain friction parameterization in two-dimensional river flood models using vegetation heights derived from airborne scanning laser altimetry. Hydrol. Process. 2003, 17, 1711–1732. [Google Scholar] [CrossRef]
- Antonarakis, A.S. The Potential of LiDAR in Recovering Physical Data on Floodplain Vegetation to Parameterise Flow Resistance. Ph.D. Thesis, Cambridge University, UK, 6 May 2008. [Google Scholar]
- Kouwen, N. Field estimation of the biomechanical properties of grass. J. Hydraul. Res. 1988, 26, 559–568. [Google Scholar] [CrossRef]
- Kouwen, N.; Fathi-Moghadam, M. Friction factors for coniferous trees along rivers. J. Hydraul. Eng. ASCE 2000, 126, 732–740. [Google Scholar] [CrossRef]
- Abu-Aly, T.R.; Pasternack, G.B.; Wyrick, J.R.; Barker, R.; Massa, D.; Johnson, T. Effects of LiDAR-derived, spatially distributed vegetation roughness on two-dimensional hydraulics in a gravel-cobble river at flows of 0.2 to 20 times bankfull. Geomorphology 2014, 206, 468–482. [Google Scholar] [CrossRef]
- Katul, G.G.; Wiberg, P.; Albertson, J.; Hornberger, G. A mixing layer theory for flow resistance in shallow streams. Water Resour. Res. 2002, 38. [Google Scholar] [CrossRef]
- Nathanson, M.; Kean, J.W.; Grabs, T.J.; Seibert, J.; Laudon, H.; Lyon, S.W. Modeling rating curves using remotely sensed LiDAR data. Hydrol. Process. 2012, 26, 1427–1434. [Google Scholar] [CrossRef]
- Laudon, H.; Taberman, I.; Ågren, A.; Futter, M.; Ottosson-Löfvenius, M.; Bishop, K. The Krycklan Catchment Study—A flagship infrastructure for hydrology, biogeochemistry and climate research in the boreal landscape. Water Resour. Res. 2013, 49, 1–5. [Google Scholar]
- Bishop, K.H.; Grip, H.; O’Neill, A. The origins of acid runoff in a hillslope during storm events. J. Hydrol. 1990, 116, 35–61. [Google Scholar] [CrossRef]
- Lyon, S.W.; Laudon, H.; Seibert, J.; Mörth, M.; Tetzlaff, D.; Bishop, K.H. Controls on snowmelt water mean transit times in northern boreal catchments. Hydrol. Process. 2010, 24, 1672–1684. [Google Scholar] [CrossRef]
- Grabs, T.; Bishop, K.; Laudon, H.; Lyon, S.W.; Seibert, J. Riparian zone hydrology and soil water total organic carbon (TOC): Implications for spatial variability and upscaling of lateral riparian TOC exports. Biogeosciences 2012, 9, 3901–3916. [Google Scholar] [CrossRef]
- Blom, S.A.T.A. Projektrapport 1110 Krycklan; 1110 Krycklan: Gothenburg, Sweden, 2008. [Google Scholar]
- Kean, J.W.; Smith, J.D. Calculation of stage-discharge relations for gravel bedded channels. J. Geophys. Res. Earth Surf. 2010, 115, 1–15. [Google Scholar] [CrossRef]
- Kean, J.W.; Smith, J.D. Generation and verification of theoretical rating curves in the Whitewater River basin, Kansas. J. Geophys. Res. 2005, 110, 1–17. [Google Scholar]
- Long, C.E.; Wiberg, P.L.; Nowell, A.R.M. Evaluation of von Karman’s constant from integral flow parameters. J. Hydraul. Eng. ASCE 1993, 119, 1182–1190. [Google Scholar] [CrossRef]
- Lyon, S.W.; Nathanson, M.; Spans, A.; Grabs, T.; Laudon, H.; Temnerud, J.; Bishop, K.; Seiber, J. Specific discharge variability in a boreal landscape. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Tetzlaff, D.; Soulsby, C.; Buttle, J.; Capell, R.; Carey, S.K.; Laudon, H.; McDonnell, J.; McGuire, K.; Seibert, S.; Shanley, J. Catchments on the cusp: Structural and functional change in northern ecohydrology. Hydrol. Process. 2013, 27, 766–774. [Google Scholar] [CrossRef]
- Bishop, K.; Buffam, I.; Erlandsson, M.; Fölster, J.; Laudon, H.; Seibert, J.; Temnerud, J. Aqua Incognita: The unknown headwaters. Hydrol. Process. 2008, 22, 1239–1242. [Google Scholar] [CrossRef]
- Edson, C.; Wing, M.G. Airborne Light Detection and Ranging (LiDAR) for Individual Tree Stem Location, Height, and Biomass Measurements. Remote Sens. 2011, 3, 2494–2528. [Google Scholar] [CrossRef]
- Maltamo, M.; Eerikäinen, K.; Packalén, P.; Hyyppä, J. Estimation of stem volume using laser scanning-based canopy height metrics. Forestry 2006, 79. [Google Scholar] [CrossRef]
- McMillan, H.K.; Westerberg, I.K. Rating curve estimation under epistemic uncertainty. Hydrol. Process. 2015, 29. [Google Scholar] [CrossRef]
- Graf, W.L. Damage control: Restoring the physical integrity of America’s rivers. Ann. Assoc. Am. Geogr. 2001, 91, 1–27. [Google Scholar] [CrossRef]
- Di Baldassarre, G.; Claps, P. A hydraulic study on the applicability of flood rating curves. Hydrol. Res. 2011, 42, 10–19. [Google Scholar] [CrossRef]
- Brown, K. Water scarcity: Forecasting the future with spotty data. Science 2002, 297, 926–927. [Google Scholar] [CrossRef] [PubMed]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lyon, S.W.; Nathanson, M.; Lam, N.; Dahlke, H.E.; Rutzinger, M.; Kean, J.W.; Laudon, H. Can Low-Resolution Airborne Laser Scanning Data Be Used to Model Stream Rating Curves? Water 2015, 7, 1324-1339. https://doi.org/10.3390/w7041324
Lyon SW, Nathanson M, Lam N, Dahlke HE, Rutzinger M, Kean JW, Laudon H. Can Low-Resolution Airborne Laser Scanning Data Be Used to Model Stream Rating Curves? Water. 2015; 7(4):1324-1339. https://doi.org/10.3390/w7041324
Chicago/Turabian StyleLyon, Steve W., Marcus Nathanson, Norris Lam, Helen E. Dahlke, Martin Rutzinger, Jason W. Kean, and Hjalmar Laudon. 2015. "Can Low-Resolution Airborne Laser Scanning Data Be Used to Model Stream Rating Curves?" Water 7, no. 4: 1324-1339. https://doi.org/10.3390/w7041324
APA StyleLyon, S. W., Nathanson, M., Lam, N., Dahlke, H. E., Rutzinger, M., Kean, J. W., & Laudon, H. (2015). Can Low-Resolution Airborne Laser Scanning Data Be Used to Model Stream Rating Curves? Water, 7(4), 1324-1339. https://doi.org/10.3390/w7041324







