Abstract
Extracting surface water distribution with satellite imagery has been an important subject in remote sensing. Spectral indices of water only use information from a limited number of bands, thus they may have poor performance from pixels contaminated by ice/snow, clouds, etc. The detection algorithms using information from all spectral bands, such as constrained energy minimization (CEM), could avoid this problem to some extent. However, these are mostly designed for hyperspectral imagery, and may fail when applied to multispectral data. It has been proved that adding linearly irrelevant data to original data could improve the performance of CEM. In this study, two kinds of linearly irrelevant data are added for water extraction: the spectral indices and the spectral similarity metric data. CEM is designed for targets with low-probability distribution in an image, but water bodies do not always satisfy this condition. We thereby impose a sensible coefficient for each pixel to form the weighted autocorrelation matrix. In this study, the weight is based on the orthogonal subspace projection, so this new method is named Orthogonal subspace projection Weighted CEM (OWCEM). The newly launched Landsat 8 images over two lakes, the Hala Lake in China with ice/snow distributed in the north, and the Huron Lake in North America, a lake with a very large surface area, are selected to test the accuracy and robustness of our algorithm. The Kappa coefficient and the receiver operating characteristic (ROC) curve are calculated as an accuracy evaluation standard. For both lakes, our method can greatly suppress the background (including ice/snow and clouds) and extract the complete water surface with a high accuracy (Kappa coefficient > 0.96).
1. Introduction
Surface water information is vital for water resources, climate, and agriculture studies [1]. Surface water change is critically important for studies on the land use/cover (LULC), climate, and other forms of environmental change in the world. With the rapid development of remote sensing technology, satellite data can provide continuous coverage of the earth’s surface both in space and in time. Thus remotely sensed data has become an important source for earth surface change monitoring [2]. Applications using remote sensing related to water resources include flood hazard/damage assessment and management, change in surface water resources, water quality assessment and monitoring, and water-borne disease epidemiology [3].
To date, a number of water extraction techniques using optical imagery have been developed, which can be categorised into four basic types: (a) statistical pattern recognition techniques including supervised [4,5,6] and unsupervised classification methods [7]; (b) linear unmixing [8]; (c) single-band thresholding [9,10]; and (d) spectral indices [3,11,12,13,14].
Among these, the most commonly used category is the spectral index due to its ease of use. McFeeters [11] developed the normalized difference water index (NDWI) using the reflectance of the green (band 2) and near-infrared (band 4) bands of Landsat TM (Thematic Mapper). Rogers and Kearney [15] used another NDWI for water extraction where they applied bands 3 and 5 of Landsat TM. Xu [12] revised McFeeters’s NDWI to overcome the inseparability of built up areas and named it the modified NDWI (MNDWI), in which the SWIR (short wave infrared) band (Landsat TM band 5) was used to replace the NIR (near infrared) band (band 4) in McFeeters’s NDWI. MNDWI is one of the most widely used water indices for a variety of applications, including surface water mapping, land use/cover change analyses, and ecological research [16,17,18]. Feyisa et al. [3] introduced a new automated water extraction index (AWEI) improving the classification accuracy in areas that include shadow and dark surfaces. The index includes two indices: AWEInsh and AWEIsh. They are a linear combination of the blue (band 1), green (band2), NIR (band4), SWIR 1 (band 5), and SWIR 2 (band 6) bands of Landsat TM. AWEInsh is mainly used in areas with an urban background, while AWEIsh is primarily designed to remove shadow pixels.
However, the extraction result of the above water index-based methods may not be ideal. For example, when using these indices, pixels with ice/snow or clouds can also show a high value, sometimes even higher than water pixels. The main reason is that they only use partial spectral information, and have not taken the background information into consideration. In other words, a simple band combinations like NDWI or AWEI cannot differentiate pixels containing liquid water from pixels containing water in other form, such as ice/snow or cloud. One way to solve this problem is to use information from all bands, together with the statistical differences between water and background.
With hyperspectral data, a series of algorithms have been developed for target detection and successfully applied for various applications [19,20,21]. The common hyperspectral detection algorithms include orthogonal subspace projection (OSP) [22,23,24], constrained energy minimization (CEM) [20,22], and matched filter (MF) [21,25,26,27,28,29,30,31,32]. The OSP uses the linear mixture model and white Gaussian noise assumption. It requires the spectral signature of both target and background. It is usually hard for OSP to produce optimal results in real time. CEM is a linear filter, which constrains a desired target signature while minimizing the total energy of the output of other unknown signatures. CEM requires prior spectral knowledge of a target and utilizes second-order statistical information on images. Under the assumption of a low-probability distribution for the target in an image, the CEM detector can distinguish the target of interest from the background very well. Comparative studies show that the CEM generally outperforms the OSP in terms of eliminating an unidentified signal sources and suppressing noise. However, they are closely related and essentially equivalent provided that the noise is white with large SNR (single-to-noise ratio) [23]. In a Bayes or Neyman–Pearson case, when the target and background classes follow multivariate normal distributions with the same covariance matrix, an MF detector can get optimal detection results. In fact, the MF and CEM detectors have a very similar mathematical formula, and the main difference is that an MF detector requires the data to be centralised first.
The above target detection algorithms can exhibit very good performance in hyperspectral remote sensing. However, they may fail for multispectral imagery due to the lack of spectral bands. Ren et al. [33] have proposed a generalised constrained energy minimization (GCEM) for detecting targets in multispectral images with a dimensionality expansion approach. They expanded bands by generating the second-order correlated and nonlinearly correlated new variables, producing a total of (L2 + 5L)/2 new variables, where L is the number of bands. GCEM outperforms CEM for multispectral imagery but it is very sensitive to noise and the selection of the desired target signature.
Geng et al. [34] have proved that adding any newly derived variable linearly uncorrelated with the original image, even a noisy band, would be beneficial to the performance of CEM in terms of output energy. The conclusion serves a theoretical base to improve the performance of CEM for multispectral target detection. That is to increase the dimensionality of data by adding new variables that can be derived from the original data but are not linearly correlated with the original data. According to this theory, more un-correlated data means better performance, but on the other hand, more data also means greater computational complexity and memory requirement. GCEM has provided a way for data expansion, but it is not target-oriented and the number of variables added is huge. For example, for a 7-band multispectral data, it will produce 42 additional channels. If the added channels cannot highlight the difference between the target and background, their impact to increase CEM’s performance is of little use and may increase the sensitivity to the target signature selection instead. So how to add useful data for water extraction is a key problem that is of interest to us.
Another problem related to CEM for water extraction is that water bodies in an image may not always satisfy the low-probability distribution constraint. For large targets, CEM would shine with both high rates of omission and false positive errors. This can be attributed to the fact that the autocorrelation matrix used in CEM is calculated from both target and background pixels. So, when the target size is large in an image, the performance of CEM would be poor. Geng et al. [35] have proposed a new strategy by multiplying a weight coefficient for each pixel in the process of constructing the autocorrelation matrix, which aims to lessen the contribution of pixels with spectral characteristics similar to the target. We followed this idea and developed a new weight expression according to the idea of OSP, named the OSP-weighted CEM (OWCEM). In this paper, we introduce this new strategy for water detection with multispectral images.
2. Study Areas and Data Source
2.1. Test Sites
Two water bodies of different areas were selected. One was the Hala Lake (see Figure 1a), located in Qinghai Province, China, with an estimated water surface area of 590 km2. It is surrounded by high mountain ridges, such as the glaciated Shule Nanshan, along the northern to northwestern fringe of the basin [36]. Ice/snow surrounding the lake is an important reason for choosing Hala Lake. It helps us to assess the accuracy of OWCEM when ice/snow exists. The other one was Huron Lake, which has a very large area. It is bounded on the east by Ontario, Canada, and on the west by the state of Michigan of the United States (see Figure 1b). Lake Huron is the second-largest of the Great Lakes, with a surface area of 59,600 km2. Lake Huron was selected to evaluate the performance of our algorithm when the area percentage of water in an image is large.
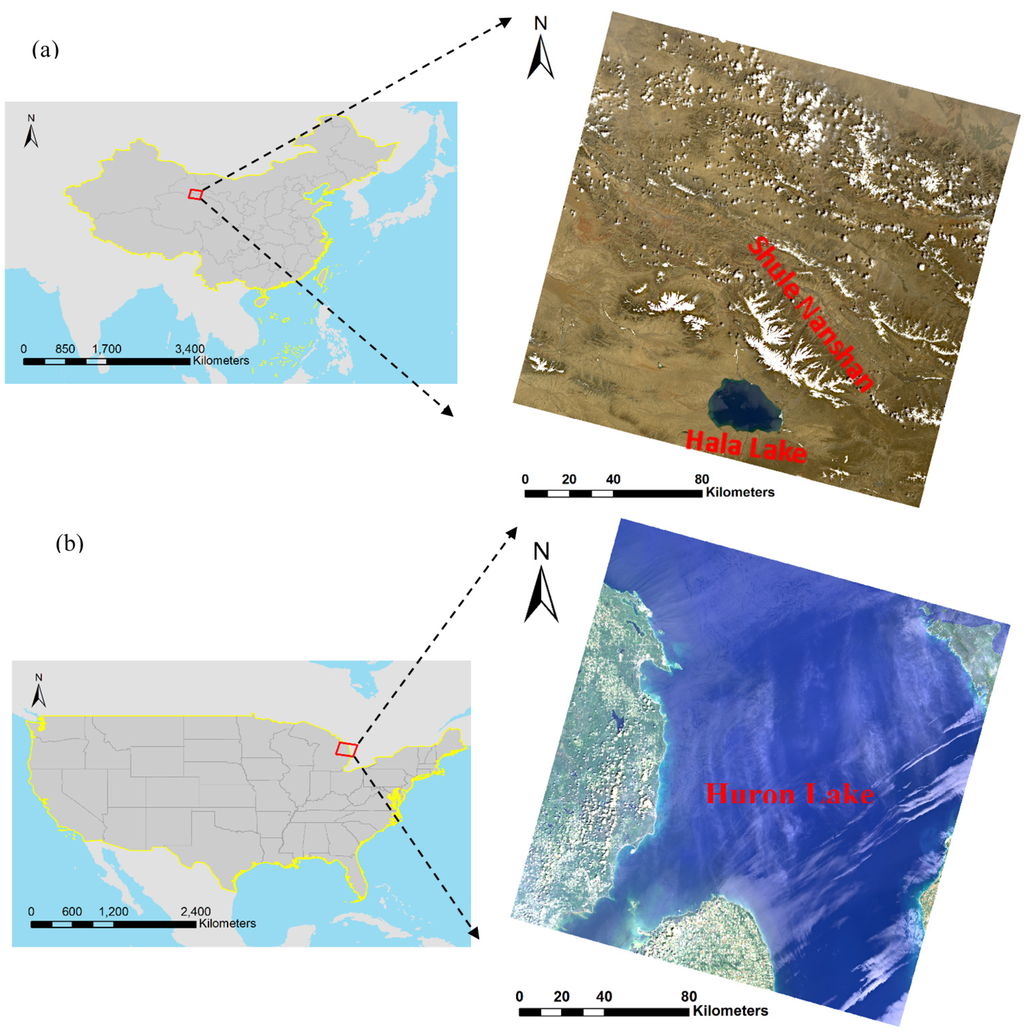
Figure 1.
The locations of study areas: (a) Hala Lake and (b) Lake Huron.
2.2. Landsat Images
Landsat 8 Operational Land Imager (OLI)/Thermal Infrared Sensor (TIRS) images were selected for their improved signal to noise performance over Thematic Mapper (TM) and Enhanced Thematic Mapper Plus (ETM+) images. The band allocations among TM, ETM+, and OLI/TIRS are shown in Table 1. The images were acquired from the United States Geological Survey (USGS) Global Visualization Viewer (GLOVIS) portal (http://earthexplorer.usgs.gov/). To test the robustness of our algorithm to the existence of cloud, images with clouds were purposely selected on purpose. All Landsat images used were at the L1T level. The radiometric processing was done automatically using the Global Mapper (GM) software package developed in [37]. This processing included atmospheric correction and the topographic correction. Descriptions of the Landsat 8 images used in this study are presented in Table 2.

Table 1.
The band designations between Landsat 5/7 and Landsat 8.
| Sensor | Bands | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Costal Aerosol | Blue | Green | Red | NIR | SWIR 1 | SWIR 2 | Panchromatic | Cirrus | TIRS 1 | TIRS 2 | |
| TM | - | 1 | 2 | 3 | 4 | 5 | 7 | - | - | 6 | |
| ETM+ | - | 1 | 2 | 3 | 4 | 5 | 7 | 8 | - | 6 | |
| OLI/TIRS | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |

Table 2.
Description of Landsat OLI/TIRS scenes and corresponding reference data.
| Test Site | Path/Row | Central Latitude/Longitude | Acquisition Date | Image Size | Cloud Cover | Water Cover | Reference Data |
|---|---|---|---|---|---|---|---|
| Hala Lake | 135/033 | 38°89' N/97°69' E | 01/06/2013 | 7691/7501 | 5.08% | 1.75% | FROM-GLC: base image acquired on 09/08/2009 |
| Huron Lake | 020/029 | 44°59' N/82°71' W | 13/07/2013 | 7901/8021 | 1.29% | 76.40% | FROM-GLC: base image acquired on 20/09/2009 |
2.3. Reference Data
The reference data used in the accuracy assessment was selected from the land cover map with the same path and row of the Finer Resolution Observation and Monitoring of Global Land Cover (FROM-GLC) [37] product using Landsat TM images. Due to the difference between the acquisition dates of the images used in FROM-GLC and our study, there exist some mismatches. However, we have carefully examined the land cover maps with our Landsat 8 images, and found that the mismatching portion was actually statistically very low. Therefore, the corresponding land cover maps of FROM-GLC were used as ground reference images in this study (see Table 2).
3. Methods
3.1. CEM
CEM is originally derived from the linearly constrained minimized variance adoptive beam-forming in the field of digital signal processing. It uses a finite impulse response (FIR) filter to constrain the desired signature by a specific gain while minimizing the output energy of the filter [20,22].
Assume that we are given a finite set of observations S = {x1, x2, …, xN}, where xi = (xi1, xi2, …, xiL)T for 1 ≤ i ≤ N is a sample pixel vector; N is the total number of pixels, and L is the number of bands (generally L << N). Suppose that the desired signature d is also known a priori. The objective of the CEM is to design an FIR linear filter
w = {w1, w2, …, wL}T to minimize the output power subject to the constraint,
. Then the problem yields:
where
turns out to be the sample autocorrelation matrix. The solution to (1) is called the CEM operator with a weight vector wCEM given by:
The CEM technique has been successfully applied to small target detection from hyperspectral data, since the number of bands for a hyperspectral image is usually large enough to distinguish the target from other ground objects spectrally. If we want to utilise CEM on images with fewer bands, one possible way is to add artificial variables. Geng et al. [34] proved that adding any linearly irrelevant data to the original data, even if that data was noisy, would always be beneficial to the performance of CEM in terms of output energy. According to this theory, we can use CEM on multiband images by adding bands with useful information, such as spectral index data.
3.2. Band Expansion
In order to improve the performance of CEM, we need to expand the dimensionality of the multispectral image. The data added should satisfy two criteria: (1) the data should not be the linear expression of the original bands; and (2) the data should highlight the characteristics of the target while suppressing that of the background. According to the previous knowledge on water in remote sensing, two kinds of data could be added. The first one is the spectral index, and the second is the spectral similarity metric with the target.
3.2.1. Water Index
So far, two water indices have shown their superiority in many applications related to water. The first one is the MNDWI:
In Landsat 8’s band designation, we can rewrite MNDWI as:
The second is Feyisa’s AWEI, which includes two indices for non-shadow and shadow surfaces, respectively:
AWEInsh = 4×(band3 − band6) − (0.25 × band5 + 2.75 × band7)
AWEIsh = band2 + 2.5 × band3 − 1.5 × (band5 + band6) − 0.25 × band7
Clearly, MNDWI is the non-linear expression of band 3 and 6, so we can directly use it in OWCEM. But AWEInsh and AWEIsh are the linear expressions of band 2, 3, 5, 6, and 7. To satisfy the linearly irrelevant constraint, we can modify the two indices as MAWEInsh and MAWEIsh:
MAWEInsh = AWEInsh/(band3 + band5 + band6 + band7)
MAWEIsh = AWEIsh/(band2 + band3 + band5 + band6 + band7)
3.2.2. Spectral Similarity Metrics
The common indices to measure the similarity between two spectra include correlation (corr), Euclidean distance (d), spectral angle distance (SAD), and spectral information distance (SID) [38]. For two spectra (pixels), x = (x1, x2,…,xL)T nd y = (y1, y2,…,yL)T, the corr, d, SAD and SID metrics can be defined as follows:
where
and
d = ||x-y||
SID = D(x||y) + D(y||x)
Therefore in our algorithm, we use 14 channels: 7 Landsat 8 bands (band 1–7), 3 water indices (MNDWI, MAWEInsh, MAWEIsh), and 4 spectral similarity metrics (corr, SAD, d and SID). The additional 7 new variables can help improve CEM’s performance on water detection, since they are generated according to people’s understanding of the spectral properties.
3.3. CEM Based on Orthogonal Subspace Projection-Weighted Autocorrelation Matrix
Besides the limitation of the number of bands, another problem when using CEM to extract water in Landsat images is that CEM has a low-probability distribution assumption for a target. In the CEM detector expression (Equation (3)), the function of R−1 is to suppress the background. However, when calculating the autocorrelation matrix R, all pixels, including the target pixels, will be involved. When the target is small, the influence of including target vectors when calculating R can be neglected. But this influence cannot be ignored in the case of a large target. For this reason CEM is mostly considered as a small target detector.
However, water in a Landsat image is not always “small.” The proportion of water could be large, for example, the seawater in an image of a coastal area. Therefore, when calculating R, we should eliminate the influence of target vectors to R as much as possible. Geng et al. [35] proposed a way to reconstruct R, which they named the weighted autocorrelation matrix R*, and defined as:
where c is a constant; f(x) is a monotonically increasing function for x ≥ 0 with f(0) = 0; g(x,y) is the function to measure the spectral similarity between vector x and y, which decreases as the similarity of x and y increases. For example, let f(g(x,y)) be the Euclidean distance between x and y, i.e., f(g(x,y)) = ||x − y||. If xi = d, we have f(g(xi,d)) = 0, which indicates that the contribution of the target to R* is zero. On the other hand, if xi is a background vector, we have f(g(xi,d)) > 0. Therefore, R* mostly reflects the two-order statistics of the background.
The Euclidean distance emphasizes the difference in spectral value, but it cannot reflect the dissimilarity in spectral shape. In this paper, we introduce another way to separate the target from the background by applying the OSP operator [22,23,24] P = I − dd+, where d+ is the pseudo-inversion of d. Let
and f(x) = x, then we have:
We name this new R* as the orthogonal subspace projection-weighted (OW) autocorrelation matrix, and the new CEM detector as the OWCEM detector. In this study, we apply OWCEM to the original data with 7 additional variables, as illustrated in Figure 2. Besides the Landsat series data, OWCEM can also be applied to other multispectral data, such as the multispectral images from the Sentinel 2 satellite that is scheduled to be launched soon.
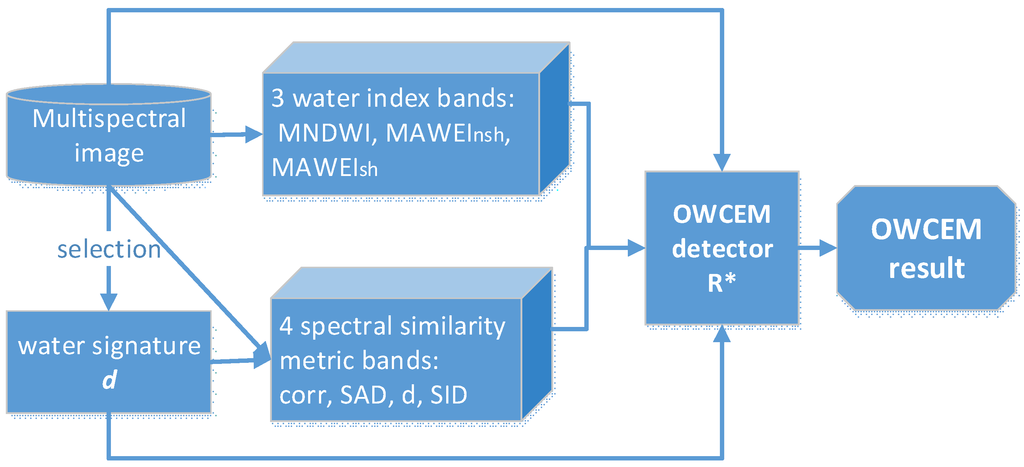
Figure 2.
Flowchart of OWCEM algorithm for water extraction with the multispectral image.
3.4. Pure Water Signature Extraction
It should be noted that the target signature, d, is needed for both CEM and OWCEM. However, the spectrum of water varies as its composition and depth changes. Sivanpillai et al. [7] categorise water as clear water, green water, and muddy/turbid water. Sun et al. [39] have followed this categorization. The colour of green water is dominated by the phytoplankton or floating hydrophytes. Usually, clear water in true color images appears blue or dark blue and muddy/turbid water appears yellow. However, in addition to muddy/turbid water, but also shallow water appears yellow. Thus, in this paper, according to the colour, we classify water into three classes: blue water, green water, and yellow water. Their typical signature curves are shown in Figure 3. It can be seen that blue water has the highest reflectance in the blue bands, while green water has high reflectance in the green bands. The spectrum of yellow water is very similar to that of ice/snow, but with a much lower value.
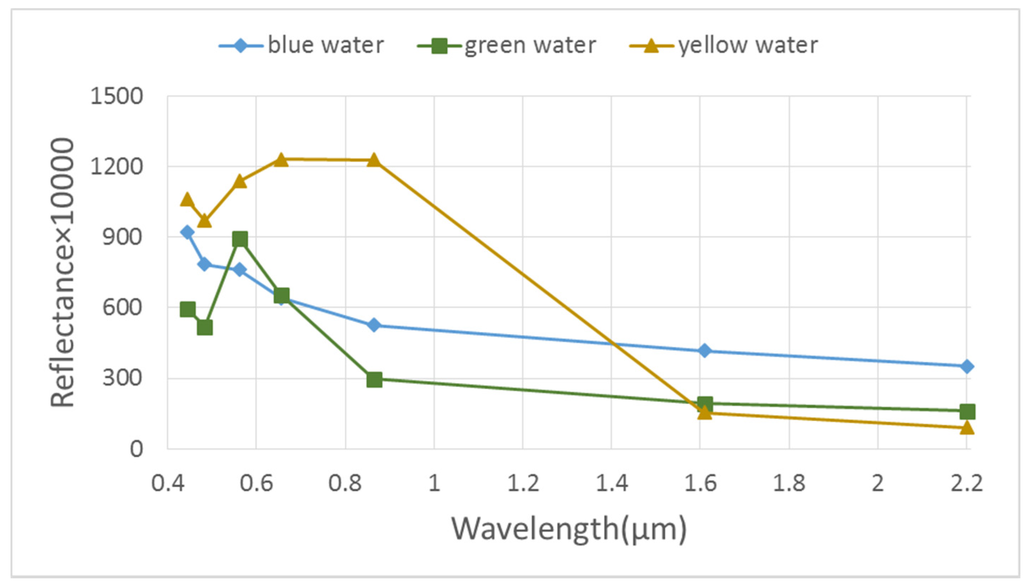
Figure 3.
The spectral signatures of three water colors.
A pure water signature can be extracted by endmember extraction algorithms [40,41], or by using water signatures in a spectral library. In this study, for similarity, we manually pick some pure water points in the image for each kind of water based on the ground reference maps. Water pixels with different reflectance levels are selected, and their mean spectrum is calculated as d for CEM and OWCEM. The total number of pixels selected does not have to be large, but the selected pixels should have representative spectral signatures.
4. Results
In this study, we compared our method, OWCEM with 14 channels, with the water indices MNDWI, AWEInsh, AWEIsh, and CEM with only the original 7 bands. Strictly speaking, both CEM and OWCEM are detection operators and can be applied to data with any number of channels. However, we simplified OWCEM for “OWCEM applied to 14 channels (Landsat 8 band 1–7 MNDWI, MAWEInsh, MAWEIsh, corr, SAD, d, and SID)” and CEM for “CEM with original 7 bands (Landsat 8 band 1–7)” in the following content. In addition, the Kappa coefficient and the receiver operating characteristic (ROC) curves were calculated to evaluate the performance of the five algorithms.
4.1. Hala Lake
Within the Landsat 8 image, the Hala Lake is a small target, which only occupies 1.57% of the image. However, both ice/snow and cloud exist in the image, as shown in Figure 1a. The middle area of Hala Lake is blue, while some edge areas appear dark green. In this study, three pixels for these two kinds of water were selected as the representatives for CEM and OWCEM, as shown in Figure 4.
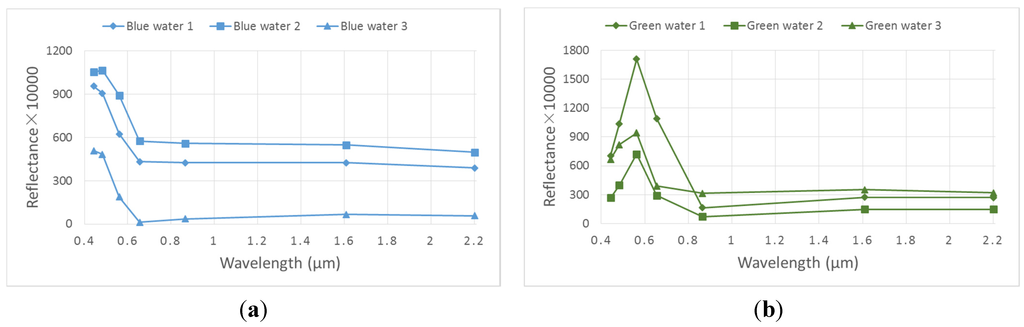
Figure 4.
The spectral curves of blue (a) and green (b) water for the Hala Lake image.
The outputs of the five algorithms are presented in Figure 5. Visually, OWCEM could suppress the background more efficiently compared to water indices and CEM. Water indices have extremely high values in ice/snow areas (Figure 5b–d), while CEM has high values in cloudy areas (Figure 5e). For a quantitative comparison with the ground reference map, the water extraction binary results are required. The most commonly used binarisation is to partition the image by setting a threshold. However, there is no fixed threshold or threshold range for the three published water indices and CEM. For a fair comparison, we adopted the following strategy: first, determine the total number of water pixels from the reference image, denoted as N; second, sort the resulting image (images in Figure 5) in descending order and mark the first N pixels as water (images in Figure 6). To extract the whole water area for CEM and OWCEM, we selected the larger value from the results of the blue and green water for each pixel; finally, the ROC curves and Kappa coefficients of all algorithms were generated.

Figure 5.
The results of MNDWI, AWEInsh, AWEIsh, CEM, and OWCEM for blue and green water for the Hala Lake image. (a) True colour image; (b) MNDWI; (c) AWEInsh; (d) AWEIsh; (e) CEM (blue water); (f) CEM (green water); (g) OWCEM (blue water); and (h) OWCEM (green water).
The final water extraction maps for all methods are shown in Figure 6. A visual comparison indicates that OWCEM produces a better accuracy of water mapping than the water indices and CEM. Only the ice/snow areas are extracted by MNDWI, AWEInsh, and AWEIsh, as shown in Figure 6b–d. The central part of Hala Lake is missed by CEM, and some ice/snow and cloud areas are extracted by CEM. This is because when extracting blue water, the CEM output shows a higher value in those cloudy and ice/snow areas than those in blue water areas (Figure 5e). OWCEM can extract the complete Hala Lake, and some small ponds and rivers around, but no ice/snow or cloudy areas. However, due to the acquisition time difference (refer to Table 2), there does exist some omissions on small rivers and ponds. For example, the long river across the reference image from the upper-left to the lower-right has not been extracted completely by OWCEM. The corresponding zoom-in images are shown in Figure 7. The reason for this is that the river water was partially frozen at the acquisition time for the Hala Lake image. Yet, those areas are small, so the Kappa coefficient (see Table 3) is still very high for OWCEM (0.9647). The Kappa coefficients of MNDWI, AWEInsh and AWEIsh are negative, because no water, but only ice/snow and cloud were extracted. The ROC curves of the five methods are shown in Figure 8. It can be seen that the overall performance of OWCEM is better than that for the other four methods. It yields closely to the (0, 1) of the ROC space, representing OWCEM as an almost perfect classifier.

Figure 6.
Comparison of water extraction results of the five algorithms for Hala Lake image: (a) Reference data; (b) MNDWI; (c) AWEInsh; (d) AWEIsh; (e) CEM; (f) OWCEM.
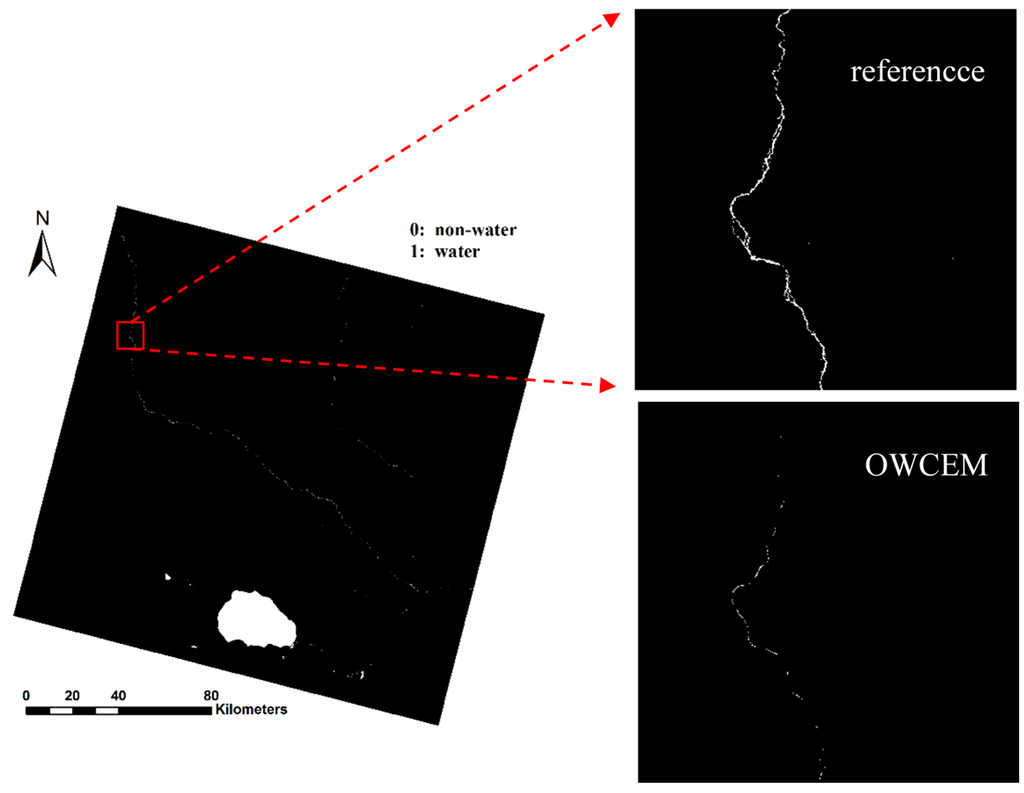
Figure 7.
Comparison of a subarea of a river in the Hala Lake image between the reference and OWCEM result.

Table 3.
The kappa coefficients of the five algorithms for Hala and Lake Huron images.
| Classifier | MNDWI | AWEInsh | AWEIsh | CEM | OWCEM |
|---|---|---|---|---|---|
| Hala Lake | −0.0076 | −0.0152 | −0.0145 | 0.4744 | 0.9647 |
| Lake Huron | 0.9843 | 0.9843 | 0.9772 | 0.8473 | 0.9928 |
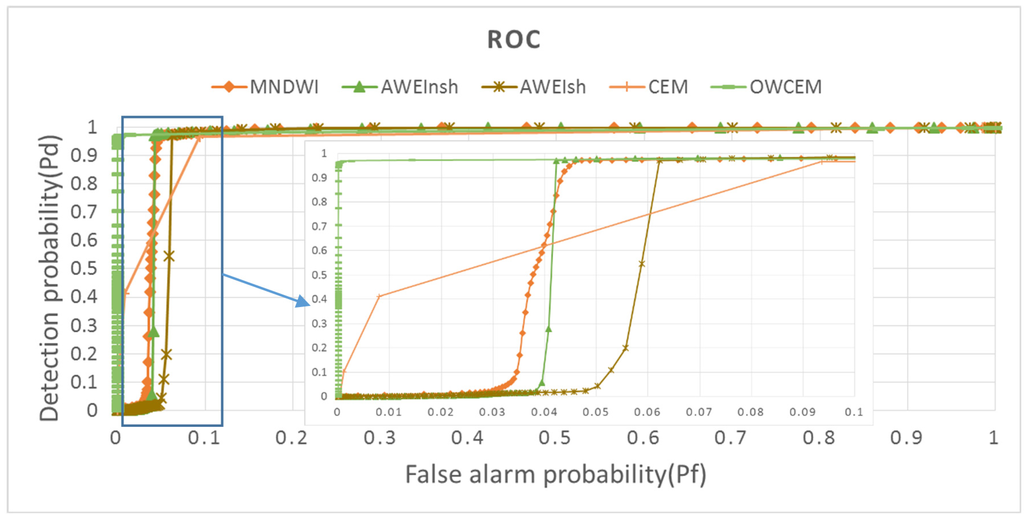
Figure 8.
The ROC curves of the five methods for the Hala Lake image.
4.2. Lake Huron
Unlike Hala Lake, Huron Lake occupies the majority of the Landsat 8 image (about 76.4%), as shown in Figure 1b. In this image, no ice/snow pixels exist. However, thin clouds present on most lake areas, and some thick clouds appear on the land area (Figure 1b). Most parts of the lake are blue, even when covered by thin cloud. The water at the shore areas appears light green. The signatures of blue and green water selected for d are shown in Figure 9.
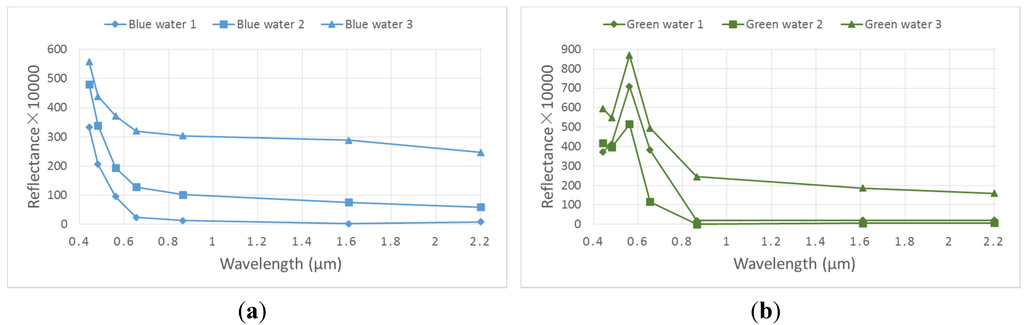
Figure 9.
The spectral curves of blue (a) and green (b) water for the Lake Huron image.
The results of the five algorithms are presented in Figure 10. Comparatively speaking, the result of OWCEM shows the strongest contrast between the blue/green water and the background, especially for the blue water. For MNDWI, AWEInsh, and AWEIsh, their combinations of bands have also enhanced the cloud area above land (see Figure 10b–d)). The CEM result for blue water has the worst contrast effect, because blue water in this image is not a “small target” and only the 7 original bands were used.


Figure 10.
The results of MNDWI, AWEInsh, AWEIsh, CEM, and OWCEM for blue water and OWCEM for green water in the Lake Huron image: (a) True color image; (b) MNDWI; (c) AEWInsh; (d) AWEIsh; (e) CEM (blue); (f) CEM (green); (g) OWCEM (blue); and (h) OWCEM (green).
The water extraction procedure is the same as that for Hala Lake, and the results are shown in Figure 11. MNDWI, AWEInsh, and AWEIsh have all missed some water areas covered by thicker cloud, but extracted some land areas with thick clouds (Figure 12c–e). CEM has the worst performance. Both cloud and cloud shadow areas on the land part have been extracted by CEM (Figure 12f). In addition, some water areas near the bank have been missed. The water area extracted by OWCEM is much more complete and even the water areas covered by light cloud have been extracted. However, water covered by very thick cloud cannot be extracted by OWCEM either (Figure 12g). The kappa coefficients of the five algorithms are tabulated in Table 3. OWCEM has the highest value (0.9928) while CEM has the lowest (0.8473). The ROC curves are shown in Figure 13. The performance of MNDWI is very close to that of OWCEM. Overall, OWCEM still performs best, even though the percentage of water is very large in the image. To further investigate the influence of target size on CEM, we applied CEM to the 14-channel data. The corresponding kappa coefficient became even lower (0.3290), which again indicates that CEM has poor performance for a large size targets, and may perform worse when more data is added. The main reason for this is that the autocorrelation matrix R of this image used in the CEM detector mostly represents the statistical information on water, not the background. By introducing a weight when constructing the autocorrelation matrix, OWCEM has no limit on target size.
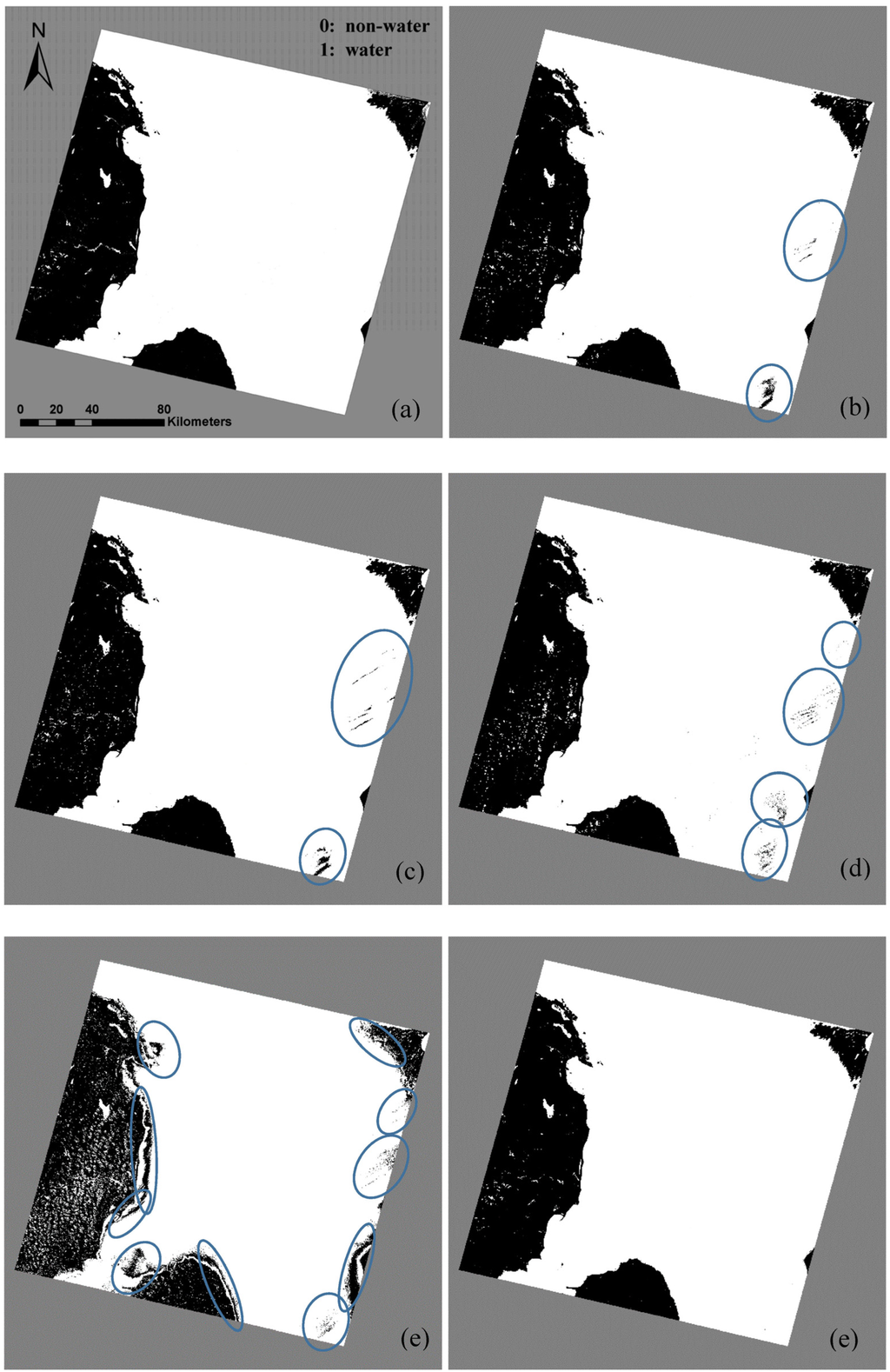
Figure 11.
Comparison of water extraction results of the five algorithms for the Lake Huron image. Areas in circles indicate the missing water areas. (a) Reference data; (b) MNDWI; (c) AWEInsh; (d) AWEIsh; (e) CEM; and (f) OWCEM.

Figure 12.
Details of water extraction results using the five algorithms for the Lake Huron image: (a) True colour image; (b) reference; (c) MNDWI; (d) AWEInsh; (e) AWEIsh; (f) CEM; and (g) OWCEM.
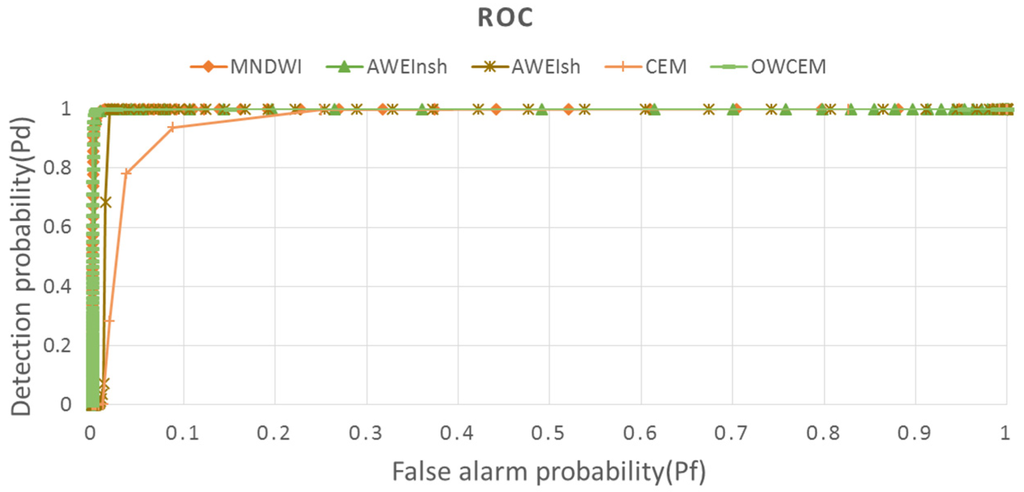
Figure 13.
The ROC curves of the five algorithms for the Lake Huron image.
4.3. Analysis on Correlation between Channels
The above results on the two lakes indicate that adding water index and spectral similarity metric channels in OWCEM can greatly improve the accuracy of water mapping. Table 4 and Table 5 tabulate the correlation coefficients between the 7 additional channels and all 14 channels used in the Hala Lake and Lake Huron images. We find that the correlation coefficients between the water indices, and the correlation coefficients between corr, SAD, and SID are high. Also, the d channel has a high correlation with the VNIR (visible and near-infrared) bands. To assess the influence of the channel correlation to the result of OWCEM, we conducted a comparison study by adding (1) a zero mean Gaussian distributed random noise with a standard deviation of one, denoted as n1; (2) an existing channel disturbed by a small Gaussian distributed random noise with a mean of zero and a standard deviation of 0.0001, denoted as n2; and (3) a water index/spectral similarity metric.

Table 4.
The correlation coefficient matrix for the data set used in the Hala Lake image.
| Channel | MNDWI | MAWEInsh | MAWEIsh | corr | SAD | d | SID | n1 | MADWI + n2 | Corr + n2 |
|---|---|---|---|---|---|---|---|---|---|---|
| B1 | 0.8092 | 0.7894 | 0.6789 | 0.7224 | −0.7271 | 0.9281 | −0.5889 | −0.0003 | 0.8092 | 0.7224 |
| B2 | 0.8028 | 0.7821 | 0.6678 | 0.7107 | −0.7214 | 0.9365 | −0.5873 | −0.0003 | 0.8028 | 0.7107 |
| B3 | 0.7612 | 0.7349 | 0.6100 | 0.6526 | −0.6973 | 0.9624 | −0.5815 | −0.0003 | 0.7612 | 0.6526 |
| B4 | 0.7027 | 0.6726 | 0.5408 | 0.5797 | −0.6578 | 0.9755 | −0.5622 | −0.0003 | 0.7027 | 0.5797 |
| B5 | 0.5568 | 0.5293 | 0.3927 | 0.4341 | −0.5592 | 0.9773 | −0.4983 | −0.0002 | 0.5568 | 0.4341 |
| B6 | −0.4072 | −0.4587 | −0.4006 | −0.4457 | 0.0447 | 0.3687 | −0.1337 | −0.0001 | −0.4072 | −0.4457 |
| B7 | −0.3466 | −0.4085 | −0.3409 | −0.3981 | −0.0032 | 0.4068 | −0.1828 | −0.0001 | −0.3466 | −0.3981 |
| MNDWI | 1.0000 | 0.9934 | 0.9380 | 0.9135 | −0.8212 | 0.6131 | −0.6612 | −0.0002 | 1.0000 | 0.9135 |
| MAWEInsh | 0.9934 | 1.0000 | 0.9430 | 0.9179 | −0.7834 | 0.5758 | −0.6059 | −0.0002 | 0.9934 | 0.9179 |
| MAWEIsh | 0.9380 | 0.9430 | 1.0000 | 0.8907 | −0.7662 | 0.4877 | −0.6228 | −0.0003 | 0.9380 | 0.8907 |
| Corr | 0.9135 | 0.9179 | 0.8907 | 1.0000 | −0.7217 | 0.5031 | −0.5101 | −0.0002 | 0.9135 | 1.0000 |
| SAD | −0.8212 | −0.7834 | −0.7662 | −0.7217 | 1.0000 | −0.6286 | 0.9010 | 0.0002 | −0.8212 | −0.7217 |
| d | 0.6131 | 0.5758 | 0.4877 | 0.5031 | −0.6286 | 1.0000 | −0.5740 | −0.0003 | 0.6131 | 0.5031 |
| SID | −0.6612 | −0.6059 | −0.6228 | −0.5101 | 0.9010 | −0.5740 | 1.0000 | 0.0002 | −0.6612 | −0.5101 |

Table 5.
The correlation coefficient matrix for the data set used in the Lake Huron image.
| Channel | MNDWI | MAWEInsh | MAWEIsh | Corr | SAD | d | SID | n1 | MNDWI + n2 | Corr + n2 |
|---|---|---|---|---|---|---|---|---|---|---|
| B1 | −0.1217 | −0.1842 | −0.1519 | −0.1056 | −0.0199 | 0.8368 | −0.0299 | −0.0001 | −0.1217 | −0.1056 |
| B2 | −0.1539 | −0.2128 | −0.1824 | −0.1368 | 0.0046 | 0.8543 | −0.0015 | −0.0001 | −0.1539 | −0.1368 |
| B3 | −0.3625 | −0.3824 | −0.3705 | −0.3655 | 0.2165 | 0.9321 | 0.2241 | 0.0001 | −0.3625 | −0.3655 |
| B4 | −0.3316 | −0.3677 | −0.3371 | −0.3445 | 0.1875 | 0.9282 | 0.1787 | 0.0000 | −0.3316 | −0.3445 |
| B5 | −0.8559 | −0.7331 | −0.7715 | −0.8981 | 0.8484 | 0.7830 | 0.8754 | 0.0004 | −0.8559 | −0.8981 |
| B6 | −0.7625 | −0.6909 | −0.6890 | −0.8210 | 0.7032 | 0.9015 | 0.7106 | 0.0004 | −0.7624 | −0.8210 |
| B7 | −0.6181 | −0.5957 | −0.5680 | −0.6761 | 0.5204 | 0.9464 | 0.5097 | 0.0002 | −0.6181 | −0.6761 |
| MNDWI | 1.0000 | 0.9547 | 0.9690 | 0.8948 | −0.8303 | −0.5075 | −0.8658 | −0.0005 | 1.0000 | 0.8948 |
| MAWEInsh | 0.9547 | 1.0000 | 0.9851 | 0.7579 | −0.6469 | −0.4524 | −0.6802 | −0.0004 | 0.9547 | 0.7579 |
| MAWEIsh | 0.9690 | 0.9851 | 1.0000 | 0.7743 | −0.6782 | −0.4427 | −0.7359 | −0.0005 | 0.9690 | 0.7743 |
| Corr | 0.8948 | 0.7579 | 0.7743 | 1.0000 | −0.9578 | −0.5923 | −0.9322 | −0.0005 | 0.8948 | 1.0000 |
| SAD | −0.8303 | −0.6469 | −0.6782 | −0.9578 | 1.0000 | 0.4879 | 0.9730 | 0.0005 | −0.8303 | −0.9578 |
| d | −0.5075 | −0.4524 | −0.4427 | −0.5923 | 0.4879 | 1.0000 | 0.4676 | 0.0002 | −0.5075 | −0.5923 |
| SID | −0.8658 | −0.6802 | −0.7359 | −0.9322 | 0.9730 | 0.4676 | 1.0000 | 0.0005 | −0.8658 | −0.9322 |
The resulting kappa coefficients are listed in Table 6. Though n1 has very low correlation with the other channels (see Table 4 and Table 5), the kappa coefficient is not increased when added. This is a consequence of the fact that n1 contains little useful information. On the other hand, adding MNDWI + n2 and corr + n2, which are highly correlated with MNDWI and corr, respectively, will be of no benefit in improving performance either, because those channels have no extra information. However, when the other water index/spectral similarity metric channel is added, the kappa coefficient increased, as shown in Table 6. For example, adding d can further increase the kappa coefficient, although it has a high correlation with the VNIR bands. Therefore, only adding data with extra useful information can improve the performance of OWCEM. This useful information is derived from people’s physical understanding of the target. For example, the water indices added in this paper contain people’s empirical knowledge about the spectral characteristics of the water.

Table 6.
The kappa coefficients for different combinations of channels used in OWCEM.
| Data used for OWCEM | Hala Lake | Lake Huron |
|---|---|---|
| 7 Landsat bands, MNDWI | 0.8024 | 0.9428 |
| 7 Landsat bands, MNDWI, n1 | 0.8024 | 0.9428 |
| 7 Landsat bands, MNDWI, MNDWI + n2 | 0.8022 | 0.9427 |
| 7 Landsat bands, MNDWI, MAWEIsh | 0.9638 | 0.9761 |
| 7 Landsat bands, MNDWI, MAWEIsh, d | 0.9640 | 0.9916 |
| 7 Landsat bands, corr | 0.5505 | 0.9907 |
| 7 Landsat bands, corr, n1 | 0.5500 | 0.9907 |
| 7 Landsat bands, corr, corr + n2 | 0.5501 | 0.9907 |
| 7 Landsat bands, corr, SAD | 0.9263 | 0.9927 |
5. Discussion and Perspectives
From the results at Hala and Huron Lakes, we find that water indices are more sensitive to ice/snow while CEM is more sensitive to cloud. OWCEM has a better suppression effect on both snow/ice and clouds. From the spectral curves of water and ice/snow, it can be observed that the SWIR bands of both water and ice/snow have a lower reflectance compared to the VIS and NIR bands. Thus, to some extent, there does exist some similarity between water and ice/snow. However, ice/snow has a much higher reflectance value than water. Therefore, adding Euclidean distance data could help OWCEM to distinguish water from ice/snow. The spectral signature for thin cloud is much more complicated, which usually varies as the ground objects below change. Therefore, it is hard to say which specific additional channel plays a more important role for OWCEM to suppress cloud. We think all additional channels make some contribution. For example, from Figure 5 and Figure 10 we can see that both MNDWI and AWEInsh have a better suppression effect on cloud than CEM, although this is not particularly obvious.
Another advantage of our algorithm is that OWCEM is less sensitive to the selection for d than CEM. Both OWCEM and CEM use the same pixels for calculating ds, but CEM has missed some water areas in results of both lakes (see Figure 6e and Figure 11e). This implies that a target pixel with a slightly different signature in shape or value from the desired signature d may be considered as an undesirable or background pixel by CEM. However, the situation for OWCEM is much better. This is because the additional water indices can enhance the information for all water types, thus lowering the impact caused by the spectral differences in the original bands between waters. In practical applications, the most representative water samples should be selected for OWCEM for better performance.
Therefore, regardless of the distribution of the target, the main advantage for OWCEM outperforming CEM is the added channels. Suitable additional data could help OWCEM to avoid the drawbacks of CEM in many aspects. From the above analysis, we can conclude that data which both reflects the common characteristics of various water types and that highlights the difference between water to background should be included in OWCEM. In this study, we only show one combination of added channels, and the result is encouraging. Thus, other useful information could also be tried in the future, such as shape information, texture, etc.
OWCEM is a supervised classifier, which requires water training samples as input. In fact, the ground truth maps are generated using the support vector machine (SVM) classifier by selecting samples for 11 level-1 and 28 level-2 land cover types, including water, ice, snow and clouds, etc. From the comparison results between OWCEM and the reference maps, we can see that the performance of our algorithm is comparable to that of SVM. However, OWCEM requires much less prior knowledge on samples, which could therefore save a lot of time in sample selection and adjustment. Moreover, OWCEM outputs are also suitable for the classification of water types by setting a different d value for different kinds of water. Taking Hala Lake as an example, by classifying the water types by choosing a larger OWCEM value, we can get a water-type map of Hala Lake, as shown in Figure 14.
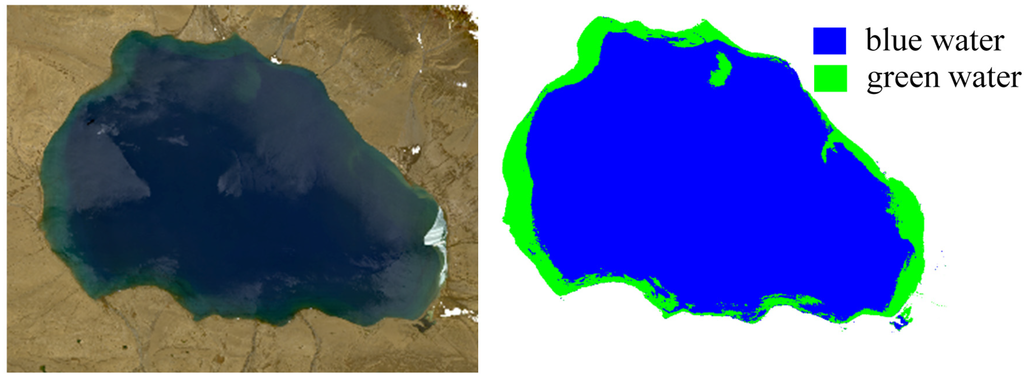
Figure 14.
The classification result of Hala Lake by OWCEM.
In addition, it should be pointed out here that the water map in Figure 6 and Figure 11 are extracted by the new strategy to achieve a fair comparison. However, people tend to use threshold segmentation or other classifiers for further water extraction. Here, we computed two different indices, the separability index (SI) [42] and the Jeffries–Matusita (J–M) distance, to measure the degree of separation between the target and the background. From Figure 15, we can see that OWCEM has the highest value in both indices, which indicates that water and non-water area are more easily separable with the OWCEM result than with the other four. The values from OWCEM usually range between −1 and 1. The threshold value can be determined automatically or manually. Through multiple tries, we found that OWCEM could achieve a stable threshold range. For these two tests, the suitable threshold is around 0.3.
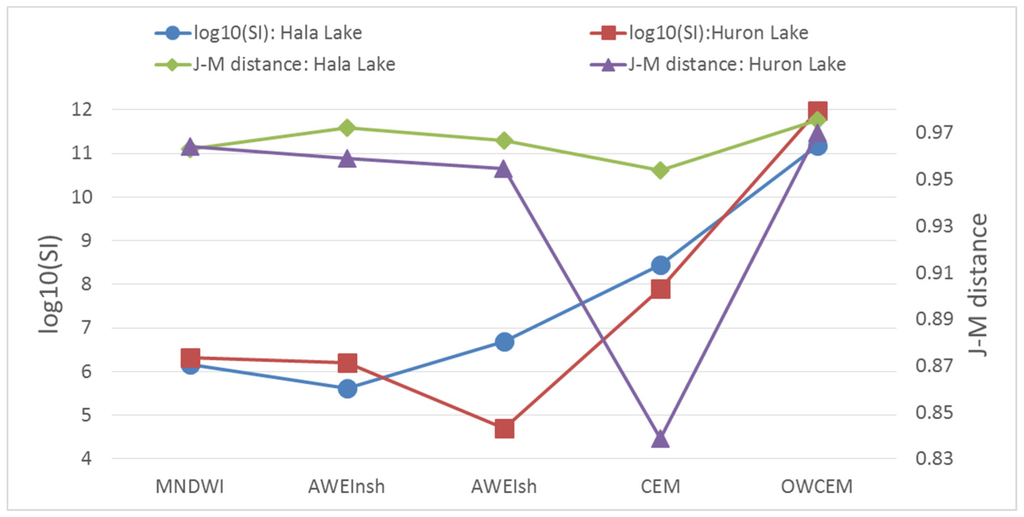
Figure 15.
The SI and J–M distance of the five algorithms.
6. Conclusions
The OWCEM developed in this research can deal with a targets having a large probability distribution. Compared to water indices and CEM, our new algorithm can achieve a consistent performance with considerably improved accuracy even when ice/snow and/or clouds exist. Our algorithm is also suitable for other multi-band images. The process used in this study can be regarded as a standard procedure for applying a CEM-derived or CEM-similar hyperspectral target detection algorithms from multispectral imagery. Moreover, besides water, other ground objects with unique signatures, such as green vegetation and urban objects, could also be extracted in the same way.
Acknowledgments
Co-funding of the project leading to these results by the National Basic Research Program of China (973 Program) under Grant Number 2015CB953701 is kindly acknowledged.
Author Contributions
Luyan Ji: Primary researcher and writer of the research publication; Xiurui Geng, Kang Sun, and Peng Gong: Technical expertise to the research publication; Yongchao Zhao: Landsat 8 image atmospheric correction software developer.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Roberts, N.; Taieb, M.; Barker, P.; Damnati, B.; Icole, M.; Williamson, D. Timing of the younger dryas event in east africa from lake-level changes. Nature 1993, 366, 146–148. [Google Scholar] [CrossRef]
- Gong, P. Remote sensing of environmental change over china: A review. Chin. Sci. Bull. 2012, 57, 2793–2801. [Google Scholar] [CrossRef]
- Feyisa, G.L.; Meilby, H.; Fensholt, R.; Proud, S.R. Automated water extraction index: A new technique for surface water mapping using landsat imagery. Remote Sens. Environ. 2014, 140, 23–35. [Google Scholar] [CrossRef]
- Sun, F.; Zhao, Y.; Gong, P.; Ma, R.; Dai, Y. Monitoring dynamic changes of global land cover types: Fluctuations of major lakes in china every 8 days during 2000–2010. Chin. Sci. Bull. 2014, 59, 171–189. [Google Scholar] [CrossRef]
- McIver, D.K.; Friedl, M.A. Using prior probabilities in decision-tree classification of remotely sensed data. Remote Sens. Environ. 2002, 81, 253–261. [Google Scholar] [CrossRef]
- Tulbure, M.G.; Broich, M. Spatiotemporal dynamic of surface water bodies using landsat time-series data from 1999 to 2011. ISPRS J. Photogramm. Remote Sens. 2013, 79, 44–52. [Google Scholar] [CrossRef]
- Sivanpillai, R.; Miller, S.N. Improvements in mapping water bodies using aster data. Ecol. Inform. 2010, 5, 73–78. [Google Scholar] [CrossRef]
- Sethre, P.R.; Rundquist, B.C.; Todhunter, P.E. Remote detection of prairie pothole ponds in the devils lake basin, north dakota. GISci. Remote Sens. 2005, 42, 277–296. [Google Scholar] [CrossRef]
- Work, E.A., Jr.; Gilmer, D.S. Utilization of satellite data for inventorying prairie ponds and lakes. Photogramm. Eng. Remote Sens. 1976, 42, 685–694. [Google Scholar]
- Rundquist, D.C.; Lawson, M.P.; Queen, L.P.; Cerveny, R.S. The relationship between summer-season rainfall events and lake-surface area. J. Am. Water Resour. Assoc. 1987, 23, 493–508. [Google Scholar] [CrossRef]
- McFeeters, S.K. The use of the normalized difference water index (NDWI) in the delineation of open water features. Int. J. Remote Sens. 1996, 17, 1425–1432. [Google Scholar] [CrossRef]
- Xu, H. Modification of normalised difference water index (NDWI) to enhance open water features in remotely sensed imagery. Int. J. Remote Sens. 2006, 27, 3025–3033. [Google Scholar] [CrossRef]
- Boland, D.H. Trophic Classification of Lakes Using Landsat-1 (erts-1) Multispectral Scanner Data; U.S. Environmental Protection Agency: Corvallis, OR, USA, 1976; p. 265.
- Ji, L.; Zhang, L.; Wylie, B. Analysis of dynamic thresholds for the normalized difference water index. Photogramm. Eng. Remote Sens. 2009, 75, 1307–1317. [Google Scholar] [CrossRef]
- Rogers, A.S.; Kearney, M.S. Reducing signature variability in unmixing coastal marsh thematic mapper scenes using spectral indices. Int. J. Remote Sens. 2004, 25, 2317–2335. [Google Scholar] [CrossRef]
- Duan, Z.; Bastiaanssen, W.G.M. Estimating water volume variations in lakes and reservoirs from four operational satellite altimetry databases and satellite imagery data. Remote Sens. Environ. 2013, 134, 403–416. [Google Scholar] [CrossRef]
- Poulin, B.; Davranche, A.; Lefebvre, G. Ecological assessment of phragmites australis wetlands using multi-season spot-5 scenes. Remote Sens. Environ. 2010, 114, 1602–1609. [Google Scholar] [CrossRef]
- Hui, F.; Xu, B.; Huang, H.; Yu, Q.; Gong, P. Modelling spatial-temporal change of poyang lake using multitemporal landsat imagery. Int. J. Remote Sens. 2008, 29, 5767–5784. [Google Scholar] [CrossRef]
- Chang, C.-I.; Althouse, M.L.G.; Sun, T.-L. Unsupervised interference rejection approach to target detection and classification for hyperspectral imagery. Opt. Eng. 1998, 37, 735–743. [Google Scholar] [CrossRef]
- Farrand, W.H.; Harsanyi, J.C. Mapping the distribution of mine tailings in the coeur d’alene river valley, idaho, through the use of a constrained energy minimization technique. Remote Sens. Environ. 1997, 59, 64–76. [Google Scholar] [CrossRef]
- Manolakis, D.; Shaw, G. Detection algorithms for hyperspectral imaging applications. IEEE Signal Proc. Mag. 2002, 19, 29–43. [Google Scholar] [CrossRef]
- Harsanyi, J.C. Detection and Classification of Subpixel Spectral Signatures in Hyperspectral Image Sequences; University of Maryland: College Park, MD, USA, 1993. [Google Scholar]
- Du, Q.; Ren, H.; Chang, C.-I. A comparative study for orthogonal subspace projection and constrained energy minimization. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1525–1529. [Google Scholar] [CrossRef]
- Arora, M.K.; Bansal, S.; Khare, S.; Chauhan, K. Comparative assessment of some target detection algorithms for hyperspectral images. Def. Sci. J. 2013, 63, 53–62. [Google Scholar] [CrossRef]
- Manolakis, D.; Shaw, G.; Keshava, N. Comparative analysis of hyperspectral adaptive matched filter detector. Proc. SPIE 2000. [Google Scholar] [CrossRef]
- Chen, J.Y.; Reed, I.S. A detection algorithm for optical targets in clutter. IEEE Trans. Aerosp. Electron. Syst. 1987, AES-23, 46–59. [Google Scholar] [CrossRef]
- Manolakis, D.; Lockwood, R.; Cooleyb, T.; Jacobson, J. Is there a best hyperspectral detection algorithm? Proc. SPIE 2009. [Google Scholar] [CrossRef]
- Manolakis, D.; Lockwood, R.; Cooleyb, T.; Jacobson, J. Hyperspectral detection algorithms: Use covariances or subspaces? Proc. SPIE 2009. [Google Scholar] [CrossRef]
- DiPietro, R.S.; Manolakis, D.; Lockwood, R.; Cooleyb, T.; Jacobson, J. Performance evaluation of hyperspectral detection algorithms for sub-pixel objects. Proc. SPIE 2010. [Google Scholar] [CrossRef]
- Manolakis, D.; Marden, D.; Kerekes, J.; Shaw, G. On the statistics of hyperspectral imaging data. Proc. SPIE 2001. [Google Scholar] [CrossRef]
- Funk, C.C.; Theiler, J.; Roberts, D.A.; Borel, C.C. Clustering to improve matched filter detection of weak gas plumes in hyperspectral thermal imagery. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1410–1420. [Google Scholar] [CrossRef]
- Minet, J.; Taboury, J.; Goudail, F.; Péalat, M.; Roux, N.; Lonnoy, J.; Ferrec, Y. Influence of band selection and target estimation error on the performance of the matched filter in hyperspectral imaging. Appl. Opt. 2011, 50, 4276–4284. [Google Scholar] [CrossRef] [PubMed]
- Ren, H.; Wang, C.-M.; Chang, C.-I.; Liu, J.-M.; Yang, C.-W.; Ma, D.-J.; Chieu, B.-C.; Lo, C.-S.; Chung, P.-C. Generalized constrained energy minimization approach to subpixel target detection for multispectral imagery. Opt. Eng. 2000, 39, 1275–1281. [Google Scholar] [CrossRef]
- Geng, X.; Ji, L.; Sun, K.; Zhao, Y. CEM: More bands, better performance. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1–5. [Google Scholar] [CrossRef]
- Geng, X.; Zhao, Y. Principle of small target detection for hyperspectral imagery. Sci. China Earth Sci. 2007, 50, 1225–1231. [Google Scholar] [CrossRef]
- Wünnemann, B.; Wagner, J.; Zhang, Y.; Yan, D.; Wang, R.; Shen, Y.; Fang, X.; Zhang, J. Implications of diverse sedimentation patterns in hala lake, qinghai province, china for reconstructing late quaternary climate. J. Paleolimnol. 2012, 48, 725–749. [Google Scholar] [CrossRef]
- Gong, P.; Wang, J.; Yu, L.; Zhao, Y.; Zhao, Y.; Liang, L.; Niu, Z.; Huang, X.; Fu, H.; Liu, S.; et al. Finer resolution observation and monitoring of global land cover: First mapping results with landsat tm and etm+ data. Int. J. Remote Sens. 2012, 34, 2607–2654. [Google Scholar] [CrossRef]
- Chang, C.-I. An information-theoretic approach to spectral variability, similarity, and discrimination for hyperspectral image analysis. IEEE Trans. Inf. Theory 2000, 46, 1927–1932. [Google Scholar] [CrossRef]
- Sun, F.; Sun, W.; Chen, J.; Gong, P. Comparison and improvement of methods for identifying waterbodies in remotely sensed imagery. Int. J. Remote Sens. 2012, 33, 6854–6875. [Google Scholar] [CrossRef]
- Geng, X.; Xiao, Z.; Ji, L.; Zhao, Y.; Wang, F. A gaussian elimination based fast endmember extraction algorithm for hyperspectral imagery. ISPRS J. Photogramm. Remote Sens. 2013, 79, 211–218. [Google Scholar] [CrossRef]
- Ji, L.; Geng, X.; Yu, K.; Zhao, Y. A new non-negative matrix factorization method based on barycentric coordinates for endmember extraction in hyperspectral remote sensing. Int. J. Remote Sens. 2013, 34, 6577–6586. [Google Scholar] [CrossRef]
- Acito, N.; Resta, S.; Diani, M.; Corsini, G. Robust technique for anomalous change detection in airborne hyperspectral imagery based on automatic and adaptive band selection. Opt. Eng. 2013, 52. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).