Experimental Measurement of Diffusive Extinction Depth and Soil Moisture Gradients in a Dune Sand Aquifer in Western Saudi Arabia: Assessment of Evaporation Loss for Design of an MAR System
Abstract
:1. Introduction

2. Background and Methods
2.1. Collection of Sand Samples from Dune Fields
2.2. Grain Size Distribution Analyses
2.3. Laboratory Porosity and Hydraulic Conductivity Measurements
2.4. Calibration of Moisture Sensors
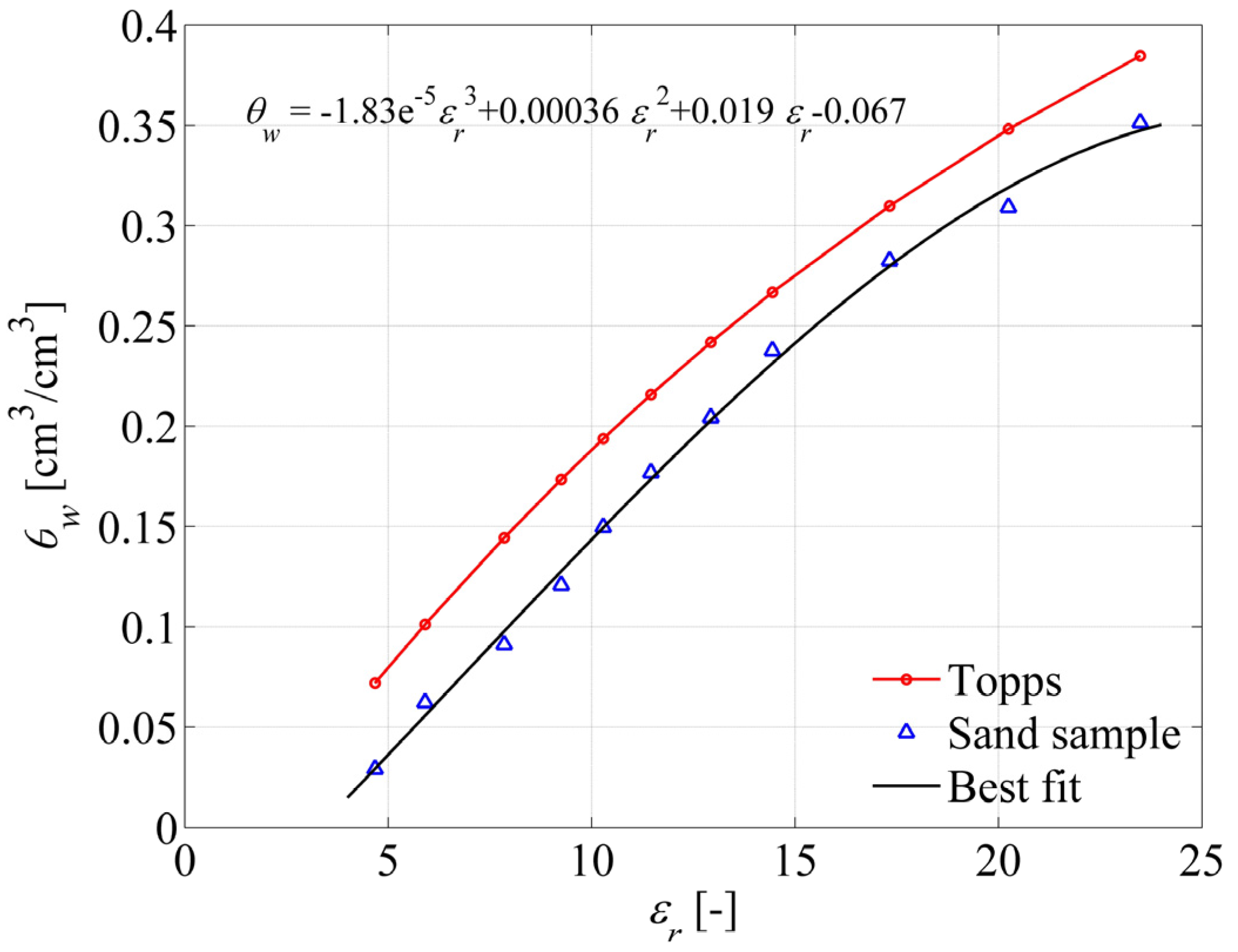
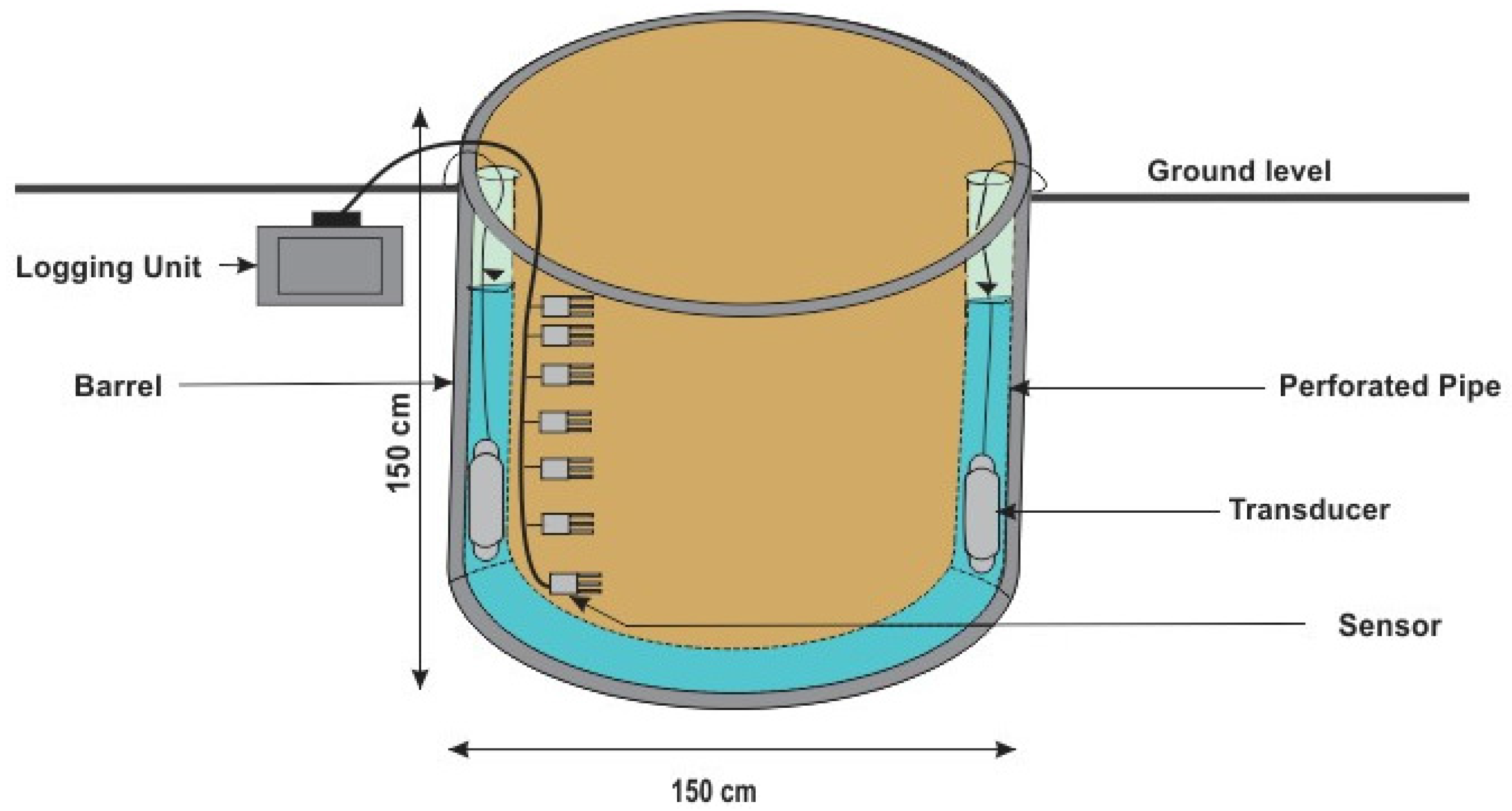
2.5. Experimental Design and Instrumentation

2.6. Hydrodynamic Modeling
3. Results
3.1. Physical Properties of the Media
| Parameter | Sample 1 | Sample 2 | Sample 3 | Sample 4 | Sample 5 |
|---|---|---|---|---|---|
| Porosity | 0.41 | - | 0.33 | - | 0.40 |
| Hydraulic Conductivity (m/day) | 6.48 | 3.30 (?) | 6.75 | 7.57 | 7.54 |
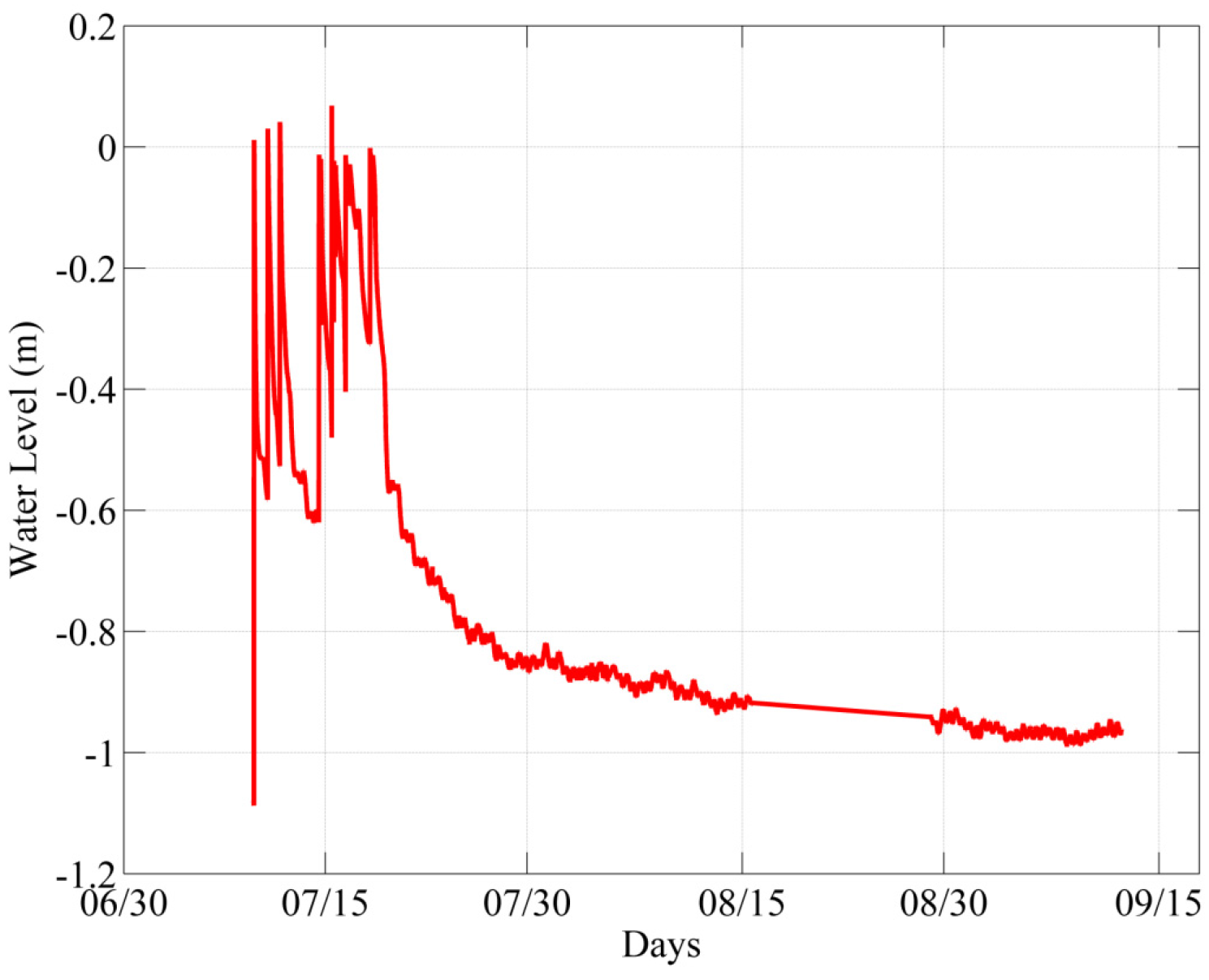
3.2. Water Level Profile
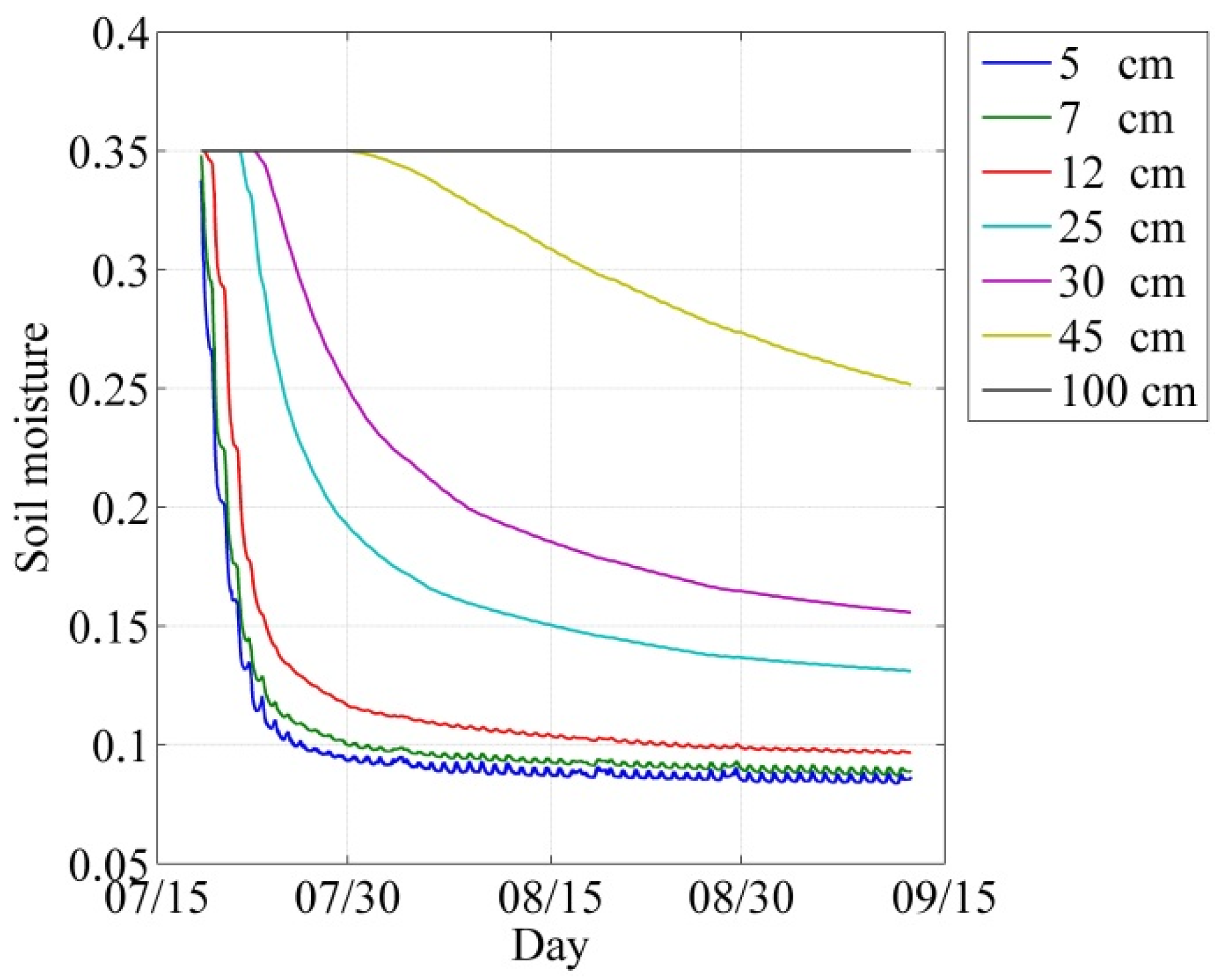
3.3. Soil Moisture Content Profile

3.4. Temperature Profile

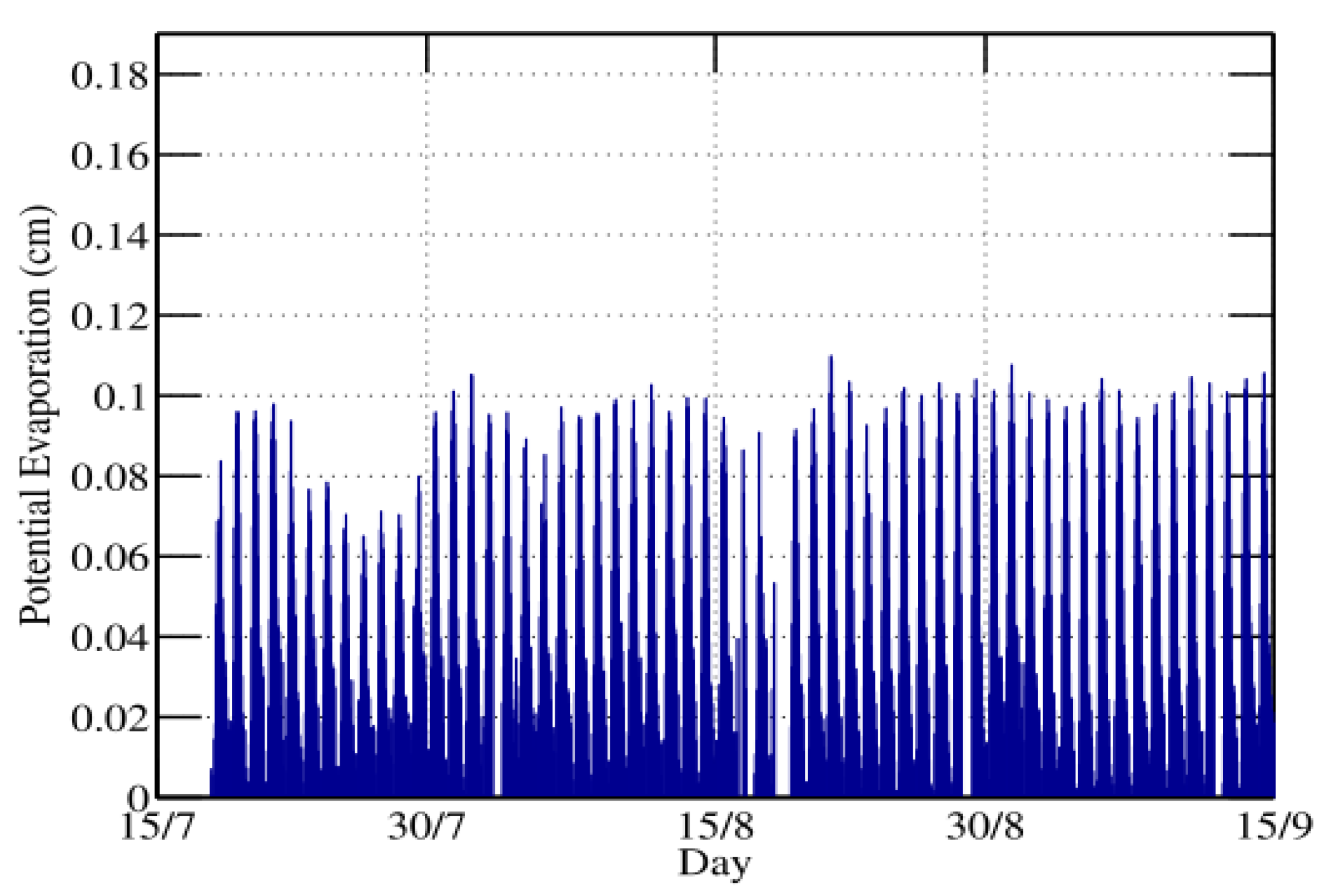
3.5. Hydrodynamic Modeling Results

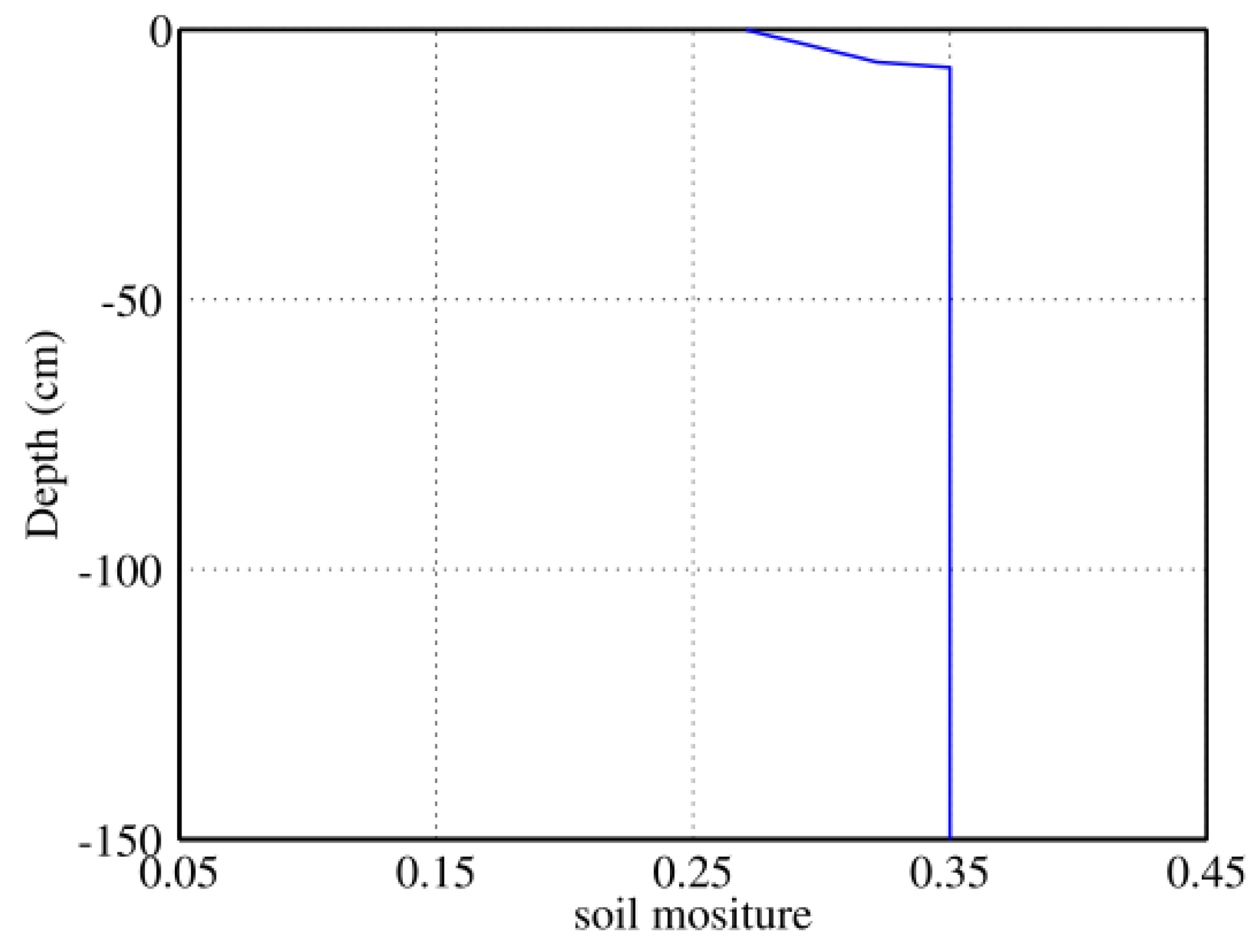
3.6. Comparison of Sensor and MVG Model Results
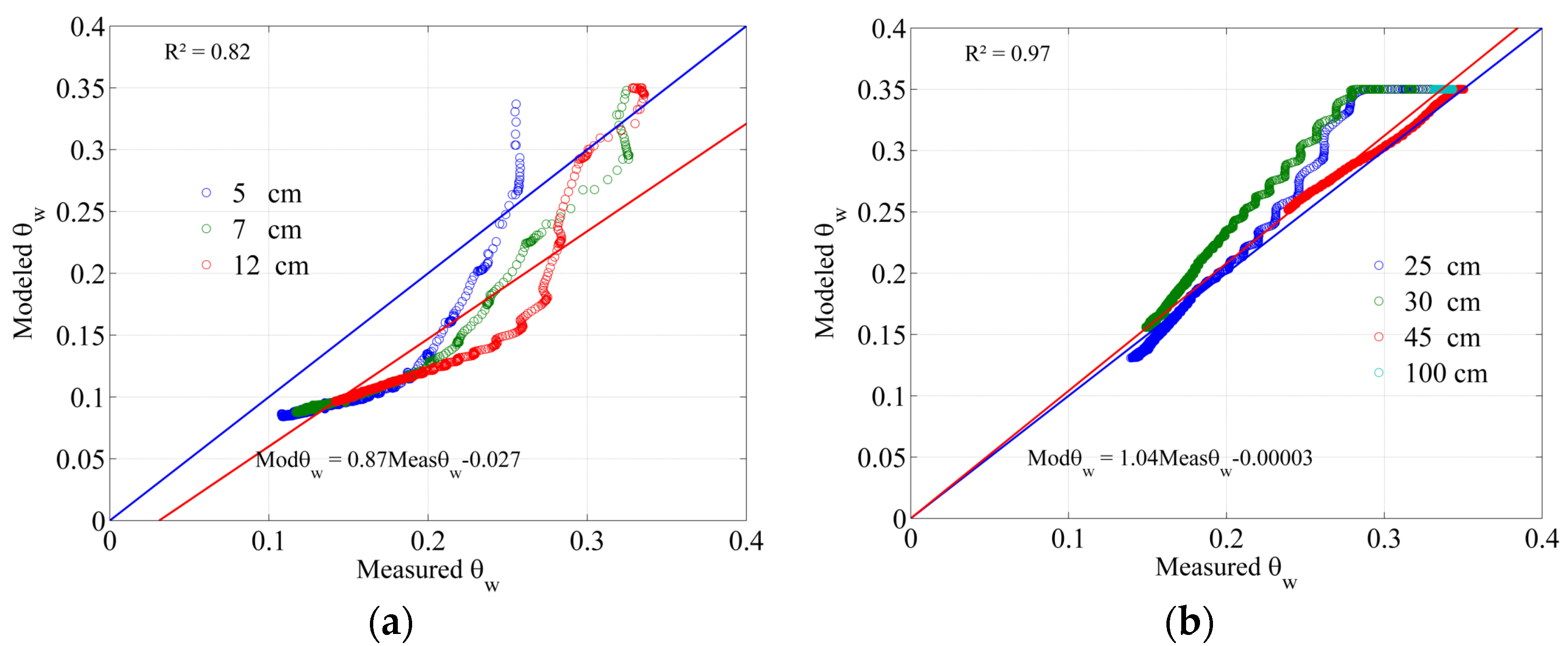
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Subyani, A.M. Geostatistical study of annual and mean rainfall patterns in southwest Saudi Arabia. Hydrol. Sci. J. 2004, 49, 803–817. [Google Scholar] [CrossRef]
- Sen, Z. Wadi Hydrology; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2008. [Google Scholar]
- Maliva, R.G.; Missimer, T.M. Arid Lands Water Evaluation and Management; Springer: Heidelberg, Germany, 2012. [Google Scholar]
- Abdulrazzak, M.J.; Morel-Seytoux, H.J. Recharge from an ephemeral stream following wetting front arrival to water table. Water Resour. Res. 1983, 19, 194–200. [Google Scholar] [CrossRef]
- Sorman, A.U.; Abdulrazzak, M.J. Infiltration-recharge through wadi beds in arid regions. Hydrol. Sci. J. 1993, 38, 173–186. [Google Scholar] [CrossRef]
- Missimer, T.M.; Drewes, J.E.; Amy, G.; Maliva, R.G.; Keller, S. Restoration of wadi aquifers by artificial recharge with treated wastewater. Groundwater 2012, 50, 514–527. [Google Scholar] [CrossRef] [PubMed]
- AlSarmi, S.; Washington, R. Recent observed climate change over the Arabian Peninsula. J. Geophys. Res. 2011, 166, D11109. [Google Scholar] [CrossRef]
- Almazroui, M. Simulation of present and future climate of Saudi Arabia using a regional climate model (PRECIS). Int. J. Climatol. 2013, 9, 2247–2259. [Google Scholar] [CrossRef]
- Al-Muttair, F.F.; Sendil, U.; Al-Turbak, A.S. Management of recharge dams in Saudi Arabia. J. Water Res. Plan. Manag. 1994, 120, 749–763. [Google Scholar] [CrossRef]
- Missimer, T.M.; Guo, W.; Maliva, R.G.; Rosas, J.; Jadoon, K.Z. Enhancement of wadi recharge using dams coupled with aquifer storage and recovery wells. Environ. Earth Sci. 2014, 73, 1303–1315. [Google Scholar] [CrossRef]
- Lopez, O.; Stenchikov, G.; Missimer, T.M. Water management during climate change using aquifer storage and recovery in a dunefield in western Saudi Arabia. Environ. Res. Lett. 2014, 9. [Google Scholar] [CrossRef]
- Vandenbohede, A.; van Houtte, E.; Lebbe, L. Sustainable groundwater extraction in coastal areas: A Belgian example. Environ. Geol. 2009, 57, 735–747. [Google Scholar] [CrossRef]
- Thoa, N.T.K.; Arduino, G.; Giang, N.V.; van, P.T.K.; Vuong, B.T. The model for management of aquifer recharge in sand dune area of Bac Binh, Binh Thuan, Vietnam. J. Earth Sci. 2006, 28, 389–410. [Google Scholar]
- Dillion, P. Aquifer storage and recovery with stormwater and reclaimed water in Australia. In Proceedings of the UNESCO-VIETNAM Artificial Recharge in South East Asia, Ho Chin Minh City, Virtnam, 15–17 December 2004.
- Lopez, O.M.; Jadoon, K.Z.; Missimer, T.M. Method of relating grain size distribution to hydraulic conductivity in dune sands to assist in assessing managed aquifer recharge projects: Wadi Khulays dune field, western Saudi Arabia. Water 2015, 7, 6411–6426. [Google Scholar] [CrossRef]
- Droogers, P.; Allen, R.G. Estimating reference evapotranspiration under inaccurate data conditions. Irrig. Drain. Syst. 2002, 16, 33–45. [Google Scholar] [CrossRef]
- Inmark, S.; Irmak, A.; Allen, R.; Jones, J. Solar and net radiation-based equations to estimate reference evapotranspiration in humid climates. J. Irrig. Drain. Eng. 2003, 129, 336–347. [Google Scholar]
- Shah, N.; Nachabe, M.; Ross, M. Extinction depth and evapotranspiration from ground water under selected land covers. Ground Water 2007, 45, 329–338. [Google Scholar] [CrossRef] [PubMed]
- Xiao, X.; Li, B.; Sauer, T.; Heitman, J.; Ren, T. Cumulative soil water evaporation as a function of depth and time. Vadose Zone J. 2000, 10, 1016–1022. [Google Scholar] [CrossRef]
- Hellwig, D.H.R. Evaporation of water from sand, 1: Experimental set-up and climate influence. J. Hydrol. 1973, 18, 93–108. [Google Scholar] [CrossRef]
- Hellwig, D.H.R. Evaporation of water from sand, 2: Diurnal variations. J. Hydrol. 1973, 18, 109–118. [Google Scholar] [CrossRef]
- Hellwig, D.H.R. Evaporation of water from sand, 4: The influence of the depth of the water table and the particle size distribution of the sand. J. Hydrol. 1973, 18, 109–118. [Google Scholar] [CrossRef]
- Soylu, M.E.; Istanbulluoglu, E.; Lenters, J.D.; Wang, T. Quantifying the impact of groundwater depth on evapotranspiration in a semi-arid grassland region. Hydrol. Earth Syst. Sci. 2011, 15, 787–806. [Google Scholar] [CrossRef]
- Wang, X. Vapor flow resistance of dry soil layer to soil water evaporation in arid environment: An overview. Water 2015, 7, 4552–4574. [Google Scholar] [CrossRef]
- Tanner, W.F.; Balsillie, J.H. Environmental Granulometry; Special Publication No. 40; Florida Geological Survey: Tallahassee, FL, USA, 1995. [Google Scholar]
- United States Department of Agriculture-Natural Resources Conservation Service (USDA-NRCS). Soil Survey Laboratory Methods Manual; Report No. 42, Version 4.0; National Soil Center: Lincoln, NE, USA, 2004.
- American Society for Testing and Materials (ASTM). Standard Test Method for Permeability of Granular Soils, ASTM Standard D2434–68; ASTM: West Conshocken, PA, USA, 2006. [Google Scholar]
- Topp, S.; Grasmueck, M.; Vega, S.; Viggiano, D.A. Electromagnetic determination of soil water content: Measurement in coaxial transmission lines. Water Res. 1980, 16, 574–582. [Google Scholar] [CrossRef]
- Jadoon, K.Z.; Weihermüller, L.; Scharnagl, B.; Kowalsky, M.B.; Bechtold, M.; Hubbard, S.S.; Vereecken, H.; Lambot, S. Estimation of soil hydraulic parameters in the field by integrated hydrogeophysical inversion of time-lapse ground-penetrating radar data. Vadose Zone J. 2012, 11, 1–17. [Google Scholar] [CrossRef]
- Dimitrov, M.; Vanderborght, J.; Kostov, K.G.; Jadoon, K.Z.; Weihermuller, L.; Jackson, T.J.; Bindlish, R.; Pachepsky, Y.; Schwank, M.; Vereecken, H. Soil hydraulic parameters and surface soil moisture of a tilled bare soil plot inversely derived from L-band brightness temperatures. Vadose Zone J. 2014, 13, 1–18. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Christman, M.; Reedy, R.C.; Porro, I.; Simunek, J.; Flerchinger, G.N. Intercode comparisons for simulating water balance of surficial sediments in semiarid regions. Water Res. 2002, 38, 1323–1339. [Google Scholar] [CrossRef]
- Saito, H.J.; Simunek, J.; Mohanty, B. Numerical analyses of coupled water, vapor and heat transport in the vadose zone. Vadose Zone J. 2006, 5, 784–800. [Google Scholar] [CrossRef]
- Mualem, Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Res. 1976, 12, 513–522. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A closed form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Vereecken, H. Estimating the unsaturated hydraulic conductivity from theoretical models using simple soil properties. Geodema 1995, 65, 81–92. [Google Scholar] [CrossRef]
- Noborio, K.; McInnes, K.J.; Heilman, J.L. Two-dimensional model for water, heat, and solute transport in furrow-irrigated soil: II. Field evaluation. Soil Sci. Soc. Am. J. 1996, 60, 1010–1021. [Google Scholar] [CrossRef]
- Nimmo, J.R.; Miller, E.E. The temperature dependence of isothermal moisture vs. potential characteristics of soils. Soil Sci. Soc. Am. J. 1986, 50, 1105–1113. [Google Scholar] [CrossRef]
- Nassar, I.N.; Horton, R. Simultaneous transfer of heat, water, and solute in porous media: I. Theoretical development. Soil Sci. Soc. Am. J. 1992, 56, 1350–1356. [Google Scholar] [CrossRef]
- Wentworth, C.K. A scale of grade and class terms for clastic sediments. J. Geol. 1922, 30, 377–392. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Smith, M. Crop Evapotranspiration: Guidelines for Computing Crop Water Requirements; Irrigation and Drainage Paper 56; Food and Agriculture Organization of the United Nations: Roma, Italy, 1998. [Google Scholar]
- Scharnagl, B.; Vrugt, J.; Vereecken, H.; Herbst, M. Inverse modeling of in situ soil water dynamics: Investigation the effect of different prior distributions of the soil hydraulic parameters. Hydrol. Earth Syst. Sci. 2011, 15, 3043–3059. [Google Scholar] [CrossRef]
- Chuhan, F.A.; Kjeldstad, A.; Bjorlykke, K.; Hoeg, K. Experimental compression of loose sands: Relevance to porosity reduction during burial in sedimentary basins. Can. Geotech. J. 2003, 40, 997–1011. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mughal, I.; Jadoon, K.Z.; Mai, P.M.; Al-Mashharawi, S.; Missimer, T.M. Experimental Measurement of Diffusive Extinction Depth and Soil Moisture Gradients in a Dune Sand Aquifer in Western Saudi Arabia: Assessment of Evaporation Loss for Design of an MAR System. Water 2015, 7, 6967-6982. https://doi.org/10.3390/w7126669
Mughal I, Jadoon KZ, Mai PM, Al-Mashharawi S, Missimer TM. Experimental Measurement of Diffusive Extinction Depth and Soil Moisture Gradients in a Dune Sand Aquifer in Western Saudi Arabia: Assessment of Evaporation Loss for Design of an MAR System. Water. 2015; 7(12):6967-6982. https://doi.org/10.3390/w7126669
Chicago/Turabian StyleMughal, Iqra, Khan Z. Jadoon, P. Martin Mai, Samir Al-Mashharawi, and Thomas M. Missimer. 2015. "Experimental Measurement of Diffusive Extinction Depth and Soil Moisture Gradients in a Dune Sand Aquifer in Western Saudi Arabia: Assessment of Evaporation Loss for Design of an MAR System" Water 7, no. 12: 6967-6982. https://doi.org/10.3390/w7126669
APA StyleMughal, I., Jadoon, K. Z., Mai, P. M., Al-Mashharawi, S., & Missimer, T. M. (2015). Experimental Measurement of Diffusive Extinction Depth and Soil Moisture Gradients in a Dune Sand Aquifer in Western Saudi Arabia: Assessment of Evaporation Loss for Design of an MAR System. Water, 7(12), 6967-6982. https://doi.org/10.3390/w7126669






