State of the Art of Online Monitoring and Control of the Coagulation Process
Abstract
:1. Introduction
1.1. The Relevance of the Coagulation Process
1.2. Parameters and Physical Sensors Related to Coagulation
1.3. The Floc Formation Process
| Monitoring stage | Parameter | Commonly Measured | Occasionally Measured | Commonly Used for Dosing Control | Occasionally Used for Dosing Control |
|---|---|---|---|---|---|
| Raw water (inlet) | Flow | X | X | ||
| pH | X | X | |||
| Temperature | X | ||||
| Conductivity | X | ||||
| Turbidity | X | X | |||
| Suspended solids | X | X | |||
| UV-absorbance | X | X | |||
| Color | X | X | |||
| TOC | X | ||||
| Ortho-P | X | ||||
| Total-P | X | ||||
| Particle counter | X | ||||
| Coagulated water (immediately after dosing of coagulants) | pH | X | X | ||
| Streaming current | X | X | |||
| Zeta potential | X | ||||
| Finished water (outlet) | pH | X | X | ||
| Turbidity | X | X | |||
| Suspended solids | X | ||||
| UV-absorbance | X | ||||
| Color | X | ||||
| TOC | X | ||||
| Ortho-P | X | ||||
| Total-P | X |
2. Direct Use of Online Parameters for Dosing Control
2.1. General Approach
- Feed-forward control based on raw water quality;
- Feed-backward control based on dosed water quality;
- Feed-backward control based on treated water quality.
2.2. Feed-Forward Control Based on Raw Water Quality

2.3. Feed-Backward Control Based on Dosed Water Quality

2.4. Feed-Backward Control Based on Finished Water Quality
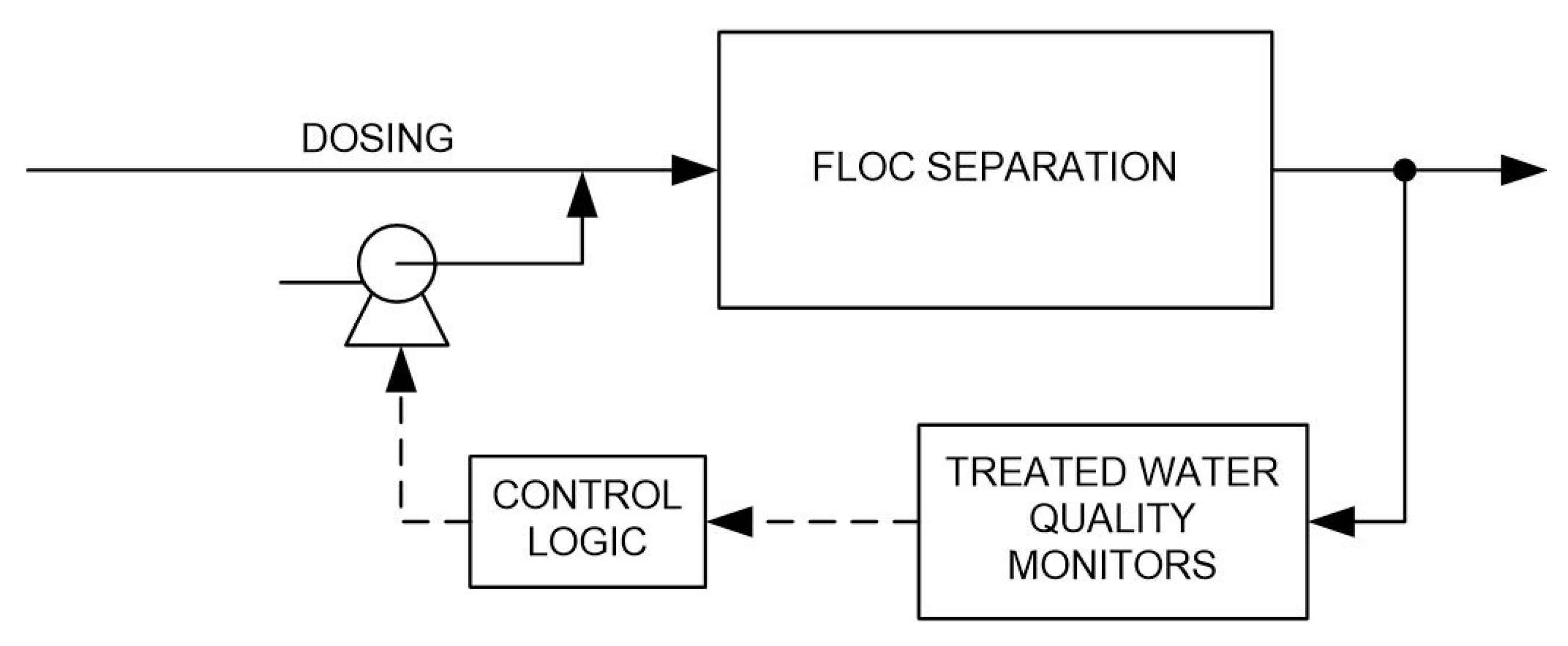
3. Indirect Use of Online Parameters for Dosing Control
3.1. Development of Software Sensors for Dosing Control
- Multivariate regression analysis;
- Artificial neural network models (ANN);
- Fuzzy logic models.
3.2. Multivariate Regression Analysis
3.3. Artificial Neural Network Models (ANN)
3.4. Fuzzy Logic Models
4. Practical Applications
5. Research Needs
6. Conclusions
Acknowledgments
Conflicts of Interest
References
- Ratnaweera, H. Phosphorus recovery from wastewater—Should we rebuild our wastewater treatment plants? VANN 2013, 04, 551–556. (In Norwegian) [Google Scholar]
- Dhiman, R. Speciality Chemicals for Water Treatment: The Global Market; Report No. CHM050A; BCC Research: Wellesley, MA, USA, 2008; p. 101. [Google Scholar]
- Hagmeyer, G.; Gimbel, R.; Kiepke, O.; Dautzenberg, W. Flocculation/Ultrafiltration for drinking water treatment of reservoir water. In Proceedings of the AWWA Membrane Technology Conference, San Antonio, TX, USA, 4–7 March 2001. [CD-ROM].
- Amirtharajah, A.; Mills, K.M. Rapid-mix design for mechanisms of alum coagulation. J. Am. Water Works Assoc. 1982, 74, 210–216. [Google Scholar]
- American Water Works Association (AWWA). Operational Control of Coagulation and Filtration Processes. In Manual of Water Supply Practices M37, 3rd ed.; AWWA: Denver, CO, USA, 2011. [Google Scholar]
- TeKippe, R.J.; Ham, R.K. Coagulation Testing: A Comparison of Techniques, Part I. J. AWWA 1970, 62, 594–602. [Google Scholar]
- TeKippe, R.J.; Ham, R.K. Coagulation Testing: A Comparison of Techniques, Part II. J. AWWA 1970, 62, 620–628. [Google Scholar]
- Dentel, S.K. Coagulation Control in Water Treatment. Crit. Rev. Environ. Control 1991, 21, 41–135. [Google Scholar] [CrossRef]
- Ratnaweera, H. Coagulant Dosing Control—A Review. In Chemical Water and Wastewater Treatment VIII; Hahn, H.H., Hoffmann, E., Ødegaard, H., Eds.; IWA Publishing: London, UK, 2004; pp. 10–18. [Google Scholar]
- Shutova, Y.; Baker, A.; Bridgeman, J.; Henderson, R.K. Spectroscopic characterisation of dissolved organic matter changes in drinking water treatment: From PARAFAC analysis to online monitoring wavelengths. Water Res. 2014, 54, 159–169. [Google Scholar] [CrossRef] [PubMed]
- Bernhardt, H.; Schell, H. Experience in coagulant control by use of a charge titration unit. J. Water Supply Res. Technol. Aqua 1996, 45, 19–27. [Google Scholar]
- Gregory, J. Monitoring particle aggregation processes. Adv. Colloid Interface Sci. 2009. [Google Scholar] [CrossRef] [PubMed]
- Sharp, E.; Norris, R. Using online zeta potential measurements for coagulation control: A first for the UK water industry. In Proceedings of the 6th IWA Specialist Conference on Natural Organic Matter in Drinking Water, Malmö, Sweden, 7–10 September 2015.
- Thomas, D.N.; Judd, S.J.; Fawcett, N. Flocculation Modelling: A Review. Water Res. 1999, 33, 1579–1592. [Google Scholar] [CrossRef]
- Wistrom, A.; Farrell, J. Simulation and system identification of dynamic models for flocculation control. Water Sci. Technol. 1998, 37, 181–192. [Google Scholar] [CrossRef]
- Schuetz, S.; Piesche, M. A model of the coagulation process with solid particles and flocs in a turbulant flow. Chem. Eng. Sci. 2002, 57, 4357–4368. [Google Scholar] [CrossRef]
- Kim, J.W.; Kramer, T.A. Improved models for fractal colloidal agglomeration: Computationally efficient algorithms. Colloids Surf. A Physicochem. Eng. Asp. 2005, 254, 33–49. [Google Scholar] [CrossRef]
- Jackson, P.J.; Tomlinson, E.J. Automatic Coagulation Control—Evaluation of Strategies and Techniques. Water Supply 1986, 4, 55–67. [Google Scholar]
- Hernebring, C. Rapid Methods for the Determination of Required Alum Dosage in Surface Water Treatment Plants. Vatten 1987, 43, 209–219. (In Swedish) [Google Scholar]
- Eikebrokk, B.; Fettig, J. Treatment of Coloured Surface Water by Coagulation/Direct Filtration: Effect of Water Quality, Type of Coagulant and Filter Aids. In Chemical Water and Wastewater Treatment I; Hahn, H.H., Klute, R., Eds.; Springer-Verlag: Berlin, Germany, 1990; pp. 361–376. [Google Scholar]
- Edzwald, J.K. Coagulation in Drinking Water Treatment: Particles, Organics, and Coagulants. Water Sci. Technol. 1993, 27, 21–35. [Google Scholar]
- Edzwald, J.K.; Kaminski, G.S. A Practical Method for Water Plants to Select Coagulant Dosing. J. NEWWA 2009, 123, 11–27. [Google Scholar]
- Archer, A.D.; Singer, P.C. An evaluation of the relationship between SUVA and NOM coagulation using the ICR database. J. AWWA 2006, 98, 110–123. [Google Scholar]
- Edwards, M. Predicting DOC Removal during Enhanced Coagulation. J. AWWA 1997, 89, 78–89. [Google Scholar]
- Van Leeuwen, J.; Holmes, M.; Heidenreich, C.; Daly, R.; Fisher, I.; Kastl, G.; Sathasivan, A.; Bursill, D. Modelling the Application of Inorganic Coagulants and pH Control Reagents for Removal of Organic Matter from Drinking Waters. In Proceedings of the MODSIM Conference—Integrated Modelling of Biophysical, Social and Economic Systems for Resource Management Solutions, Townsville, Australia, 14–17 July 2003; [CD-ROM]. pp. 1835–1840.
- Van Leeuwen, J.; Holmes, M.; Kaeding, U.; Daly, R.; Bursill, D. Development and implementation of the software mEnCo© to predict coagulant doses for DOC removal at full-scale WTPs in South Australia. J. Water Supply Res. Technol. Aqua 2009, 58, 291–298. [Google Scholar] [CrossRef]
- Murshed, M.F.; van Leeuwen, J.A.; Chow, C.W.K.; Drikas, M. Modification of jar testing protocol combined with mEnCo model predicted dose to predict dissolved organic matter removal for surface water. Water Sci. Technol. Water Supply 2014, 14, 358–366. [Google Scholar] [CrossRef]
- Wang, D.; Xie, J.; Chow, C.W.; Xing, L.; van Leeuwen, J. Characterization and predicting DOM treatability by enhanced coagulation. Water Sci. Technol. Water Supply 2012, 13, 147–157. [Google Scholar] [CrossRef]
- Xie, J.; Wang, D.; van Leeuwen, J.; Zhao, Y.; Xing, L.; Chow, W.C. pH modeling for maximum dissolved organic matter removal by enhanced coagulation. J. Environ. Sci. 2012, 24, 276–283. [Google Scholar] [CrossRef]
- Xianjun, D.; Ping, Y.; Songtao, S. Study on Modeling of Coagulant Dosage System in Water Purification Process. Inf. Technol. J. 2013, 12, 2651–2655. [Google Scholar] [CrossRef]
- Stedmon, C.A.; Markager, S.; Bro, R. Tracing dissolved organic matter in aquatic environments using a new approach to fluorescence spectroscopy. Mar. Chem. 2003, 82, 239–254. [Google Scholar] [CrossRef]
- Ohno, T.; Bro, R. Dissolved organic matter characterization using multiway spectral decomposition of fluorescence landscapes. Soil Sci. Soc. Am. J. 2003, 70, 2028–2037. [Google Scholar] [CrossRef]
- Sanchez, N.; Skeriotis, A.; Miller, C. A PARAFAC-Based Long-Term Assessment of DOM in a Multi-Coagulant Drinking Water Treatment Scheme. Environ. Sci. Technol. 2014, 48, 1582–1591. [Google Scholar] [CrossRef] [PubMed]
- Critchley, R.F.; Smith, E.O.; Pettit, P. Automatic Coagulation Control at Water Treatment Plants in the North-West Region of England. Water Environ. J. 1990, 4, 535–543. [Google Scholar] [CrossRef]
- Adgar, A.; Cox, C.S.; Jones, C.A. Enhancement of coagulation control using the streaming current detector. Bioprocess Biosyst. Eng. 2005, 27, 349–357. [Google Scholar] [CrossRef] [PubMed]
- Yavich, A.A.; van de Wege, J. Chemical feed control using coagulation computer models and a streaming current detector. Water Sci. Technol. 2013, 67, 2814–2821. [Google Scholar] [CrossRef] [PubMed]
- Oh, J.I.; Lee, S.H. Influence of streaming potential on flux decline of microfiltration with in-line rapid pre-coagulation process for drinking water production. J. Membr. Sci. 2005, 254, 39–47. [Google Scholar] [CrossRef]
- Nam, S.W.; Jo, B.I.; Kim, M.K.; Kim, W.K.; Zoh, K.D. Streaming current titration for coagulation of high turbidity water. Colloids Surf. A Physicochem. Eng. Asp. 2013, 419, 133–139. [Google Scholar] [CrossRef]
- Byun, S.; Kwon, J.H.; Kim, M.K.; Park, K.Y.; Lee, S. Automatic control of polymer dosage using streaming potential for waterworks sludge conditioning. Sep. Purif. Technol. 2013, 57, 230–236. [Google Scholar] [CrossRef]
- Gregory, J.; Nelson, D.W. Monitoring aggregations in flowing suspension. Colloids Surface 1986, 18, 175–188. [Google Scholar] [CrossRef]
- Huang, C.; Chen, G.S. Use of the Fiber-Optical Monitor in Evaluating the State of Flocculation. Water Res. 1996, 30, 2723–2727. [Google Scholar] [CrossRef]
- Staaks, C.; Fabris, R.; Lowe, T.; Chow, C.; van Leeuwen, J.; Drikas, M. Coagulation assessment and optimisation with a photometric dispersion analyser and organic characterisation for natural organic matter removal performance. Chem. Eng. J. 2011, 168, 629–634. [Google Scholar] [CrossRef]
- Zouloubis, A.I.; Tzoupanos, N. Alternative cost-effective preparation method of PAC coagulant agent: Characterization and comparative application for water/wastewater treatment. Desalination 2010, 250, 339–344. [Google Scholar] [CrossRef]
- Hopkins, D.C.; Ducoste, J.J. Characterizing flocculation under heterogeneous turbulence. J. Colloid Interface Sci. 2003, 264, 184–194. [Google Scholar] [CrossRef]
- Huang, C.; Liu, C.B. Automatic Control for Chemical Dosing in Laboratory-scale Coagulation Process by Using an Optical Monitor. Water Res. 1996, 30, 1924–1929. [Google Scholar] [CrossRef]
- Cheng, W.P.; Kao, Y.P.; Yu, R.F. A novel method for on-line evaluation of floc size in coagulation process. Water Res. 2008, 42, 2691–2697. [Google Scholar] [CrossRef] [PubMed]
- Cheng, W.P.; Chang, J.N.; Chen, P.H.; Yu, R.F.; Huang, Y.W. Turbidity fluctuation as a measure of floc size in a coagulation pilot study. Desalination Water Treat. 2011, 30, 98–104. [Google Scholar] [CrossRef]
- Cheng, W.P.; Chen, P.H.; Yu, R.F.; Chang, J.N. Assessing Coagulant Dosage in Full-Scale Drinking Water Treatment Plants Using Nephelometry. Environ. Eng. Sci. 2012, 29, 212–217. [Google Scholar] [CrossRef]
- Sangu, Y.; Yokoi, H.; Tadokoro, H.; Tachi, T. Development of automatic coagulant dosage control technology for rapid changes of raw water quality parameters. Water Sci. Technol. Water Supply 2012, 12, 918–925. [Google Scholar] [CrossRef]
- Sangu, Y.; Yokoi, H.; Tadokoro, H.; Tachi, T. Verification of automatic coagulant dosage control technology based on aluminium concentration at a water treatment plant quality. Water Sci. Technol. Water Supply 2015, 15, 25–33. [Google Scholar] [CrossRef]
- Lin, J.; Huang, C.; Chin, C.; Pan, J. Coagulation dynamics of fractal flocs induced by enmeshment and electrostatic patch mechanisms. Water Res. 2008, 42, 4457–4466. [Google Scholar] [CrossRef] [PubMed]
- Xiao, F.; Huang, J.H.; Zhang, B.; Cui, C. Effects of low temperature on coagulation kinetics and floc surface morphology using alum. Desalination 2009, 237, 201–213. [Google Scholar] [CrossRef]
- Jin, Y. Use of a High Resolution Photographic Technique for Studying Coagulation/Flocculation in Water Treatment. Master’s Thesis, University of Saskatchewan, Saskatchewan, Canada, 3 June 2005. [Google Scholar]
- Yu, R.F.; Cheng, W.P.; Huang, H.D. On-line Assessment of the Particle Separation in Chemical Flocculant Suspension by Image Analysis. In Proceedings of the International Conference on Particle Separation, Berlin, Germany, 18–20 June 2012; pp. 53–57.
- Raspati, G.S.; Leiknes, T.O.; Meyn, T. Fractal Dimension Analysis of Flocs in In-line Coagulation-Microfiltration of Natural Organic Matter (NOM). Sep. Sci. Technol. 2013, 48, 2713–2723. [Google Scholar] [CrossRef]
- Jarvis, P.; Jefferson, B.; Gregory, J.; Parsons, S.A. A review of floc strength and breakage. Water Res. 2005, 39, 3121–3137. [Google Scholar] [CrossRef] [PubMed]
- Kurita Water Industries. Launch of a Water Treatment Management Service Using the Newly Developed Mobile Water Quality Analyzer, S.sensing MA. Available online: http://www.kurita.co.jp/english/aboutus/press140331.html (accessed on 10 September 2014).
- Sivchenko, N.; Kvaal, K.; Ratnaweera, H. Image analysis of flocs and mathematical modelling applied to coagulation-flocculation process. In Proceedings of the IWA Specialist Conference “Advances in Particle Science and Separation: From mm to nm Scale and Beyond”, Sapporo, Japan, 15–18 June 2014.
- Tse, I.C.; Swetland, K.; Weber-Shirk, M.L.; Lion, L.W. Method for quantitative analysis of flocculation performance. Water Res. 2011, 45, 3075–3084. [Google Scholar] [CrossRef] [PubMed]
- Blankert, B.; Betlem, B.H.L.; Roffel, B. Development of a control system for in-line coagulation in an ultrafiltration process. J. Membr. Sci. 2007, 301, 39–45. [Google Scholar] [CrossRef]
- Futselaar, H.; Blankert, B.; Spanjer, T.; Spenkelink, F. Ultrafiltration used as pre-treatment for SWRO desalination: Dynamic coagulant control under extreme conditions. Desalination Water Treat. 2013, 51, 407–415. [Google Scholar] [CrossRef]
- Wei, L.; Ratnaweera, H.; Heping, S. Better treatment efficiencies and process economics with real-time coagulant dosing control. In Proceedings of the Instrumentation, Control and Automation ICA 2013 Conference, Narbonne, France, 18–20 September 2013.
- Manamperuma, L.; Ratnaweera, H.; Rathnaweera, S. Retrofitting coagulant dosing control using real-time water quality measurements to reduce coagulant consumption. In Proceedings of the Instrumentation, Control and Automation Conference (ICA) 2013, Narbonne, France, 18–20 September 2013.
- Storhaug, R. Methods for Improving Chemical Phosphorus Removal in Municipal Wastewater Treatment Plants; Report No. 166; Norwegian Water BA: Hamar, Norway, 2009. (In Norwegian) [Google Scholar]
- Tik, S.; Vanrolleghem, P.A. Modelling and control of a full-scale chemically enhanced primary treatment. In Proceedings of the International Conference on Particle Separation, Berlin, Germany, 18–20 June 2012; Jekel, M., Ed.; pp. 329–330.
- AlGhazzawi, A.; Lennox, B. Model predictive control monitoring using multivariate statistics. J. Process Control 2009, 19, 314–327. [Google Scholar] [CrossRef]
- Franceschi, M.; Girou, A.; Carro-Diaz, A.M.; Maurette, M.T.; Puech-Costes, E. Optimisation of the coagulation-flocculation process of raw water by optimal design method. Water Res. 2002, 36, 3561–3572. [Google Scholar] [CrossRef]
- Trinh, T.K.; Kang, L.S. Response surface methodological approach to optimize the coagulation-flocculation process in drinking water treatment. Chem. Eng. Res. Des. 2011, 89, 1126–1135. [Google Scholar] [CrossRef]
- Juntunen, P.; liukkonen, M.; Pelu, M.; Lehtola, M.; Hiltunen, Y. Modelling of Water Quality: An Application to a Water Treatment Process. Appl. Comput. Intell. Soft Comput. 2012. [Google Scholar] [CrossRef]
- Juntunen, P.; Liukkonen, M.; Lehtola, M.; Hiltunen, Y. Dynamic soft sensors for detecting factors affecting turbidity in drinking water. J. Hydroinf. 2013, 15, 416–426. [Google Scholar] [CrossRef]
- Ratnaweera, H.; Lu, L.; Lindholm, O. Simulation Program for Wastewater Coagulation. In Chemical Water and Wastewater Treatment VII; Hahn, H.H., Hoffmann, E., Ødegaard, H., Eds.; IWA Publishing: London, UK, 2002; pp. 253–260. [Google Scholar]
- Ratnaweera, H.; Smozcynski, L.; Lewandowski, A.; Bielecka, M. Efficient Coagulant Dosing Control in Wastewater Treatment. Pol. Acad. Sci. 2005, 505, 347–352. [Google Scholar]
- Annadurai, G.; Sung, S.S.; Lee, D.J. Simultaneous removal of turbidity and humic acid from high turbidity stormwater. Adv. Environ. Res. 2004, 8, 713–725. [Google Scholar] [CrossRef]
- Ghafari, S.; Abdul Aziz, H.; Isa, M.H.; Zinatizadeh, A. Application of response surface methodology (RSM) to optimize coagulation-flocculation treatment of leachate using poly-aluminium chloride (PAC) and alum. J. Hazard. Mater. 2009, 163, 650–656. [Google Scholar] [CrossRef] [PubMed]
- Adlan, M.N.; Palaniandy, P.; Aziz, H.A. Optimization of coagulation and dissolved air flotation (DAF) treatment of semi-aerobic landfill leachate using response surface methodology (RSM). Desalination 2011, 277, 74–82. [Google Scholar] [CrossRef]
- Guida, M.; Mattei, M.; Della Rocca, C.; Melluso, G.; Meric, S. Optimization of alum-coagulation/flocculation for COD and TSS removal from five municipal wastewater. Desalination 2007, 211, 113–127. [Google Scholar] [CrossRef]
- Paliwal, M.; Kumar, U.A. Neural networks and statistical techniques: A review of applications. Expert Syst. Appl. 2009, 36, 2–17. [Google Scholar] [CrossRef]
- Ráduly, B.; Gernaey, K.V.; Capodaglio, A.G.; Mikkelsen, P.S.; Henze, M. Artificial neural networks for rapid WWTP performance evaluation: Methodology and case study. Environ. Modell. Softw. 2007, 22, 1208–1216. [Google Scholar] [CrossRef]
- Zhang, Q.; Staney, S.J. Real-Time Water Treatment Process Control with Artificial Neural Network. J. Environ. Eng. 1999, 125, 153–159. [Google Scholar] [CrossRef]
- Baxter, C.W.; Stanley, S.J.; Zhang, Q. Development of a full-scale artificial neural network for the removal of natural organic matter by enhanced coagulation. Aqua 1999, 48, 129–136. [Google Scholar] [CrossRef]
- Baxter, C.W.; Shariff, R.; Stanley, S.J.; Smith, D.W.; Zhang, Q.; Saumer, E.D. Model-based advanced process control of coagulation. Water Sci. Technol. 2002, 45, 9–17. [Google Scholar] [PubMed]
- Valentin, N.; Denoeux, T. A neural network-based software sensor for coagulation control in a water treatment plant. Intell. Data Anal. 2001, 5, 23–39. [Google Scholar]
- Bloch, G.; Denoeux, T. Neural networks for process control and optimization: Two industrial applications. ISA Trans. 2003, 42, 39–51. [Google Scholar] [CrossRef]
- Yu, R.F.; Kang, S.F.; Liaw, S.L.; Chen, M.C. Application of artificial neural network to control the coagulant dosing in water treatment plant. Water Sci. Technol. 2000, 42, 403–408. [Google Scholar]
- Joo, D.S.; Choi, D.J.; Park, H. The Effects of Data Preprocessing in the Determination of Coagulant Dosing Rate. Water Res. 2000, 34, 3295–3302. [Google Scholar] [CrossRef]
- Maier, H.R.; Morgan, N.; Chow, C. Use of artificial neural networks for predicting optimal alum doses and treated water quality parameters. Environ. Modell. Softw. 2004, 19, 1189–1195. [Google Scholar] [CrossRef]
- Zhang, H.; Luo, D. Application of an expert system using neural network to control the coagulant dosing in water treatment plant. J. Control Theory Appl. 2004, 2, 89–92. [Google Scholar] [CrossRef]
- Lamrini, B.; Benhammou, A.; Le Lann, M.V.; Karama, A. A neural software sensor for online prediction of coagulant dosage in a drinking water treatment plant. Transact. Inst. Meas. Control 2005, 27, 195–213. [Google Scholar] [CrossRef]
- Hernandez, H.; Le Lann, M.V. Development of a Neural Sensor for On-line Predictions of Coagulant Dosage in a Potable Water Treatment Plant in the Way of its Diagnosis. In Advances in Artificial Intelligence, IBERAMA-SBIA; Springer-Verlag: Berlin, Germany, 2006; pp. 249–257. [Google Scholar]
- Wu, G.D.; Lo, S.L. Predicting real-time coagulant dosage in water treatment by artificial neural networks and adaptive network-based fuzzy inference system. Eng. Appl. Artif. Intell. 2008, 21, 1189–1195. [Google Scholar] [CrossRef]
- Wu, G.D.; Lo, S.L. Effects of data normalization and inherent-factor on decision of optimal coagulant dosage in water treatment by artificial neural network. Expert Syst. Appl. 2010, 37, 4974–4983. [Google Scholar] [CrossRef]
- Kriti, S.; Smita, J. Artificial Neural Network Modelling of Shyamala Water Works, Bhopal MP, India. Res. J. Recent Sci. 2013, 2, 26–28. [Google Scholar]
- Kumar, J.S.; Poongodi, P.; Balakumaran, P. Artificial Intelligence Based Alum Dosage Control in Water Treatment Plant. Int. J. Eng. Technol. 2013, 5, 3344–3350. [Google Scholar]
- Dellana, S.A.; West, D. Predictive modelling for wastewater applications: Linear and nonlinear approaches. Environ. Modell. Softw. 2009, 24, 96–106. [Google Scholar] [CrossRef]
- Zheng, H.; Zhu, G.; Jiang, S.; Tshukudu, T.; Xiang, X.; Zhang, P.; He, Q. Investigations of coagulation-flocculation process by performance optimization, model prediction and fractal structure of flocs. Desalination 2011, 269, 148–156. [Google Scholar] [CrossRef]
- Liu, J.C.; Wu, M.D. Fuzzy control of coagulation reaction through streaming current monitoring. Water Sci. Technol. 1997, 36, 127–134. [Google Scholar] [CrossRef]
- Ratnaweera, H.; Anderssen, E.; Seim, F.; Njål, E.; Nilsen, N.K. Fuzzy Control in Water Supply- Pilot Project; NIVA Report OR-3849; Norwegian Institute for Water Research: Oslo, Norway, 1998; p. 38. [Google Scholar]
- Chen, C.L.; Hou, P.L. Fuzzy model identification and control system design for coagulation chemical dosing of potable water. Water Sci. Technol. Water Supply 2006, 6, 97–104. [Google Scholar] [CrossRef]
- Heddam, S.; Bermad, A.; Dechemi, N. ANFIS-based modelling for coagulant dosage in drinking water treatment plant: A case study. Environ. Monit. Assess. 2012, 184, 1953–1971. [Google Scholar] [CrossRef] [PubMed]
- Wan, J.Q.; Huang, M.Z.; Ma, Y.W.; Guo, W.J.; Wang, Y.; Zhang, H.P. Control of the Coagulation Process in a Paper-mill Wastewater Treatment Process Using a Fuzzy Neural Network. Chem. Biochem. Eng. Q. 2010, 24, 425–435. [Google Scholar]
- Kramer, L.; Horger, J. Streaming Current Monitor Used to Optimize Coagulant Dosages. WaterWorld 2001, 17, 10–14. [Google Scholar]
- Boruszenko, P.; Haley, J.; Thompson, K.C. On-line Analysis—A Water Company Perspective. Available online: http://www.rsc.org/images/JohnHaleyYWS5thNovCambridge_tcm18-143639.pdf (accessed on 16 November 2015).
- Naidoo, P.; van der Walt, J.J. Artificial Neural Networks as a Chemical Dosing Budgeting Tool. Available online: http://www.ewisa.co.za/literature/files/ID107%20Paper102%20van%20der%20walt%20M.pdf (accessed on 16 November 2015).
- Cooperative Research Centre (CRC) for Water Quality and Treatment. Natural Organic Matter—Understanding and Controlling the Impact on Water Quality and Water Treatment Processes. Available online: http://www.waterra.com.au/publications/document-search/ (accessed on 16 November 2015).
- Schlegel, S. Coagulant demand of large wastewater treatment plants with dosage control. Korresp. Abwasser 2009, 50, 1442–1446. (In German) [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ratnaweera, H.; Fettig, J. State of the Art of Online Monitoring and Control of the Coagulation Process. Water 2015, 7, 6574-6597. https://doi.org/10.3390/w7116574
Ratnaweera H, Fettig J. State of the Art of Online Monitoring and Control of the Coagulation Process. Water. 2015; 7(11):6574-6597. https://doi.org/10.3390/w7116574
Chicago/Turabian StyleRatnaweera, Harsha, and Joachim Fettig. 2015. "State of the Art of Online Monitoring and Control of the Coagulation Process" Water 7, no. 11: 6574-6597. https://doi.org/10.3390/w7116574
APA StyleRatnaweera, H., & Fettig, J. (2015). State of the Art of Online Monitoring and Control of the Coagulation Process. Water, 7(11), 6574-6597. https://doi.org/10.3390/w7116574