Empirical Formulas for Calculation of Negative Pressure Difference in Vacuum Pipelines
Abstract
:1. Introduction
- The working effectiveness (including energy consuming) of the vacuum pipelines depends mainly on the ratio of the volume of introduced air to the volume of sewage (f), and to a lesser degree on the pipeline diameter and its configuration. The highest effectiveness was shown by the systems with relatively low ratio of f.
- Whirls in emptying wells can cause a 40% reduction of the velocity of sewage flow in pipelines. To avoid this, the well outlet should be placed in the sidewall of the well, not in the bottom.
- The required difference of pressures (negative pressure in the vacuum tank) should take into consideration the total height of elevation, not only the difference between elevations of the beginning and end of the pipeline (net height).
- Coefficients of linear resistance of two-phase mixtures flowing in vacuum pipelines cannot be determined from dependences for one-phase flows, though the latter can be a rough approximation of the former—the nearer to zero the phase volume ratio f is, the better.
- in steady conditions without air sucking, i.e., during the tests the emptying valve was open all the time and the vacuum pipeline continuously sucked only water with a set flow rate;
- in steady conditions with air sucking, i.e., during the tests the emptying valve was open all the time and the vacuum pipeline continuously sucked water and air with a set flow rates;
- in unsteady conditions, i.e., during the tests the emptying valve was opened in random way (the opening time was set) and the vacuum pipeline sucked water first and then air.
- in steady conditions, without air suction, the following occur: bubbly flow, slug air flow, stratified air flow, annular flow, wave flow, air flow, slug flow, intermittent flow (projective);
- in steady conditions, with air suction, the following occur: projective flow, bubbly flow, slug flow, foam flow, wave flow, stratified flow, annular flow;
- in unsteady conditions, the following occur: foam flow, bubbly flow, projective flow (intermittent), slug air flow, stratified air flow, wave flow.
2. Methodology of Derivation of Structural Equation
- Δpvr—difference of negative pressure along the vacuum pipeline length, kg·m−1·s−2;
- pvzp—negative pressure in the vacuum container, kg·m−1·s−2;
- d—vacuum pipeline internal diameter, m;
- L—vacuum pipeline length, m;
- Qw—water flow rate, m3·s−1;
- Qp—air flow rate, m3·s−1;
- ρw—water density, kg·m−3;
- ρp—air density, kg·m−3;
- μw—water dynamic viscosity, kg·m−1·s−1;
- μp—air dynamic viscosity, kg·m−1·s−1;
- g—gravitational acceleration, m·s−2;
- k—absolute roughness coefficient, m.
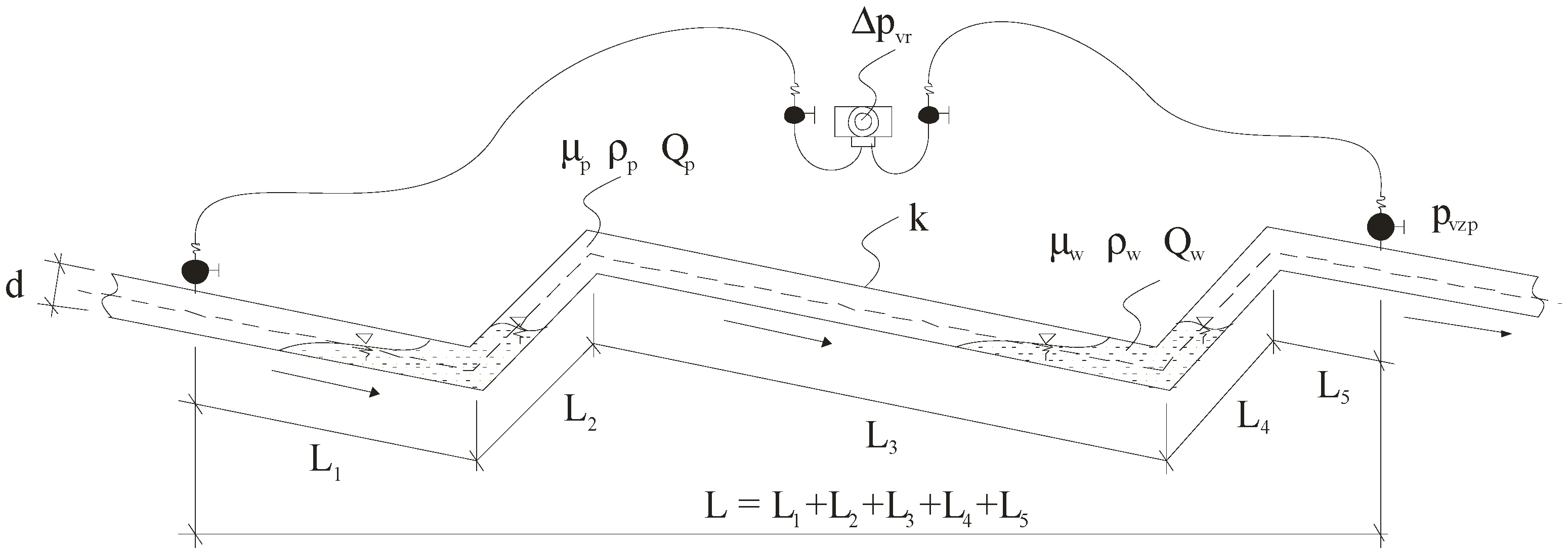
- ρw, μw—determine the physical properties of water,
- ρp, μp—determine the physical properties of air;
- d, k, L—characterize the object of the investigations, i.e., the vacuum pipelines—these quantities are constant;
- pvzp, Qw, Qp—determine so-called input parameters, enabling the intentional action on the object of the investigations—these quantities are controllable and under control;
- Δpvr—determines so-called output parameter—it is the response of the object of the investigations to the input parameters.
- π1—determines the quotient of the forces evoked by the negative pressure difference to the friction forces;
- π2 and π3—determines the quotient of the forces evoked by the negative pressure to the dynamic forces;
- π4—determines the quotient of the air friction (viscosity) forces to the water friction (viscosity) forces;
- π5—determines the quotient of the air flow to the water flow;
- π6—determines the quotient of the gravity forces to the dynamic forces evoked by the water flow;
- π7—determines the relative roughness of the internal surface of the pipeline.
3. Experimental Procedures
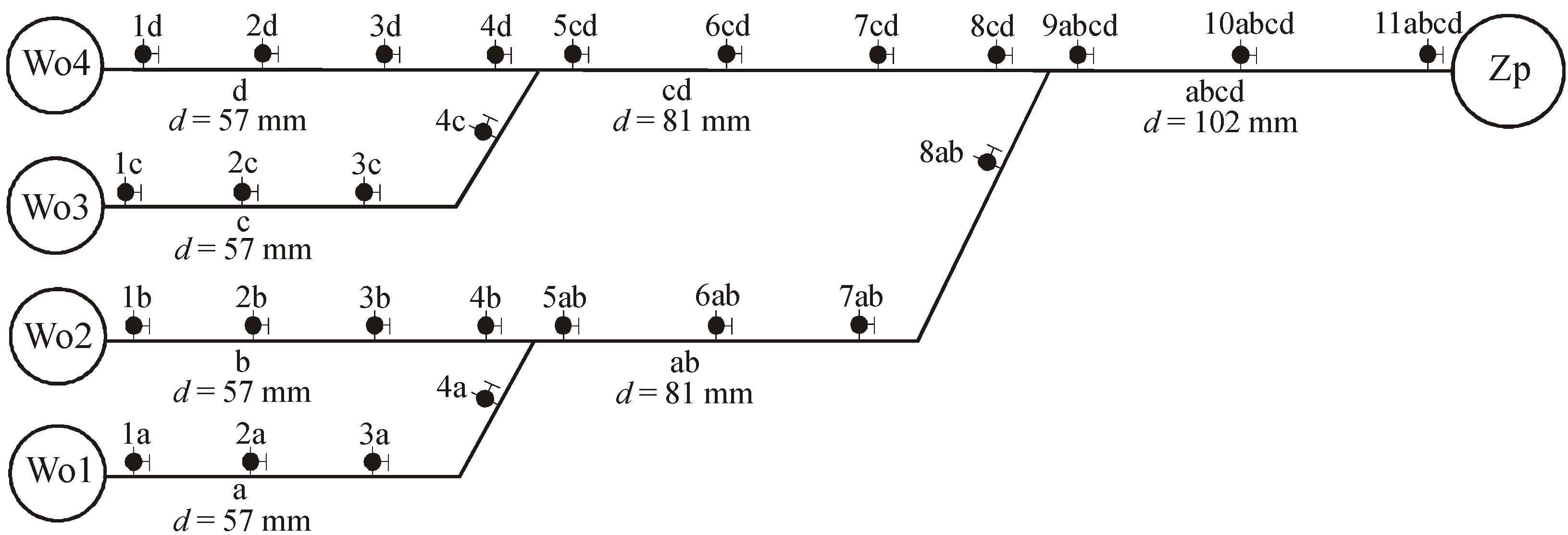
3.1. Description of Experimental Installation of Vacuum Sewage System
- for an internal diameter of 57 mm–96 m;
- for an internal diameter of 81 mm–44 m;
- for an internal diameter of 102 mm–42 m.
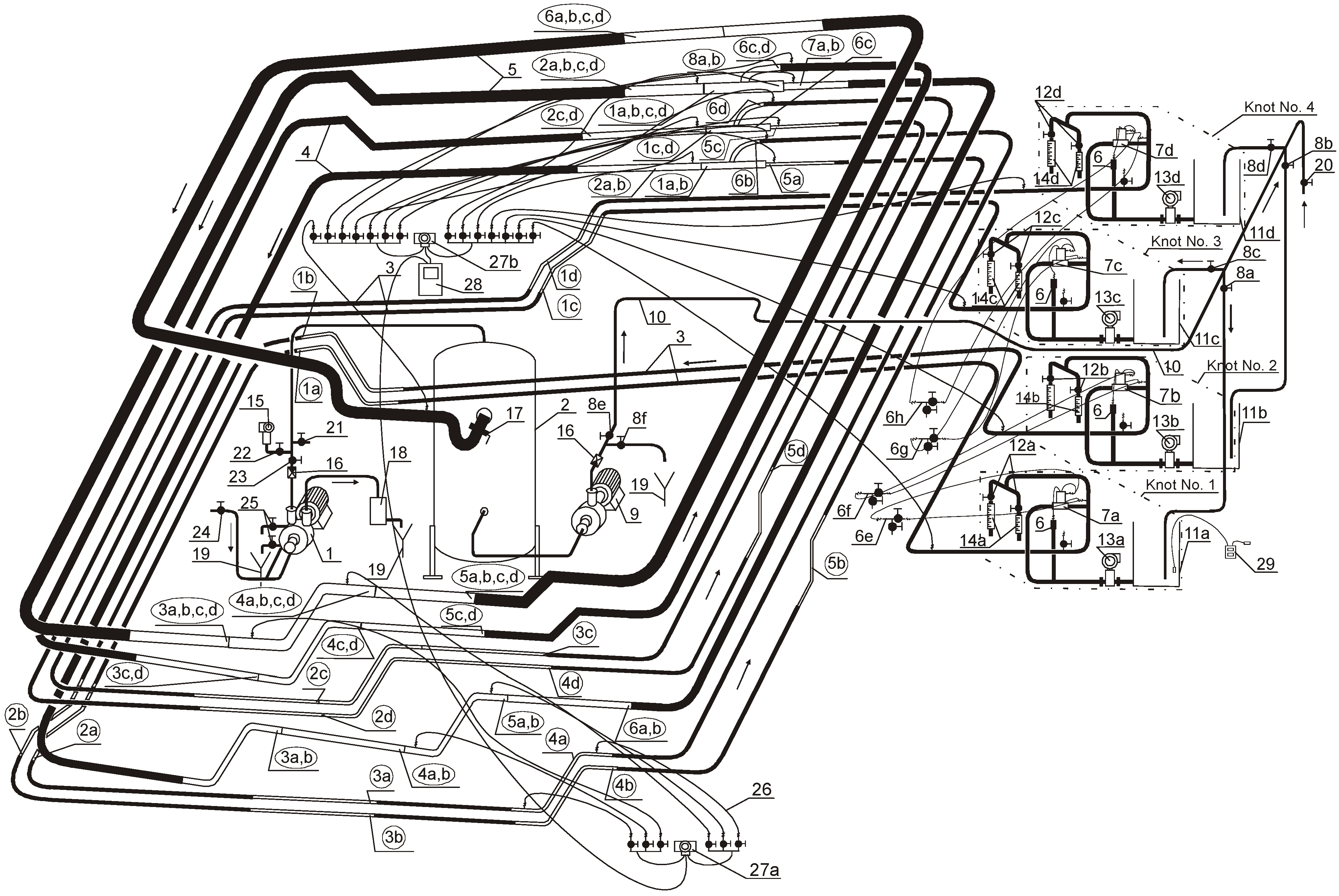
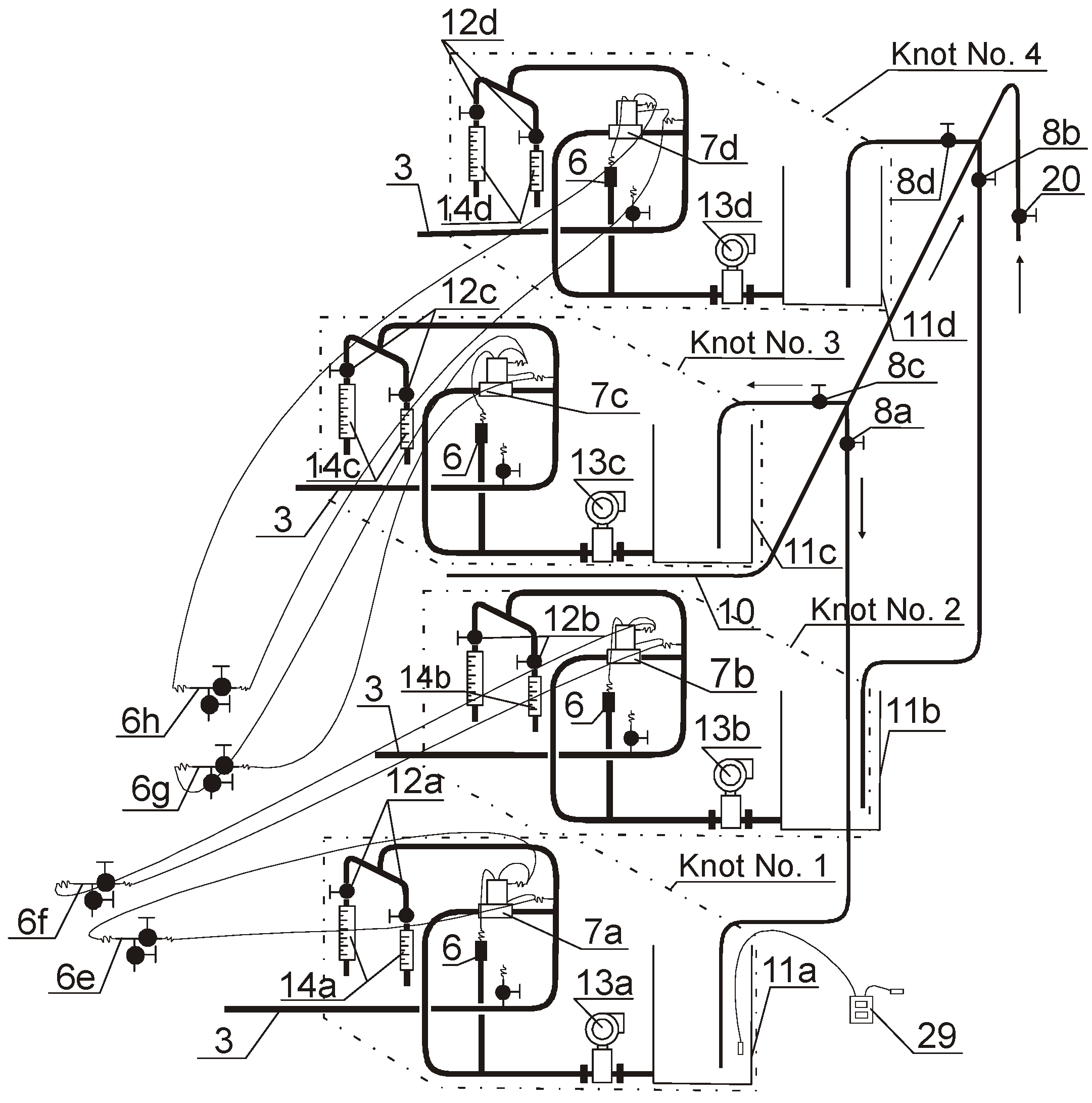
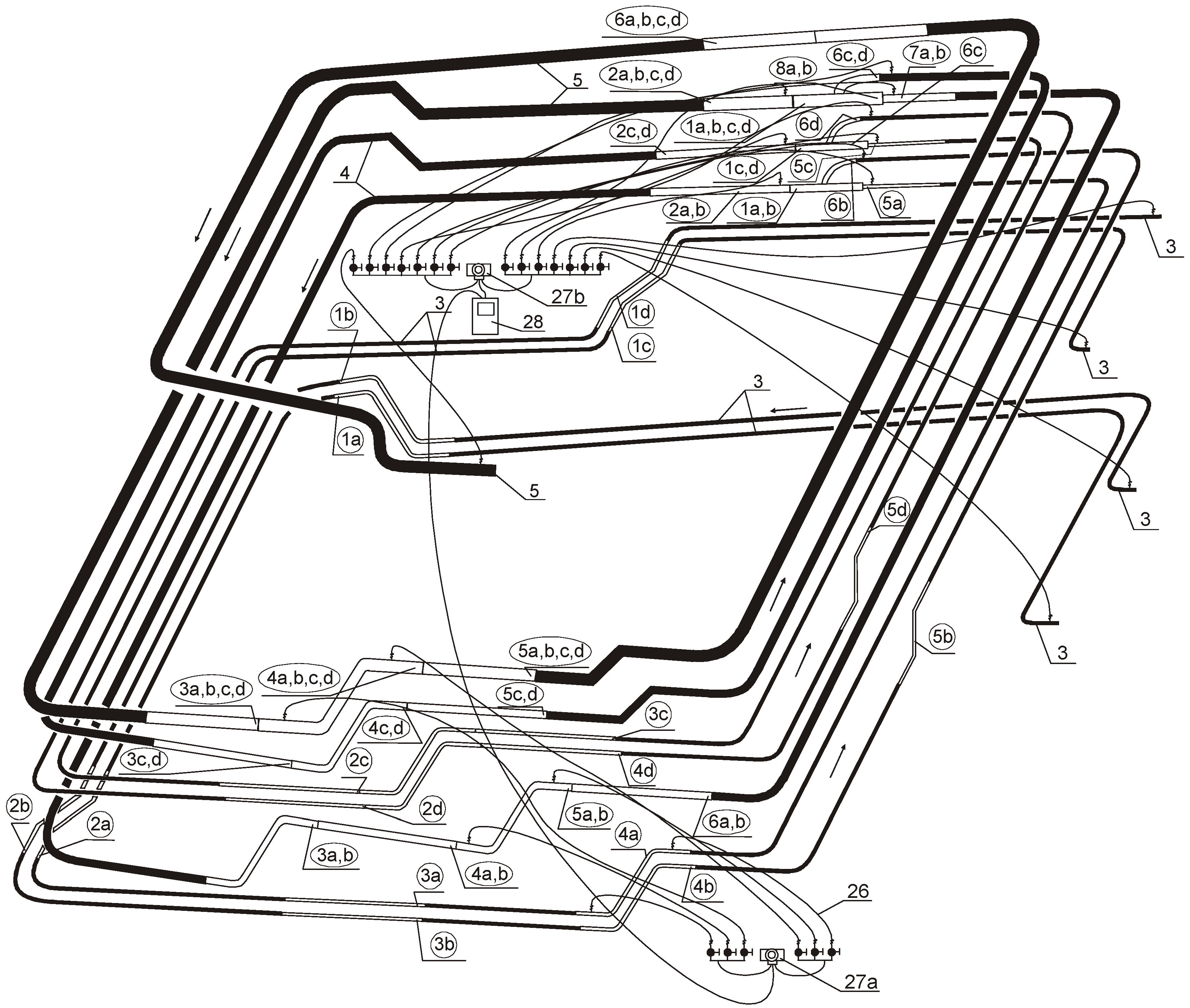
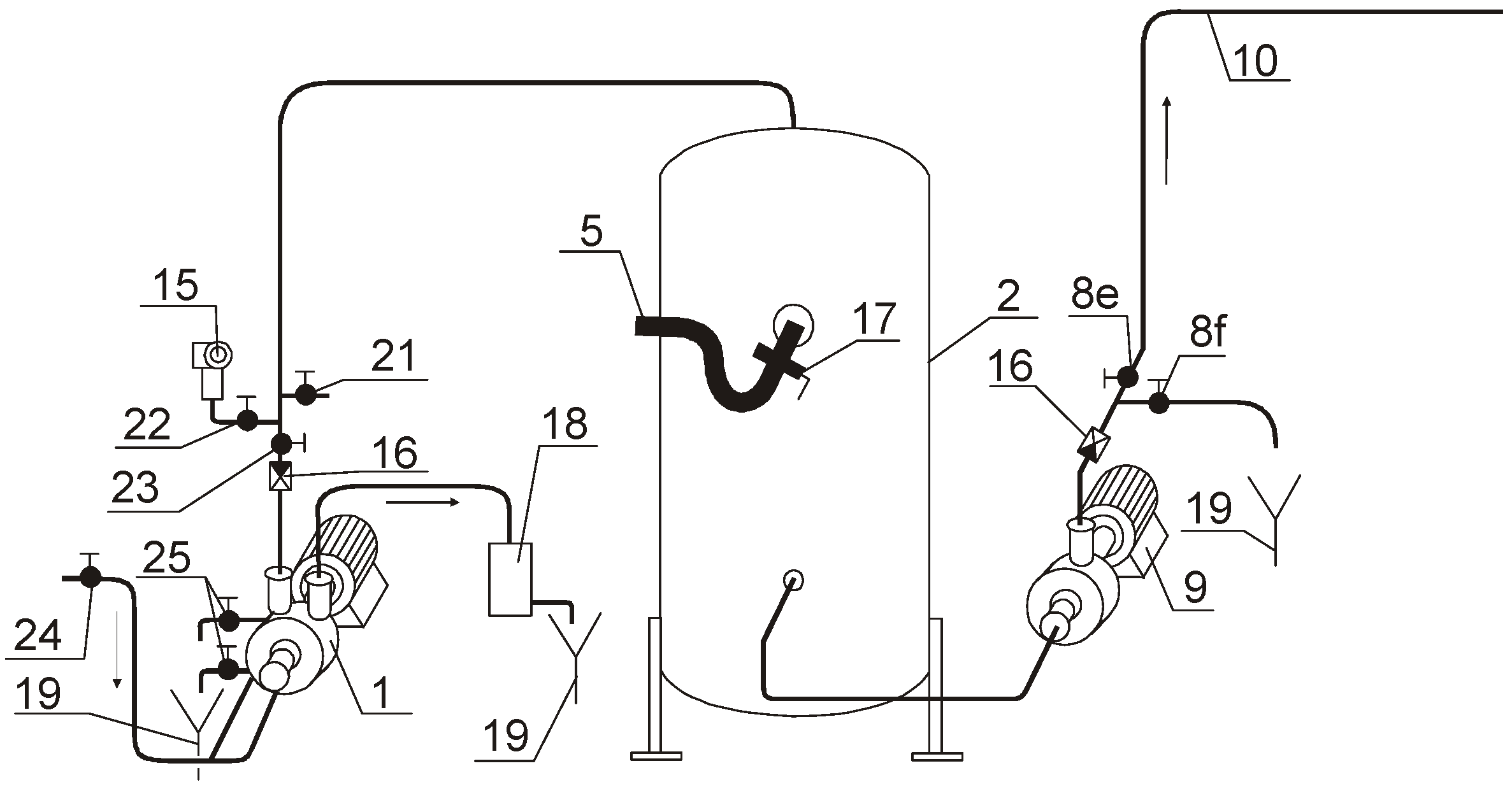
3.2. Methodology of Measurements
4. Results and Discussion
- Δpvr—negative pressure difference in pipeline, Pa;
- pvzp—negative pressure in vacuum container, kg·m−1·s−2;
- d—pipeline internal diameter, m;
- L—pipeline length, m;
- Qw—water flow rate, m3·s−1;
- Qp—air flow rate, m3·s−1;
- ρw—water density, kg·m−3;
- ρp—air density, kg·m−3;
- μw—water dynamic viscosity, kg·m−1·s−1;
- μp—air dynamic viscosity, kg·m−1·s−1;
- g—gravitational acceleration, m·s−2;
- k—absolute roughness coefficient, m.
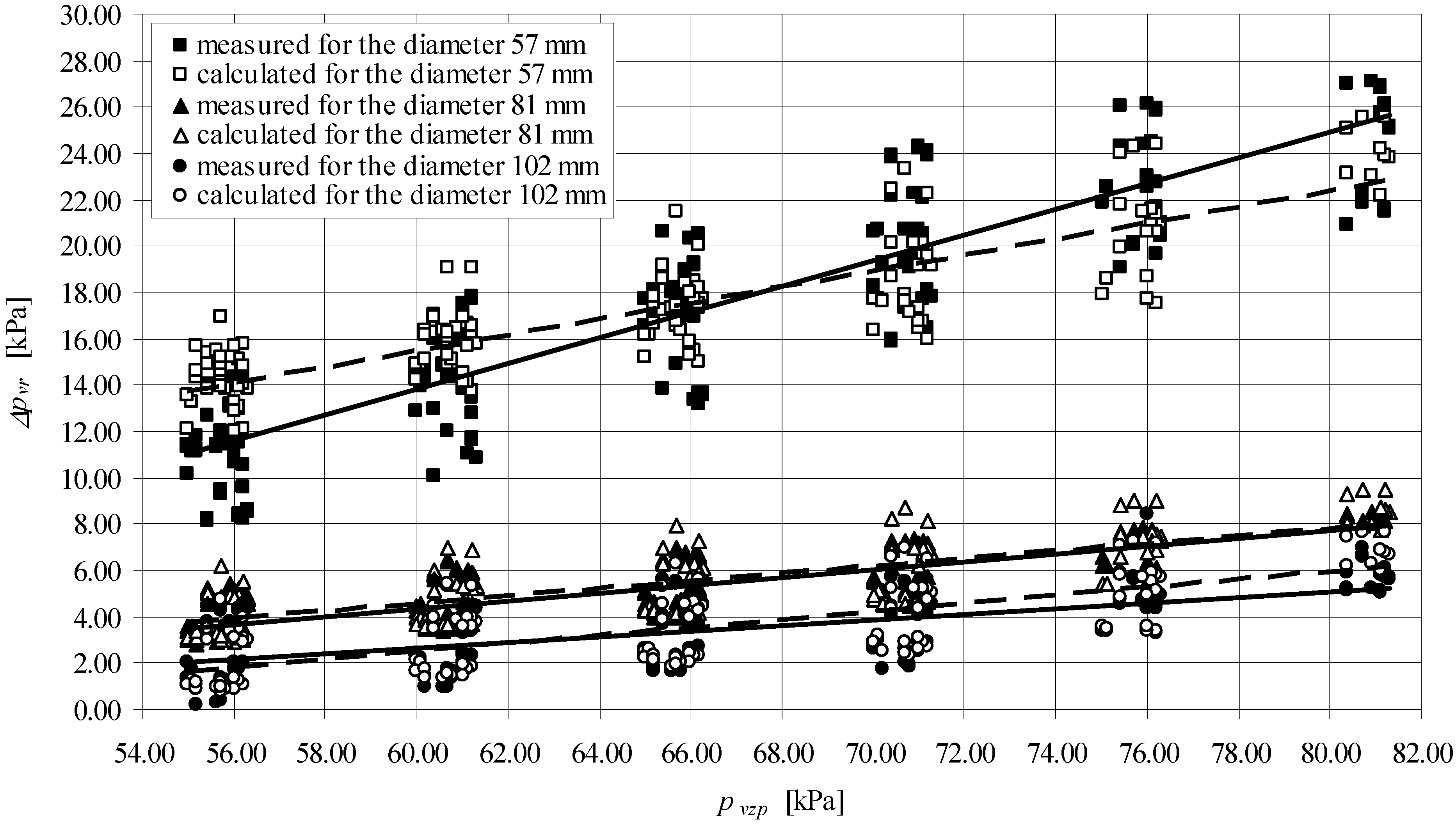
- d = 0.057 m; d = 0.081 m; d = 0.102 m;
- 55 kPa < pvzp < 81 kPa;
- 4.80 m3·h−1 < Qw < 15.40 m3·h−1;
- 4.00 m3·h−1 < Qp < 40.00 m3·h−1;
- 1.2046 kg·m−3 < ρp < 1.2154 kg·m−3;
- 998.2478 kg·m−3 < ρw < 998.5148 kg·m−3;
- 1.0113·10−3 kg·m−1·s−1 < μw < 1.0788·10−3 kg·m−1·s−1;
- 1.7970·10−5 kg·m−1·s−1 < μp < 1.8150·10−5 kg·m−1·s−1;
5. Conclusions
Acknowledgments
Conflicts of Interest
References
- Worksheet A 116, Part 1, Vacuum Drainage Outside of Buildings; ATV-DVWK Rules and Standards; Deutsche Vereinigung fur Wasserwirtschaft, Abwasser und Abfal e.V.: Hennef, Germany, 2004.
- Vacuum Sewage Systems Outside Buildings; PN-EN 1091; Polski Komitet Normalizacyjny: Warsaw, Poland, 2002. (In Polish)
- Dolecki, J. Analysis of economical effectiveness of vacuum sewage systems. Ochr. Środo. 1984, 3–4, 78–81. (In Polish) [Google Scholar]
- Alternative Wastewater Collection Systems; Manual, EPE/625/1-91/024; United States Environmental Protection Agency: Washington, DC, USA, 1991.
- Grabarczyk, C.; Kanclerz, A. Analysis and mathematical description of operating conditions of vacuum-force pumping station of vacuum sewage system. Zesz. Probl. Postęp. Nauk Rol. 1998, 458, 45–55. (In Polish) [Google Scholar]
- Kalenik, M. Hydraulic operating conditions of vacuum sewage system. Gaz Woda i Tech. Sanit. 2004, 4, 125–130. (In Polish) [Google Scholar]
- Kalenik, M.; Ćwiek, A. Investigations of the vacuum sewage net under exploitation in AIRVAC system. Gaz Woda i Tech. Sanit. 2005, 3, 26–30. (In Polish) [Google Scholar]
- Kalenik, M. Methods of dimensioning of vacuum sewage systems. Inżynieria Ekologiczna 2001, 5, 82–90. (In Polish) [Google Scholar]
- Kalenik, M. Experimental investigations of hydraulic resistance on lifts in pipelines of a vacuum sewage system. Environ. Prot. Eng. 2008, 34, 59–73. [Google Scholar]
- Kalenik, M. Experimental investigations of interface valve flow capacity in the RoeVac type vacuum sewage system. Environ. Prot. Eng. 2014, 40, 127–138. [Google Scholar]
- Kalenik, M. Non-Conventional Sewage Systems; Wyd. SGGW: Warsaw, Poland, 2011. (In Polish) [Google Scholar]
- Taitel, Y.; Dukler, A.E. A Model for Predicting Flow Regime Transitions in Horizontal and Near Horizontal Gas—Liquid Flow. Am. Inst. Chem. Eng. J. 1976, 22, 47–55. [Google Scholar] [CrossRef]
- Mamajew, W.A.; Odiszarija, G.E.; Kłanczuk, W.O.; Toczein, A.A.; Semenow, N.I. Flows of Gaseous Mixtures in Pipelines; Nedra: Moscow, Russia, 1978. (In Russian) [Google Scholar]
- Troniewski, L.; Ulbrich, R. Determination of a type of two-phase gas-liquid flow. Inż. i Aparat. Chem. 1987, 13, 13–16. (In Polish) [Google Scholar]
- Orzechowski, Z. Two-Phase Flows; PWN: Warsaw, Poland, 1990. (In Polish) [Google Scholar]
- Uollik, G. One-Dimensional Two-Phase Flows; Izd. Mir: Moscow, Russia, 1986. (In Russian) [Google Scholar]
- Tchiskholm, D. Two-Phase Flows in Pipelines and Heat Exchangers; Nedra: Moscow, Russia, 1986. (In Russian) [Google Scholar]
- Cazarez-Candia, O.; Benitez-Centeno, O.C.; Espinosa-Paredes, G. Two-fluid model for transient analysis of slug flow in oil wells. Int. J. Heat Fluid Flow 2011, 32, 762–770. [Google Scholar] [CrossRef]
- Maron, W.I. Hydraulics of Two-Phase Flow in Pipelines; Łan. Saint-Petersburg: Moscow, Russia; Krasnodar, Russia, 2012. (In Russian) [Google Scholar]
- Ratkovicha, N.; Majumderb, S.K.; Bentzena, T.R. Empirical correlations and CFD simulations of vertical two-phase gas-liquid (Newtonian and non-Newtonian) slug flow compared against experimental data of void fraction. Chem. Eng. Res. Design 2012. Available online: http://dx.doi.org/10.1016/j.cherd.2012.11.002 (accessed on 30 December 2014). [Google Scholar]
- Spedding, P.L.; Nguyen, V.T. Regime Maps for Air Water Two Phase Flow. Chem. Eng. Sci. 1980, 35, 779–793. [Google Scholar] [CrossRef]
- Weisman, J.; Duncan, D.; Gibson, J.; Crawford, T. Effects of fluid properties and pipe diameter on two-phase flow patterns in horizontal lines. Int. J. Multiph. Flow 1979, 5, 437–462. [Google Scholar] [CrossRef]
- Dukler, A.E.; Wicks, M., III; Cleveland, R.G. Frictional Pressure Drop in Two-Phase Flow: A. A Comparison of Existing Correlations For Pressure Loss and Holdup. Am. Inst. Chem. Eng. J. 1964, 10, 38–43. [Google Scholar] [CrossRef]
- Dukler, A.E.; Wicks, M., III; Cleveland, R.G. Frictional Pressure Drop in Two-Phase Flow: B. An Approach Through Similarity Analysis. Am. Inst. Chem. Eng. J. 1964, 10, 44–51. [Google Scholar] [CrossRef]
- Lockhart, R.W.; Martinelli, R.C. Proposed Correlation of Data for Isothermal Two-Phase, Two-Component Flow in Pipes. Chem. Eng. Prog. 1949, 45, 39–48. [Google Scholar]
- Dolecki, J. Principles of hydraulic calculations of conduits for sewage transport in gas-liquid mix system. Gaz Woda i Tech. Sanit. 1983, 9, 282–284. (In Polish) [Google Scholar]
- Dolecki, J. Principles of design and possibilities of application of vacuum sewage system. Ochr. Środo. 1986, 1–2, 61–64. (In Polish) [Google Scholar]
- Chenoweth, J.M.; Martin, M.W. Turbulent Two-Phase Flow. Petrol. Ref. 1955, 34, 151–155. [Google Scholar]
- Hughmark, G.A. Holdup in gas-liquid flow. Chem. Eng. Prog. 1962, 58, 62–65. [Google Scholar]
- Hughmark, G.A. Pressure Drop in Horizontal and Vertical Cocurrent Gas-Liquid Flow. Ind. Eng. Chem. Fundam. 1963, 2, 315–321. [Google Scholar] [CrossRef]
- Hughmark, G.A.; Pressburg, B.S. Holdup and Pressure Drop with Gas-Liquid Flow in a Vertical Pipe. Am. Inst. Chem. Eng. J. 1961, 7, 677–682. [Google Scholar] [CrossRef]
- Irikura, M.; Maekawa, M.; Hosokawa, S.; Tomiyama, A. Numerical simulation of slugging of stagnant liquid at a V-shaped elbow in a pipeline. Appl. Math. Model. 2014, 38, 4238–4248. [Google Scholar] [CrossRef]
- Skillman, E.P. Design Criteria for Vacuum Wastewater Transfer Systems in Advanced Base Applications; Civil Engineering Laboratory: Port Hueneme, CA, USA, 1979. [Google Scholar]
- Li, M.; Tang, Y.; Li, J.; Meng, P. A two-phase hydrodynamic model for transport pipelines in vacuum sewage systems. Appl. Mech. Mater. 2013, 275–277, 508–512. [Google Scholar]
- Dukler, A.E.; Hubbard, M.G. A Model for Gas—Liquid Slug Flow in Horizontal and Near Horizontal Tubes. Ind. Eng. Chem. Fundam. 1975, 14, 337–347. [Google Scholar] [CrossRef]
- Dolecki, J. Fundamentals of Design of Vacuum Sewage Systems and Evaluation of Their Economical Usefulness. Ph.D. Thesis, Faculty of Sanitary and Water Engineering, Warsaw Technical University, Warsaw, Poland, 1983. [Google Scholar]
- Grabarczyk, C.; Kalenik, M.; Kanclerz, A. Theoretical and Experimental Investigations of Hydraulic Operating Conditions of Vacuum Sewage Systems in Rural Settlements; Final Report on the Realization of the Research Project No. 5P06H06719; Scientific Research Committee Resources, Department of Civil Engineering of Warsaw University of Life Sciences: Warsaw, Poland, 2003. (In Polish) [Google Scholar]
- Kalenik, M. Experimental Researches of Hydraulic Flow Conditions in Collectors of Vacuum Sewage System; Final Report on the Realization of the Research Project of WULS No. 50405250012; Scientific Research Committee Resources, Department of Civil Engineering of Warsaw University of Life Sciences: Warsaw, Poland, 2005. (In Polish) [Google Scholar]
- Boulos, P.F.; Lansey, K.E.; Karney, B.W. Comprehensive Water Distribution Systems Analiysis Handbook for Engineers and Planners, 2nd ed.; MWH Soft, Inc. Publ.: Pasadena, CA, USA, 2006. [Google Scholar]
- Bergant, A.; Simpson, A.R.; Tijsseling, A.S. Water hammer with column separation: A historical review. J. Fluids Struct. 2006, 22, 135–171. [Google Scholar] [CrossRef]
- Collins, R.P.; Boxall, J.B.; Karney, B.W.; Brunone, B.; Meniconi, S. How severe can transients be after a sudden depressurization? J. Am. Water Works Assoc. AWWA 2012, 104, E243–E251. [Google Scholar] [CrossRef]
- De Cachard, F.; Delhaye, J.M. A slug-churn flow model for small-diameter airlift pumps. Int. J. Multiph. Flow 1996, 22, 627–649. [Google Scholar] [CrossRef]
- Fan, W.; Chen, J.; Pan, Y.; Huang, H.; Chen, C.-T.A.; Chen, Y. Experimental study on the performance of air-lift pump for artificial upwelling. Ocean Eng. 2013, 59, 47–57. [Google Scholar] [CrossRef]
- Hanafizadeh, P.; Ghanbarzadeh, S.; Saidi, M.H. Visual technique for detection of gas-liquid two-phase flow regime in the air lift pump. J. Pet. Sci. Eng. 2011, 75, 327–335. [Google Scholar] [CrossRef]
- Kassab, S.Z.; Kandil, H.A.; Warda, H.A.; Ahmed, W.H. Air-lift pumps characteristics under two-phase flow conditions. Int. J. Heat Fluid Flow 2009, 30, 88–98. [Google Scholar] [CrossRef]
- Kassab, S.Z.; Kandil, H.A.; Warda, H.A.; Ahmedb, W.H. Experimental and analytical investigations of airlift pumps operating in three-phase flow. Chem. Eng. J. 2007, 131, 273–281. [Google Scholar] [CrossRef]
- Kim, S.H.; Sohn, C.H.; Hwang, J.Y. Effects of tube diameter and submergence ratio on bubble pattern and performance of air-lift pump. Int. J. Multiph. Flow 2014, 58, 195–204. [Google Scholar] [CrossRef]
- Mahrous, A.-F. Performance of airlift pumps: Single-stage vs. multistage air injection. Am. J. Mech. Eng. 2014, 2, 28–33. [Google Scholar] [CrossRef]
- Mahrous, A.-F. Performance study of an air-lift pump with bent riser tube. Wseas Trans. Appl. Theor. Mech. 2013, 2, 136–145. [Google Scholar]
- Mahrous, A.-F. Numerical Study of Solid Particles-Based Airlift Pump Performance. Wseas Trans. Appl. Theor. Mech. 2012, 3, 221–230. [Google Scholar]
- Meng, Q.; Wang, C.; Chen, Y.; Chen, J. A simplified CFD model for air-lift artificial upwelling. Ocean Eng. 2013, 72, 267–276. [Google Scholar] [CrossRef]
- Yoshinaga, T.; Sato, Y. Performance of an air-lift pump for conveying coarse particles. Int. J. Multiph. Flow 1996, 22, 223–238. [Google Scholar] [CrossRef]
- Wahba, E.M.; Gadalla, M.A.; Abueidda, D.; Dalaq, A.; Hafiz, H.; Elawadi, K.; Issa, R. On the performance of air-lift pumps: From analytical models to large eddy simulation. J. Fluids Eng. 2014, 11, 111301:1–111301:7. [Google Scholar] [CrossRef]
- Esen, I.I. Experimental investigation of a rectangular air lift pump. Adv. Civil Eng. 2010. Article ID 789547. [Google Scholar] [CrossRef]
- Fujimoto, H.; Murakami, S.; Amura, A.; Takuda, H. Effect of local pipe bends on pump performance of a small air-lift system in transporting solid particles. Int. J. Heat Fluid Flow 2004, 25, 996–1005. [Google Scholar] [CrossRef]
- Mahrous, A.-F. Experimental study of airlift pump performance with s-shaped riser tube bend. Int. J. Eng. Manuf. 2013, 1, 1–12. [Google Scholar] [CrossRef]
- Nicklin, D.J. The air lift pump: Theory and optimization. Trans. Inst. Chem. Eng. 1963, 41, 29–39. [Google Scholar]
- Kalenik, M. Investigations of hydraulic operating conditions of air lift pump with three types of air-water mixers. Ann. Wars. Univ. Life Sci. SGGW Land Reclam. 2015, 47, 69–85. [Google Scholar] [CrossRef]
- Kasprzak, W.; Lysik, B. Dimensional Analysis in Experiment Planning; PWN: Wrocław, Poland; Warsaw, Poland; Cracow, Poland; Gdańsk, Poland, 1978. (In Polish) [Google Scholar]
- Kasprzak, W.; Lysik, B. Dimensional Analysis. Algorithmic Procedures of Experiment Service; WNT: Warsaw, Poland, 1988. (In Polish) [Google Scholar]
- Kasprzak, W.; Lysik, B. Problems of construction of mathematical model of process in experiment methodology. Stud. Filozof. 1976, 2, 109–120. (In Polish) [Google Scholar]
- Kasprzak, W.; Lysik, B.; Pomierski, R. Formal principles of construction of mathematical model and object identification. Arch. Autom. i Telemech. 1970, 15, 431–426. (In Polish) [Google Scholar]
- Kokar, M. Determination of mathematical model form with use of dimensional analysis. Inż. Chem. 1975, 1, 103–124. (In Polish) [Google Scholar]
- Kokar, M. Outline of procedure of formulation of physical laws in language of dimensional analysis. Inż. Chem. 1979, 9, 361–369. (In Polish) [Google Scholar]
- Kokar, M. Algorithmization of dimensional analysis. Inż. Chem. 1974, 2, 277–286. (In Polish) [Google Scholar]
- Mitosek, M. Fluid Mechanics in Environmental Engineering; Warsaw Technical University: Warsaw, Poland, 1999. (In Polish) [Google Scholar]
- Muller, L. Application of dimensional analysis in investigations of models; Polskie Wydawnictwo Naukowe: Warsaw, Poland, 1983. (In Polish) [Google Scholar]
- Orzechowski, Z.; Prywer, J.; Zarzycki, R. Problem Book of Fluid Mechanics in Environmental Engineering; WNT: Warsaw, Poland, 2001. (In Polish) [Google Scholar]
- Statistica 6, Computer Program; StatSoft Polska Sp. z o. o.: Cracow, Poland, 2006.
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kalenik, M. Empirical Formulas for Calculation of Negative Pressure Difference in Vacuum Pipelines. Water 2015, 7, 5284-5304. https://doi.org/10.3390/w7105284
Kalenik M. Empirical Formulas for Calculation of Negative Pressure Difference in Vacuum Pipelines. Water. 2015; 7(10):5284-5304. https://doi.org/10.3390/w7105284
Chicago/Turabian StyleKalenik, Marek. 2015. "Empirical Formulas for Calculation of Negative Pressure Difference in Vacuum Pipelines" Water 7, no. 10: 5284-5304. https://doi.org/10.3390/w7105284
APA StyleKalenik, M. (2015). Empirical Formulas for Calculation of Negative Pressure Difference in Vacuum Pipelines. Water, 7(10), 5284-5304. https://doi.org/10.3390/w7105284




