Empirical Modeling of Spatial 3D Flow Characteristics Using a Remote-Controlled ADCP System: Monitoring a Spring Flood

Abstract

The use of acoustic Doppler current profilers (ADCP) for measuring streamflow and discharge is becoming increasingly widespread. The spatial distribution of flow patterns is useful data in studying riverine habitats and geomorphology. Until now, most flow mapping has focused on measurements along a series of transects in a channel. Here, we set out to measure, model and analyze the 3D flow characteristics of a natural river over a continuous areal extent, quantifying flow velocity, 3D flow directions, volumes, water depth and their changes over time. We achieved multidimensional spatial flow measurements by deploying an ADCP on a remotely-controlled boat, combined with kinematic GNSS positioning and locally-monitored water level data. We processed this data into a 3D point cloud of accurately positioned individual 3D flow measurements that allows the visual analysis of flow velocities, directions and channel morphology in 3D space. We demonstrate how this allows monitoring changes of flow patterns with a time series of flow point clouds measured over the period of a spring flood in Finnish Lapland. Furthermore, interpolating the raw point cloud onto a 3D matrix allows us to quantify volumetric flow while reducing noise in the data. We can now quantify the volumes of water moving at certain velocities in a given reach and their location in 3D space, allowing, for instance, the monitoring of the high-velocity core and its changes over time.

1. Introduction

The flow characteristics of water in a river influence both the channel morphology and the riverine habitats, which are of great interest to fluvial scientists and engineers alike, for instance in the fields of hydro-power or other in-channel construction, as well as habitat restoration [1] or pollution dispersion [2]. These are complex dynamic processes that have thus far been challenging to map over a continuous spatial extent. The spatial distribution of flow patterns is useful knowledge in studying riverine habitats [3] and geomorphology [4], especially in meander bends, where the distribution of flow velocities is non-uniform, both in the down-stream and the cross-stream direction [5,6]. Flow field data of high spatial resolution will be beneficial for investigations of fluvial processes—especially in river channels with complex flow structures, such as meandering or braided channels, at confluences or diffluences or around engineered objects, such as dams or bridge pylons, to name but a few—as well as in calibrating and validating computational models over complex river reaches.

The use of acoustic Doppler current profilers (ADCP) for measuring streamflow [7] and discharge is becoming increasingly widespread [8]. The principles of the operation of ADCPs are described in great detail, for instance, in Muste et al. [9] and Gunawan et al. [10]. Briefly, ADCP measurements derive flow velocity from the Doppler shift of the measured return of an emitted acoustic signal that is reflected off suspended matter in the water column. The information from a combination of several (usually three or four) acoustic beams is used to calculate the mean velocity and flow direction, based on the assumption that the acoustic scatterers move at the same speed as the water and that flow is homogeneous over the area covered by the beams. These locally-averaged flow measurements are split vertically into cells (bins) that each represent a flow vector at a certain depth. When deployed from a moving vessel, a series of these velocity components measured perpendicular to the cross-section produces a transect of flow vectors across a stream, usually represented in the form of a raster, where each raster cell represents one flow vector. Generally, this series of measurements in a transect is used to calculate discharge. Several researchers have used a series of such transect measurements to analyze flow characteristics in natural streams [11,12].

Most flow mapping has focused on measurements along a series of transects in a channel measured using either an ADCP [13,14,15,16] or an acoustic Doppler velocimeter (ADV) [17,18,19,20]. Parsons et al. [15] developed a set of software tools that facilitates the analysis and visualization of such transect-based measurements, and they showcase several impressive examples where a series of transects is used to characterize the 3D flow of several river reaches. The transect-based approach gives insight into the flow field in 3D, along the transect and through the water column. This approach is, however, limited in providing information of the areal flow field over a river reach, leaving considerable gaps between the transects.

Another approach is to employ sampling trajectories that move beyond the classical transect arrangement towards a more spatial coverage, either surveying a dense pattern of transects intended for spatial interpolation [21] or employing a spatially irregular or continuous survey pattern [22,23,24,25], employing real-time kinematic GPS for accurate positioning of the flow measurements. This approach allows the investigation of the areal flow field by generating, for instance, depth-averaged flow maps along with bathymetry maps. However, the third dimension of flow variation in the water column is not represented in a 2D flow field map. Dinehart and Burau [22] interpolated ADCP-measured flow vectors onto a 3D grid in order to represent the flow field in three dimensions at the reach scale. Tsubaki et al. [26] also presented an interesting interpolation method for modeling the 3D flow distribution based on ADCP-measured data, dividing the flow data into depth layers, thereby creating an areal 3D flow field. However, a method for rapidly measuring and visualizing areal 3D flow field data and visualizing it in a virtual 3D environment for analysis has thus far not been presented.

The aim of this paper is to measure, model and analyze multitemporal 3D flow characteristics of a natural river over a continuous areal extent, quantifying flow velocity, 3D flow directions, volumes, water depth and their changes over time:

First, we present a measurement and empirical modeling method that combines areal ADCP flow data with highly accurate positional data to yield a 3D point cloud of measured flow properties. The new processing method presented makes it possible to represent the raw measured three-dimensional flow field at the reach scale in a virtual 3D environment.

Second, we demonstrate how this methodology can be used to capture river reaches at different scales and resolutions, from a several km-long reach at a coarse resolution, down to focusing on one meander bend at high resolution.

Third, we model and analyze the 3D flow field in a meander bend over a two-week time period of a snow-melt-induced flood event. We analyze the spatial distribution of the high-velocity core and its movement, as well as changes in vertical flow patterns and river bed topography over the time period of the flood event.

Finally, we use a 3D interpolation to transform the raw data onto a regular grid, which enables us to conduct a quantitative analysis of flow volumes and the volumetric distribution of different flow velocities in a given reach of a river.

The focus of this paper is on presenting the survey and empirical modeling methodology representing raw measured flow data as a 3D point cloud and to show how it can be applied to analyze 3D flow fields. A detailed geomorphological analysis will be the subject of a future publication and is therefore beyond the scope of this work.

2. Study Area

The field data for this study was collected from a 3.7-km reach of the Pulmanki River in Northern Lapland (69°56' N, 28°2' E). The Pulmanki River flows in a valley of glaciofluvial deposits surrounded by fell country. The river meanders northwards into Lake Pulmanki on the Finnish side and flows out of the lake on the Norwegian side to continue its flow towards the Tana River. Our study area is located immediately upstream of Lake Pulmanki. The study reach includes eight meanders.

We placed particular focus on one meander bend where we collected data at a higher spatial and temporal density than in the whole reach in order to be able to compare the utility of this methodology at different scales. The meander bend area of interest (AOI) is 220 m in length and is located 1 km upstream of Lake Pulmanki, with a thalweg distance of 1.8 km (Figure 1).

Figure 1. (A) Map locating the study area showing the Tana River watershed and the Pulmankijoki sub-watershed in grey, with the study reach marked in red; (B) Point cloud of raw measured flow data of the meander bend AOI (220 m) on 17 May 2013, visualized in CloudCompare, looking downstream. The coloring represents horizontal flow velocity (m/s).

Figure 1. (A) Map locating the study area showing the Tana River watershed and the Pulmankijoki sub-watershed in grey, with the study reach marked in red; (B) Point cloud of raw measured flow data of the meander bend AOI (220 m) on 17 May 2013, visualized in CloudCompare, looking downstream. The coloring represents horizontal flow velocity (m/s).

In our study area, the Pulmanki River is about 20–30 m wide during summer low flow, depending on the water level. The riverbed consists mostly of sandy sediments. These sediments accumulate as point bars on the inside of the meanders. Kasvi et al. [6] and Alho and Mäkinen [27] describe the geomorphology of this study site in great detail.

The typical discharges of the Pulmanki River vary between about 4 m³s⁻¹ during summer low flow and 70 m³s⁻¹ during the annual snow-melt-induced spring flood. The water level can be two to four meters higher during flood time than during summer low flow, depending on the size of the flood. Fieldwork for this study captured the rising stage of the spring flood during the latter half of May 2013.

3. Methods and Data

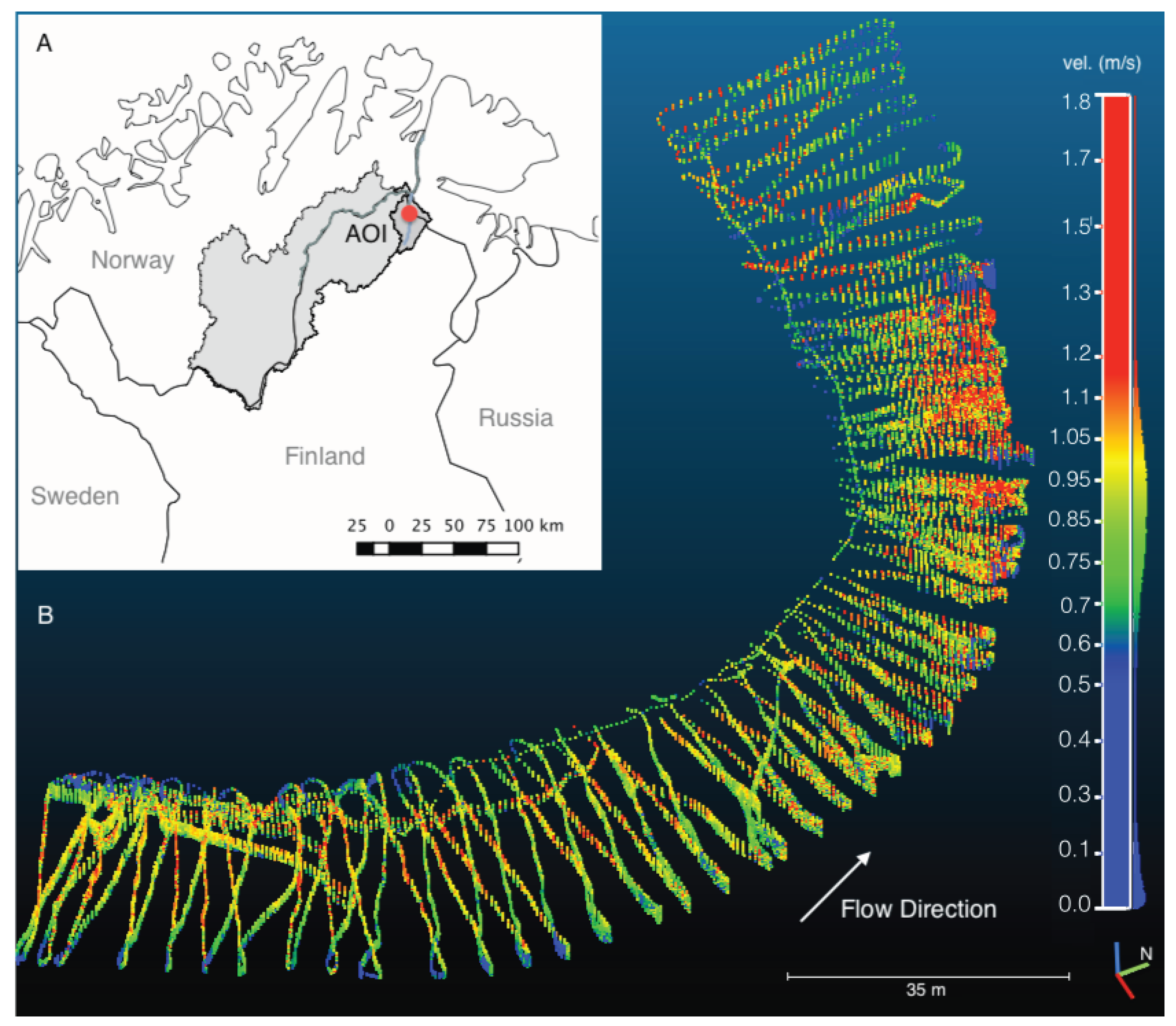
We set out to create a model of measured flow characteristics that is spatially accurate in 3D and contains flow velocities and 3D flow directions of a spatially continuous area as a time-integrated snapshot of the measurement period of about two hours.

The way we represent spatial flow data in 3D is as a LiDAR-like (light detection and ranging) point cloud [28] that contains flow parameters as scalar fields. Unlike a LiDAR point cloud, which generally aims to represent primarily the surface of a 3D object, the point clouds we create here contain data from the entire water column. Furthermore, unlike a LiDAR point cloud, this one is semi-systematic in its structure, that is the points are irregularly spaced, but they are vertically stacked, albeit at varying vertical spacing.

Creating multidimensional flow data point clouds involves a range of field methods and data post-processing. Figure 2 shows the main components of the set-up in the field and how the field measurements relate to the final data product. The process is described in detail below.

Figure 2. Diagram of the flow measurement set-up and concept. (A) The new spatial modeling of flow vectors as a 3D point cloud containing surface points, flow velocity and direction points in the water column and river bed elevation points; (B) This subfigure contrasts the more traditional method of representing flow as a series of transects.

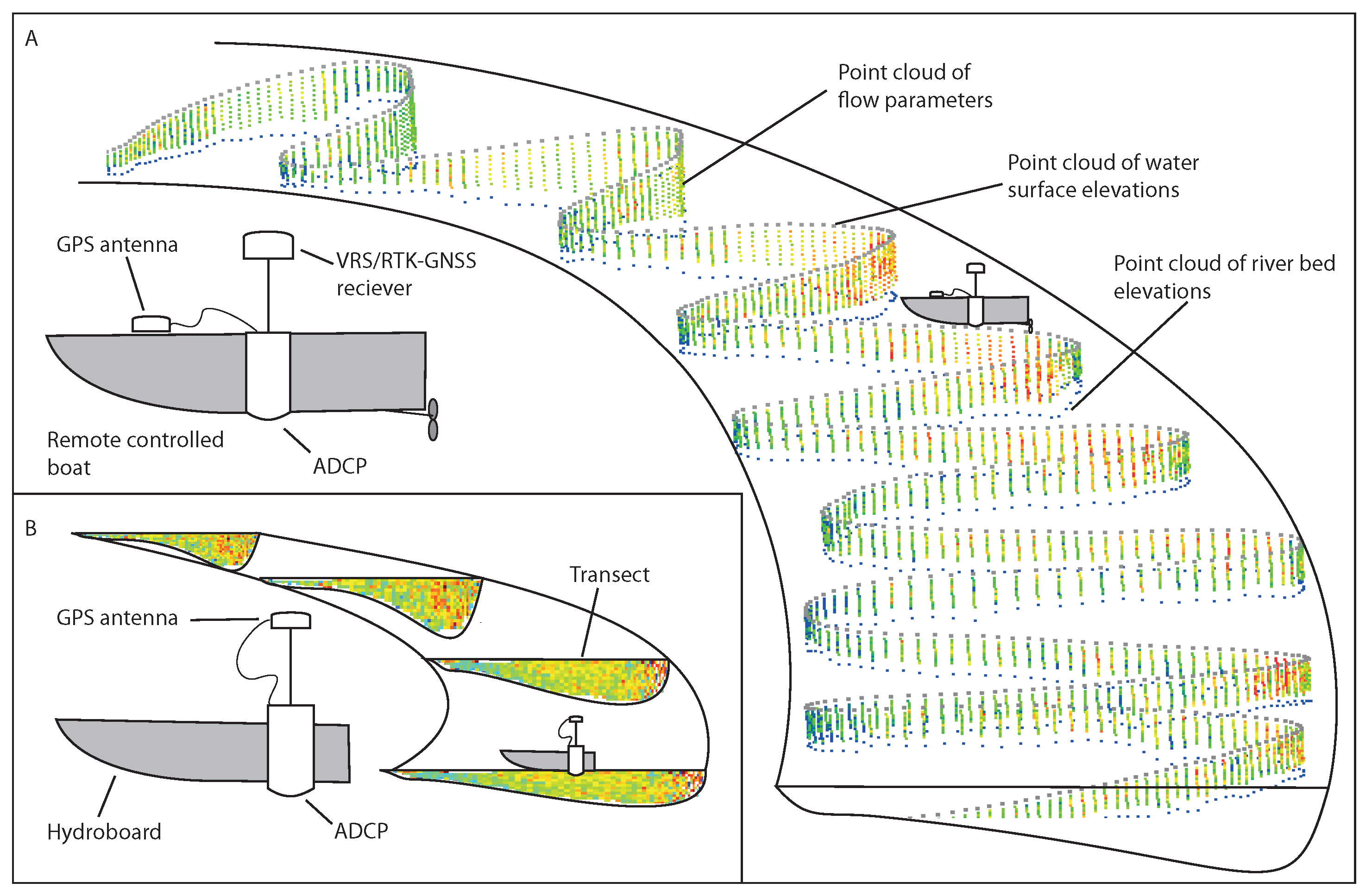
Figure 2. Diagram of the flow measurement set-up and concept. (A) The new spatial modeling of flow vectors as a 3D point cloud containing surface points, flow velocity and direction points in the water column and river bed elevation points; (B) This subfigure contrasts the more traditional method of representing flow as a series of transects.

3.1. Field Data

We conducted field measurements during a nine-day period (16–24 May 2013) that included the rising stage of the spring flood. Flow measurements were conducted daily at the meander bend AOI and every second day over the whole reach studied. Measurements of the meander bend AOI took about two hours to complete.

3.1.1. Remote-Controlled ADCP

We used a Sontek RiverSurveyor M9 ADCP mounted to a custom-built remote-controlled mini-boat (RCflow) to survey a dense pattern of flow measurements at the meander bend AOI. The boat is 1.43-m long and 0.425-m wide with the sensor emerging from the hull without its edge protruding at a water depth of 0.06 m. The hull is designed to minimize drag and turbulence, so that the boat can move against a fairly strong current and cause minimal interference to the measurements. RCflow makes it possible to survey even shallow reaches in sub-meter depths that cannot be accessed by larger boats. The boat is propelled by an electric motor powered by either NiCad or LiPo battery sets providing 20,000 mA/h. This allows for uninterrupted measurements exceeding 2 h, depending on flow conditions and the load required.

To measure the long reaches of the study area, we mounted a Sontek S5 ADCP to a Hydroboard floating platform attached with a pole to a motorboat (Figure 3). This allowed us to cover a greater distance and better cope with the current than the battery-operated RC boat. We aimed for boat speeds not exceeding 1 ms⁻¹.

Figure 3. ADCP-GNSS set-up on a remote-controlled boat (A) and on the Hydroboard tethered to a zodiac (B). A Trimble R8 GNSS receiver is mounted on the GPS pole of the ADCP exactly above the sensor, and the ADCP’s GPS antenna is mounted on the deck of the vessel.

Figure 3. ADCP-GNSS set-up on a remote-controlled boat (A) and on the Hydroboard tethered to a zodiac (B). A Trimble R8 GNSS receiver is mounted on the GPS pole of the ADCP exactly above the sensor, and the ADCP’s GPS antenna is mounted on the deck of the vessel.

Both ADCPs had the SmartPulseHD feature enabled. Using this measurement mode, the sensor simultaneously emits coherent and incoherent pulses, potentially at multiple frequencies, and a processing algorithm selects the best return signal for the given water depth and velocity. The Sontek M9 uses 3.0-MHz, 1.0-MHz and 0.5-MHz and the S5 uses 3.0-MHz and 1.0-MHz pulses. The ADCP sample measurements were carried out in discharge measurement mode using the ADCPs’ differential GPS (DGPS) for tracking. Bottom tracking was not an option, because the sandy river bed is mobile during the spring flood. Measurements were collected in a zig-zag pattern as very long transects and later exported as raw data in MATLAB format. The ADCPs measure one sample (also referred to as an ensemble) each second, and each sample is divided vertically into separate cells, also referred to as bins. The number of cells depends on water depth, and the cell height is dynamically adjusted depending on depth and speed. Measurement cells may be as small as 2 cm in shallow (<1.5 m), slow moving (<0.4 ms⁻¹) water or as large as 2 m in depths over 20 m. In our case, depths did not exceed 4 m, so the maximum cell size was 0.2 m.

By design, ADCPs average the flow of increasingly large areas into one measurement cell, with increasing distance from the sensor. That is, the measurement sample is in the shape of a pyramid consisting of different layers [9,29]. Each layer in the sample pyramid is one measurement cell. The true horizontal size of the measurement cell depends on the angle of the receivers on the sensor. Both Sontek ADCPs have the receivers arranged in a Janus configuration at a 25° angle. This means that, typically, the first cell measured after the blanking distance [30] (the space too close to the sensor to measure, generally 25 cm) is 0.03 m²; at a 1-m depth, the cell is 0.45 m², and at 2 m depth, the cell is 1.77 m² in area, while both cells may be the same thickness, say 0.1 m. Conceptually, however, the measurement sample is treated as a column of stacked cells, each of the same size, the width of which depends on the distance between consecutive samples, which depends on the boat speed. The measured value is often considered as a point located at the center of the cell, vertically and horizontally [9] centered under the instrument. In fact, the center position of the cell that the measured value is assigned to is never actually measured, since the sensor integrates measured return signals from the four beams that surround the center point, but do not actually cover the area directly below the sensor.

3.1.2. Positioning (GNSS)

Creating 3D point clouds of flow data requires accurate absolute positioning of each measurement. In order to obtain the best possible absolute positioning, we mounted a Trimble R8 Global Navigation Satellite System (GNSS) operating in virtual reference station (VRS) mode onto the RiverSurveyor’s GPS antenna pole instead of the ADCP’s own GPS antenna, which, even when using real-time kinematic (RTK) correction, only achieves a relative positional accuracy of 2 cm, due to the fact that the base station estimates its own position using its own GPS antenna, and does so anew, every time the base station is booted. This gives the ADCP’s positional data DGPS-level accuracy in absolute terms, even though the points within one measurement have RTK-level precision relative to each other. If it were possible to set up the ADCP’s RTK base station over a known reference point and input those coordinates to the station along with the necessary offsets at millimeter accuracy, the use of a second GNSS would not be necessary. The location of the base station’s antenna cannot be input using Sontek’s RiverSurveyor Live software, making an external GNSS solution necessary. However, in the interest of completeness, it should be noted that the more recent optional HydroSurveyor software does give the option to input base station coordinates, which results in absolute RTK-GPS positioning.

VRS-GNSS (also known as network RTK) is a virtualized version of RTK-GNSS, using real-time kinematic positioning, but rather than using a physical base station in the field, the VRS receiver gets its correction data through a GPRS-based (general packet radio service) Internet connection. A computing centre gathers real-time satellite data from a network of base stations around the country, based on which a virtual base station in the vicinity of the rover is computed and the virtual correction data transmitted to the receiver in real time. It is also possible to download the correction data at a later time for post-processing purposes. Given that the field site is within range of a GPRS network, the VRS system is much more convenient and faster to set up than a physical base station. Furthermore, the fact that the virtual base station can be located very closely to the measurement and can even be updated when measurements spread over a large area, minimizes baseline length-dependent errors common in GNSS positioning.

The Trimble R8 GNSS makes use of both the GPS and GLONASS satellite systems, which greatly improves coverage, particularly at these high latitudes. Despite having a large number of satellites available, a river channel remains a challenging environment for rapid and accurate GNSS positioning, particularly near steep banks. Fortunately, trees at the riverbank did not represent much of an obstacle during the spring flood, since they had not grown any foliage yet.

The Sontek’s own GPS antenna was mounted on the bow of the RCflow or the Hydroboard to collect satellite timestamp data (cf. Figure 2 and Figure 3). We use GPS timestamps later to merge the GNSS and ADCP data. The appropriate GPS offsets were included in the ADCP set-up parameters, so as not to affect the tracking ability of the ADCP. The integrated GPS receives differential corrections (DGPS) from the Satellite-based Augmentation System (SBAS) satellite network, giving it a nominal accuracy of 1 m or better. These DGPS data are used by the ADCP for tracking (cf. Section 3.1.1).

The R8 GNSS was set to collect raw data at 10 Hz, while the RiverSurveyor’s internal GPS collects data at 1 Hz, concurrent with its flow measurements. Given that these measurements do not necessarily take place at the peak of each second and that, like many instruments, the specified 1-Hz interval of the ADCP is theoretical and exhibits slight variation about that value in reality, this made it necessary to collect the actual positioning data at 10 Hz. At that rate, it is impossible for the GNSS to process differential corrections in real time, so we opted to post-process the data and calculate the baselines using correction data from the VRS network. This process gives us positional data at a precision of ±0.05 m or better in XYZ. Measurements with lower estimated precision were discarded in post-processing.

The 10-Hz VRS-GNSS positional data were subsequently merged with the 1-Hz flow measurements using the GPS timestamps included in the data from the RiverSurveyor’s own GPS. The precision of the timestamp is 0.1 s, so the possible horizontal error introduced by this process is at most 0.5 × boat speed, that is, half the distance between two subsequent flow measurements, which, given boat speeds of <1 ms⁻¹, amounts to at most ±0.05 m. Table 1 gives an overview of the number of GNSS points, ADCP points for each measurement day at the meander bend AOI, as well as the number of points remaining after merging the two datasets.

3.1.3. Water Level Data

Water levels were continuously measured along the study reach at 15-min intervals using pressure transducers (Solinst Gold Leveloggers) mounted to concrete slabs that were sunk to the riverbed at the beginning of the field work period and left to collect data throughout the ice-free period (Figure 4). The pressure transducers of these devices have an accuracy of ±0.005 m. Seven Leveloggers were positioned throughout the study area, three of which were located at the meander bend under investigation, one upstream, one in the middle of the bend in the deepest part of the meander and one downstream of the bend (Figure 5). The loggers were positioned far enough from the bank to be in deep enough water to remain submerged during summer low flow conditions.

Table 1. The number of points measured for each day at the meander bend AOI. GNSS points is the number of accepted points after baseline calculation (RMSE <0.05 m). ADCP points are raw measured point samples (ensembles). 3D points are the number of points in the point cloud for each day, and interpolated points are the number of points in the regular matrix interpolated from the original point cloud. 3D point density denotes the number of points per m³ in the meander bend AOI.

Date	GNSS Points	ADCP Sample Points	3D Points	Interpolated 3D Points	3D Point Density in Meander (pts m−3)
May 6	82,823	7,444	70,556	2,587	15.2
May 17	92,047	8,006	64,944	3,030	11.9
May 18	497,716	17,293	155,584	3,243	2.2
May 19	110,001	6,217	49,112	4,928	5.5
May 20	96,532	8,552	69,397	4,983	7.7
May 21	59,871	4,422	36,884	4,456	4.6
May 23	87,028	6,368	49,744	5,703	4.8
May 24	51,064	4,138	36,708	4,836	4.2

Table 1. The number of points measured for each day at the meander bend AOI. GNSS points is the number of accepted points after baseline calculation (RMSE <0.05 m). ADCP points are raw measured point samples (ensembles). 3D points are the number of points in the point cloud for each day, and interpolated points are the number of points in the regular matrix interpolated from the original point cloud. 3D point density denotes the number of points per m³ in the meander bend AOI.

Date	GNSS Points	ADCP Sample Points	3D Points	Interpolated 3D Points	3D Point Density in Meander (pts m−3)
May 6	82,823	7,444	70,556	2,587	15.2
May 17	92,047	8,006	64,944	3,030	11.9
May 18	497,716	17,293	155,584	3,243	2.2
May 19	110,001	6,217	49,112	4,928	5.5
May 20	96,532	8,552	69,397	4,983	7.7
May 21	59,871	4,422	36,884	4,456	4.6
May 23	87,028	6,368	49,744	5,703	4.8
May 24	51,064	4,138	36,708	4,836	4.2

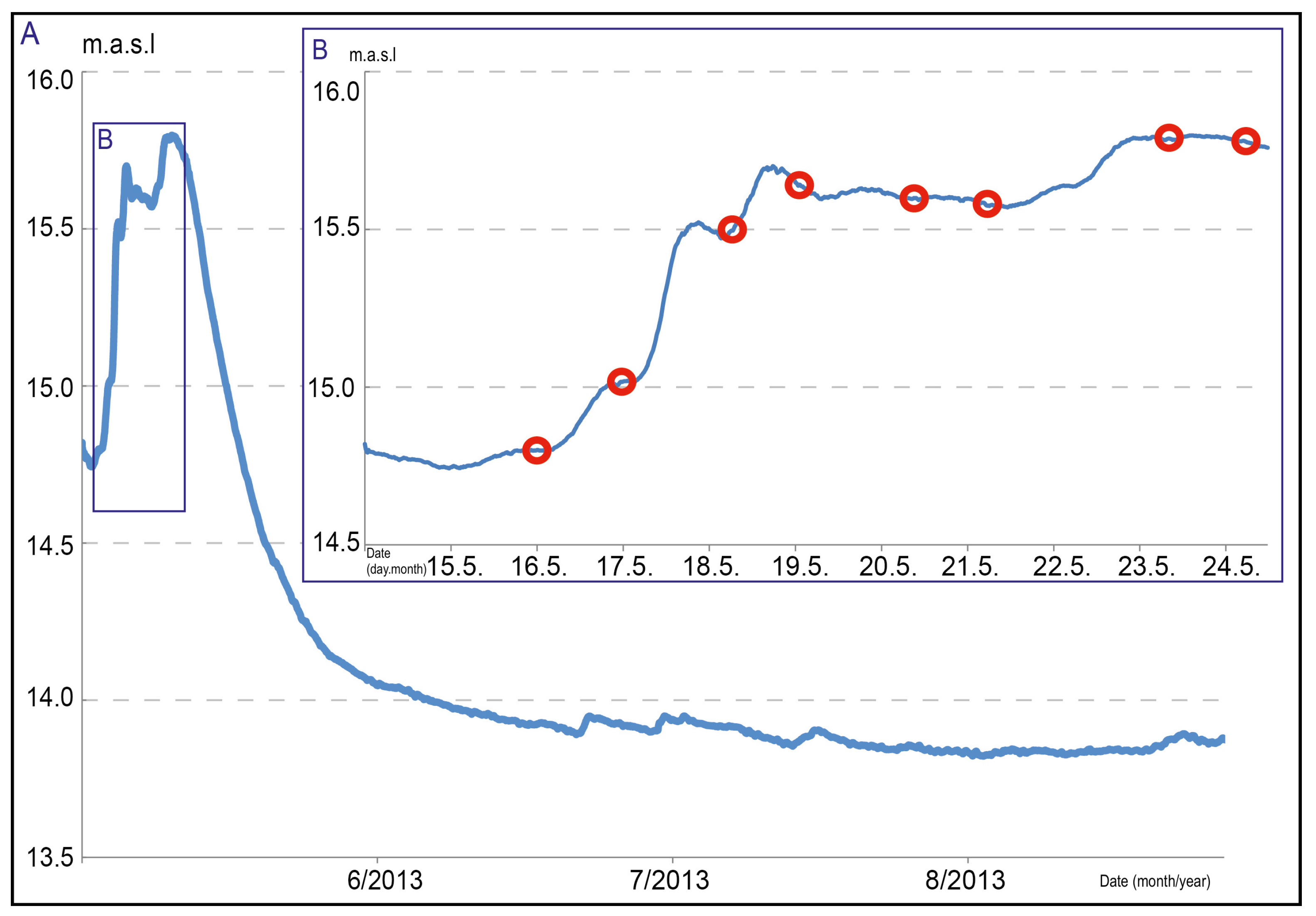
Figure 4. (A) Hydrograph of the ice-free period for 2013 of the Pulmanki River; (B) The rising stage of the spring flood is in meters above sea level (m.a.s.l). ADCP-flow measurement times are indicated with red circles.

Figure 4. (A) Hydrograph of the ice-free period for 2013 of the Pulmanki River; (B) The rising stage of the spring flood is in meters above sea level (m.a.s.l). ADCP-flow measurement times are indicated with red circles.

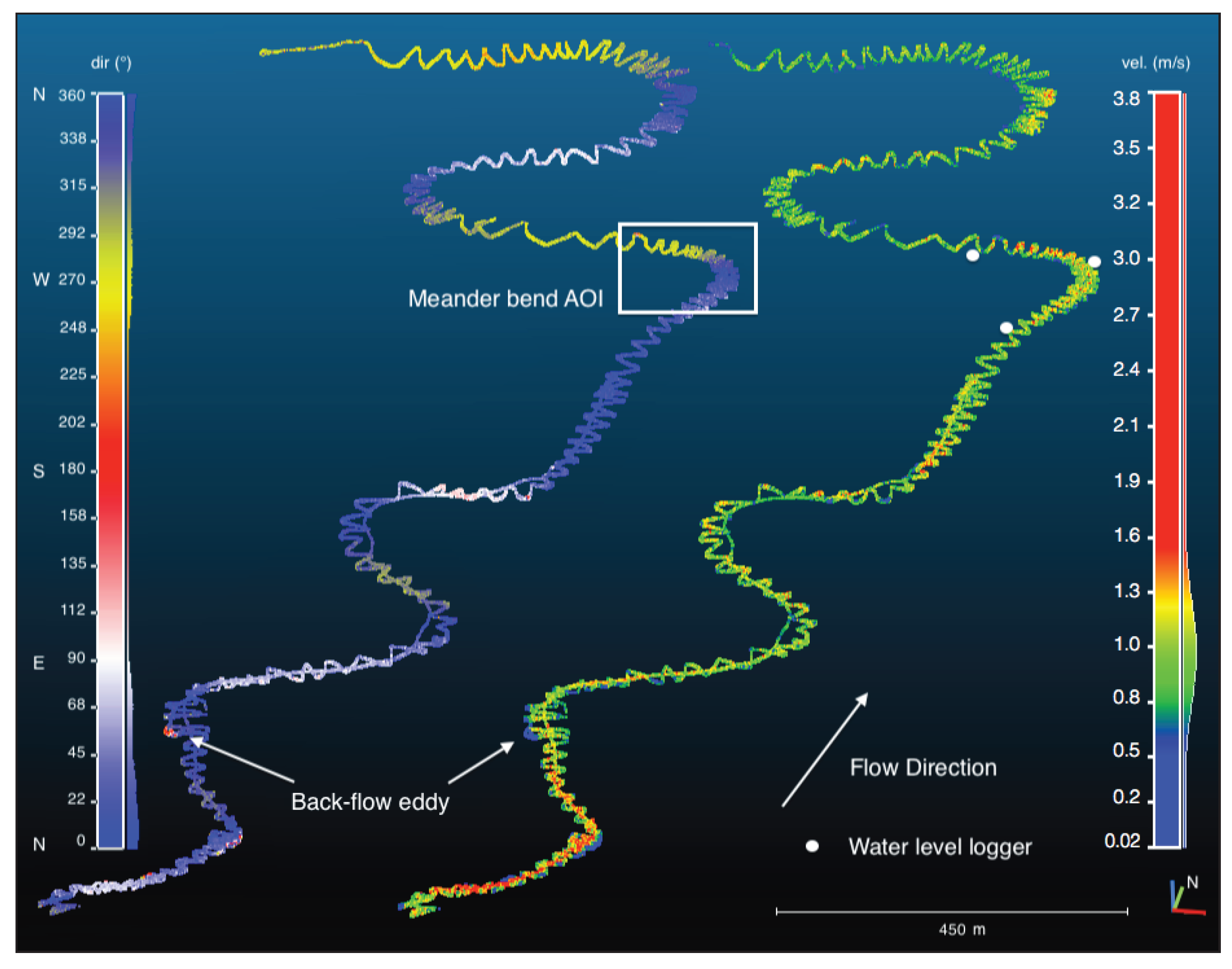
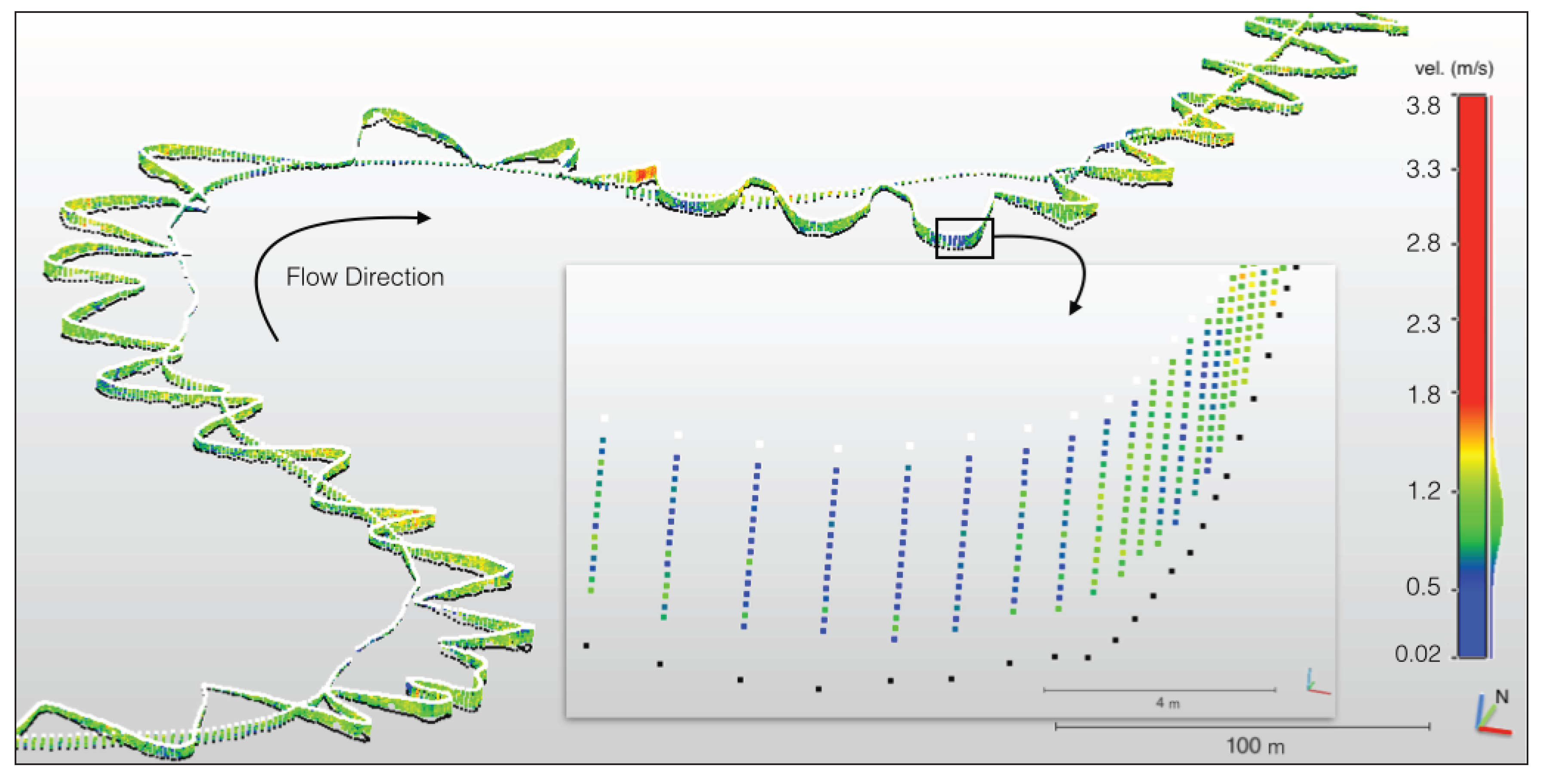
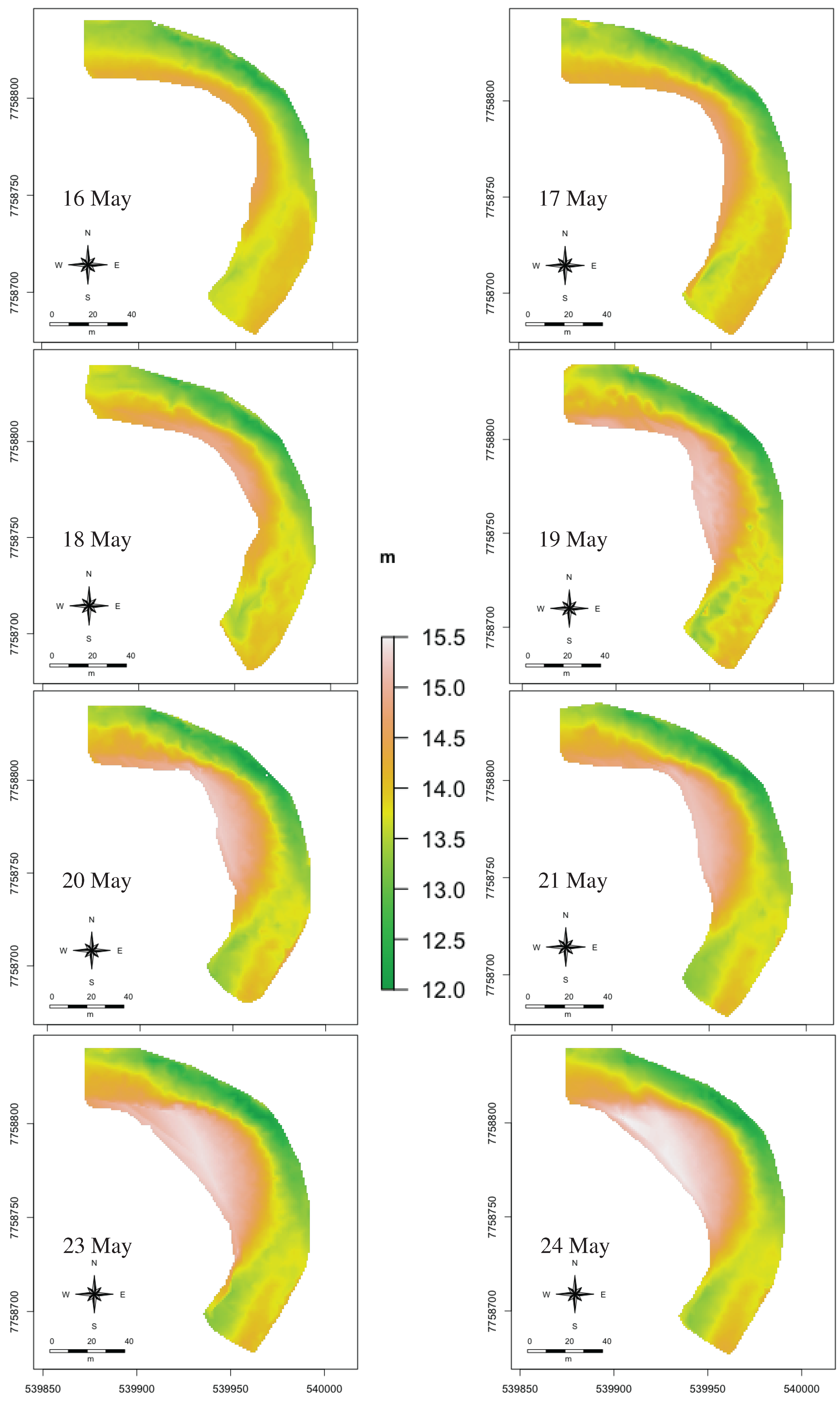
Figure 5. Point cloud of raw measured flow data of the whole study reach (3.7 km) on 18 May 2013 looking downstream. The left-hand plot shows flow directions in degrees from the north and the right-hand plot shows flow velocities in m/s. A back-flow eddy location is clearly detectable in the plot of flow directions. The location of the meander bend AOI is indicated by a box, and the approximate locations of the water level loggers are indicated by three points. The actual water level loggers were located about 2 m from the shore at low water, but for ease of visualization, approximate locations are shown here.

Figure 5. Point cloud of raw measured flow data of the whole study reach (3.7 km) on 18 May 2013 looking downstream. The left-hand plot shows flow directions in degrees from the north and the right-hand plot shows flow velocities in m/s. A back-flow eddy location is clearly detectable in the plot of flow directions. The location of the meander bend AOI is indicated by a box, and the approximate locations of the water level loggers are indicated by three points. The actual water level loggers were located about 2 m from the shore at low water, but for ease of visualization, approximate locations are shown here.

The water levels were measured at the beginning and the end of the study period using VRS-GNSS topography point measurements. The topography point method involves measuring a series of consecutive points and averaging the resulting coordinates in order to increase accuracy by averaging small positional errors that may result from slight movements of the GNSS receiver. This results in a measurement with better than 2-cm precision [31], which is suitable, given that the gradient of the river reach translates to a height difference of 0.2 m from the upstream to the downstream end of the reach. RTK-GNSS has previously been successfully used for water surface reconstructions [32,33,34].

The Leveloggers log pressure and temperature data. A Barologger was located near the middle of the study reach to collect atmospheric pressure data for post-processing the pressure data of the Leveloggers into water depths. Figure 4 shows the hydrograph measured by the water level loggers at the meander bend AOI for the ice-free period of 2013.

3.2. Data Processing

All ADCP data were exported to MATLAB format. The GNSS data were post-processed using VRS correction data from the Finnish virtual reference station network (http://www.vrsnet.fi). Baselines were calculated, and points with a positional accuracy better than 0.05 m were retained and exported as CSV (Table 1), including UTC timestamp information.

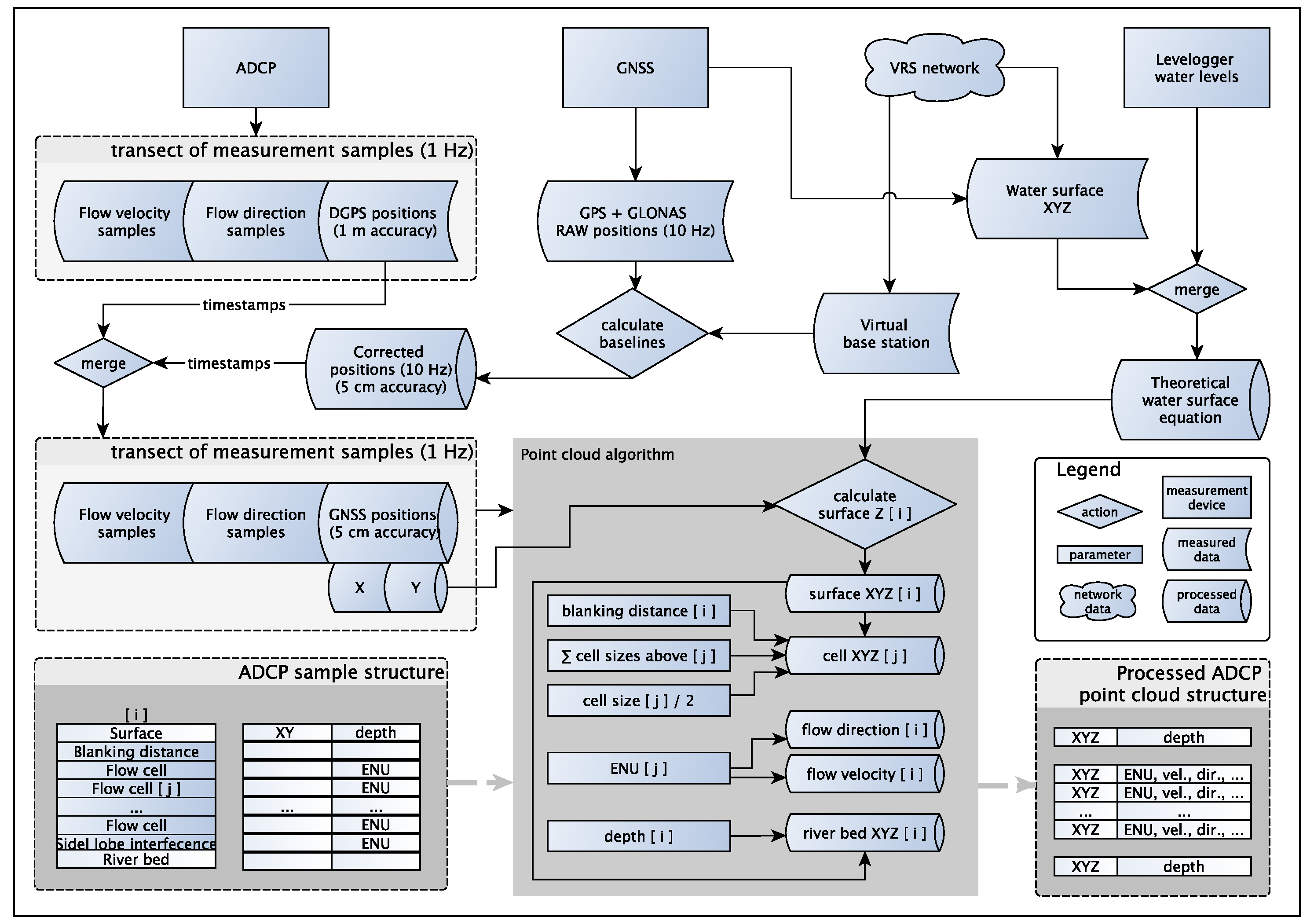
Further processing was carried out in R [35]. Figure 6 outlines the conceptual processing flow. The GNSS position data were merged with the ADCP flow data using the GPS timestamps. The continuous water level measurements were used to create a localized time-specific water surface model. The water surface model is created by fitting a plane through the water surface elevations at the three level logger locations at the time of measurement:

ax + by + cz = d

(1)

where a, b and c are the level logger points; x, y and z are their respective coordinates and d is the distance from a level plane. Given the locations of the water level loggers (Figure 5) with the upstream and downstream logger near the inside of the meander bend and the middle logger near the outside of the bend at the bend apex, we consider that this surface accounts for the possible superelevation of the water surface that is expected to be found in meander bends. In reality, though, at this particular meander bend, this effect is smaller than the vertical accuracy of the GNSS.

Figure 6. Conceptual process of creating a point cloud of flow data from ADCP, virtual reference station (VRS)-GNSS and water level measurements. A simplified conceptual view of the original ADCP sample structure is shown, where one measurement sample [ i ] consists of a series of superimposed flow measurement cells [ j ], each of which contains flow parameters. This is contrasted with the processed point cloud structure, where each cell becomes its own unit with spatial information i.e., a 3D spatial point, as well as additionally computed flow parameters (direction from north, velocity), calculated from the ENUvalues of the original cells, that is the velocity magnitude to the east, the north and up. Here, the individual point elements are shown superimposed in the “processed ADCP point cloud structure”, only to show how their positions relate to the original measurement structure.

Figure 6. Conceptual process of creating a point cloud of flow data from ADCP, virtual reference station (VRS)-GNSS and water level measurements. A simplified conceptual view of the original ADCP sample structure is shown, where one measurement sample [ i ] consists of a series of superimposed flow measurement cells [ j ], each of which contains flow parameters. This is contrasted with the processed point cloud structure, where each cell becomes its own unit with spatial information i.e., a 3D spatial point, as well as additionally computed flow parameters (direction from north, velocity), calculated from the ENUvalues of the original cells, that is the velocity magnitude to the east, the north and up. Here, the individual point elements are shown superimposed in the “processed ADCP point cloud structure”, only to show how their positions relate to the original measurement structure.

The flow data were registered to this water surface in order to avoid small remaining inaccuracies in the vertical component of the positioning. Whereas an accuracy of 5 cm or better horizontally is more than adequate for the purpose of 3D flow measurements in a river, in the vertical, this can leave a notable roughness to the water surface that was not present in the field. This artificial surface roughness would propagate to all measurement points in the water column. The water surface of the Pulmanki River is very calm, even during high water, with at most small ripples caused by wind (cf. Figure 3). For measuring purposes, the water surface can be considered flat. We therefore consider the Levelogger-based water surface to be more accurate as vertical positioning than each measurement’s individual GNSS-measured elevation. The variation in the water surface elevations during the measurement period was considerably smaller than the vertical precision of the VRS-GNSS (Table 2). The water surface elevation of each flow measurement sample was thus added to the dataset.

The ADCP automatically compensates tilting of the sensor caused by movement of the boat using its internal inertial measurement unit (IMU). The tilt sensor of the ADCP has a angular resolution of 1°.

The RiverSurveyor ADCP measures one sample each second. A sample is one vertical measurement (ensemble) that is divided into a number of cells (bins). In effect, this splits each vertical into a number of measurements, each with its own flow direction and velocity. The number of cells per sample depends on water depth and is dynamically adjusted by the RiverSurveyor’s internal algorithms. In practice, the cell size varies between 0.02 and 0.2 m.

The raw flow velocity measurements for each cell for each beam for each sample were used to calculate 3D flow vectors for each measurement cell. Flow directions were calculated in degrees clockwise from north, and horizontal velocity was calculated using ENU velocity components. This allows representing velocity as a magnitude parameter independent of flow direction.

In order to create a 3D point cloud of 3D flow data, the elevation of each measurement cell was calculated:

C_e = W_s − C₁ − ((n − 1) ∗ C_s) + C_s/2

(2)

where C_e is the elevation of a flow measurement cell; W_s is the Levelogger-based water surface elevation at the sample-specific location; C₁ is the depth of the first measurement cell, that is the blanking distance (this varies for each sample, but is generally around 0.25 m); n is the number of cells in a given sample and C_s is the cell size of a given sample. This locates the sample elevation vertically in the center of the cell in question, in line with the conceptual location of ADCP measurements (cf. Section 3.1.1). Similarly, river bed elevation was calculated by subtracting measured depth from the water surface elevation.

Thus, a point cloud of flow measurements was created, containing XYZ coordinates for each measurement, ENU coordinates of measured flow velocities, as well as flow velocity, direction, water surface, water depth, bed elevation and a UTC timestamp.

These points were subsequently interpolated in 3D using MATLAB to create a regular 3D matrix of points to create an evenly-spaced point cloud that is somewhat easier to visually analyze than the raw measured data. The point cloud was interpolated at different densities: 1 m, 2 m, 3 m and 4 m horizontally and 0.2 m vertically. The best interpolation density among these was determined to be 3 m horizontally and 0.2 m vertically. This is closest to the actual spacing of the measured data when considering the spacing of the zig-zag pattern, and while creating a large number of points, it is computationally manageable and visually not overwhelming, so that interpretation of the flow patterns is actually possible. The vertical spacing was selected to correspond to the most common large cell size of the ADCP measurements. A 0.2-m vertical spacing also results in a fair number of layers in shallow water without being overwhelming in deeper sections. Figure 7 illustrates the spatial relation of the interpolated point cloud data to the originally measured point cloud data.

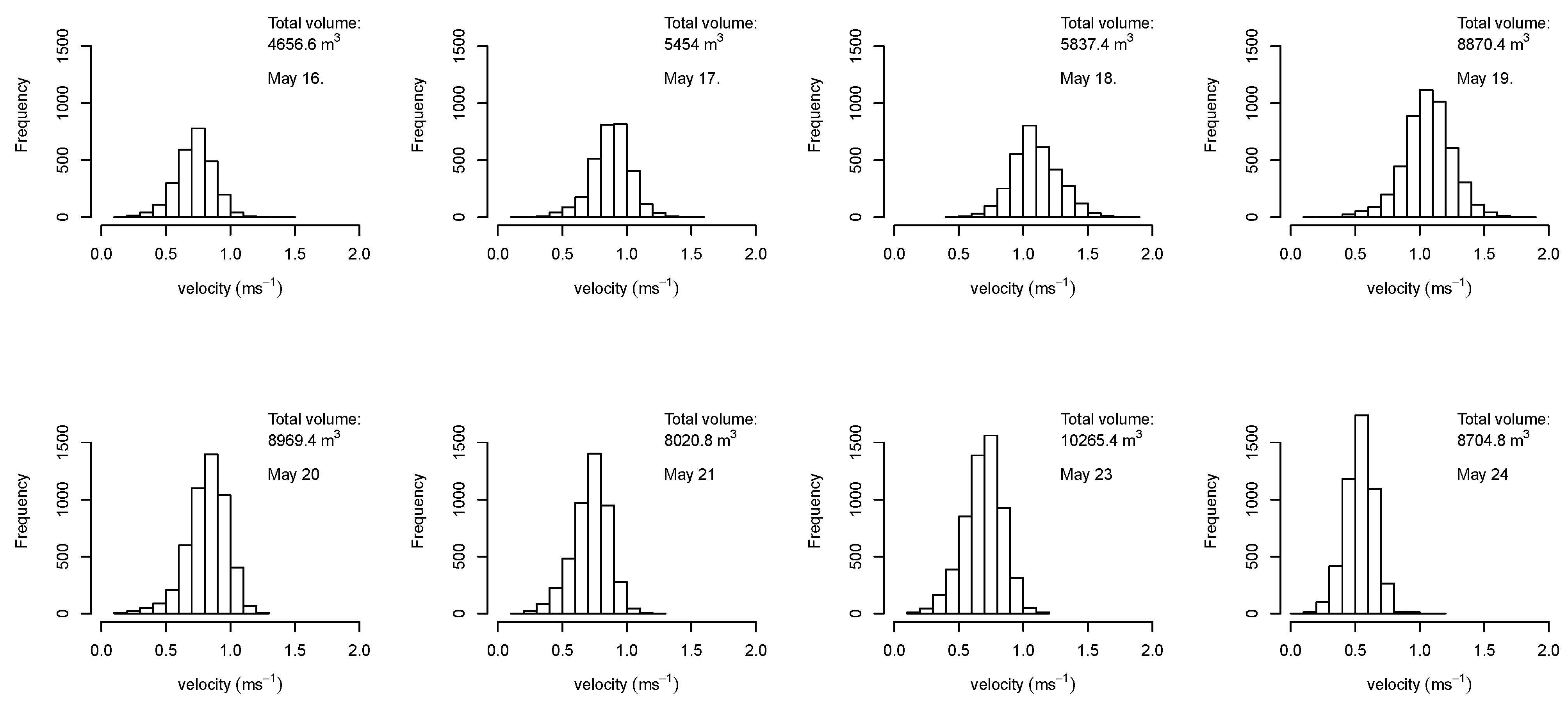
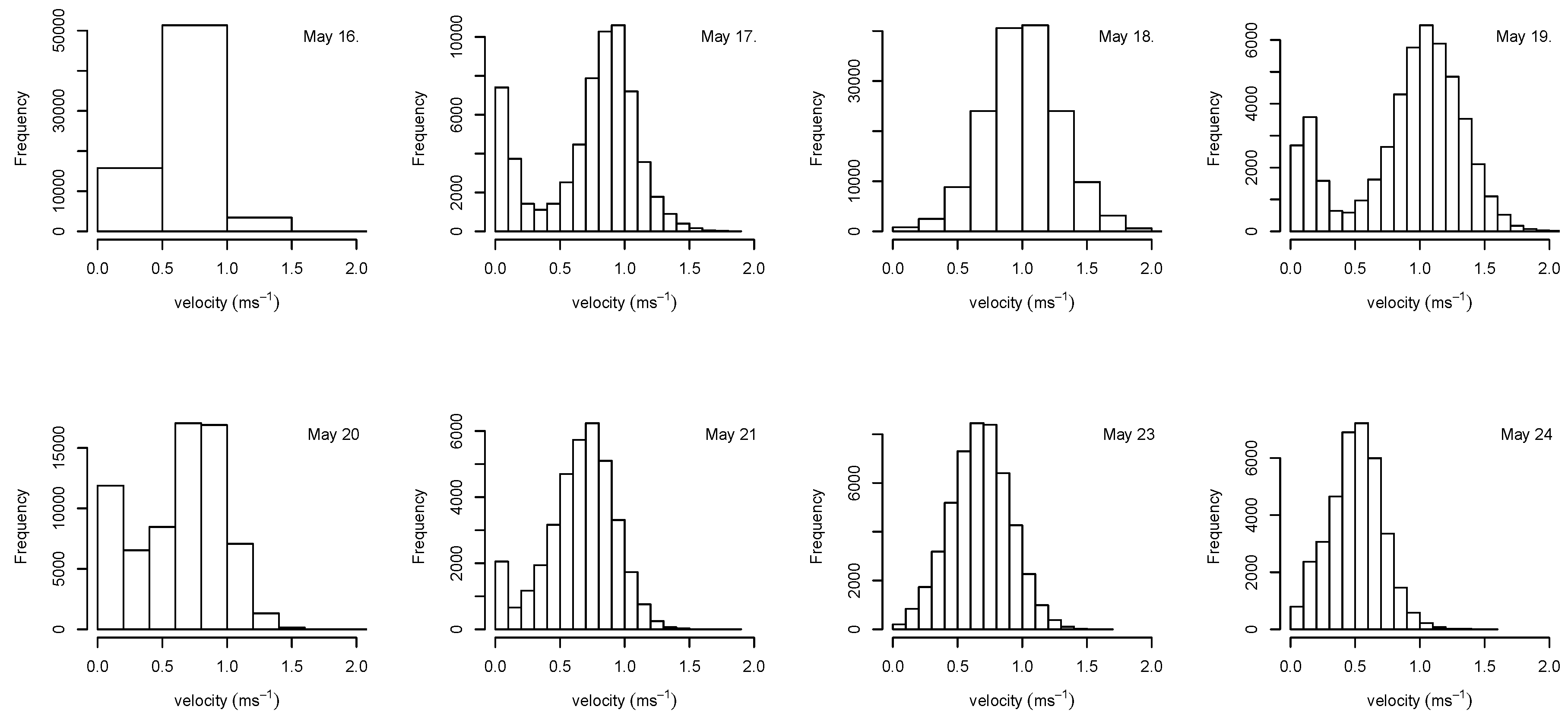
Table 2. Results of the 3D-interpolated point clouds for Venesärkkä for each day: time of measurement, temperature (°C) mean T and standard deviation σ T during measurement period, water level elevation mean wl (metres above sea level) and standard deviation σ wl, slope (m), minimum velocity min v, mean velocity v, maximum velocity max. v (ms⁻¹), min, mean and max. depths d (m), discharge Q (m³s⁻¹), total volume of water vol (m³), volume of water moving at velocities of <0.5 m³, 0.5–1.0 m³, 1.0–1.2 m³ and >1.2 m³.

Day	Time	T	σ T	wl	σ wl	Slope	Min d	d	Max d	Min v	v	Max v	Q	vol	vol < 0.5	vol 0.5–1	vol 1–1.2	vol > 1.2
16	19:30–21:35	5.0	0.056	14.818	0.006	0.0010	0.35	1.38	2.61	0.12	0.72	1.43		4656.6	306.0	4249.8	88.2	12.6
17	17:00–19:00	6.2	0.084	15.025	0.007	0.0013	0.30	1.55	2.83	0.17	0.88	1.52	35.28	5454.0	90.0	4329.0	937.8	97.2
18	19:20–19:40	5.0	0.002	15.493	0.002	0.0008	0.59	1.99	3.40	0.46	1.10	1.84	57.81	5837.4	3.6	1711.8	2552.4	1569.6
19	13:41–15:25	3.5	0.100	15.64	0.004	0.0006	0.37	2.12	3.62	0.17	1.06	1.82	66.00	8870.4	70.2	3013.2	3835.8	1951.2
20	17:57–20:05	4.7	0.163	15.601	0.001	0.0001	0.33	2.09	3.67	0.12	0.82	1.29	47.63	8969.4	300.6	7810.2	851.4	7.2
21	12:52–14:06	3.8	0.035	15.597	0.001	0.0000	0.38	2.12	3.63	0.20	0.72	1.24	42.16	8020.8	586.8	7342.2	90.0	1.8
23	19:59–21:37	9.3	0.040	15.787	0.001	0.0000	0.39	2.25	3.90	0.10	0.69	1.19	46.42	10265.4	1087.2	9068.4	109.8	0.0
24	21:17–22:25	10.1	0.019	15.763	0.000	0.0000	0.28	2.17	3.84	0.09	0.54	1.12	33.33	8704.8	3076.2	5626.8	1.8	0.0

Table 2. Results of the 3D-interpolated point clouds for Venesärkkä for each day: time of measurement, temperature (°C) mean T and standard deviation σ T during measurement period, water level elevation mean wl (metres above sea level) and standard deviation σ wl, slope (m), minimum velocity min v, mean velocity v, maximum velocity max. v (ms⁻¹), min, mean and max. depths d (m), discharge Q (m³s⁻¹), total volume of water vol (m³), volume of water moving at velocities of <0.5 m³, 0.5–1.0 m³, 1.0–1.2 m³ and >1.2 m³.

Day	Time	T	σ T	wl	σ wl	Slope	Min d	d	Max d	Min v	v	Max v	Q	vol	vol < 0.5	vol 0.5–1	vol 1–1.2	vol > 1.2
16	19:30–21:35	5.0	0.056	14.818	0.006	0.0010	0.35	1.38	2.61	0.12	0.72	1.43		4656.6	306.0	4249.8	88.2	12.6
17	17:00–19:00	6.2	0.084	15.025	0.007	0.0013	0.30	1.55	2.83	0.17	0.88	1.52	35.28	5454.0	90.0	4329.0	937.8	97.2
18	19:20–19:40	5.0	0.002	15.493	0.002	0.0008	0.59	1.99	3.40	0.46	1.10	1.84	57.81	5837.4	3.6	1711.8	2552.4	1569.6
19	13:41–15:25	3.5	0.100	15.64	0.004	0.0006	0.37	2.12	3.62	0.17	1.06	1.82	66.00	8870.4	70.2	3013.2	3835.8	1951.2
20	17:57–20:05	4.7	0.163	15.601	0.001	0.0001	0.33	2.09	3.67	0.12	0.82	1.29	47.63	8969.4	300.6	7810.2	851.4	7.2
21	12:52–14:06	3.8	0.035	15.597	0.001	0.0000	0.38	2.12	3.63	0.20	0.72	1.24	42.16	8020.8	586.8	7342.2	90.0	1.8
23	19:59–21:37	9.3	0.040	15.787	0.001	0.0000	0.39	2.25	3.90	0.10	0.69	1.19	46.42	10265.4	1087.2	9068.4	109.8	0.0
24	21:17–22:25	10.1	0.019	15.763	0.000	0.0000	0.28	2.17	3.84	0.09	0.54	1.12	33.33	8704.8	3076.2	5626.8	1.8	0.0

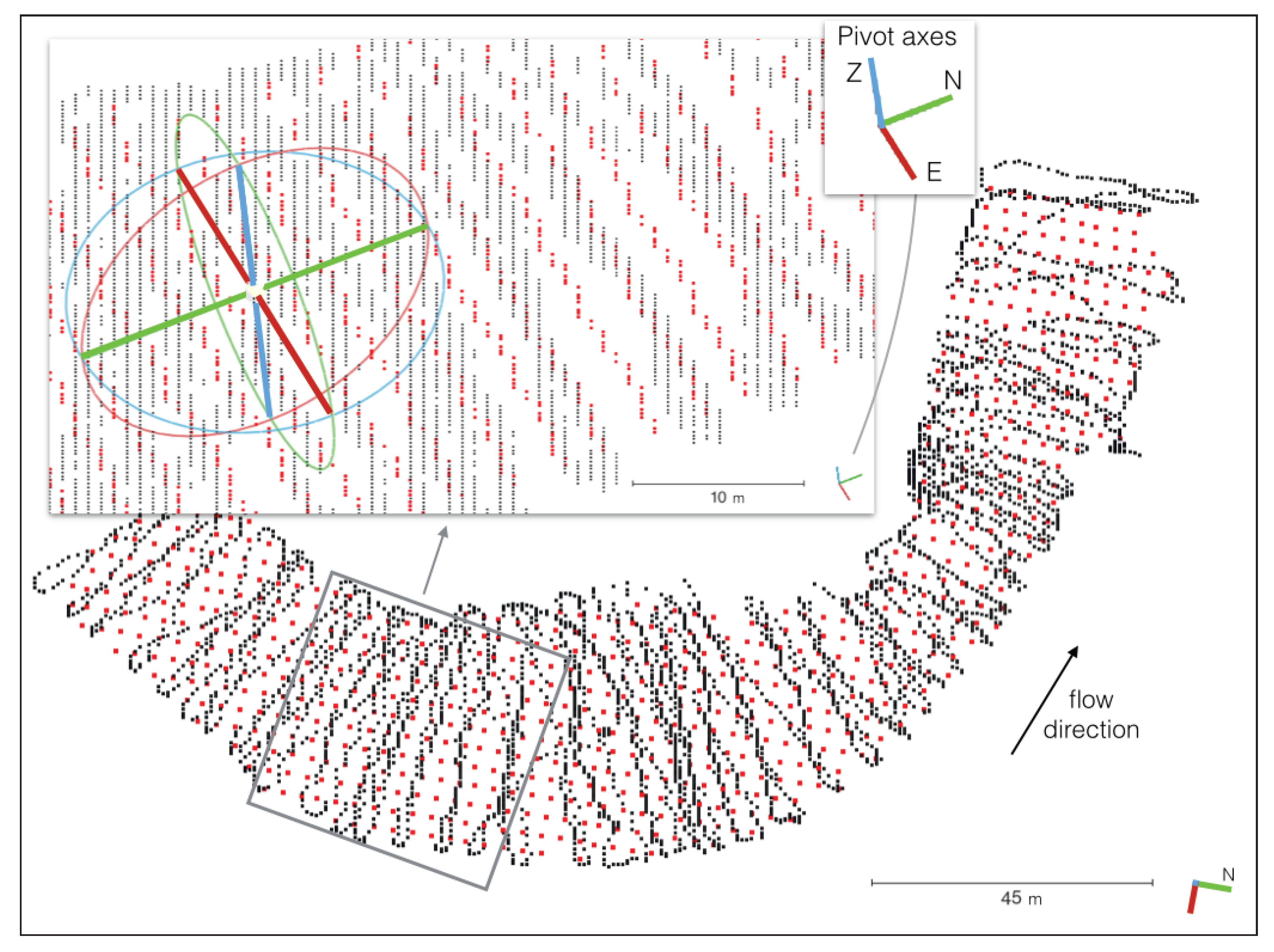
Figure 7. Comparison of original (black) vs. interpolated (red) data example of 19 May in plane view. The insert shows a close-up viewed at an angle (a 3D pivot sphere is included for spatial reference), to illustrate how the vertical dimension compares between the measured and interpolated point clouds. The point density in the interpolation matrix is sparser vertically and compared to the original sample line, along the line. The density is similar when considering the line spacing of the original zig-zag pattern. The pivot axes in this 3D plot, as well as in all subsequent plots indicate the view angle, with the green north-south axis pointing towards the north (substituting the north arrow), the red east-west axis pointing towards the east and the blue vertical axis pointing upwards, normal to the N-E plane.

Figure 7. Comparison of original (black) vs. interpolated (red) data example of 19 May in plane view. The insert shows a close-up viewed at an angle (a 3D pivot sphere is included for spatial reference), to illustrate how the vertical dimension compares between the measured and interpolated point clouds. The point density in the interpolation matrix is sparser vertically and compared to the original sample line, along the line. The density is similar when considering the line spacing of the original zig-zag pattern. The pivot axes in this 3D plot, as well as in all subsequent plots indicate the view angle, with the green north-south axis pointing towards the north (substituting the north arrow), the red east-west axis pointing towards the east and the blue vertical axis pointing upwards, normal to the N-E plane.

In order to create a realistic interpolation of the 3D flow structure in the stream, a Delaunay triangulation-based interpolation was applied to interpolate the velocity, angle, direction, surface elevation and depth values of the raw point cloud. A 3D network of triangular planes is created using the scattered raw points; the network is then sampled into a regular voxel space (a 3D matrix) of a defined resolution (here, 3 m × 3 m × 0.2 m). A natural neighbor interpolation is used to interpolate values of each voxel (each cell in the matrix) using the Delaunay network. All input data, as well as all the interpolations use the exact same section of the river. That is, all point clouds have the same length of thalweg; only the width of the water area changes with the stage of the flood.

4. Results

4.1. Analyzing 3D Flow Field Point Clouds

The 3D flow field point cloud data can be visually analyzed by borrowing tools from the LiDAR community. We used the open-source point cloud processing software, CloudCompare [36], to visualize the raw flow data. Figure 8 shows an example of flow velocities along with the water surface points and the river bed points. The dataset in this figure consists of a sparser zig-zag pattern used to survey the whole AOI. This sparser pattern helps to illustrate how the point cloud represents flow velocities in the water column. The shape of the river bed is indicated by the depth of the water column represented together with the river bed points. The pattern of deep water on the outside of the meander bends and shallow water towards the inside of the bends is clearly visible in the shape of the point cloud. The gap between the river bed and the deepest measured point shows the size of the bottom estimate caused by side-lobe interference at the end of the sample profile. Figure 1 shows the denser zig-zag pattern employed on the meander bend AOI in order to get a more detailed model of the flow characteristics at this location. The velocity distribution throughout the meander bend can be clearly detected with slow speeds on the inside of the bend in the shallow areas and the high velocities concentrated towards the outside of the bend downstream of the apex. The measurement samples on the very outside of the bend show that the velocity is slowed down by friction on the vertical bank. Furthermore, a little bay with a slow moving back flow can be seen downstream of the apex.

Figure 8. Point cloud of raw measured flow data from 18 May 2013, visualized in CloudCompare, looking downstream. The image shows a 800 m-long section of a 3.7 km-long measurement. The coloring represents flow velocity in m/s. The water surface points are indicated in white, and the river bed points are black. The insert illustrates how the ADCP measurement samples are converted into a series of stacked points in 3D space. The depth of the water column is reflected in the number of vertically-stacked points.

Figure 8. Point cloud of raw measured flow data from 18 May 2013, visualized in CloudCompare, looking downstream. The image shows a 800 m-long section of a 3.7 km-long measurement. The coloring represents flow velocity in m/s. The water surface points are indicated in white, and the river bed points are black. The insert illustrates how the ADCP measurement samples are converted into a series of stacked points in 3D space. The depth of the water column is reflected in the number of vertically-stacked points.

Figure 5 shows the point cloud of the whole river reach under investigation visualized in the same manner as Figure 8. Naturally, detail is less visible at this scale. However, flow patterns can nevertheless be detected with low velocities consistently on the inside of the meander bends along the point bars and high velocity flows mostly towards the outside of meander bends starting at the bend apexes. The highest velocities can be seen at the beginning of the reach, both on the straight section, as well as through the first meander.

Figure 9 shows the flow velocities on the interpolated 3D matrix for each measurement day, minus 22 May. The GNSS data on 22 May was problematic and could not be processed with the ADCP data to produce a flow point cloud. This data visualization can be rotated freely in all directions in a virtual 3D space on screen. Here, the visualization angle was chosen so as to show a series of pseudo-transects. Due to the regular spacing on of the 3D grid, it is possible to visualize pseudo-transects from many angles to get different views of the same dataset in a way that is familiar and easy to interpret. All data in Figure 9 are at the same scale, so the increase in flow velocities during the rising stage of the flood can be clearly seen, along with the shift of the fast flowing water away from the deeper part of the channel near the outside of the bend and into the shallows over the inundated point bar, after the peak of the flood on 19 May.

4.2. Analyzing High Velocity Core Changes in 3D

In order to gain a better understanding of the distribution of the high velocity core (HVC) from the measured spatial flow data, we visualized high velocity flows only. Figure 10 shows the HVC as the top 20% of flow velocities on the interpolated point cloud, colored according to velocity. The slower velocity points are indicated by smaller grey dots in order to give the three-dimensional context to the HVC. At the beginning of the flood, the flow follows the classical pattern described by Leopold and Wolman [37] and Dietrich and Smith [5], with the HVC located in the deep parts of the channel, near the outside of the bend. The fast flow is wide in the shallows upstream of the apex, nearly hugging the inside bank. At the bend apex, there is a drop-off, and the HVC drops into the deeper part of the channel near the outside of the bank. This situation largely remains until the flood reaches its peak on 19 May. After that, the HVC drops in nominal velocity and shifts away from the outside of the bend to flow over the now inundated part of the point bar. The HVC is now wider and less distinct than during the rising stage of the flood. This situation remains until the end of the measurement period.

Figure 9. 3D point cloud of flow velocities colored according to velocity magnitude (ms⁻¹). A triangulation of the river bed is included to enhance the visualization. The Z-axis is exaggerated by a factor of two.

Figure 9. 3D point cloud of flow velocities colored according to velocity magnitude (ms⁻¹). A triangulation of the river bed is included to enhance the visualization. The Z-axis is exaggerated by a factor of two.

Figure 10. Visualizing the high velocity core (HVC) as a 3D point cloud of flow velocities viewed at an angle, looking downstream. The view angle is indicated by the rotational axes. The HVC here is the top 20% of velocities for each day. The HVC is colored according to velocity (ms⁻¹). The points with velocities lower than the HVC are shown in light grey to give the three-dimensional context. The Z-axis is exaggerated by a factor of two. The river bed model of 23 May is shown to give a consistent spatial context.

Figure 10. Visualizing the high velocity core (HVC) as a 3D point cloud of flow velocities viewed at an angle, looking downstream. The view angle is indicated by the rotational axes. The HVC here is the top 20% of velocities for each day. The HVC is colored according to velocity (ms⁻¹). The points with velocities lower than the HVC are shown in light grey to give the three-dimensional context. The Z-axis is exaggerated by a factor of two. The river bed model of 23 May is shown to give a consistent spatial context.

4.3. Visualizing Vertical Flow

Since the 3D point cloud includes flow coordinates in three directions, the flow patterns can be interpreted to determine upwelling or downwelling patterns, as well as their changes through time and changing discharges and water levels.

The flow patterns can not only be interpreted to determine upwelling or downwelling patterns, but also to find turbulence, indicated by a local mixture of flow in both directions. One way to analyze these patterns is to plot the point clouds showing vertical motion (Figure 11).

Figure 11. Vertical flow velocities. The color scale is symmetrical centered on zero, meaning horizontal flow. Positive values indicate upwards flow motion (upwelling), and negative values indicate downwards flow motion (downwelling). The Z-axis is exaggerated by a factor of two. The river bed model of 23 May is shown for spatial context.

Figure 11. Vertical flow velocities. The color scale is symmetrical centered on zero, meaning horizontal flow. Positive values indicate upwards flow motion (upwelling), and negative values indicate downwards flow motion (downwelling). The Z-axis is exaggerated by a factor of two. The river bed model of 23 May is shown for spatial context.

Before the water starts rising, the motion is mostly horizontal (16 May), with some upwelling near the river bed in the deepest part of the meander bend. As soon as the water rises, the flow starts moving more vertically too (17 May), with a fairly clear pattern of the water in the meander bend moving in a downward direction in the shallow parts near the point bar, with some upwelling in the deeper part towards the outside bank. The same pattern intensifies on 18 May. It needs to be considered, though, that the sampling pattern on that day was coarse; hence, more of the data is relying on interpolation than on the other days. By 19 May, as the flood reaches its preliminary peak, the water is downwelling towards the drop-off at the peak of the point bar, then it moves mostly horizontally in the deeper part of the channel with some upwelling continuing there, as on the previous days. Towards the exit of the meander, an overturning motion starts, with downwelling near the surface and upwelling from below. Thereafter, the water body seems to be split into layers of vertical motion, with the top layer generally descending and the bottom layers rising. This tendency remains until the end of the measurement period, but decreases in magnitude on 23 May, as the lake effect becomes more pronounced and velocities have decreased from the flood peak. During the high water stages, the inundated point bar is dominated by downwelling water, whereas the main part of the channel is dominated by horizontal motion with upwelling near the bottom.

4.4. Bathymetry

In addition to the flow velocities and direction, the method presented here also allows for easy modeling of the river bathymetry, especially because of the dense survey pattern. The surface elevation and water depth were included in the interpolation algorithm presented in Section 3.2. Subtracting depth from the surface elevation gives river bed elevation. The points were interpolated to a surface by a triangulated irregular network interpolation. Figure 12 shows the evolution of the river bed at the meander bend AOI over the study period.

The bathymetric model created from the ADCP points gives a synoptic view of the shape of the river bed, albeit with some small artifacts caused by the measurement pattern. The time series of river bed elevations reveals how the pool on the upstream end of the AOI erodes deeper every day and slowly progresses downstream to connect to the deeper part of the channel near the outside of the bend. At the same time, the submerged point on the outside edge on the upstream end decreases over time.

Figure 12. River bathymetry. Bed topography is shown as elevation in meters above sea level.

Figure 12. River bathymetry. Bed topography is shown as elevation in meters above sea level.

4.5. Numerical Analysis

The interpolation of the point cloud into a regular matrix allows us, for the first time, to calculate new parameters based on field-measured data of the river section under investigation, that would otherwise only be possible to derive from numerical modeling. Each 3D point in the matrix represents a known volume, known as a voxel (analogous to a pixel in a 2D raster space). Because of this property, it becomes possible to calculate the total volume of water in the AOI: a voxel size of 3 × 3 × 0.2 equals a volume of 1.8 m³, so the total number of voxels times 1.8 gives a fairly good estimate of the total volume of water in the river reach at a given stage of the flood. Furthermore, it becomes possible to evaluate the volume of water moving at a certain velocity or a range of velocities. That way, the high-velocity core can be quantified with reasonable accuracy. Table 2 lists total volumes, along with volumes of water moving at velocities of <0.5 m³, 0.5–1.0 m³, 1.0–1.2 m³ and >1.2 m³. Figure 13 shows the flow velocity distribution for each measurement day as histograms.

Figure 13. Histogram plots of 3D interpolated flow velocity lattice illustrating the changes in magnitude and flow speed distribution during the measurement period. All plots use the same scale. One frequency unit represents 1.8 m³ of water, as per the 3D interpolation. Only measured volume is represented here. The top layer of water that is not captured by the ADCP, the local speeds of which are unknown, is not included in this analysis.

Figure 13. Histogram plots of 3D interpolated flow velocity lattice illustrating the changes in magnitude and flow speed distribution during the measurement period. All plots use the same scale. One frequency unit represents 1.8 m³ of water, as per the 3D interpolation. Only measured volume is represented here. The top layer of water that is not captured by the ADCP, the local speeds of which are unknown, is not included in this analysis.

The data presented in Table 2 and Figure 13 show that the velocities are largely normally distributed and that the total volume of water in the meander bend AOI increases during the rising stage of the flood, along with water levels and discharge, as one would expect. However, the peak velocities of the whole measurement period are concentrated on 18 and 19 May, reaching 1.8 ms⁻¹ with a mean velocity exceeding 1 ms⁻¹. Thereafter, while water levels and, as a consequence, total volumes of water increase until May 23, the peak velocities decrease, and most of the water is moving at speeds slower than 1 ms⁻¹. This is reflected in the discharge values measured on these days. Discharge peaks on May 19 at 66 m³s⁻¹ and then drops overnight by almost 20 m³s⁻¹, while the water level only decreased by 5 cm during the same time period. The total volume of water in the meander bend AOI increases by 99 m³, but the volume of water moving at speeds over 1 ms⁻¹ drops by about 5000 m³, while the volume moving at over 1.2 m³s⁻¹ drops by nearly 200 m³ to almost zero overnight.

5. Discussion

5.1. Feasibility of Representing 3D Flow in 3D Space

The results show that it is possible to create a three-dimensional model of measured flow velocity and flow direction as a point cloud. The raw point clouds of measured data (Figure 1) give us a synoptic view of a time-averaged flow situation in 3D. When interpreting these data, it is important to consider the time and space dimensions involved. The whole point cloud is a time-integrated representation of a given situation, while at the same time, each individual measured point is a snapshot of the flow at that particular position and one particular instant. Therefore, the model implicitly assumes that the flow situation is constant throughout the measurement period. This is on top of the assumption of locally horizontally homogeneous flow implicit in all ADCP measurements, due to the way that measurements of three or four divergent beams are integrated into one value [38]. Turbulence, eddies and hysteresis are ignored in this case, because it is impossible to measure the entire water body over the desired spatial extent at once. This assumption of constant flow is the same in discharge measurements using ADCP, even though, in the case of a single transect, the time-integration is smaller. Petrie et al. [16] found the number of transect measurements to control the accuracy with which moving vessel ADCP measurements are able to model the spatial distribution of flow, while noting that the time-averaged flow velocities obtained from fixed-vessel measurements could not be reproduced by four spatially interpolated transects. They did not determine how many transects would be required to give an accurate representation of the spatial distribution of the mean flow. Petrie et al. [16] analyzed transects, so the spatial distribution that they refer to is along a cross-section, rather than areal or in 3D. Nevertheless, the zig-zag pattern employed in the present study, spatially averaged into a 3D matrix, replicates an averaged series of transect measurements that, in the real world, are rarely spatially concordant.

In the case of this study, we monitored the water levels and temperatures throughout the measurement period. These parameters give an indication of the stability of the flow situation throughout the measurement period. The mean temperatures and water levels for each measurement are listed in Table 2 along with their corresponding standard deviations. The largest standard deviation of water level was 0.007 m and occurred on 17 May, as the water level was rising rapidly, thereafter declining towards zero. This means that the assumption of a constant flow situation became increasingly valid during the field measurement period.

Temperature also gives an indication of how constant the situation remained. The largest standard deviation of temperature during one measurement period was 0.16 °C. The ADCP measures water temperature at the sensor with each measurement sample, so any changes in temperature, as it affects water density and the effect of this on the propagation of sound, is already included in the flow measurements.

The duration of each measurement for the meander bend AOI was around two hours, and the measurement for the whole 3.7-km reach with a sparser survey pattern was around five hours. The duration of a survey is an important consideration, relative to the prevailing flow conditions at the time. During any rapid change in the hydrograph, such as the rising stage of a flood, it is important to adjust the measurement density, so that the reach under investigation can be surveyed in a few hours, whereas during summer low flow conditions, for instance, it may be perfectly acceptable to extend a survey over several days, allowing the freedom to measure a longer reach and/or at a higher density. For instance, Guerrero and Lamberti [23] found a two-day measurement period to be adequate for minimizing hydrological non-stationarity effects, whereas Jamieson et al. [13] found a five-hour measurement time to be acceptable for capturing large-scale 3D flow features. The fairly rapid survey during the spring flood conditions means that the time-integrated snapshots we achieved here should give a good overview of the overall situation. Given that an instant survey of the flow field of the entirety of a given reach is impossible, a compromise between survey density and time has to be struck with the steadiness of the flow conditions in mind.

The time-integrated point cloud may be regraded as a better representation of the overall three-dimensional flow field than each individual point is of the mean flow at that particular position, meaning that, while individual measurement points may erroneous, the synthesis of all points is nevertheless able to represent the big picture. ADCP measurements are well known to include noise (see González-Castro and Muste [38] for a detailed break-down of all error sources involved in ADCP measurements), both when considering single measurement samples and classical transects, but the averages of the measured values have been shown to give a very good approximation of the actual situation measured [9]. Rennie [24] found the uncertainty of depth-averaged velocities to be smaller than the uncertainty of single-cell measurements. Each individual measurement cell on each sample represents the average of the return signals measured. The assumption is that flow within each cell is horizontally homogeneous, so any deviation from this assumption caused by small eddies or turbulence results in noise. In order to get truly accurate velocity measurements, stationary measurements with several tens of seconds of measuring time need to be employed [9,23,39]. This, however, is not possible in moving vessel measurements. In the same manner, the raw point clouds are likely to include noise, that is erroneous values on the individual point level, but the overall representation of the hydrological conditions of the time-integrated measurement period should be fairly good. Jamieson et al. [13] argued that spatially-interpolated data may better represent the flow field compared to a series of transects. Visual interpretation of the raw point cloud (cf. Figure 1 and Figure 5) certainly allows us to get insight into the flow pattern, with zones of high and low velocities, as well as back flows clearly distinguishable (cf. Figure 5). The scale of features to be mapped, such as eddies or vortices in particular situations, needs to be included in the above-mentioned compromise of area and resolution. In a relatively small river, such as the Pulmanki, measuring 3D flow at a dense resolution can be feasible, and smaller features can be captured that way than in a larger river. On the other hand, in larger rivers, smaller features are unlikely to be of great interest, so a coarser resolution can still allow the mapping of site-specific features of importance in reasonable time, so that the time-integration does not overstretch the steady flow assumption.

One aspect that remains to be investigated in the future is the extent to which areas that look noisy in the raw point clouds are actually caused by measurement errors or whether they represent a real situation that is locally non-uniform. For now, we reason that noise in the raw data is likely to result from instrument noise inherent in ADCP measurements, possibly in combination with imprecision in the compass and IMU, as discussed above. Positioning errors are smaller than the distance between measurement samples, so they are unlikely to cause noise in the flow data. One important aspect is the inability of the measurement method to represent the whole water body at the same instant in time. On the other hand, a flow field measured as a transect is also a time-integrated measurement. The survey pattern causes measurements that are spatially close together to not necessarily be adjacent in the time series of the measurement. While each sample has two temporally adjacent samples, other samples in the immediate spatial vicinity are from a different line in the zig-zag pattern and, therefore, are temporally more distant. Some noise may therefore be introduced by high-frequency non-stationary properties of the flow, which may cause apparent noise, even without measurement errors.

5.2. Discussion of Interpolated Flow Volumes

Given that average values resulting from ADCP-measured data are known to be more accurate than individual measurement cells or, in our case, 3D points, spatial interpolation is a good way to remove noise from data and gain a more simple and, possibly, a more accurate and realistic model of the hydrological situation. The 3D interpolation described in Section 3.2 serves to simplify the raw point cloud into a regular grid. This spatial averaging shrinks the conceptual gap between the time-integrated measurements consisting of time-specific snapshots to a time-integrated model consisting of spatially- and time-averaged points. Oberg and Mueller [7] determined that measurement duration was the most important factor in reducing uncertainty in flow measurements. Even though the interpolation integrates only a relatively small time span into one point, this does increase the measurement duration of the interpolated point data compared to the instantaneous measurements represented in the raw point cloud. Each point in the 3D matrix represents a locally-averaged flow velocity, direction and depth value. This local averaging implicitly introduces short-term time averaging, not just of the previous and subsequent second, but including points from neighboring lines of the zig-zag pattern, which may be close by, but measured over a minute away in time. In a way, the 3D interpolation acts as a low-pass filter that removes small local variation and, therefore, can be considered to remove short-term variability. It has been reasoned [13,25] that the interpolation of spatially densely measured data reduces uncertainty in velocity measurements. Jamieson et al. [13] concluded that the spatial smoothing resulting from interpolation reduces variance in ADCP velocities, but that, at the same time, this elimination of temporal fluctuations may reduce our capacity to capture complex flow fields, while still enabling the mapping of large-scale eddies or turbulence.

While no longer representing raw measured data, the 3D-interpolated model is still based exclusively on measured 3D data, as opposed to a computational model.

The matrix resulting from the interpolation allows us to express 3D points in terms of volume (voxel), both total volume of water in a certain reach or volumes of water moving at certain velocities. Clearly, the volumes derived in this manner are estimates, since they are based on the number of voxels without taking into account that voxels near the river bed may not be cubic in reality. This inaccuracy is analogous to an irregular 2D polygon represented as a raster, which, at its edge, is only an abstraction of a real line, exhibiting a jaggedness depending on the resolution of the raster. The boundary of an irregular voxel space, as is the river bed, exhibits the same kind of jaggedness, but on a surface, instead of a line. Considering that the ADCP’s ability to measure flow and related parameters accurately in the immediate vicinity of the river bed is limited [40], this voxel space may be in any case the best approximation to be had in that area.

The effect of the abstraction of the raw measurements, and the raw shape of the water column, into the 3D voxel space is evident when comparing the histograms of flow velocities of the raw data points (Figure 14) to the interpolated points (Figure 13). The raw flow data contains a considerable amount of low velocity flow measurement points, whereas these are absent in the interpolated point cloud. This is likely due to the above-mentioned edge behavior of the voxels. Much of the edge data that contains the majority of low velocities near the river bed and the shallow areas on the inside of the meander bend gets abstracted into voxels that contain higher velocities.

Moreover, since this analysis pertains to measured data, the portion of the river that is not captured by the ADCP, notably the blanking distance near the sensor [40,41,42], is excluded from these volumes. The area near the river bed that is not captured by the ADCP due to side-lobe interference [8,29] is only represented insofar as the lower level voxels intrude into this space. Nevertheless, the part of the river that is measured can be analyzed this way.

Figure 14. Histogram plots of raw ADCP-measured flow velocities illustrating the changes in magnitude and flow speed distribution during the measurement period. Because of the differing number of points measured each day, the histograms have individual Y-axes.

Figure 14. Histogram plots of raw ADCP-measured flow velocities illustrating the changes in magnitude and flow speed distribution during the measurement period. Because of the differing number of points measured each day, the histograms have individual Y-axes.

5.3. Decreasing Discharge at High Water Levels

The time series of 3D point cloud measurements showed that during the second half of the measured spring flood flow velocity and, by association, discharge decreased while water levels remained high. The slope values can give an indication as to why this may be the case. The meander bend in question is in close proximity upstream of Lake Pulmanki. The water level of the lake rises during the rising stage of the flood. During this process, the slope of the water surface in the lower reaches of the Pulmanki River decreases, until the lake level actually reaches the area under investigation, at which point the slope is zero (20–21 May) (Table 2). This backwater effect of the lake causes the velocities and, by association, the discharges to decrease, while water levels and the total volume of water increase.

The astute reader will have noticed that there is an inconsistency in this logic, when examining the data closely, or, alternatively, that there is an inconsistency in the data, when considering this logic. Assuming that the explanation of the lake effect holds, as observation and most of the data in Table 2 suggests, one has to wonder why the total volume of water can be found to increase between 19 and 20 May, while the water level momentarily decreases. Assuming that the Levelogger data is correct, this points to a possible weakness in the volume estimation from the interpolated point cloud. The 3D matrix is created based on the extent of the data and the specified voxel size. This has the effect that a small change in water level, and, therefore, depth, may cause extra voxels to be added or lost, near the river bed. The voxels in this case have a vertical extent of 0.2 m. The 99 m³ in question amount to 55 voxels out of 4983, on 20 May. The voxels have similar spatial properties as a 2D raster in that they are a somewhat coarse approximation of the real phenomenon represented, with the coarseness being related to the pixel size of the raster or, in this case, the voxel size of the 3D matrix. This coarseness may account for the noted discrepancy in the volume data, as the edges of a raster object are, by their nature, imprecise, and in the case of what is essentially a 3D raster, the edge is not just a line, but a whole surface.

Another factor influencing the creation of the 3D matrix is the spatial distribution or coverage of the points in the original point cloud. While we attempted to cover the same area in the same way at the same density every day, it is naturally impossible to get the exact same sample point density every time.

However, even when taking these limitations of the 3D matrix into account, the data still allow an unprecedented assessment of flow velocities in terms of volume based on the measured data.

6. Conclusions

In this paper, we demonstrated that it is possible to analyze the areal 3D flow field at the reach scale by creating an areal three-dimensional model of 3D flow parameters in a natural environment as a point cloud, based exclusively on measured data. The RCflow set-up, consisting of an ADCP coupled with a precision GNSS mounted on a remote-controlled boat, makes it possible to survey river reaches rapidly, including shallow areas that cannot be accessed by a larger boat. The raw flow data, while containing noise, gives a good synoptic time-integrated snapshot of a complex 3D flow field. In addition, a bathymetric model can be created to complement the flow data. Depending on the site-specific features to be investigated and the prevalent flow conditions, different measurement densities can be used to find a compromise between survey time, area and the scale of flow features to be captured.

A simplified view of the point cloud can be achieved by abstracting the raw data into a regular 3D matrix that represents the water column as a regularly-spaced point cloud. These data can be easily visualized as either a point cloud of flow velocities or flow directions overlaid on a river bed model and underlying a water surface model in most any point cloud visualization software that is commonly used in the domain of laser scanning. Three-dimensional flow can be analyzed by visualizing vertical flow velocities, as well as horizontal or total flow velocities or flow directions. Such an analysis is best performed viewing the data in 3D visualization software. The density of the point cloud can make pattern detection of flow in this analysis quite challenging, especially when representing such complex and dense data on the 2D medium of paper without the ability to rotate or zoom the point cloud. For 2D analysis, a more traditional representation of 3D flow as a series of transects [15,43] may be preferable. The interpolated 3D matrix can be interpreted as a dense series of transects and should lend itself to this type of analysis, allowing the additional freedom of choosing the direction of the transects at the visualization time (with no limitation on streamwise directions), rather than at the measurement time.

In this paper, we presented a modeling methodology to create a spatially-accurate 3D representation of the 3D flow-field in the form of a point cloud. Naturally, these data can be used to derive other flow parameters than what is directly measured. For instance, Laamanen et al. [44] demonstrated how the data can be dissected into layers and used to calculate shear velocity and how this affects bed erosion and deposition. Simple bed change detection can be performed, as well. All of these applications rely on the absolute positional accuracy of the dataset achieved by combining RTK-GNSS with the ADCP. These data may also serve as measured reference boundary conditions for a 3D computational hydraulic model in a natural setting, such as employed in Kasvi [45]. Williams et al. [21] demonstrated how a dense series of transects can serve both as calibration and reference data for a 2D hydraulic model in a braided natural river. Guerrero et al. [46] used an ADCP in an areal sampling pattern in combination with multi-beam sonar to calibrate and validate a 2D morphodynamic model investigating the movement of suspended sediment. Such a comparison may reveal the strengths and weaknesses of this measurement-based model and theoretical models alike.

We have developed this methodology in the hopes that it may prove useful and allow new insights for investigators in the fields of hydrology, fluvial geomorphology, river habitat studies and environmental monitoring.