Next Article in Journal
Rainfall Enhances Vegetation Growth but Does the Reverse Hold?
Previous Article in Journal
Multilayer Numerical Modeling of Flows through Vegetation Using a Mixing-Length Turbulence Model
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Water
Volume 6
Issue 7
10.3390/w6072104
water-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Sensitivity of Subjective Decisions in the GLUE Methodology for Quantifying the Uncertainty in the Flood Inundation Map for Seymour Reach in Indiana, USA

by
Younghun Jung
1,
Venkatesh Merwade
2,
Soojun Kim
3,
Narae Kang
4,
Yonsoo Kim
4,
Keonhaeng Lee
5,
Gilho Kim
5 and
Hung Soo Kim
4,*
1
Institute of Environmental Research, Kangwon National University, Chuncheon-si, Gangwon-do 200-701, Korea
2
School of Civil Engineering, Purdue University, 550 Stadium Mall Drive, West Lafayette, IN 47907, USA
3
Columbia Water Center, Earth Institute, Columbia University, New York, NY 10027, USA
4
Department of Civil Engineering, Inha University, Incheon-si 402-751, Korea
5
Water Resources Research Division, Water Resources and Environment Research Department, Korea Institute of Civil Engineering and Building Technology, Goyang-si, Gyeonggi-do 411-712, Korea
*
Author to whom correspondence should be addressed.
Water 2014, 6(7), 2104-2126; https://doi.org/10.3390/w6072104
Submission received: 30 May 2014 / Revised: 4 July 2014 / Accepted: 10 July 2014 / Published: 23 July 2014
Browse Figures
Versions Notes

Abstract

:
Generalized likelihood uncertainty estimation (GLUE) is one of the widely-used methods for quantifying uncertainty in flood inundation mapping. However, the subjective nature of its application involving the definition of the likelihood measure and the criteria for defining acceptable versus unacceptable models can lead to different results in quantifying uncertainty bounds. The objective of this paper is to perform a sensitivity analysis of the effect of the choice of likelihood measures and cut-off thresholds used in selecting behavioral and non-behavioral models in the GLUE methodology. By using a dataset for a reach along the White River in Seymour, Indiana, multiple prior distributions, likelihood measures and cut-off thresholds are used to investigate the role of subjective decisions in applying the GLUE methodology for uncertainty quantification related to topography, streamflow and Manning’s n. Results from this study show that a normal pdf produces a narrower uncertainty bound compared to a uniform pdf for an uncertain variable. Similarly, a likelihood measure based on water surface elevations is found to be less affected compared to other likelihood measures that are based on flood inundation area and width. Although the findings from this study are limited due to the use of a single test case, this paper provides a framework that can be utilized to gain a better understanding of the uncertainty while applying the GLUE methodology in flood inundation mapping.

1. Introduction

Flood inundation mapping plays a major role in conveying flood risk information to decision makers and the general public for planning purposes and relief operations. Flood inundation mapping involves an integrated modeling approach that involves hydrology, hydraulics and geospatial analysis. The accuracy of the final flood inundation maps is affected by the uncertainty in the input data and modeling techniques, including model parameters. As a result, several studies have reported the role of uncertainty in flood inundation mapping. There are many techniques available for uncertainty analysis, such as a Bayesian forecasting system [1], generalized likelihood uncertainty estimate (GLUE) [2], parameter estimation (PEST) [3], a methodology based on the fuzzy extension principle [4], the Gaussian approach [5], the simultaneous optimization and data assimilation (SODA) method [6] and sequential data assimilation [7]. Among these techniques, the GLUE method has found widespread implementation in various studies related to uncertainty analysis in environmental and hydrologic modeling, including flood mapping (e.g., [8,9,10,11,12]).
The GLUE method uses Monte Carlo simulations in conjunction with Bayesian theory to produce parameter distributions conditioned on available data and associated uncertainty bounds. The parameter distributions are generated based on parameter sets that can produce acceptable model outputs in comparison with observed data. The criterion for an acceptable model is based on the definition of a user-specified informal likelihood measure in realistic cases or the reversed formal statistical error in ideal cases [13]. While GLUE has found widespread application in flood inundation mapping [14,15,16] because of its simple and flexible conceptual structure, it has been debated in several studies with regard to the choice of formal and informal likelihood measures for model calibration and uncertainty estimation [6,17,18,19,20,21,22,23,24]. Specifically, the subjectivity involved in defining the informal likelihood measure and the criteria for defining acceptable versus unacceptable models have been argued from a statistical point of view. Even studies that implement formal likelihood measures through sequential data assimilation [7,25] and multi-model averaging have been reported to have their own weaknesses. Furthermore, the use of formal likelihood measure needs an exact definition of the error model between the observations and the predictions, including information on heteroscedasticity and autocorrelation [26]. While the subjectivity related to the informal likelihood measure in GLUE cannot be ignored, the GLUE methodology based on the concept of a true model [27] is potentially useful to estimate uncertainty in flood inundation mapping for data-poor environments where a formal likelihood is not available. This characteristic of the GLUE methodology is similar to the concept of approximation Bayesian computation (ABC), which uses an accept-reject method and allows for the selection of both formal and informal likelihood measures [28].
As mentioned above, subjective decisions are required for the implementation of GLUE in flood inundation mapping. For example, the selection of a likelihood measure can produce different uncertainty bounds for a flood inundation map. However, an investigation of the prior and posterior probability distributions of model variables can provide information that may be useful in making appropriate choices while applying the GLUE methodology. Accordingly, the objective of this paper is to assess the sensitivity of the effect of the selection of likelihood measures and cut-off thresholds used in selecting behavioral and non-behavioral models in the GLUE methodology using a single case study. This objective is accomplished by applying the GLUE methodology, including Monte Carlo simulations with hydraulic modeling and terrain analysis for a reach along the White River in Seymour, Indiana (Seymour reach). Figure 1 shows the procedures of this study.
Water 06 02104 g001 1024
Figure 1. Study procedures.
Figure 1. Study procedures.
Water 06 02104 g001

2. Study Area and Data

The White River is one of the major rivers in Indiana and is a tributary of the Wabash River, which joins the Ohio River before draining to the Mississippi River. The Seymour reach selected in this study is 5.5 km-long, and its floodplain is relatively flat with a U-shaped valley (Figure 2). The geometric data for the Seymour reach contains 9 digitized cross-sections extracted from a 1.5-m resolution digital elevation model (DEM) developed by the Information Technology Services at Indiana University in Bloomington, IN. The DEM data for the Seymour Reach is generated from digital orthophotographs taken in 2006. The vertical accuracy of these data in terms of root mean square error (RMSE) is found to be 0.69 m for the study area and is verified by comparing the DEM-derived elevations with twelve bench mark points in the area. The average width of Seymour reach cross-sections is about 3.9 km, with an average spacing of 700 m. Seymour reach is selected because of the availability of an observed flood inundation map for a historical flood in June 2008. The flooding of June 2008, was one of the worst in modern history and led to the evacuation of more than 100 homes in the area.
Water 06 02104 g002 1024
Figure 2. Study area (East Fork of the White River, near Seymour, Indiana).
Figure 2. Study area (East Fork of the White River, near Seymour, Indiana).
Water 06 02104 g002

3. Methodology

The objective of this paper is to investigate the effect of the selection of likelihood measures and cut-off thresholds for behavioral and non-behavioral models in the GLUE methodology. The methodology involves the following steps: (i) generation of random numbers from an assumed prior pdf for model variables; (ii) Monte Carlo simulations for each model variable evaluated with different likelihood measures; (iii) selection of multiple cut-off thresholds for each model variable and likelihood measure; and (iv) comparison of the uncertainty bounds for individual combinations of the model variable, likelihood measure and cut-off threshold. Each step is described below in more detail.

3.1. Selection of Prior pdfs and Random Number Generation

Although many variables, including topography, the modeling approach and parameters and designed discharge add uncertainty in flood inundation mapping; the three variables that have received the most attention in literature are used in this study [29,30,31,32]. These variables include topography, discharge and the Manning’s n (roughness) parameter in hydraulic modeling. The range of uncertainty in topography is dictated by its accuracy. The cross-sections for the Seymour reach used in this study are derived from a DEM that has an RMSE of ±0.69 m. The error in topographic data affects the cross-sectional area and the slope between the cross-sections, and it finally propagates to water surface profiles produced from hydraulic modeling of river channels [33,34]. The discharge data obtained from the United States Geological Survey (USGS) are estimated by a rating curve that converts the observed flood stage to a discharge value. By using USGS field measurements of stage (H) and discharge (Q) at the White River gauging station, a stage-discharge rating relationship (Equation (4)) is developed through regression.
Q = 10(1.58+1.44·logH)
The flow corresponding to the observed stage of 19.67 m is 2729.7 m3/s. The regression equation for the stage-discharge rating curve is developed assuming a Student’s t distribution [34,35]. Using a 95% confidence interval, a stage of 19.67 m gives a lower bound of 2257 m3/s and an upper bound of 3301 m3/s. These lower and upper bounds define the uncertainty range for discharge. Manning’s n values are generally adopted from the literature [36] and are adjusted by trial and error during calibration. The uncertainty range for Manning’s n is established by using published values from Chow [37] and by using guidance from Acrement and Schneider [38]. Acrement and Schneider provide guidance on assigning Manning’s n values based on bed material, degree of channel bed irregularity, variations in the channel cross-section, the relative effect of obstructions, vegetation and the degree of channel meandering. Romanowicz and Beven [10] found that the effective roughness coefficients change with flood magnitude, but this factor is not directly incorporated in this study, because we think that the selection of Manning’s n values from a range will account for this change indirectly.
In most practical cases, it is difficult to obtain information about the distribution of input data, as well as the model parameters in the absence of historical data. Therefore, many applications in flood inundation modeling assume the prior pdfs of model variables simply to be uniform. This simple assumption for model variables might be necessary when conducting very large computations in order to obtain behavioral variables. In this study, the model variables, specifically stream discharge, Manning’s n and elevation, are randomly selected from uniform and normal pdfs and then combined for an input dataset in the GLUE methodology (see Table 1 and Table 2). Although just using normal and uniform pdfs may not provide comprehensive results, these distributions are commonly used in such studies [2,14,39]. Once the uncertainty range and prior pdf is known, random values can be extracted for Monte Carlo simulations in the GLUE method. In the case of Manning’s n, the uncertainty range is converted to a percentage of the initial Manning’s n value used in the hydraulic model, and then, the selected random percentage change is applied to all cross-sections. For example, if all cross-sections have three Manning’s n values of 0.04 (left bank), 0.06 (main channel) and 0.05 (right bank), a random number of 20% would increase the Manning’s n values to 0.048 (left bank), 0.072 (main channel) and 0.06 (right bank) at all cross-sections to represent the change in the initial values. Similarly, if a random value for topography indicates a vertical error in a DEM, it is added to the initial elevation. For example, a random number of −0.1 m will reduce the elevations in the DEM by 0.1 m. For discharge, a random value is selected applied as the input flow value to the Hydrologic Engineering Centers River Analysis System (HEC-RAS) model.
Table
Table 1. Combinations of prior pdfs for model variables. The model variable is denoted by AB: A indicates a model variable, such as topography (T), discharge (Q) and Manning’s n (N); B means a prior pdf of a normal (N) and uniform (U) type.
Table 1. Combinations of prior pdfs for model variables. The model variable is denoted by AB: A indicates a model variable, such as topography (T), discharge (Q) and Manning’s n (N); B means a prior pdf of a normal (N) and uniform (U) type.
CombinationCase 1Case 2Case 3Case 4Case 5Case 6Case 7Case 8
pdfTNQNNNTNQNNUTNQUNNTNQAUNUTUQNNNTUQNNUTUQUNNTUQUNU
Table
Table 2. The upper and lower boundary of the random variable (RV) for the parameters, where the units of RV are t-values with a 95% confidence interval for discharge and meters for topography. The unit of RV is dimensionless for Manning’s n.
Table 2. The upper and lower boundary of the random variable (RV) for the parameters, where the units of RV are t-values with a 95% confidence interval for discharge and meters for topography. The unit of RV is dimensionless for Manning’s n.
Initial (Variables)Model variables updated by random variable (RV)RV
LowerUpper
Ni, Manning’s nN = Ni (1 + RV)−0.3750.375
Qi, DischargeQ = Qi *1000286RV (m3/s)−1.9631.963
Ti, TopographyT = Ti + RV (m)−0.690.69

3.2. Monte Carlo Simulations

Monte Carlo simulations are conducted by using the HEC-RAS model to create the water surface elevation at each cross-section presented in Figure 2. HEC-RAS is a one-dimensional (1D) hydraulic model based on an energy equation and Manning’s equation; and HEC-RAS can simulate the basic profile and the total conveyance for steady and unsteady flow conditions in river channels, including floodplains. The output from HEC-RAS is then used to create a water surface, which is then subtracted from the topography to get a flood inundation map. Some previous studies (e.g., [40]) illustrated that a 2D hydraulic model is able to produce a more realistic flood inundation compared to a 1D hydraulic model. However, the use of a 1D model in this study is justified, because the Seymour Reach is a relatively straight reach with a flat terrain, where the main channel and the floodplain act as a single channel.
The data for the HEC-RAS model involves the geometric data, flow data, Manning’s n and boundary conditions. Generally, geometric data in the HEC-RAS model is obtained by HEC-GeoRAS, which is an ArcGIS tool that allows the extraction of cross-sections by reading information from a DEM and a land use map and exporting this information to HEC-RAS. In the HEC-RAS model used for this study, a downstream condition of normal depth is used as the boundary condition, and steady flow conditions are assumed for a flood event. HEC-RAS provides one water surface elevation per cross-section. In order to get the inundation extent, these values must be interpolated to create a surface. A Visual Basic script is written to get the water surface elevations (m) from HEC-RAS and interpolate by using a triangle-based linear interpolation (MATLAB function “griddata”) [41] to get a water surface. In this study, Monte Carlo simulations are performed with random variables selected from a combination of prior pdfs for each variable. A total of 40,000 simulations are conducted, including 5000 simulations corresponding to each of eight prior pdf combinations in Table 1.

3.3. Subjectivities in the GLUE Processes

A likelihood measure is a key factor in the GLUE methodology, because the uncertainty bounds can be narrowed or widened by the choice of a particular likelihood measure. GLUE can use a likelihood measure based on formal statistical functions under ideal settings or assumptions (e.g., non-minimum error variance or non-maximum likelihood Beven [42,43], but most often, informal likelihood measures are used in the absence of ideal conditions or consistent error structure in the data. Among the several likelihood functions proposed in the literature, inverse error variance and Nash–Sutcliffe efficiency are representative likelihood functions [2,44,45,46,47], but these functions are difficult to apply to non-temporal data, such as a flood inundation map. Therefore, the F-statistic, which considers the spatial distribution of flood extent, has been used as a likelihood measure in flood inundation mapping [12,48,49]. The selection of a likelihood measure depends on the availability of observed data against which model output can be compared. For this study, observed flood inundation map provides information on the spatial extent of the flood, so a measure based on spatial extent can be used. The observed flood inundation map can also be intersected with a digital elevation model to get the corresponding water surface elevations and the water surface top width at each cross-section. Thus, the extent, elevation and width of the water surface can all be used individually to define a likelihood function. Under ideal conditions, a likelihood measure based on extent should not give different results for a likelihood measure based on elevation, but typically, this is not the case [44]. Any of these measures, however, can be used successfully as an objective function to evaluate the hydraulic performance without much difference in the final outcome, but their use as a likelihood measure in uncertainty estimation through Monte Carlo simulations will produce different outcomes, due to an unknown error structure. Accordingly, to test the sensitivity of likelihood measures on GLUE, three different likelihood measures are explored in this study. These measures include: (i) the sum of the absolute errors in inundation width (W; Equation (3)); (ii) the sum of absolute errors in the water surface elevation (E; Equation (4)); and (iii) the F-statistic that describes the overall matching of the observed flood inundation area with the model’s predicted area (F; Equation (5)). It should be noted that these measures are informal. In addition, the measures related to elevation or width may take other forms, such as the root mean square error in water surface elevations or widths, but we think the form probably will not affect the sensitivity analysis.
Water 06 02104 i001
where L[M(Θ, I)] is a likelihood measure by model prediction (M) for given parameter (Θ) and a set of input data (I); Piis a penalty function; and r is a cut-off threshold.
Water 06 02104 i002
where Wm,i and Wo represent the i-th iteration of the modeled water surface width and observed water surface width, respectively for the j-th cross-section among a total of N cross-sections. In this study, the unit of the W likelihood measure is m−1.
Water 06 02104 i003
where Em,i and Eo represent the i-th iteration of the modeled water surface elevation and the observed water surface elevation, respectively, for the j-th cross-section among a total of N cross-sections. In this study, the unit of the E likelihood measure is m−1.
Water 06 02104 i004
where Ao indicates the observed inundation area; Ap refers to the predicted flood inundation area and Aop represents the intersection of both the observed and the predicted inundation areas. In this study, the unit of the F likelihood measure is dimensionless. Typically, observed data, such as the inundation extent used in this study, have errors associated with them, and incorporating this error is difficult in the absence of any additional data. Therefore, error in the observed data is assumed to be negligible in this study to obtain a conservative analysis from the uncertainty point of view.
After selecting a likelihood measure to compare the outcome of all simulations with observations, a cut-off threshold is selected to divide the simulations between two categories: behavioral and non-behavioral. In most GLUE applications, there are suggested criterions in defining the cut-off threshold, but limited to only several functions, such as cumulative error, the Willmot index of agreement, Chiew and MacMahon and the cumulative absolute error [50,51,52]. Typically, a tighter cut-off threshold leads to a small number of behavioral model or acceptable datasets, while a relaxed cut-off threshold produces a large number of acceptable datasets. An acceptable dataset in GLUE refers to the model variables that are associated with the behavioral models. Because of the subjectivity involved in selecting behavioral models, a procedure that involves a comparison of prior and posterior pdfs of model variables is used in this study. It is assumed that a model variable that yields robust posterior pdfs for different cut-off thresholds is less sensitive, because the values of model variables are spread across the potential predicted range regardless of the threshold. A posterior pdf is considered robust if it does not change its form with regard to the prior pdf and cut-off thresholds. A posterior pdf for a model variable is determined by using the values of the variable from behavioral models that are created by using a cut-off threshold. For example, if all models are selected as behavioral models (no cut-off threshold), the prior and posterior pdfs are identical for a given model variable. Therefore, the number of behavioral models and the type of posterior pdfs for a model variable vary with different cut-off thresholds and likelihood measures. In this regard, Monte Carlo simulations were conducted for combinations of variables (Table 1) and the condition of variables (Table 2).

3.4. Uncertainty Quantification

For each output from Monte Carlo simulations, the W, E and F likelihood measures are calculated by using Equations (2)–(4). Uncertainty bounds in flood inundation areas are individually quantified by using all simulations for W, E and F likelihood measures. These uncertainty bounds correspond to 100% behavioral models (no cut-off thresholds) and are then compared with uncertainty bounds obtained by using cut-off thresholds and likelihood measures.

4. Results

4.1. Monte Carlo Simulations

The results from Monte Carlo simulations are presented using scatter plots (Figure 3). Each scatter plot represents the change in the likelihood measure (y-axis) with respect to change in the model variable (x-axis) for a given combination of prior pdf. As expected from the prior information of model variables, the plots generated from uniform prior pdfs have more scatter compared to that from normal prior pdfs. The scatter plots related to the F likelihood measure, which considers both the water surface elevation and flood extent, are more concentrated in the top for all model variables (topography, discharge and Manning’s n) (Figure 3a). The F likelihood measure shows more scatter for negative uncertainties in topography and Manning’s n, but the scatter is symmetric for discharge. In particular, positive uncertainty in topography produces high F likelihood measure values, but the scatter in the F likelihood measure increases as the uncertainty shifts towards the negative range. The scatter is highest for the maximum negative uncertainty in topography.
The scatter plots for the W likelihood measure (W), which considers only the flood width, show horizontal layers for all model variables (Figure 4b). From these results, it may seem that the W likelihood measure is inappropriate to use, but the layers in the scatter plot are produced mainly due to the rectangular shape of the valley. For example, the inundation width at a given cross-section in a rectangular valley is not affected by variations in water surface elevations. Similarly, if a cross-section has a step-like geometry, a layer is created in the scatter plot when the water surface moves from one step to another. However, the W likelihood measure may not produce layers in a river with a V-shaped valley. Thus, the W likelihood measure can be appropriate to use in floodplains with V-shaped valleys. In the case of a rectangular valley, the selection of an appropriate likelihood measure depends on the flood magnitude. For smaller floods, the W likelihood measure can be more proper than E likelihood, because the flood extent width may easily change with a small variation of the water surface elevation at different cross-sections. However, for a larger flood that fills the valley, the E likelihood measure is more appropriate to use than the W likelihood measure, because the flood extent width may not change with varying water surface elevations.
The E likelihood measure (E), which is based only on the vertical difference between simulated and observed water surface elevations, shows different scatter for negative and positive uncertainties in topography (Figure 3c). The scatter plots of the E likelihood measure for discharge and Manning’s n are relatively symmetric in comparison with the scatter for topography. It is also possible from the scatter plot to guess the prior pdf based on the symmetry of the scatter. For example, for a normal prior pdf, the scatter in the dot plot is symmetric along a vertical line, with a greater concentration of dots in the center. On the other hand, the scatter plot for a variable with uniform pdf is evenly symmetric. Similarly, a symmetric scatter plot indicates relatively a less sensitive variable compared to a variable that has an asymmetric plot. Based on the symmetry of dot plots for the F and E likelihood measures, discharge seems to be less sensitive compared to topography and Manning’s n for the Seymour Reach.
Water 06 02104 g003 1024
Figure 3. Dot plots of model variables (T, Q and N) based on likelihood measures and the combination of the prior pdfs (Cases 1 and 8), where the x-axis indicates the error ranges of variables and the y-axis shows the likelihood measures. (a) F likelihood measure; (b) W likelihood measures (103 m−1); (c) E likelihood measures (103 m−1).
Figure 3. Dot plots of model variables (T, Q and N) based on likelihood measures and the combination of the prior pdfs (Cases 1 and 8), where the x-axis indicates the error ranges of variables and the y-axis shows the likelihood measures. (a) F likelihood measure; (b) W likelihood measures (103 m−1); (c) E likelihood measures (103 m−1).
Water 06 02104 g003

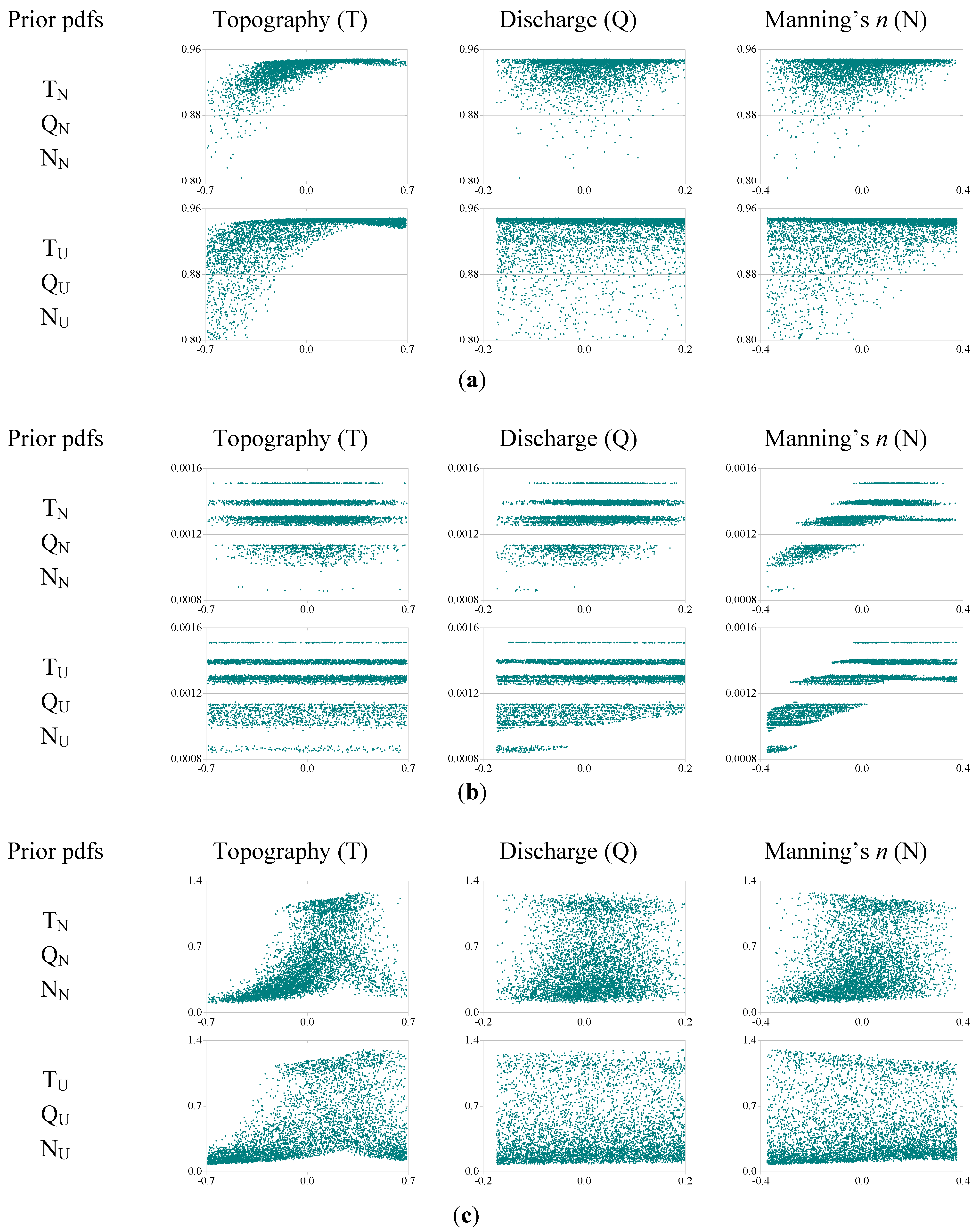
4.2. Effect of Likelihood Measures, Prior/Posterior pdf and Thresholds on GLUE

Table 3 presents the uncertainty bounds from GLUE based on the F and E likelihood measures for each combination of prior pdf (Table 1) used in this study. The flood inundation areas with a 90% uncertainty bound (lower 5% and upper 95%) for the Seymour Reach range from 9.29 to 10.98 km2 for the F likelihood measure and 10.13 to 10.92 km2 for the E likelihood measure. It is also evident that when all model variables are randomly selected from a uniform distribution, wider uncertainty bounds are obtained with all of the likelihood measures. As a result, the E likelihood measure produced the smallest uncertainty bound in the inundation area with an average value of 0.68 km2 and a standard deviation of 0.1 km2. This means that the E likelihood measure produced robust uncertainty bounds regardless of the prior pdf types of model variables. Overall, the 90% uncertainty bounds considering prior pdf with the F and E likelihood measures range from 0.55 to 1.69 km2. The maximum difference in uncertainty bounds is about 11% of the base area (10.57 km2). Considering only the effect of the prior pdf, the maximum differences in uncertainty bounds are 6% (F likelihood measure) and 2% (E likelihood measure) of the base area. From these results, the effect of the prior pdf type, including its subjectivity on uncertainty quantification, is illustrated.
Table
Table 3. Uncertainty bounds based on the likelihood measure and prior pdfs of variables (units: km2).
Table 3. Uncertainty bounds based on the likelihood measure and prior pdfs of variables (units: km2).
LMCase12345678AVGSD
UB
FLower 5%9.839.729.829.669.469.369.459.299.570.21
Upper 95%10.8910.9210.9010.9210.9510.9810.9610.9810.940.04
Bound1.061.201.081.261.491.621.521.691.360.25
ELower 5%10.3210.2710.3110.2510.1610.1410.1410.1310.210.08
Upper 95%10.8z710.8810.8710.8910.9210.9210.9210.9210.900.02
Bound0.550.610.560.640.760.780.780.790.680.10
Notes: UB: Uncertainty bounds; LM: Likelihood Measure; AVG: Average; SD: Standard Deviation.
For a given likelihood measure, a cut-off threshold plays a role in determining the posterior pdf of an uncertain variable. Figure 4 and Figure 5 show the posterior pdfs of the model variables for the top 1% and 100% of the E and F likelihood measures. Results for the W likelihood measures are not appropriate in this study, because the W likelihood measure is largely affected by valley shapes and, hence, not included. The posterior pdf of each model variable has a different shape for different cut-off thresholds. Regardless of the prior pdf combinations, robust posterior pdfs are obtained for topography for a cut-off threshold of the top 1% of the F and E likelihood measures (Figure 4). A cut-off threshold of 100% for the F and E likelihood measures does not produce any change in the shape of posterior pdfs of all model variables compared to prior pdfs (Figure 5). If the posterior pdf produced by a cut-off threshold of 100% likelihood measure is used as the updated prior pdf in the model parameter optimization using GLUE, the 100% threshold makes it difficult to search the optimal parameter in a model. However, a 100% threshold can be used to quantify the uncertainty bound in a flood inundation area propagated from the initial deterministic error in model variables. From these results, the threshold gives a significant contribution to the posterior pdf of variables.
Water 06 02104 g004 1024
Figure 4. The posterior pdfs of model variables for the top 1% of the E and F likelihood measures. The x-axis is the change of uncertainty in the model variable, and the y-axis indicates the probability.
Figure 4. The posterior pdfs of model variables for the top 1% of the E and F likelihood measures. The x-axis is the change of uncertainty in the model variable, and the y-axis indicates the probability.
Water 06 02104 g004
Water 06 02104 g005 1024
Figure 5. The posterior pdfs of the model variables for the top 100% of the E and F likelihood measures. The x-axis is the change of uncertainty in the model variable and the y-axis indicates the probability.
Figure 5. The posterior pdfs of the model variables for the top 100% of the E and F likelihood measures. The x-axis is the change of uncertainty in the model variable and the y-axis indicates the probability.
Water 06 02104 g005
Figure 6 shows how the ranges of model variable values from posterior pdfs change as the cut-off threshold is changed from 1% to 100% for the F and E likelihood measures. Among the three variables, discharge does not show any change in the range of values for most cut-off thresholds for the F and E likelihood measures (middle in Figure 6). The lower bound of topography becomes narrower as the cut-off threshold become smaller for the F and E likelihood measures (left in Figure 6). In the range for Manning’s n, the upper bound becomes abruptly narrower as the cut-off threshold becomes smaller than 5% for both likelihood measures (right in Figure 6). Overall, most cut-off thresholds produce similar trends in the ranges of model variables for the F and E likelihood measures.
Water 06 02104 g006 1024
Figure 6. The ranges of model variables based on likelihood measures corresponding to 1%, 5%, 10%, 20%, 50% and 100% cut-off thresholds. (a) Topography error; (b) Discharge change rate; (c) Manning’s n change rate. (Note: the F and E indicate the F and E likelihood measures, respectively. The lower 5% and upper 95% are the lower 5% and upper 95% uncertainty bounds corresponding to the likelihood measures).
Figure 6. The ranges of model variables based on likelihood measures corresponding to 1%, 5%, 10%, 20%, 50% and 100% cut-off thresholds. (a) Topography error; (b) Discharge change rate; (c) Manning’s n change rate. (Note: the F and E indicate the F and E likelihood measures, respectively. The lower 5% and upper 95% are the lower 5% and upper 95% uncertainty bounds corresponding to the likelihood measures).
Water 06 02104 g006

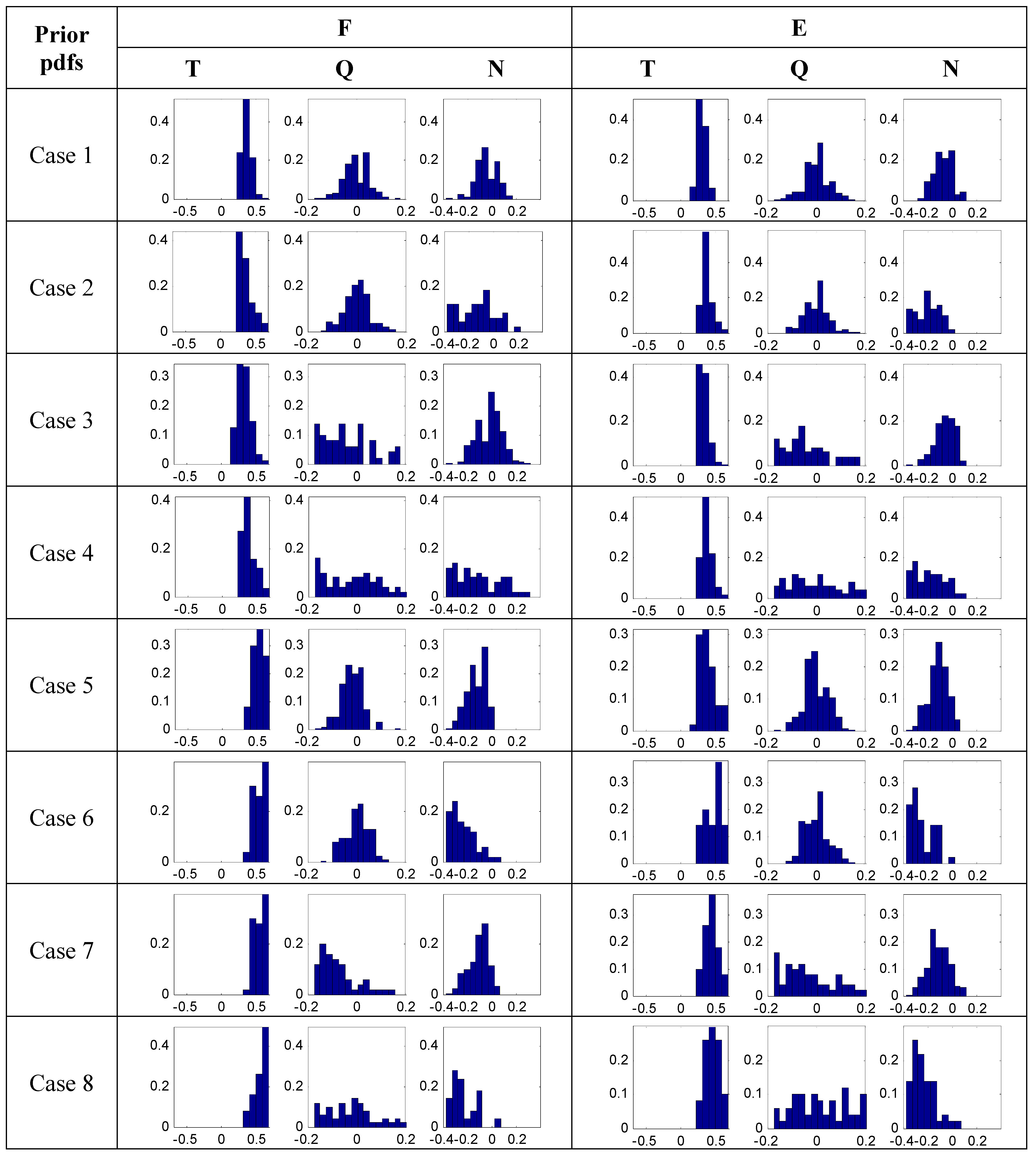
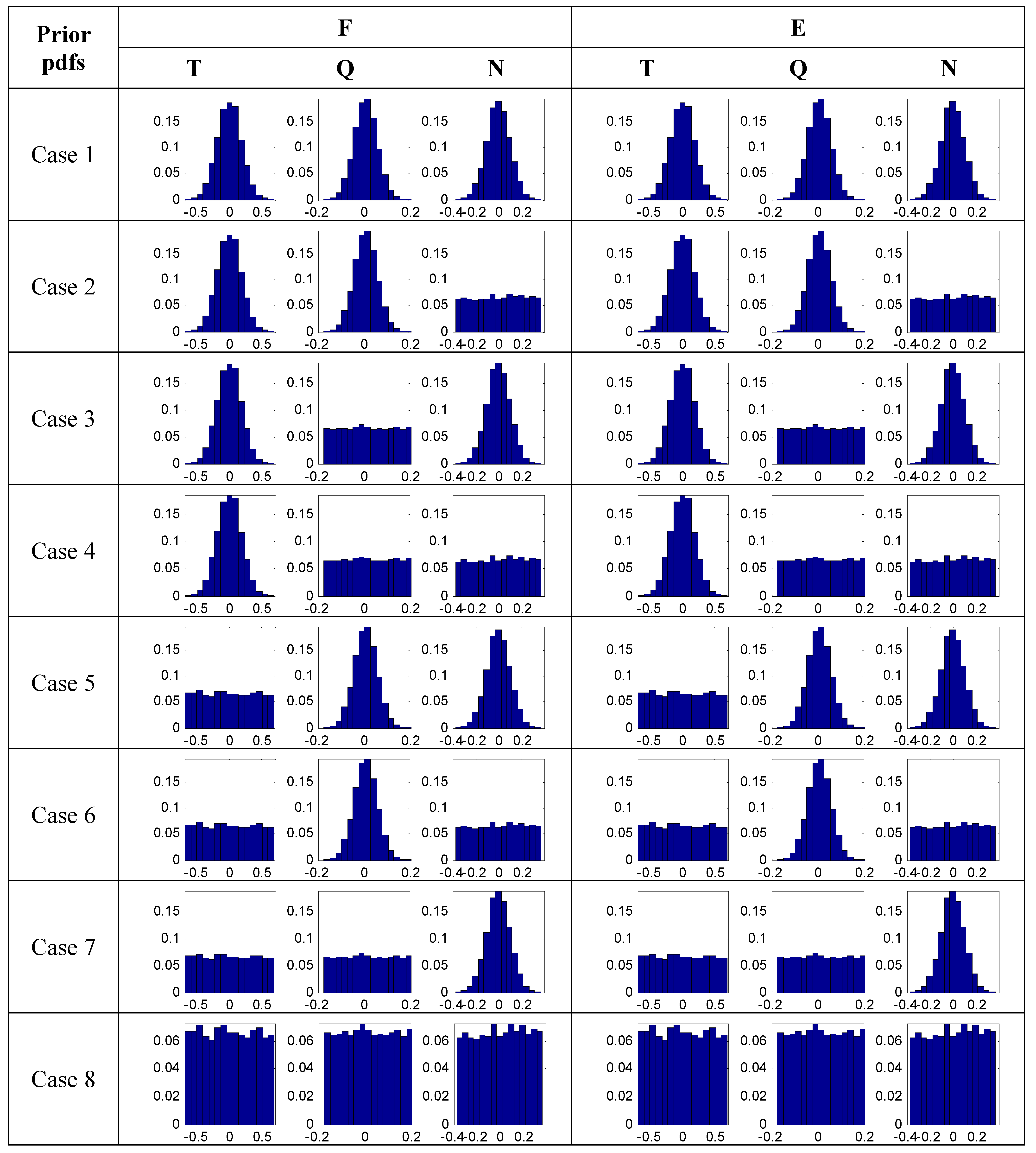
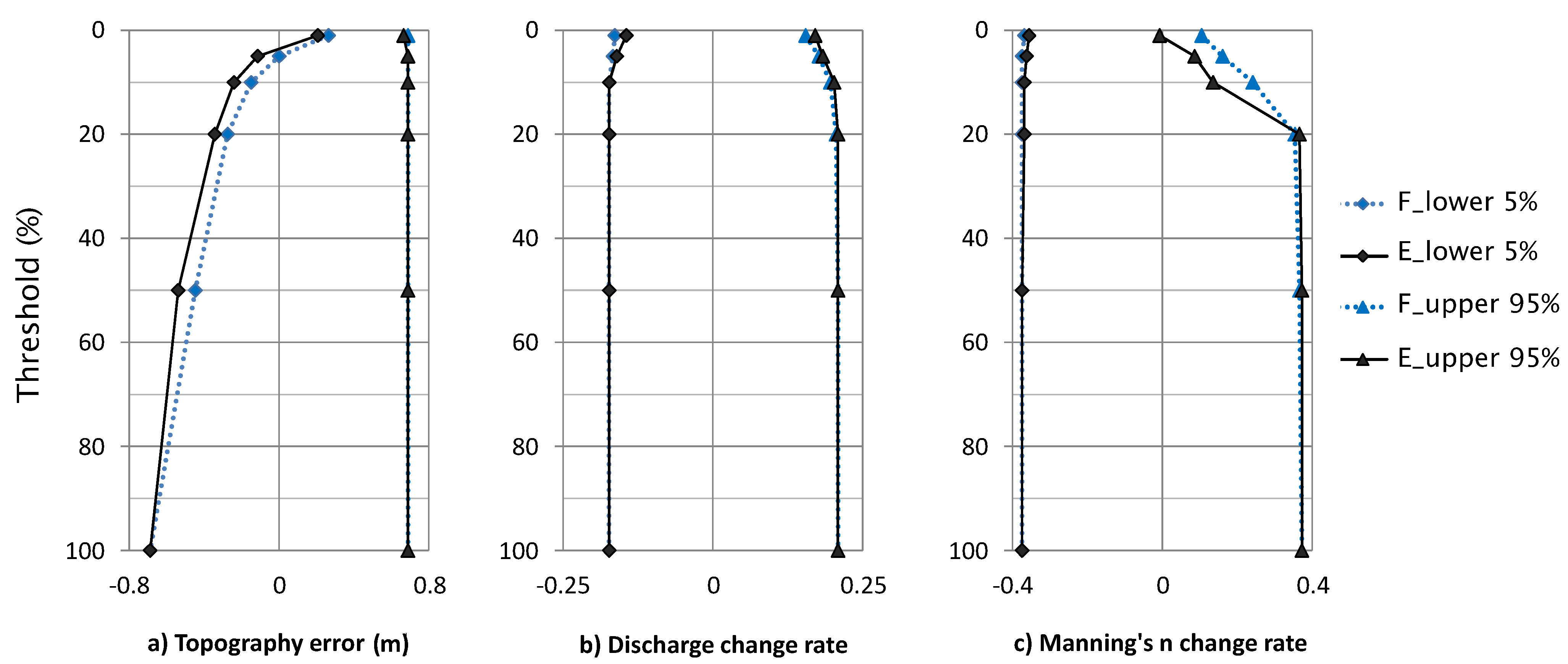
4.3. Uncertainty Quantification

In this study, behavioral models for the F and E likelihood measures are determined by various cut-off thresholds. These behavioral models are used to estimate the cdf of the flood inundation area. In this regard, Figure 7 shows the cdf results based on the F and E likelihood measures selected by the top 1%, 5%, 10%, 20%, 50% and 100% thresholds. Uncertainty boundaries between the F and E likelihood measures are significantly different for the 100% threshold, but slightly different for other thresholds. Table 4 and Table 5 shows the quantitative results of the uncertainty bound in the flood inundation area for the top 1%, 5%, 10%, 20%, 50% and 100% of the F and E likelihood measures. The estimated uncertainty bound ranges from 0.031 to 1.076 km2 for the F likelihood measure and from 0.026 to 0.557 km2. Considering the base inundation area of 10.57 km2 for the Seymour Reach, the top 100% F likelihood measure produces 10% uncertainty of the base area in the flood inundation area, while the E likelihood measure produces 5% uncertainty of the base area. For the 100% threshold (no criteria) in this study, the F likelihood measure delivers a twice higher uncertainty than the E likelihood measure. In the case of the top 50% threshold, both the F and E likelihood measures produce about 2.5% uncertainty of the base area. From this result, as the error involved in the combination of the model variables is larger, uncertainty is more sensitive to the flood inundation area by the F likelihood measure than the E likelihood measure.
Water 06 02104 g007 1024
Figure 7. Comparison of the generalized likelihood uncertainty estimation (GLUE) results based on the F and E likelihood measure: (a) F likelihood measure; (b) E likelihood measure.
Figure 7. Comparison of the generalized likelihood uncertainty estimation (GLUE) results based on the F and E likelihood measure: (a) F likelihood measure; (b) E likelihood measure.
Water 06 02104 g007
Table
Table 4. F likelihood measure values, the number of datasets and the uncertainty bounds corresponding to the thresholds where a threshold indicates a percentage of total simulation (e.g., top 10% of best likelihood measures), the E likelihood measure shows the value calculated by the E likelihood function and the number of accepted datasets shows the number of datasets selected by the threshold. The uncertainty bound means 90% bounds between the lower 5% bound and the upper 95% bound for the inundation area.
Table 4. F likelihood measure values, the number of datasets and the uncertainty bounds corresponding to the thresholds where a threshold indicates a percentage of total simulation (e.g., top 10% of best likelihood measures), the E likelihood measure shows the value calculated by the E likelihood function and the number of accepted datasets shows the number of datasets selected by the threshold. The uncertainty bound means 90% bounds between the lower 5% bound and the upper 95% bound for the inundation area.
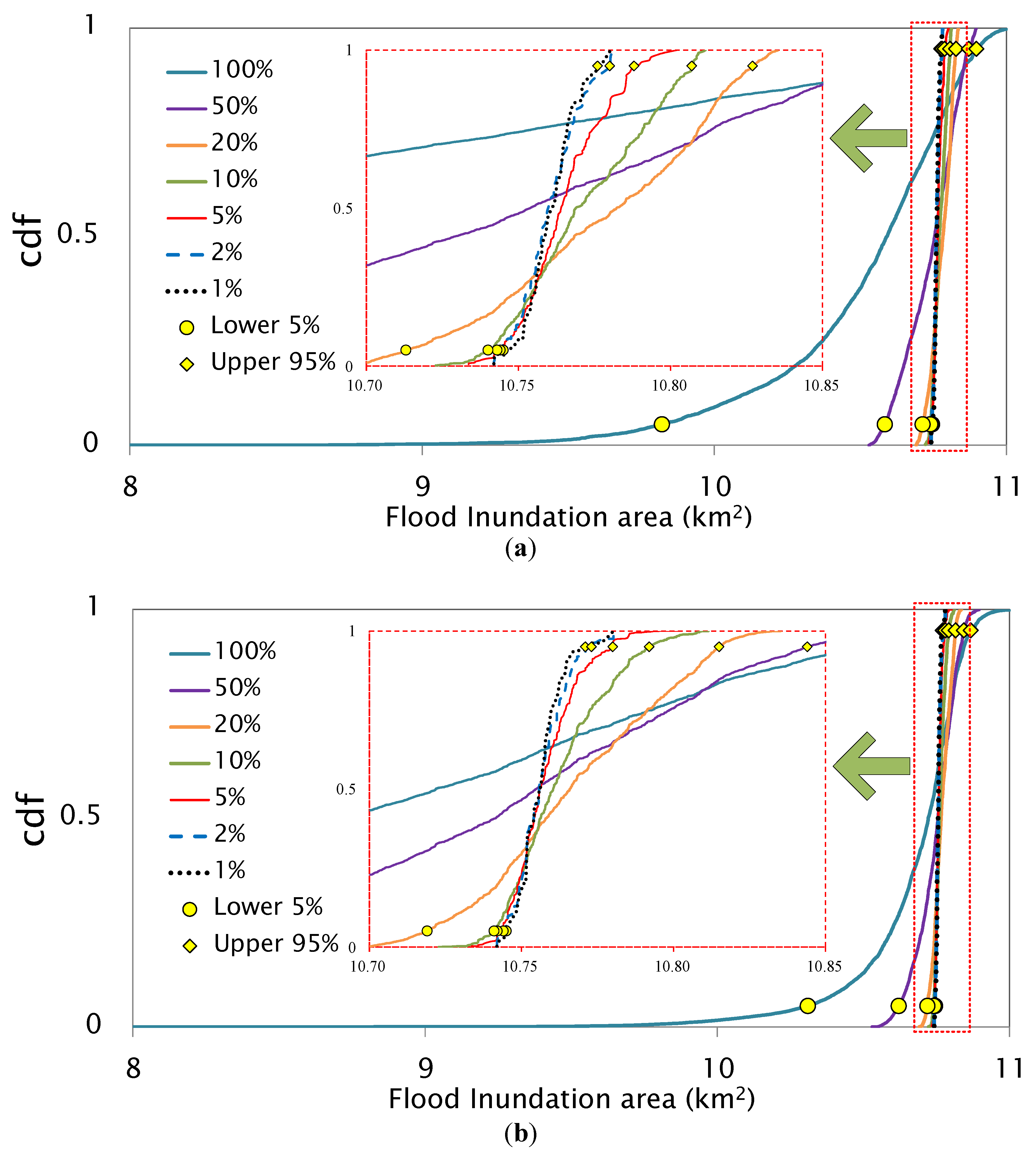
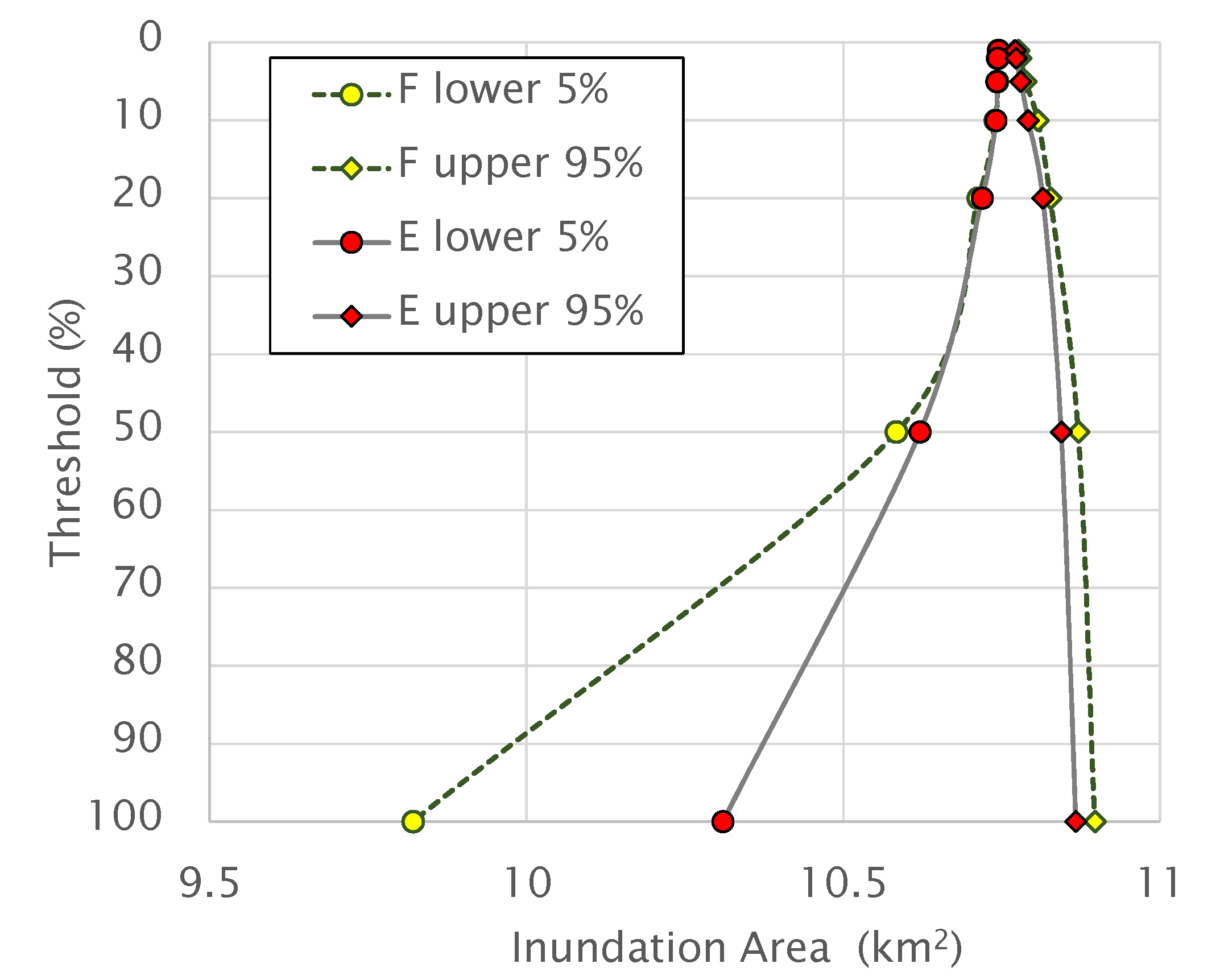
Threshold (%)F Likelihood MeasureNo. of Accepted Dataset5% Lower Bound (L) (km2)95% Upper Bound (U) (km2)Uncertainty Bound (U–L) (km2)
10.94795010.74510.7760.031
20.947810010.74410.7800.036
50.947625010.74310.7880.045
100.947350010.74010.8070.067
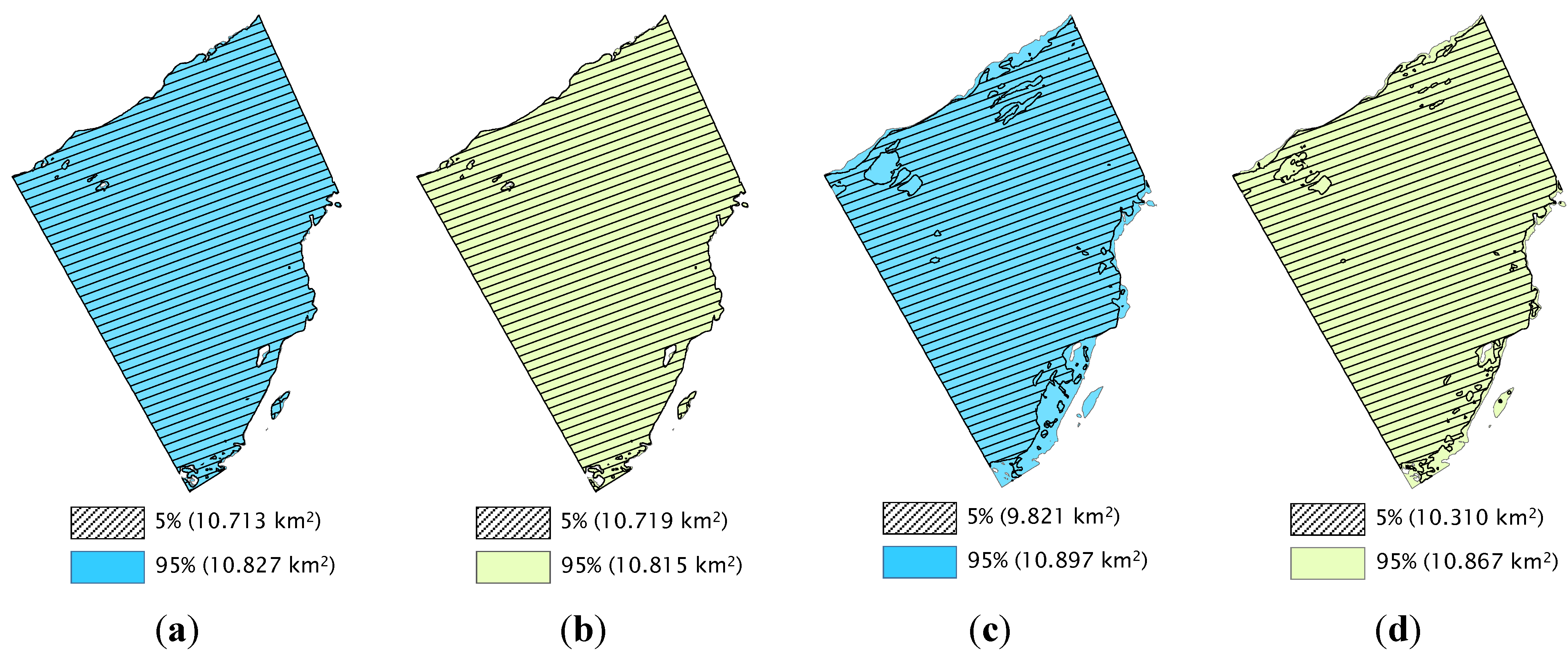
200.9468100010.71310.8270.114
500.9444250010.58410.8710.287
1000.749950009.82110.8971.076
Table
Table 5. E likelihood measure values, the number of datasets and the uncertainty bounds corresponding to the thresholds.
Table 5. E likelihood measure values, the number of datasets and the uncertainty bounds corresponding to the thresholds.
Threshold(%)E Likelihood Measure (km−1)No. of Accepted Dataset5% Lower Bound (L) (km2)95% Upper Bound (U) (km2)Uncertainty Bound (U–L) (km2)
11.2155010.74510.7710.026
21.19610010.74410.7730.029
51.15625010.74210.7800.038
101.09550010.74110.7920.051
200.879100010.71910.8150.096
500.41250010.62110.8440.286
1000.093500010.31010.8670.557
As the cut-off threshold is relaxed with a low likelihood measure, the uncertainty bound for the inundation area is wider (Figure 8). In particular, the change in lower bounds is greater than the change in upper bounds. Moreover, the uncertainty bounds changed slightly from the top 50% to the top 1% threshold. The uncertainty bounds of the F likelihood measure are entirely wider than ones of the E likelihood measure. However, the difference in uncertainty of the E and F likelihood measures becomes smaller from the top 50% threshold. In this regard, Figure 9 shows the spatial comparisons of the 5% and 95% uncertainty bounds based on the F and E likelihood measures with the top 20% and 100% thresholds. Specifically, a and b of Figure 9 are the flood inundation maps considering uncertainty based on the top 20% F and E likelihood measures, and the spatial difference between a and b of Figure 9 is tiny. However, the spatial difference between the flood inundation maps based on the top 100% F and E likelihood measures can be easily found in c and d of Figure 9.
Water 06 02104 g008 1024
Figure 8. Uncertainty bounds according to the thresholds based on the F and E likelihood measures.
Figure 8. Uncertainty bounds according to the thresholds based on the F and E likelihood measures.
Water 06 02104 g008
Water 06 02104 g009 1024
Figure 9. Inundation areas for Seymour Reach. (a) Inundation area by taking the top 20% of the F likelihood measures; (b) Inundation area by taking the top 20% of the E likelihood measures; (c) Inundation area by taking the top 100% of the F likelihood measures; (d) Inundation area by taking the top 100% of the E likelihood measure; where, 5 and 95 indicate the lower 5% and the higher 95% inundation areas, respectively.
Figure 9. Inundation areas for Seymour Reach. (a) Inundation area by taking the top 20% of the F likelihood measures; (b) Inundation area by taking the top 20% of the E likelihood measures; (c) Inundation area by taking the top 100% of the F likelihood measures; (d) Inundation area by taking the top 100% of the E likelihood measure; where, 5 and 95 indicate the lower 5% and the higher 95% inundation areas, respectively.
Water 06 02104 g009

5. Discussion

Simulation and prediction of flood inundation extent involves incorporating uncertainty at various levels, including input data, model structure and observations. The GLUE methodology has been used in several past studies to account for the uncertainty in flood inundation mapping [53,54,55]. Some studies that have used GLUE have acknowledged the subjective nature of the decisions that need to be made in the GLUE methodology. Specifically, the choice of likelihood measure and the selection of behavioral versus non-behavioral models are subjective in nature. Typically, the choice of likelihood measure depends on the observed data for the floodplain. Many studies in flood inundation mapping use the F-statistic as the likelihood measure, because of its ability to capture the spatial extent of the entire flood (e.g., [12,48,49]). Some studies also use the extent data [9,10] or water levels [13] to develop the likelihood measure. In a study such as the one presented here, where a map of observed inundation extent is available, the choice of the F-statistic would be considered appropriate for use in the GLUE methodology. This study used three informal likelihood measures to represent the error in the prediction of the water surface extent (W likelihood measure) at individual cross-sections, the water surface elevation (E likelihood measure) at individual cross-sections and the overall flood extent (F likelihood measure). Although the W and E likelihood measures used the same statistical function (sum of absolute error), they produced different measure distributions, because of different comparison targets (flood extent width for the W likelihood measure and water surface elevation for the E likelihood measure).
The results show that the E likelihood measure proved to be more appropriate among the three different likelihood measures for the study reach with a U-shaped valley. Thus, in addition to the available data, information related to the river valley should also be considered within the context of the sensitivity of the likelihood measure to the hydraulic model output. For a U-shaped valley, the water surface extent and, hence, the W and F likelihood measures will show no change in the extent in relation to the change in water levels for high flows. For a simple calibration process, any of the three measures can be used for assessing the performance of the model output for high flows, but all of them may behave differently when the model is run for various flow conditions. Hence, a measure that can be used for assessing performance may not necessarily prove to be an effective likelihood measure for assessing uncertainty using the GLUE methodology for a U-shaped valley. On the other hand, a flat terrain may show significant change in flood extent with slight variation in the water level. In such cases, likelihood measures, such as the W likelihood measure or the F likelihood measure, which are based on water extent, may prove to be useful compared to a measure based on water surface elevation. It is also important to note that the choice of a measure based on elevation or extent is critical in uncertainty or sensitivity analyses, but not necessarily so when assessing the performance of a model for an individual event. For example, the HEC-RAS model used in this study can be calibrated for a high flood event using any of the W, E or F likelihood measures as the objective function without significantly affecting the final flood inundation map.
Even though the selection of an appropriate likelihood measure is subjective, its choice can be guided by the availability of observed data and other factors, such as the shape of the river valley, as found in this study. The selection of behavioral and non-behavioral models to get the uncertainty bound is based on specifying an acceptable range for the model output based on observations (e.g., [12]), specifying an absolute value for the likelihood measure or specifying a behavioral threshold (e.g., [2,56]). In the absence of errors associated with the observed flood inundation map, this study used a threshold to distinguish between behavioral and non-behavioral models. With this approach, a tighter threshold produces a narrower uncertainty bound and vice versa. As a result, the range of parameter values included in the behavior models also changes for a cut-off threshold. Thus, it may be possible to get an uncertainty bound corresponding to a specific threshold, but the parameter range associated with that uncertainty bound may not necessarily include the optimum parameters.
This paper deals with the subjectivity of the selection of likelihood measures and behavioral thresholds by using discharge, topography and channel roughness as uncertain variables. In many studies involving GLUE, the first step is to select the uncertain parameter to be included in the analysis. Although uncertainty in discharge estimates, error in topography data and uncertain estimates of channel roughness are commonly used in flood inundation mapping, choosing one variable over other or their connectivity can also affect the GLUE method. Pappenberger et al. [12] studied the effect of a rating curve, channel roughness and internal boundary conditions (bridge structure) at a reach along the Alzette River in Luxembourg and found that the effect of uncertainty in the rating curve depended on the implementation of the form of the chosen bridge. The selection of a combination of variables as listed in Table 1 did take into consideration the relative effect of uncertain variables on each other, but this issue is not specifically investigated in this study. Some of these relative effects are also dictated by the flow conditions and the overall morphology of the reach. For example, as found by Pappenberger et al. [12], the effect of an uncertain rating curve is significant as long as the flow regime and the subsequent inundation was not impacted by the bridge formulation.

6. Conclusions

Considering the increased occurrence of flooding events in many parts of the world, the production of flood inundation maps has emerged as a necessary step for effective flood risk management, including relief and rescue efforts. Similarly, considering the importance of the flood inundation maps, the issue of quantifying and representing uncertainty has become more critical than ever. GLUE is one of the widely used methods in hydrology for uncertainty quantification. GLUE is a subjective method that involves making decisions on a probability distribution of the uncertain variable and the selection of likelihood measures and a cut-off threshold to develop the uncertainty bound. Depending on the choices made for the probability distribution, likelihood measure and cut-off threshold, the results may vary. This study is an attempt to explore the range in uncertainty, while applying the GLUE methodology. Eight combinations of prior pdfs are used for three uncertain variables (topography, discharge and Manning’s n) in the GLUE method, involving three different likelihood measures and multiple cut-off thresholds for defining behavioral models. While the subjectivity of the GLUE methodology is widely discussed in the literature, a framework to quantify the effect of these subjective decisions on the final result does not exist. This study is an attempt to develop such a framework. Based on the results from only one study area used in this study, the following conclusions are drawn:
  • Results from this study show that the uncertainty bound in GLUE is affected by the type of prior pdf, and that the use of a normal prior pdf for a model variable produces a narrower uncertainty bound compared to a uniform prior pdf.
  • Among the three likelihood measures used in this study, the E likelihood measure (Equation (3)) based on water surface elevations is found to be less affected by the combination of prior pdfs for the model variables.
  • As the threshold for defining the behavioral model increases to include more datasets, the range of values for a model variable increases in the posterior pdf. This change is more prominent in topography and Manning’s n; whereas discharge does not show much change in the range of values for different cut-off thresholds and likelihood measures.
  • The shape of the posterior pdf also changes as the cut-off threshold is changed for different likelihood measures. Usually, the number of datasets used to create an uncertainty bound decreases with tighter thresholds. In order to get a reasonable number of datasets with a tighter threshold for the smooth cdf weighted by behavioral models, a large number of simulations are needed. However, too many simulations can increase the computational burden. Therefore, the number of simulations should be determined by considering the degree of a threshold.
  • Although the findings from this study are limited due to the use of a single test case, this paper provides a framework that can be utilized to gain a better understanding of the uncertainty while applying the GLUE methodology in flood inundation mapping. In addition, the application of this framework for other study areas may provide some guidance to generalize the findings of this study, thus advancing this important topic in flood inundation mapping.

Acknowledgments

This work was supported by the National Research Foundation of Korea Grant funded by the Korean Government (NRF-2009-220-D00104).

Author Contributions

This research presented here was carried out in collaboration between all authors. Younghun Jung and Venkatesh Merwade suggested/designed this research and contributed to the writing of the paper. Soojun Kim, Narae Kang, and Yonsoo Kim conducted data analysis. Keonhaeng Lee, Gilho Kim, and Hung Soo Kim designed/conducted the research methods. All authors discussed the structure and comment on the manuscript at all stages.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Krzysztofowicz, R. Probabilistic flood forecast: Bounds and approximations. J. Hydrol. 2002, 268, 41–55. [Google Scholar] [CrossRef]
  2. Beven, K.J.; Binley, A.M. The future of distributed models: Model calibration and uncertainty prediction. Hydrol. Process. 1992, 6, 279–298. [Google Scholar] [CrossRef]
  3. Liu, Y.B.; Batelaan, O.; De Smedt, F.; Poórová, J.; Velcická, L. Automated Calibration Applied to a GIS Based Flood Simulation Model Using PEST. In Floods, from Defence to Management, Proceedings of the 3rd International Symposium on Flood Defence, Nijmegen, The Netherlands, 25–27 May 2005; Van Alphen, J., van Beek, E., Taal, M., Eds.; CRC Press: Boca Raton, FL, USA, 16 February 2006. [Google Scholar]
  4. Maskey, S.; Guinot, V.; Price, R.K. Treatment of precipitation uncertainty in rainfall-runoff modelling: A fuzzy set approach. Adv. Water Resour. 2004, 27, 889–898. [Google Scholar] [CrossRef]
  5. Montanari, A.; Brath, A. A stochastic approach for assessing the uncertainty of rainfall-runoff simulations. Water Resour. Res. 2004, 40. [Google Scholar] [CrossRef]
  6. Vrugt, J.A.; Diks, C.G.H.; Gupta, H.V.; Bouten, W.; Verstraten, J.M. Improved treatment of uncertainty in hydrologic modeling: Combining the strengths of global optimization and data assimilation. Water Resour. Res. 2005, 41. [Google Scholar] [CrossRef]
  7. Moradkhani, H.K.L.; Hsu, H.; Gupta, S. Sorooshian Uncertainty assessment of hydrologic model states and parameters: Sequential data assimilation using the particle filter. Water Resour. Res. 2005, 41. [Google Scholar] [CrossRef]
  8. Aronica, G.; Nasello, C.; Tucciarelli, T. 2D multilevel model for flood wave propagation in flood-affected areas. J. Water Resour. Plan. Manag. 1998, 124, 210–217. [Google Scholar] [CrossRef]
  9. Romanowicz, R.; Beven, K.J. Dynamic real-time prediction of flood inundation probabilities. Hydrol. Sci. J. 1998, 43, 181–196. [Google Scholar] [CrossRef]
  10. Romanowicz, R.J.; Beven, K.J. Estimation of flood inundation probabilities as conditioned on event inundation maps. Water Resour. Res. 2003, 39. [Google Scholar] [CrossRef]
  11. Pappenberger, F.; Beven, K.J.; Hunter, N.; Gouweleeuw, B.; Bates, P.; de Roo, A.; Thielen, J. Cascading model uncertainty from medium range weather forecasts (10 days) through a rainfall-runoff model to flood inundation predictions within the European Flood Forecasting System (EFFS). Hydrol. Earth Syst. Sci. 2005, 9, 381–393. [Google Scholar] [CrossRef]
  12. Pappenberger, F.; Beven, K.J.; Frodsham, K.; Romanovicz, R.; Matgen, P. Grasping the unavoidable subjectivity in calibration of flood inundation models: A vulnerability weighted approach. J. Hydrol. 2007, 333, 275–287. [Google Scholar] [CrossRef]
  13. Romanowicz, R.; Beven, K.J.; Tawn, J. Bayesian Calibration of Flood Inundation Models. In Floodplain Processes; Anderson, M.G., Walling, D.E., Bates, P.D., Eds.; Wiley: Chichester, UK, 1996; pp. 333–360. [Google Scholar]
  14. Heidari, A.; Saghafian, B.; Maknoon, R. Assessment of flood forecasting lead time based on generalized likelihood uncertainty estimation approach. Stoch. Environ. Res. Risk Assess. 2006, 20, 363–380. [Google Scholar] [CrossRef]
  15. Horritt, M.S. A methodology for the validation of uncertain flood inundation models. J. Hydrol. 2006, 326, 153–165. [Google Scholar] [CrossRef]
  16. Hunter, N.M. Utility of different data types for calibrating flood inundation models within a GLUE framework. Hydrol. Earth Syst. Sci. 2005, 9, 412–430. [Google Scholar] [CrossRef]
  17. Mantovan, P.; Todini, E. Hydrological forecasting uncertainty assessment: Incoherence of the GLUE methodology. J. Hydrol. 2006, 330, 368–381. [Google Scholar] [CrossRef]
  18. Mantovan, P.; Todini, E.; Martina, M. Reply to comment by Keith Beven, Paul Smith and JimFreer on “Hydrological forecasting uncertainty assessment: Incoherence of the GLUE methodology”. J. Hydrol. 2007, 338, 319–324. [Google Scholar] [CrossRef]
  19. Todini, E.P. Comment on: “On undermining the science?” by Keith Beven. Hydrol. Process. 2007a, 21, 1633–1638. [Google Scholar] [CrossRef]
  20. Todini, E.P. Hydrological catchment modelling: Past, present and future. Hydrol. Earth Syst. Sci. 2007b, 11, 468–482. [Google Scholar] [CrossRef]
  21. Todini, E.; Mantovan, P. Hydrological catchment modelling: Past, present and future. Hydrol. Earth Syst. Sci. 2007, 11, 468–482. [Google Scholar] [CrossRef]
  22. Beven, K.J.; Smith, P.J.; Freer, J.E. Comment on “Hydrological forecasting uncertainty assessment: Incoherence of the GLUE methodology” by Pietro Mantovan and Ezio Todini. J. Hydrol. 2007, 338, 315–318. [Google Scholar] [CrossRef]
  23. Beven, K.J.; Smith, P.J.; Freer, J.E. So just why would a modeller choose to be incoherent? J. Hydrol. 2008, 354, 15–32. [Google Scholar] [CrossRef]
  24. Beven, K.J. Environmental Modelling: An Uncertain Future? Routledge: London, UK, 2009; p. 310. [Google Scholar]
  25. Vrugt, J.A.; Robinson, B.A. Treatment of uncertainty using ensemble methods: Comparison of sequential data assimilation and Bayesian model averaging. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
  26. Sorooshian, S. Parameter estimation of rainfall run-off models with heteroscedastic streamflow errors—noninformative data case. J. Hydrol. 1981, 52, 127–138. [Google Scholar] [CrossRef]
  27. McMillan, H.; Clark, M. Rainfall-runoff model calibration using informal likelihood measures within a Markov chain Monte Carlo sampling scheme. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
  28. Robert, C.; Casella, G. Monte Carlo Statistical Methods, 2nd ed.; Springer: New York, NY, USA, 2004. [Google Scholar]
  29. Vazquez, R.F.; Feyen, L.; Feyen, J.; Refsgaard, J.C. Effect of grid size on effective parameters and model performance of the MIKE-SHE code. Hydrol. Process. 2002, 16, 355–372. [Google Scholar] [CrossRef]
  30. Bates, P.D.; Marks, K.J.; Horritt, M.S. Optimal use of high-resolution topographic data in flood inundation models. Hydrol. Process. 2003, 17, 537–557. [Google Scholar] [CrossRef]
  31. Parodi, U.; Ferraris, L. Influence of stage discharge relationships on the annual maximum discharge statistics. Nat. Hazards 2004, 31, 603–611. [Google Scholar] [CrossRef]
  32. Merwade, V.M.; Olivera, F.; Arabi, M.; Edleman, S. Uncertainty in flood inundation mapping—Current issues and future directions. J. Hydrol. Eng. 2008a, 13, 608–620. [Google Scholar]
  33. Kenward, T.; Lettenmaier, D.; Wood, E.F.; Fielding, E. Effects of digital elevation model accuracy on hydrologic predictions. Remote Sens. Environ. 2000, 74, 432–444. [Google Scholar] [CrossRef]
  34. Vaze, J.; Teng, J.; Spencer, G. Impact of DEM accuracy and resolution on topographic indices. Environ. Model. Softw. 2010, 25, 1086–1098. [Google Scholar] [CrossRef]
  35. Herschy, R.W. Streamflow Measurement; Elsevier: London, UK, 1985. [Google Scholar]
  36. Montgomery, D.C.; Peck, A.P.; Vining, G.G. Introduction to Linear Regression Analysis; Wiley: New York, NY, USA, 2001. [Google Scholar]
  37. Chow, V.T. Open-Channel Hydraulics; McGraw- Hill Book Co.: New York, NY, USA, 1959; p. 80. [Google Scholar]
  38. Arcement, G.J.; chneider, V.R. Guide for Selecting Manning’s Roughness Coefficients for Natural Channels and Flood Plains US; Geological Survey Water Supply Paper 2339; US Government Printin Office: Washington, DC, USA, 1989; p. 38. [Google Scholar]
  39. Xiong, L.; O’Connor, K.M. An empirical method to improve the prediction limits of the GLUE methodology in rainfall—Runoff modeling. J. Hydrol. 2008, 349, 115–124. [Google Scholar] [CrossRef]
  40. Cook, A.; Merwade, V. Effect of topographic data, geometric configuration and modeling approach on flood inundation mapping. J. Hydrol. 2009, 377, 131–142. [Google Scholar] [CrossRef]
  41. Watson, D.F.; Phillip, G.M. Triangle based interpolation. Math. Geol. 1984, 8, 779–795. [Google Scholar] [CrossRef]
  42. Beven, K.J. A manifesto for the equifinality thesis. J. Hydrol. 2006, 320, 18–36. [Google Scholar] [CrossRef] [Green Version]
  43. Beven, K.J. On doing better hydrological science. Hydrol. Process. 2008, 22, 3549–3553. [Google Scholar] [CrossRef]
  44. Freer, J.; Beven, K.; Ambroise, B. Bayesian estimation of uncertainty in runoff prediction and the value of data: An application of the GLUE approach. Water Resour. Res. 1996, 32, 2161–2173. [Google Scholar] [CrossRef]
  45. Ratto, M.S.; Tarantola, A. Saltelli Sensitivity analysis in model calibration: GSA-GLUE approach. Comput. Phys. Commun. 2001, 136, 212–224. [Google Scholar] [CrossRef]
  46. Kinner, D.A.; Stallard, R.F. Identifying storm flow pathways in a rainforest catchment using hydrological and geochemical modelling. Hydrol. Process. 2004, 18, 2851–2875. [Google Scholar] [CrossRef]
  47. Uhlenbrook, S.; Sieber, A. On the value of experimental data to reduce the prediction uncertainty of a process-oriented catchment model. Environ. Model. Softw. 2005, 20, 19–32. [Google Scholar] [CrossRef]
  48. Aronica, G.; Bates, P.D.; Horritt, M.S. Assessing the uncertainty in distributed model predictions using observed binary pattern information within GLUE. Hydrol. Process. 2002, 16, 2001–2016. [Google Scholar] [CrossRef]
  49. Horritt, M.S.; Bates, P.D. Effects of spatial resolution on a raster based model of flood flow. J. Hydrol. 2001, 253, 239–249. [Google Scholar] [CrossRef]
  50. Willmott, C. On the validation of models. Phys. Geogr. 1981, 2, 184–194. [Google Scholar]
  51. Willmott, C. Some comments on the evaluation of model performance. Bull. Am. Meterol. Soc. 1982, 63, 1309–1313. [Google Scholar] [CrossRef]
  52. Pappenberger, F.; Beven, K. Functional classification and evaluation of hydrographs based on multicomponent mapping. Int. J. River Basin Manag. 2004, 2, 1–8. [Google Scholar]
  53. Blazkova, S.; Beven, K.J. Uncertainty in flood estimation. Struct. Infrastruct. Eng. Maint. manag. Life-Cycle Des. Perform. 2009, 5, 325–332. [Google Scholar] [CrossRef]
  54. Mason, D.C.; Bates, P.D.; Dall’Amico, J.T. Calibration of uncertain flood inundation models using remotely sensed water levels. J. Hydrol. 2009, 368, 224–236. [Google Scholar] [CrossRef]
  55. Jung, Y.; Merwade, V. Uncertainty quantification in flood inundation mapping using generalized likelihood uncertainty estimate and sensitivity analysis. J. Hydrol. Eng. 2012, 17, 507–520. [Google Scholar] [CrossRef]
  56. Hornberger, G.M.; Beven, K.J.; Cosby, B.J.; Sappington, D.E. Shenandoah watershed study: Calibration of the topography-based, variable contributing area hydrological model to a small forested catchment. Wat. Resour. Res. 1985, 21, 1841–1850. [Google Scholar] [CrossRef]

Share and Cite

MDPI and ACS Style

Jung, Y.; Merwade, V.; Kim, S.; Kang, N.; Kim, Y.; Lee, K.; Kim, G.; Kim, H.S. Sensitivity of Subjective Decisions in the GLUE Methodology for Quantifying the Uncertainty in the Flood Inundation Map for Seymour Reach in Indiana, USA. Water 2014, 6, 2104-2126. https://doi.org/10.3390/w6072104

AMA Style

Jung Y, Merwade V, Kim S, Kang N, Kim Y, Lee K, Kim G, Kim HS. Sensitivity of Subjective Decisions in the GLUE Methodology for Quantifying the Uncertainty in the Flood Inundation Map for Seymour Reach in Indiana, USA. Water. 2014; 6(7):2104-2126. https://doi.org/10.3390/w6072104

Chicago/Turabian Style

Jung, Younghun, Venkatesh Merwade, Soojun Kim, Narae Kang, Yonsoo Kim, Keonhaeng Lee, Gilho Kim, and Hung Soo Kim. 2014. "Sensitivity of Subjective Decisions in the GLUE Methodology for Quantifying the Uncertainty in the Flood Inundation Map for Seymour Reach in Indiana, USA" Water 6, no. 7: 2104-2126. https://doi.org/10.3390/w6072104

APA Style

Jung, Y., Merwade, V., Kim, S., Kang, N., Kim, Y., Lee, K., Kim, G., & Kim, H. S. (2014). Sensitivity of Subjective Decisions in the GLUE Methodology for Quantifying the Uncertainty in the Flood Inundation Map for Seymour Reach in Indiana, USA. Water, 6(7), 2104-2126. https://doi.org/10.3390/w6072104

Article Metrics

Back to TopTop