A Web-Based Model to Estimate the Impact of Best Management Practices
Abstract
:1. Introduction


2. Methodology
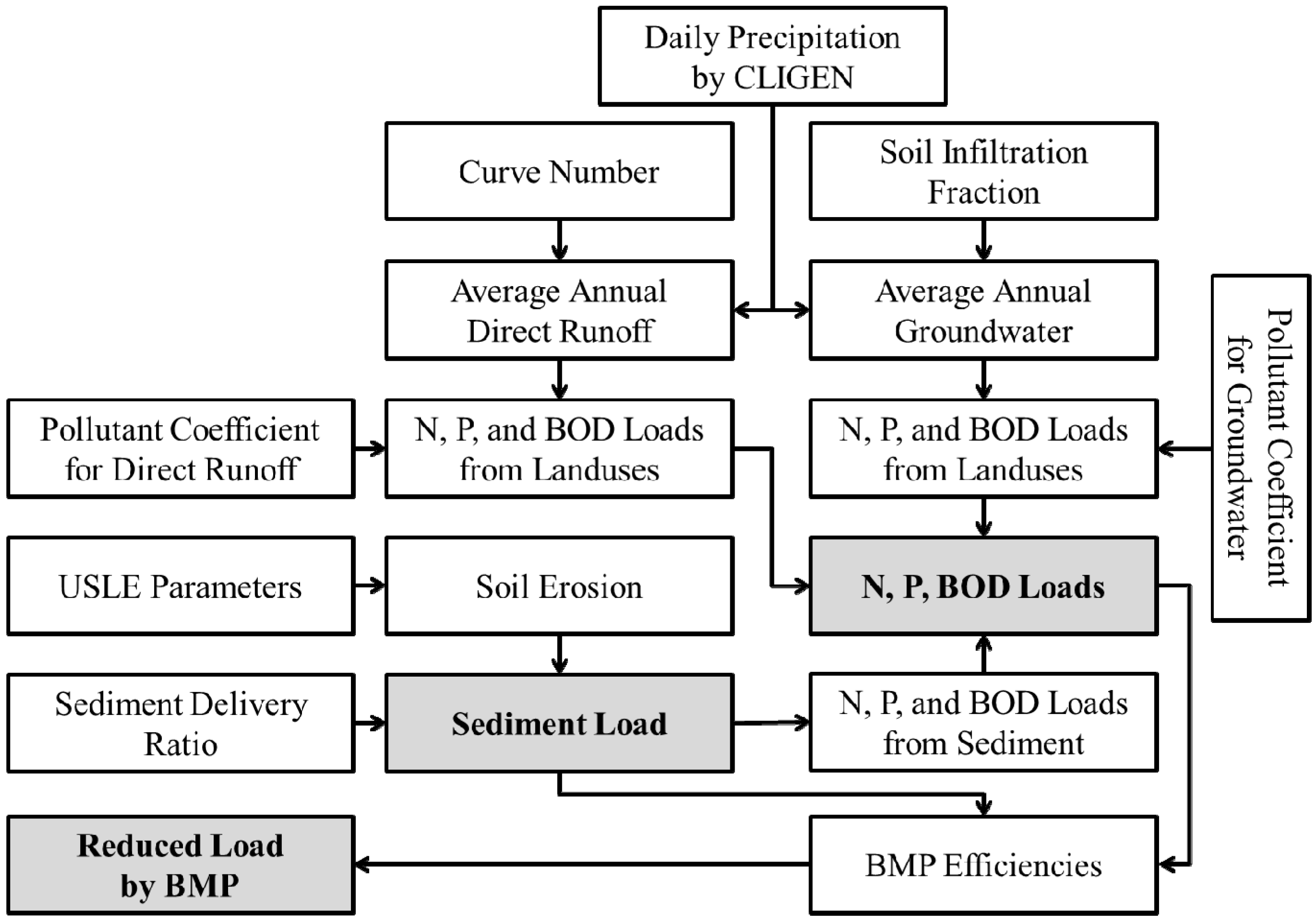
2.1. Average Annual Direct Runoff Computations


| Station Number | Station Name | Period |
|---|---|---|
| USC00120676 | Berne WWTP | 1949–1999 |
| USC00121747 | Columbus | 1921–2010 |
| USC00121869 | Crane NSA | 1943–1959 |
| USW00014848 | South Bend Michiana Regional Airport | 1948–2012 |
| USC00128999 | Valparaiso Waterworks | 1985–2000 |
| USC00129138 | Wabash | 1989–2004 |
| USC00129430 | West Lafayette 6 NW | 1989–2012 |
| USC00129678 | Winchester AAP 3 | 1989–2012 |
| USC00121229 | Cambridge City 3 N | 1975–1992 |
| USC00123547 | Greensburg | 1933–1941 |
| USC00127125 | Princeton 1 W | 1898–1952 |
| USC00127875 | Scottsburg | 1897–2000 |
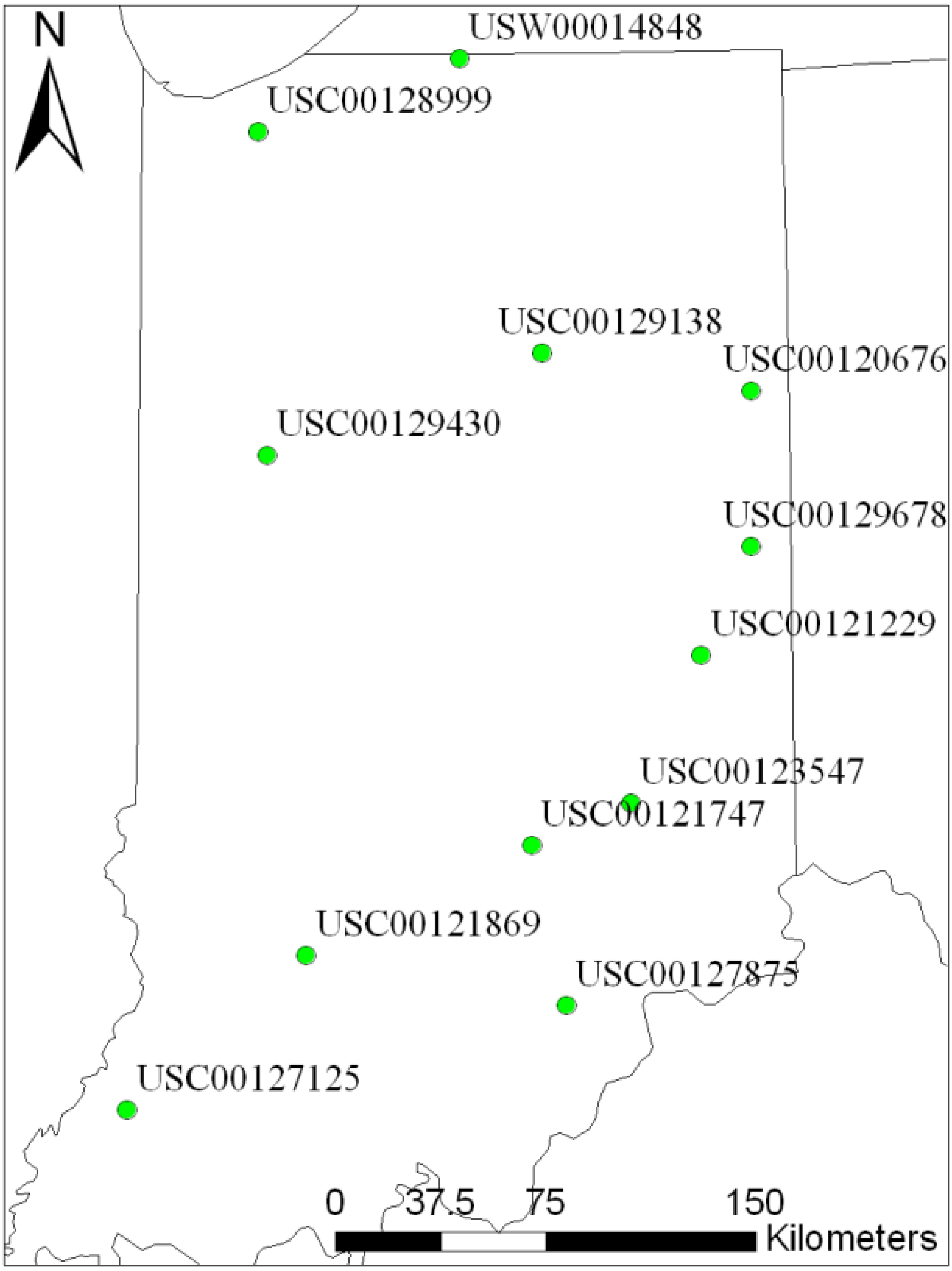
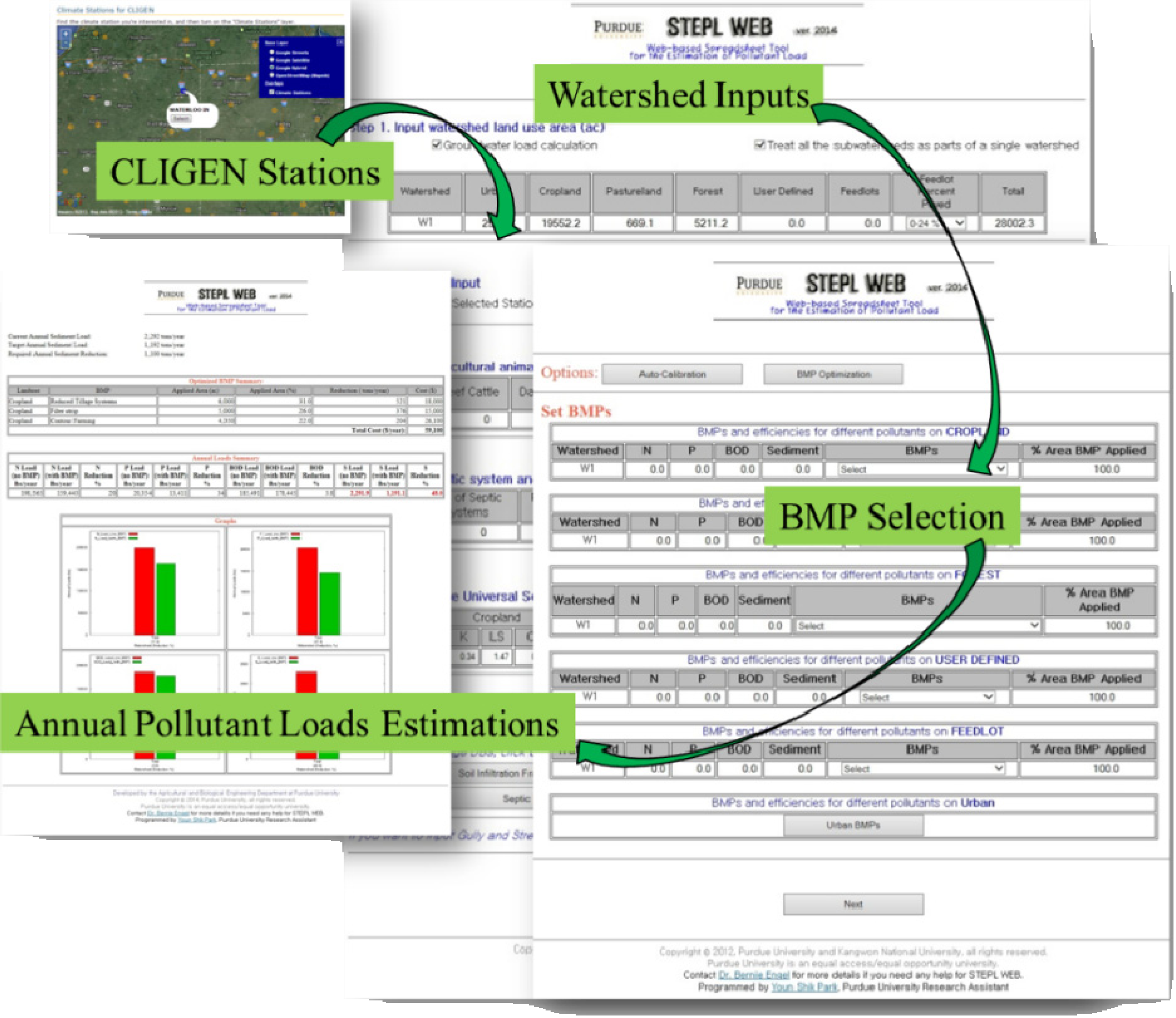
2.2. Web Interfaces and CLIGEN Use
| Land use | Best Manage Practices and Low Impact Development Practices |
|---|---|
| Cropland | Contour Farming, Diversion, Filter Strip, Reduced Tillage Systems, |
| Stream Bank Stabilization and Fencing, Terrace | |
| Forest | Road Dry Seeding, Road Grass and Legume Seeding, Road Hydro Mulch, |
| Road Straw Mulch, Road Tree Planting, Site Preparation/Hydro Mulch/Seed/Fertilizer, | |
| Site Preparation/Hydro Mulch/Seed/Fertilizer/Transplants, | |
| Site Preparation/Steep Slope Seeder/Transplant, | |
| Site Preparation/Straw/Crimp Seed/Fertilizer/Transplant, | |
| Site Preparation/Straw/Crimp/Net, Site Preparation/Straw/Net/Seed/Fertilizer/Transplant, | |
| Site Preparation/Straw/Polymer/Seed/Fertilizer/Transplant | |
| Feedlots | Diversion, Filter Strip, Runoff Management System, Solids Separation Basin, |
| Solids Separation Basin w/Infiltration Bed, Terrace, Waste Management System, | |
| Waste Storage Facility | |
| Urban | Alum Treatment, Bioretention Facility, Concrete Grid Pavement, Dry Detention, |
| Extended Wet Detention, Filter Strip-Agricultural, Grass Swales, Infiltration Basin, | |
| Infiltration Devises, Infiltration Trench, LID/Cistern, LID/Cistern + Rain Barrel, | |
| LID/Rain Barrel, LID/Bioretention, LID/Dry Well, LID/Filter/Buffer Strip, | |
| LID/Infiltration Swale, LID/Infiltration Trench, LID/Vegetated Swale, LID/Wet Swale, | |
| Oil/Grit Separator, Porous Pavement, Sand Filter/Infiltration Basin, Sand Filters, | |
| Settling Basin, Vegetated Filter Strips, Weekly Street Sweeping, Wet Pond, | |
| Wetland Detention, WQ Inlet w/Sand Filter, WQ Inlets |
2.3. Auto-Calibration Modules
2.4. Optimization of Best Management Practices

3. Results and Discussion
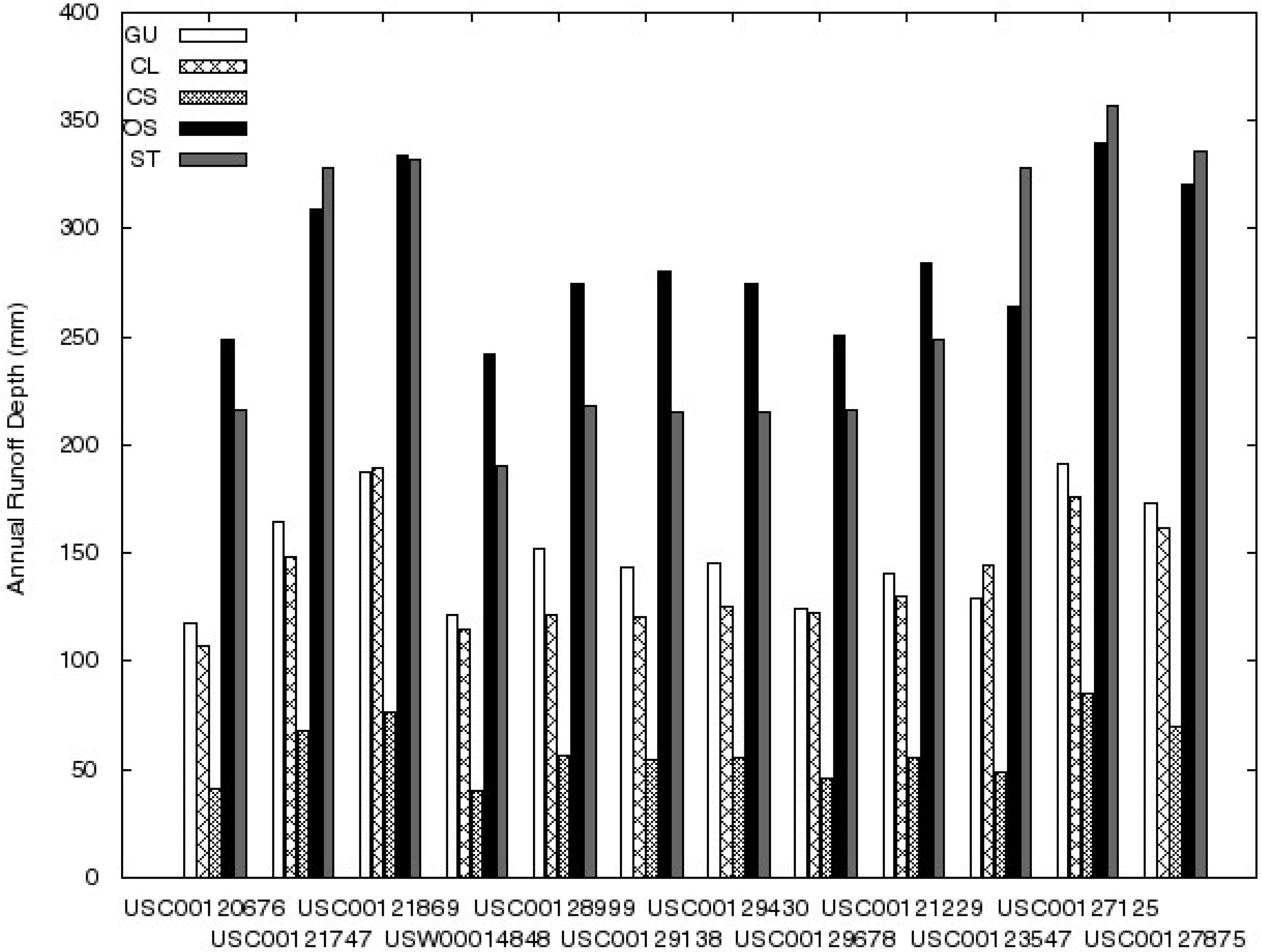
3.1. Average Annual Direct Runoff Computations
| Station | Precipitation (mm) | Average Annual Direct Runoff Depth (mm) | TC8 | |||||
|---|---|---|---|---|---|---|---|---|
| PN1 | PC2 | GU3 | CL4 | CS5 | OS6 | ST7 | ||
| USC00120676 | 963.8 | 940.7 | 117.4 | 107.4 | 41.6 | 248.6 | 216.0 | 78 |
| USC00121747 | 1077.0 | 1027.1 | 164.9 | 147.9 | 68.0 | 309.4 | 327.8 | 76 |
| USC00121869 | 1128.1 | 1146.3 | 187.7 | 189.3 | 76.1 | 334.4 | 331.8 | 76 |
| USW00014848 | 970.7 | 950.5 | 121.1 | 114.5 | 40.2 | 242.5 | 190.7 | 78 |
| USC00128999 | 1008.6 | 958.9 | 152.6 | 121.4 | 56.0 | 274.4 | 218.4 | 76 |
| USC00129138 | 1025.7 | 925.5 | 143.8 | 120.8 | 54.5 | 280.4 | 215.2 | 77 |
| USC00129430 | 996.0 | 935.1 | 145.3 | 125.1 | 55.6 | 274.8 | 215.2 | 77 |
| USC00129678 | 931.3 | 951.8 | 124.8 | 122.6 | 45.8 | 250.8 | 216.2 | 77 |
| USC00121229 | 1044.5 | 1027.8 | 141.1 | 130.3 | 55.6 | 284.4 | 249.1 | 77 |
| USC00123547 | 994.8 | 1047.9 | 129.6 | 144.1 | 48.4 | 263.9 | 327.8 | 77 |
| USC00127125 | 1080.4 | 1069.2 | 191.4 | 176.4 | 85.6 | 339.9 | 357.0 | 75 |
| USC00127875 | 1097.9 | 1078.6 | 173.0 | 161.6 | 69.6 | 320.8 | 335.7 | 76 |
3.2. Application of STEPL WEB

| Land use | Area (km2) | Percentage (%) |
|---|---|---|
| Urban | 10.4 | 8.1 |
| Cropland | 79.2 | 61.3 |
| Pasture | 2.7 | 2.1 |
| Forest | 21.1 | 16.3 |
| Water | 15.7 | 12.2 |
| Total | 129.1 | 100.0 |
| Model Parameters | HSG | A | B | C | D |
|---|---|---|---|---|---|
| Curve Number | Urban | 83/90 | 89/97 | 92/98 | 93/98 |
| Cropland | 67/73 | 78/85 | 85/92 | 89/97 | |
| Pastureland | 49/53 | 69/75 | 79/86 | 84/91 | |
| Forest | 39/42 | 60/65 | 73/79 | 79/86 | |
| Soil Infiltration Fraction | Urban | 0.36/0.31 | 0.24/0.21 | 0.12/0.01 | 0.06/0.05 |
| Cropland | 0.45/0.39 | 0.30/0.26 | 0.15/0.13 | 0.08/0.07 | |
| Pastureland | 0.45/0.39 | 0.30/0.26 | 0.15/0.13 | 0.08/0.07 | |
| Forest | 0.45/0.39 | 0.30/0.26 | 0.15/0.13 | 0.08/0.07 | |
| Pollutant Coefficient Phosphorus (mg/L) | Urban | 0.30/0.18 | |||
| Cropland | 0.50/0.30 | ||||
| Pastureland | 0.30/0.18 | ||||
| Forest | 0.10/0.06 | ||||
| Sediment Delivery Ratio | 0.42 × (0.3861 × Area (km2))−0.1350/0.02 × (0.3861 × Area (km2))−0.1350 | ||||
| Model Outputs | Measured | Predicted |
|---|---|---|
| Direct Runoff | 16.7 × 106 m3/year | 16.7 × 106 m3/year |
| Baseflow | 25.9 × 106 m3/year | 25.6 × 106 m3/year |
| Sediment | 237 ton/year | 245 ton/year |
| Phosphorus | 2.3 ton/year | 2.3 ton/year |
4. Conclusions
Conflicts of Interest
References
- Kang, M.S.; Park, S.W.; Lee, J.J.; Yoo, K.H. Applying SWAT for TMDL programs to a small watershed containing rice paddy fields. Agric. Water Manag. 2006, 79, 72–92. [Google Scholar] [CrossRef]
- Park, Y.S.; Park, J.H.; Jang, W.S.; Ryu, J.C.; Kang, H.; Choi, J.; Lim, K.J. Hydrologic response unit routing in SWAT to simulate effects of vegetative filter strip for South-Korean conditions. Water 2011, 3, 819–842. [Google Scholar] [CrossRef]
- Park, Y.S.; Engel, B.A.; Shin, Y.; Choi, J.; Kim, N.W.; Kim, S.J.; Kong, D.S.; Lim, K.J. Development of Web GIS-based VFSMOD System with three modules for effective vegetative filter strip design. Water 2013, 5, 1194–1210. [Google Scholar] [CrossRef]
- Patil, A.; Deng, Z. Bayesian approach to estimating margin of safety for total maximum daily load development. J. Environ. Manag. 2011, 92, 910–918. [Google Scholar] [CrossRef]
- Pease, L.M.; Oduor, P.; Padmanabhan, G. Estimating sediment, nitrogen, and phosphorus loads from the pipestem creek watershed, North Dakota, using AnnAGNPS. Comput. Geosci. 2010, 36, 282–291. [Google Scholar] [CrossRef]
- Richards, C.E.; Munster, C.L.; Vietor, D.M.; Arnold, J.G.; White, R. Assessment of a turfgrass sod best management practice on water quality in a suburban watershed. J. Environ. Manag. 2008, 86, 229–245. [Google Scholar] [CrossRef]
- Tetra Tech, Inc. User’s Guide Spreadsheet Tool for the Estimation of Pollutant Load (STEPL) Version 4.1; Tetra Tech, Inc.: Fairfax, VA, USA, 2011. [Google Scholar]
- Commonwealth Biomonitoring. Little River Watershed Diagnostic Study; Commonwealth Biomonitoring: Indianapolis, IN, USA, 2009. [Google Scholar]
- FDEP (Florida Department of Environmental Protection). State of Florida FY2010 Section 319(h) Grant Work Plan; FDEP: Tallahassee, FL, USA, 2009. [Google Scholar]
- Keegstra, N.; Parks, J.; Linden, L.V. Whiskey Creek Final Report; Calvin College: Grand Rapids, MI, USA, 2012. [Google Scholar]
- USDA-NRCS (U.S. Department of Agriculture, Natural Resources Conservation Service). National Engineering Handbook; USDA-NRCS: Washington, DC, USA, 1985; Section 4; pp. 1–20. [Google Scholar]
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large area hydrologic modeling and assessment—Part 1: Model development. J. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Leonard, R.A.; Knisel, W.G.; Still, D.A. GLEAMS: Groundwater loading effects on agricultural management. Trans. ASAE 1987, 30, 1403–1428. [Google Scholar] [CrossRef]
- Lim, K.J.; Engel, B.A.; Tang, Z.; Muthukrishnan, S.; Choi, J.; Kim, K. Effects of calibration on L-THIA GIS runoff and pollutant estimation. J. Environ. Manag. 2006, 78, 35–43. [Google Scholar] [CrossRef]
- Williams, J.R.; LaSeur, V. Water yield model using SCS CN curve numbers. J. Hydraul. Eng. 1976, 102, 1241–1253. [Google Scholar]
- Williams, J.R.; Arnold, J.G.; Srinivasan, R. The APEX Model; BRC Report No. 00–06; Blackland Research and Extension Center, Texas Agricultural Experiment Station, Texas A & M University System: Temple, TX, USA, 2000. [Google Scholar]
- Tedela, N.H.; McCutcheon, S.C.; Rasmussen, T.C.; Hawkins, R.H.; Swank, W.T.; Campbell, J.L.; Adams, M.B.; Jackson, C.R.; Tollner, E.W. Runoff curve numbers for 10 small forested watersheds in the mountains of the eastern United States. J. Hydrol. Eng. 2012, 17, 1188–1198. [Google Scholar] [CrossRef]
- USDA-NRCS (U.S. Department of Agriculture, Natural Resources Conservation Service). Urban Hydrology for Small Watersheds; USDA-NRCS: Washington, DC, USA, 1986; Chapter 2; pp. 1–8. [Google Scholar]
- Baltas, E.A.; Dervos, N.A.; Mimikou, M.A. Technical note: Determination of the SCS initial abstraction ratio in an experimental watershed in Greece. Hydrol. Earth Syst. Sci. 2007, 11, 1825–1829. [Google Scholar] [CrossRef]
- Shi, Z.; Chen, L.; Fang, N.; Qin, D.; Cai, C. Research on the SCS-CN initial abstraction ratio using rainfall-runoff event analysis in the Three Gorges Area, China. Catena 2009, 77, 1–7. [Google Scholar] [CrossRef]
- Woodward, D.E.; Hawkins, R.H.; Jiang, R.; Hjelmfelt, A.T.; Van Mullem, J.A. Runoff curve number method: Examination of the initial abstraction ratio. In Proceedings of World Water & Environmental Resources Congress 2003 and Related Symposia, Philadelphia, PA, USA, 23–26 June 2003; American Society of Civil Engineers: Philadelphia, PA, USA, 2003. [Google Scholar]
- Web-based LDC Tool Homepage. Available online: https://engineering.purdue.edu/~ldc/ (accessed on 17 April 2013).
- National Climatic Data Center Homepage. Available online: https://www.ncdc.noaa.gov (accessed on 23 March 2013).
- Nicks, A.D.; Lane, L.J. USDA-Water Erosion Prediction Project: Hillsploe Profile Model Documentation; USDA-ARS National Soil Erosion Research Laboratory: West Lafayette, IN, USA, 1989. [Google Scholar]
- Zhang, X.C.; Garbrecht, J.D. Evaluation of CLIGEN precipitation parameters and their implication on WEPP runoff and erosion prediction. Trans. ASAE 2003, 46, 311–320. [Google Scholar]
- Elliot, W.J.; Arnold, C.D. Validation of the weather generator CLIGEN with precipitation data from Uganda. Trans. ASAE 2001, 44, 53–58. [Google Scholar] [CrossRef]
- Lim, K.J.; Engel, B.A. Extension and enhancement of National Agricultural Pesticide Risk Analysis (NAPRA) WWW decision support system to include nutrients. Comput. Electron. Agric. 2003, 38, 227–236. [Google Scholar] [CrossRef]
- USDA-NRCS (U.S. Department of Agriculture, Natural Resources Conservation Service). Sediment sources, yields, and delivery ratios. In National Engineering Handbook; USDA-NRCS: Washington, DC, USA, 1983; Chapter 6; pp. 5–8. [Google Scholar]
- Park, Y.S.; Kim, J.; Kim, N.W.; Kim, S.J.; Jeon, J.H.; Engel, B.A.; Jang, W.; Lim, K.J. Development of new R, C, and SDR modules for the SATEEC GIS system. Comput. Geosci. 2010, 36, 726–734. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems; University of Michigan Press: Ann Arbor, MI, USA, 1975. [Google Scholar]
- Lim, K.J.; Park, Y.S.; Kim, J.; Shin, Y.C.; Kim, N.W.; Kim, S.J.; Jeon, J.H.; Engel, B.A. Development of genetic algorithm-based optimization module in WHAT system for hydrograph analysis and model application. Comput. Geosci. 2010, 36, 936–944. [Google Scholar] [CrossRef]
- Toğan, V.; Daloğlu, T.A. An improved genetic algorithm with initial population strategy and self-adaptive member grouping. Comput. Struct. 2008, 86, 1204–1218. [Google Scholar] [CrossRef]
- Ashkar, F.; Mahdi, S. Fitting the log-logistic distribution by generalized moments. J. Hydrol. 2006, 328, 694–703. [Google Scholar] [CrossRef]
- Hong, Y.; Yeh, N.; Chen, J. The simplified methods of evaluating detention storage volume for small catchment. Ecol. Eng. 2006, 26, 355–364. [Google Scholar] [CrossRef]
- Neupauer, R.M.; Borcher, B. A MATLAB implementation of the minimum relative entropy method for linear inverse problems. Comput. Geosci. 2001, 27, 757–762. [Google Scholar] [CrossRef]
- Arabi, M.; Govindaraju, R.S.; Hantush, M.M. Cost-effective allocation of watershed management practices using a genetic algorithm. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Garen, D.C.; Moore, D.S. Curve number hydrology in water quality modeling: Uses, abuses, and future directions. J. Am. Water Resour. Assoc. 2005, 41, 377–388. [Google Scholar] [CrossRef]
- Water Quality Targets. Available online: http://www.in.gov/idem/nps/3484.htm (accessed on 21 October 2013).
- Runkel, R.L.; Crawford, C.G.; Cohn, T.A. Load Estimator (LOADEST):A Fortran Program for Estimating Constituent Loads in Streams and Rivers; U.S. Geological Survey Techniques and Methods: Reston, VA, USA, 2004. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Park, Y.S.; Engel, B.A.; Harbor, J. A Web-Based Model to Estimate the Impact of Best Management Practices. Water 2014, 6, 455-471. https://doi.org/10.3390/w6030455
Park YS, Engel BA, Harbor J. A Web-Based Model to Estimate the Impact of Best Management Practices. Water. 2014; 6(3):455-471. https://doi.org/10.3390/w6030455
Chicago/Turabian StylePark, Youn Shik, Bernie A. Engel, and Jon Harbor. 2014. "A Web-Based Model to Estimate the Impact of Best Management Practices" Water 6, no. 3: 455-471. https://doi.org/10.3390/w6030455
APA StylePark, Y. S., Engel, B. A., & Harbor, J. (2014). A Web-Based Model to Estimate the Impact of Best Management Practices. Water, 6(3), 455-471. https://doi.org/10.3390/w6030455




