Feasibility Study of a Simple and Low-Cost Device for Monitoring Trihalomethanes Presence in Water Supply Systems Based on Statistical Models
Abstract
:1. Introduction
2. Materials and Methods
2.1. Characterization of Data
| Parameter | Average | Standard Deviation |
|---|---|---|
| Total Organic Carbon (mg/L) | 2.10 | 0.66 |
| Combined Residual Chlorine (mg/L) | 0.80 | 0.31 |
| Free Residual Chlorine (mg/L) | 0.61 | 0.29 |
| Bicarbonates (mg/L) | 229.94 | 76.40 |
| Conductivity (μS/cm) | 1172.76 | 615.89 |
| Chloride (mg/L) | 221.56 | 153.67 |
| Temperature (°C) | 19.5 | 4.2 |
| Total THM (μg/L) | 105.80 | 63.61 |
2.2. Statistical Method
2.3. Device Description
- pH
- TOC
- Cl−
- Bicarbonate
- Conductivity
- Temperature
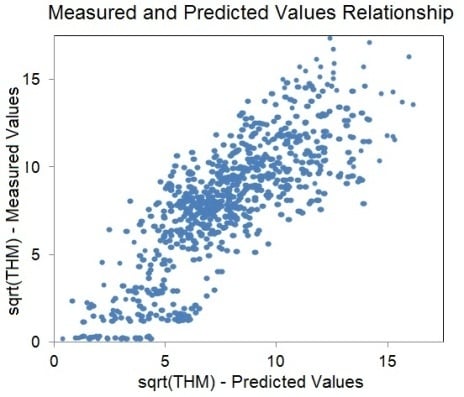
3. Results and Discussion
- TOC (Total Organic Carbon)
- TOC and ln(σ)
- TOC, ln(σ) and Combined Residual Chlorine (CRC)
- TOC, ln(σ), CRC, and pH
- TOC, ln(σ), CRC, pH and ln(Bc)
- TOC, ln(σ), CRC, pH, ln(Bc) and Temperature
| Dependent Variable | aj | βj | t | Significance |
|---|---|---|---|---|
| Total Organic Carbon (TOC) | 1.583 (0.071) | 0.533 | 22.229 | 0.000 |
| ln(σ) | 2.713 (0.131) | 0.459 | 20.736 | 0.000 |
| ln(Bc) | −1.307 (0.192) | −0.153 | −6.804 | 0.000 |
| Combined residual chlorine (CRC) | 3.744 (0.253) | 0.399 | 14.773 | 0.000 |
| pH | 2.427 (0.270) | 0.206 | 8.992 | 0.000 |
| Temperature | 0.102 (0.021) | 0.115 | 4.783 | 0.000 |

4. Conclusions
- -
- Total organic carbon (TOC)
- -
- Combined residual chlorine (CRC)
- -
- Conductivity
- -
- pH
- -
- Bicarbonates
- -
- Temperature.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Cantor, K.P.; Hoover, R.; Hartge, P.; Mason, T.J.; Silverman, D.T.; Levin, L.I. Drinking water source and risk of bladder cancer: A case—Control study. In Water Chlorination, Volume VI: Chemistry, Environmental Impact and Health Effects; Jolley, R.L., Bull, R.J., Davisw, W.P., Katz, S., Roberts, M.H., Jacobs, V.A., Eds.; CRC Press: Boca Raton, FL, USA, 1985; pp. 145–152. [Google Scholar]
- Cantor, K.P.; Lynch, C.F.; Hildesheim, M. Chlorinated drinking water and risk of glioma: A case—Control study in Iowa, USA. Epidemiology 1996, 7, S83. [Google Scholar] [CrossRef]
- Monarca, S.; Zani, C.; Richardson, S.D.; Thruston, A.D.; Moretti, J.M.; Feretti, D.; Villarini, M.A. New approach to evaluating the toxicity and genotoxicity of disinfected drinking water. Water Res. 2004, 38, 3809–3819. [Google Scholar] [CrossRef] [PubMed]
- Abdullah, M.D.; Yew, C.H.; Ramli, M.S. Formation, modeling and validation of trihalomethanes (THM) in Malaysian drinking water: A case study in the districts of Tampin, Negeri Sembilan and Sabak Bernam, Selangor, Malaysia. Water Res. 2003, 37, 4637–4644. [Google Scholar] [CrossRef] [PubMed]
- Sadiq, R.; Rodriguez, M.J. Fuzzy synthetic evaluation of disinfection by-products—A risk-based indexing system. J. Environ. Manag. 2004, 73, 1–13. [Google Scholar] [CrossRef]
- Directive, C. 98/83/EC of 3 November 1998 on the quality of water intended for human consumption. Off. J. Eur. Communities 1998, 5, 1–23. [Google Scholar]
- Sadiq, R.; Rodriguez, M.J. Disinfection by-products (DBPs) in drinking water and predictive models for their occurrence: A review. Sci. Total Environ. 2004, 321, 21–46. [Google Scholar] [CrossRef] [PubMed]
- Nokes, C.J.; Fenton, E.; Randall, C.J. Modelling the Formation of Brominated Trihalomethanes in Chlorinated Drinking Waters. Water Res. 1999, 33, 3557–3568. [Google Scholar] [CrossRef]
- Brown, D.; West, J.R.; Courtis, B.J.; Bridgeman, J. Modelling THMs in Water Treatment and Distribution Systems. ICE Proc. Water Manag. 2010, 163, 1–10. [Google Scholar] [CrossRef]
- Kulkarni, P.; Chellam, S. Disinfection by-product formation following chlorination of drinking water: Artificial neural network models and changes in speciation with treatment. Sci. Total Environ. 2010, 408, 4202–4210. [Google Scholar] [CrossRef] [PubMed]
- Westerhoff, P.; Debroux, J.; Amy, G.L.; Gatel, D.; Mary, V.; Cavard, J. Applying DBP models to full-scale plants. J. Am. Water Works Assoc. 2000, 92, 89–102. [Google Scholar]
- Sohn, J.; Amy, G.; Cho, J.; Lee, Y.; Yoon, Y. Disinfectant decay and disinfection by-products formation model development: Chlorination and ozonation by-products. Water Res. 2004, 38, 2461–2478. [Google Scholar] [CrossRef]
- Hong, H.C.; Liang, Y.; Han, B.P.; Mazumder, A.; Wong, M.H. Modeling of trihalomethane (THM) formation via chlorination of the water from Dongjiang River (source water for Hong Kong’s drinking water). Sci. Total Environ. 2007, 385, 48–54. [Google Scholar] [CrossRef]
- Uyak, V.; Ozdemir, K.; Toroz, I. Multiple linear regression modeling of disinfection by products formation in Istanbul drinking water reservoirs. Sci. Total Environ. 2007, 378, 269–280. [Google Scholar] [CrossRef] [PubMed]
- Singer, P.C.; Chang, S.D. Correlations between trihalomethanes and total organic halides formed during water treatment. J. Am. Water Works Assoc. 1989, 81, 61–65. [Google Scholar]
- Singer, P.C.; Obolensky, A.; Greiner, A. DBPs in chlorinated North Carolina drinking water. Am. Water Works Assoc. 1995, 87, 83–92. [Google Scholar]
- Chen, W.J.; Weisel, C.P. Halogenated DBP concentrations in a distribution system. J. Am. Water Works Assoc. 1998, 90, 151–163. [Google Scholar]
- Arora, H.; le Chevallier, M.W.; Dixon, K.L. DBP occurrence survey. J. Am. Water Works Assoc. 1997, 89, 60–68. [Google Scholar]
- Gallard, H.; von Gunten, U. Chlorination of natural organic matter: Kinetics of chlorination and of THM formation. Water Res. 2002, 36, 65–74. [Google Scholar] [CrossRef] [PubMed]
- Gang, D.; Clevenger, T.E.; Banerji, S.K. Relationship of chlorine decay and THMs formation to NOM size. J. Hazard. Mater. 2003, A96, 1–12. [Google Scholar] [CrossRef]
- Engerholm, B.A.; Amy, G.L. A predictive model for chloroform formation from humic acid. J. Am. Water Works Assoc. 1983, 75, 418–423. [Google Scholar]
- Adin, A.; Katzhendler, J.; Alkaslassy, D.; Rav-Acha, C. Trihalomethane formation in chlorinated drinking water: A kinetic model. Water Res. 1991, 25, 797–805. [Google Scholar] [CrossRef]
- Clark, R.M.; Sivaganesan, M. Predicting chlorine residuals and formation of TTHMs in drinking water. J. Environ. Eng. 1998, 124, 1203–1210. [Google Scholar] [CrossRef]
- Clark, R.M.; Thurnau, R.C.; Sivaganesan, M.; Ringhand, P. Predicting the formation of chlorinated and brominated by-products. J. Environ. Eng. 2001, 127, 493–501. [Google Scholar] [CrossRef]
- Golfinopoulos, S.K.; Arhonditsis, G.B. Quantitative assessment of trihalomethane formation using simulations of reaction kinetics. Water Res. 2002, 36, 2856–2868. [Google Scholar] [CrossRef] [PubMed]
- Gang, D.D.; Segar, R.L., Jr.; Clevenger, T.E.; Banerji, S.K. Using chlorine demand to predict THM and HAA9 formation. J. Am. Water Works Assoc. 2002, 94, 76–86. [Google Scholar]
- Campos, I.; Alcañiza, M.; Aguado, D.; Barat, R.; Ferrer, J.; Gil, L.; Marrakchi, M.; Martínez-Mañez, R.; Soto, J.; Vivancos, J.L. A voltammetric electronic tongue as tool for water quality monitoring in wastewater treatment plants. Water Res. 2012, 46, 2605–2614. [Google Scholar] [CrossRef] [PubMed]
- Gil, L.; Barat, J.M.; García-Breijo, E.; Ibañez, J.; Martínez-Máñez, R.; Soto, J.; Llobet, E.; Brezmes, J.; Aristoy, M.C.; Toldrá, F. Fish freshness analysis using metallic potentiometric electrodes. Sens. Actuators B Chem. 2008, 131, 362–370. [Google Scholar] [CrossRef]
- Paixão, T.R.L.C.; Bertotti, M. Fabrication a disposable voltammetric electronic tongues by using Prussian Blue films electrodeposited onto CD-R gold surfaces and recognition of milk adulteration. Sens. Actuators B Chem. 2009, 137, 266–273. [Google Scholar] [CrossRef]
- Parra, V.; Arrieta, A.; Fernández-Escudero, J.A.; García, H.; Apetrei, C.; Rodríguez-Méndez, M.L.; de Saja, J.A. E-Tongue based on a hybrid array of voltammetric sensors based on phthalocyanines, perylene derivatives and conducting polymers: Discrimination capability towards red wines elaborated with different variety of grapes. Sens. Actuators B Chem. 2006, 115, 54–61. [Google Scholar] [CrossRef]
- Parra, V.; Arrieta, A.A.; Fernández-Escudero, J.A.; Rodríguez-Mendez, M.L.; de Saja, J.A. Electronic tongue based on chemically modified electrodes and voltammetry for the detection of adulterations in wines. Sens. Actuators B Chem. 2006, 118, 448–453. [Google Scholar] [CrossRef]
- Francioso, L.; Bjorklund, R.; Krantz-Rulcker, T.; Siciliano, P. Classification of multiple defect concentrations in white wine by platinum microelectrode voltammetry. Sens. Actuators B Chem. 2007, 125, 462–467. [Google Scholar] [CrossRef]
- Winquist, F.; Bjorklund, R.; Krantz-Rülcker, C.; Lundström, I.; Östergren, K.; Skoglund, T. An electronic tongue in the dairy industry. Sens. Actuators B Chem. 2005, 111, 299–304. [Google Scholar] [CrossRef]
- Collier, W.A.; Baird, D.B.; Park-Ng, Z.A.; More, N.; Hart, A.L. Discrimination among milks and cultured dairy products using screen-printed electrochemical arrays and an electronic nose. Sens. Actuators B Chem. 2003, 92, 232–239. [Google Scholar] [CrossRef]
- Mimendia, A.; Gutierrez, J.M.; Leija, L.; Hernandez, P.R.; Favari, L.; Muñoz, R.; del Valle, M.A. Review of the use of the potentiometric electronic tongue in the monitoring of environmental systems. Environ. Model. Softw. 2010, 25, 1023–1030. [Google Scholar] [CrossRef]
- Nayak, K.; Supreetha, B.S.; Deccaraman, M.; Nayak, V. E-Nose System to Detect E-Coli in Drinking Water of Udupi District. Int. J. Eng. Res. Dev. 2012, 1, 58–64. [Google Scholar]
- Winquist, F.; Olsson, J.; Eriksson, M. Multicomponent analysis of drinking water by a voltammetric electronic tongue. Anal. Chim. Acta 2011, 683, 192–197. [Google Scholar] [PubMed]
- Kundu, P.K.; Chatterjee, A.; Panchariya, P.C. Electronic Tongue System for Water Sample Authentication: A Slantlet-Transform-Based Approach. IEEE Trans. Instrum. Meas. 2011, 60, 1959–1966. [Google Scholar] [CrossRef]
- Urano, K.; Wada, H.; Takemasa, T. Empirical rate equation for Trihalomethane formation with chlorination of humic substances in water. Water Res. 1983, 17, 1797–1802. [Google Scholar] [CrossRef]
- Morrow, C.M.; Minear, R.A. Use of regression models to link raw water characteristics to Trihalomethane concentrations in drinking water. Water Res. 1987, 21, 41–48. [Google Scholar] [CrossRef]
- Golfinopoulus, S.K.; Xilourgidis, N.K.; Kostopoulou, M.N.; Lekkas, T.D. Use of a multiple regression model for predicting trihalomethane formation. Water Res. 1998, 32, 2821–2829. [Google Scholar] [CrossRef]
- Golfinopoulus, S.K.; Arhonditsis, G.B. Multiple regression models: A methodology for evaluating trihalomethane concentrations in drinking water for raw water characteristics. Chemosphere 2002, 47, 1007–1018. [Google Scholar] [CrossRef] [PubMed]
- Mosteller, F.; Tukey, J.W. Data Analysis and Regression; Addison-Wesley: Reading, MA, USA, 1977. [Google Scholar]
- Chowdhury, S.; Champagne, P.; McLellan, P.J. Models for predicting disinfection by product (DBP) formation in drinking waters: A chronological review. Sci. Total Environ. 2009, 407, 4189–4206. [Google Scholar] [CrossRef] [PubMed]
- Sanz, D.A.; Unigarro, E.A.; Osma, J.F.; Segura-Quijano, F. Low cost wireless passive microsensors for the detection of hazardous compounds in water systems for control and monitoring. Sens. Actuators B Chem. 2013, 178, 26–33. [Google Scholar] [CrossRef]
- Tian, K.; Dasgupta, P.K. A permeable membrane capacitance sensor for ionogenic gases application to the measurement of total organic carbon. Anal. Chim. Acta 2009, 652, 245–250. [Google Scholar] [CrossRef] [PubMed]
- Fraser, K.J.; Curto, V.F.; Coyle, S.; Byrne, R.; Benito-Lopez, F.; Diamond, D.; Schazmann, B.; Owens, R.M.; Malliaras, G.G. Wearable electromechamical sensors for monitoring performance athletes. In Proceedings of the SPIE 8118 Organic Semiconductors in Sensors and Bioelectronics IV, San Diego, CA, USA, 21–25 August 2011.
- Diamond, D.; Coyle, S.; Scarmagnani, S.; Hayes, J. Wireless Sensor Networks and Chemo-Biosensing. Chem. Rev. 2008, 108, 652–679. [Google Scholar] [CrossRef] [PubMed]
- Benco, J.S.; Foos, J.S. Planar Bicarbonate Sensor. United States Patent 5554272, 10 August 1995. [Google Scholar]
- Wang, D.; Hu, P.; Xu, J.; Dong, X.; Pan, Q. Fast response chlorine gas sensor based on mesoporous SnO2. Sens. Actuators B Chem. 2009, 140, 383–389. [Google Scholar] [CrossRef]
- Chou, J.C.; Ye, G.C.; Wu, D.G.; Chen, C.C. Fabrication of the array chlorine ion sensor based on microfluidic device framework. Solid-State Electron. 2012, 77, 87–92. [Google Scholar] [CrossRef]
- Hilhorst, M.A. A Pore Water Conductivity Sensor. Soil Sci. Soc. Am. J. 2000, 64, 1922–1925. [Google Scholar]
- Vaz, A.; Ubarretxena, A.; Zalbide, I.; Pardo, D.; Solar, H.; García-Alonso, A. Full Passive UHF Tag with a Temperature Sensor Suitable for Human Body Temperature Monitoring. IEEE Trans. Circuits Syst. II Express Briefs 2010, 57, 95–99. [Google Scholar] [CrossRef]
- Rodriguez, M.J.; Sérodes, J.B. Spatial and temporal evolution of trihalomethanes in three water distribution systems. Water Res. 2001, 35, 1572–1586. [Google Scholar] [CrossRef] [PubMed]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rivadeneyra, A.; García-Ruiz, M.J.; Delgado-Ramos, F.; González-Martínez, A.; Osorio, F.; Rabaza, O. Feasibility Study of a Simple and Low-Cost Device for Monitoring Trihalomethanes Presence in Water Supply Systems Based on Statistical Models. Water 2014, 6, 3590-3602. https://doi.org/10.3390/w6123590
Rivadeneyra A, García-Ruiz MJ, Delgado-Ramos F, González-Martínez A, Osorio F, Rabaza O. Feasibility Study of a Simple and Low-Cost Device for Monitoring Trihalomethanes Presence in Water Supply Systems Based on Statistical Models. Water. 2014; 6(12):3590-3602. https://doi.org/10.3390/w6123590
Chicago/Turabian StyleRivadeneyra, Almudena, Maria Jesús García-Ruiz, Fernando Delgado-Ramos, Alejandro González-Martínez, Francisco Osorio, and Ovidio Rabaza. 2014. "Feasibility Study of a Simple and Low-Cost Device for Monitoring Trihalomethanes Presence in Water Supply Systems Based on Statistical Models" Water 6, no. 12: 3590-3602. https://doi.org/10.3390/w6123590
APA StyleRivadeneyra, A., García-Ruiz, M. J., Delgado-Ramos, F., González-Martínez, A., Osorio, F., & Rabaza, O. (2014). Feasibility Study of a Simple and Low-Cost Device for Monitoring Trihalomethanes Presence in Water Supply Systems Based on Statistical Models. Water, 6(12), 3590-3602. https://doi.org/10.3390/w6123590