Modeling Flood Inundation Induced by River Flow and Storm Surges over a River Basin
Abstract
:1. Introduction
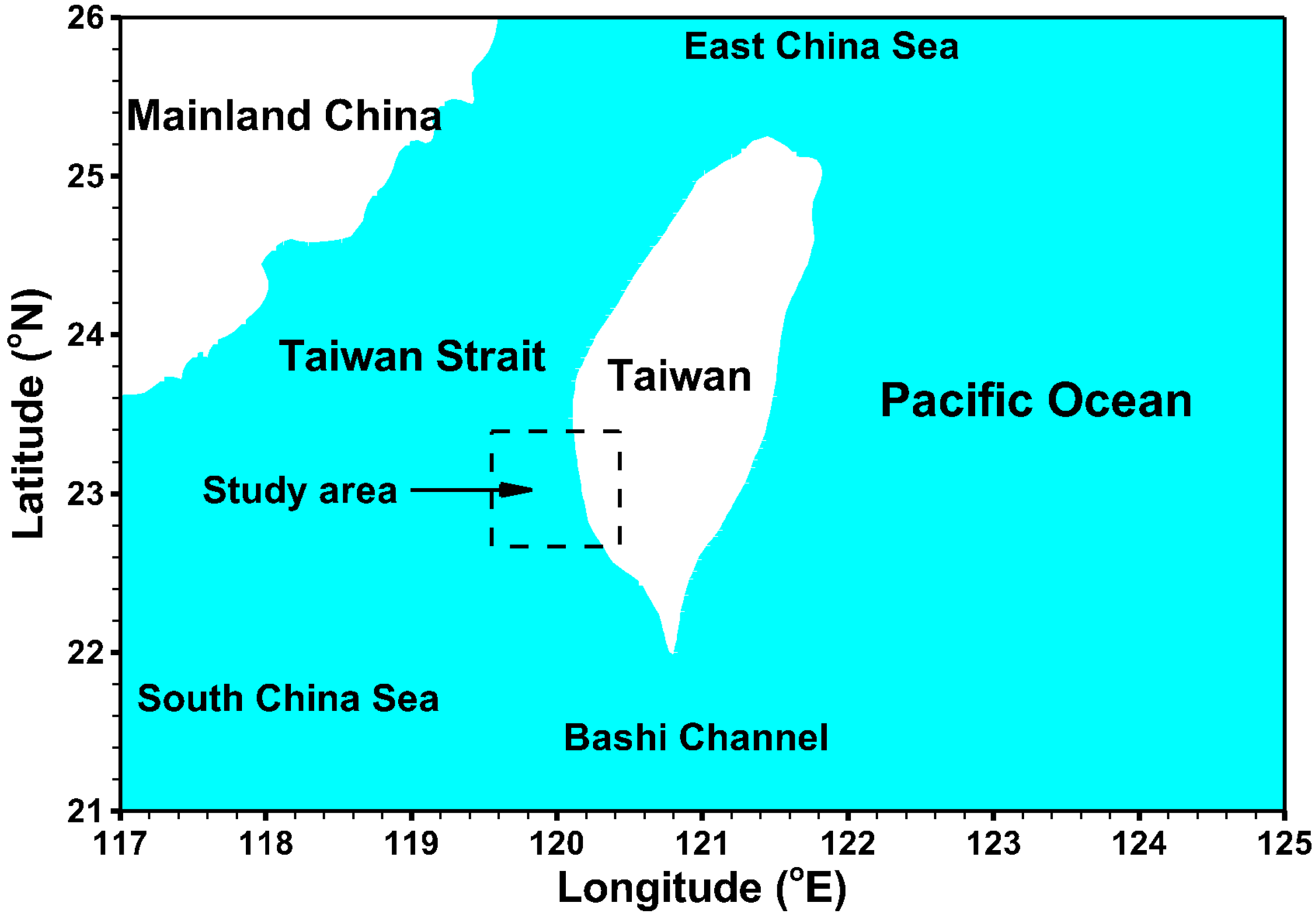
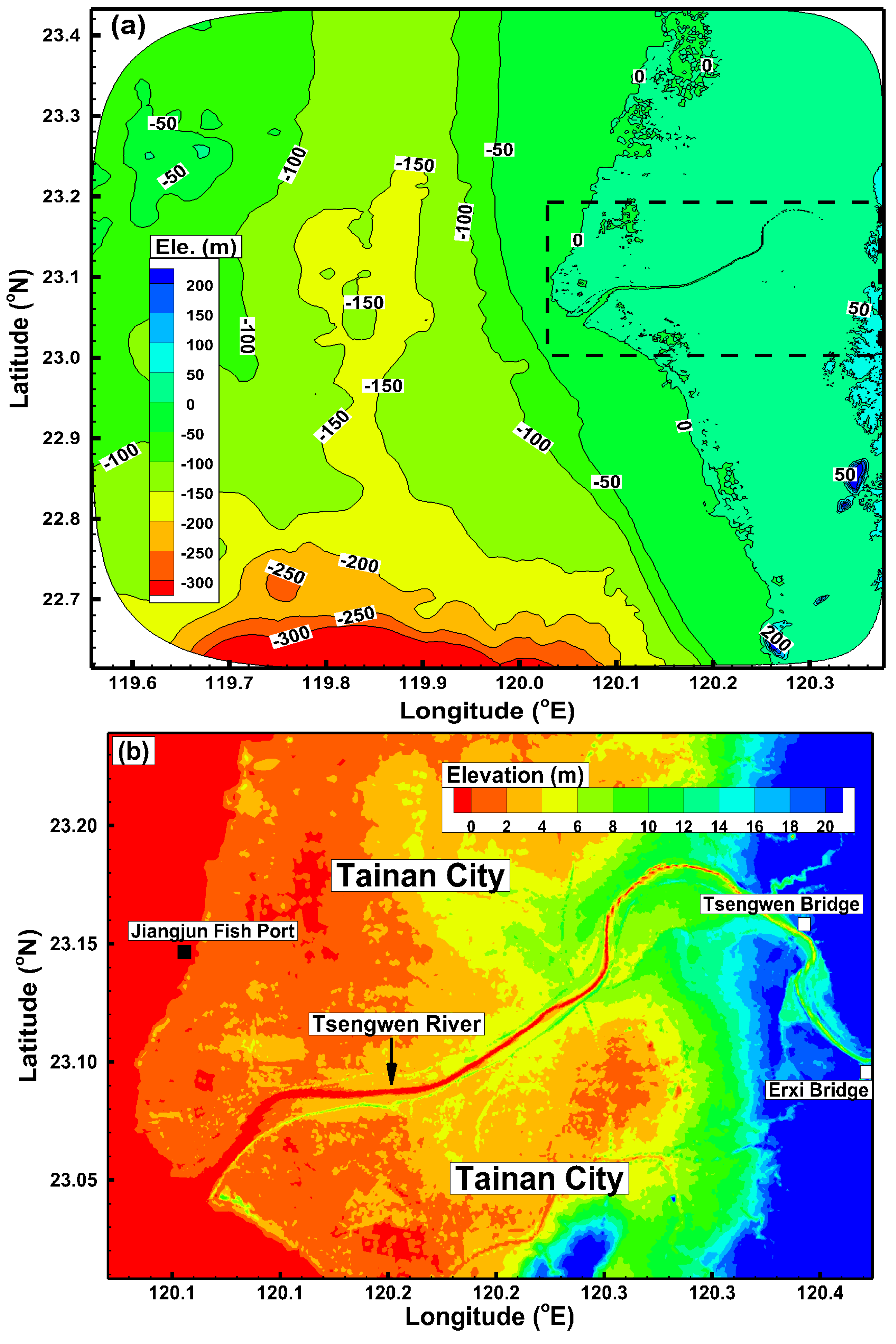
2. Description of Study Area
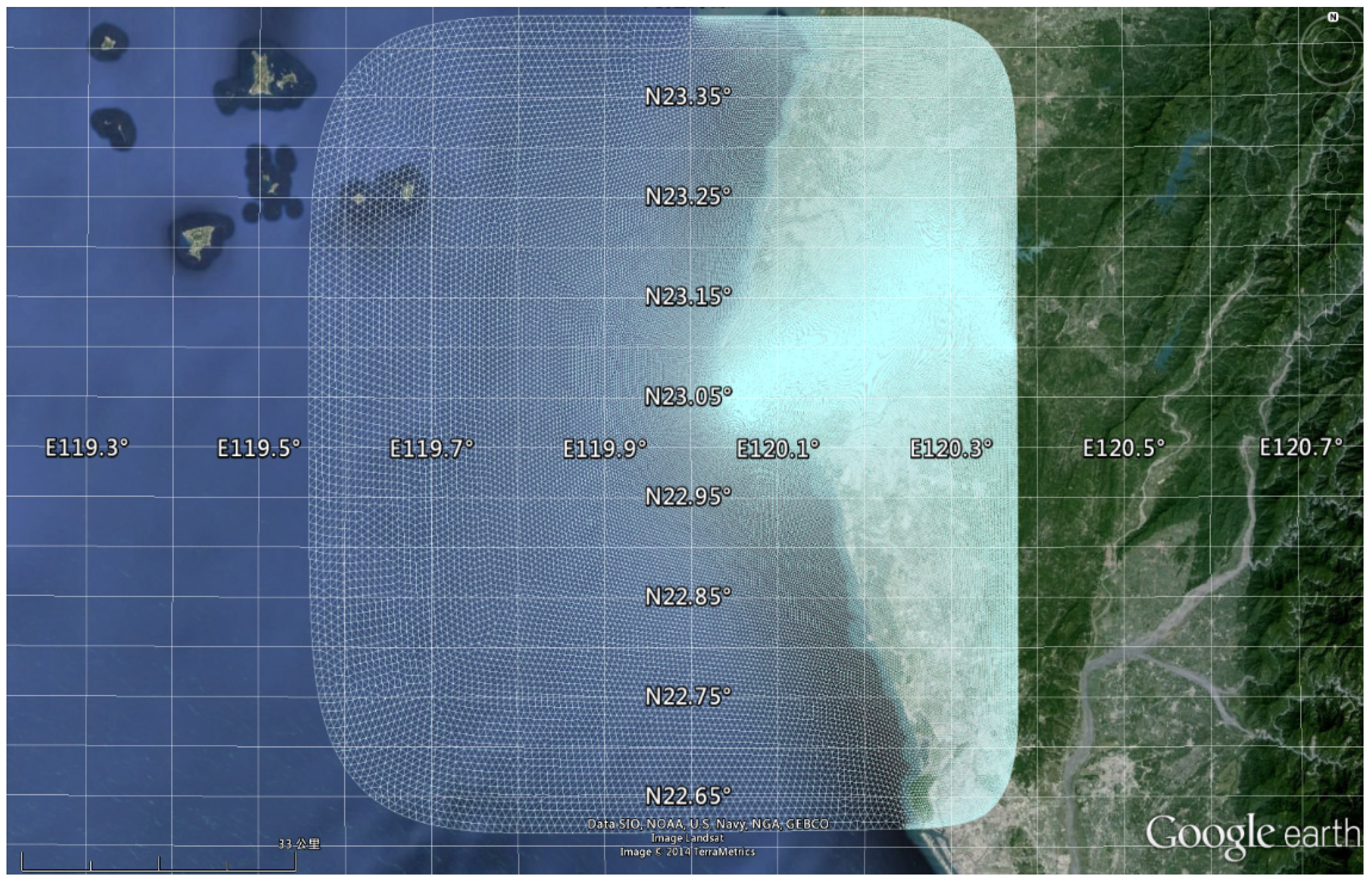
3. Model Descriptions
3.1. Governing Equations
3.2. Prototypical Typhoon Model
3.3. Model Implementation
3.4. Indices of Simulation Performance
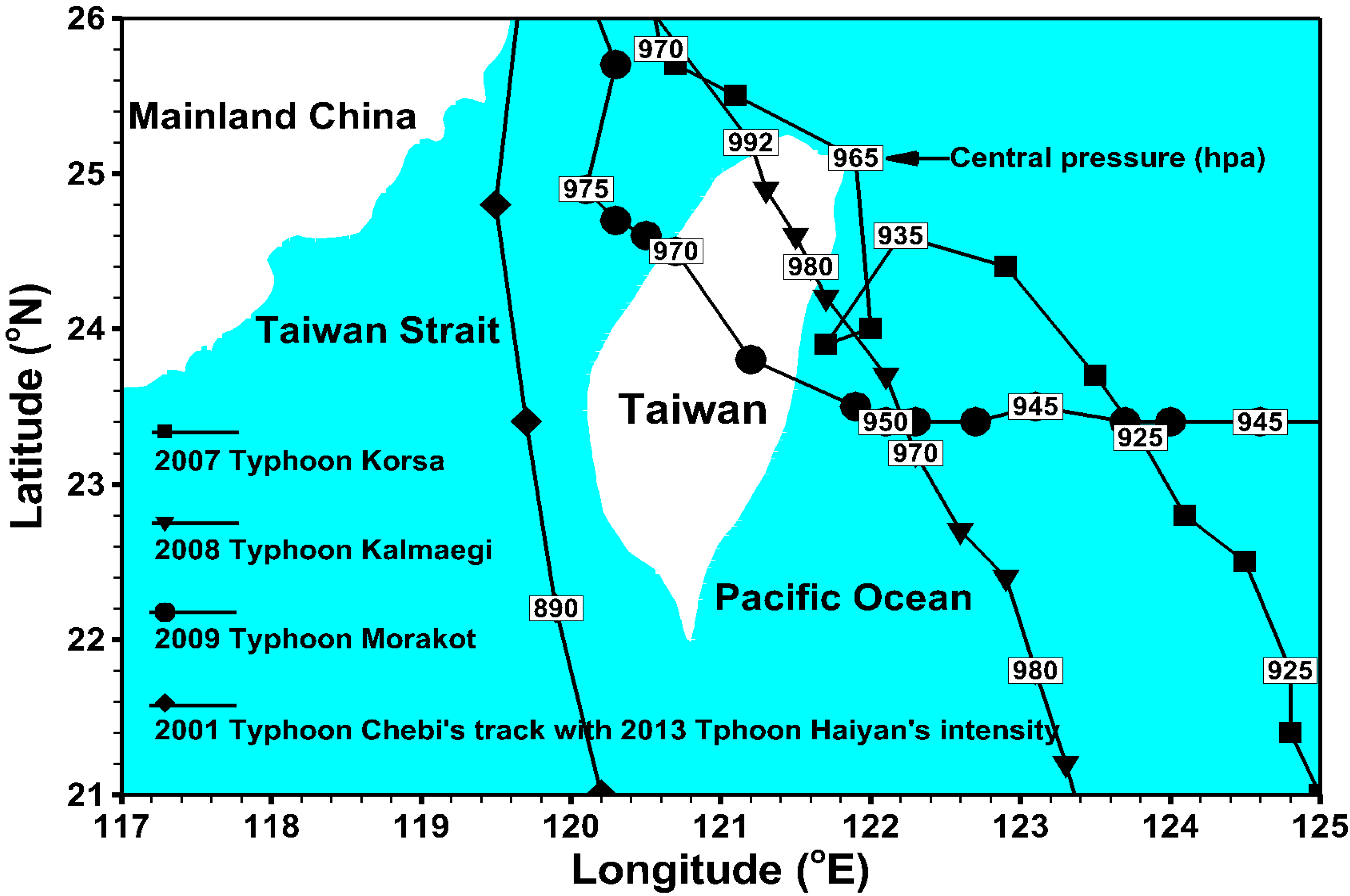
4. Model Validation
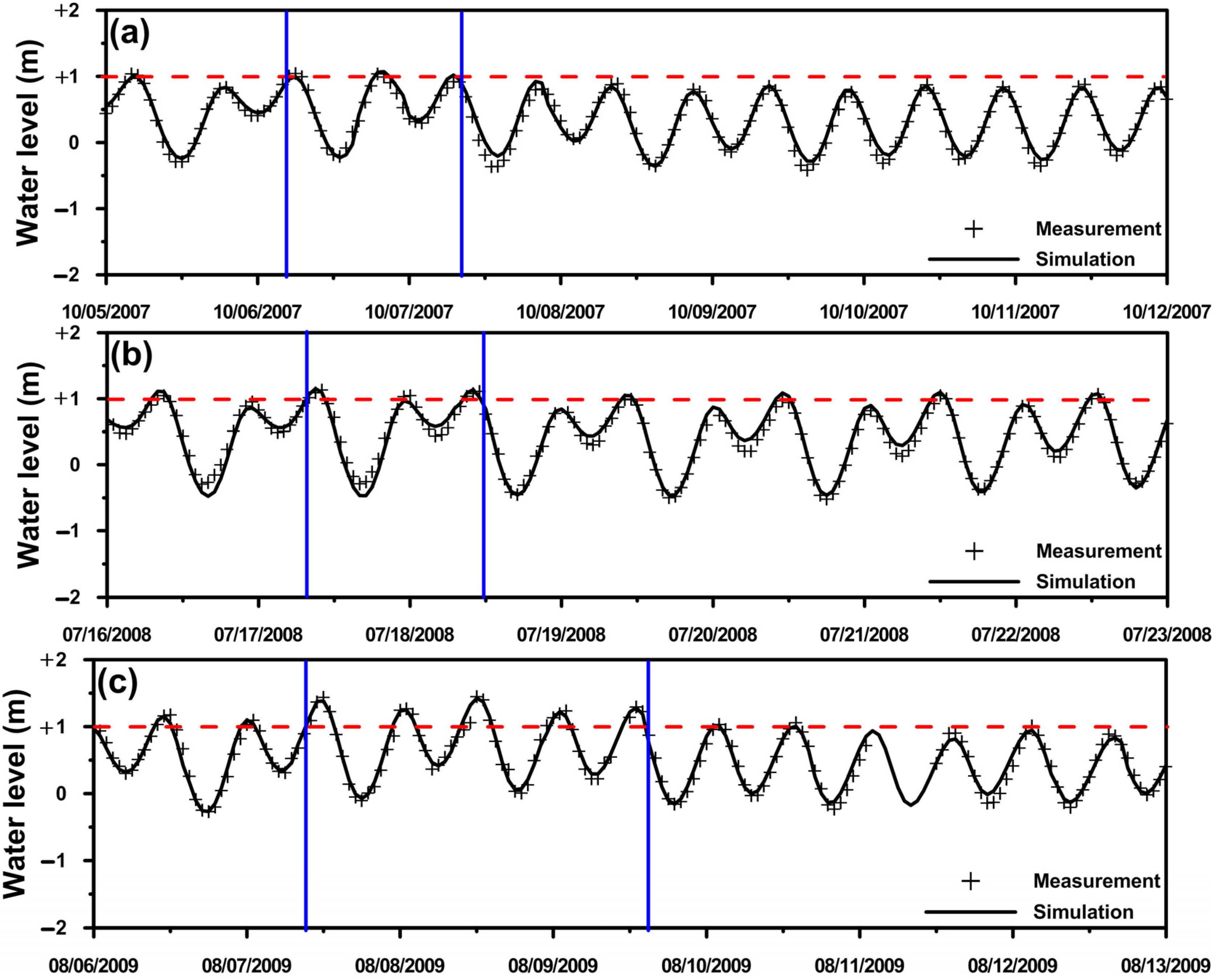

| Typhoon | Jianjun Fish Port | Tsengwen Bridge | ||||
|---|---|---|---|---|---|---|
| MAE (m) | RMSE (m) | SRE (%) | MAE (m) | RMSE (m) | SRE (%) | |
| Typhoon Krosa (2007) | 0.06 | 0.08 | 1.41 | 0.71 | 0.87 | 8.72 |
| Typhoon Kalmaegi (2008) | 0.07 | 0.09 | 1.55 | 0.47 | 0.63 | 4.14 |
| Typhoon Morakot (2009) | 0.07 | 0.09 | 1.26 | 0.91 | 1.10 | 9.90 |
5. Model Applications and Discussion
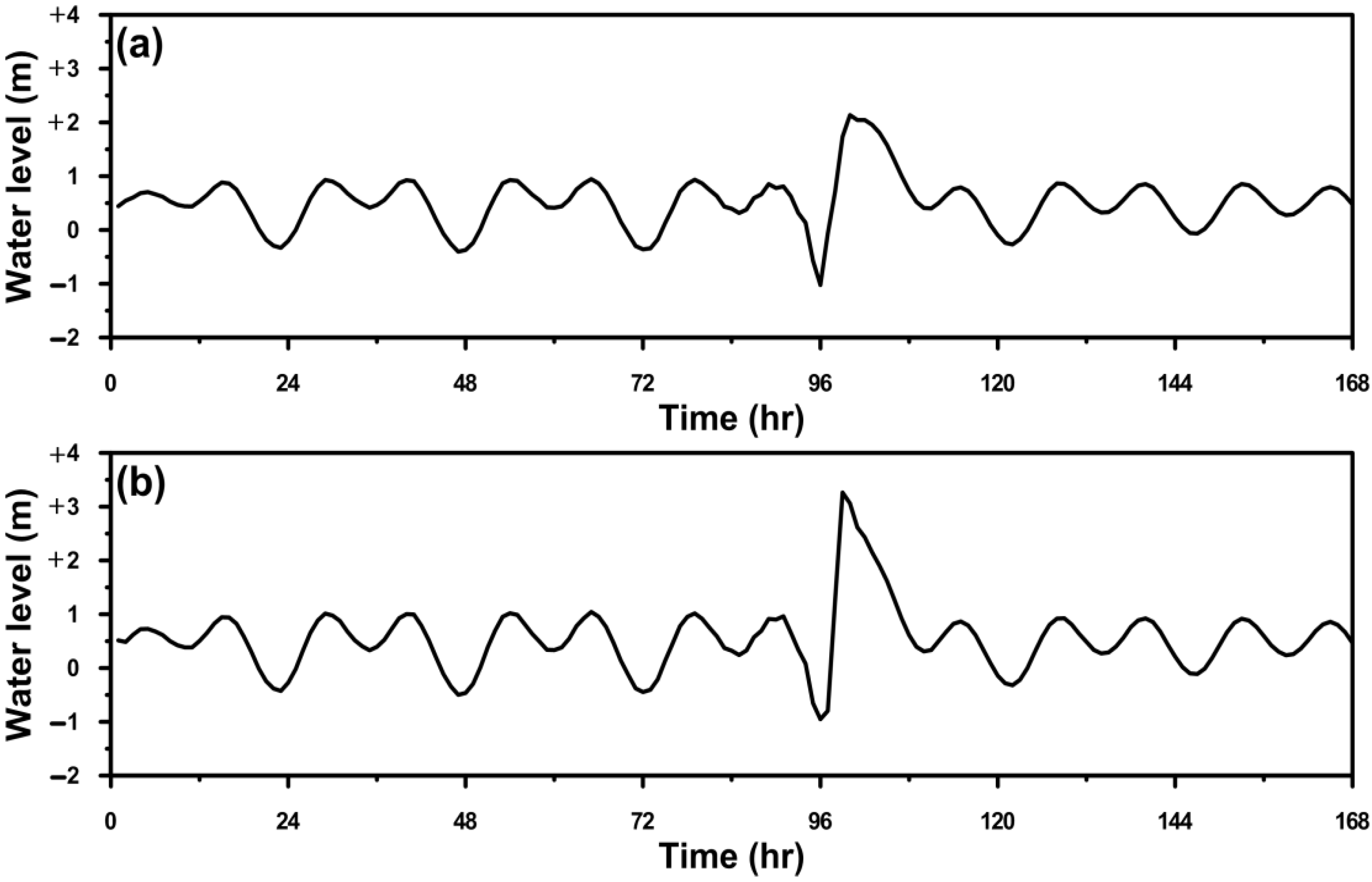
5.1. Effect of Storm Surge
5.2. Effect of Freshwater Discharge


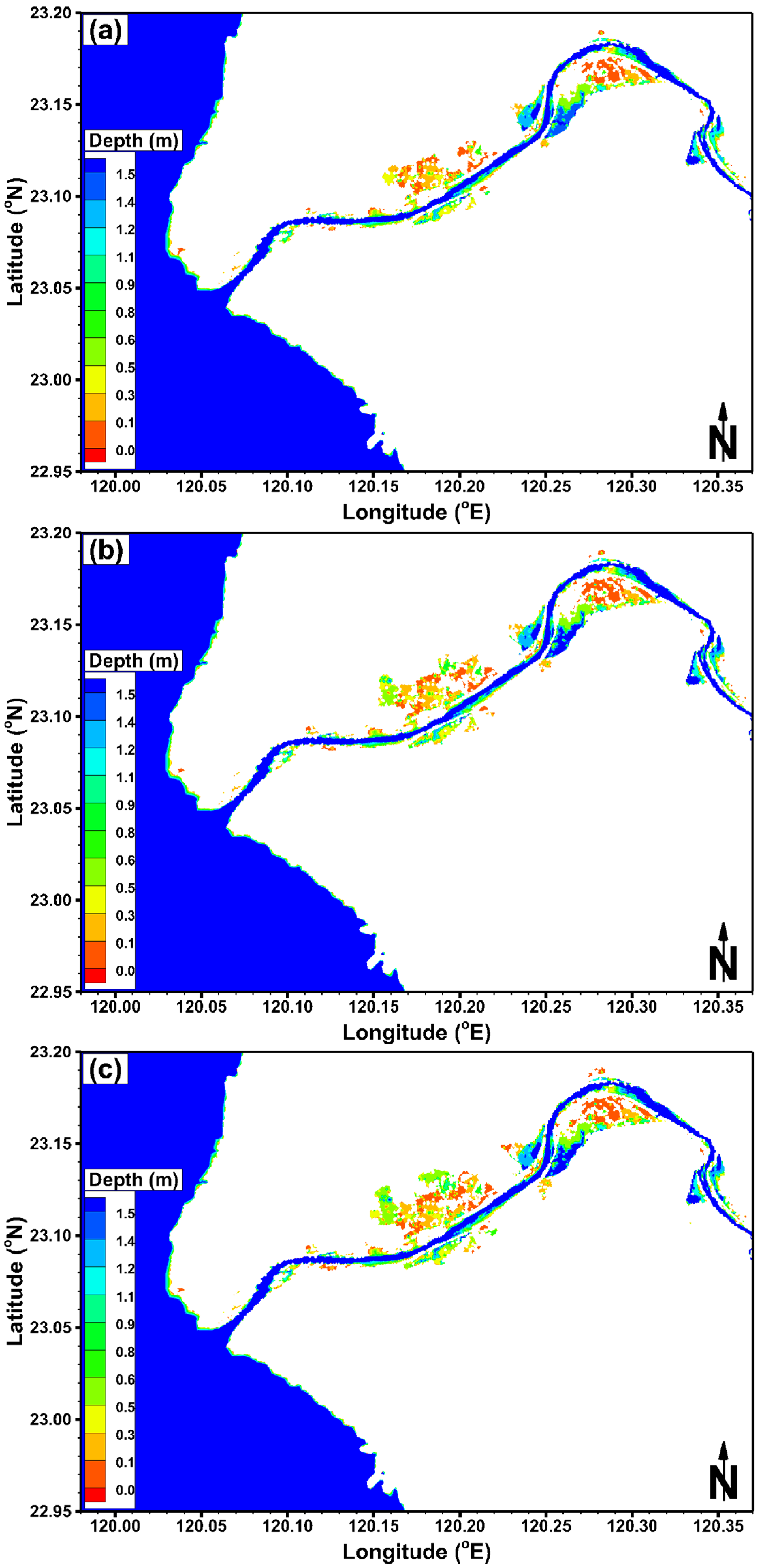
| Inundation Condition | Effect of Storm Surge | Effect of Freshwater Discharge | ||
|---|---|---|---|---|
| Return Period | ||||
| 50 Year | 100 Year | 200 Year | ||
| Inundation area (km2) | 60 | 21 | 25 | 30 |
| Maximum inundation depth (m) | 1.98 | 1.53 | 1.56 | 1.58 |
5.3. Effect of Storm Surge Combined with Freshwater Discharge

6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Flather, R.A. Storm surges. In Encyclopaedia of Ocean Science; Steele, J., Thorpe, S., Turekian, K., Eds.; Academia: San Diego, CA, USA, 2001; pp. 2882–2892. [Google Scholar]
- Bertin, X.; Bruneau, N.; Breilh, J.; Fortunato, A.B.; Karpytchev, M. Importance of wave age and resonance in storm surges: The case Xynthia, Bay of Biscay. Ocean Model. 2012, 42, 16–30. [Google Scholar]
- Turner, A.B.; Colby, J.D.; Csontos, R.M.; Batten, M. Flood modeling using a synthesis of multi-platform LiDAR data. Water 2013, 5, 1533–1560. [Google Scholar]
- Forunato, A.B.; Rodrigues, M.; Dias, J.M.; Lopes, C.; Olivera, A. Generating inundation maps for a coastal lagoon: A case study in the Ria de Aveiro (Portugal). Ocean Eng. 2013, 64, 60–71. [Google Scholar] [CrossRef]
- Chen, W.B.; Liu, W.C.; Hsu, M.H. Predicting typhoon-induced storm surge tide with a two-dimensional hydrodynamic model and artificial neural network model. Nat. Hazards Earth Sys. Sci. 2012, 12, 3799–3809. [Google Scholar] [CrossRef]
- Dietsche, D.; Hagen, S.C.; Bacopoulos, P. Storm surge simulation for Hurricane Hugo (1989): On the significance of inundation areas. J. Waterw. Port Coast. Ocean Eng. 2007, 133, 183–191. [Google Scholar] [CrossRef]
- Jones, J.E.; Davis, A.M. Storm surge computations for the west coast of Britain using a finite element model (TELEMAC). Ocean Dynam. 2008, 58, 337–363. [Google Scholar] [CrossRef]
- Weisberg, R.H.; Zheng, L. Hurricane storm surge simulations comparing three-dimensional with two-dimensional formulaitons based on an Ivan-like storm over the Tampa Bay, Florida region. J. Geophs. Res. 2008, 113. [Google Scholar] [CrossRef]
- Xia, M.; Xia, L.; Pietrafesa, L.J.; Peng, M. A numerical study of storm surge in the Cape Fear River Estuary and adjacent coast. J. Coast. Res. 2008, 24, 159–167. [Google Scholar] [CrossRef]
- Rego, J.L.; Li, C. Storm surge propagation in Galveston Bay during Hurricane Ike. J. Mar. Syst. 2010, 82, 265–279. [Google Scholar] [CrossRef]
- Xu, H.; Zhang, K.; Shen, J.; Li, Y. Storm surge simulation along U.S. Ease and Gulf Coasts using multi-scale numerical model approach. Ocean Dynam. 2010, 60, 1597–1619. [Google Scholar] [CrossRef]
- You, S.H.; Lee, W.J.; Moon, K.S. Comparison of storm surge/tide predictions between a 2-D operational forecast system, the regional tide/storm surge model (RTSM), and the 3-D regional ocean modeling system (ROMS). Ocean Dynam. 2010, 60, 443–459. [Google Scholar] [CrossRef]
- Krestenitis, Y.N.; Androulidakis, Y.S.; Kontos, Y.N.; Georgakopoulos, G. Coastal inundation in the north-eastern Mediterranean coastal zone due to storm surge events. J. Coast. Conserv. 2011, 15, 353–368. [Google Scholar] [CrossRef]
- Orton, P.; Georgas, N.; Blumberg, A.; Pullen, J. Detailed modeling of recent severe storm tides in estuaries on the New York City region. J. Geophys. Res. 2012, 117. [Google Scholar] [CrossRef]
- Sheng, Y.P.; Alymov, V.; Paramygin, V.A. Simulation of storm surge, wave, and inundation in the Outer Banks and Chesapeake Bay during Hurricane Isabel in 2003: The importance of waves. J. Geophy. Res. 2010, 115. [Google Scholar] [CrossRef]
- Vested, H.J.; Jensen, H.R.; Petersen, H.M.; Jorgensen, A.; Machenhauer, B. An operational hydrographic warning system for the North Sea and Danish Belts. Cont. Shelf Res. 1992, 12, 65–81. [Google Scholar] [CrossRef]
- Li, Y.S.; Zhang, M.Y. Dynamic coupling of wave and surge models by Eulerian-Lagrangian method. J. Waterw. Port Coast. Ocean Eng. 1997, 123, 1–7. [Google Scholar] [CrossRef]
- Shen, J.; Zhang, K.; Xiao, C.; Gong, W. Improved prediction of storm surge inundation with a high-resolution unstructured grid model. J. Coast. Res. 2006, 22, 1309–1319. [Google Scholar] [CrossRef]
- Peng, M.; Xie, L.; Pietrafesa, L.J. A numerical study of storm surge and inundation in the Croatan-Albemarle-Pamlico Estuary System. Estuar. Coast. Shelf Sci. 2004, 59, 121–137. [Google Scholar] [CrossRef]
- Xie, L.; Kiu, H.; Liu, B.; Bao, S. A numerical study of the effect of hurricane wind asymmetry on storm surge and inundation. Ocean Model. 2011, 36, 71–79. [Google Scholar] [CrossRef]
- Lewis, M.; Bates, P.; Horsburgh, K.; Neal, J.; Schumann, G. A storm surge inundation model of the northern Bay of Bengal using publicly available data. Quart. J. Roy. Meteor. Soc. 2013, 139, 358–369. [Google Scholar] [CrossRef]
- Dyer, K.R. Estuaries: A Physical Introduction; Wiley: New York, NY, USA, 1997. [Google Scholar]
- Hong, E.; Huang, T.C.; Yu, H.S. Morphology and dynamic sedimentology in front or the retreating Tsengwen Delta, Southwestern Taiwan. Terre. Atmos. Ocean. Sci. 2004, 15, 565–587. [Google Scholar]
- Zhang, Y.L.; Baptista, A.M. SELFE: A semi-implicit Eulerian-Lagrangian finite-element model for cross-scale ocean circulation. Ocean Model. 2008, 21, 71–96. [Google Scholar] [CrossRef]
- Large, W.G.; Pond, S. Open ocean momentum flux measurements in moderate to strong winds. J. Phys. Oceanogr. 1981, 11, 324–336. [Google Scholar] [CrossRef]
- Powell, M.D.; Vickery, P.J.; Reinhold, T.A. Reduced drag coefficient for high wind speeds in tropical cyclones. Nature 2003, 422, 279–283. [Google Scholar] [CrossRef] [PubMed]
- Holland, G.J. An analytical model of the wind and pressure profiles in hurricanes. Mon. Weather Rev. 1980, 108, 1212–1218. [Google Scholar] [CrossRef]
- Hubbert, G.D.; Holland, G.J.; Leslie, L.M.; Manton, M.J. A real-time system for forecasting tropical cyclone storm surges. Weather Forecast. 1991, 6, 86–97. [Google Scholar] [CrossRef]
- Medeiros, S.C.; Hagen, S.C. Review of wetting and drying algorithms for numerical tidal flow models. Int. J. Numer. Method. Fluid. 2012, 71, 473–487. [Google Scholar] [CrossRef]
- Zu, T.; Gana, J.; Erofeevac, S.Y. Numerical study of the tide and tidal dynamics in the South China Sea. Deep Sea Res. I Ocean. Res. Pap. 2008, 55, 137–154. [Google Scholar] [CrossRef]
- Water Resources Agency. The Analysis of Storm Rainfall and River Discharge during the Typhoon Morakot in 2009; Technical Report; Water Resources Agency: Taipei, Taiwan, 2009. [Google Scholar]
- Condon, A.J.; Sheng, Y.P. Evaluation of coastal inundation hazard for present and future climates. Nat. Hazards 2012, 62, 345–373. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, W.-B.; Liu, W.-C. Modeling Flood Inundation Induced by River Flow and Storm Surges over a River Basin. Water 2014, 6, 3182-3199. https://doi.org/10.3390/w6103182
Chen W-B, Liu W-C. Modeling Flood Inundation Induced by River Flow and Storm Surges over a River Basin. Water. 2014; 6(10):3182-3199. https://doi.org/10.3390/w6103182
Chicago/Turabian StyleChen, Wei-Bo, and Wen-Cheng Liu. 2014. "Modeling Flood Inundation Induced by River Flow and Storm Surges over a River Basin" Water 6, no. 10: 3182-3199. https://doi.org/10.3390/w6103182
APA StyleChen, W.-B., & Liu, W.-C. (2014). Modeling Flood Inundation Induced by River Flow and Storm Surges over a River Basin. Water, 6(10), 3182-3199. https://doi.org/10.3390/w6103182






