Abstract
Growing water scarcity, due to growing populations and varying natural conditions, puts pressure on irrigation systems, which often are the main consumptive water users. Therefore, water resources management to improve the allocation of limited water supplies is essential. In this study, a non-linear programming optimization model with an integrated soil/water balance is developed to determine the optimal reservoir release policies and the optimal cropping pattern around Doroudzan Dam in the South-West of Iran. The proposed model was solved using a genetic algorithm (GA). Four weather conditions were identified by combining the probability levels of rainfall, evapotranspiration and inflow. Moreover, two irrigation strategies, full irrigation and deficit irrigation were modeled under each weather condition. The results indicate that for all weather conditions the total farm income and the total cropped area under deficit irrigation were larger than those under full irrigation. In addition, our results show that when the weather conditions and the availability of water changes the optimal area under corn and sugar beet decreases sharply. In contrast, the change in area cropped with wheat is small. It is concluded that the optimization approach has been successfully applied to Doroudzan Dam region. Thus, decision makers and water authorities can use it as an effective tool for such large and complex irrigation planning problems.
1. Introduction
Water scarcity is a global problem, but it is most severe in arid and semi-arid regions.Often, increasing water demands due to population growth further aggravate the problem [1]. At the global level, the agricultural sector is the largest consumer of water resources. Consequently, this sector is heavily impacted by water scarcity and yield reduction may result in a decline of food security worldwide [2].
Hence, improvements in agricultural water management are needed. Optimization of irrigation systems and improvement of water resource allocations through appropriate multi-cropping patterns and irrigation scheduling are considered as crucial responses to address water scarcity [3].
Iran is a water scarce country due to the low precipitation, high evaporation and the temporal and spatial variation of rainfall. According to the International Water Management Institute (IWMI), Iran is furthermore one of the countries under critical water scarcity conditions [4].
The Doroudzan Dam is one of the largest reservoirs in the Fars province (Southwest Iran). This province is one of the leading regions in terms of agricultural production in Iran and the most important producer of wheat [5]. Due to a decrease in rainfall over the past years, which has resulted in a severe reduction of the water storage in the Doroudzan dam, the irrigation sector in this region is under pressure [5,6]. As water scarcity intensifies, better management of irrigation water is becoming an issue of paramount importance.
Several researchers have developed optimization and simulation models for planning and management of irrigation systems. Ghahraman and Sepaskhah [7] for example developed a stochastic dynamic programming optimization model for the optimal allocation of water to a predetermined multiple cropping pattern in Khorasan province, Iran. Raju and Kumar [8] applied a genetic algorithm (GA) for irrigation planning of the Sri Ram Sagar Project, in Andhra Pradesh, India. Kumar et al. [9] also proposed an irrigation allocation model to determine relative yield under a specified cropping pattern in Karnataka State, India using a GA. Similarly, Georgiou and Papamichail [10] developed anon-linear programming optimization model to determine the optimal reservoir release policies and the optimal cropping pattern in Chalkidiki region, Greece. Regulwar and Anand Raj [11] finally a monthly multi objective genetic algorithm fuzzy optimization model for two conflicting objectives of a multi reservoir system in the Godavari river sub basin, in Maharashtra state, India.
In this paper, the same biophysical modeling approach as presented in [10] is used. However the system they studied was very small. Building further on their study we constructed a non-linear programming optimization model for determining optimal reservoir release policies and optimal cropping patterns for a large and more complex system. In addition the model developed is solved using a GA. The objective function of the model maximizes the total farm income, which is based on the crop-water production functions developed by Jensen [12]. As in the study [10] rainfall, evapotranspiration and inflow are considered as being stochastic in our study. The optimization process therefore makes use of a simulated series of rainfall, evapotranspiration and inflow and in the model expected values of the aforementioned parameters corresponding to different probabilities are used for the runs. In this way, by combining the various probability levels of rainfall, evapotranspiration and inflow, four weather conditions are distinguished. Furthermore, the application of two irrigation strategies, namely, full irrigation and deficit irrigation modeled under the four weather conditions. Predicted outputs of the full irrigation approach were compared with the results obtained from deficit irrigation approach.
2. Materials and Methods
2.1. Study Area and Data
The study considers the Doroudzan Dam in Fars province, Southwest Iran (Figure 1). This dam, with a storage capacity of 960 × 106 m3 is designed to supply water to irrigate 114,500 ha. The areas currently irrigated with this water under modern or traditional irrigation and drainage networks are 60,000 ha in Ramjrd and Marvdasht, 7000 ha from Pol-e-Khan to Band-e-Amir and 47,500 ha from Band-e-Amir to Korbal. The dam also provides drinking water to the cities of Marvdasht and Shiraz. The average inflow of this dam between 1987 and 2009 was 1141 × 106 m3, with a maximum of 2509 × 106 m3 and a minimum of 254 × 106 m3 [6].
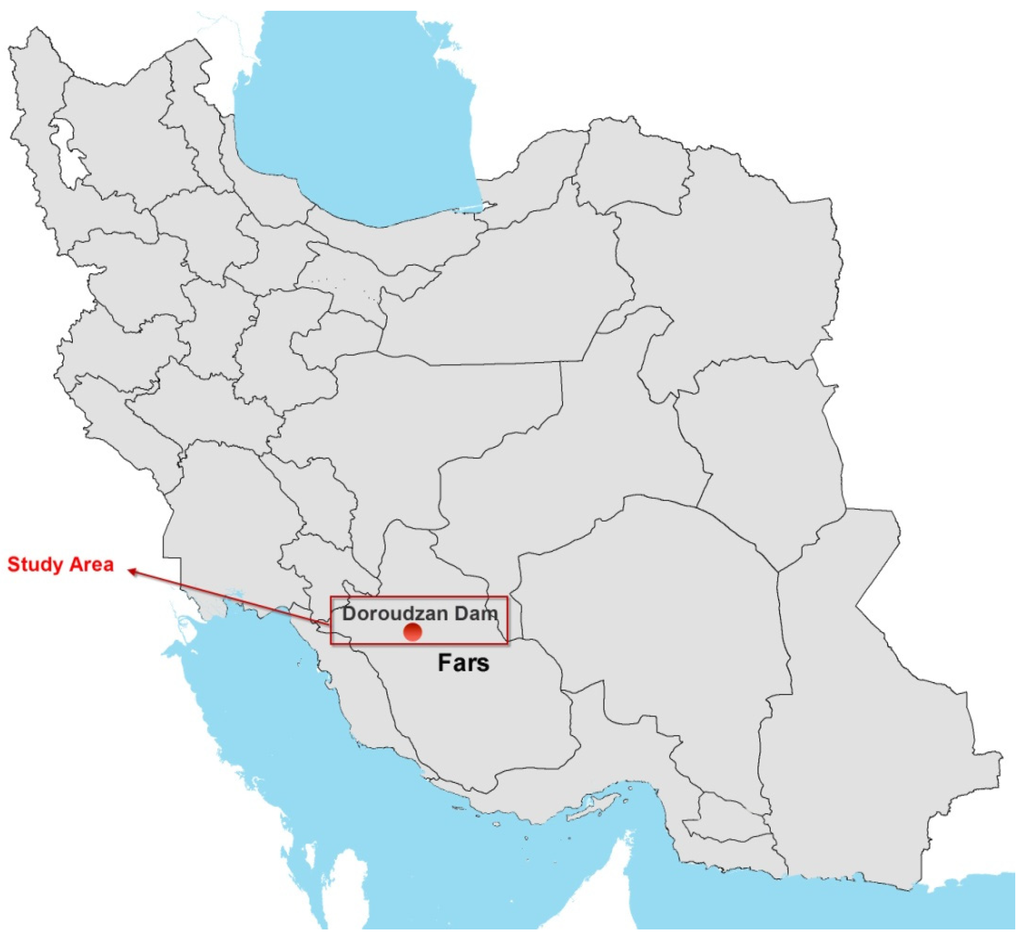
Figure 1.
A general map of Iran illustrating the location of the study area.
Five crops are considered in our optimization model: Wheat, canola and barley as winter crops and corn and sugar beet as summer crops. These are the most important crops in the study area. Table 1 presents the characteristics of these crops including production costs, gross margins, yield response factors for different growing stages, planting day and length of growing season.

Table 1.
Some critical data for the indicated crops in study area.
| Growth Stage | Parameter | Crop | ||||
|---|---|---|---|---|---|---|
| Wheat | Corn | Sugar Beet | Barley | Canola* | ||
| Establishment | Ky **,a | 0.01 | 0.07 | 0.12 | 0 | - |
| Early vegetation | 0.2 | 0.4 | 2 | 0.12 | - | |
| Late Vegetation | 0.2 | 0.4 | 2 | 0.15 | - | |
| Flowering | 0.6 | 1.5 | - | 1.5 | - | |
| Yield formation | 0.5 | 0.5 | 0.36 | 0.4 | - | |
| Ripening | 0.01 | 0.2 | 0.12 | 0.14 | - | |
| Gross margin (106Rls/ha)b | 17 | 27 | 36 | 15 | 41 | |
| Production cost (106Rls/ha)b | 4 | 12 | 14 | 3 | 7 | |
| Planting day b | 21 October | 22 June | 21 March | 21 October | 12 October | |
| Length of growing season(days)b | 220 | 110 | 200 | 210 | 240 | |
Notes:* Sensitivity index of canola to water stress for three growing stages: Vegetation, flowering and ripening is equal to 0.18, 0.41, and 0.28, respectively [13]; ** Ky is the yield response factor which quantifies the response of yield to water supply. It relates relative yield decrease to relative ET deficit for different growing stages; a [14], b [15].
The crop yields are calculated using the Jensen water productivity model. Based on the reported yield response factors, the sensitivity indexes (λ) for this model for all growing stages were computed from a polynomial function [16] and time intervals using the procedure developed by Tsakiris [17]. This is explained in Section 2.3.1. The sensitivity index of canola however was extracted directly from Shabani [13].
The gross margins reported in this table are obtained by multiplying maximum crop yield with product price. The production costs are the summation of all costs such as seeds, fertilizers, pesticides, machinery, harvesting, etc.
In addition, the irrigation season is considered to start in October and to end in October of the following year. The year is divided into 36 periods, with each month consisting of three sub-periods.
The maximum reservoir capacity is planned to be 960 × 106 m3 and the dead capacity 300 × 106 m3. Although the proposed optimization model can handle heterogeneous soils, the soil under study was considered to be homogeneous with a field capacity (FC) of 0.3 cm3/cm3 and a permanent wilting point (PWP) of 0.15 cm3/cm3.
The reference evapotranspiration is calculated using the FAO Penman–Monteith equation [18]. It was derived from daily climatic data (mean temperature, radiation, relative humidity and wind speed). A dataset of 22 years (1987–2009) was available from the Zarghan meteorological station (Latitude 29° 47' N, Longitude 52° 43' E).
2.2. Stochastic Generation of Climatic Data
Because climatic data for the full operation life of the reservoir is not available a synthetic time series is constructed for rainfall, evapotranspiration and inflow. Moreover, rainfall, evapotranspiration and inflow are considered to be stochastic. The optimization model is therefore run for expected values of the aforementioned parameters corresponding to different probabilities.
The synthetic series of 37 years (=the operation life of the reservoir) for rainfall, evapotranspiration and inflow were generated by applying mathematical models to data from the Zarghan weather station.
In this paper, rainfall data generation is a two-stage process whereby rainfall occurrence (i.e., wet or dry day) is based on a first order two state Markov chain and rainfall amount is sampled from the gamma distribution (Appendix) [10].
The evapotranspiration is synthetically generated using Monte Carlo simulation (Appendix) [19].
The synthetic monthly inflows were generated using an autoregressive moving average exogenous variables (ARMAX) model, which represents the relationship between inflow and precipitation (Appendix) [20].
Generated values of rainfall, evapotranspiration and inflow are used to calculate frequency curves from which expected values corresponding to different probability of exceedance were obtained.
By combining the various probability levels of rainfall, evapotranspiration and inflow, four weather conditions are defined [21]: Hot and dry, dry, normal and wet weather conditions, corresponding to the probability levels of exceedance of rainfall, evapotranspiration and inflow. This is presented in Table 2.

Table 2.
Four defined weather conditions.
| Weather Condition | Probability Level of Exceedance | ||
|---|---|---|---|
| Evapotranspiration (%) | Rainfall (%) | Inflow (%) | |
| Hot and dry | 20 | 100 (no rain) | 100 |
| Dry | 40 | 80 | 80 |
| Normal | 50 | 50 | 50 |
| Wet | 60 | 20 | 20 |
2.3. Model Formulation
The model is developed to determine the optimal cropping pattern and irrigation scheduling for the major crops in the study area. The reservoir storage constitutes the system’s state variable, whereas the system’s inputs, commonly referred to as decision variables, are the cultivated areas, and the water releases from the reservoir to satisfy irrigation requirements for each crop during each time interval. Six sets of constraints are considered in this study: The soil moisture balance, the state equation of the reservoir, the reservoir storage, the irrigation requirements of each crop with the corresponding reservoir release, the yield and the cultivated area. Meanwhile, the developed mathematical model for irrigation planning is solved using a (GA) with 145 decision variables and 431 constraints.
2.3.1. Objective Function
Following objective function, which maximizes the total farm income, is considered for the optimal operation of the reservoir and the irrigation of n crops at any time interval j during the irrigation season [10]:
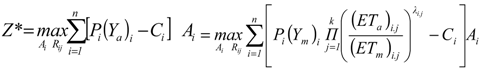 Here n is the number of crops; k is the number of time intervals; i is the crop index and j refers to the time interval; Z* is total farm income (Rls) (US $1~10,000 Rials (Rls) in 2009); Pi is the price of crop i (Rls kg−1); Rij is the reservoir release for crop i during time interval j; Ci is the production cost of crop i (Rls ha−1); Ai is the cultivated area of crop i (ha); Ya is the actual yield (kg ha−1); Ym is maximum crop yield under the given management conditions with unlimited water supply (kg ha−1); ETa is the actual evapotranspiration (mm); ETm is the maximum evapotranspiration (mm), which is the product of a crop factor Kc and the reference evapotranspiration; the Kc for three growing stages (initial, middle, end) were extracted from Shabani [14]; λi,j is the sensitivity index of crop i to water stress during time interval j.
Here n is the number of crops; k is the number of time intervals; i is the crop index and j refers to the time interval; Z* is total farm income (Rls) (US $1~10,000 Rials (Rls) in 2009); Pi is the price of crop i (Rls kg−1); Rij is the reservoir release for crop i during time interval j; Ci is the production cost of crop i (Rls ha−1); Ai is the cultivated area of crop i (ha); Ya is the actual yield (kg ha−1); Ym is maximum crop yield under the given management conditions with unlimited water supply (kg ha−1); ETa is the actual evapotranspiration (mm); ETm is the maximum evapotranspiration (mm), which is the product of a crop factor Kc and the reference evapotranspiration; the Kc for three growing stages (initial, middle, end) were extracted from Shabani [14]; λi,j is the sensitivity index of crop i to water stress during time interval j.
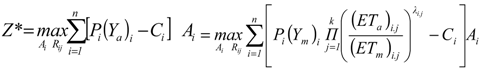
As mentioned above the estimations of the crop production are based on the production functions developed by Jensen [12].
Following polynomial function relates the sensitivity indexes at each growing stage used in the model of Jensen to the yield response factors (Ky) [16]:
where Ky for all growing stages of the crops was obtained in Table 1.
λ = 0.2418ky3 − 0.1768ky2 + 0.9464ky − 0.0177
A procedure was developed for estimating the crop sensitivity to water deficiency at given time intervals using Jensen’s crop water production function [17].
Under a full irrigation strategy, the reservoir releases are forced to be equal to the full irrigation water requirements over the entire crop periods. Therefore, under this condition, ETa = ETm, Ya = Ym and the relative yield (Ya/Ym) is fixed to unity. The Equation (1) may be reduced to [10]:
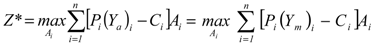
2.3.2. Constraints
Reservoir Constraint
The reservoir water balance is governed by the following reservoir storage continuity equation [10]:
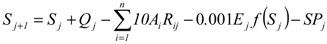
Here Sj is the reservoir storage at the beginning of time interval j, (m3); Qj is the reservoir inflow during time interval j (m3); Ej is the reservoir surface area evaporation rate (mm) during time interval j. This is computed from the de Bruin equation [22], further f(Sj) is the reservoir surface area in time interval j (m2), which is related to the storage of the reservoir and SPj is the overflow loss from the spillway during time interval j (m3). Like in [10] the rainfall on the reservoir area is considered as negligible and therefore is not included in the model.
The reservoir storage at any time interval is bound to be between an upper limit (full reservoir, Smax) and a lower limit (dead storage, Smin). Thus, it is possible to remove the overflow variable SPj from Equation (4) and rewrite it as a state Equation (5), where the reservoir storage is the state:
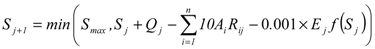
Soil Moisture Constraint
The soil water balance equation for a given crop i during time interval j was given by [23]:
(SMin )i.j + 1 = (SMin )i.j + ERAIN i.j + IRi.j − (ETa )i.j + (ASM i.j + 1 − ASM i.j) − DPij
Here SMin is the initial soil moisture level (mm); ERAINij is the effective rainfall for crop i in time interval j (mm); which is computed by the procedure described by e.g., [24,25]; IRij is irrigation water allocated to crop i in time interval j (mm); ASMi.j is the available soil moisture (mm) for crop i in time interval j and DPij is deep percolation for crop i in time interval j (mm).
In the beginning of the irrigation season, soil moisture is assumed to be at field capacity (FC) for all soils and crops. The available soil moisture is computed from field capacity, permanent wilting point (PWP) and root depth (RD). The initial soil water content is considered constant through deeper layers of the soil. As the root deepens, a contribution of this extra water is added to the water in the soil balance equation (ASMi.j in Equation (6)), a sine function was adopted for assessing time patterns of root growth [26]. At the beginning of every time interval, any water added (ERAINi.j and IRi.j) is computed as if it was done instantaneously.
Irrigation application efficiency (AE) of <100% causes some percolation of water below the root zone (surface runoff was ignored for simplicity). Therefore, the following constraint was included in the model’s structure to guarantee deep percolation amounts [10]:
DPij ≥ IRi.j (1 − AE)
Crop Irrigation Requirements and Reservoir Releases
The irrigation requirement (IRmax)i,j of crop i during a given time interval j depends on the initial soil moisture level, the effective rainfall, the potential evapotranspiration and the remaining moisture. It can therefore be given by [27]:
(IRmax )i,j = max {0,(1 − pij)ASM i.j + (ETm )i.j − (SM in )i.j − ERAIN i.j }
Here IRmax is the maximum irrigation requirement (mm); pij is the soil moisture depletion factor under no stress condition for crop i in time interval j. This according to Allen et al. [18] depends on the specific evapotranspiration of the crop and the maximum evapotranspiration (ETm).
The maximum releases from the reservoir are given by [16]:
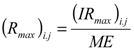
Here Rmax is the maximum release from reservoir to meet the irrigation requirements, ME is the mean irrigation efficiency, including the application efficiency and the conveyance efficiency.
ETa Constraint
The actual evapotranspiration (ETa) is given by e.g., [28,16]:
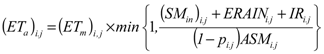
Bounds
The decision variables in the model are the cultivated areas and the irrigation releases while the state variable is storage. The lower and upper limits for these variables are the following:
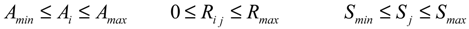
Furthermore, in this study, a socio economic constraint is introduced to guarantee a minimum production. The minimum relative yield (Ya/Ym) for all crops is therefore set at 0.70.
2.4. Solution Technique
The optimization model is solved using a GA. The methodology of a GA involves coding, fitness function computation, and operations of reproduction, crossover, and mutation [29]. A constrained problem is converted into an un-constrained problem in a GA by introducing a penalty function as follows [9]:
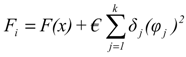
Here Fi is the fitness value; F(x) is the objective function value, k is the number of constraints, € is −1 for maximization and +1 for minimization; δj is the penalty coefficient; and φj is the amount of violation. The GA has been implemented in the MATLAB language [30]. As explained in the Genetic Algorithm and Direct Search users’ guide of the MATLAB software, population size needs to be at least twice the number of variables for enough searches in the variables’ space, so that the individuals in each population span the space being searched. In our case, the number of variables is 145. Therefore, the population size is 300. The mutation probability considered to vary adaptively from 0.2 to a small value when we are near to optimal solutions. It helps us to explore the search space in the beginning of optimization and to prevent missing the near optimized solutions at the end. Different settings for Crossover in genetic algorithm can be used to see which one gives the best results. The implemented coding runs the function GA multi times; varying crossover from zero to one in increments of 0.05. A schematic diagram is given in Figure 2.
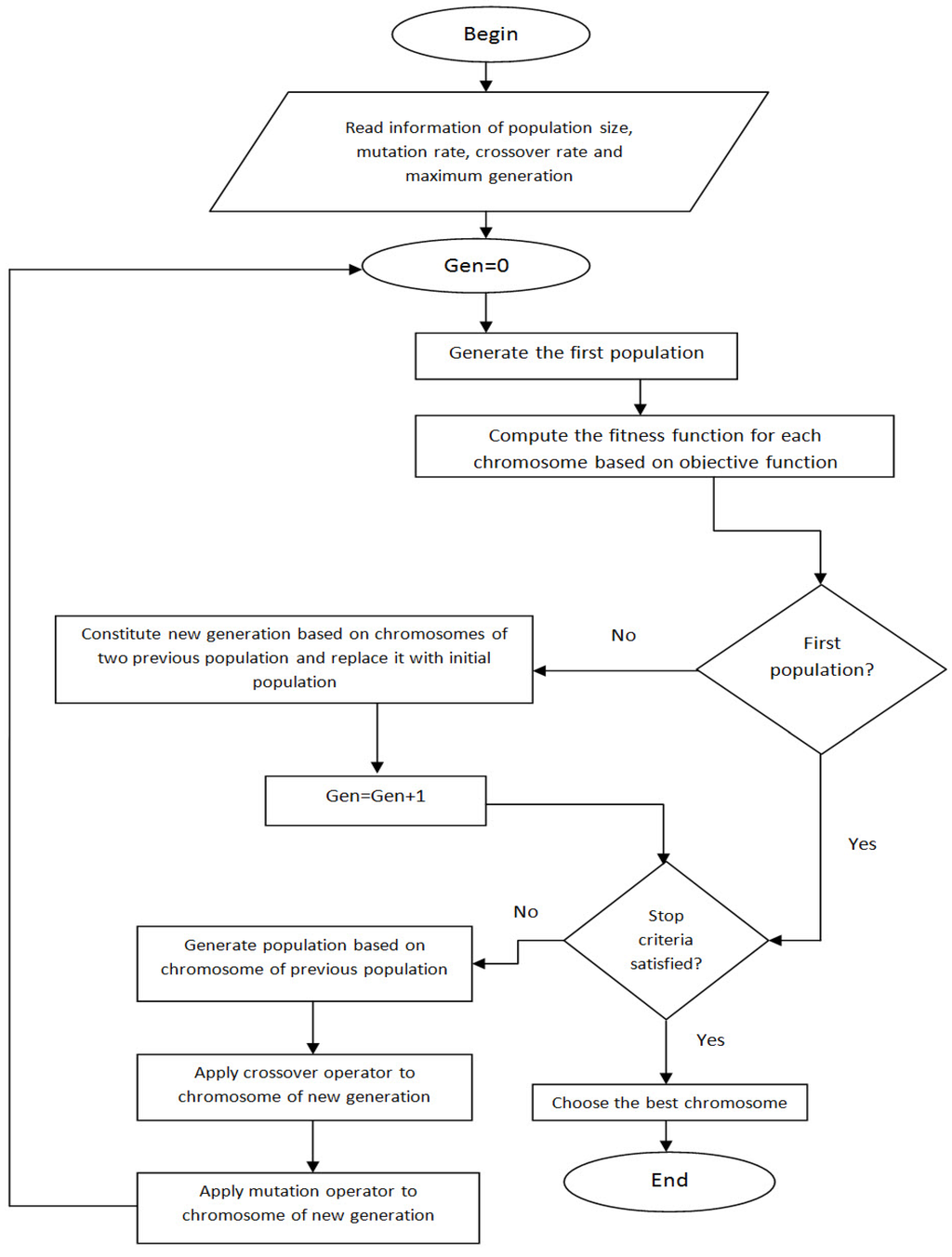
Figure 2.
Schematic diagram of the Genetic Algorithm (GA).
3. Results and Discussion
3.1. Results from the Stochastic Generation
By applying the models, which were described in the “Stochastic generation section” to the historical data, a synthetic series of 37 years duration for rainfall, evapotranspiration and inflow was generated.
Figure 3 shows the comparison between the monthly means and the monthly standard deviation of the measured rainfall, evapotranspiration, inflow (1987–2009) with the averages of the generated rainfall, evapotranspiration, and inflow time series respectively. It is observed that the monthly means and the monthly standard deviations of the generated synthetic rainfall, evapotranspiration, and inflow are close to those of the measured rainfall, evapotranspiration and inflow. This confirms the fact that Markov chain, Monte Carlo simulation and ARMAX model are suitable for generating synthetic rainfall evapotranspiration, and inflow data respectively. By taking into account all the aforementioned probabilities, with the help of frequency curves the ten-day rainfall, evapotranspiration and inflow levels are shown in Figure 4.
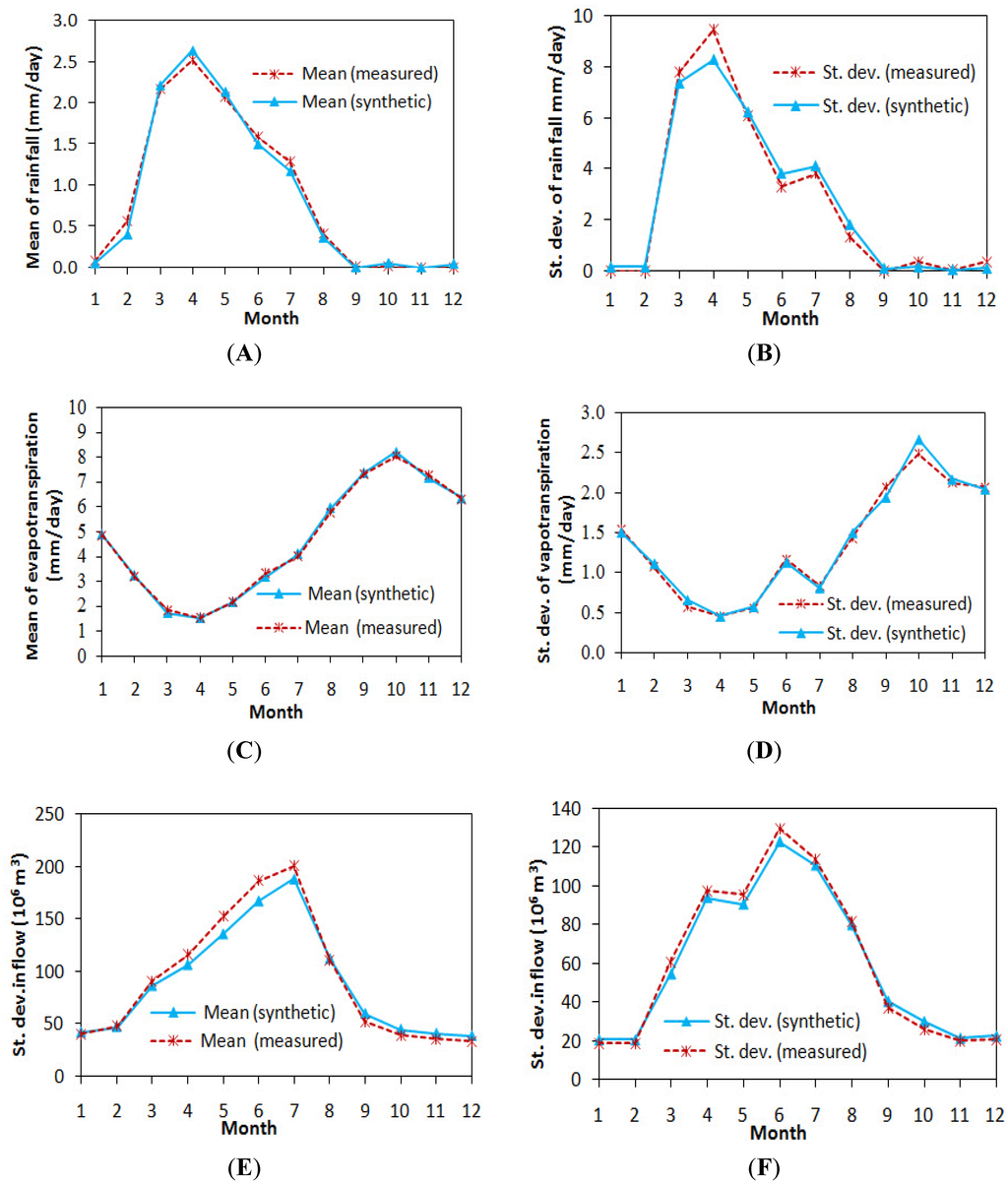
Figure 3.
(A) means of rainfall; (B) standard deviation of rainfall; (C) means of evapotranspiration; (D) standard deviation of evapotranspiration; (E) means of inflow; (F) standard deviation of inflow.
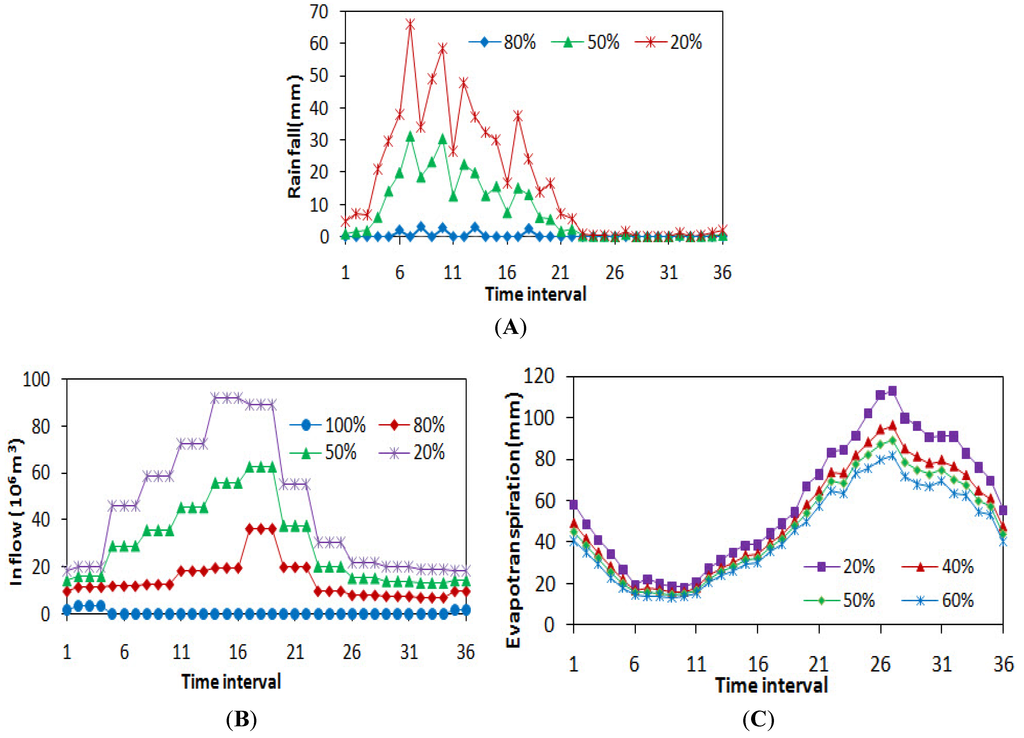
Figure 4.
(A) Ten day rainfall levels; (B) Ten day evapotranspiration levels; (C) Ten day inflow levels.
3.2. Results from the Genetic Algorithm (GA)
The optimization method described above was used to compute the optimal cropping pattern and irrigation scheduling for five major crops: Wheat, canola, barley as winter crops, corn and sugar beet as summer crops under different weather conditions.
Performance of the Genetic Algorithm
Figure 5 depicts the fitness values for the number of iterations under dry weather conditions using the GA. The stopping criterion for the GA is that the fitness function remained constant. As can be seen, this model indicates appropriate performance, as the model tends to converge to a maximum to after 200 iterations. For wet and normal weather conditions similar results were obtained (data are not shown).
The model did not find a feasible solution under hot and dry weather conditions. The reason is that the initial reservoir storage and the inflow during the irrigation season were insufficient to irrigate the crops given the imposed constraints of the minimum desired area (Amin) and the minimum desired relative yield (Ya/Ym).
The optimization model was run based on the expected values of rainfall, evapotranspiration and inflow corresponding to the different probability levels of exceedance (i.e., dry, normal and wet weather conditions) to allocate area to crops and irrigation water to crops.
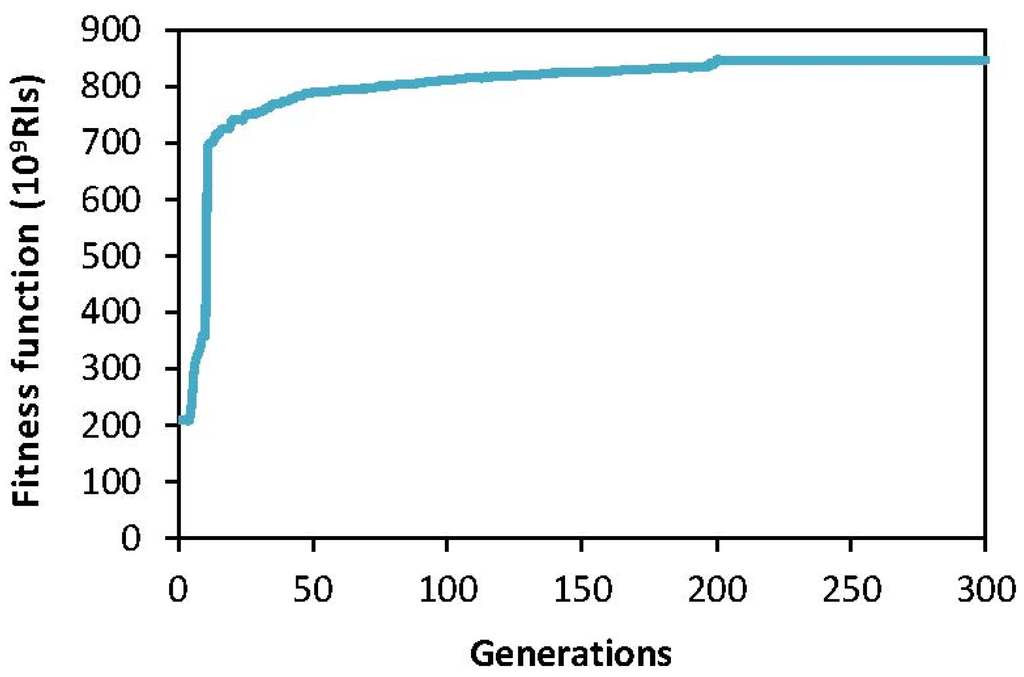
Figure 5.
Fitness function for dry weather condition.
To fix the GA parameters, the model was run for various values of population size, number of generations, crossover and mutation probabilities. It is found that the appropriate parameters for the number of generations, the population size and the crossover probability are 300, 300 and 0.6 respectively. In addition, the mutation function was set to the “adapt feasible” option.
The relative yields under the three weather conditions are given in Table 3. Table 3 demonstrates that results of the optimization model correspond to a deficit irrigation strategy because the relative yield of some crops is less than one.

Table 3.
Relative yield (Ya/Ym (of crops under study corresponding to various weather conditions.
| Crop | Relative Yield (Ya/Ym) | ||
|---|---|---|---|
| Wet | Normal | Dry | |
| Wheat | 1 | 1 | 0.98 |
| Barley | 1 | 1 | 1 |
| Corn | 1 | 1 | 1 |
| Sugar beet | 0.98 | 0.91 | 0.78 |
| Canola | 1 | 0.88 | 0.7 |
The resulting allocation of irrigation water from the reservoir, the cropped areas and the total farm income are shown in Table 4. The allocation of irrigation water and the cropped area for each crop depends on factors such as the net profit per unit of yield, production cost, the potential yield per ha, the minimum water application needed for getting the maximum yield and the total amount of irrigation water available.
The cultivation area under wheat (as winter crop) and corn (as summer crop) is larger than that of other crops (Table 4). For example, under wet weather conditions, the optimal areas under wheat, canola, barley, corn and sugar beet were 73,916 ha, 2183 ha, 15,412 ha, 19,090 ha and 2992 ha respectively. The net profit for canola is higher than that for wheat (Table 1). However, wheat is selected as the optimum crop because the depth of water required for canola was much higher than that of wheat. Similarly, the net profit for sugar beet is higher than that for corn (Table 1). However, the cultivation area under corn is maximized because the depth of water required for corn was lower than that for sugar beet. Under wet weather condition, the allocation of irrigation water from the reservoir for wheat, canola, barley, corn and sugar beet was 399 mm, 544 mm, 447 mm, 626 mm and 890 mm respectively.

Table 4.
Optimum water allocation from reservoir, optimum cultivation area of different crops and total income under various weather conditions.
| Crop | Wet | Normal | Dry | ||||
|---|---|---|---|---|---|---|---|
| Water (mm) | Area (ha) | Water (mm) | Area (ha) | Water (mm) | Area (ha) | ||
| Wheat | 399 | 73,916 | 381 | 74,776 | 412 | 56,308 | |
| Corn | 626 | 19,090 | 696 | 15,466 | 721 | 875 | |
| Sugar beet | 890 | 2,992 | 951 | 2477 | 858 | 98 | |
| Barley | 447 | 15,412 | 346 | 15,584 | 567 | 5,004 | |
| Canola | 544 | 2,183 | 462 | 1,731 | 620 | 642 | |
| TOTAL | Deficit irrigation | 2,906 | 113,594 | 2,836 | 110,034 | 3,178 | 62,927 |
| Full irrigation | - | 111,952 | - | 107,157 | - | - | |
| Total income (106Rls) | Deficit irrigation | 1,621,097 | 1,541,267 | 847,417 | |||
| Full irrigation | 1,584,404 | 1,522,755 | - | ||||
Our results show that when the weather conditions and the availability of water change the area under corn and sugar beet decreases sharply. The area under corn is reduced from 19,090 ha under wet weather condition to 875 ha under dry weather conditions (Table 4). Corn and sugar beet are more sensitive to drought and require a maximum depth of irrigation water. Therefore, it is very difficult to grow corn and sugar beet in the summer season without sufficient supply of irrigation water. However, the change in area cropped with wheat is small because wheat requires less irrigation water. The optimal allocation of irrigation water from the reservoir for wheat production under dry, normal and wet weather conditions was 412, 381 and 399 mm respectively (Table 4). Consequently, weather conditions and water availability are dominant factors affecting cropping pattern, compared to other factors such as the net profit per unit of yield, production cost and the potential yield per ha.
Meanwhile, it is observed that the total farm income is reduced from 1,621,097(106 Rls) under wet weather condition to 847,417(106 Rls) under dry weather condition (Table 4).
It is interesting to compare the results for the two irrigation strategies, namely, the full irrigation and the deficit irrigation (Table 4). In certain cases where under dry weather conditions, there was no feasible solution for the optimization problem using full irrigation, a feasible solution could be reached using deficit irrigation.
As shown in Table 4, for all weather conditions the total farm income and the total cropped area under deficit irrigation are larger than those under full irrigation. Under wet weather condition, for example the total income increased from 1,584,404 to 1,621,097(106 Rls) and total cropped areas increased from 111,952 to 113,594 (ha). The total farm income thus increased by extending the total cropped area, and allowing deficit irrigation for some crops.
4. Conclusions
In this study, a non-linear programming optimization model with an integrated soil/water balance has been developed for determining an optimal reservoir release policy and the optimal cropping pattern for the Doroudzan Dam region in the Fars province (Southwest Iran). The optimization model was solved with a genetic algorithm (GA) using MATLAB [30]. Four weather conditions were identified by combining the probability levels of rainfall, evapotranspiration and inflow. Moreover, two irrigation strategies, full irrigation and deficit irrigation were modeled under each weather condition.
The results indicate that for all weather conditions the total farm income and the total cropped area under deficit irrigation were larger than those under full irrigation. In certain cases of dry weather conditions deficit irrigation gave a feasible solution. Therefore, deficit irrigation strategy is suggested as a management technique to improve allocation of the limited water supplies, especially under dry weather conditions. The solutions provide optimal water-allocation and crop pattern for all weather conditions. The cultivation area under wheat (as winter crop) and corn (as summer crop) is larger than that of other crops. In addition, our results show that when the weather conditions and the availability of water changes the area under corn and sugar beet decreases sharply. Corn and sugar beet require a maximum depth of irrigation water. In contrast, the change in area cropped with wheat is small because wheat requires less irrigation water. Therefore, it is recommended to replace low water requiring crops with high water requiring crops. In addition, it is concluded that the optimization approach has been successfully applied to the Doroudzan Dam region. Thus, decision makers and water authorities can use it as an effective tool for such large and complex irrigation planning problems.
Appendix
Rainfall occurrence is modeled using a first-order Markov chain approach whereby each day can be either wet (W) or dry (D). The transitional probability matrix is given in Equation (A1) below:
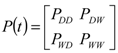 where PDD = conditional probability that a dry day is followed by a dry day; PDW= conditional probability that a wet day is followed by a dry day; PWD = conditional probability that a dry day is followed by a wet day; PWW = conditional probability that a wet day is followed by a wet day. However, by definition, PWD = 1 − PDD and PDW = 1 − PWW and thus, only two probabilities need be calculated from historical data, the other two being calculated from these:
where PDD = conditional probability that a dry day is followed by a dry day; PDW= conditional probability that a wet day is followed by a dry day; PWD = conditional probability that a dry day is followed by a wet day; PWW = conditional probability that a wet day is followed by a wet day. However, by definition, PWD = 1 − PDD and PDW = 1 − PWW and thus, only two probabilities need be calculated from historical data, the other two being calculated from these:
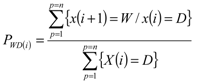
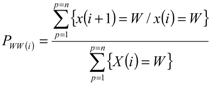 where PWD(i) = the probability that if day i is dry, then day i + 1 will be wet. These probabilities, in combination with a random number generator from uniform distribution, are then used to generate series of wet and dry days. Given the state of the preceding day (W or D), a random number of uniform distribution is generated and compared with the appropriate probability (PWD if preceding day D and PWW if preceding day W). If the number generated is greater than the probability, then the day is recorded as wet, otherwise, it is dry. The process is continued until the end of the year, the last day of one year becoming the preceding day for the start of the next. Given that a day is wet, rainfall amounts are calculated by sampling from the gamma distribution [10].
where PWD(i) = the probability that if day i is dry, then day i + 1 will be wet. These probabilities, in combination with a random number generator from uniform distribution, are then used to generate series of wet and dry days. Given the state of the preceding day (W or D), a random number of uniform distribution is generated and compared with the appropriate probability (PWD if preceding day D and PWW if preceding day W). If the number generated is greater than the probability, then the day is recorded as wet, otherwise, it is dry. The process is continued until the end of the year, the last day of one year becoming the preceding day for the start of the next. Given that a day is wet, rainfall amounts are calculated by sampling from the gamma distribution [10].
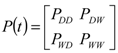
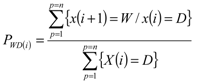
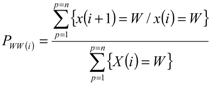
Gamma distribution has two parameters, the shape and the scale parameters. The probability density function (pdf) of the gamma distribution is given by [10]:
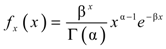 where α = the shape parameter (α > 0); β = the scale parameter (β > 0); and Γ(0) is the Gamma function.
where α = the shape parameter (α > 0); β = the scale parameter (β > 0); and Γ(0) is the Gamma function.
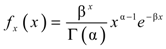
A1. Monte Carlo Simulation
Monte Carlo simulation is based on repeatedly sampling from a chance process.
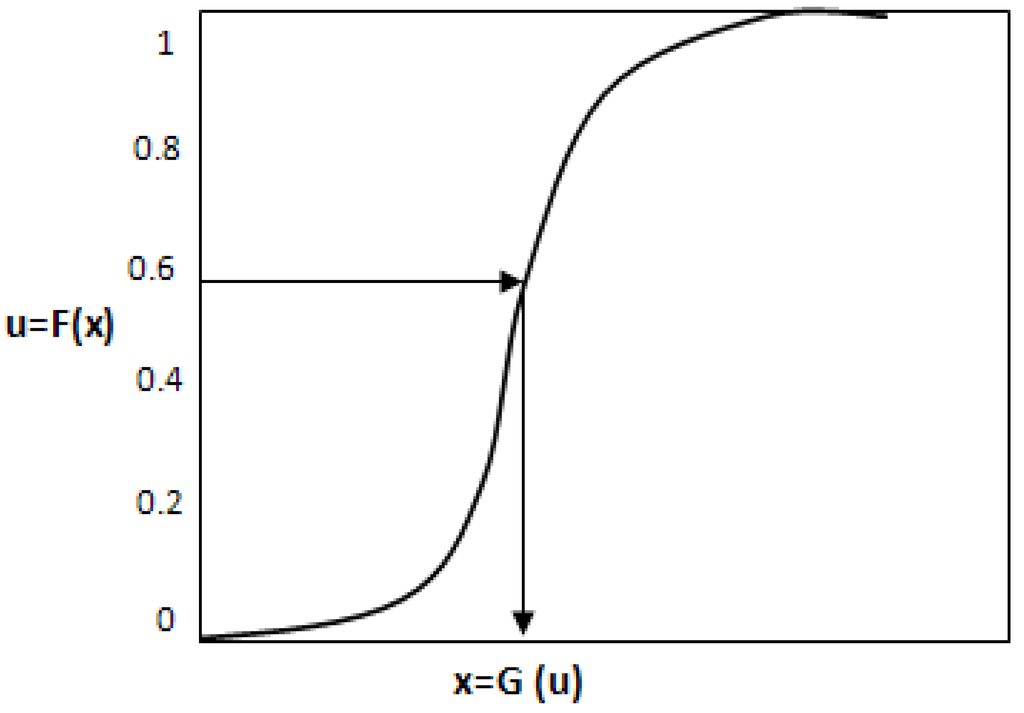
Figure A1.
The principle of Monte Carlo sampling.
As illustrated in the figure, the cumulative probability scale in this case has been divided in to five equi-probable intervals. Therefore a random integer (1, 2…, 5) is generated to pick an interval. A new random number is then generated to determine where within the interval the sampled value of F(x) should lie. As ordinary Monte Carlo sampling, x is then calculated for the value of F(x) by putting this into x=G(u), where u now is first scaled to lie in the range of F(x) corresponding to the chosen interval of x. The same procedure is repeated for the required number of iterations with the provision that intervals once chosen are not eligible to be sampled again—they are already represented in the sampled set [19].
A2. ARMAX Model
ARMAX model represents the relationship between inflow and precipitation and is written as [10]:
where t = discrete time; yt = inflow time series; xt = precipitation time series; et = normally independently distributed white noise residual with mean zero and variance σ2; φ(B) = 1 + φ1B − φ2B2 − .... − φ pB p non seasonal autoregressive (AR) operator of order p; θ(B) = 1 − θ1B − θ2B2 − .... − θ qB P non seasonal moving average (MA) operator of order q and ω(B) = ω0 − ω1B − ω2B2 − ... − ω rB r operator of order r in the numerator of the transfer r function; B = backward shift operator defined by Byt = yt−1.
φ ( B ) yt = ω ( B ) xt + θ ( B ) et
Conflicts of Interest
The authors declare no conflict of interest.
References
- Mariolakos, I. Water resources management in the framework of sustainable development. J. Desalin. 2007, 213, 147–151. [Google Scholar]
- Olesen, J.E.; Bindi, M. Consequences of climate change for European agricultural productivity, land use and policy. J. Agron. 2002, 16, 239–262. [Google Scholar]
- Moradi-Jalal, M.; Haddad, O.B.; Marino, M.A.; Karney, B.W. Reservoir operation in assigning optimal multi-crop irrigation areas. J. Agric. Water Manag. 2007, 90, 149–159. [Google Scholar]
- Seckler, D.; Amarasinghe, U.; Molden, D.; Radhika, D.; Randolph, B. World Water Demand and Supply 1990 to 2025: Scenarios and Issues; Research Report 19; International Water Management Institute: Colombo, Sri Lanka, 1998. [Google Scholar]
- Hayati, D.; Karami, E. Typology of causes of poverty: The perception of Iranian farmers. J. Econ. Psychol. 2005, 26, 884–901. [Google Scholar]
- Fars Regional Water Organization. Islamic Republic of Iran Ministry of Energy. 2009. Available online: http://www.frrw.ir (accessed on 31 December 2009).
- Ghahraman, B.; Sepaskhah, A.R. Optimal allocation of water from a single reservoir to an irrigation project with predetermined multiple cropping patterns. J. Irrig. Sci. 2002, 21, 127–137. [Google Scholar]
- Raju, K.S.; NageshKumar, D. Irrigation planning using genetic algorithms. J. Water Res. Manag. 2004, 182, 163–176. [Google Scholar]
- Nagesh Kumar, D.; Raju, K.S.; Ashok, B. Optimal reservoir operation for irrigation of multiple crops using genetic algorithms. J. Irrig. Drain. Eng. 2006, 132, 123–129. [Google Scholar]
- Georgiou, P.E.; Papamichai, D.M. Optimization model of an irrigation reservoir for water allocation and crop planning under various weather conditions. J. Irrig. Sci. 2008, 26, 487–504. [Google Scholar]
- Regulwar, D.G.; Anand Raj, P. Development of 3-D optimal surface for operation policies of a multi reservoir in fuzzy environment using genetic algorithm for river basin development and management. J. Water Res. Manag. 2008, 22, 595–610. [Google Scholar]
- Jensen, M.E. Water Consumption by Agricultural Plants. In Water Deficits and Plants Growth; Academic Press: New York, NY, USA, 1968; Volume 2, pp. 1–22. [Google Scholar]
- Shabani, A. Effect of Water Stress on Different Growth Stages of Oilseed Rape (Brassica Napus). Master’s Thesis, Agricultural University, Shiraz, Iran, 2006. [Google Scholar]
- Shabani, M.K. Optimal Management of Irrigation Water Allocation and Cropping Pattern in Doroudzan Irrigation and Drainage Network Using Geographic Information System. Master’s Thesis, Agricultural University, Shiraz, Iran, 2007. [Google Scholar]
- Fars agricultural Organization. Islamic Republic of Iran Ministry of Agriculture. 2009. Available online: http://www.fars.agri-jahad.ir (accessed on 31 December 2009).
- Georgiou, P.E.; Papamichail, D.M.; Vougioukas, S.G. Optimal irrigation reservoir operation and simultaneous multi-crop cultivation area selection using simulated annealing. J. Irrig. Drain. 2006, 55, 129–144. [Google Scholar]
- Tsakiris, G. A method for applying crop sensitivity factors in irrigation scheduling. J. Agric. Water Manag. 1982, 5, 335–343. [Google Scholar]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration: Guidelines for Computing Crop Water Requirements; FAO Irrigation and drainage paper 56; Food and Agriculture Organization of the United Nations: Rome, Italy, 1998. [Google Scholar]
- Hardaker, J.B.; Huirne, B.M.; Anderson, R.; Lien, G. Coping with Risk in Agriculture; Commonwealth Agricultural Bureaux International (CABI) Publishing: London, UK, 2004. [Google Scholar]
- Makridakis, S.; Wheelwright, S.C.; Hyndman, R.J. Forecasting: Methods and Applications, 3rd ed.; Wiley: New York, NY, USA, 1998. [Google Scholar]
- Raes, D.; Sahli, A.; van Looij, J.; ben Mechlia, N.; Persoons, E. Charts for guiding irrigation in real time. J. Irrig. Drain. Syst. 2000, 14, 343–352. [Google Scholar]
- De Bruin, H.A.R. A simple model for shallow lake evaporation. J. Appl. Meteorol. 1978, 17, 1132–1134. [Google Scholar]
- Ghahraman, B.; Sepaskhah, A.R. Linear and non-linear optimization models for allocation of a limited water supply. J. Irrig. Drain. 2004, 53, 39–54. [Google Scholar]
- Bos, M.G.; Vos, J.; Feddes, R.A. CRIWAR 2.0: A Simulation Model on Crop Irrigation Water Requirements; International Institute for Land Reclamation and Improvement Publication: Nairobi, Kenya, 1996; No. 46. [Google Scholar]
- USDA Soil Conservation Service. Irrigation water requirements. In National Engineering Handbook; USDA Soil Conservation Service: Washington, DC, USA, 1993; Chapter 2; p. 283. [Google Scholar]
- Borg, H.; Grimes, D.W. Depth development of roots with time: An empirical description. J. Trans. ASAE 1986, 29, 194–197. [Google Scholar]
- Vedula, S.; Mujumdar, P.P. Optimal reservoir operation for irrigation multiple crops. J. Water Res. Res. 1992, 28, 1–9. [Google Scholar]
- Doorenbos, J.; Kassam, A.H. Yield Response to Water; FAO Irrigation and drainage paper 56; Food and Agriculture Organization of the United Nations: Rome, Italy, 1979. [Google Scholar]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization and Machine Learning; Addision-Wesley: Reading, MA, USA, 2000. [Google Scholar]
- MATLAB software. The language of technical computing. Version 7.4.0.287(R2007a). Math Works Inc: Natick, MA, USA.
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).