Sensitivity of Surface Runoff to Drought and Climate Change: Application for Shared River Basins
Abstract
:1. Introduction
- (1)
- predict the likely proportional change (%) in the annual runoff available for the downstream country; and
- (2)
- anticipate the standardized Reconnaissance Drought Index (RDIst) and SDI values due to a wide range of possible future climate change.
2. Materials and Methods
2.1. Meteorological Drought Severity (MDS)
2.2. Streamflow Drought Index
| Condition | Range |
|---|---|
| Extremely wet | (SDI and RDIst) ≥2.00 |
| Very wet | 1.5 ≤ (SDI and RDIst) < 2.00 |
| Moderately wet | 1.00 ≤ (SDI and RDIst) < 1.50 |
| Near normal | −1.00 < (SDI and RDIst) < 1.00 |
| Moderately dry | −1.50 < (SDI and RDIst) ≤ −1.00 |
| Severely dry | −2.00 < (SDI and RDIst) ≤ −1.50 |
| Extremely dry | (SDI and RDIst) ≤ 2.00 |
2.3. Rainfall-Runoff Model
2.4. Methodological Approach
- The Medbasin-M rainfall-runoff model was calibrated using the monthly P and PET data for the period of twelve hydrologic years (1962−1973) for which unimpaired streamflow data were observed and used for model calibration. The climatic conditions for the calibration period were mostly near to normal, with some years characterised by moderately wet or moderately dry conditions (Table 1). This allowed the unbiased calibration of the model. About 75% and 92% of the annual precipitations during the calibrated period were between the mean −SD and the mean +SD, and between mean − 2SD and mean + 2SD, respectively. The minimum, mean and the maximum annual precipitations were 520 mm, 729 mm and 1,187 mm, respectively. The SD was approximately 201 mm. The annual precipitation observed in 1969 was interpreted as an outlier. No other outliers were observed over the calibration time interval. The minimum, mean and maximum PET values were 1,215 mm, 1,287 mm and 1,364 mm, respectively. The SD was about 58 mm. No outliers were observed.
- The simulation results were validated using monthly climatic data (P and PET) and the unregulated observed runoff for a period of nine water years (1974−1982). Some statistical goodness-of-fit tools were employed for calibrating the model and validating the simulation results. These measures are r, RMSE, MAE and IoA ([34,35] for the latter). The following formulas (Equations (8) to (11)) were applied:where , and are the observed runoff, simulated runoff and the means of the observed and simulated runoffs, respectively. N is the number of years and i is the time step.
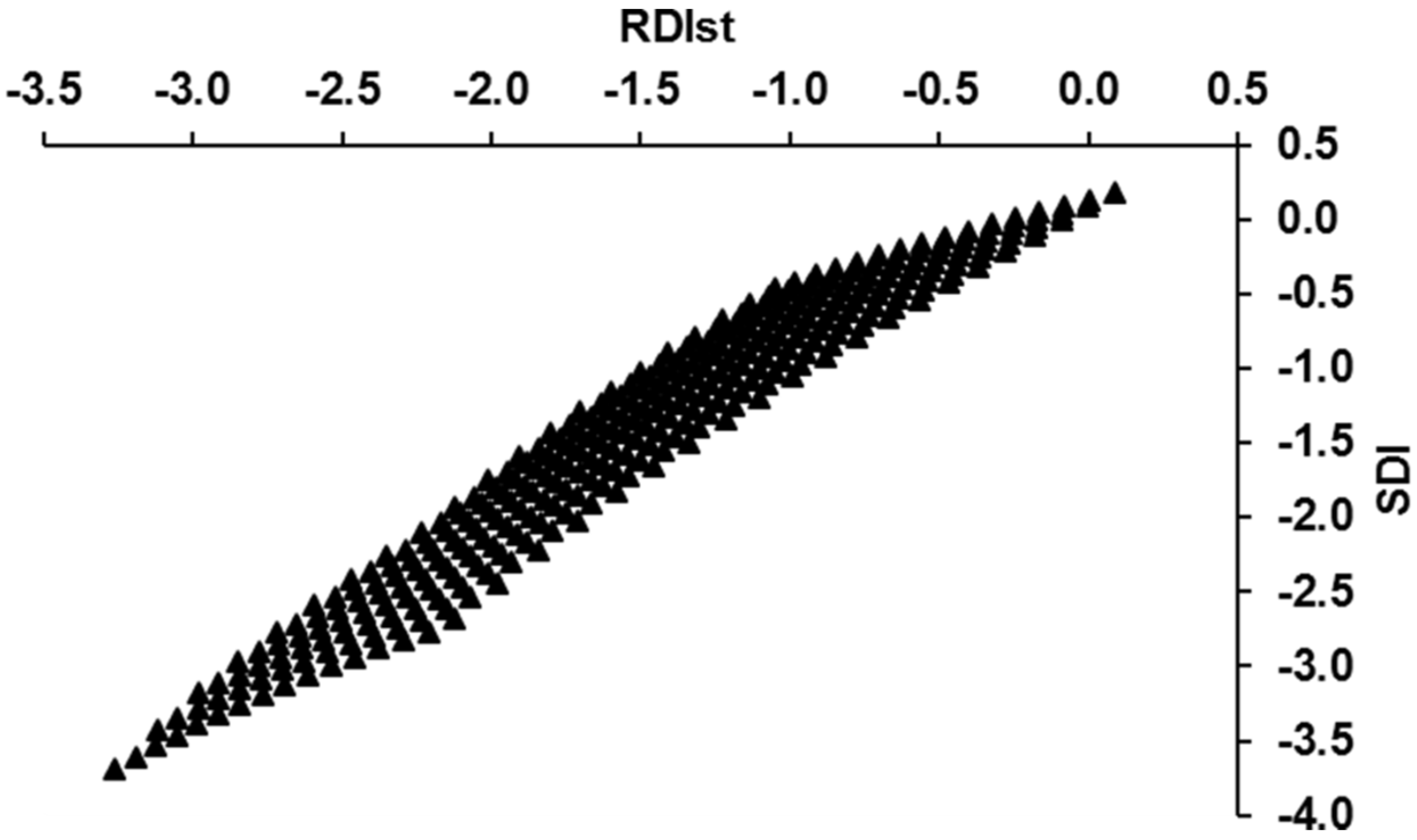
- The RDIst values were calculated over a time window of 30 years between 1962 and 1991. This was performed to specify which period represents nearly the normal climatic condition (on average) and to assess the constants a and b of the linear Equations (12) and (13):where , and SDI are the standardized form of the RDI, the initial form of the RDI and the streamflow drought index, respectively. , , and are constants. The period of nearly normal climatic condition expresses the timeframe in which no extreme RDIst values were witnessed and when, on average, the RDIst value is close to zero. The period of eight water years (1975 to 1982), which characterised the normal condition, was used for running the climatic scenarios. Moreover, the period between 1975 and 1982 was devoid of any considerable human construction activities (e.g., hydraulic control structures and large-scale irrigation schemes) in the upstream country, Iran.
- The Medbasin-M model was used to compute the reference mean annual runoff for the normal climatic condition.
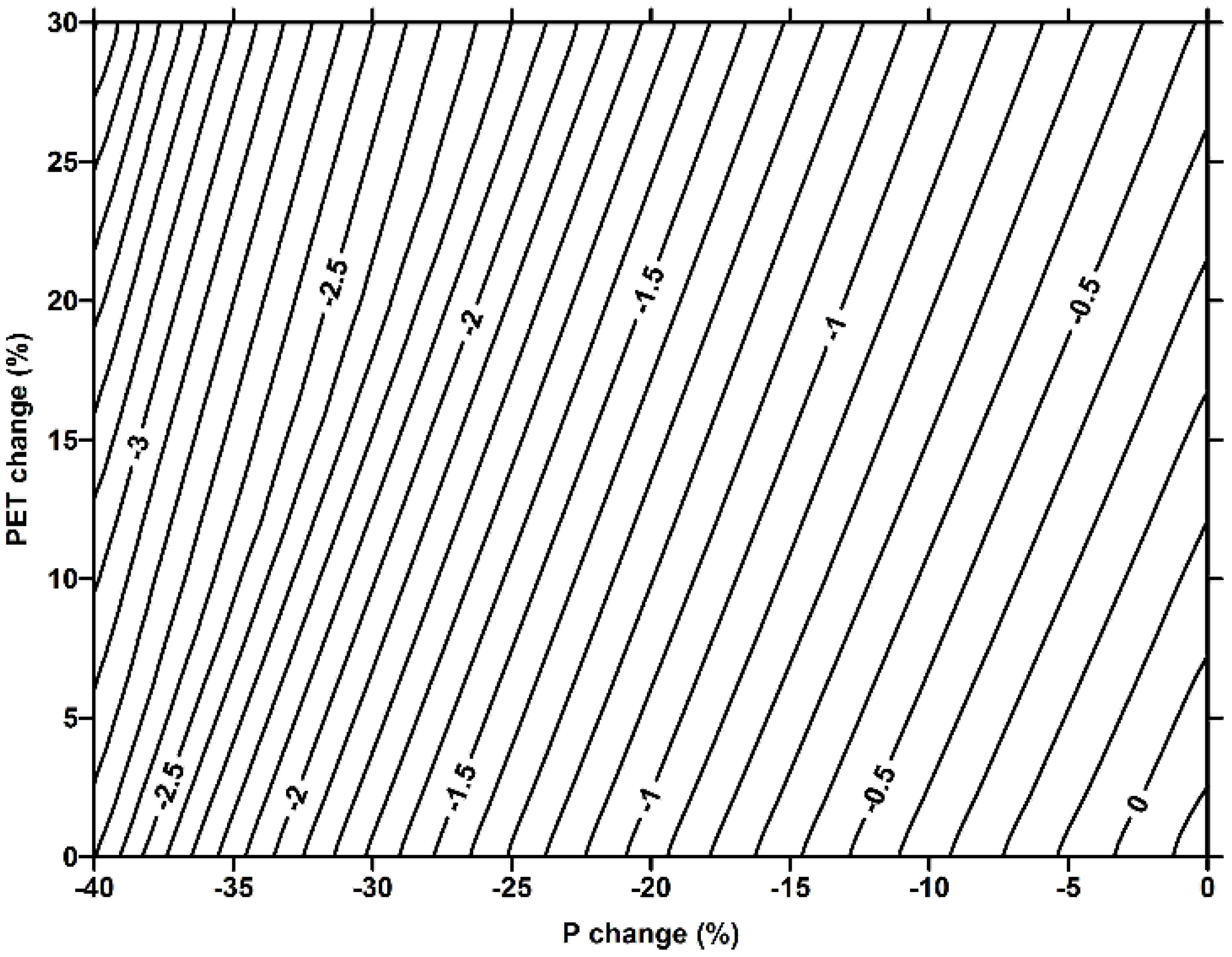
- The Fifth Assessment Report of the IPCC [1] suggests that the region where the examined basin is located is likely to face a decline in precipitation amount and an increase in mean air temperature as part of climate change. The IPCC [36] highlighted that the annual average river runoff availability is projected to decrease by between 10% and 30% over some dry regions at mid-latitudes by 2050. Some impacted regions presently have water-stressed areas. Furthermore, an increase in drought spells is also projected for mid-latitudes. The IPCC reports also point out with high confidence (defined by IPCC) that climate change has the potential to exacerbate water resource stresses in most regions of Asia. The regional projections of temperature and precipitation in Asia based on a so-identified A2-forced emission scenario using the Atmosphere-Ocean General Circulation Model (AOGCM) simulations show that the rate of decrease in precipitation could reach −40% in winter (between December and February) and −50% in summer (between June and August). The increase in temperature would be in the order of +10% in winter and +6% in summer. It should be noted that these predictions should be considered as valid until the end of the 21st century. The synthetic scenarios for assessing the runoff sensitivity to climate change were formulated through an incremental shift of the historical P and PET values by a 2% step for a P reduction range from 0% to −40% and a PET increase from 0% to +30%. Correspondingly, 336 scenarios were developed, representing the mutual impact of deviations in P and PET values that lie within the aforementioned assortment of scenarios. These scenarios include all possible basin-wide climate change projections, as well as a wide array of drought severity conditions. The Medbasin-M model was repetitively used to simulate the runoff for the 336 scenarios.
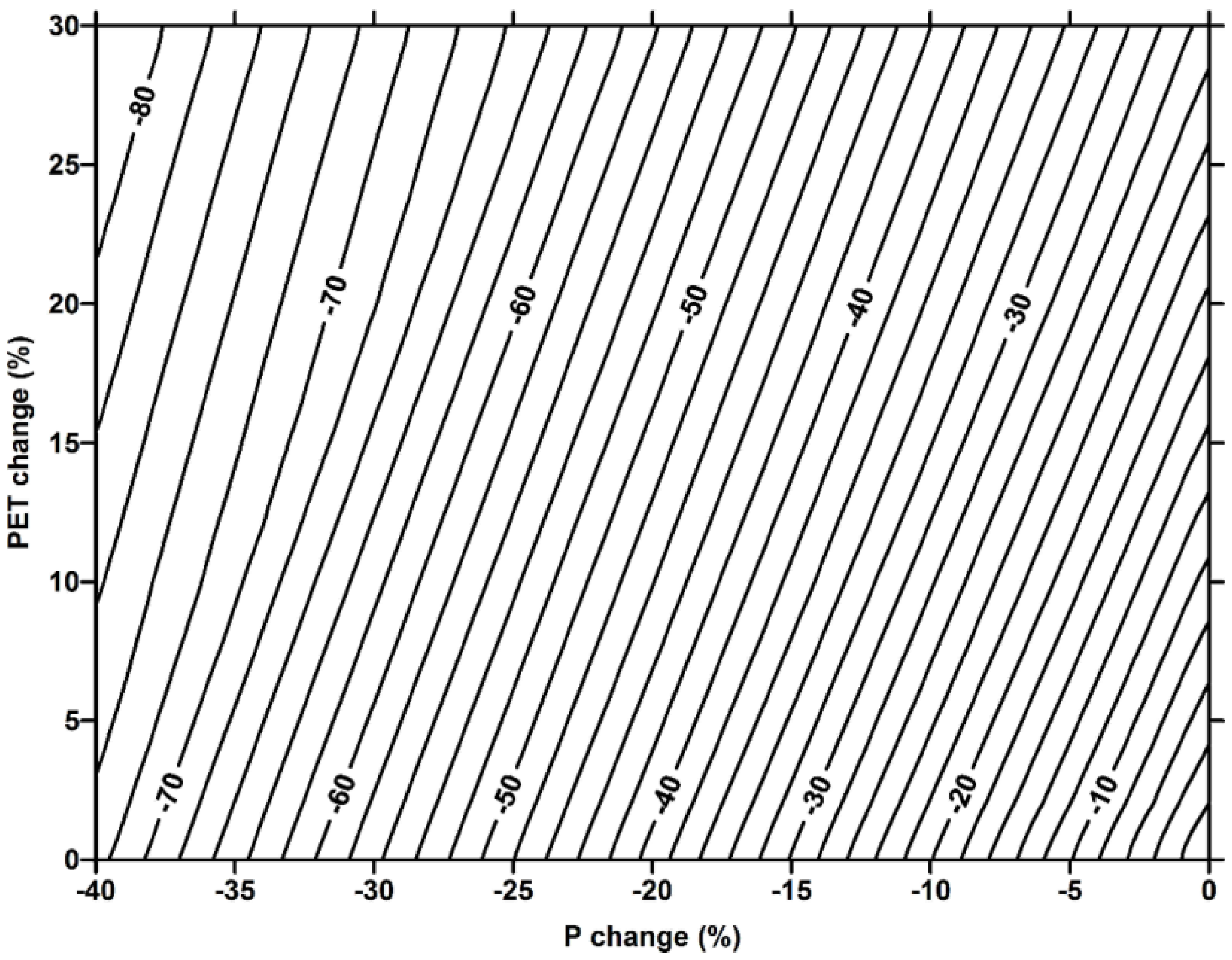
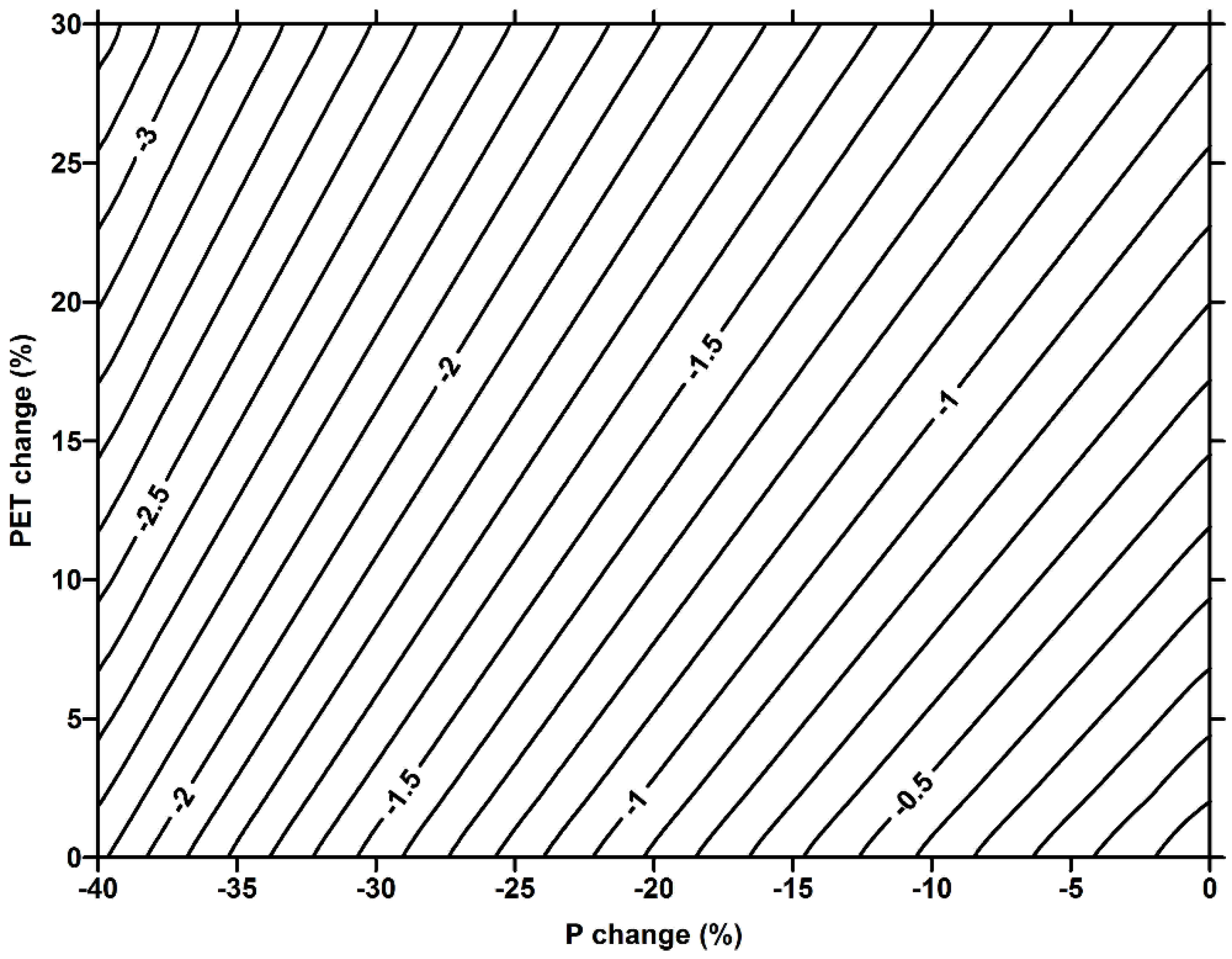
- The anticipated proportional change in the annual runoff (%), corresponding to each scenario, was determined relative to the reference mean annual runoff.
- A nomograph was used for estimating the projected proportional change (%) in the climate-impacted runoff. The predictable proportional changes in the runoff represent the anticipated runoff reductions (%) relative to the long-term unimpaired mean annual runoff under the normal climatic condition.
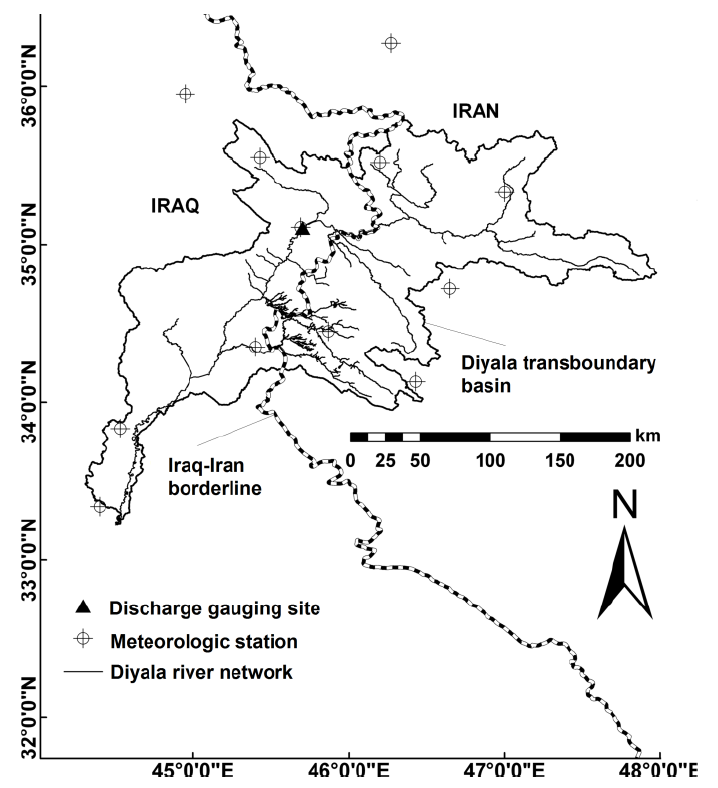
2.5. Study Area and Data Availability
3. Results and Discussion
3.1. Model Calibration and Simulation Results after Validation

3.2. Anticipated Runoff for Various Climatic Scenarios

4. Conclusions and Recommendations
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Intergovernmental Panel on Climate Change. Climate Change 2014: Impacts, Adaptation, and Vulnerability. Available online: http://www.ipcc.ch/report/ar5/wg2 (accessed on 5 May 2014).
- Niemeyer, S. New Drought Indices. In Proceedings of the 1st International Conference on Drought Management: Scientific and Technological Innovations (option Méditerranéennes, series A, No. 80), Zaragoza, Spain, 12–14 June 2008.
- Cloppet, E. Agricultural Drought Indices in France and Europe: Strengths, Weaknesses, and Limitations. In Proceedings of the Expert Meeting, Murcia, Spain, 2–4 June 2010.
- Zarch, M.A.A.; Malekinezhad, H.; Mobin, M.H.; Dastorani, M.T.; Kousari, M.R. Drought monitoring by reconnaissance drought index (RDI) in Iran. Water Res. Manag. 2011, 25, 3485–3504. [Google Scholar] [CrossRef]
- Talaee, P.H.; Tabari, H.; Ardakani, S.S. Hydrological drought in the west of Iran and possible association with large-scale atmospheric circulation patterns. Hydrol. Proc. 2012, 28, 764–773. [Google Scholar] [CrossRef]
- Rasheed, A.M.M. Analysis of rainfall drought periods in the North of Iraq using standard precipitation index (SPI). Al Rafidain Eng. J. 2010, 18, 60–72. [Google Scholar]
- United Nations Educational, Scientific and Cultural Organization. Integrated Drought Risk Management–DRM National Framework for Iraq-Executive Summary; Technical Report; UNESCO-Iraq office: Baghdad, Iraq, 2013. [Google Scholar]
- Tigkas, D. Drought Characterisation and Monitoring in Regions of Greece. Eur. Water 2008, 23–24, 29–39. [Google Scholar]
- Pangalou, D.; Tigkas, D.; Vangelis, H.; Tsakiris, G.; Nanou-Giannarou, A. Drought severity thresholds and drought management in Greece. Adv. Nat. Technol. Hazards Res. 2009, 26, 243–256. [Google Scholar]
- Dogan, S.; Berltay, A.; Singh, V.P. Comparison of multi-monthly rainfall-based drought severity indices, with application to semi-arid Konya closed basin, Turkey. J. Hydrol. 2012, 470–471, 255–268. [Google Scholar]
- Al-Qinna, M.I.; Hammouri, N.A.; Obeidat, M.M.; Ahmad, F.Y. Drought analysis in Jordan under current and future climates. Clim. Change 2011, 106, 421–440. [Google Scholar] [CrossRef]
- Tarawneh, Q.Y. Quantification of drought in the Kingdom of Saudi Arabia. Int. J. Water Res. Arid Environ. 2013, 2, 125–133. [Google Scholar]
- Tsakiris, G.; Vangelis, H. Establishing a drought index incorporating evapotranspiration. Eur. Water 2005, 9–10, 3–11. [Google Scholar]
- Khalili, D.; Farnoud, T.; Jamshidi, H.; Kamgar-Haghighi, A.A.; Zand-Parsa, S. Comparability analyses of the SPI and RDI meteorological drought indices in different climatic zones. Water Res. Manag. 2011, 25, 1737–1757. [Google Scholar] [CrossRef]
- Elagib, N.A.; Elhag, M.M. Major Climate indicators of ongoing drought in Sudan. J. Hydrol. 2011, 409, 612–625. [Google Scholar] [CrossRef]
- Nalbantis, I. Drought and streamflow. Eur. Water 2008, 23–24, 65–76. [Google Scholar]
- Nalbantis, I.; Tsakiris, G. Assessment of hydrological drought revisited. Water Res. Manag. 2009, 23, 881–897. [Google Scholar]
- Allen, P.; Harmel, R.D.; Dunbar, J.A.; Arnold, J.G. Upland contribution of sediment and runoff during extreme drought: A study of the 1947–1956 drought in the Blackland Prairie, Texas. J. Hydrol. 2011, 407, 1–11. [Google Scholar] [CrossRef]
- Tsakiris, G.; Nalbantis, I.; Pangalou, D.; Tigkas, D.; Vangelis, H. Drought Meteorological Monitoring Network Design for the Reconnaissance Drought Index (RDI). Available online: http://www.iamz.ciheam.org/medroplan/zaragoza2008/Sequia2008/Session1/D.Tigkas.pdf (accessed on 1 May 2014).
- Bonsal, B.; Regier, M. Historical comparison of the 2001/2002 drought in the Canadian prairies. Clim. Res. 2007, 33, 229–242. [Google Scholar] [CrossRef]
- Tsakiris, G.; Pangalou, D.; Vangelis, H. Regional drought assessment based on the Reconnaissance Drought Index (RDI). Water Res. Manag. 2007, 21, 821–833. [Google Scholar] [CrossRef]
- Tigkas, D.; Vangelis, H.; Tsakiris, G. The RDI as a composite climatic index. Eur. Water 2013, 41, 17–22. [Google Scholar]
- Tigkas, D.; Vangelis, H.; Tsakiris, G. The Drought Indices Calculator (DrinC). In Proceedings of the 8th International Conference of EWRA: Water Resources Management in an Interdisciplinary and Changing Context, Porto, Portugal, 26–29 June 2013.
- Tigkas, D.; Vangelis, H.; Tsakiris, G. DrinC: A software for drought analysis based on drought indices. Earth Sci. Inform. 2014, in press. [Google Scholar]
- Al-Faraj, F.A.M.; Scholz, M. Assessment of temporal hydrologic anomalies coupled with drought impact for a transboundary river flow regime. The Diyala watershed case study. J. Hydrol. 2014, 517, 64–73. [Google Scholar]
- Al-Faraj, F.A.M.; Scholz, M. Impact of upstream anthropogenic river regulation on downstream water availability in transboundary river watersheds. Int. J. Water Res. Dev. 2014, in press. [Google Scholar]
- Doorenbos, J.; Pruitt, W.O. Guidelines for Predicting Crop Water Requirements. In Food and Agriculture Organisation (FAO) of the United Nations–Irrigation and Drainage Paper 24, 2nd ed.; FAO: Rome, Italy, 1977. [Google Scholar]
- Tigkas, D.; Tsakiris, G. Medbasin: A Mediterranean rainfall–runoff software package. Eur. Water 2004, 5–6, 3–11. [Google Scholar]
- Tigkas, D.; Vangelis, H.; Tsakiris, G. Drought and climate change impact on streamflow in small watersheds. Sci. Total Environ. 2012, 440, 33–41. [Google Scholar] [CrossRef] [PubMed]
- Giakoumakis, S.; Dercas, N.; Karantounias, G. Validation of a Simple Water Balance Model in Pinios River Basin (Peloponnese, Greece). In Proceedings of the 6th International Conference of the European Water Resources Association (EWRA) on Sharing a Common Vision for Our Water Resources, Menton, France, 7–10 September 2005.
- Soil Conservation Service. National Engineering Handbook. Section 4 on Hydrology; Department of Agriculture: Washington, DC, USA, 1972.
- Gregory, M.A.; Cunningham, B.A.; Schmidt, M.F.; Mack, B.W. Estimating Soil Storage Capacity for Stormwater Modeling Applications. In Proceedings of the 6th Biennial Conference on Stormwater Research and Watershed Management, Southwest Florida, FL, USA, 14–17 September 1999.
- United States Department of Agriculture. Urban hydrology for small watersheds. In Technical Release 55 (TR-55), 2nd ed.Natural Resources Conservation Service, Conservation Engineering Division: Washington, DC, USA, 1986. [Google Scholar]
- Willmott, C.J. On the validation of models. Phys. Geogr. 1981, 2, 184–194. [Google Scholar]
- Willmott, C.J.; Robesonb, S.M.; Matsuuraa, K. A refined index of model performance. Int. J. Climatol. 2012, 32, 2088–2094. [Google Scholar] [CrossRef]
- Intergovernmental Panel on Climate Change (IPCC). Climate Change 2007: Impacts, Adaptation, and Vulnerability; Contribution of Working Group II to the Fourth Assessment Report of the IPCC; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Harza Engineering Company and Binnie & Partners. Hydrological Survey of Iraq; Discharges for Selected Gauging Stations in Iraq, Report; Harza Engineering Company: Chicago, IL, USA; Binnie & Partners: London, UK, 1958. [Google Scholar]
- Harza Engineering Company and Binnie & Partners. Hydrological Survey of Iraq; Discharges for Selected Gauging Stations in Iraq, Report; Harza Engineering Company: Chicago, IL, USA; Binnie & Partners: London, UK, 1959. [Google Scholar]
- Harza Engineering Company and Binnie & Partners. Hydrological Survey of Iraq; Main Report; Harza Engineering Company: Chicago, IL, USA; Binnie & Partners: London, UK, 1963. [Google Scholar]
- Ministry of Agriculture and Water Resources-Kurdistan Regional Government (MA and WR-KRG). Various Official Data Sets, General Directorate of Dams and Reservoirs and Directorate for Operation of Derbandikhan; MA and WR-KRG: Erbil and Sulaymaniya, Iraq, 2013.
- Food and Agriculture Organization of the United Nations (FAO). Hydrogeology of Northern Iraq, Volume 1–Climate, Hydrology, Geomorphology and Geology; FAO: Rome, Italy, 2004. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Faraj, F.A.M.; Scholz, M.; Tigkas, D. Sensitivity of Surface Runoff to Drought and Climate Change: Application for Shared River Basins. Water 2014, 6, 3033-3048. https://doi.org/10.3390/w6103033
Al-Faraj FAM, Scholz M, Tigkas D. Sensitivity of Surface Runoff to Drought and Climate Change: Application for Shared River Basins. Water. 2014; 6(10):3033-3048. https://doi.org/10.3390/w6103033
Chicago/Turabian StyleAl-Faraj, Furat A. M., Miklas Scholz, and Dimitris Tigkas. 2014. "Sensitivity of Surface Runoff to Drought and Climate Change: Application for Shared River Basins" Water 6, no. 10: 3033-3048. https://doi.org/10.3390/w6103033
APA StyleAl-Faraj, F. A. M., Scholz, M., & Tigkas, D. (2014). Sensitivity of Surface Runoff to Drought and Climate Change: Application for Shared River Basins. Water, 6(10), 3033-3048. https://doi.org/10.3390/w6103033