Pump as Turbine (PAT) Design in Water Distribution Network by System Effectiveness †
Abstract
:1. Introduction
- The capability of the PAT performance in hydraulic or electrical regulation;
- The flexibility of the PAT under working conditions slightly different from the design values;
- The reliability of the PAT based on the lifecycle of its components.
2. PAT Design Skills
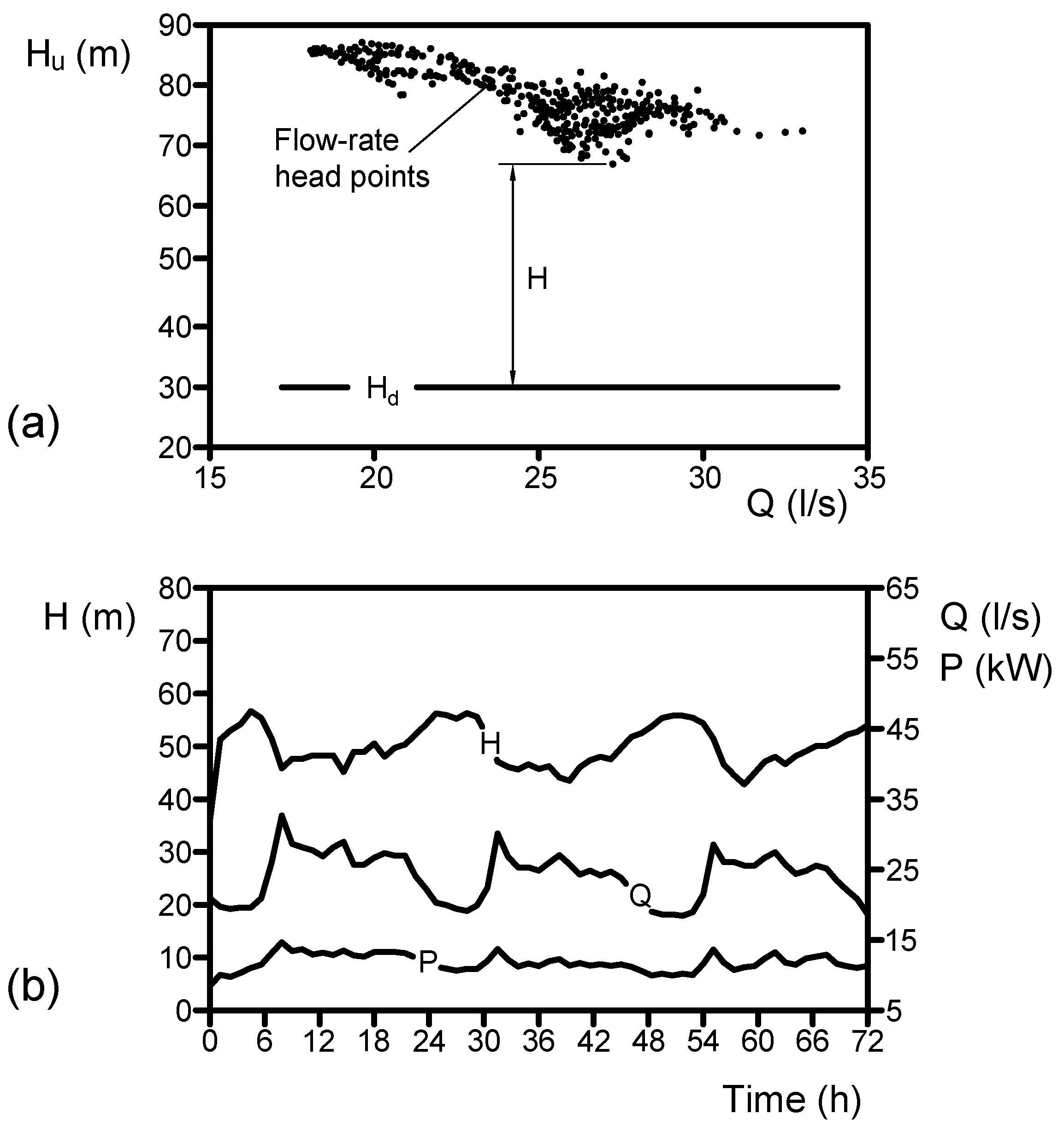
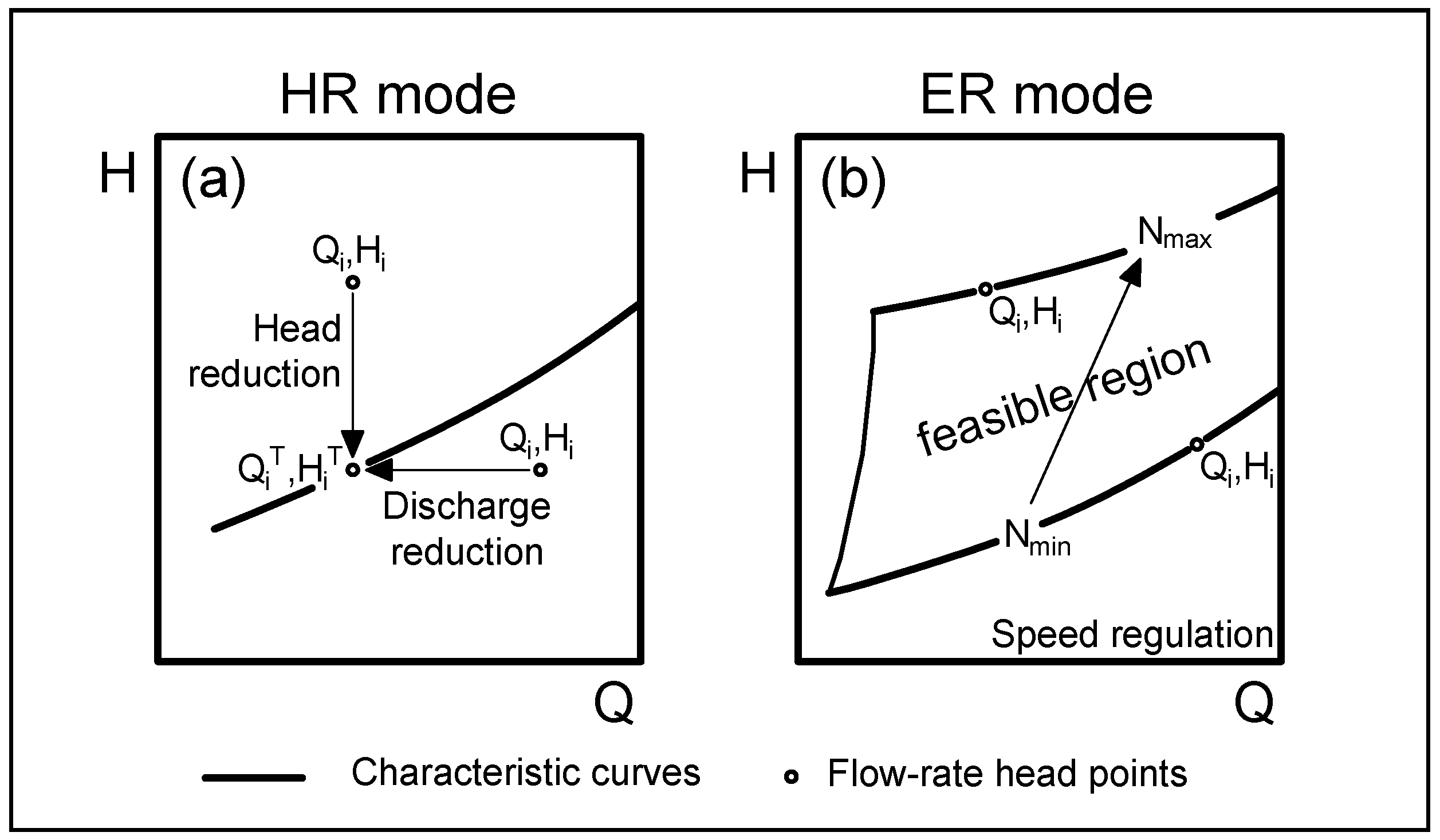
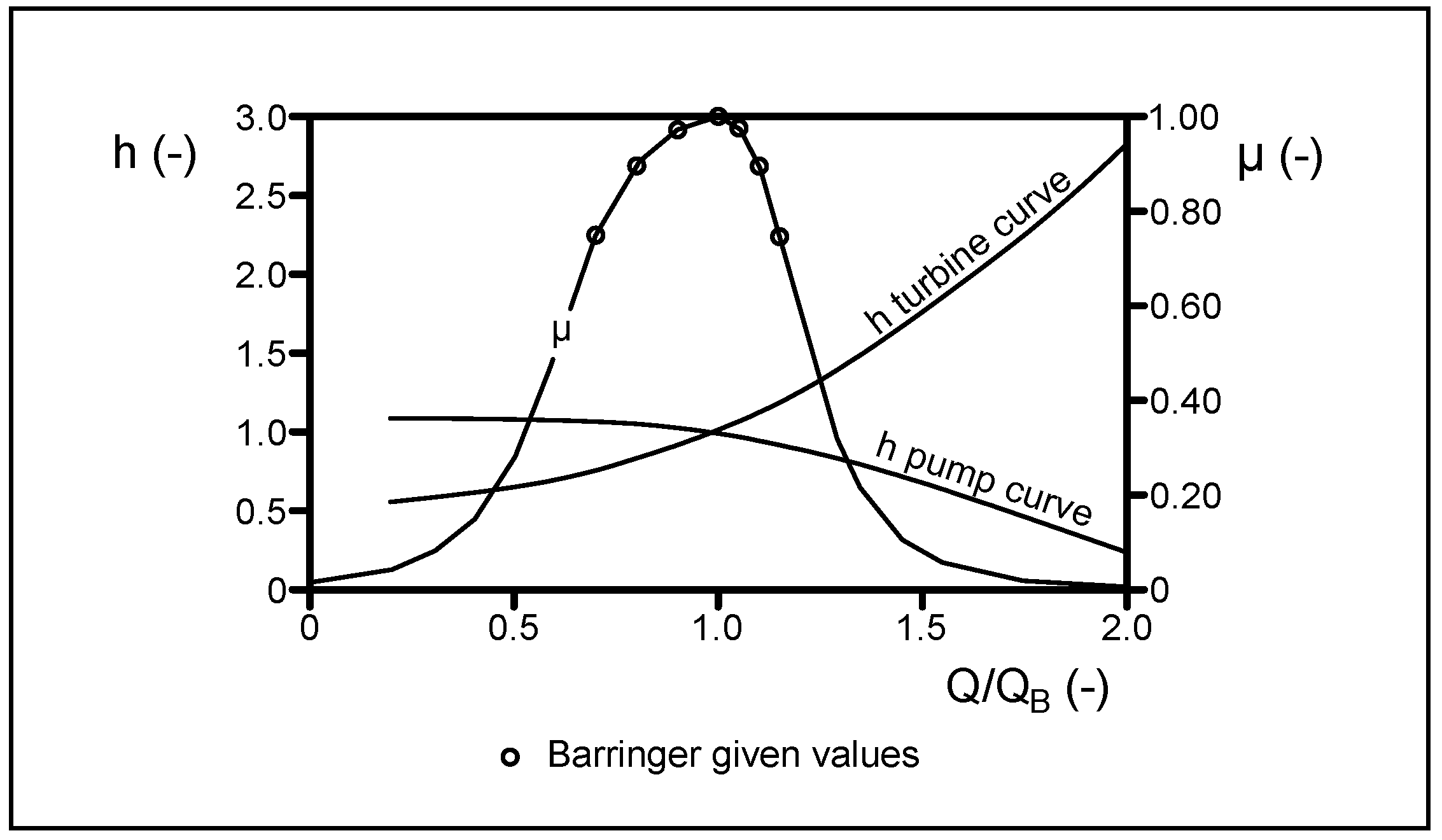
3. System Effectiveness
- performs its intended production activity according to expectation;
- performs for a variation around the design value;
- operates for a given time without failure.
3.1. System Capability
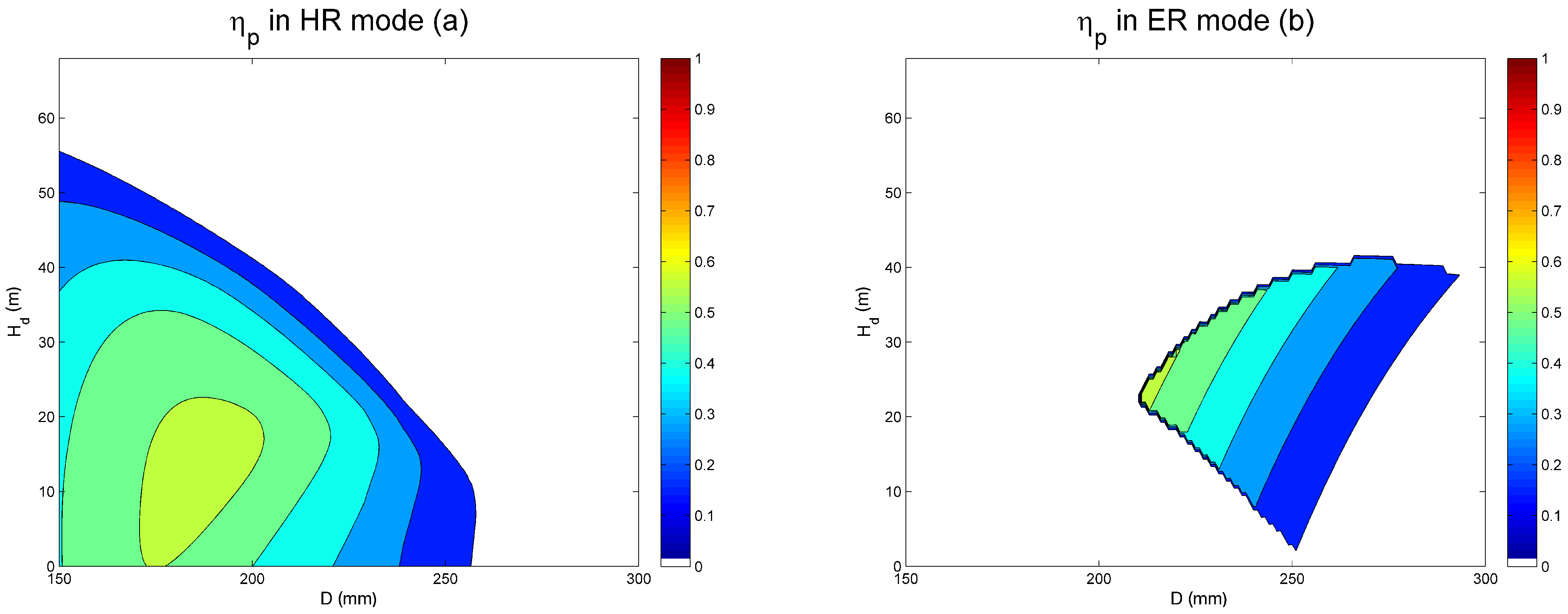
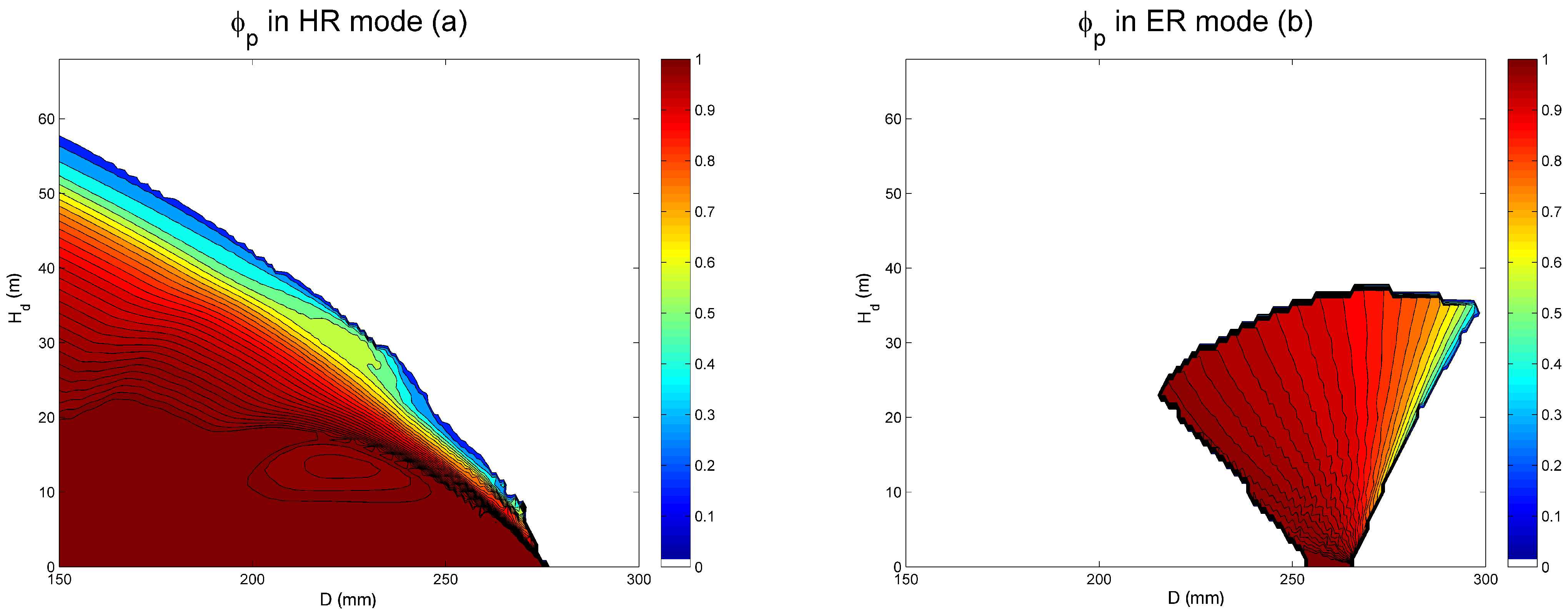
3.2. System Flexibility
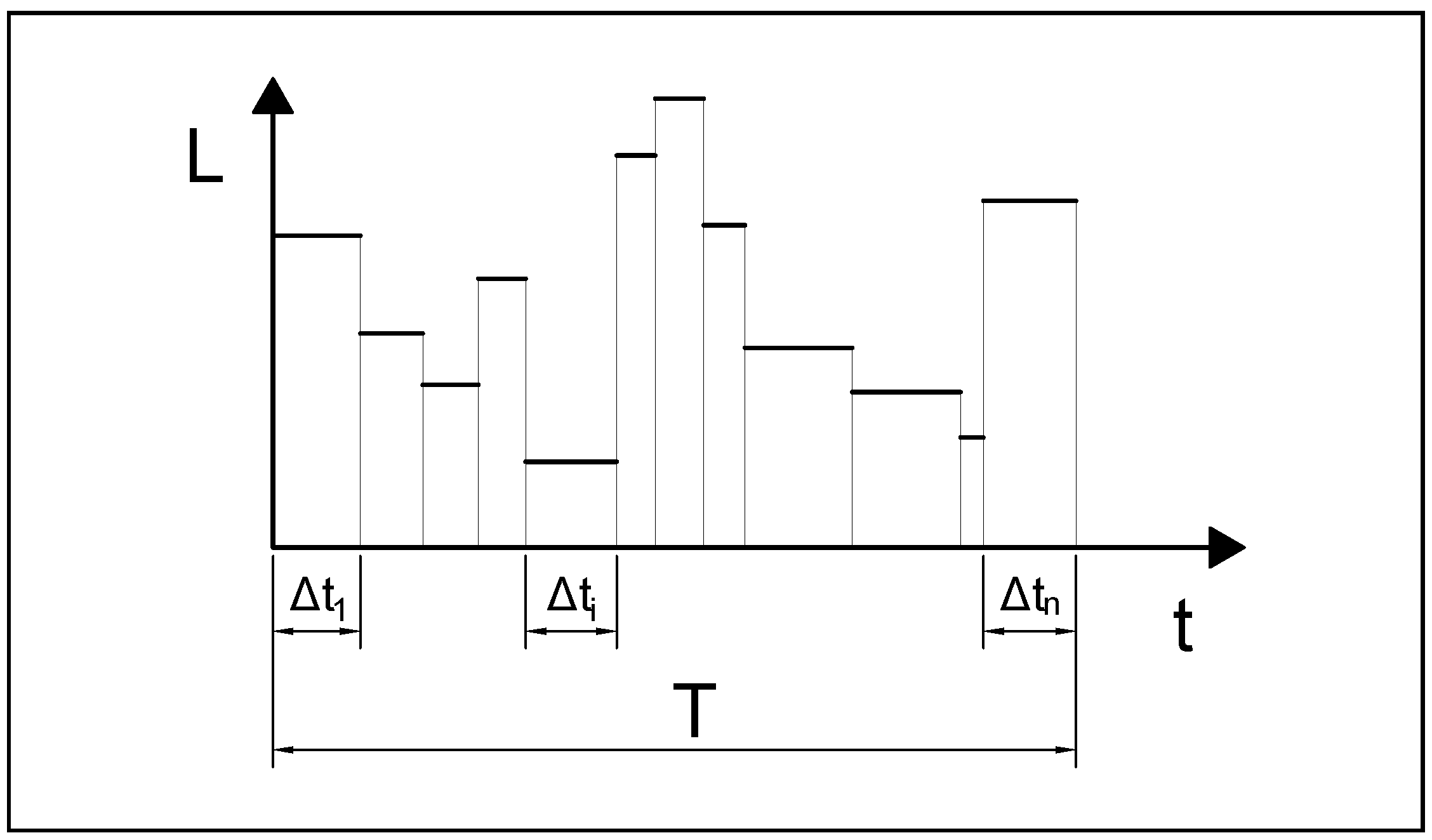
3.3. System Reliability
| American National | Enhanced ANSI | American Petroleum | |
|---|---|---|---|
| Standards Institute (ANSI) | Industry (API) | ||
| 0.70 | 0.73 | 0.75 | |
| 0.88 | 0.89 | 0.90 | |
| 0.97 | 0.97 | 0.98 | |
| 0.97 | 0.97 | 0.98 | |
| 0.88 | 0.89 | 0.90 | |
| 0.70 | 0.73 | 0.75 |
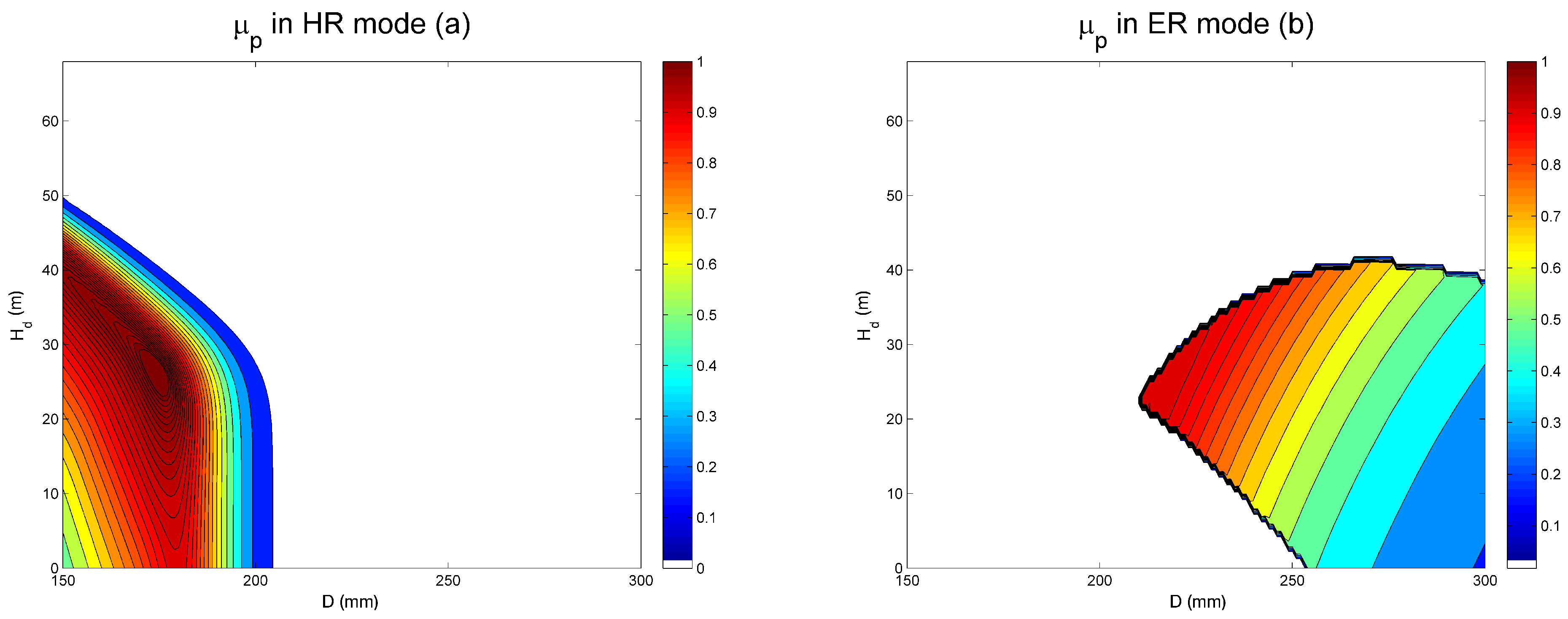
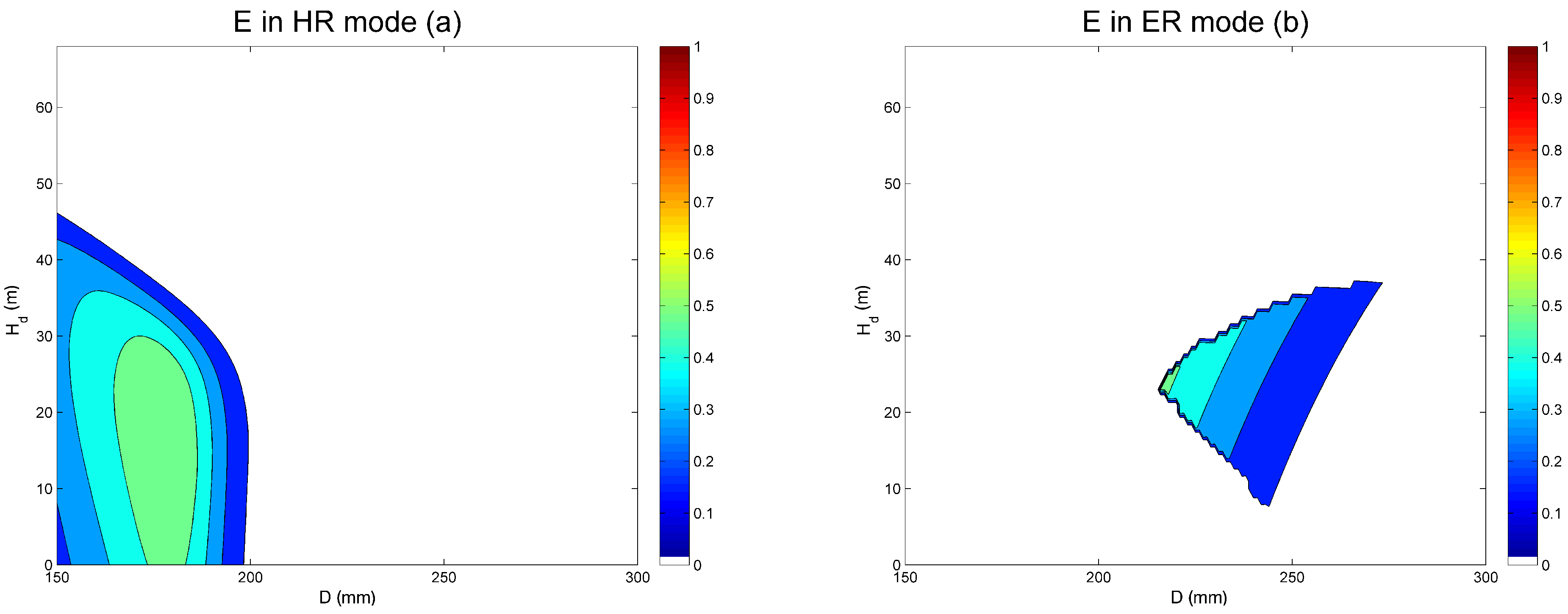
4. PAT Design by System Effectiveness
| VOS | 10 | 20 | 30 | 35 | |
|---|---|---|---|---|---|
| VOS | 186 | 191 | 181 | 176 | |
| 0.590 | 0.595 | 0.532 | 0.483 | ||
| 0.997 | 0.984 | 0.952 | 0.893 | ||
| 0.878 | 0.666 | 0.868 | 0.603 | ||
| E | 0.517 | 0.390 | 0.440 | 0.260 | |
| VOS | 179 | 178 | 171 | 163 | |
| 0.567 | 0.549 | 0.499 | 0.439 | ||
| 0.999 | 0.990 | 0.956 | 0.923 | ||
| 0.933 | 0.976 | 0.98 5 | 0.971 | ||
| E | 0.529 | 0.531 | 0.471 | 0.394 |
| VOS | 10 | 20 | 30 | 35 | |
|---|---|---|---|---|---|
| VOS | 237 | 216 | 222 | 234 | |
| 0.313 | 0.527 | 0.549 | 0.513 | ||
| 0.000 | 0.000 | 0.000 | 0.000 | ||
| 0.704 | 0.914 | 0.917 | 0.899 | ||
| E | 0.000 | 0.000 | 0.000 | 0.000 | |
| VOS | 239 | 221 | 231 | 250 | |
| 0.298 | 0.495 | 0.495 | 0.410 | ||
| 0.977 | 0.976 | 0.957 | 0.924 | ||
| 0.686 | 0.894 | 0.891 | 0.809 | ||
| E | 0.199 | 0.432 | 0.422 | 0.306 |
5. Conclusions
Acknowledgments
Conflict of Interest
References
- Punys, P.; Dumbrauskas, A.; Kvaraciejus, A.; Vyciene, G. Tools for small hydropower plant resource planning and development: A review of technology and applications. Energies 2011, 4, 1258–1277. [Google Scholar] [CrossRef]
- Koch, F.; Prasch, M.; Bach, H.; Mauser, W.; Appel, F.; Weber, M. How will hydroelectric power generation develop under climate change scenarios? A case study in the upper danube basin. Energies 2011, 4, 1508–1541. [Google Scholar]
- Nazif, S.; Karamouz, M.; Tabesh, M.; Moridi, A. Pressure management model for urban water distribution networks. Water Resour. Manag. 2010, 24, 437–458. [Google Scholar] [CrossRef]
- Araujo, L.; Ramos, H.; Coelho, S. Pressure control for leakage minimisation in water distribution systems management. Water Resour. Manag. 2006, 20, 133–149. [Google Scholar] [CrossRef]
- Vairavamoorthy, K.; Lumbers, J. Leakage reduction in water distribution systems: Optimal valve control. J. Hydraul. Eng. 1998, 124, 1146–1154. [Google Scholar] [CrossRef]
- Da Conceicao Cunha, M.; Ribeiro, L. Tabu search algorithms for water network optimization. Eur. J. Oper. Res. 2004, 157, 746–758. [Google Scholar] [CrossRef]
- Prasad, T.; Park, N. Multiobjective genetic algorithms for design of water distribution networks. J. Water Resour. Plan. Manag. 2004, 130, 73–82. [Google Scholar] [CrossRef]
- Vasan, A.; Simonovic, S. Optimization of water distribution network design using differential evolution. J. Water Resour. Plan. Manag. 2010, 136, 279–287. [Google Scholar] [CrossRef]
- Almandoz, J.; Cabrera, E.; Arregui, F.; Cabrera, E.; Cobacho, R. Leakage assessment through water distribution network simulation. J. Water Resour. Plan. Manag. 2005, 131, 458–466. [Google Scholar] [CrossRef]
- Tucciarelli, T.; Criminisi, A.; Termini, D. Leak analysis in pipeline systems by means of optimal valve regulation. J. Hydraul. Eng. 1999, 125, 277–285. [Google Scholar] [CrossRef]
- Walsky, T.; Bezts, W.; Posluzny, E.; Weir, M.; Withman, B. Modeling leakage reduction through pressure control. J. Am. Water Works Assoc. 2006, 98, 148–155. [Google Scholar]
- Prescott, S.; Ulanicki, B. Improved control of pressure reducing valves in water distribution networks. J. Hydraul. Eng. 2008, 134, 56–65. [Google Scholar] [CrossRef]
- Del Giudice, G.; Di Cristo, C. Sampling design for water distribution networks. Prog. Water Resour. 2003, 8, 181–190. [Google Scholar]
- Liberatore, S.; Sechi, G. Location and calibration of valves in water distribution networks using a scatter-search meta-heuristic approach. Water Resour. Manag. 2009, 23, 1479–1495. [Google Scholar] [CrossRef]
- McNabola, A.; Coughlan, P.; Williams, A. The Technical and Economic Feasibility of Energy Recovery in Water Supply Networks. In Proceedings of International Conference on Renewable Energy and Power Quality, Las Palmas de Gran Canaria, Spain, 13–15 April 2011.
- Corcoran, L.; McNabola, A.; Coughlan, P. Energy Recovery Potential of the Dublin Region Water Supply Network; Water Congress on Water, Climate and Energy: Dublin, Ireland, 2012. [Google Scholar]
- Filion, Y.; MacLean, H.; Karney, B. Life cycle energy analysis of a water distribution system. J. Infrastruct. Syst. 2004, 10, 120–130. [Google Scholar] [CrossRef]
- Paish, O. Small hydro power: Technology and current status. Renew. Sustain. Energy Rev. 2002, 6, 537–556. [Google Scholar] [CrossRef]
- Sammartano, V.; Aricò, C.; Carravetta, A.; Fecarotta, O.; Tucciarelli, T. Banki-michell optimal design by computational fluid dynamics testing and hydrodynamic analysis. Energies 2013, 6, 2362–2385. [Google Scholar] [CrossRef]
- Carravetta, A.; Giugni, M. Functionality Factors in the Management and Rehabilitation of Water Networks. In Management of Water Networks, Proceedings of Conference Efficient Management of Water Networks, Design and Rehabilitation Techniquesa, Ferrara, Italy, May 2006; Franco Angeli Editore: Milano, Italy, 2006. [Google Scholar]
- Yassi, Y.; Hashemloo, S. Improvement of the efficiency of the Agnew micro hydro turbine at part loads due to installing guide vanes mechanism. Energy Convers. Manag. 2010, 51, 1970–1975. [Google Scholar] [CrossRef]
- Zakkour, P.; Gatarell, M.; Gochin, R.; Lester, J. Developing a sustainable energy strategy for a water utility. Part II: A review of potential technologies and approaches. J. Environ. Manag. 2002, 66, 115–125. [Google Scholar]
- Arriaga, M. Pump as turbine a pico-hydro alternative in lao peoples democratic republic. Renew. Energy 2010, 35, 1109–1115. [Google Scholar] [CrossRef]
- Nautiyal, H.; Varun; Kumar, A. Reverse running pumps analytical, experimental and computational study: A review. Renew. Sustain. Energy Rev. 2010, 14, 2059–2067. [Google Scholar] [CrossRef]
- Carravetta, A.; Fecarotta, O.; Ramos, H. Numerical Simulation on Pump as Turbine: Mesh Reliability and Performance Concerns. In Proceedings of the IEEE International Conference on Clean Electrical Power, Ischia, Italy, 14–16 June 2011; Franco Angeli Editore: Milano, Italy, 2011. [Google Scholar]
- Vicinanza, D.; Ciardulli, F.; Buccino, M.; Calabrese, M.; Koefed, J. Wave loadings acting on an innovative breakwater for energy production. J. Coast. Res. 2011, 64, 608–612. [Google Scholar]
- Vicinanza, D.; Margheritini, L.; Kofoed, J.; Buccino, M. The SSG wave energy converter: Performance, status and recent developments. Energies 2012, 5, 193–226. [Google Scholar] [CrossRef]
- Buccino, M.; Banfi, D.; Vicinanza, D.; Calabrese, M.; Del Giudice, G.; Carravetta, A. Non breaking wave forces at the front face of seawave slotcone generators. Energies 2012, 5, 4779–4803. [Google Scholar] [CrossRef]
- Bryden, G.; Couch, S. ME1-marine energy extraction: Tidal resource analysis. Renew. Energy 2006, 31, 133–139. [Google Scholar] [CrossRef]
- Carcangiu, S.; Montisci, A. A Building-Integrated Eolic System for the Exploitation of Wind Energy in Urban Areas. In Proceedings of the 2012 IEEE International Energy Conference and Exhibition (ENERGYCON), Florence, Italy, 9–12 September 2012; pp. 172–177.
- Vieira, F.; Ramos, H.M. Hybrid solution and pump-storage optimization in water supply system efficiency: A case study. Energy Policy 2008, 36, 4142–4148. [Google Scholar] [CrossRef]
- Vieira, F.; Ramos, H.M. Optimization of operational planning for wind/hydro hybrid water supply systems. Renew. Energy 2009, 34, 928–936. [Google Scholar] [CrossRef]
- Carravetta, A.; Del Giudice, G.; Fecarotta, O.; Ramos, H. Energy production in water distribution networks: A PAT design strategy. Water Resour. Manag. 2012, 26, 3947–3959. [Google Scholar] [CrossRef]
- Carravetta, A.; Del Giudice, G.; Fecarotta, O.; Ramos, H. PAT design strategy for energy recovery in water distribution networks by electrical regulation. Energies 2013, 6, 411–424. [Google Scholar] [CrossRef]
- Carravetta, A.; Fecarotta, O.; Sinagra, M.; Tucciarelli, T. A cost benefit analisys for hydropower production in water distribution networks by pump as turbine (PAT). J. Water Resour. Plan. Manag. 2013. [Google Scholar] [CrossRef]
- Suter, P. Representation of pump characteristics for calculation of water hammer. Sulzer Tech. Rev. 1966, 4, 45–48. [Google Scholar]
- Fecarotta, O.; Carravetta, A.; Ramos, H. CFD and comparisons for a pump as turbine: Mesh reliability and performance concerns. Int. J. Energy Environ. 2011, 2, 39–48. [Google Scholar]
- Dörfler, P. “Neo-Suterian” Pump-Turbine Characteristics and Their Benefits. In Proceedings of the 4th International Conference on Earth and Environmental Science, Timisoara, Romania, 20–24 September 2010; IOP Publishing: Bristol, UK, 2010; Volume 12. [Google Scholar]
- Barringer, H.P. Life Cycle Cost and Good Practices. In Proceedings of the NPRA Maintenance Conference, San Antonio, TX, USA, 19–22 May 1998; Barringer & Associates, Inc.: Humble, TX, USA, 1998. [Google Scholar]
- Barringer, H.P. A Life Cycle Cost Summary. In Proceedings of the International Conference of Maintenance Societies, Perth, Australia, 20–23 May 2003.
- Cheong, L. International Report on Unaccounted for Water and Economics of Leak Detection. In Proceedings of the IWA World Conference, Budapest, Hungary, October 1993.
- Kececioglu, D.; Tian, X. Reliability education: A historical perspective. IEEE Trans. Reliab. 1998, 47, SP390–SP398. [Google Scholar] [CrossRef]
- Pecht, M. Product Reliability, Maintainability, and Supportability Handbook; CRC: Boca Raton, FL, USA, 2009. [Google Scholar]
- Raheja, D.; Lindsley, M. Defect-Free Manufacturing in the Nineties. In Proceedings of the 1991 IEEE National Conference on Aerospace and Electronics, Dayton, OH, USA, 20–24 May 1991; pp. 1019–1022.
- Clements, R. Handbook of Statistical Methods in Manufacturing; Prentice-Hall: Upper Saddle River, NJ, USA, 1991. [Google Scholar]
- Tung, Y.; Yen, B.; Melching, C. Hydrosystems Engineering Reliability Assessment and Risk Analysis; McGraw-Hill Professional: New York, NY, USA, 2006. [Google Scholar]
- Kapur, K.; Lamberson, L. Reliability in Engineering Design; John Wiley and Sons: New York, NY, USA, 1977; Volume 1. [Google Scholar]
- Trivedi, K. Probability and Statistics with Reliability, Queuing, and Computer Science Applications; John Wiley and Sons: New York, NY, USA, 2002. [Google Scholar]
- Carderock, D. Handbook of Reliability Prediction Procedures for Mechanical Equipment; Naval Surface Warfare Center: West Bethesda, MD, USA, 1992. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Carravetta, A.; Del Giudice, G.; Fecarotta, O.; Ramos, H.M. Pump as Turbine (PAT) Design in Water Distribution Network by System Effectiveness. Water 2013, 5, 1211-1225. https://doi.org/10.3390/w5031211
Carravetta A, Del Giudice G, Fecarotta O, Ramos HM. Pump as Turbine (PAT) Design in Water Distribution Network by System Effectiveness. Water. 2013; 5(3):1211-1225. https://doi.org/10.3390/w5031211
Chicago/Turabian StyleCarravetta, Armando, Giuseppe Del Giudice, Oreste Fecarotta, and Helena M. Ramos. 2013. "Pump as Turbine (PAT) Design in Water Distribution Network by System Effectiveness" Water 5, no. 3: 1211-1225. https://doi.org/10.3390/w5031211
APA StyleCarravetta, A., Del Giudice, G., Fecarotta, O., & Ramos, H. M. (2013). Pump as Turbine (PAT) Design in Water Distribution Network by System Effectiveness. Water, 5(3), 1211-1225. https://doi.org/10.3390/w5031211








