Abstract
The impacts of flood events that occurred in autumn 2011 in the Italian regions of Liguria and Tuscany revived the engagement of the public decision-maker to enhance the synergy of flood control and land use planning. In this context, the design of efficient flood risk mitigation strategies and their subsequent implementation critically relies on a careful vulnerability analysis of the fixed and mobile elements exposed to flood hazard. In this paper we develop computation schemes enabling dynamic vulnerability and risk analyses for a broad typological variety of elements at risk. To show their applicability, a series of prime examples are discussed in detail, e.g. a bridge deck impacted by the flood and a car, first displaced and subsequently exposed to collision with fixed objects. We hold the view that it is essential that the derivation of the computational schemes to assess the vulnerability of endangered objects should be based on classical and fluid mechanics. In such a way, we aim to complement from a methodological perspective the existing, mainly empirical, vulnerability and risk assessment approaches and to support the design of effective flood risk mitigation strategies by defusing the main criticalities within the systems prone to flood risk.
1. Introduction
Natural hazards, vulnerability and risk in mountain regions have increasingly become a focus of political attention in recent years [1]. On a European level, the Directive on the Assessment and Management of Flood Risks addressed to the Member States (Flood Directive) was issued in 2007 as one of the three components of the European Action Programme on Flood Risk Management. It was recognized that flood events have the potential to severely compromise economic development and to undermine the economic activities of the community [2,3]. Due to the increasing imbalance between values at risk and level of protection in flood prone areas, concentrated action is needed at all levels to avoid severe flood impacts on human life and property. The analysis of flood risk at different scales with a commensurate degree of detail is a valuable basis, not only for priority setting and further financial and political decisions regarding flood risk management, but also for the identification on a technical level of the most promising solutions to the risk mitigation problems at hand [4,5].
Acknowledging the fact that flood risk governance is a multi-faceted field of interdisciplinary activities [6,7], an essential condition for success in defusing the criticalities of risk generation mechanisms is the engineering design of possible alternatives indicating feasible and cost-effective ways of reducing risks.
The societal need to reduce flood risks is not the same as an unbounded willingness to invest public money for any solution pathway proposed. Envisaged solutions must be convincing, both from a technical and economic viewpoint and also be sustainable from an ecological perspective [8,9]. A reliable and tailored risk assessment entails the definition of scenarios composed of different levels, namely: (1) exposure scenarios, (2) vulnerability scenarios, (3) analyses of the values at risk, resulting in (4) risk scenarios [10,11].
These components have multiple functional dependencies among each other, resulting in compound intersections both in space and time.
To remove the root causes of risk generation mechanisms it is necessary to mirror the spatial and temporal evolution of flood risk, in particular sub-events (e.g., bridge clogging and levee failure) [12] which may trigger significant raising of hazard levels, leading to flooding configurations which may induce the uncontrolled floating of mobile objects (e.g., vehicles).
Departing from these premises and from a dynamic conceptualization of vulnerability, we approach its assessment from an engineering science perspective (entailing analyses based on fluid and classical mechanics), according to the following methodological skeleton: (1) Hydrodynamic computation of time-dependent flood intensities resulting for each element at risk in a succession of loading configurations; (2) Modeling the mechanical response of objects impacting against one another through static, elasto-static and kinetic analyses; (3) Characterizing the mechanical response through proper structural damage variables and (4) economic valuation of the losses as a function of the quantified damage variables.
We will exemplify the calculations for potentially mobile objects exposed to flood load exceeding a given probability.
Unveiling the significant risk generation mechanisms, both methodologically and computationally, is of great value for the planning of functionally efficient mitigation measures that are able to provide a higher degree of risk reduction than conventional mitigation strategies. These computational schemes will be embedded in the general framework of cost-benefit analysis for the appraisal of flood risk mitigation projects [11,13]. By making explicit risk dynamics and cost generation mechanisms, the scope of application of cost-benefit analysis is expanded beyond its classical role as a decision-support tool and linked to the core of the planning process.
2. The Dynamic Conceptualization of Vulnerability
It has repeatedly been claimed that there exists a lack of studies related to the spatio-temporal development of risk and the underlying vulnerability of the elements at risk [6,14].
Space is—along with time—a key factor when information on vulnerability and risk is assessed, since risk materializes only as a consequence of the physical overlap between hazardous events and elements at risk [15,16].
As a point of departure, we assume that the results of flood hazard analysis are given in the form of  flood scenarios exceeding a known probability (1/recurrence interval)
flood scenarios exceeding a known probability (1/recurrence interval)  . Each flood scenario
. Each flood scenario  is characterized by a succession in time
is characterized by a succession in time  ,
,  , of triples of intensity maps with respect to the computational domain
, of triples of intensity maps with respect to the computational domain  (flow depth maps -
(flow depth maps - 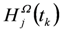 , maps of flow velocities in
, maps of flow velocities in  and
and 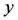 direction, symbolized with
direction, symbolized with  and
and 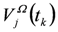 )
)
 flood scenarios exceeding a known probability (1/recurrence interval)
flood scenarios exceeding a known probability (1/recurrence interval)  . Each flood scenario
. Each flood scenario  is characterized by a succession in time
is characterized by a succession in time  ,
,  , of triples of intensity maps with respect to the computational domain
, of triples of intensity maps with respect to the computational domain  (flow depth maps -
(flow depth maps - 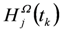 , maps of flow velocities in
, maps of flow velocities in  and
and 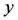 direction, symbolized with
direction, symbolized with  and
and 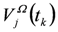 )
)The assessment of the time-varying vulnerability of the generic object  ,
, 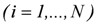 , assumed to be potentially movable, entails for each time-step
, assumed to be potentially movable, entails for each time-step  a computational procedure as follows:
a computational procedure as follows:
 ,
, 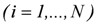 , assumed to be potentially movable, entails for each time-step
, assumed to be potentially movable, entails for each time-step  a computational procedure as follows:
a computational procedure as follows:(1) Analysis of hydrodynamics, which entails the determination of the process intensities at the object location  namely
namely 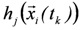 ,
, 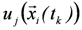 ,
, 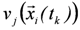 .
.
 namely
namely 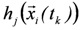 ,
, 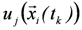 ,
, 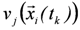 .
.(2) Mechanical analysis of the considered object, which entails:
- Assessment of the geometrical and physical properties of the object in question, the transporting fluid and the environment,
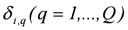 and
and  respectively. Introduction of necessary idealized situations for mechanical analysis.
respectively. Introduction of necessary idealized situations for mechanical analysis. - Identification of the physical damage variables
 which describe the expected structural damage properly (e.g., displacement of the object, critical stress conditions, strains and deformations). Restoring the original values of these variables entails monetary expenditure.
which describe the expected structural damage properly (e.g., displacement of the object, critical stress conditions, strains and deformations). Restoring the original values of these variables entails monetary expenditure. - Drawing the free body diagram of the object indicating the loading conditions (e.g., acting forces),
 , determined by the local process intensities (compare procedural step 1), and the corresponding reactive forces
, determined by the local process intensities (compare procedural step 1), and the corresponding reactive forces  .
. - Choice of a proper coordinate system and check whether a 3D, 2D or a 1D analysis is suitable. (e.g., plane rigid body kinetics versus 3D motion).
- Iterative analysis of the statics, elastostatics and kinetics of the considered object
 aiming at quantifying the physical damage variables
aiming at quantifying the physical damage variables  with respect to
with respect to  and
and  . For complex problems, a combination of analytical and numerical techniques has to be employed. Special cases can be solved analytically by introducing simplifying engineering assumptions (see next section and mathematical appendix).
. For complex problems, a combination of analytical and numerical techniques has to be employed. Special cases can be solved analytically by introducing simplifying engineering assumptions (see next section and mathematical appendix).
(3) Valuation and economic assessment of vulnerability  : establishing a functional relationship between the damage state of the object under consideration expressed through quantification of the physical damage variables
: establishing a functional relationship between the damage state of the object under consideration expressed through quantification of the physical damage variables  and the corresponding expected monetary loss
and the corresponding expected monetary loss 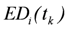 in relation to the reinstatement value
in relation to the reinstatement value  of the object
of the object  , thus:
, thus:
 : establishing a functional relationship between the damage state of the object under consideration expressed through quantification of the physical damage variables
: establishing a functional relationship between the damage state of the object under consideration expressed through quantification of the physical damage variables  and the corresponding expected monetary loss
and the corresponding expected monetary loss 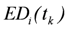 in relation to the reinstatement value
in relation to the reinstatement value  of the object
of the object  , thus:
, thus: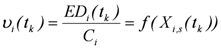 (1)
(1)3. Worked out Example Problems
In this section we elaborate two prime examples to illustrate the procedure outlined in the previous section. We prefer starting with a mainly didactical example containing in a simplified fashion: the full set of conceptual elements of the presented procedure. Thereafter, in a second step, we will approach a more complex problem.
The first problem is a stylized version of a process chain which occurred frequently during the catastrophic flash flood events in the Italian regions Liguria and Tuscany in autumn 2011, namely the so called “vehicle risk problem”.
A large number of vehicles were parked in dedicated parking zones on inclined planes prone to flooding. With increasing flow depths and velocities, incipient motion of these objects began. The objects were displaced either by sliding due to the reduced friction or more rapidly by floating as soon as the lift forces exceeded gravity. Along the displacement pathways the objects collided with fixed obstacles and were consequently severely damaged as a result of these impacts.
Let us consider in our simplified setting a vehicle in an initially resting condition on an inclined plane which is flooded uniformly with constant flow depth and constant velocity. A fixed obstacle is placed at a known distance in the direction of motion. The task consists of formulating a simple vulnerability model, assuming that the extent of damage depends only on the deformation due to the impact energy. Following the previously outlined general procedure we obtain:
(1) Hydrodynamic analysis: Determination of the process intensities at the object’s location  :
:
 :
:Due to the uniform flow conditions, the following process intensities can be assumed:
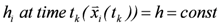 ,
, 
(2) Mechanical analysis:
a. Assessment of the geometrical and physical properties  and
and  respectively:
respectively:
 and
and  respectively:
respectively:We approximate, for simplicity only, the geometrical shape of the vehicle as a rectangular solid and the obstacle is assumed to be a vertical wall (compare Figure 1a,b).
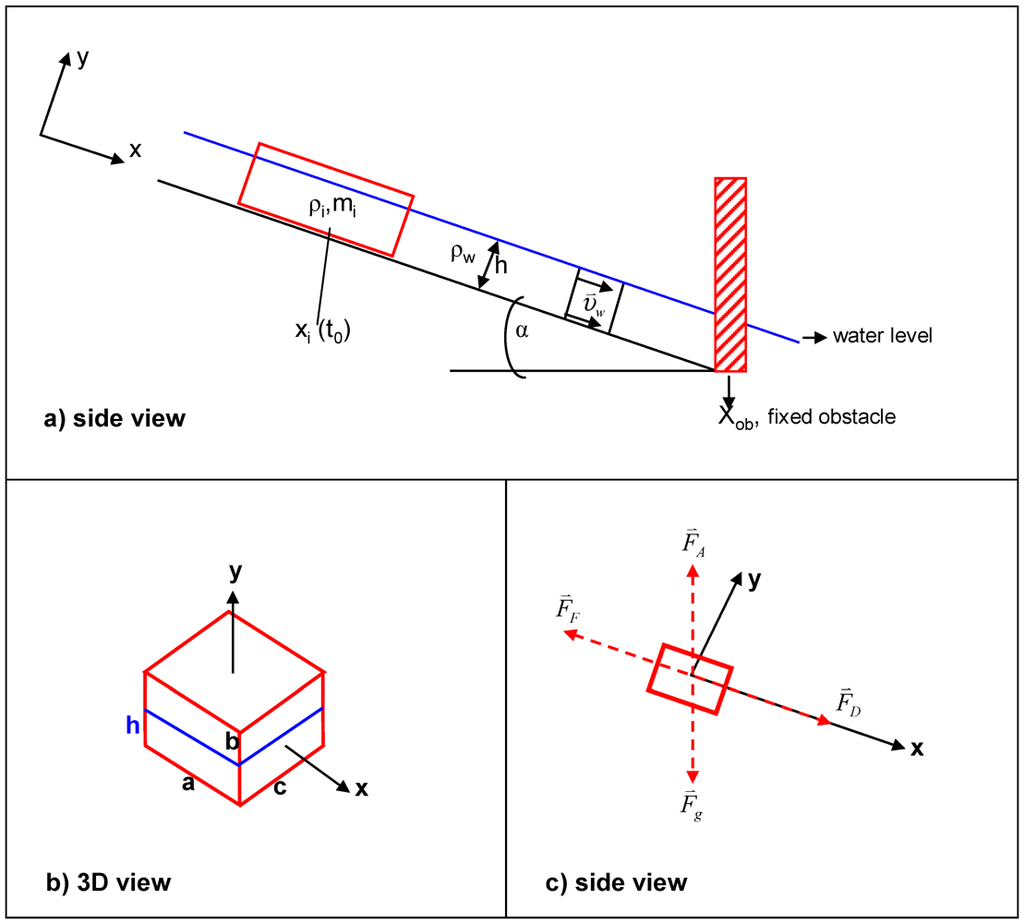
Figure 1.
System sketch (a and b) and free body diagram (c).
b. In this simplified setting the deformation depth  (after collision) is the only relevant physical damage variable of interest.
(after collision) is the only relevant physical damage variable of interest.
 (after collision) is the only relevant physical damage variable of interest.
(after collision) is the only relevant physical damage variable of interest.c. The free body diagram with the loading conditions and the reactive forces is shown in Figure 1c.  is the drag force,
is the drag force,  is gravity, whereas
is gravity, whereas  is the force due to friction and
is the force due to friction and  is the lift force.
is the lift force.
 is the drag force,
is the drag force,  is gravity, whereas
is gravity, whereas  is the force due to friction and
is the force due to friction and  is the lift force.
is the lift force.d. The Cartesian x, y coordinate system is chosen in such a way that the x-axis coincides with the direction of potential translational motion of the rigid body: (compare Figure 1). The rigid body kinetics are described according to the conceptual scheme outlined in Scheme 1.
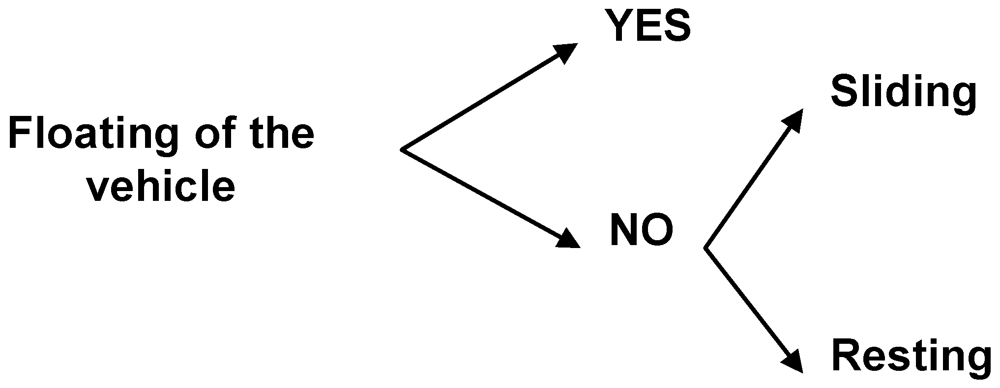
Scheme 1.
Conceptual scheme for the analysis of the rigid body kinetics.
According to this scheme the kinetic problem is analyzed as a planar problem to check whether incipient uplift displacement or sliding in the x direction may take place.
If neither the incipient floating nor the sliding condition is given, equilibrium conditions are satisfied.
e. Static, kinetic and elasto-static analyses. Throughout we indicate the velocity of the object and of the fluid as  and
and  respectively. The drag force in flow direction is generally expressed as
respectively. The drag force in flow direction is generally expressed as 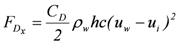 , where
, where 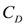 is the drag coefficient,
is the drag coefficient,  is the density of the fluid,
is the density of the fluid,  is the flow depth (or the submerged object depth,
is the flow depth (or the submerged object depth,  , once floating occurs) and
, once floating occurs) and  is the width of the object. The force due to friction acting in the opposite direction is expressed as
is the width of the object. The force due to friction acting in the opposite direction is expressed as 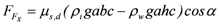 , where
, where  indicates the static or dynamic friction coefficient, depending on whether the object is in motion or not,
indicates the static or dynamic friction coefficient, depending on whether the object is in motion or not,  is the acceleration due to gravity,
is the acceleration due to gravity,  are the geometrical parameters of the object and
are the geometrical parameters of the object and  is the inclination angle of the plane. The force due to gravity is given by
is the inclination angle of the plane. The force due to gravity is given by 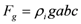 , and the lift force that the object is subjected to, is
, and the lift force that the object is subjected to, is  (
(  in the case of floating).
in the case of floating).
 and
and  respectively. The drag force in flow direction is generally expressed as
respectively. The drag force in flow direction is generally expressed as 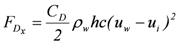 , where
, where 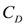 is the drag coefficient,
is the drag coefficient,  is the density of the fluid,
is the density of the fluid,  is the flow depth (or the submerged object depth,
is the flow depth (or the submerged object depth,  , once floating occurs) and
, once floating occurs) and  is the width of the object. The force due to friction acting in the opposite direction is expressed as
is the width of the object. The force due to friction acting in the opposite direction is expressed as 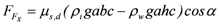 , where
, where  indicates the static or dynamic friction coefficient, depending on whether the object is in motion or not,
indicates the static or dynamic friction coefficient, depending on whether the object is in motion or not,  is the acceleration due to gravity,
is the acceleration due to gravity,  are the geometrical parameters of the object and
are the geometrical parameters of the object and  is the inclination angle of the plane. The force due to gravity is given by
is the inclination angle of the plane. The force due to gravity is given by 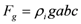 , and the lift force that the object is subjected to, is
, and the lift force that the object is subjected to, is  (
(  in the case of floating).
in the case of floating).i. Floating condition check:
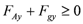 or
or 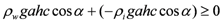
yields:
 (2)
(2)If this condition (Equation 2) is not satisfied then the sliding condition check is performed.
ii. Sliding condition check:
 (3)
(3)and
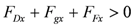 or
or 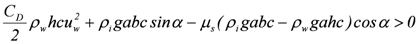
yields:
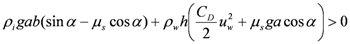 (4)
(4)iii. Kinetic analysis for the floating case:
Expressing the Newton’s second law, 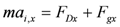 , as
, as
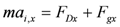 , as
, as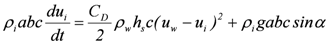 , yields the differential equation:
, yields the differential equation: .
.with  , we obtain the differential equation for the sliding case:
, we obtain the differential equation for the sliding case:
 , we obtain the differential equation for the sliding case:
, we obtain the differential equation for the sliding case: (5)
(5)And integrating with respect to time the solution of Equation 5, which is the velocity of the floating object  , we obtain its displacement as follows:
, we obtain its displacement as follows:
 , we obtain its displacement as follows:
, we obtain its displacement as follows: (6)
(6)iv. Kinetic analysis for the sliding case:
Analogously to the floating case, Newton’s second law, 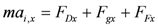 , can be expressed as:
, can be expressed as:
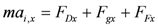 , can be expressed as:
, can be expressed as:
or more concisely, as a differential equation of the form:
 (7)
(7)Equation 6 can be employed again to calculate the displacements.
The differential Equations 5 and 7 can be solved numerically by applying the Runge-Kutta Method. The solution [6] is straightforward.
In Annex 1, analytical solutions for velocities (compare Equations 5 and 7) and displacements (compare Equation 6) for both the floating and the sliding kinetics are provided for flow-depths or velocities held constant both in space and time.
v. Computation of the deformation depth  due to collision of object
due to collision of object  with the fixed obstacle:
with the fixed obstacle:
 due to collision of object
due to collision of object  with the fixed obstacle:
with the fixed obstacle:Making the conservative assumption that a central impact takes place, we employ an empirical quadratic equation that links the impact energy (per unit width)  with the deformation depth
with the deformation depth  :
:
 with the deformation depth
with the deformation depth  :
: (8)
(8)where  and
and  are empirically defined stiffness coefficients, with units [N/m] and [N/m2].
are empirically defined stiffness coefficients, with units [N/m] and [N/m2].
 and
and  are empirically defined stiffness coefficients, with units [N/m] and [N/m2].
are empirically defined stiffness coefficients, with units [N/m] and [N/m2].The kinetic energy per unit width of the object just before the obstacles collide:
 (9)
(9)Empirical crash tests [17] indicate that reasonable restitution coefficient values for approximately inelastic collisions are close to zero, hence we assume that the kinetic energy is entirely available for deformation, thus:
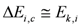
yielding:  (10)
(10)
 (10)
(10)(3) Valuation and economic assessment of vulnerability
A suitable functional relationship between the damaged state of the considered object and the corresponding vulnerability is of the type:
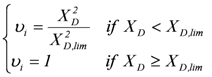 (11)
(11)where  corresponds to a deformation depth, which, once reached, completely destroys the market value of the vehicle.
corresponds to a deformation depth, which, once reached, completely destroys the market value of the vehicle.
 corresponds to a deformation depth, which, once reached, completely destroys the market value of the vehicle.
corresponds to a deformation depth, which, once reached, completely destroys the market value of the vehicle.The second problem addressed in this paper has demonstrated its relevance in the recent flood events in Italy. A large number of bridges were clogged by driftwood. In addition to inundations triggered by backwater effects, severe direct structural damage also resulted.
In extreme cases, bridge decks (superstructures) were displaced from their supports, resulting in significant direct losses and restrictions to normal economic activity.
The procedure outlined in the previous section is now applied to the bridge deck problem. Again it is assumed that the damage extent is well captured by the displacement of the bridge deck. It is assumed that dynamic vulnerability equals unity as soon as the displacement of the superstructure reaches a critical value for which the equilibrium of the moments of the forces acting on the structure can no longer be satisfied.
(1) Hydrodynamic analysis: Determination of the Process Intensities at the Location of the Object  .
.
 .
. We assume throughout that steady water profiles corresponding to the design discharge are given. These can easily be computed applying the energy equation. It is essential that flow depths and the associated average cross-sectional velocities are known for four reference cross-sections: proceeding in the downstream in upstream direction the first cross-section is located at a certain distance from the bridge where the flow is to be considered as fully expanded. The second control cross-section is placed immediately downstream of the bridge and represents the section where constriction flow switches to expansion flow. The third cross-section is placed immediately upstream of the bridge. The fourth cross-section is placed further upstream of the bridge where the backwater is fully developed. In Figure 2(a–d) the structural characteristics and all relevant process intensity values are indicated for a control volume with defined cross-sections.
(2) Mechanical Analysis
a. Assessment of the geometrical and physical properties  and
and  respectively:
respectively:
 and
and  respectively:
respectively:The reader is referred to Figure 2 were all geometrical and physical properties are indicated. The control volume for the mechanical analysis is confined by sections 2 and 3 respectively. It is assumed that the flow depths  and
and  remain unaltered during the possible displacement of the bridge deck. Expressed another way, the hydrodynamic loadings at the boundaries of the moving control volume are held constant (compare Figure 2c).
remain unaltered during the possible displacement of the bridge deck. Expressed another way, the hydrodynamic loadings at the boundaries of the moving control volume are held constant (compare Figure 2c).
 and
and  remain unaltered during the possible displacement of the bridge deck. Expressed another way, the hydrodynamic loadings at the boundaries of the moving control volume are held constant (compare Figure 2c).
remain unaltered during the possible displacement of the bridge deck. Expressed another way, the hydrodynamic loadings at the boundaries of the moving control volume are held constant (compare Figure 2c).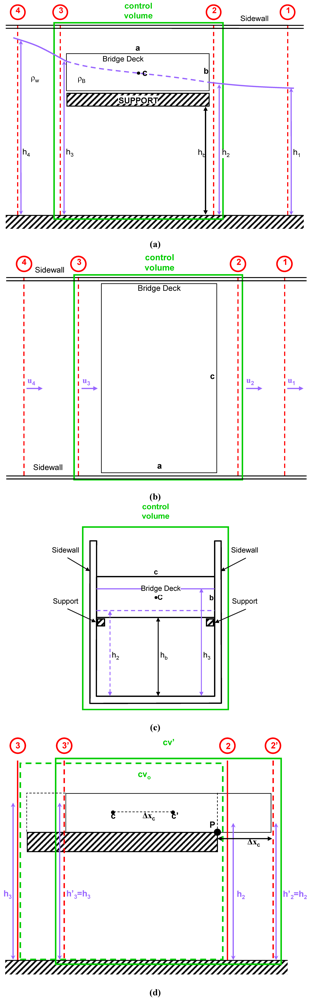
Figure 2.
Prospects of the bridge: hydrodynamic and geometrical parameters, necessary idealizations and definition of the control volume. (a) side view; (b) top down view; (c) font view; (d) control volumes.
b. Identification of the physical damage variables: The relevant physical damage variable is the displacement of the center of mass  , which ranges from 0 (stable bridge, no displacement) to a maximum value
, which ranges from 0 (stable bridge, no displacement) to a maximum value  where the equilibrium condition
where the equilibrium condition  (
(  = moments around P) is no longer satisfied:
= moments around P) is no longer satisfied:
 , which ranges from 0 (stable bridge, no displacement) to a maximum value
, which ranges from 0 (stable bridge, no displacement) to a maximum value  where the equilibrium condition
where the equilibrium condition  (
(  = moments around P) is no longer satisfied:
= moments around P) is no longer satisfied: (12)
(12)if  and
and  , which corresponds to the severest loading condition before the bridge starts to be submerged,
, which corresponds to the severest loading condition before the bridge starts to be submerged,  simplifies to:
simplifies to:
 and
and  , which corresponds to the severest loading condition before the bridge starts to be submerged,
, which corresponds to the severest loading condition before the bridge starts to be submerged,  simplifies to:
simplifies to: (13)
(13)Once  , we assume that the damage corresponds to the reinstatement value of the bridge deck and hence
, we assume that the damage corresponds to the reinstatement value of the bridge deck and hence 
 , we assume that the damage corresponds to the reinstatement value of the bridge deck and hence
, we assume that the damage corresponds to the reinstatement value of the bridge deck and hence 
c, d. Free body diagram (compare Figure 3) and coordinate system.
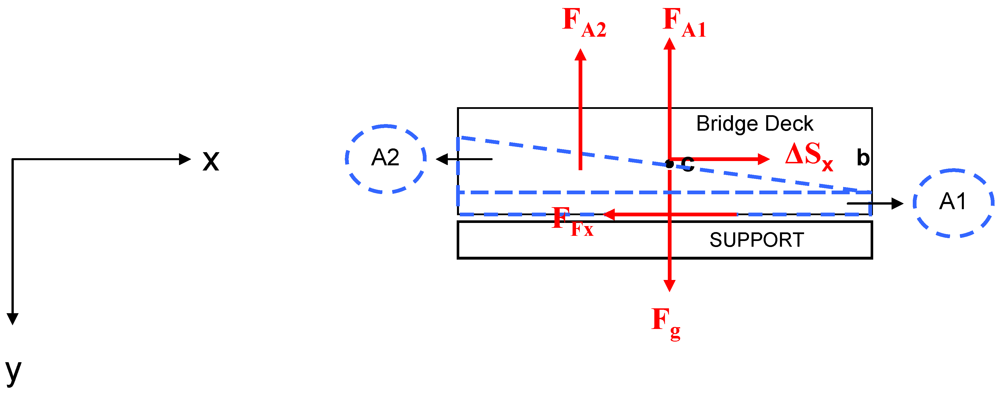
Figure 3.
Free body diagram of the bridge deck impacted by the flood.
e. Iterative analysis of the statics, elastostatics and kinetics.
i. Sliding condition:
The sliding condition, 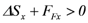 , entails a comparison between the net hydrodynamic force on the bridge structure
, entails a comparison between the net hydrodynamic force on the bridge structure  and the reactive friction force
and the reactive friction force  .
.
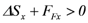 , entails a comparison between the net hydrodynamic force on the bridge structure
, entails a comparison between the net hydrodynamic force on the bridge structure  and the reactive friction force
and the reactive friction force  .
. The net hydrodynamic force is given by the difference, 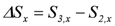 , whereas
, whereas  and
and  are the forces acting on the control volume in section 3 and 2 respectively, thus:
are the forces acting on the control volume in section 3 and 2 respectively, thus:
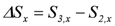 , whereas
, whereas  and
and  are the forces acting on the control volume in section 3 and 2 respectively, thus:
are the forces acting on the control volume in section 3 and 2 respectively, thus:  and
and  , therefore:
, therefore:
The friction force can be expressed as,  , where
, where  is the force due to gravity,
is the force due to gravity,  and
and  are the lift force components (compare Figure 3):
are the lift force components (compare Figure 3):
 , where
, where  is the force due to gravity,
is the force due to gravity,  and
and  are the lift force components (compare Figure 3):
are the lift force components (compare Figure 3): 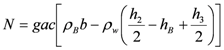 and
and  .
.Thus the sliding condition can be written as:
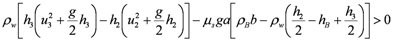 (14)
(14)ii. Kinetics of sliding:
According to Newton’s second law the differential equation for the sliding case is:
 with
with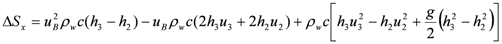 and
and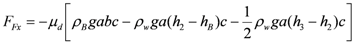 .
.Inserting and simplifying, one obtains:
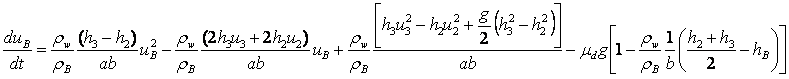
which can compactly be written as:
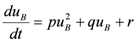 (15)
(15)with the coefficients
 ,
,  ,
,
In Annex 1 analytical solutions for velocities (compare Equation 15) and displacements (compare Equation 6) are provided for the sliding kinetics for flow-depths or velocities held constant at the cross sections delimiting the control volume.
(3) Valuation and economic assessment of vulnerability
A suitable functional relationship between the damaged state of the considered object and the corresponding vulnerability is of the type:
 (16)
(16)4. A Formal Cost-Benefit Analysis Framework Based on Dynamic Risk Assessment
Major interrelated requirements have to be met by the risk management process [18]. These include the assessment of (1) the risk mitigation performance of planned mitigation strategies; (2) the cost-plan for each strategy which shall be considered from a life-cycle perspective; and (3) of the net present value resulting from the benefits and costs, both evaluated on an annual basis, carried by the available mitigation alternatives. Considering the peculiarities of public investment decisions to mitigate natural hazard risk, specifically associated long-term capital commitments and the occurring interdependencies between these long-term commitments and important economic activities in mountain regions (above all arising from tourism and trading), the required analytical effort has to be balanced.
4.1. Risk Assessment
Based on the fully probabilized flood scenarios,  with
with  , and the location
, and the location  of each element at risk, assumed to be potentially movable in the general case, their time-varying vulnerability
of each element at risk, assumed to be potentially movable in the general case, their time-varying vulnerability  can be tracked as outlined, both in theory and practice, in the two preceding sections.
can be tracked as outlined, both in theory and practice, in the two preceding sections.
 with
with  , and the location
, and the location  of each element at risk, assumed to be potentially movable in the general case, their time-varying vulnerability
of each element at risk, assumed to be potentially movable in the general case, their time-varying vulnerability  can be tracked as outlined, both in theory and practice, in the two preceding sections.
can be tracked as outlined, both in theory and practice, in the two preceding sections.Assuming that different location matrices 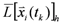 with
with  reflect the exposure scenarios for the entire object set, and that each exposure scenario has a defined probability
reflect the exposure scenarios for the entire object set, and that each exposure scenario has a defined probability  , we can quantify the time-dependent expected loss
, we can quantify the time-dependent expected loss  for an object at risk
for an object at risk  , for a specified flood scenario
, for a specified flood scenario  and for its exposure configuration
and for its exposure configuration  as:
as:
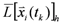 with
with  reflect the exposure scenarios for the entire object set, and that each exposure scenario has a defined probability
reflect the exposure scenarios for the entire object set, and that each exposure scenario has a defined probability  , we can quantify the time-dependent expected loss
, we can quantify the time-dependent expected loss  for an object at risk
for an object at risk  , for a specified flood scenario
, for a specified flood scenario  and for its exposure configuration
and for its exposure configuration  as:
as: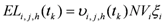 (17)
(17)where 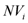 is the reinstatement value of the considered element
is the reinstatement value of the considered element  and
and  is a depreciation coefficient reflecting the element’s obsolescence [19].
is a depreciation coefficient reflecting the element’s obsolescence [19].
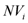 is the reinstatement value of the considered element
is the reinstatement value of the considered element  and
and  is a depreciation coefficient reflecting the element’s obsolescence [19].
is a depreciation coefficient reflecting the element’s obsolescence [19].The overall risk, quantified on an annual basis, resulting from the expected monetary losses for all elements at risk, considering the entire set of exposure scenarios and flood impacts, can be written as:
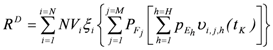 (18)
(18)where  is the last time-step considered.
is the last time-step considered.
 is the last time-step considered.
is the last time-step considered.For practical purposes it can be convenient to track the dynamic risk in time as follows:
 (19)
(19)In the adopted conceptualization of flood hazard risk (compare Equations 17 to 19), the expected losses are expressed monetarily, which entails an economic valuation of the elements at risk. We restrict our analysis to tangible loss, namely damage to capital stocks or resource flows which can be specified in monetary terms, neglecting damages to assets which are not traded and are therefore difficult to transfer into monetary values [20].
With reference to object categories valued through economic approaches using market values (e.g., reinstatement value for structures) we report a general scheme to structurally dissect complex objects and make them accessible to economic valuation in risk assessment.
Hence, in dissecting a complex object (e.g., a production plant) we distinguish between:
- a. vertically extending fixed structures (e.g., walls of the buildings) impacted directly by the flood process;
- b. particular superstructures impacted directly (e.g., bridge decks) or indirectly (e.g., roofs) by the flood process.
- c. installations and/or mobile objects (e.g., machines and cars) impacted directly by the flood process.
For completeness two supplementary categories have to be considered that are also affected by flooding: sediment and wood deposition;
- d. surfaces (areas) for different land use purposes (e.g., agricultural land, but also parking areas and roads); and
- e. biotic systems (e.g., wood, but also orchards).
The direct economic reference for a valuation of object parts belonging to the categories (a,b) is the determination of the reinstatement value,  , which can be calculated by:
, which can be calculated by:
 , which can be calculated by:
, which can be calculated by: (20)
(20)where NV is the reinstatement value of the considered object:  is the required quantity of input
is the required quantity of input  to perform the construction workflow unit
to perform the construction workflow unit  ; and
; and  is the unitary of the construction workflow unit
is the unitary of the construction workflow unit  .
.
 is the required quantity of input
is the required quantity of input  to perform the construction workflow unit
to perform the construction workflow unit  ; and
; and  is the unitary of the construction workflow unit
is the unitary of the construction workflow unit  .
.For the category (c), the estimation of the market value,  , of the equipment components is calculated as follows:
, of the equipment components is calculated as follows:
 , of the equipment components is calculated as follows:
, of the equipment components is calculated as follows: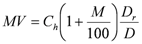 (21)
(21)where MV is the most probable market value of the equipment component under consideration.  is the purchase price;
is the purchase price;  is the cost increment from the year of purchase to the year of valuation:
is the cost increment from the year of purchase to the year of valuation:  is the residual economic life (in years) and
is the residual economic life (in years) and  is the economic lifespan (in years).
is the economic lifespan (in years).
 is the purchase price;
is the purchase price;  is the cost increment from the year of purchase to the year of valuation:
is the cost increment from the year of purchase to the year of valuation:  is the residual economic life (in years) and
is the residual economic life (in years) and  is the economic lifespan (in years).
is the economic lifespan (in years).For category (d) it is relevant to determinate the costs of clearing-up operations and the necessary reinstatements to re-establish the original functionally.
In case of object category (e), the economic valuation is carried out by determining the capital value of the biotic system under consideration through suitable capitalization formulas.
The next methodological step consists of embedding the dynamic risk notion into the mathematical apparatus of cost-benefit analysis.
We assume throughout that the public sector seeks to create system modifications maximizing the difference between annual savings in terms of risk reductions and the annual costs of the investment project through flood risk mitigation investments, entailing construction costs at the beginning of the investment lifecycle and maintenance expenditures throughout the lifecycle.
The flood risk mitigation performance,  ,of a strategy
,of a strategy 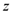 ,
,  (compare also Figure 4), can be evaluated by taking the difference between the annual risks (
(compare also Figure 4), can be evaluated by taking the difference between the annual risks (  and
and  , respectively), calculated by taking the difference of the integrals of the Expected Damage (ED) Probability curves (
, respectively), calculated by taking the difference of the integrals of the Expected Damage (ED) Probability curves ( 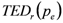 and
and 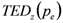 with
with  indicating the probability of exceeding, mirroring the current situation, mirroring the current situation (subscript
indicating the probability of exceeding, mirroring the current situation, mirroring the current situation (subscript  ) and the hypothesized situation with the implemented strategy respectively (subscript
) and the hypothesized situation with the implemented strategy respectively (subscript 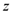 ):
):
 ,of a strategy
,of a strategy 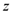 ,
,  (compare also Figure 4), can be evaluated by taking the difference between the annual risks (
(compare also Figure 4), can be evaluated by taking the difference between the annual risks (  and
and  , respectively), calculated by taking the difference of the integrals of the Expected Damage (ED) Probability curves (
, respectively), calculated by taking the difference of the integrals of the Expected Damage (ED) Probability curves ( 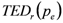 and
and 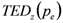 with
with  indicating the probability of exceeding, mirroring the current situation, mirroring the current situation (subscript
indicating the probability of exceeding, mirroring the current situation, mirroring the current situation (subscript  ) and the hypothesized situation with the implemented strategy respectively (subscript
) and the hypothesized situation with the implemented strategy respectively (subscript  ):
):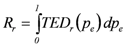 (22)
(22)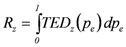 (23)
(23) (24)
(24)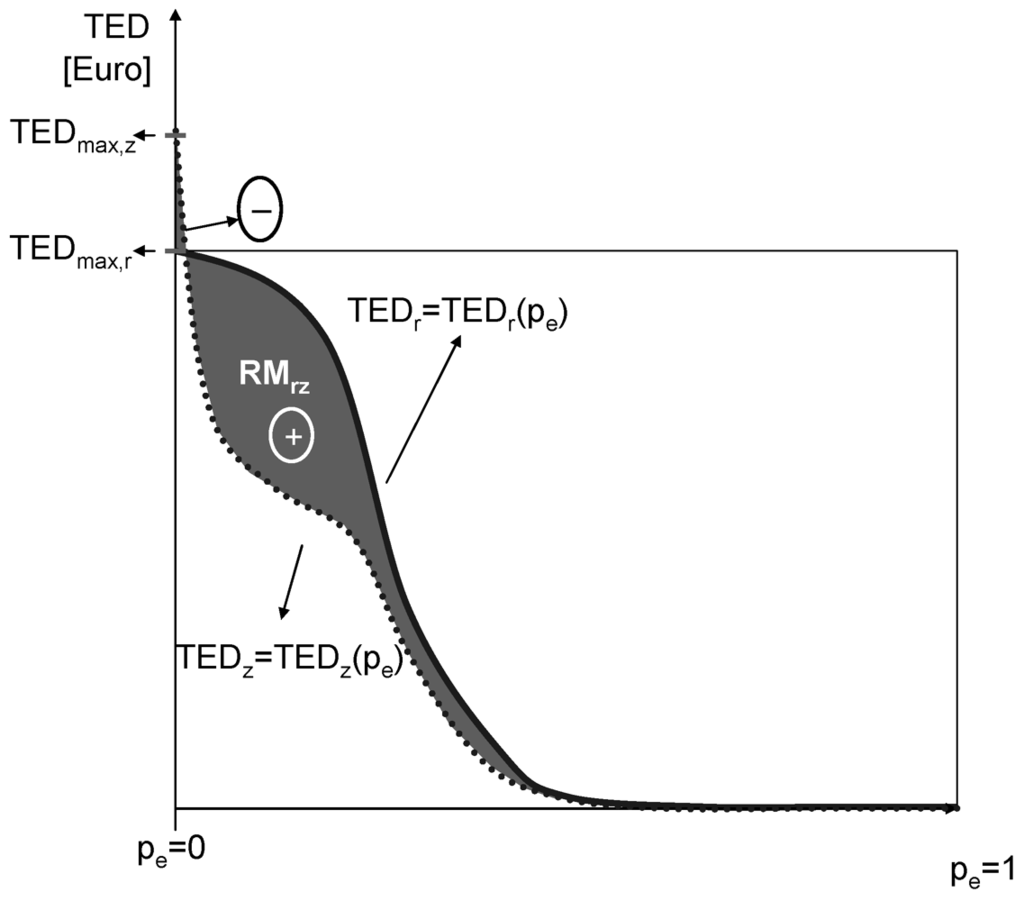
Figure 4.
Graphical representation of the risk mitigation performance  of a mitigation strategy
of a mitigation strategy 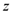 .
.
 of a mitigation strategy
of a mitigation strategy 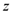 .
.
As shown in Figure 4, the implementation of flood risk mitigation strategies entailing the construction of active protection measures (e.g., check dams, dykes, local protection measures) also increases the number and the value of the objects at risk exposed to flood impact ( 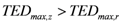 ). As one may note, for extreme events with
). As one may note, for extreme events with  that tends to zero,
that tends to zero,  is larger than
is larger than 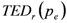 . This is due to the fact that under extreme loading conditions the elements of the protection system would also be damaged. Structures forming the protection systems feature a “dual nature” [21], as they are designed to mitigate natural process-related hazards, but on the other hand are prone to be damaged throughout their lifecycle by the same processes they should mitigate and their effectiveness thus declines over time.
. This is due to the fact that under extreme loading conditions the elements of the protection system would also be damaged. Structures forming the protection systems feature a “dual nature” [21], as they are designed to mitigate natural process-related hazards, but on the other hand are prone to be damaged throughout their lifecycle by the same processes they should mitigate and their effectiveness thus declines over time.
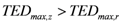 ). As one may note, for extreme events with
). As one may note, for extreme events with  that tends to zero,
that tends to zero,  is larger than
is larger than 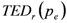 . This is due to the fact that under extreme loading conditions the elements of the protection system would also be damaged. Structures forming the protection systems feature a “dual nature” [21], as they are designed to mitigate natural process-related hazards, but on the other hand are prone to be damaged throughout their lifecycle by the same processes they should mitigate and their effectiveness thus declines over time.
. This is due to the fact that under extreme loading conditions the elements of the protection system would also be damaged. Structures forming the protection systems feature a “dual nature” [21], as they are designed to mitigate natural process-related hazards, but on the other hand are prone to be damaged throughout their lifecycle by the same processes they should mitigate and their effectiveness thus declines over time.The annual costs  associated to the implementation of the strategy
associated to the implementation of the strategy 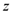 can be computed knowing the cost plan -
can be computed knowing the cost plan - 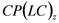 over its entire lifecycle of duration
over its entire lifecycle of duration  years.
years.
 associated to the implementation of the strategy
associated to the implementation of the strategy 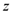 can be computed knowing the cost plan -
can be computed knowing the cost plan - 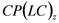 over its entire lifecycle of duration
over its entire lifecycle of duration  years.
years. Mathematically, a cost plan is a vector containing the foreseen expenditures as elements for each year, namely 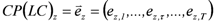 , with
, with  .
.
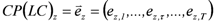 , with
, with  .
.The net present value,  ,associated to the implementation of the strategy can be calculated as:
,associated to the implementation of the strategy can be calculated as:
 ,associated to the implementation of the strategy can be calculated as:
,associated to the implementation of the strategy can be calculated as: (25)
(25)Normally, as shown in Figure 5, 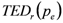 and
and  are not available as smooth functions, but have to be obtained by linear interpolation between a finite number of value pairs
are not available as smooth functions, but have to be obtained by linear interpolation between a finite number of value pairs 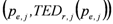 and
and 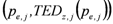 , respectively) corresponding to the consequences in terms of expected damage of the
, respectively) corresponding to the consequences in terms of expected damage of the  flood hazard under consideration.
flood hazard under consideration.
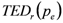 and
and  are not available as smooth functions, but have to be obtained by linear interpolation between a finite number of value pairs
are not available as smooth functions, but have to be obtained by linear interpolation between a finite number of value pairs 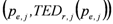 and
and 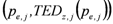 , respectively) corresponding to the consequences in terms of expected damage of the
, respectively) corresponding to the consequences in terms of expected damage of the  flood hazard under consideration.
flood hazard under consideration. 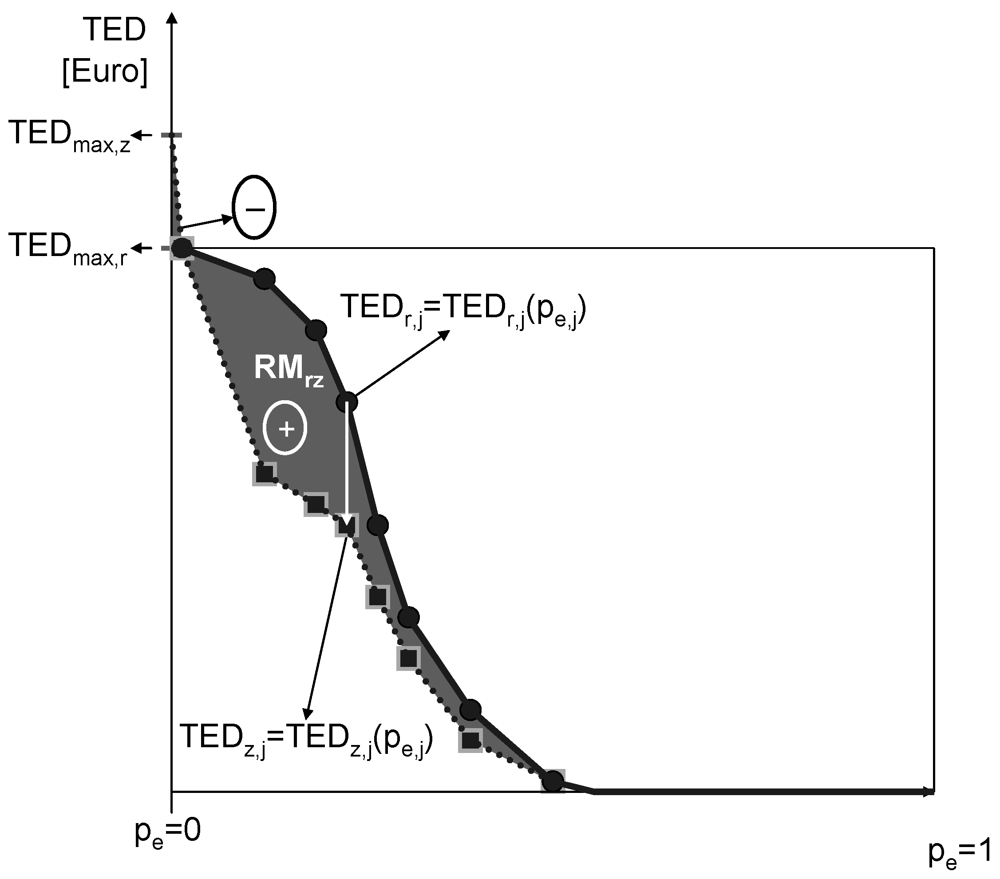
Figure 5.
Graphical representation of the risk mitigation performance  of a mitigation strategy
of a mitigation strategy  assuming only a finite number of value pairs (
assuming only a finite number of value pairs ( 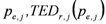 and
and 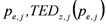 , respectively).
, respectively).
 of a mitigation strategy
of a mitigation strategy 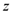 assuming only a finite number of value pairs (
assuming only a finite number of value pairs ( 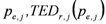 and
and 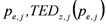 , respectively).
, respectively).
In the case illustrated by Figure 5, Equations 22, 23 and 24 have to be rewritten as:
 (26)
(26) (27)
(27)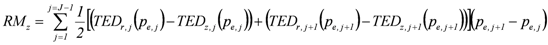 (28)
(28)Figure 6 shows the general case characterized by variability in damage potential though time (e.g., wealth moving into flood prone areas) and variability in risk mitigation performance of the strategy z.
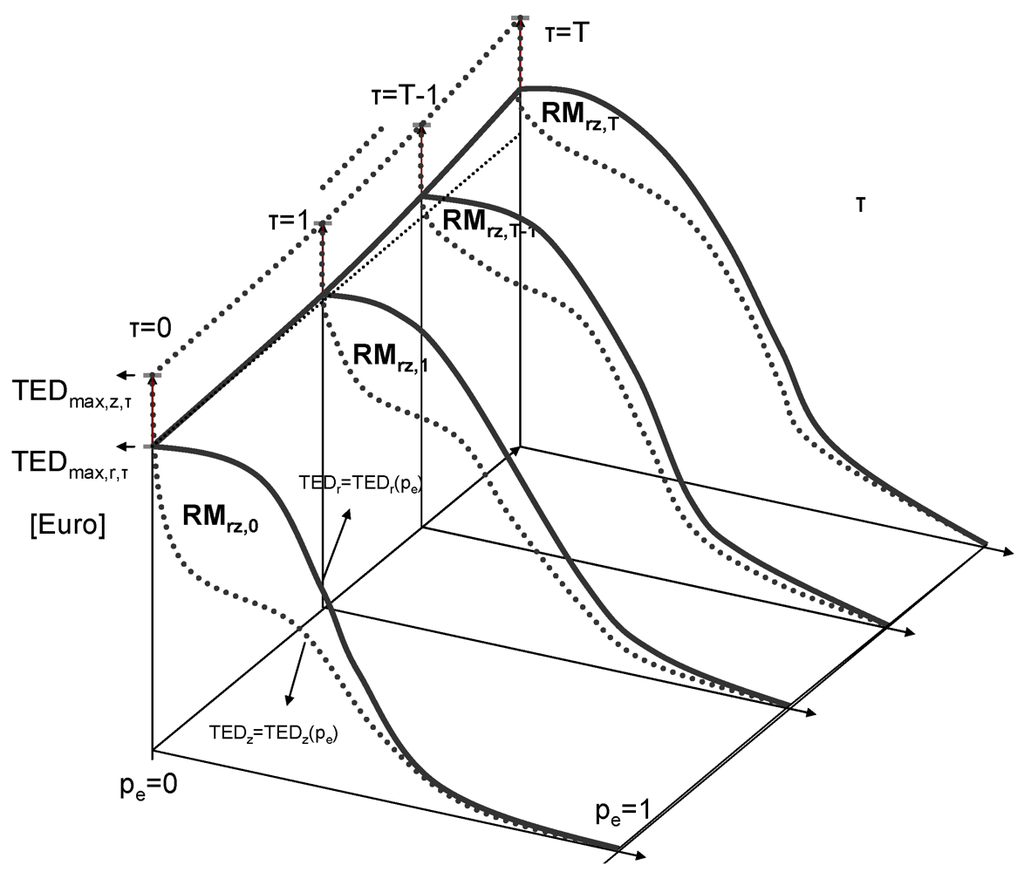
Figure 6.
Graphical representation of the risk mitigation performance  of a mitigation strategy
of a mitigation strategy 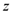 , assuming variability in damage potential and risk mitigation performance through time.
, assuming variability in damage potential and risk mitigation performance through time.
 of a mitigation strategy
of a mitigation strategy 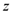 , assuming variability in damage potential and risk mitigation performance through time.
, assuming variability in damage potential and risk mitigation performance through time.
From a mathematical perspective we need (i) a cost plan (vector containing as elements the foreseen expenditures for each year 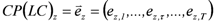 , with
, with  and (ii) the flow of risk mitigation benefits for each year
and (ii) the flow of risk mitigation benefits for each year  , with
, with  .
.
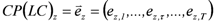 , with
, with  and (ii) the flow of risk mitigation benefits for each year
and (ii) the flow of risk mitigation benefits for each year  , with
, with  .
.The net present value,  ,associated to the implementation of the strategy z can be calculated as:
,associated to the implementation of the strategy z can be calculated as:
 ,associated to the implementation of the strategy z can be calculated as:
,associated to the implementation of the strategy z can be calculated as: (29)
(29)5. Conclusions
The evolution in Europe in recent centuries, mainly consisting in a shift from a strong agricultural orientation to a service industry and leisure-centered society, has carried ever-increasing pressures in terms of usage of alpine areas and nearby regions for settlement, industry and recreation. These dynamics resulted into conflicts between human needs and their satisfaction on the one hand and naturally-determined conditions on the other [22]. The economic bottlenecks emerging on a global level further restricted the margins of public investments to reduce flood hazard by realizing costly technical protection measures. Partly as a reaction and partly in anticipation, the European Flood Directive was issued, introducing the concept of risk as a basis for the management of natural hazards. Moreover, it was reaffirmed that an informed decision-making process regarding public investments to mitigate natural hazards could take advantage of sound cost-benefit analyses. Such an in-depth analysis entails the quantification of net benefits of risk mitigation strategies, which mainly derive from the associated reductions in terms of flood risk in relation to the prior level of risk and the expenditures needed for implementation. Besides the probabilities and intensities of the flood hazards, the determination of the physical vulnerability of impacted objects is a crucial element in risk analysis.
Therefore, in this paper, we have discussed in-depth the fundamental notion of physical vulnerability from a dynamic perspective, introducing a methodological and analytical apparatus to derive computational schemes for different categories of elements at risk.
We worked out two prime examples demonstrating the full applicability of the suggested procedural workflow. In the “vehicle risk” problem we illustrated how to subsume under the vulnerability concept the damage generation mechanism given by the interplay of static, kinetic and elasto-static effects. Concerning the “bridge deck displacement problem”, we could neglect elasto-static effects in analyzing the damage generation mechanism.
In a dedicated annex we provided analytic solutions for special cases of the two example problems.
In our opinion, linking the vulnerability assessment to engineering mechanics furthers the idea that the utility of cost-benefit analysis goes far beyond pure selection of the optimal management option out of an available bundle, if employed in earlier phases of the risk management process as an additional planning tool. Analyzing the time-varying vulnerability of elements at risk having a crucial impact on the expected consequences of flood impacts is increasingly becoming essential for a broad spectrum of activities within the risk governance process [23,24].
Intervention planning for example, which is recognized to be an effective tool to mitigate flood risk, is strongly based on the quality of the analysis of both the spatial and the temporal dynamics either of the flood hazard process or of the corresponding damaging impacts. Hazard and risk studies are valuable tools, especially if they contain an accurate time-varying representation of vulnerability for land use planning.
As mentioned earlier, we embedded the dynamic notion of vulnerability and risk into the formal framework of cost-benefit analysis. By making explicit risk dynamics and cost generation mechanisms, we have contributed to an expansion of the classical scope of application of cost-benefit analysis, promoting its use earlier in the planning process to enhance the search for both technically-feasible and economically-efficient solutions. Strengthening the link between physics and the economics of risk and expressing in monetary terms the annual risk reduction achievable by the envisaged investment projects may support a rational prioritization of public investment flows for the mitigation of flood risk (i.e., risk-based decision making).
In order to improve the risk-based selection of optimal mitigation strategies, an economic valuation of the elements at risk is necessary. In a dedicated section we have reviewed suitable existing valuation techniques.
References
- United Nations, Resolutions Adopted by the Conference. Report of the United Nations Conference on Environment and Development: New York, NY, USA, 1993.
- Commission of the European Communities. Directive 2007/60/EC of the European Parliament and of the Council of 23 October 2007 on the Assessment and Management of Flood Risks. Official Journal of the European Union: Luxembourg, 6 November 2007. Available online: http://eur-lex.europa.eu/LexUriServ/LexUriServ.do?uri=OJ:L:2007:288:0027:0034:EN:PDF (accessed on 12 October 2010).
- Commission of the European Communities. Communication from the Commission to the Council, the European Parliament, the European Economic and Social Committee and the Committee of the Regions. Flood risk management eFlood prevention, protection and mitigation. 2004. Available online: http://eur-lex.europa.eu/LexUriServ/LexUriServ.do?uri=COM:2004:0472: FIN:EN:PDF (accessed on 27 October 2010).
- Mazzorana, B.; Fuchs, S. A Conceptual planning tool for hazard and risk management. In Proceedings of the Internationales Symposium Interpraevent, Taipei, Taiwan, 26-30 April 2010; pp. 828–837.
- Merz, B.; Kreibich, H.; Schwarze, R.; Thieken, A. Assessment of economic flood damage. Nat. Hazards Earth Syst. Sci. 2010, 10, 1697–1724. [Google Scholar] [CrossRef]
- Parker, D.J.; Green, C.H.; Thompson, P.M. Urban Flood Protection Benefits: A Project Appraisal Guide; Gower Technical Press: Aldershot, UK, 1987. [Google Scholar]
- Perman, R.; Ma, Y.; Common, M.; Maddison, D.; Mcgilvray, J. Natural Resource and Environmental Economics; Addison-Wesley: Boston, MA, USA, 2011. [Google Scholar]
- Fuchs, S. Mountain Hazard Vulnerability and Risk. Habilitation Thesis, Innsbruck University, Innsbruck, Austria, 2009. [Google Scholar]
- Mazzorana, B.; Comiti, F.; Scherer, C.; Fuchs, S. Developing consistent scenarios to assess flood hazards in mountain streams. J. Environ. Manag. 2011, 94, 112–124. [Google Scholar]
- Mazzorana, B.; Fuchs, S. Fuzzy formative scenario analysis for woody material transport related risks in mountain torrents. Environ. Model. Softw. 2010, 25, 1208–1224. [Google Scholar] [CrossRef]
- Smith, K.; Ward, R. Floods: Physical Processes and Human Impacts; John Wiley & Sons: Chichester, UK, 1998. [Google Scholar]
- Comiti, F.; Mao, L.; Preciso, E.; Picco, L.; Marchi, L.; Borga, M. Large wood and flash floods: Evidences from the 2007 Event in the Davca Basin (Slovenia). In Monitoring, Simulation, Prevention and Remediation of Dense and Debris Flow II; de Wrachien, D., Lenzi, M.A., Brebbia, C.A., Eds.; WIT-Press: Southampton, UK, 2008; pp. 173–182. [Google Scholar]
- Hanley, N.; Spash, C. Cost-Benefit Analysis and the Environment; Edward Elgar: Cheltenham, UK, 1994. [Google Scholar]
- Keiler, M.; Sailer, R.; Jörg, P.; Weber, S.; Zischg, A.; Sauermoser, S. Avalanche risk assessment—A multi-temporal approach, results from Galtür, Austria. Nat. Hazards Earth Syst. Sci. 2006, 6, 637–651. [Google Scholar] [CrossRef]
- Papathoma-Köhle, M.; Kappes, M.; Keiler, M.; Glade, T. Physical vulnerability assessment for alpine hazards: State of the art and future needs. Nat. Hazards 2011, 58, 645–680. [Google Scholar]
- Mileti, D. Disasters by Design; Joseph Henry Press: Washington, DC, USA, 1999. [Google Scholar]
- Daily, J.; Strickland, R.; Daily, J. Crush analysis with under-rides and the coefficient of restitution. In Proceedings of the 24th Annual Special Problems in Traffic Crash Reconstruction; Bloomington, IL, USA: 24-28 April 2006.
- Kruschwitz, L. Investitionsrechnung; 12. Aufl., Oldenbourg Wisssenschaftsverlag GmbH: München, Germany, 2008. [Google Scholar]
- Drees, G.; Paul, W. Kalkulation von Baupreisen; Beuth Verlag: Berlin, Germany, 2011. [Google Scholar]
- Gallerani, V.; Viaggi, D.; Zanni, G. Manuale di Estimo; McGraw-Hill: Milano, Italy, 2011. [Google Scholar]
- Dell’Agnese, A.; Mazzorana, B.; Comiti, F.; von Maravic, P.; D’Agostino, V. Assessing the physical vulnerability of check dams through an empirical damage index. La Houille Blanche. in submit.
- Keiler, M.; Fuchs, S. Berechnetes risiko. Mit sicherheit am rande der gefahrenzone. In Geographische Risikoforschung. Zur Konstruktion verräumlichter Risiken und Sicherheiten; Egner, H., Pott, A., Eds.; Franz Steiner: Stuttgart, Germany, 2010; pp. 51–68. [Google Scholar]
- Renn, O. Concepts of risk: An interdisciplinary review. Part 1: Disciplinary risk concepts. GAIA 2008, 17, 50–66. [Google Scholar]
- Renn, O. Concepts of risk: An interdisciplinary review. Part 2: Integrative approaches. GAIA 2008, 17, 196–204. [Google Scholar]
Mathematical Appendix
Let us recall Equations 5 and 7 for the case of a floating or sliding free rigid body
 (floating case)
(floating case) (sliding case)
(sliding case)and the Equation of sliding for the bridge case (Equation 15):

In each of the above cases, the evolution of the system is described by the following Cauchy problem, for a suitable choice of the constant parameters  ,
,  ,
, 
 ,
,  ,
, 
 (A1)
(A1) 
The choice for the variable and the parameters in the various cases is reported in the following table:
| Case |  |  |  |  |
|---|---|---|---|---|
| Floating rigid body |  |  |  |  |
| Sliding rigid body |  | 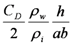 |  | 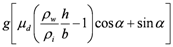 |
| Bridge |  | 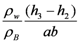 | 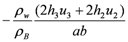 | 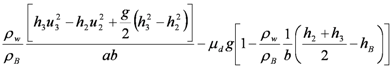 |
The analytical solution can be found by separation of variables and gives rise to different forms of the solution, depending on the sign of the constant  . In fact one has
. In fact one has
 . In fact one has
. In fact one has
Writing explicitly the integral and inverting we have
 (A2)
(A2)The equation for the position can then be found by integration. For the free rigid body we have

while for the bridge we just have  By the above equation we have
By the above equation we have
 By the above equation we have
By the above equation we have
Let us now specialize the above results for the three different cases.
A1.1. Floating Rigid Body
We have  and since obviously
and since obviously  the condition
the condition  is always satisfied. If we assume that the initial velocity of the object is zero and that
is always satisfied. If we assume that the initial velocity of the object is zero and that  we have
we have
 and since obviously
and since obviously  the condition
the condition  is always satisfied. If we assume that the initial velocity of the object is zero and that
is always satisfied. If we assume that the initial velocity of the object is zero and that  we have
we have (A3)
(A3) and
 (A4)
(A4) A1.2. Free Sliding Rigid Body
In this case 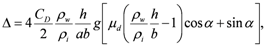 whose sign depends on that of
whose sign depends on that of  since
since  Let
Let 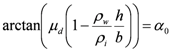 be the critical angle; the sliding condition assures that
be the critical angle; the sliding condition assures that  Thus if
Thus if  we have as before
we have as before
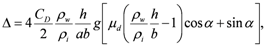 whose sign depends on that of
whose sign depends on that of  since
since  Let
Let 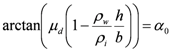 be the critical angle; the sliding condition assures that
be the critical angle; the sliding condition assures that  Thus if
Thus if  we have as before
we have as before (A5)
(A5) and
 (A6)
(A6) If  setting
setting  we get
we get
 setting
setting  we get
we get (A7)
(A7) and
 (A8)
(A8) for  we have
we have
 we have
we have (A9)
(A9) And
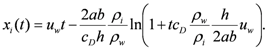 (A10)
(A10) A1.3. Bridge
In this case
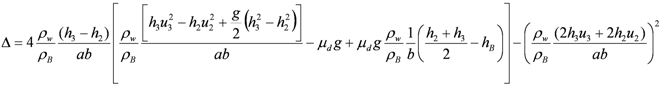
and since  it can be shown that
it can be shown that  always. Thus, given that the initial velocity of the bridge is zero, setting
always. Thus, given that the initial velocity of the bridge is zero, setting  the solution in this case is given by
the solution in this case is given by
 it can be shown that
it can be shown that  always. Thus, given that the initial velocity of the bridge is zero, setting
always. Thus, given that the initial velocity of the bridge is zero, setting  the solution in this case is given by
the solution in this case is given by (A11)
(A11) and
 (A12)
(A12) © 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).