Water Radiolysis: Influence of Oxide Surfaces on H2 Production under Ionizing Radiation
Abstract
:1. Introduction
2. Water Radiolysis: A Brief Historical Survey

3. Mechanism of Water Radiolysis
3.1. The Three Stages
- (1)
- The physical stage, which is achieved about 1 fs after the initial matter-ionizing radiation interaction, consists in energy deposition followed by fast relaxation processes. This leads to the formation of ionized water molecules (H2O+), excited water molecules (H2O*) and sub-excitations electrons (e−).
- (3)
- During the physico-chemical stage (10−15–10−12 s), numerous processes occur, including ion-molecule reaction (2), dissociative relaxation (3), autoionization of excited states, thermalization of subexcitation electrons (solvation of electrons) (4), hole diffusion, etc.
- (3)
- During the chemical stage (10−12–10−6 s), the species react in the tracks and then diffuse in solution. They can thus react with each other and also with surrounding molecules (in the solute). The track of the particles expands because of the diffusion of radicals and their subsequent chemical reactions. Recombination becomes unimportant after ca. 1 µs for low-LET radiation.
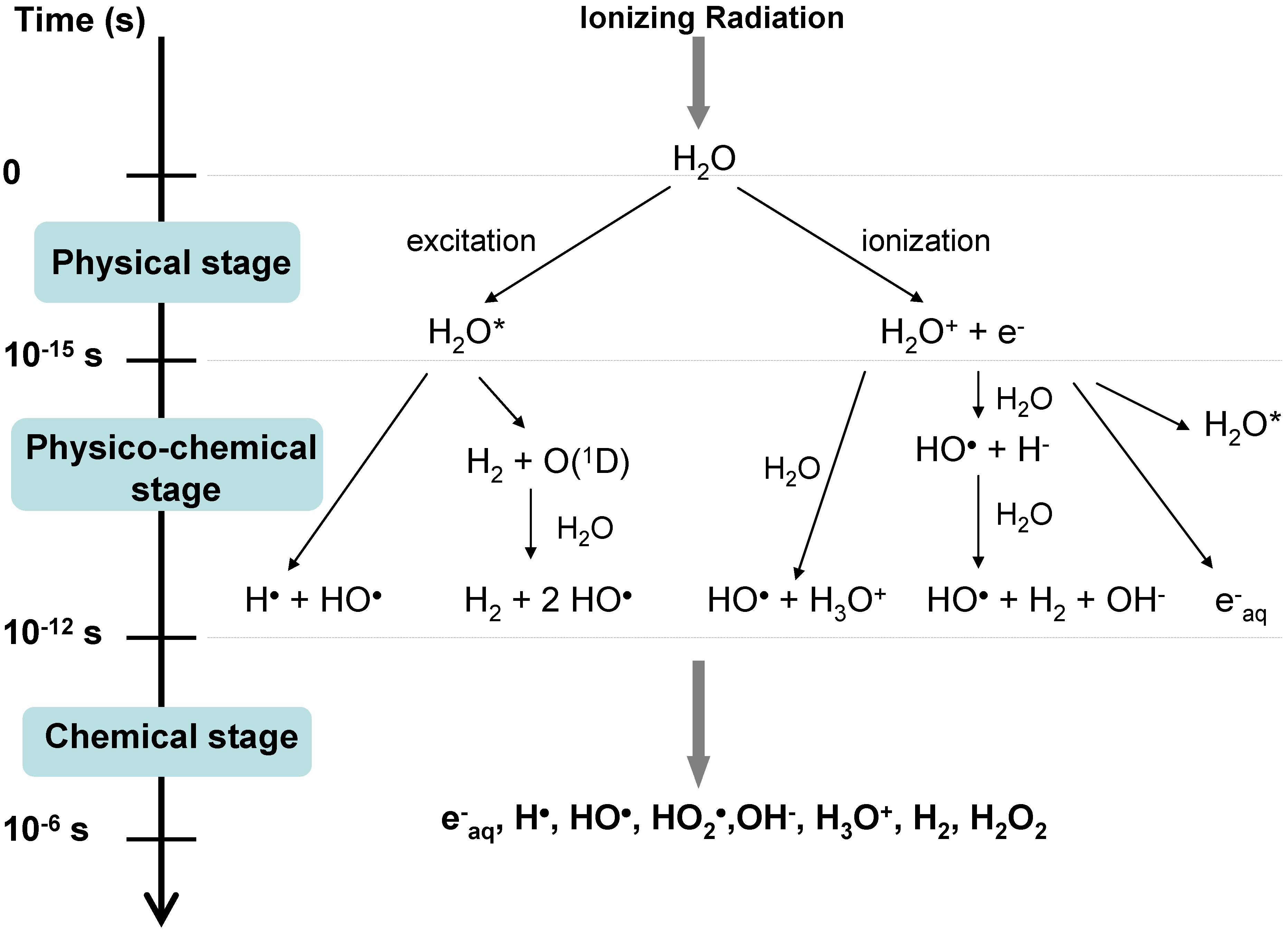
3.2. Radiolytic Yields
| Radiation | e−aq | ●OH | H● | H2 | H2O2 | HO2● |
|---|---|---|---|---|---|---|
| γ Electrons (0.1–10 MeV) pH = 3–11 | 0.28 | 0.28 | 0.06 | 0.047 | 0.073 | 0.0027 |
| γ Electrons (0.1–10 MeV) pH = 0.5 | 0 | 0.301 | 0.378 | 0.041 | 0.081 | 0.0008 |
| 5.3 MeV α particles (210Po) pH = 0.5 | 0 | 0.052 | 0.062 | 0.163 | 0.150 | 0.011 |
3.3. Main Reactions
| Reaction | Rate constant (1010 mol−1 dm3 s−1) |
|---|---|
| 0.55 | |
| 2.50 | |
| 0.78 | |
| 3.00 | |
| 2.30 | |
| 0.55 | |
| 2.00 | |
| 14.0 |
4. Water Radiolysis and H2 Production in Heterogeneous Systems at Oxide/Water Interfaces
4.1. Modification of H2 Radiolytic Yields in Heterogeneous Oxide/Water Systems
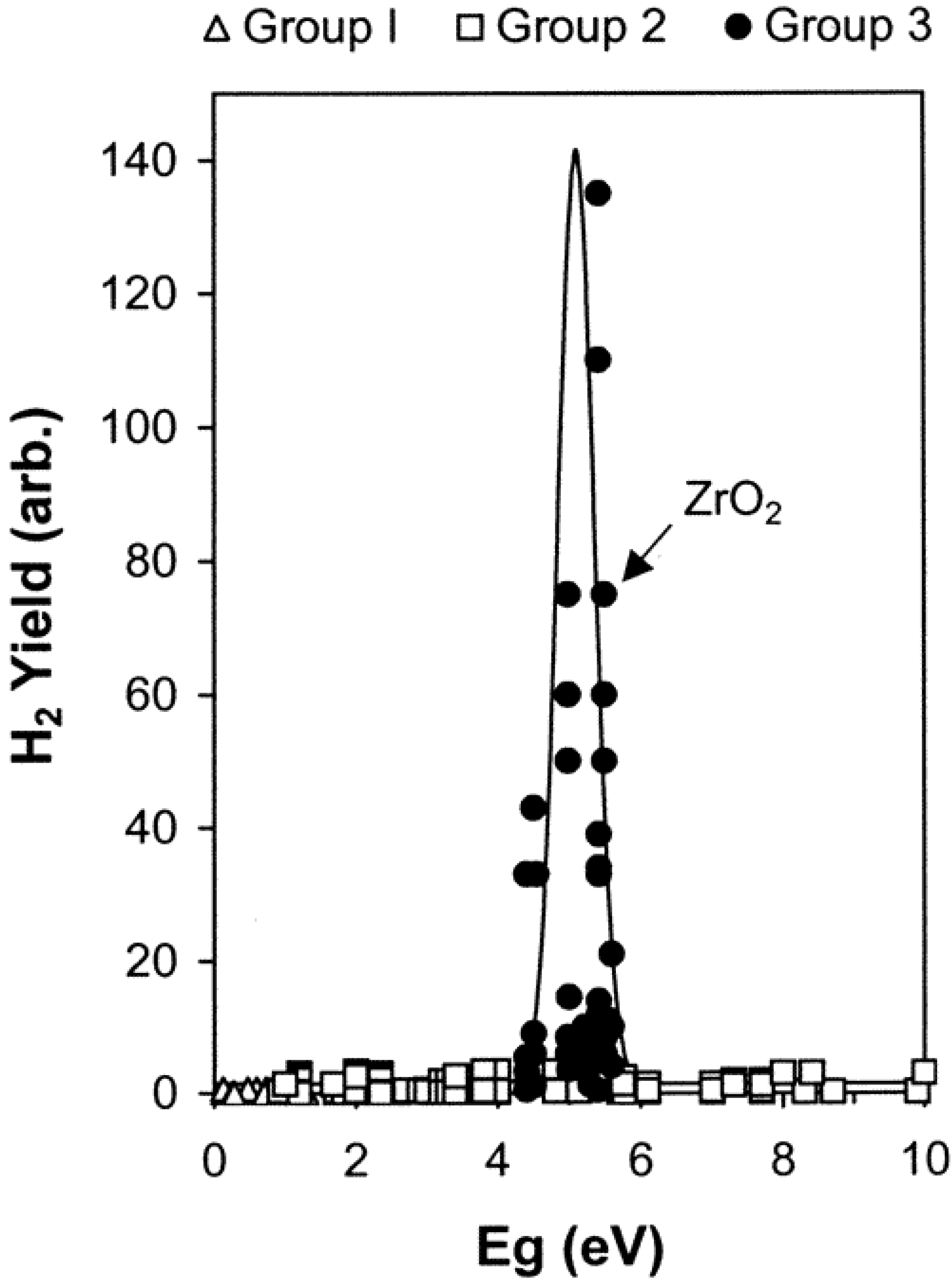
4.2. Mechanisms Accounting for H2 Production in Oxide/Water Systems
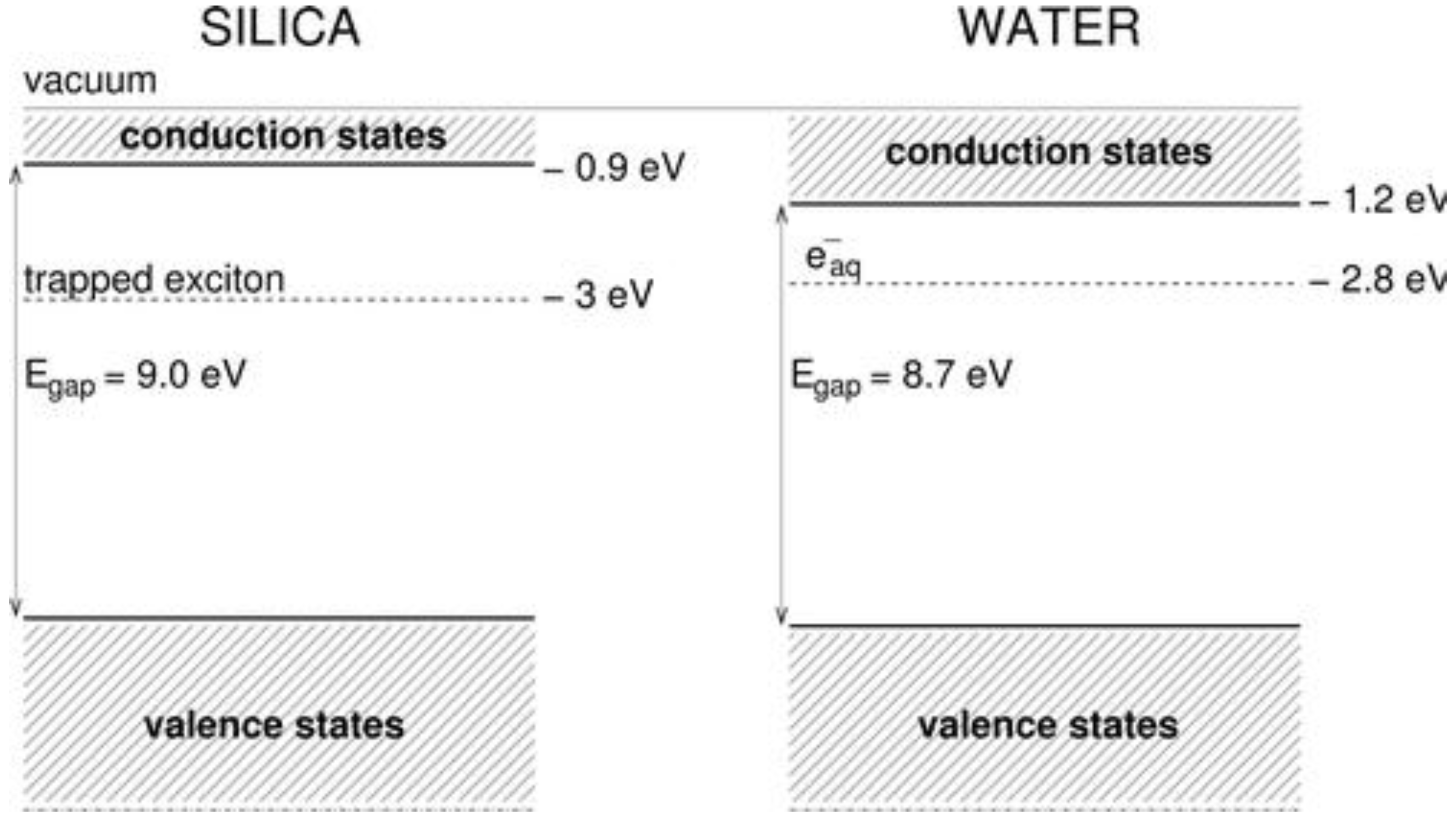
4.3. The Fate on Electrons and Holes—A Textbook Case: Silica
4.4. Parameters Affecting the Dihydrogen Yield
- the doping of the oxide [60];
- the crystal phase [89];
- the exciton migration distance. Higher distances favor exciton exciton recombination or self-trapping instead of their reaction at the interface [90];
- The water adsorption form (physisorbed/chemisorbed water) [81]. The measure of H2 production from 10 MeV-electron irradiation on mesoporous silica has shown that adsorbed water (physisorbed water) is attacked preferentially. Silanol groups (chemisorbed water) are only attacked when they are in majority with respect to adsorbed water. However, they are much less efficient in producing H2 [81];
- the dose rate of the irradiation. In the case of high dose rate irradiation, the H2 yields are much smaller than in the case of γ-irradiation with low dose rate; most of the received energy is not used for H2 production but for recombination of excitons on defect sites (cathodoluminescence) or exciton-exciton reaction [90]. The accumulation of defects under irradiation can provide an additional deactivation pathway for excitons [91]: this is indeed the principle of cathodoluminescence spectroscopy [92]. Therefore, less excitons can reach the surface to induce H2 production and the dihydrogen yields are then strongly decreased [90];
- the LET value of the particles. Contrary to the phenomena described in the bulk phase, the H2 yields for water adsorbed on zirconia were found to exhibit a marked decrease in the case of 5 MeV helium ion radiolysis as compared to γ-radiolysis. The heavy ions induce the formation of much more Frenkel defects in zirconia than the γ-radiolysis, which prevents the excitons from migrating to the surface [93].
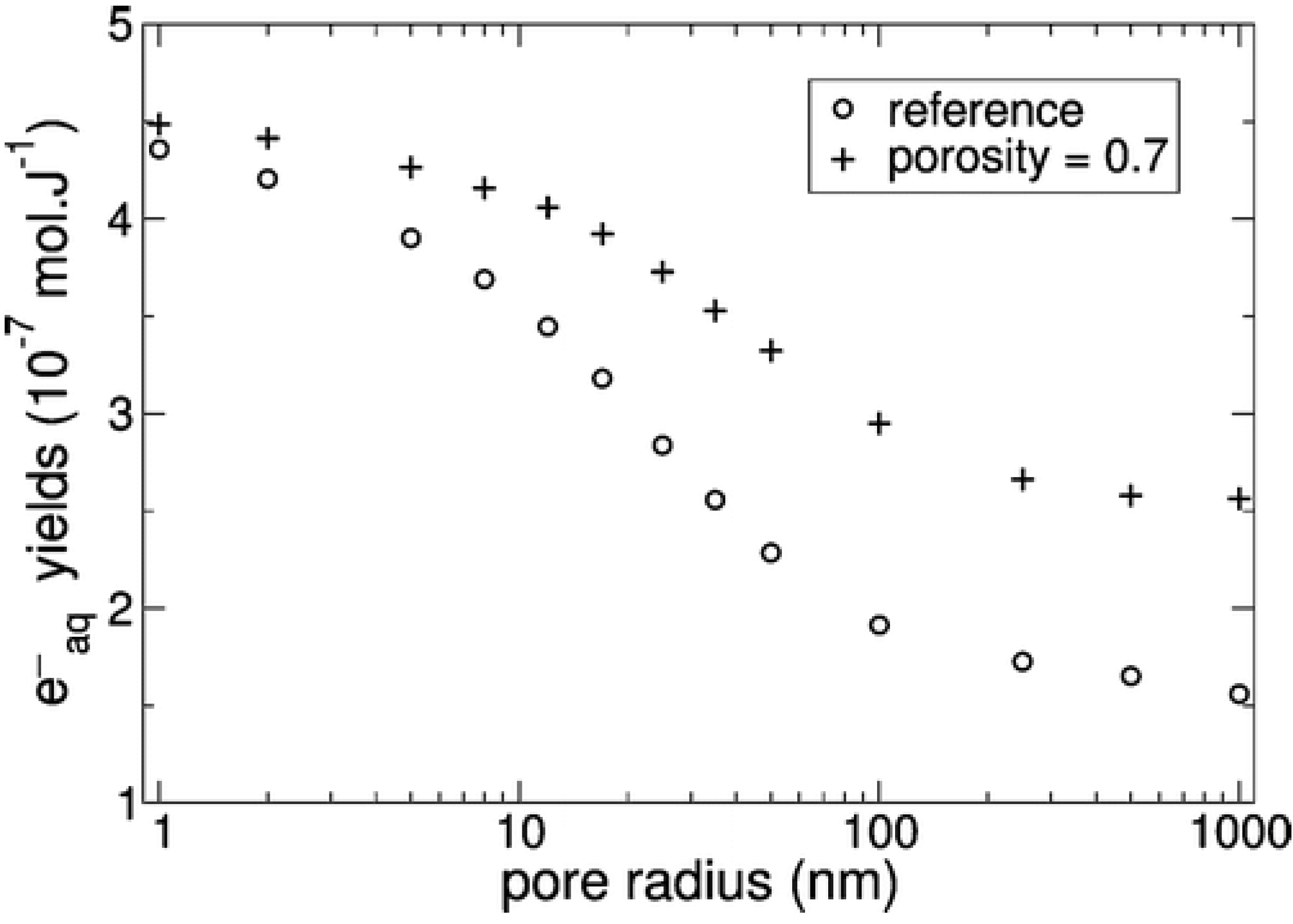
4.5. Modification of Kinetics upon Confinement
5. Conclusions
References
- Schmid, T.E.; Dollinger, G.; Hable, V.; Greubel, C.; Zlobinskaya, O.; Michalski, D.; Molls, M.; Roeper, B. Relative biological effectiveness of pulsed and continuous 20 MeV protons for micronucleus induction in 3D human reconstructed skin tissue. Radiother. Oncol. 2010, 95, 66–72. [Google Scholar] [CrossRef]
- Maquille, A.J.; Jiwan, J.L.H.; Tilquin, B. Radiosterilization of drugs in aqueous solutions may be achieved by the use of radioprotective excipients. Int. J. Pharm. 2008, 349, 74–82. [Google Scholar] [CrossRef]
- Guo, Z.B.; Tang, D.Y.; Liu, X.G.; Zheng, Z. Gamma irradiation-induced Cd2+ and Pb2+ removal from different kinds of water. Rad. Phys. Chem. 2008, 77, 1021–1026. [Google Scholar] [CrossRef]
- Katayama, T.; Nakauma, M.; Todoriki, S.; Phillips, G.O.; Tada, M. Radiation-induced polymerization of gum arabic (Acacia senegal) in aqueous solution. Food Hydrocolloid. 2006, 20, 983–989. [Google Scholar] [CrossRef]
- Bouniol, P.; Bjergbakke, E. A comprehensive model to describe radiolytic processes in cement medium. J. Nucl. Mat. 2008, 372, 1–15. [Google Scholar] [CrossRef]
- Early Developments in Radiation Chemistry; Kroh, J. (Ed.) Royal Society of Chemistry: Cambridge, UK, 1989.
- Jonah, C.D. A short history of the radiation chemistry of water. Radiat. Res. 1995, 144, 141–147. [Google Scholar] [CrossRef]
- Ferradini, C.; Jay-Gerin, J.P. La radiolyse de l’eau et des solutions aqueuses: historique et actualité. Can. J. Chem. 1999, 77, 1542–1575. [Google Scholar] [CrossRef]
- Zimbrick, J.D. Radiation research society 1952–2002 Radiation chemistry and the Radiation Research Society: A history from the beginning. Radiat. Res. 2002, 158, 127–140. [Google Scholar] [CrossRef]
- Giesel, F. Uber Radium und radioactive Stoffe. Ber. Dtsch. Chem. Ges. 1902, 35, 3608–3611. [Google Scholar] [CrossRef]
- Giesel, F. Uber den Emanationskörper aus Pechblende. Ber. Dtsch. Chem. Ges. 1903, 36, 342–347. [Google Scholar] [CrossRef]
- Kernbaum, M. Sur la décomposition de l'eau par les rayons béta du radium et par les rayons ultra-violets. Le Radium 1909, 6, 225–228. [Google Scholar] [CrossRef]
- Debierne, A. Recherches sur les gaz produits par les substances radioactives. Décomposition de l'eau. Ann. Phys. (Paris) 1914, 2, 97–127. [Google Scholar]
- Allen, A.O. Radiation chemistry of aqueous solutions. J. Phys. Colloid Chem. 1948, 52, 479–490. [Google Scholar] [CrossRef]
- Barr, N.F.; Allen, A.O. Hydrogen atoms in the radiolysis of water. J. Phys. Chem 1959, 63, 928–931. [Google Scholar] [CrossRef]
- Hayon, E.; Allen, A.O. Evidence for two kinds of “H atoms” in the radiation chemistry of water. J. Phys. Chem. 1961, 65, 2181–2185. [Google Scholar] [CrossRef]
- Czapski, G.; Schwarz, H.A. The nature of the reducing radical in water radiolysis. J. Chem. Phys 1962, 66, 471–474. [Google Scholar] [CrossRef]
- Collinson, E.; Dainton, F.S.; Smith, D.R.; Tazuké, S. Evidence for the unit negative charge on the “hydrogen atom” formed by the action of ionising radiation on aqueous systems. Proc. Chem. Soc. 1962, 140–141. [Google Scholar]
- Keene, J.P. Kinetics of radiation-induced chemical reactions. Nature 1960, 188, 843–844. [Google Scholar] [CrossRef]
- Hart, E.J.; Boag, J.W. Absorption spectrum of the hydrated electron in water and in aqueous solutions. J. Am. Chem. Soc. 1962, 84, 4090–4095. [Google Scholar] [CrossRef]
- Boag, J.W.; Hart, E.J. Absorption spectra in irradiated water and some solutions. Nature 1963, 197, 45–47. [Google Scholar] [CrossRef]
- Keene, J.P. Optical absorption in irradiated water. Nature 1963, 197, 47–48. [Google Scholar] [CrossRef]
- Stein, G. Some aspects of the radiation chemistry of organic solutes. Disc. Faraday Soc. 1952, 12, 227–234. [Google Scholar] [CrossRef]
- Platzman, R.L. Physical and Chemical Aspects of Basic Mechanisms in Radiobiology; Magee, J.L., Kamen, M.D., Platzman, R.L., Eds.; National Research Council: Washington, DC, USA, 1953; p. 22. [Google Scholar]
- Weiss, J. Radiation chemistry. Annu. Rev. Phys. Chem. 1953, 4, 143–166. [Google Scholar] [CrossRef]
- Weiss, J. Primary processes in the action of ionizing radiations on water: formation and reactivity of self-trapped electrons (‘polarons’). Nature 1960, 186, 751–752. [Google Scholar] [CrossRef]
- Burton, M. General discussion. Disc. Faraday Soc. 1952, 12, 317–318. [Google Scholar]
- Bonet-Maury, P.; Lefort, M. Formation of hydrogen peroxide in water irradiated with X- and alpha-rays. Nature 1948, 162, 381–382. [Google Scholar] [CrossRef] [PubMed]
- Magee, J.L. Theory of radiation chemistry. I. Some effects of variation in ionization density. J. Am. Chem. Soc. 1951, 73, 3270–3275. [Google Scholar]
- Samuel, A.H.; Magee, J.L. Theory of radiation chemistry. II. Track effects in radiolysis of water. J. Chem. Phys. 1953, 21, 1080–1087. [Google Scholar]
- Schwarz, H.A. Applications of the spur diffusion model to the radiation chemistry of aqueous solutions. J. Phys. Chem. 1969, 73, 1928–1937. [Google Scholar] [CrossRef]
- Hunt, J.W.; Thomas, J.K. Pulse-radiolysis studies of the formation of triplet excited states in cyclohexane solutions of naphtalene and anthracene. J. Chem. Phys. 1967, 46, 2954–2958. [Google Scholar] [CrossRef]
- Bronskill, M.J.; Hunt, J.W. A pulse-radiolysis system for the observation of short-lived transients. J. Phys. Chem. 1968, 72, 3762–3766. [Google Scholar] [CrossRef]
- Bronskill, M.J.; Taylor, W.B.; Wolff, R.K.; Hunt, J.W. Design and performance of a pulse radiolysis system capable of picosecond time resolution. Rev. Sci. Instrum. 1970, 41, 333–340. [Google Scholar] [CrossRef] [PubMed]
- Jonah, C.D. A wide-time range pulse radiolysis system of picosecond time resolution. Rev. Sci. Instrum. 1975, 46, 62–66. [Google Scholar] [CrossRef]
- Kobayashi, H.; Tabata, Y. A 20 ps time resolved pulse radiolysis using two linacs. Nucl. Inst. and Meth. Phys. Res. B 1985, 10-11, 1004–1006. [Google Scholar] [CrossRef]
- Wishart, J.F.; Cook, A.R.; Miller, J.R. The LEAF picosecond pulse radiolysis facility at Brookhaven National Laboratory. Rev. Sci. Instrum. 2004, 75, 4359–4366. [Google Scholar] [CrossRef]
- Marignier, J.-L.; de Waele, V.; Monard, H.; Gobert, F.; Larbre, J.-P.; Demarque, A.; Mostafavi, M.; Belloni, J. Time-resolved spectroscopy at the picosecond laser-triggered electron accelerator ELYSE. Rad. Phys. Chem. 2006, 75, 1024–1033. [Google Scholar] [CrossRef]
- Bronskill, M.J.; Wolff, R.K.; Hunt, J.W. Picosecond pulse radiolysis studies. I. The solvated electron in aqueous and alcohol solutions. J. Chem. Phys 1970, 53, 4201–4210. [Google Scholar]
- Jonah, C.D.; Matheson, M.S.; Miller, J.R.; Hart, E.J. Yield and decay of the hydrated electron from 100 ps to 3 ns. J . Phys. Chem. 1976, 80, 1267–1270. [Google Scholar] [CrossRef]
- Bartels, D.M.; Cook, A.R.; Mudaliar, M.; Jonah, C.D. Spur decay of the solvated electron in picosecond radiolysis measured with time-correlated absorption spectroscopy. J. Phys. Chem. A 2000, 104, 1686–1691. [Google Scholar] [CrossRef]
- Muroya, Y.; Lin, M.; Wu, G.; Iijima, H.; Yoshii, K.; Ueda, T.; Kudo, H.; Katsumura, Y. A re-evaluation of the initial yield of the hydrated electron in the picosecond time range. Rad. Phys. Chem. 2005, 72, 169–172. [Google Scholar] [CrossRef]
- Jonah, C.D.; Miller, J.R. Yield and decay of the OH radical from 200 ps to 3 ns. J. Phys. Chem. 1977, 81, 1974–1976. [Google Scholar] [CrossRef]
- Buxton, G.V. Radiation Chemistry. Principles and Applications; Farhataziz, Rodgers, M.A.J., Eds.; Verlag Chemie Publishers: Weinheim, Germany, 1987. [Google Scholar]
- Spinks, J.W.T.; Woods, R.J. An Introduction to Radiation Chemistry, 3rd ed.; Wiley-Interscience publication: New York, NY, USA, 1990. [Google Scholar]
- Ferradini, C.; Jay-Gerin, J.P. The effect of pH on water radiolysis: a still open question. A minireview. Res. Chem. Intermed. 2000, 26, 549–565. [Google Scholar] [CrossRef]
- LaVerne, J.A.; Schuler, R.H. Decomposition of water by very high linear energy transfer radiations. J. Phys. Chem. 1983, 87, 4564–4565. [Google Scholar] [CrossRef]
- Allen, A.O.; Hochanadel, C.J.; Ghormley, J.A.; Davis, T.W. Decomposition of water and aqueous solutions under mixed fast neutron and gamma radiation. J. Phys. Chem. 1952, 56, 575–586. [Google Scholar] [CrossRef]
- Pastina, B.; Isabey, J.; Hickel, B. The influence of water chemistry on the radiolysis of the primary coolant water in pressurized water reactors. J. Nucl. Mat. 1999, 264, 309–318. [Google Scholar] [CrossRef]
- Pastina, B.; LaVerne, J.A. Effect of molecular hydrogen on hydrogen peroxide in water radiolysis. J. Phys. Chem. A 2001, 105, 9316–9322. [Google Scholar] [CrossRef]
- Buxton, G.V.; Greenstock, C.L.; Helman, W.P.; Ross, A.B. Critical review of rate constants for reactions of hydrated electrons, hydrogen atoms and hydroxyl radicals (●OH/●O−) in aqueous solution. J. Phys. Chem. Ref. Data 1988, 17, 513–531. [Google Scholar] [CrossRef]
- Pimblott, S.M.; LaVerne, J.A. Stochastic simulation of the electron radiolysis of water and aqueous solutions. J. Phys. Chem. A 1997, 101, 5828–5838. [Google Scholar] [CrossRef]
- Pastina, B.; LaVerne, J.A.; Pimblott, S.M. Dependence of molecular hydrogen formation in water on scavengers of the precursor to the hydrated electron. J. Phys. Chem. A 1999, 103, 5841–5846. [Google Scholar] [CrossRef]
- LaVerne, J.A.; Pimblott, S.M. New mechanism for H2 formation in water. J. Phys. Chem. A 2000, 104, 9820–9822. [Google Scholar] [CrossRef]
- Caffrey, J.M.; Allen, A.O. Radiolysis of pentane adsorbed on mineral solids. J. Phys. Chem. 1958, 62, 33–37. [Google Scholar] [CrossRef]
- Rabe, J.G.; Rabe, B.; Allen, A.O. Radiolysis and energy transfer in the adsorbed state. J. Phys. Chem. 1966, 70, 1098–1107. [Google Scholar] [CrossRef]
- Rabe, J.G.; Rabe, B.; Allen, A.O. Radiolysis in the adsorbed state. J. Am. Chem. Soc. 1964, 86, 3887–3888. [Google Scholar] [CrossRef]
- Garibov, A.A.; Gezalov, K.B.; Velibekova, G.Z.; Ramazanova, M.K.; Kasumov, R.D.; Agaev, T.N.; Gasanov, A.M. Heterogeneous radiolysis of water: effect of the concentration of water in the adsorbed phase on the hydrogen yield. High Energy Chem. 1987, 21, 416–420. [Google Scholar]
- Nakashima, M.; Masaki, N.M. Radiolytic hydrogen gas formation from water adsorbed on type Y zeolites. Radiat. Phys. Chem. 1996, 47, 241–245. [Google Scholar] [CrossRef]
- Petrik, N.G.; Alexandrov, A.B.; Vall, A.I. Interfacial energy transfer during gamma radiolysis of water on the surface of ZrO2 and some other oxides. J. Phys. Chem. B 2001, 105, 5935–5944. [Google Scholar] [CrossRef]
- LaVerne, J.A.; Tandon, L. H2 production in the radiolysis of water on CeO2 and ZrO2. J. Phys. Chem. B 2002, 106, 380–386. [Google Scholar] [CrossRef]
- Rotureau, P.; Renault, J.P.; Lebeau, B.; Patarin, J.; Mialocq, J.C. Radiolysis of confined water: Molecular hydrogen formation. Chemphyschem. 2005, 6, 1316–1323. [Google Scholar] [CrossRef] [PubMed]
- LaVerne, J.A.; Tonnies, S.E. H2 production in the radiolysis of aqueous SiO2 Suspensions and Slurries. J. Phys. Chem. B 2003, 107, 7277–7280. [Google Scholar] [CrossRef]
- Itoh, N. Self-trapped exciton model of heavy-ion track registration. Nucl. Inst. and Meth. Phys. Res. B 1996, 116, 33–36. [Google Scholar] [CrossRef]
- Itoh, C.; Tanimura, K.; Trukhin, A.N. Time-resolved spectroscopic study of self-trapped excitons in germanium oxides. Nucl. Inst. and Meth. Phys. Res. B 1996, 116, 72–76. [Google Scholar] [CrossRef]
- Bautin, K.V.; Kudyakov, S.V.; Ogorodnikov, I.N.; Kruzhalov, A.V.; Yakovlev, V.Y. Exciton dynamics and energy transfer in beryllium oxide crystals with defects. J. Luminesc. 1998, 76-77, 467–469. [Google Scholar] [CrossRef]
- Saeta, P.N.; Greene, B.I. Primary relaxation processes at the band edge of SiO2. Phys. Rev. Lett. 1993, 70, 3588–3591. [Google Scholar] [CrossRef] [PubMed]
- Isamel-Beigi, S.; Louie, S.G. Self-trapped excitons in silicon-dioxide: mechanism and properties. Phys. Rev. Lett. 2005, 95, 154601. [Google Scholar]
- Shluger, A.; Stefanovich, E. Models of the self-trapped exciton and nearest-neighbor defect pair in SiO2. Phys. Rev. B 1990, 42, 9664–9673. [Google Scholar] [CrossRef]
- Tsai, T.E.; Griscom, D.L. Experimental evidence for excitonic mechanism of defect generation in high-purity silica. Phys. Rev. Lett. 1991, 67, 2517–2520. [Google Scholar] [CrossRef] [PubMed]
- Matsunami, N.; Hosono, H. Bi-self trapped-exciton model for Frenkel defect formation in amorphous SiO2 by proton irradiation. Phys. Rev. B 1999, 60, 10616–10619. [Google Scholar] [CrossRef]
- Hosono, H.; Kawazoe, H.; Matsunami, N. Experimental evidence for Frenkel defect formation in amorphous SiO2 by electronic excitation. Phys. Rev. Lett. 1998, 80, 317–320. [Google Scholar] [CrossRef]
- Stevens-Kalceff, M.A. Electron-irradiation-induced radiolytic oxygen generation and microsegregation in silicon dioxide polymorphs. Phys. Rev. Lett. 2000, 84, 3137–3140. [Google Scholar] [CrossRef] [PubMed]
- Shluger, A.L.; Gavartin, J.L.; Szymanski, M.A.; Stoneham, A.M. Atomistic modelling of radiation effects: Towards dynamics of exciton relaxation. Nucl. Inst. and Meth. Phys. Res. B 2000, 166-167, 1–12. [Google Scholar] [CrossRef]
- Shkrob, I.A.; Trifunac, A.D. Spin-polarized H/D atoms and radiation chemistry in amorphous silica. J. Chem. Phys. 1997, 107, 2374–2385. [Google Scholar] [CrossRef]
- Silin, A.R.; Skuja, L.N. Spectroscopic properties and mutual conversion reactions of quasi-molecular hydroxyl and non-bridging oxygen defects in vitreous silica. J. Molec. Struct. 1980, 61, 145–148. [Google Scholar] [CrossRef]
- Griscom, D.L. Defect structure of glasses. J. Non-Cryst. Solids 1985, 73, 51–77. [Google Scholar] [CrossRef]
- Griscom, D.L. Thermal bleaching of X-ray-induced defect centers in high purity fused silica by diffusion of radiolytic molecular hydrogen. J. Non-Cryst. Solids 1984, 68, 301–325. [Google Scholar] [CrossRef]
- Chemirisov, S.C.; Werst, D.W.; Trifunac, A.D. Formation, trapping and kinetics of H atoms in wet zeolites and mesoporous silica. Radiat. Phys. Chem. 2001, 60, 405–410. [Google Scholar] [CrossRef]
- Tarasov, V.F.; Chemerisov, S.D.; Trifunac, A.D. H-atom electron-spin polarization in irradiated water and ice confined in the nanopores of Vycor glass. J. Phys. Chem. B 2003, 107, 1293–1301. [Google Scholar] [CrossRef]
- Brodie-Linder, N.; Le Caër, S.; Alam, M.S.; Renault, J.P.; Alba-Simionesco, C. H2 formation by electron irradiation of SBA-15 materials and the effect of CuII grafting. Phys. Chem. Chem. Phys. 2010, 12, 14188–14195. [Google Scholar] [CrossRef] [PubMed]
- Brunet, F.; Charpentier, T.; Le Caër, S.; Renault, J.P. Solid state NMR characterization of a controlled-pore glass and of the effects of electron irradiation. Solid State Nucl. Magn. Reson. 2008, 33, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Barter, C.W.; Wagner, C.D. Generation of catalytic activity in silica gel by ionizing radiation. J. Phys. Chem. 1964, 68, 2381–2383. [Google Scholar] [CrossRef]
- Thomas, J.K. Physical aspects of radiation-induced processes on SiO2, gamma-Al2O3, zeolites and clays. Chem. Rev. 2005, 105, 1683–1734. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Zhang, G.; Thomas, J.K. Spectroscopic Studies of Electron and Hole Trapping in Zeolites : Formation of Hydrated Electrons and Hydroxyl Radicals. J. Phys. Chem. B 1997, 101, 2182–2194. [Google Scholar] [CrossRef]
- Schatz, T.; Cook, A.R.; Meisel, D. Charge carrier transfer across the silica nanoparticle/water interface. J. Phys. Chem. B 1998, 102, 7225–7230. [Google Scholar] [CrossRef]
- Dimitrijevic, N.M.; Henglein, A.; Meisel, D. Charge separation across the silica nanoparticle/water interface. J. Phys. Chem. B 1999, 103, 7073–7076. [Google Scholar] [CrossRef]
- Ouerdane, H.; Gervais, B.; Zhou, H.; Beuve, M.; Renault, J.P. Radiolysis of water confined in porous silica: a simulation study of the physicochemical yields. J. Phys. Chem. C 2010, 114, 12667–12674. [Google Scholar] [CrossRef]
- LaVerne, J.A. H2 formation from the radiolysis of liquid water with zirconia. J. Phys. Chem. B 2005, 109, 5395–5397. [Google Scholar] [CrossRef] [PubMed]
- Le Caër, S.; Rotureau, P.; Brunet, F.; Charpentier, T.; Blain, G.; Renault, J.P.; Mialocq, J.-C. Radiolysis of confined water: Hydrogen production at a high dose rate. Chemphyschem. 2005, 6, 2585–2596. [Google Scholar] [CrossRef] [PubMed]
- Glinka, Y.D.; Lin, S.-H.; Chen, Y.-T. Two-photon-excited luminescence and defect formation in SiO2 nanoparticles induced by 6.4-eV ArF laser light. Phys. Rev. B 2000, 62, 4733–4743. [Google Scholar]
- Ozawa, L. Cathodoluminescence, Theory and Applications; Verlag Chemie Publishers: Weinheim, Germany, 1990. [Google Scholar]
- LaVerne, J.A.; Tandon, L. H2 production in the radiolysis of water on UO2 and other oxides. J. Phys. Chem. B 2003, 107, 13623–13628. [Google Scholar] [CrossRef]
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Le Caër, S. Water Radiolysis: Influence of Oxide Surfaces on H2 Production under Ionizing Radiation. Water 2011, 3, 235-253. https://doi.org/10.3390/w3010235
Le Caër S. Water Radiolysis: Influence of Oxide Surfaces on H2 Production under Ionizing Radiation. Water. 2011; 3(1):235-253. https://doi.org/10.3390/w3010235
Chicago/Turabian StyleLe Caër, Sophie. 2011. "Water Radiolysis: Influence of Oxide Surfaces on H2 Production under Ionizing Radiation" Water 3, no. 1: 235-253. https://doi.org/10.3390/w3010235
APA StyleLe Caër, S. (2011). Water Radiolysis: Influence of Oxide Surfaces on H2 Production under Ionizing Radiation. Water, 3(1), 235-253. https://doi.org/10.3390/w3010235




