Regionalization of SWAT Model Parameters for Use in Ungauged Watersheds
Abstract
:1. Introduction
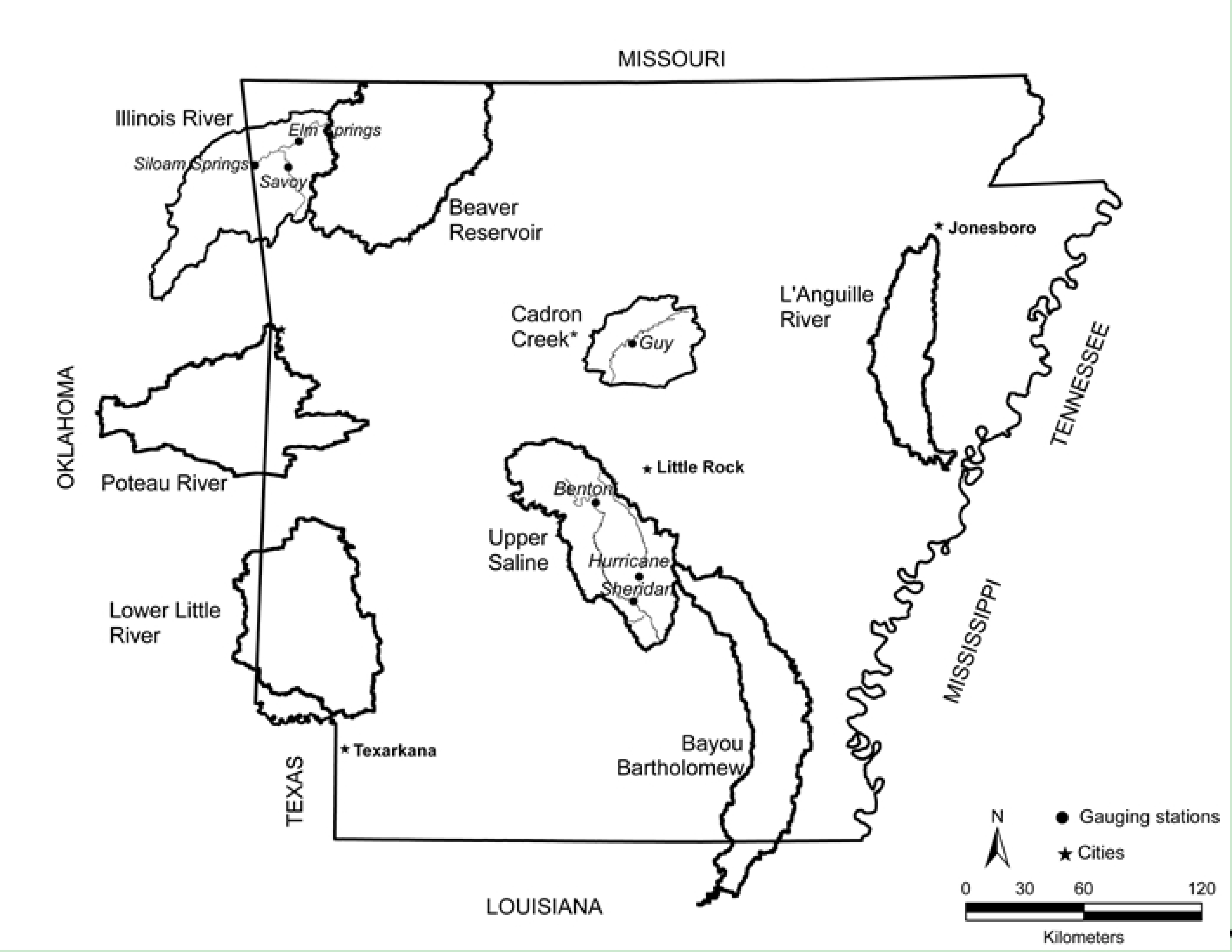
1.1. Site Description
1.2. Soil and Water Assessment Tool (SWAT) Model Description
2. Materials and Methods
| Parameter value / (Percent change from default value) | ||||||||||
| Parameter description | Symbol | Bayou Bartholomew | Beaver Reservoir | Cadron Creek | Illinois River | L'Anguille River | Lower Little River | Poteau River | Upper Saline | |
| Base flow recession factor, days | ALPHA_BF | 0.368 | 0.600 | 0.028 | 0.737 | 0.048† | 1.000 | 0.900 | 0.483 | |
| Ground water delay, days | GW_DELAY | 41 | 31† | 31 | 88 | 31 | 0.001 | 31 | 68 | |
| Ground water revaporationh coefficient | GW_REVAP | 0.04 | 0.02† | 0.30 | 0.05 | 0.08 | 0.07 | 0.02 | 0.10 | |
| Threshold depth for ground water flow to occur, mm | GWQMN | 0† | 0 | 3 | 0 | 0 | 0 | 0 | 100 | |
| Deep aquifer recharge fraction | rchrg_dp | 0.10 | 0.05† | 0.05 | 0.30 | 0.50 | 0.22 | 0.05 | 0.64 | |
| Threshold depth for revaporation to occur, mm | REVAPMN | 1† | 1 | 0 | 1 | 1 | 1 | 1 | 101 | |
| Snow fall temperature, ºC | sftmp | 0.8 | 1.0† | 1.0 | 1.0 | 0.5 | 3.4 | 1.0 | 0 | |
| Surface runoff lag coefficient, days | surlag | 0.8 | 12 | 3 | 0.6 | 0.9 | 0.2 | 10 | 1 | |
| Plant uptake compensation factor | EPCO | 0.7 | 1.0† | 0.5 | 0.9 | 1.0 | 1.0 | 1.0 | 0.2 | |
| Soil evaporation compensation factor | ESCO | 0.74 | 0.76 | 0.35 | 0.68 | 0.86 | 1.00 | 0.10 | 0.95† | |
| Average slope length, m‡ | SLSUBBSN | Varies†1 | (−1.2%) | Varies | Varies | (6.2%) | Varies | (−25.4%) | Varies | |
| Curve Number (AMChhII) ‡ | CN2 | (6.8%) | (−8.8%) | (−10.0%) | (−5.5%) | (1.8%) | (41.7%) | (10.0%) | (−26.0%) | |
| Effective channel hydraulic conductivity, mm/hr | CH_K2 | 148.9 | 0.5† | 0.03 | 15.0 | 0.5 | 0.5 | 141.0 | 1.7 | |
| Manning’s n | ch_n | 0.014† | 0.052 | 0.014 | 0.014 | 0.014 | 0.014 | 0.300 | 0.100 | |
| Soil albedo | sol_alb | 0.07 | 0.10† | 0.10 | 0.32 | 0.10 | 0.68 | 1.00 | 0.32 | |
| Available water capacity, m/m‡ | SOL_AWC | (45.7%) | Varies†2 | Varies | (43.6%) | (17.9%) | (50.0%) | (−50.0%) | (26.0%) | |
2.1. Global Average-based Parameter Regionalization
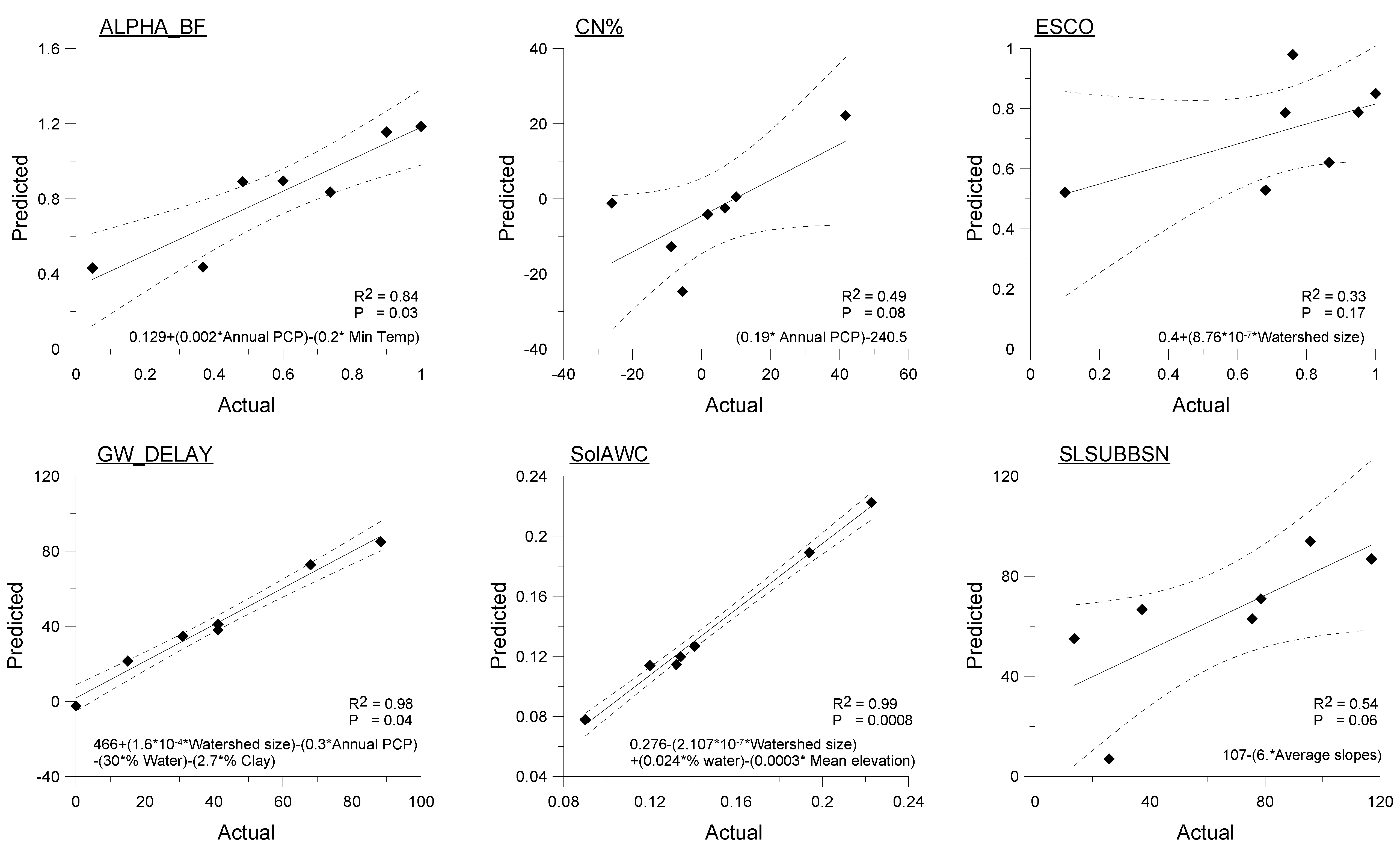
2.2. Regression-based Parameter Regionalization
| Watershed | |||||||
| Characteristics | Bayou Bartholomew | Beaver Reservoir. | Illinois River | L’Anguille River | Lower Little River | Poteau River | Upper Saline |
| Size, km2 | 4,411 | 6,616 | 1,469 | 2,517 | 5,141 | 1,383 | 4,434 |
| Annual precipitation, mm | 1,253 | 1,199 | 1,136 | 1,244 | 1,383 | 1,269 | 1,260 |
| Mean temperature, °C | 17.2 | 14.1 | 14.0 | 16.4 | 15.0 | 14.2 | 15.2 |
| Forest, % | 56 | 66 | 37 | 17 | 67 | 66 | 77 |
| Pastures/hay, % | 3 | 29 | 55 | 2 | 28 | 30 | 20 |
| Urban, % | 2 | 1 | 8 | 2 | 1 | 3 | 2 |
| Water, % | 1.16 | 3.98 | 0.27 | 1.15 | 2.68 | 0.79 | 0.97 |
| Clay, % | 27 | 17 | 17 | 18 | 16 | 19 | 17 |
| Silt, % | 59 | 46 | 60 | 71 | 33 | 48 | 29 |
| Mean elevation, m | 73 | 514 | 439 | 94 | 392 | 464 | 307 |
| Average slope, % | 3.3 | 16.6 | 8.6 | 2.1 | 7.3 | 6.7 | 6.0 |
2.3. Performance Analyses
3. Results and Discussion
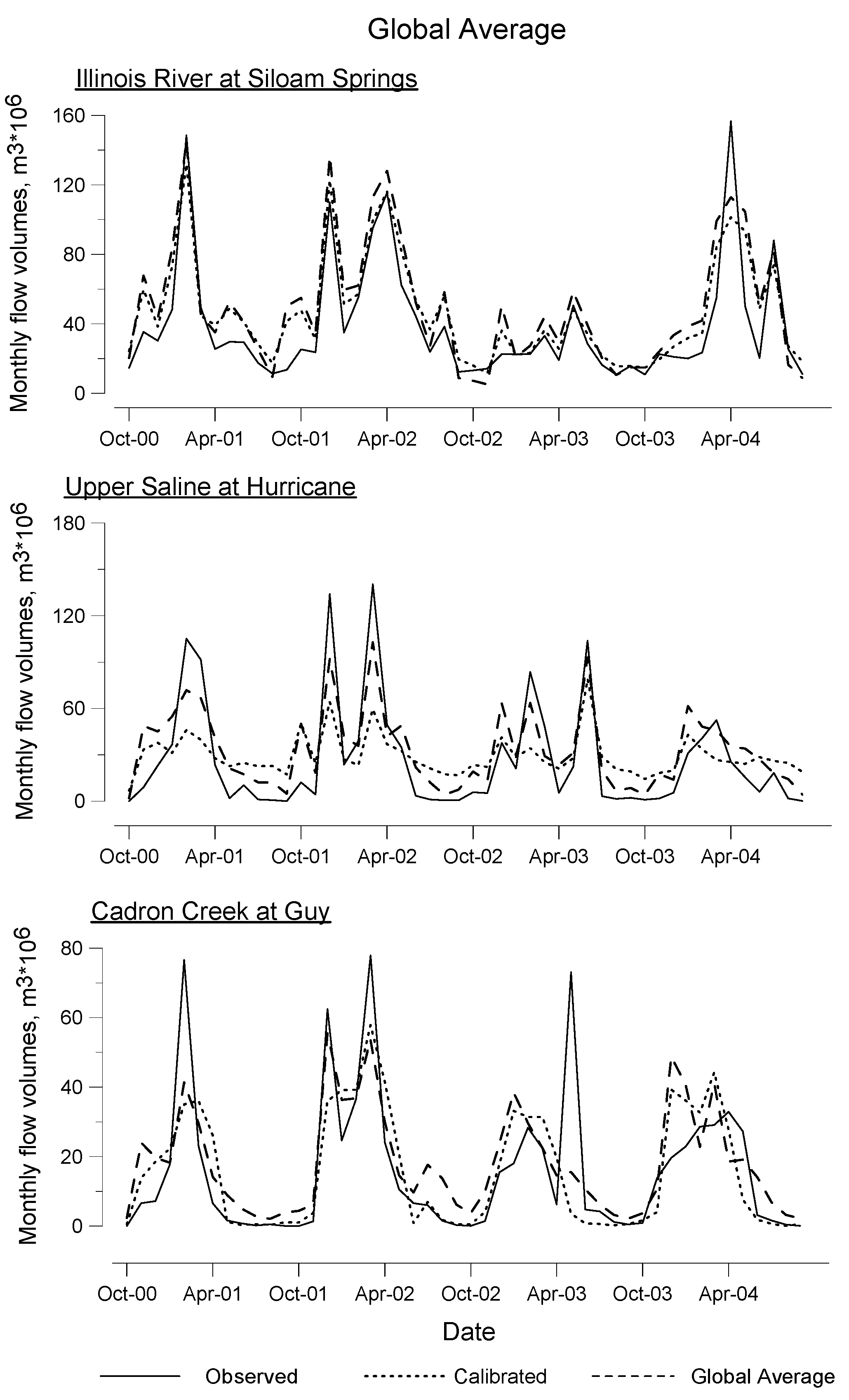
3.1. Global Averaging
| Parameter description | Parameter | Default | Global average |
| Base flow recession factor, days | ALPHA_BF | 0.048 | 0.590 |
| Ground water delay, days | GW_DELAY | 31 | 41 |
| Ground water revaporationh coefficient | GW_REVAP | 0.020 | 0.056 |
| Threshold depth for ground water flow to occur, mm | GWQMN | 0.00 | 14 |
| Deep aquifer recharge fraction | rchrg_dp | 0.050 | 0.272 |
| Threshold depth for revaporation to occur, mm | REVAPMN | 1 | 15 |
| Snow fall temperature, ºC | sftmp | 1.0 | 1.1 |
| Surface runoff lag coefficient, days | surlag | 4.00 | 3.64 |
| Plant uptake compensation factor | EPCO | 1.000 | 0.830 |
| Soil evaporation compensation factor | ESCO | 0.950 | 0.730 |
| Average slope length, m | SLSUBBSN | Varies1 | −2.9% |
| Curve Number (AMChhII) | CN2 | Varies2 | 2.8% |
| Effective channel hydraulic conductivity, mm/hr | CH_K2 | 0.5 | 44.0 |
| Manning's n | ch_n | 0.014 | 0.3‡ |
| Soil albedo | sol_alb | 0.100 | 0.370 |
| Available water capacity, m/m | SOL_AWC | Varies3 | 19.0% |
| Nash-Sutcliffe Coefficientŧ | ||||||
| C1 | C2 | C3 | C4 | |||
| Time period | Watershed | Station | Default | Calibration | Global average | Regression |
| Oct. 1998–Sept. 2000 | Upper Saline | Benton | -- | -- | -- | -- |
| Sheridan | -- | -- | -- | -- | ||
| Hurricane | −1.96 | −0.44 | −0.79 | −0.95 | ||
| Illinois River | Siloam Springs | 0.58 | 0.78 | 0.81 | 0.61 | |
| Savoy | 0.61 | 0.64 | 0.69 | 0.55 | ||
| Elm Springs | −0.20 | 0.90 | 0.81 | 0.82 | ||
| Cadron Creek | Guy | −0.39 | 0.75 | 0.49 | 0.63 | |
| Oct. 2000–Sept. 2004 | Upper Saline | Benton | 0.18 | 0.53 | 0.56 | 0.54 |
| Sheridan | 0.41 | 0.45 | 0.69 | 0.61 | ||
| Hurricane | 0.53 | 0.50 | 0.73 | 0.66 | ||
| Illinois River | Siloam Springs | 0.31 | 0.77 | 0.66 | 0.75 | |
| Savoy | 0.51 | 0.64 | 0.61 | 0.60 | ||
| Elm Springs | 0.37 | 0.77 | 0.49 | 0.83 | ||
| Cadron Creek | Guy | 0.28 | 0.45 | 0.55 | 0.53 | |
| Oct. 1998–Sept. 2004 | Upper Saline | Benton | -- | -- | -- | -- |
| (whole period) | Sheridan | -- | -- | -- | -- | |
| Hurricane | 0.42 | 0.45 | 0.67 | 0.60 | ||
| Illinois River | Siloam Springs | 0.46 | 0.79 | 0.74 | 0.71 | |
| Savoy | 0.55 | 0.64 | 0.65 | 0.58 | ||
| Elm Springs | 0.13 | 0.85 | 0.68 | 0.83 | ||
| Cadron Creek | Guy | 0.22 | 0.49 | 0.55 | 0.55 | |
3.2. Regression-based Evaluation
| Regression-based values | |||||
| Parameter description | Parameter | Default | Illinois River | Upper Saline | Cadron Creek |
| Base flow recession factor, days | ALPHA_BF | 0.048 | 0.610 | 0.640 | 1.000‡ |
| Ground water delay, days | GW_DELAY | 31 | 84 | 71 | 72 |
| Ground water revaporationh coefficient | GW_REVAP | 0.020 | 0.056* | 0.056* | 0.056* |
| Threshold depth for ground water flow to occur, mm | GWQMN | 0 | 14* | 14* | 14* |
| Deep aquifer recharge fraction | rchrg_dp | 0.050 | 0.272* | 0.272* | 0.272* |
| Threshold depth for revaporation to occur, mm | REVAPMN | 1 | 15* | 15* | 15* |
| Snow fall temperature, ºC | sftmp | 1.0 | 1.1* | 1.1* | 1.1* |
| Surface runoff lag coefficient, days | surlag | 4.00 | 3.64* | 3.64* | 3.64* |
| Plant uptake compensation factor | EPCO | 1.000 | 0.830* | 0.830* | 0.830* |
| Soil evaporation compensation factor | ESCO | 0.950 | 0.530 | 0.790 | 0.570 |
| Average slope length, m | SLSUBBSN | Varies1 | −16.0% | −10.0% | 0.0% |
| Curve Number (AMChh II) | CN2 | Varies2 | −24.2% | −0.7% | −24.0% |
| Effective channel hydraulic conductivity, mm/hr | CH_K2 | 0.5 | 44.0* | 44.0* | 44.0* |
| Manning’s n | ch_n | 0.014 | 0.3*‡ | 0.3*‡ | 0.3*‡ |
| Soil albedo | sol_alb | 0.100 | 0.370* | 0.370* | 0.370* |
| Available water capacity, m/m | SOL_AWC | Varies3 | −33.0% | −20.0% | 50.0% |
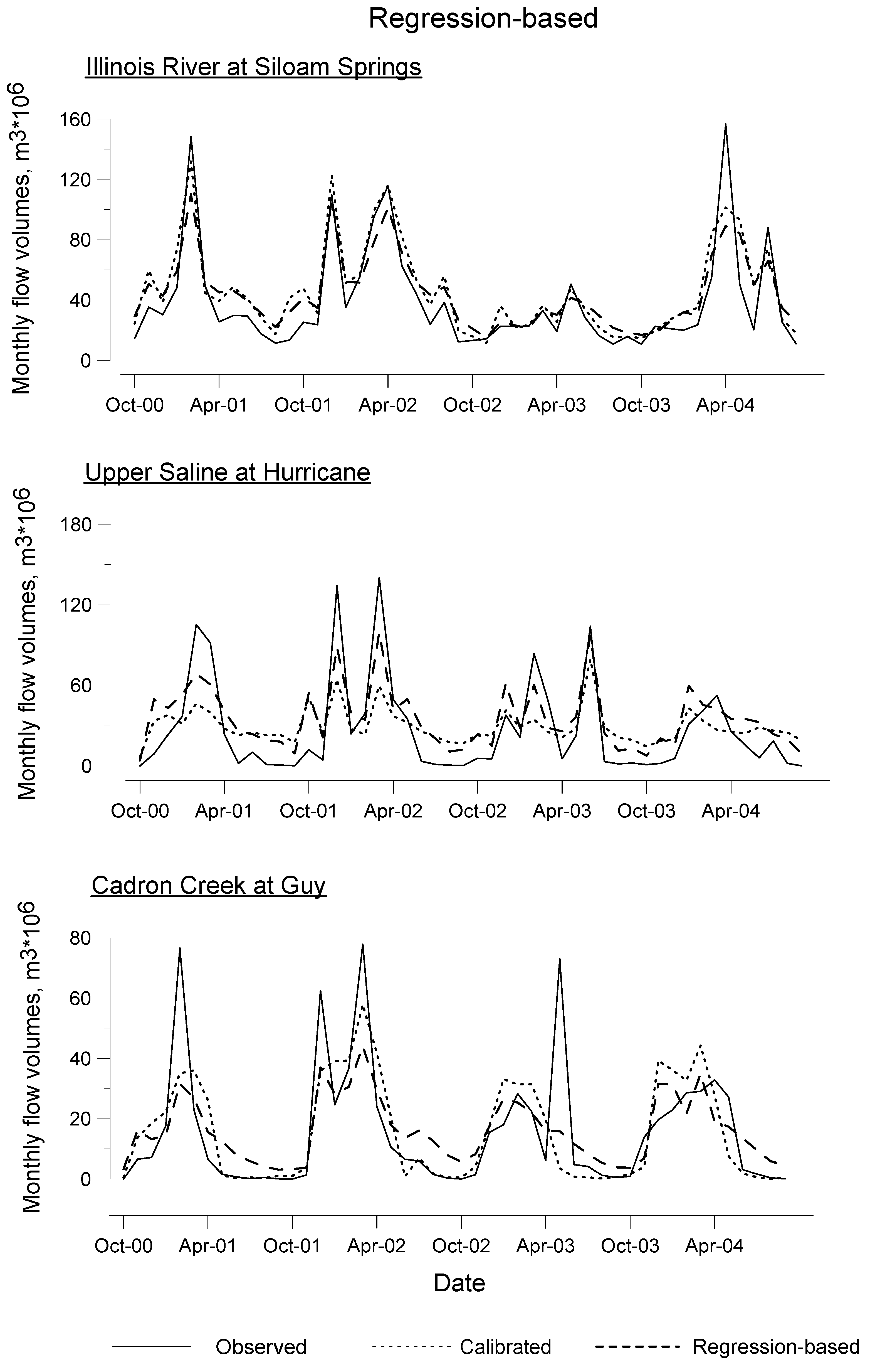
3.3. Performance Analyses of Parameter Regionalization Methods
| Nash-Sutcliffe Coefficientŧ / Dv* | ||||
| Watershed | Station | Calibration | Global Average | Regression |
| Upper Saline | Benton† | 0.16/0.31 | −0.51/0.43 | −1.07/0.51 |
| Sheridan | 0.87/0.09 | 0.61/0.28 | 0.44/0.34 | |
| Hurricane | 0.50/0.30 | 0.38/0.41 | 0.40/0.50 | |
| Illinois River | Siloam Springs | 0.78/0.16 | 0.55/0.24 | 0.92/0.09 |
| Savoy | 0.68/0.1 | 0.48/0.18 | 0.82/0.04 | |
| Elm Springs | 0.79/0.16 | 0.55/0.25 | 0.94/0.10 | |
| Cadron Creek | Guy | 0.92/−0.02 | 0.69/0.21 | 0.89/0.06 |
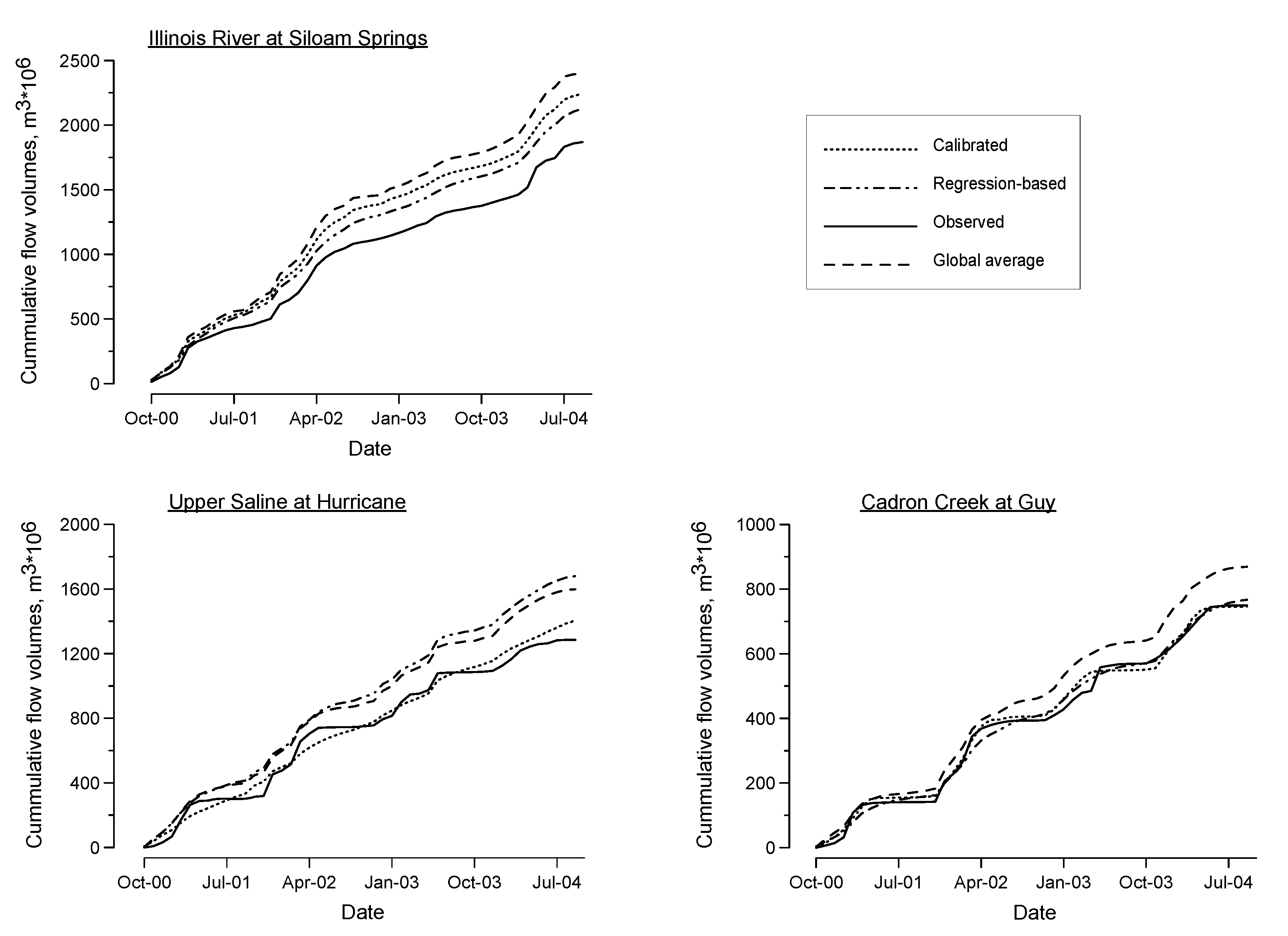
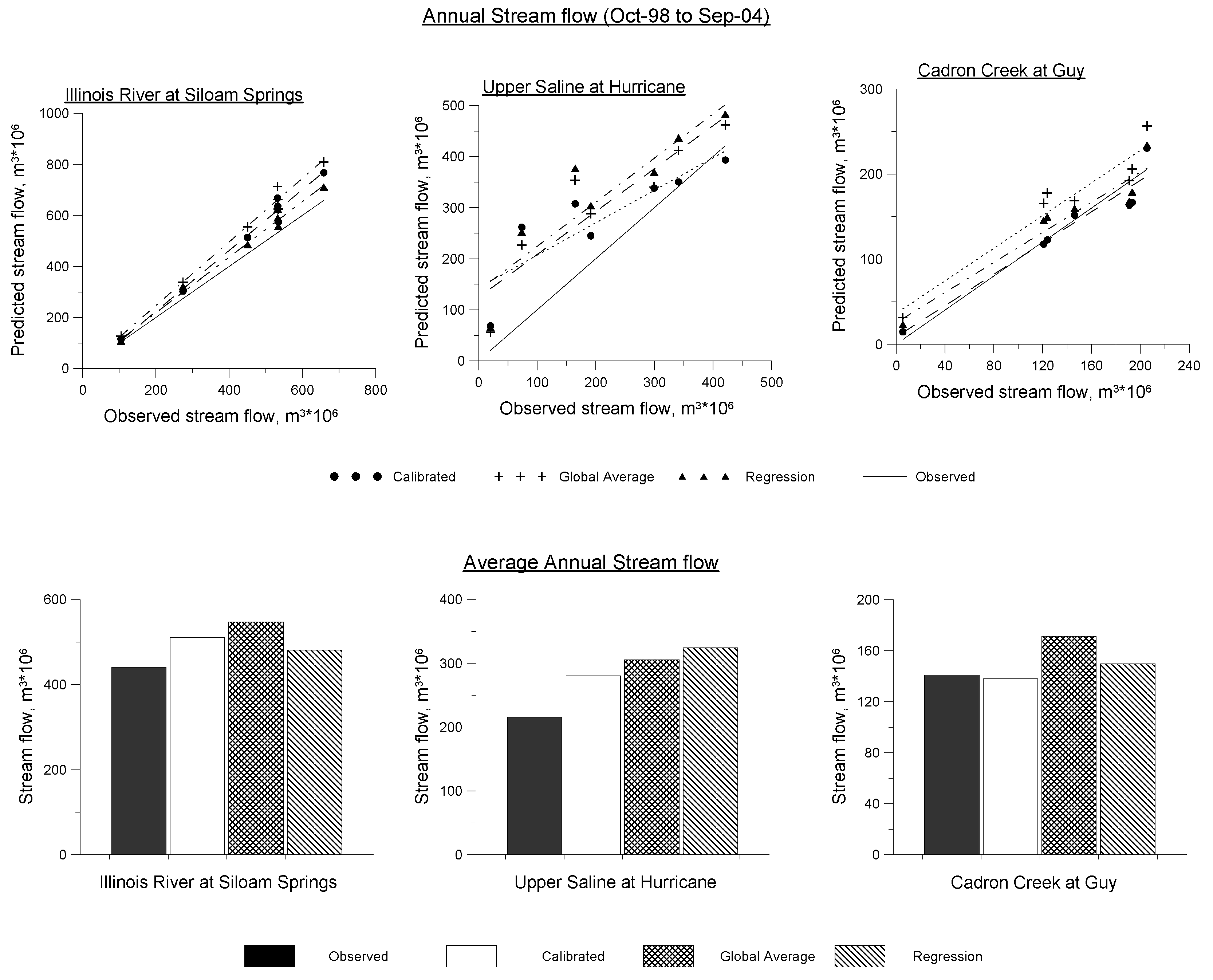
4. Conclusions
References
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large area hydrologic modeling and assessment—Part 1: Model development. J. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Bosch, D.D.; Bingner, R.L.; Theurer, F.D.; Felton, G. Evaluation of the AnnAGNPS water quality model. ASAE Paper 98-2195. American Society of Agricultural Engineers (ASAE): St. Joseph, MI, USA, 1998. [Google Scholar]
- Bouraoui, F.; Dillaha, T.A. ANSWERS-2000: Runoff and sediment transport model. J. Environ. Eng. 1996, 122, 493–502. [Google Scholar] [CrossRef]
- Johanson, R.C.; Imhoff, J.D.; Davis, H.H., Jr. Users’ Manual for Hydrological Simulation Program—Fortran (HSPF); EPA-600/9-80-015; Environmental Research Laboratory: Athens, GA, USA, 1980. [Google Scholar]
- Bicknell, B.R.; Imhoff, J.C.; Kittle, J.J.L.; Jobs, T.H.; Donigian, A.S. Hydrological Simulation Program—FORTRAN: HSPF Version 12 User’s Manual; Aqua Terra Consultants: Mountain View, CA, USA, 2001. [Google Scholar]
- Jarboe, J.E.; Hann, C.T. Calibrating a water yield model for small ungauged watersheds. Water Resour. Res. 1974, 10, 256–262. [Google Scholar] [CrossRef]
- Karlinger, M.R.; Guertin, D.P.; Troutman, B.M. Regression estimates for topological—hydrograph input. J. Water Resour. Plan. Man. 1988, 114, 446–456. [Google Scholar] [CrossRef]
- Vogel, R.M. Regional Calibration of Watershed Models. In Watershed Models; Singh, V.P., Frevert, D.K., Eds.; CRC Press: Boca Raton, FL, USA, 2006; Chapter 3; pp. 47–71. [Google Scholar]
- Bloschl, G.; Sivapalan, M. Scale Issues in Hydrological Modeling—a Review. Hydrol. Process. 1995, 9, 251–290. [Google Scholar] [CrossRef]
- Merz, R.; Bloschl, G. Regionalisation of catchment model parameters. J. Hydrol. 2004, 287, 95–123. [Google Scholar] [CrossRef]
- Magette, W.L.; Shanholtz, V.O.; Carr, J.C. Estimating selected parameters for the Kentucky Watershed Model from watershed characteristics. Water Resour. Res. 1976, 12, 472–476. [Google Scholar] [CrossRef]
- Servat, E.; Dezetter, A. Rainfall-Runoff Modeling and Water Resources Assessment in Northwestern Ivory-Coast—Tentative Extension to Ungauged Catchments. J. Hydrol. 1993, 148, 231–248. [Google Scholar] [CrossRef]
- Post, D.A.; Jakeman, A.J. Relationships between catchment attributes and hydrological response characteristics in small Australian mountain ash catchments. Hydrol. Process. 1996, 10, 877–892. [Google Scholar] [CrossRef]
- Post, D.A.; Jakeman, A.J. Predicting the daily streamflow of ungauged catchments in SE Australia by regionalising the parameters of a lumped conceptual rainfall-runoff model. Ecol. Model. 1999, 123, 91–104. [Google Scholar] [CrossRef]
- Vandewiele, G.L.; Elias, A. Monthly Water-Balance of Ungauged Catchments Obtained by Geographical Regionalization. J. Hydrol. 1995, 170, 277–291. [Google Scholar] [CrossRef]
- Kokkonen, T.S.; Jakeman, A.J.; Young, P.C.; Koivusalo, H.J. Predicting daily flows in ungauged catchments: Model regionalization from catchment descriptors at the Coweeta Hydrologic Laboratory, North Carolina. Hydrol. Process. 2003, 17, 2219–2238. [Google Scholar] [CrossRef]
- Schmidt, J.; Hennrich, K.; Dikau, R. Scales and similarities in runoff processes with respect to geomorphometry. Hydrol. Process. 2000, 14, 1963–1979. [Google Scholar] [CrossRef]
- Seibert, J. Regionalization of parameters for a conceptual rainfall-runoff model. Agr. Forest Meteorol. 1999, 98-99, 279-293. [Google Scholar]
- Watershed Boundary Dataset. Coordinated Effort between the United States Department of Agriculture-Natural Resources Conservation Service (USDA-NRCS),the United States Geological Survey (USGS),and the Environmental Protection Agency (EPA). (Created from a Variety of Sources from Each State and Aggregated into a Standard National Layer for Use in Strategic Planning and Accountability). Available online: http://datagateway.nrcs.usda.gov (accessed on 18 October 2007).
- Chaubey, I.; Matlock, M.; Costello, T.; Cooper, C.; White, K. GIS Database Development and Watershed Modeling in Arkansas Priority Watersheds; Final report submitted to Arkansas Soil and Water Conservation Commission. Project No. 04-120. In 2004.
- White, K.L.; Chaubey, I. Sensitivity analysis, calibration, and validations for a multisite and multivariable SWAT model. J. Am. Water Resour. Assoc. 2005, 41, 1077–1089. [Google Scholar] [CrossRef]
- Chaubey, I.; Matlock, M.; Garg, V. GIS Database Development and Watershed Modeling in Arkansas Priority Watersheds; Final Report submitted to the Arkansas Soil and Water Conservation Commission. Project No. 02-1400. In 2006.
- Arnold, J.G.; Fohrer, N. SWAT2000: Current capabilities and research opportunities in applied watershed modelling. Hydrol. Process. 2005, 19, 563–572. [Google Scholar] [CrossRef]
- Jayakrishnan, R.; Srinivasan, R.; Santhi, C.; Arnold, J.G. Advances in the application of the SWAT model for water resources management. Hydrol. Process. 2005, 19, 749–762. [Google Scholar] [CrossRef]
- Gitau, M.W.; Veith, T.L.; Gburek, W.J.; Jarrett, A.R. Watershed level best management practice selection and placement in the town brook watershed, New York. J. Am. Water Resour. Assoc. 2006, 42, 1565–1581. [Google Scholar] [CrossRef]
- Migliaccio, K.W.; Chaubey, I.; Haggard, B.E. Evaluation of landscape and instream modeling to predict watershed nutrient yields. Environ. Model. Softw. 2007, 22, 987–999. [Google Scholar] [CrossRef]
- Miller, S.N.; Semmens, D.J.; Goodrich, D.C.; Hernandez, M.; Miller, R.C.; Kepner, W.G.; Guertin, D.P. The Automated Geospatial Watershed Assessment tool. Environ. Model. Softw. 2007, 22, 365–377. [Google Scholar] [CrossRef]
- Gitau, M.W.; Veith, T.L.; Gburek, W.J. Farm-level optimization of BMP placement for cost-effective pollution reduction. Trans. ASAE 2004, 47, 1923–1931. [Google Scholar] [CrossRef]
- Cerucci, M.; Conrad, J.M. The use of binary optimization and hydrologic models to form Riparian buffers. J. Am. Water Resour. Assoc. 2003, 39, 1167–1180. [Google Scholar] [CrossRef]
- Neitsch, S.L.; Arnold, J.G.; Kiniry, T.R.; Williams, J.R. Soil and Water Assessment Tool. Theoretical Documentation; Texas Water Resources Institute: College Station, TX, USA, 2005. [Google Scholar]
- Water Pollution Control Federation. Design and Construction of Sanitary and Storm Sewers. Manual of Practice 9. In ASCE Manual of Engineering practice; Water Pollution Control Federation: Washington, DC, USA, 1969. [Google Scholar]
- Lane, L.J. Transmission Losses. In Soil Conservation Service. National Engineering Handbook; U.S. Government Printing Office: Washington, DC, USA, 1983; pp. 19-11–19-21. [Google Scholar]
- Kresse, T.M.; Fazio, J.A. Pesticides, Water Quality and Geochemical Evolution of Ground Water in the Alluvial Aquifer, Bayou Bartholomew Watershed, Arkansas; Arkansas Ambient Ground-Water Monitoring Program; Arkansas Department of Environmental Quality: Little Rock, AR, USA, 2002. [Google Scholar]
- Neitsch, S.L.; Arnold, J.G.; Kiniry, T.R.; Williams, J.R. Soil and Water Assessment Tool. User’s Manual; Texas Agricultural Experiment Station: Temple, TX, USA, 2001. [Google Scholar]
- Mason, C.H.; Perreault, W.D. Collinearity, power, and interpretation of multiple-regression analysis. J. Market. Res. 1991, 28, 268–280. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models: Part 1. A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar]
- Martinez, J.; Rango, A. Merits of statistical criteria for the performance of hydrological models. Water Resour. Bull. 1989, 25, 421–432. [Google Scholar] [CrossRef]
- Gassman, P.W.; Reyes, M.R.; Green, C.H.; Arnold, J.G. The soil and water assessment tool: Historical development, applications, and future research directions. Trans. ASABE 2007, 50, 1211–1250. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Engel, B.; Storm, D.; White, M.; Arnold, J.; Arabi, M. A hydrologic/water quality model application protocol. J. Am. Water Resour. Assoc. 2007, 43, 1223–1236. [Google Scholar] [CrossRef]
- Popov, E.G. Gidrologicheskie Prognozy (Hydrological Forecasts); Gidrometeoizdat: Leningrad, Russia, 1979. [Google Scholar]
- Van Liew, M.W.; Garbrecht, J. Hydrologic simulation of the Little Washita river experimental watershed using SWAT. J Am.Water Resour. Assoc. 2003, 39, 413–426. [Google Scholar] [CrossRef]
- Ramanarayanan, T.S.; Williams, J.R.; Dugas, W.A.; Hauck, L.M.; McFarland, A.M.S. Using APEX to Identify Alternative Practices for Animal Waste Management; ASAE Paper 97-2209; American Society of Agricultural Engineers (ASAE): St. Joseph, MI, USA, 1997. [Google Scholar]
- Donigan, A.S.; Love, J.T. Sediment Calibration Procedures and Guidelines for Watershed Modeling. In WEF TMDL 2003 Specialty Conference; WEF-CDROM: Chicago, IL, USA, 2003. [Google Scholar]
- Sorooshian, S.; Gupta, V.K. Model Calibration. In Computer Models of Watershed Hydrology; Singh, V.P., Ed.; Water Resources Publications: Highlands Ranch, CO, USA, 1995. [Google Scholar]
- Jacomino, V.M.F.; Fields, D.E. A critical approach to the calibration of a watershed model. J. Am. Water Resour. Assoc. 1997, 33, 143–154. [Google Scholar] [CrossRef]
© 2010 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Gitau, M.W.; Chaubey, I. Regionalization of SWAT Model Parameters for Use in Ungauged Watersheds. Water 2010, 2, 849-871. https://doi.org/10.3390/w2040849
Gitau MW, Chaubey I. Regionalization of SWAT Model Parameters for Use in Ungauged Watersheds. Water. 2010; 2(4):849-871. https://doi.org/10.3390/w2040849
Chicago/Turabian StyleGitau, Margaret W., and Indrajeet Chaubey. 2010. "Regionalization of SWAT Model Parameters for Use in Ungauged Watersheds" Water 2, no. 4: 849-871. https://doi.org/10.3390/w2040849
APA StyleGitau, M. W., & Chaubey, I. (2010). Regionalization of SWAT Model Parameters for Use in Ungauged Watersheds. Water, 2(4), 849-871. https://doi.org/10.3390/w2040849




